Арксинус что такое
Арксинус что такое
Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
sin ( a r c sin a ) = a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
Пример 1. Свойства обратных тригонометрических функций
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccos
Соответственно, для арктангенса и арккотангенса
Сумма arctg и arcctg
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинуса
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.
Арксинус что такое
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Что означает выражение
И всё.
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
Например: что такое arcsin 0,5?
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус. Что такое арктангенс, арккотангенс. То легко разберётесь, например, с таким монстром.)
Достаточно сообразить, что:
и всё. Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8). Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
 |
 |
 |
 |
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:
С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:
Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:
Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.
Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):
Надеюсь, зрительная память вас спасёт, если что. )
Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:
У какого угла синус равен 0,4?
Для ответа в градусах или радианах вам придётся открывать таблицы Брадиса, или включать солидный калькулятор. Искать там значение синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу. )
Если вы осознали этот забавный факт, то легко ответите на все подобные вопросы:
А можно записать (приблизительно) тот же самый угол через градусы. Это будет:
≈ 23,57817847820183110402. °
Осознали простой и важный смысл арков? Тогда порешаем самостоятельно. Примерчики от устных до хитрых.)
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №6. Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
Глоссарий по теме
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения 

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения 
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения 

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения 
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен 


Объяснение нового материала
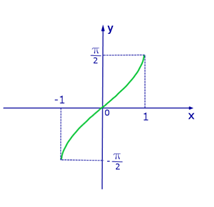
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Повторим определение еще раз:
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Значит, областью определения функции y = arcsin x является отрезок
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
Строим график функции
1. Область определения
2. Область значений
Напомним, что графики взаимно обратных функций симметричны относительно прямой
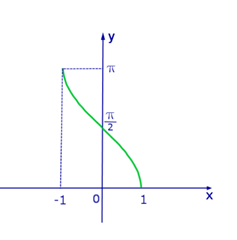
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Заполним таблицу, пользуясь определением арккосинуса.
Вот график арккосинуса:
1. Область определения
2. Область значений
Эта функция общего вида — она не является ни четной, ни нечетной.
5. Функции и являются взаимно обратными.
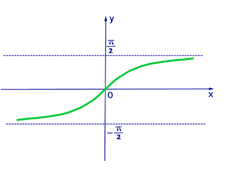
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
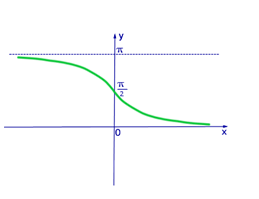
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
1. Область определения
2. Область значений
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Для четкого понимания рассмотрим пример.
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
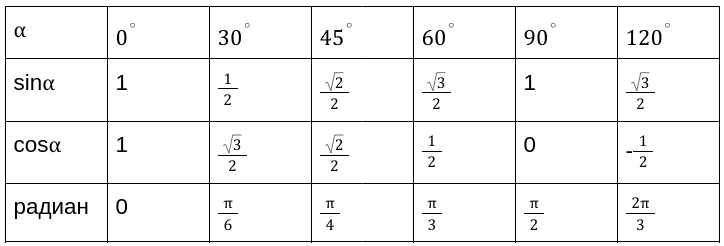
Таблица синусов основных углов предлагает такие результаты значений углов:
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | |
| a r c sin α к а к у г о л | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
| в г р а д у с а х | — 90 ° | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c sin α к а к ч и с л о | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Следуя из таблицы, находим значения арккосинуса:
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | 1 | |
| a r c cos α к а к у г о л | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 | |
| в г р а д у с а х | 180 ° | 150 ° | 135 ° | 120 ° | 90 ° | 60 ° | 45 ° | 30 ° | 0 ° | |
| a r c cos α к а к ч и с л о | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 | |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Нахождение значения arcsin, arccos, arctg и arcctg
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
Теперь разберем примеры, как они применяются в задачах.
Решение
У нас для этого есть подходящая формула следующего вида: cos ( a r c t g α ) = 1 1 + α 2
Подставляем нужное значение: cos ( a r c t g 5 ) = 1 1 + ( 5 ) 2 = 2 6
Решение
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin ( a r c cos 1 2 ) = sin π 3 = 3 2
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
sin 2 α + cos 2 α = 1 1 + c t g 2 α = 1 sin 2 α
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
Следовательно, sin ( a r c t g α ) = t g ( a r c t g α ) 1 + t g 2 ( a r c t g α ) = α 1 + α 2
Следовательно, sin ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
следует, что cos ( a r c t g α ) = c t g ( a r c c t g α ) 1 + c t g 2 ( a r c c t g α ) = α 1 + α 2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
c t g α = 1 t g α
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
А так мы выразим арккосинус через остальные обратные функции:
Формула выражения арктангенса:
Последняя часть – выражение арккотангенса через другие обратные функции:
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Решение
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Как найти арксинус: формула, свойства, функция
Понятие арксинуса
Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).
Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу. В результате с помощью синуса можно, учитывая дугу окружности, определить хорду, которая ее стягивает.
Обратная функция под названием арксинус призвана решить противоположную задачу. Арксинус обозначают \(\arcsin x\) и определяют, как угол с синусом, равным х.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для тригонометрических функций характерна периодичность. В связи с этим, обратные тригонометрические функции являются многозначными. Аркфункция обладает значением в виде множества из углов, для которых прямая тригонометрическая функция соответствует заданному числу.
(30^\circ, 150^\circ, 390^\circ, 510^\circ \dots) \right )\)
Значение синуса при этом: ½
Как правило, под обратными тригонометрическими функциями понимают ключевые значения каждой аркфункции, выделенные из ее множества значений.
Зачем нужен арксинус
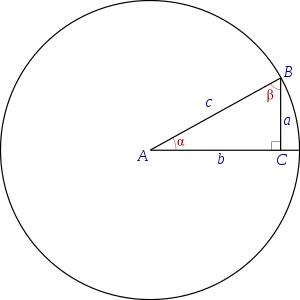
С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.
\(\alpha =\arcsin(a/c)=\arccos(b/c)=\operatorname
Получение функции arcsin с пояснением на примерах
Предположим, что существует некая функция:
Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=\arcsin x нельзя причислить к функциям.
В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:
Функция \(y=\sin x \) на отрезке \(\left[-<\frac <\pi ><2>>;<\frac <\pi ><2>>\right]\) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой \(y=\arcsin x.\)
График обратной функции является симметричным графику функции \(y=\sin x\) в рамках интервала \(\left[-<\frac <\pi ><2>>;<\frac <\pi ><2>>\right]\) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.
Определим значение выражение:
По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.
Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:
Общий ответ можно высчитать не в градусах, а в радианах:
Свойства функции arcsin
Область определения, в которой функцию можно вычислить:
\(D(\arcsin x)=[-1;1]\qquad\) (от минус единицы до плюс единицы)
Значения функций можно посчитать таким образом:
Функция arcsin обладает следующими свойствами:
Алгебра
План урока:
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
Арксинус, арккосинус, арктангенс и арккотангенс – начальные сведения
Задача, обратная нахождению значения синуса, косинуса, тангенса и котангенса данного угла (числа), подразумевает нахождение угла (числа) по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.
В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение упомянем про аркфункции и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.
Навигация по странице.
Определения, обозначения, примеры
Арксинус, арккосинус, арктангенс и арккотангенс можно определить как угол и как число. Это связано с тем, что мы определили синус, косинус, тангенс и котангенс как угла, так и числа (смотрите синус, косинус, тангенс и котангенс в тригонометрии). Остановимся на обоих подходах к определению арксинуса, арккосинуса, арктангенса и арккотангенса.
Арксинус, арккосинус, арктангенс и арккотангенс как угол
Аналогично определяются арккосинус, арктангенс и арккотангенс.
В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа можно записать более формально:
Теперь можно привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Арксинус, арккосинус, арктангенс и арккотангенс как число
Когда мы имеем дело с синусом, косинусом, тангенсом и котангенсом угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять как угол. Если же мы начинаем говорить про синус, косинус, тангенс и котангенс числа, а не угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять уже как число.
Арксинус
Смотреть что такое «Арксинус» в других словарях:
арксинус — арксинус … Орфографический словарь-справочник
арксинус — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
арксинус — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN antisine … Справочник технического переводчика
арксинус — арксинус, арксинусы, арксинуса, арксинусов, арксинусу, арксинусам, арксинус, арксинусы, арксинусом, арксинусами, арксинусе, арксинусах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
Арксинус — … Википедия
арксинус — аркс инус, а … Русский орфографический словарь
арксинус — аркси/нус, а … Слитно. Раздельно. Через дефис.
арксинус — а, ч. Кут, синус якого дорівнює даному числу … Український тлумачний словник
арксинус — іменник чоловічого роду … Орфографічний словник української мови
арксинус — арк/синус/ … Морфемно-орфографический словарь
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №6. Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
Глоссарий по теме
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения 

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения 
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения 

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения 
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен 


Объяснение нового материала
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Арксинус, арккосинус и арктангенс числа
Вы будете перенаправлены на Автор24
Рисунок 1. Единичная окружность. Автор24 — интернет-биржа студенческих работ
Рассмотрим теперь непосредственно определения для функций арксинус, арккосинус, арктангенс и арккотангенс по отдельности.
Арксинус числа
Готовые работы на аналогичную тему
График арксинуса выглядит следующим образом:
Рисунок 2. График арксинуса. Автор24 — интернет-биржа студенческих работ
Арккосинус числа
Свойства арккосинуса в сравнении с косинусом:
Рисунок 3. График арккосинуса. Автор24 — интернет-биржа студенческих работ
Арктангенс числа
Рисунок 4. График арктангенса. Автор24 — интернет-биржа студенческих работ
Арккотангенс
Свойства функции арккотангенса:
Рисунок 5. График арккотангенса. Автор24 — интернет-биржа студенческих работ
Решение:
$arccos(-\frac<-1><2>) = π – arccos(\frac<-1><2>) = π – \frac<π> <3>= \frac<2π><3>$
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 13.02.2022
Арксинус. Решение уравнения sin x = a
п.1. Понятие арксинуса
\(arcsin\frac12=\frac\pi6,\ \ arcsin\left(-\frac<\sqrt<3>><2>\right)=-\frac<\pi><3>\)
\(arcsin2\) – не существует, т.к. 2> 1
п.2. График и свойства функции y=arcsinx
п.3. Уравнение sinx=a
Углы в левой части числовой окружности записывают как разность π и арксинуса (угла справа). А остальные углы, которые превышают π по модулю, записывают через сумму арксинуса и величин, которые «не помещаются» в область значений арксинуса.
2) Решим уравнение \(sinx=0,8\)
 | Найдем точку 0,8 в числовой окружности на оси синусов (ось OY). Построим горизонталь – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках. По определению правая точка – это угол, равный arcsin0,8. Тогда левая точка – это разность развернутого угла и арксинуса, т.е. (π–arcsin0,8). Добавление или вычитание полных оборотов к каждому из решений даст другие корни. Получаем ответ: \(x_1=arcsin0,8+2\pi k,\) \(x_2=\pi-arcsin0,8+2\pi k\) |
п.4. Примеры
Пример 1. Найдите функцию, обратную арксинусу. Постройте графики арксинуса и найденной функции в одной системе координат.
Для \(y=arcsinx\) область определения \(-1\leq x\leq 1\), область значений \(-\frac\pi2\leq y\leq \frac\pi2\).
Обратная функция \(y=sinx\) должна иметь ограниченную область определения \(-\frac\pi2\leq x\leq \frac\pi2\) и область значений \(-1\leq y\leq 1\).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
 | Способ 1. Решение с помощью числовой окружности |
Пример 4*. Решите уравнения:
\(a)\ arcsin(x^2-3x+3)=\frac\pi2\) \begin
Арксинус, арккосинус, арктангенс и арккотангенс числа
Время чтения: 28 минут
Данный тип функций решают задачу вычисления и определения угловых значений по известному заданному значению тригонометрической функции.
Например, синус какого угла будет иметь значение \[\frac<1><2>\]
Данные тригонометрические функции являются обратными по значению. Они имеют множество характерных свойств:
Все остальные функции доказываются аналогично, согласно их определения.
Противоположные значения для обратных значений функций арксинус, арккосинус, арктангенс, арккотангенс
Взаимосвязь функций противоположных чисел можно записать в следующем виде:
Перейдем к доказательству записанных выражений.
Докажем, что — arcsin a находится в пределах \[-\frac<\pi> <2>до \frac<\pi><2>\] и обоснуем, что sin (-arcsin a)=-a.
Для функции арксинус справедливо неравенство, следующего вида:\[-\frac<\pi> <2>\leq \arcsin a \leq \frac<\pi><2>\].
Для того чтобы получить эквивалентное неравенство, нужно обе части равенства умножить на значение-1. После вычислений получим:\[-\frac<\pi> <2>\leq-\arcsin \mathrm \leq \frac<\pi><2>\].
Докажем, что sin ( − arcsin a ) = − a sin(-arcsin a)=-a.
Применим свойство противоположных углов и составим уравнение:
sin ( − a r c sin a ) = − sin ( a r c sin a )=-sin arcsin a.
Арккосинус доказывается следующим образом:
Записываем выражение: \[\arccos (-a)=\pi-\arccos a \text < при >a \in(-1,1)\]
Чтобы доказать оставшиеся две функции, применяются аналогичные свойства и правила.
Правило противоположных чисел позволяет упростить процесс решения и исключает все операции при вычислении с отрицательными числами.
Принцип сложения обратных тригонометрических функций
Для тригонометрических функций, прямых или обратных, характерны простые математические свойства, а именно: сложение данных.
Выполнив все необходимые операции по вычислению заданного равенства, получим следующие выражения:
Для завершения доказательства запишем формулу: \[\sin \left(\frac<\pi><2>-\arccos a\right)=\cos (\arccos a)=a\]
Сформулируем свойства рассматриваемых значений функций относительно синуса, косинуса, тангенса и котангенса.
Значение arcsin (sin a) имеет смысл в том случае, если a относится к пределам \[-\frac<\pi> <2>; \frac<\pi><2>\] и выполняется условие \[-\frac<\pi> <2>\leq a \leq \frac<\pi><2>\].
Аналогичные условия характерны и для других функций.
Пример: \[\arcsin \left(\sin \frac<8 \pi><3>\right)=\frac<8 \pi><3>\], является неверной, потому что \[\frac<8 \pi><3>\], не удовлетворяет условию.
Главные значения: arcsin, arccos, arctg и arctg
Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \[0, \pm 30,45,60,90,120 \ldots \ldots \ldots \ldots \ldots \pm 180\] градусов. Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.
Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций.
Нет времени решать самому?
Наши эксперты помогут!
Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.
Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.
Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.
И напоследок остается вычислить значения арктангенса и арккотангенса.
Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:
\[\operatorname
\[\operatorname
Далее все данные запишем в виде табличной формы.
Первая таблица для арктангенса
Вторая таблица для арккотангенса
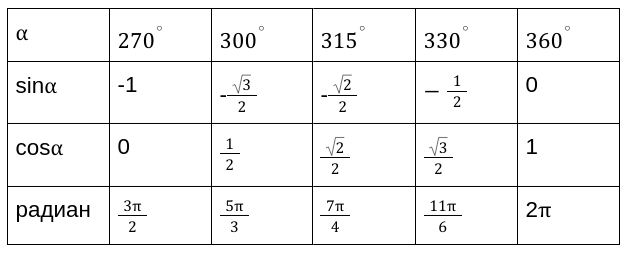
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Основные способы, которые помогут заполнить таблицу функций тригонометрии.
Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec).
На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения.
Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.
В таблице представлены следующие данные:
Мы показали, что представляет таблица, какие данные и значения отображает. Полную версию таблицы, можно найти в сборнике. Который издается каждый год. Для определения неизвестных нужно использовать следующие уже известные нам формулы:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102
Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение. Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.
Арксинус (y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).





























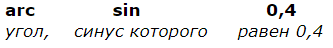
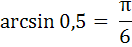

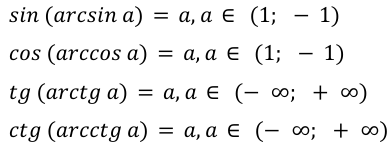
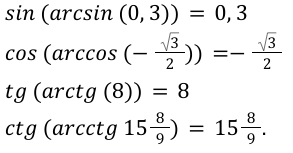

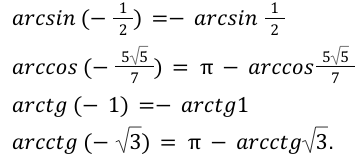
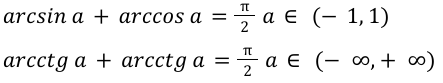
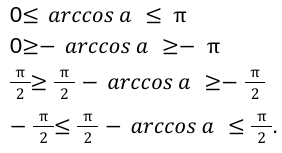
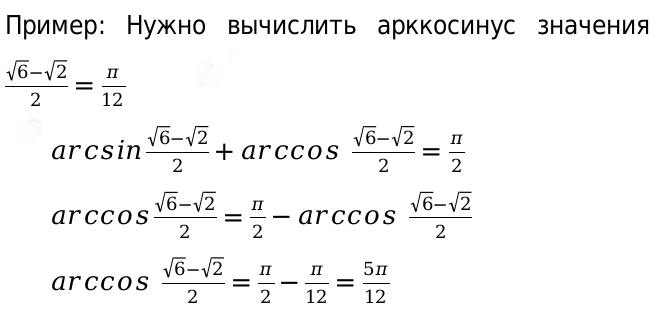
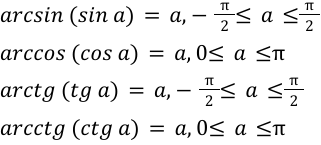
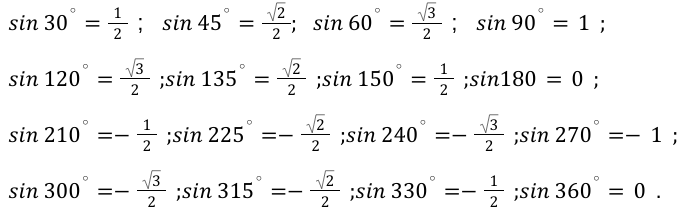


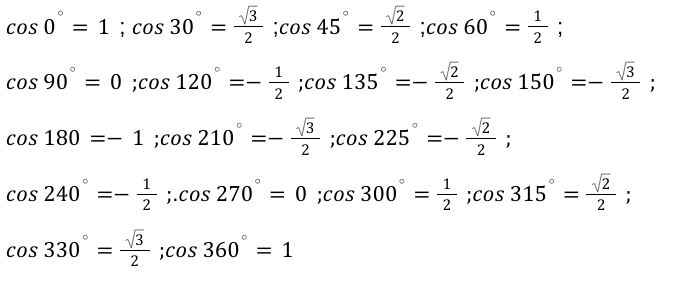
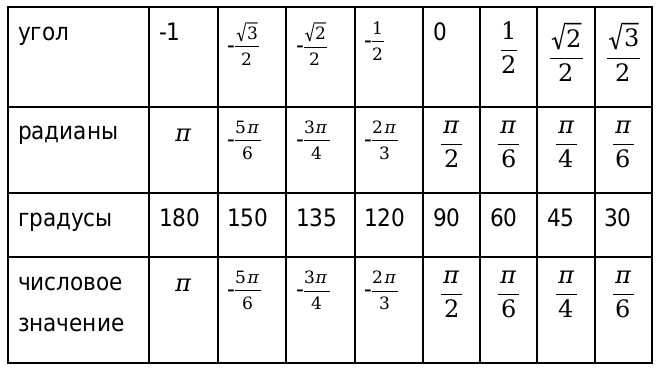
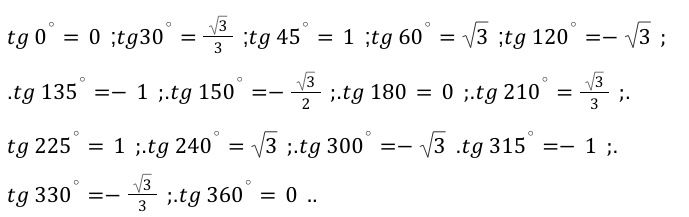
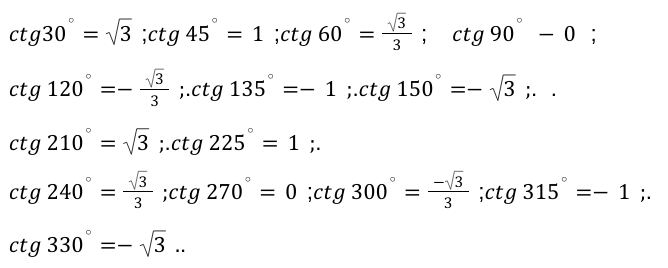
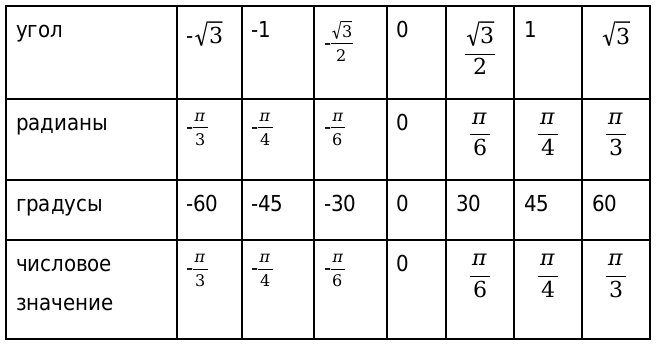
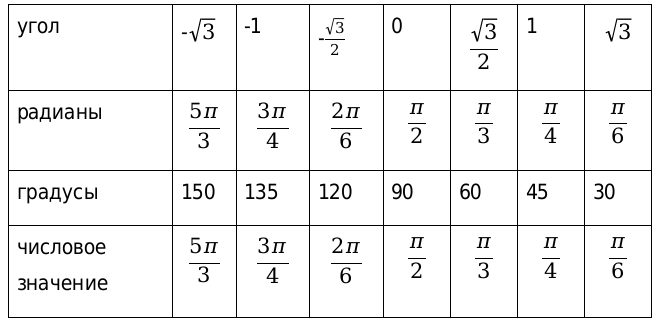

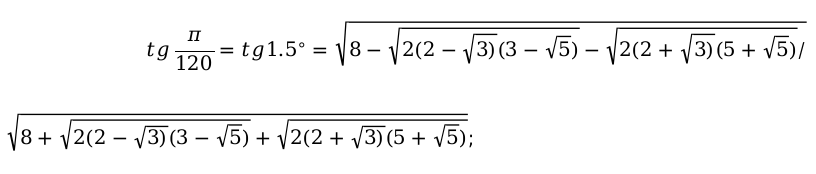











 Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!



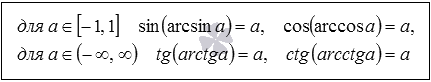

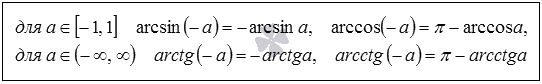
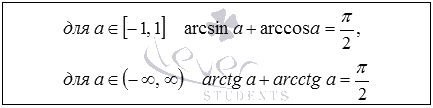

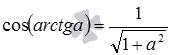 , таким образом
, таким образом 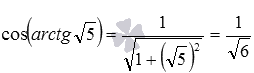 .
.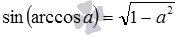 , мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем
, мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем 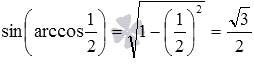 . Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату:
. Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: 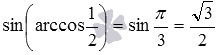 (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).
(при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).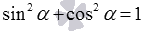 и
и 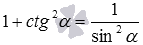 , а также учитывая, что
, а также учитывая, что 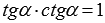 , легко получить следующие формулы
, легко получить следующие формулы 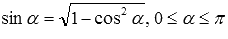 ,
, 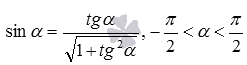 и
и 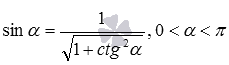 , выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.
, выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.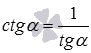 .
.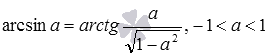 . Известно, что
. Известно, что 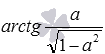 при указанных a представляет собой угол (число) от минус пи пополам до пи пополам. Более того, по формуле синуса арктангенса имеем
при указанных a представляет собой угол (число) от минус пи пополам до пи пополам. Более того, по формуле синуса арктангенса имеем 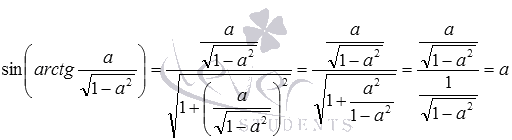 . Следовательно,
. Следовательно, 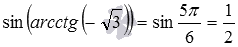 . Очевидно, что мы получили тот же результат.
. Очевидно, что мы получили тот же результат.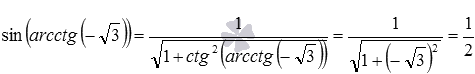 . А можно было и сразу применить формулу синуса арккотангенса вида
. А можно было и сразу применить формулу синуса арккотангенса вида 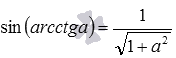 :
: 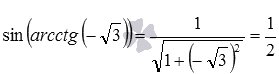 .
.














 Решим простое уравнение для
Решим простое уравнение для
 Теперь рассмотрим уравнение для
Теперь рассмотрим уравнение для
 ⇒
⇒ 

 Так как косинус определяется координатой х, то и пересекать круг будем прямыми, проходящими через соответствующие точки на оси Ох. На этом круге решаем уравнение положительного значения арккосинуса. И в том случае можем смело утверждать, что
Так как косинус определяется координатой х, то и пересекать круг будем прямыми, проходящими через соответствующие точки на оси Ох. На этом круге решаем уравнение положительного значения арккосинуса. И в том случае можем смело утверждать, что  =
=  Получается:
Получается: ⇒
⇒ 
 ⇒
⇒  Тангес угла определяется, как
Тангес угла определяется, как
 .
.