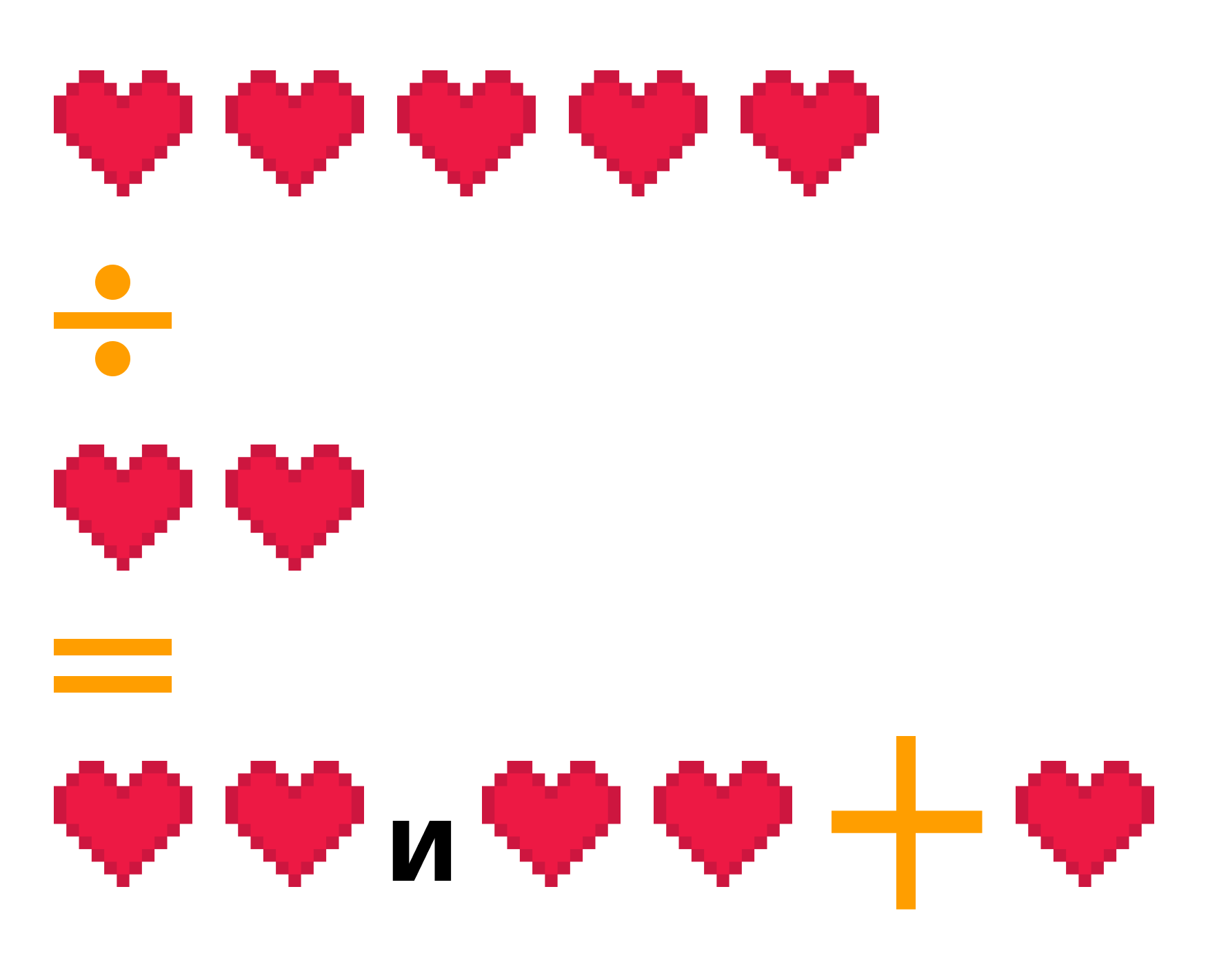Четные числа это какие

29.08.202229.08.2022 admin 0 Комментариев

Четные числа это какие

Определить чётное или нечётное число

Сколько чётных и нечётных чисел между.

Теория

Чётное ли число

Чётным является целое число, которое делится на 2 без остатка (нацело).

Все многозначные числа, оканчивающиеся на 0,2,4,6 или 8, являются чётными числами:

Примеры

Чётное ли число 10?

Десять разделилось на два без остатка, следовательно 10 является чётным числом.

Чётное ли число 1?

После деления единицы на два мы получаем нецелое число, следовательно 1 не является чётным числом.

Чётность нуля

Чётное ли число 0?

Ноль чётное число, так как оно делится на два без остатка: 0 ÷ 2 = 0

Нечётные числа

Нечетным является целое число, которое не делится на 2 без остатка.

Все многозначные числа, оканчивающиеся на 1,3,5,7 или 9, являются нечётными числами:

Пример

Для примера рассмотрим число 67. Так как оно заканчивается цифрой 7 (нечётной), уже можно утверждать, что оно нечётное. Для пущей уверенности разделим 67 на два:

67 ÷ 2 = 33.5, то есть 33 и остаток 1 (67 = 33 ⋅ 2 + 1)

Окончательно делаем вывод, что число 67 является нечётным числом.

Сколько чётных и нечётных чисел в ряду

Сколько чётных и нечётных чисел находится в ряду между n и m?

Если n и m разные по чётности

Если n и m разные по чётности числа, то есть одно из них четное, а второе нечётное, то количество чётных и нечётных чисел в ряду одинаковое:

Пример

Возьмём ряд чисел между n = 22 и m = 31:

22, 23, 24, 25, 26, 27, 28, 29, 30, 31

Определим количество чётных и нечётных чисел в этом ряду.

Так как 22 и 31 являются числами разной чётности делаем вывод, что чётных и нечётных чисел в данном ряду поровну:

5 чётных и 5 нечётных

22	24	26	28	30
23	25	27	29	31

Если n и m чётные

Если n и m чётные числа, то чётных чисел в ряду будет на одно больше, чем нечётных:

Пример

Возьмём ряд чисел между n = 10 и m = 20:

10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20

Определим количество чётных и нечётных чисел в этом ряду.

6 чётных и 5 нечётных

10	12	14	16	18	20
11	13	15	17	19

Если n и m нечётные

Если n и m нечётные числа, то чётных чисел в ряду будет на одно меньше, чем нечётных:

Пример

Возьмём ряд чисел между n = 11 и m = 19:

11, 12, 13, 14, 15, 16, 17, 18, 19

Определим количество чётных и нечётных чисел в этом ряду.

Источник

Четные числа

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

Полезное

Смотреть что такое «Четные числа» в других словарях:

Числа — Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов

Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

ЧИСЛА — ♥ ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник

«Сакральный» смысл чисел в верованиях и учениях — К материалу «07.07.07. Влюбленные всего мира поверили в магию чисел» С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров

АДДИТИВНАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в к ром изучаются задачи о разложении целых чисел на слагаемые заданного вида, а также алгебраич. и геометрич. аналоги таких задач, относящиеся к полям алгебраич. чисел и к множествам точек решетки. Эти задачи наз.… … Математическая энциклопедия

Счастливое число — В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия

НУМЕРОЛОГИЯ — методы определения скрытых истин с помощью толкования чисел. В основе нумерологии лежит идея о том, что каждое число является символом неких понятий. Например, 1 это единство, Бог, начало и неделимость; 2 двойственность, разделение, анализ,… … Символы, знаки, эмблемы. Энциклопедия

Источник

Четные и нечетные числа

О чем эта статья:

Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.

Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.

Четное число — это число, которое делится нацело на 2.

4 : 2 = 2
Это значит, что 4 — четное число.

Нечетное число — это число, которое не делится на 2 без остатка.

5 не делится на 2 без остатка — значит, 5 это нечетное число.

Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.

Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.

Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.

Свойства четных и нечетных чисел

Четные и нечетные числа чередуются друг с другом

1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.

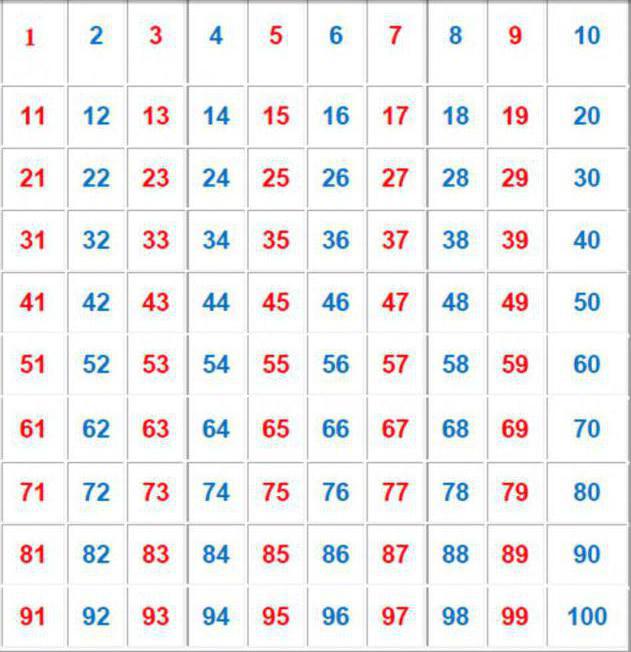
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.

1	11	21	31	41	51	61	71	81	91
2	12	22	32	42	52	62	72	82	92
3	13	23	33	43	53	63	73	83	93
4	14	24	34	44	54	64	74	84	94
5	15	25	35	45	55	65	75	85	95
6	16	26	36	46	56	66	76	86	96
7	17	27	37	47	57	67	77	87	97
8	18	28	38	48	58	68	78	88	98
9	19	29	39	49	59	69	79	89	99
10	20	30	40	50	60	70	80	90	100

Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.

Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.

Задачи для практики

Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.

Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?

1	♥	17
2	10	♥
♥	11	19
4	♥	20
5	13	♥
♥	14	22
7	15	23
8	♥	♥

Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.

Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.

X	2	4	6	8	10
X × 2
X : 2

X	2	4	6	8	10
X × 2	4	8	12	16	20
X : 2	1	2	3	4	5

2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное

Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?

Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)

Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.

Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?

Ответ: изначально у Маши в инстаграме было 46 фотографий.

Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.

1	☆	3	☆	5
6	☆	☆	9	10
☆	12	13	☆	15
16	☆	☆	19	20
☆	22	23	☆	25

Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.

Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70

Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.

Источник

Чётные и нечётные числа

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Содержание

Определения

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

С точки зрения теории сравнений, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Признак чётности

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа. 31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

История и культура

В разных странах существуют связанные с количеством даримых цветов традиции.

Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье.

В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли.

Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов, у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.

Примечания

Полезное

Смотреть что такое «Чётные и нечётные числа» в других словарях:

Нечётные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Нечётное — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Нечётное число — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Четные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Слегка избыточные числа — Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия

Совершенные числа — целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… … Большая советская энциклопедия

Квантовые числа — целые (0, 1, 2. ) или полуцелые (1/2, 3/2, 5/2. ) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия

Источник

Четные и нечетные числа

Больше онлайн заданий по математике для детей от 2 до 11 лет. Начните прямо сейчас!

Уже в дошкольном возрасте ребята узнают, что бывают четные и нечетные числа. Определить абстрактно, четное число или нечетное, бывает непросто. Зато каждому понятно, получится ли некоторое количество разделить на двоих без остатка, или нет. Объяснить ребенку четные и нечетные числа помогут занимательные упражнения.

Что такое четные и нечетные числа

Таблица четных и нечетных чисел

Чтобы быстро определить, четным или нечетным является число, можно воспользоваться таблицей до 100. В ней четные и нечетные числа будут чередоваться. В нашей таблице выделены четные числа.

100

Как объяснить ребенку четные и нечетные числа

Сначала расскажите ребенку, что такое четные и нечетные числа.

Проиллюстрируйте это на примерах – раскладывайте перед ребенком разное количество карандашей и попытайтесь разделить на две равные части. Если так получилось сделать, то число карандашей является четным. Если остался лишний карандаш – число нечетное.

Закрепляем знание о четных и нечетных числах

Запоминание приходит с практикой. Вначале пусть ребенок продолжает ряды четных или нечетных чисел, начиная с указанного вами числа. В этом упражнении пригодится навык счета через один. Следующим этапом предлагайте определить четность или нечетность любого числа. Поиграйте в игру: вы загадываете число в небольшом диапазоне и сообщаете, что оно находится между 4 и 7. А ребенок, используя вопрос: «Это четное или нечетное число?», пытается угадать задуманное число. Если ребенок угадал, то следующий вопрос задает он.

Выполните развивающие упражнения от Айкьюши

Свойства четных и нечетных чисел

Даже если ребенок не умеет складывать числа в уме, он может запомнить несколько простых правил:

Какое число 0 – четное или нечетное?

Ноль – это четное число.

Некоторые взрослые до сих пор затрудняются правильно ответить на этот вопрос. Как же это доступно объяснить детям?

Во-первых, чтобы определить четность или нечетность, нужно вспомнить какие числа называются четными – те, которые делятся на 2 без остатка. Ноль делится на 2 без остатка. Значит, ноль – четное число.

Во-вторых, мы уже знаем, что четные и нечетные числа чередуются. После ноля стоит нечетное число 1. Значит ноль – четное число.

Также поможет запомнить четность ноля тот факт, что все числа, которые заканчиваются на 0 – четные. Значит и ноль тоже четное число.

Четные и нечетные числа до 20

Чётные числа до 20:

Нечётные числа до 20:

Игры с четными и нечетными числами

Для того чтобы знания о четных и нечетных числах закрепились у малыша в памяти, регулярно используйте эти понятия в игре.

Например, в игре в магазин вы можете “печатать” для товаров ценники только с нечетными числами, выдумывая двузначные или трёхзначные числа из головы. Остается только вспомнить, на какие цифры должны оканчиваться эти числа.

Напомнить знания о четных и нечетных поможет обычное русское лото. Когда вы с ребенком заполняете фишками карточки лото, проговаривайте вслух, является ли число четным.

Айкьюша поможет легко и в игровой форме познакомиться с математикой для детей 6-7 лет. Раздел включает задания и игры по арифметике для дошкольников: счет, сложение, вычитание, сравнение, умножение, деление, изучение геометрических фигур. Познавательные уроки и занятия для развития мальчиков и девочек.

Материалы для самостоятельных занятий по математике с дошкольником

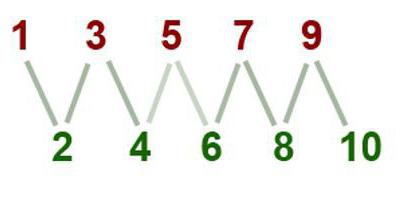
Предложите ребенку раскрасить предметы с четными числами в зеленый цвет, а с нечетными – в красный.	Распечатайте картинку и предложите ребенку продолжить последовательность четных и нечетных чисел, начиная с шеи жирафа.

Превратите изучение четных и нечетных чисел в увлекательное занятие – и ребенок без труда освоит эту непростую тему!

Источник

Чётные и нечётные числа

Чётность в теории чисел

Чётное число — целое число, которое делится на 2 без остатка: …−4,−2,0,2,4,6,8,10.

Например, 4 ─ это чётное число, его можно разделить на 2. Это помогает в сложении.

Нечётное число — целое число, которое не делится на 2 без остатка: …−3,−1,1,3,5,7,9…

Иными словами чётное и нечётное — собственные названия классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

Сложение и вычитание

Умножение:

Деление:

История и культура

Примечания

ar:أعداد فردية و زوجية bg:Четни и нечетни числа ca:Nombre senar cs:Sudá a lichá čísla da:Lige og ulige tal

el:Άρτιοι και περιττοί αριθμοί

he:מספר זוגי hu:Páros és páratlan számok io:Para e ne-para nombri is:Oddatala

lmo:Nümar díspari lt:Lyginiai ir nelyginiai skaičiai nds:Evene un unevene Tallen nl:Even nn:Oddetal og partal no:Partall pl:Liczby parzyste i nieparzyste

simple:Even number sk:Párne a nepárne čísla sl:Soda in liha števila sr:Парни и непарни бројеви sv:Jämna och udda tal th:จำนวนคู่และจำนวนคี่

ur:جفت عدد Шаблон:Ш2 Шаблон:Ш2 Шаблон:Ш2 Шаблон:Ш2

Источник

Четные и нечетные числа

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

История и культура

Примечания

Полезное

Смотреть что такое «Четные и нечетные числа» в других словарях:

Зонная пластинка Френеля — Не следует путать с линзой Френеля. Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное … Википедия

Квадратурная фазовая манипуляция — Технологии модуляции п· … Википедия

НУМЕРОЛОГИЯ — и; ж. [лат. numero считаю и греч. logos учение] Учение, основанное на вере в сверхъестественное влияние на судьбу человека, страны и т.п. сочетаний определённых чисел, цифр. ◁ Нумерологический, ая, ое. Н ие предсказания. * * * НУМЕРОЛОГИЯ… … Энциклопедический словарь

ТОПОЛОГИЯ — раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание. Непрерывная деформация это деформация фигуры, при которой не… … Энциклопедия Кольера

ХЭ ТУ И ЛО ШУ — План (карта) [[из Желтой]] реки и Письмена (документ) [[из реки]] Ло нумерологические (сян шу чжи сюэ) пространственно числовые (троично пятеричные) схемы, магический крест и магический квадрат соответственно, образованные по квадратно… … Энциклопедия Кольера

Источник

Нечётные числа

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

История и культура

Примечания

Полезное

Смотреть что такое «Нечётные числа» в других словарях:

Чётные и нечётные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Содержание 1 Определения 2 Признак чётности 3 … Википедия

Источник

Четное число

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

История и культура

Примечания

Полезное

Смотреть что такое «Четное число» в других словарях:

ЧЕТНОЕ ЧИСЛО — целое число, делящееся на 2, напр. 0, 2, 4; 2, 4. Всякое четное число можно представить в виде 2m, где m целое число … Большой Энциклопедический словарь

четное число — сущ., кол во синонимов: 2 • чет (2) • чётное число (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

четное число — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN even number … Справочник технического переводчика

четное число огней (два или большее) (в автотранспортных средствах) — четное число огней (два или большее) Одна светоизлучающая поверхность, имеющая форму полосы и расположенная симметрично по отношению к средней продольной плоскости транспортного средства, на расстоянии не менее чем на 0,4 м от края габаритной… … Справочник технического переводчика

ЧЕТНОЕ ЧИСЛО — целое число, делящееся (без остатка) на 2 … Математическая энциклопедия

ЧИСЛО — ср. количество, счетом, на вопрос: сколько? и самый знак, выражающий количество, цифра. Без числа; нет числа, без счету, многое множество. Поставь приборы, по числу гостей. Числа римские, арабские или церковные. Целое число, ·противоп. дробь.… … Толковый словарь Даля

Число — С древнейших времен различным числам приписывали тайные значения. Философы, последователи Пифагора (около 500 г. до Р.Хр.), утверждали, что числа являются основным началом и сущностью вещей и подробно определили качества и роды чисел. По их… … Словарь библейских имен

четное целое число — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN even integral number … Справочник технического переводчика

ЧИСЛО — нечетное: символ светлого, доброго, мужской аспект; четное: символ темного, женский аспект. Имеет значимую историю. У пифагорейцев трактовалось как выражение гармонии космического и человеческого порядков. В исламе рассматривалось как первооснова … Символы, знаки, эмблемы. Энциклопедия

чётное число — целое число, делящееся на 2, например 0, 2, 4; 2, 4. Всякое чётное число можно представить в виде 2m, где m целое число. * * * ЧЕТНОЕ ЧИСЛО ЧЕТНОЕ ЧИСЛО, целое число, делящееся на 2, напр. 0, 2, 4; 2, 4. Всякое четное число можно представить в… … Энциклопедический словарь

Источник

Чётные числа

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

История и культура

Примечания

Полезное

Смотреть что такое «Чётные числа» в других словарях:

Конструктивные способы определения вещественного числа — При конструктивном подходе к определению вещественного числа вещественные числа строят, исходя из рациональных, которые считают заданными. Во всех трёх нижеизложенных способах за основу берутся рациональные числа и конструируются новые объекты,… … Википедия

Двойные числа — О гиперкомплексных числах параболического типа см. дуальные числа Двойные числа или паракомплексные числа, расщепляемые комплексные числа, комплексные числа гиперболического типа гиперкомплексные числа вида « », где и вещественные… … Википедия

Счётные палочки — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Центрированные полигональные числа — Центрированные полигональные числа это класс фигурных чисел, каждое сформировано вокруг центральной точки, окружённой слоями многоугольников с постоянным числом сторон. Каждый слой содержит на одну точку больше чем предыдущий., так что… … Википедия

Источник

Нечетные числа

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

История и культура

Примечания

Полезное

Смотреть что такое «Нечетные числа» в других словарях:

КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь

сорит — (от греч. soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики

Источник

Чётное число — целое число, которое делится на 2 без остатка.
Сумма чётных чисел от 0 до 100 равна 2550.

В таблице приведены чётные числа от 0 до 100

№	число
1	0
2	2
3	4
4	6
5	8
6	10
7	12
8	14
9	16
10	18
11	20
12	22
13	24
14	26
15	28
16	30
17	32
18	34
19	36
20	38
21	40
22	42
23	44
24	46
25	48
26	50
27	52
28	54
29	56
30	58
31	60
32	62
33	64
34	66
35	68
36	70
37	72
38	74
39	76
40	78
41	80
42	82
43	84
44	86
45	88
46	90
47	92
48	94
49	96
50	98
51	100

Ряд чётных чисел от 0 до 100:

0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100

Источник

Арифметические свойства

Четными называют числа, которые при делении на 2 образуют целое число. Нечетные при том же действии дают результат с остатком (дробное число). Чтобы быстро проверить на четность двузначную цифру, нужно определить параметр для последней его цифры в десятичной записи. Если она делится на два, число является четным, в противном случае — нечетным. Метод работает для любых многозначных чисел.

Арифметические правила четных и нечетных чисел при различных операциях описаны древнегреческим математиком Пифагором до нашей эры и используются для вычислений современниками. Они помогают составлять формулы для оптимизированных расчетов в задачах с большим рядом переменных. Алгоритмы многих онлайн-калькуляторов запрограммированы с помощью таких функций.

Закономерности арифметических операций с целыми числами:

Формула четного числа: m = 2k. Формула нечетного числа: m = 2k + 1.

При уменьшении или увеличении четного числа на единицу получается нечетное и наоборот. При начертании оси с нулем в центре будет сохраняться чередование четных и нечетных чисел. Наглядно продемонстрировать феномен школьникам можно, предложив записать последовательный ряд четных чисел через запятую.

Характеристика парности у ноля

Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.

В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.

Признаки четности ноля:

Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.

Свойства группы для вычислений

Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.

Алгоритм оптимизированного решения:

Количество складываемых элементов последовательного ряда некратных двум числительным всегда соответствует квадратному корню суммы.

Примеры логических задач для решения через характеристику парности:

Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.

Ответ становится очевидным при понимании, что пройденный путь, равен расстоянию, которое необходимо пройти для возвращения к стартовой позиции. Таким образом суммарное расстояние обязано быть парным.

История и значение в культуре

Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.

Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.

Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.

У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.

Практическое применение

Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.

В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.

Парность строк помогает проверить созвучность стиха поэтам. Если мысленно пронумеровать слоги, можно подобрать слово в соответствии с ритмом произведения, так как ударные и безударные гласные являются основным ориентиром.

Источник

Чётное

Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание

Признак чётности

Арифметика

История и культура

Примечания

Полезное

Смотреть что такое «Чётное» в других словарях:

Чётное число — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Счётное слово — часть речи, служащая при счёте. В языках Юго Восточной Азии (китайском, корейском, вьетнамском, японском, малайском, индонезийском, бирманском), также маяйских, атабаскских, австронезийских и других языках обязательна. Встречается и в… … Википедия

Почётное гражданство — … Википедия

Пролётное — У этого термина существуют и другие значения, см. Пролётное. Село Пролётное укр. Пролітне крымскотат. Prolötnoye Страна … Википедия

Пулемётное гнездо — Пулемётное гнездо … Википедия

ОТСЧЁТНОЕ УСТРОЙСТВО — измерительного прибора (аналогового или цифрового), часть прибора, предназначенная для отсчитывания его показаний. О. у. аналогового прибора обычно состоит из шкалы и указателя. По типу указателя О. у. подразделяются на стрелочные и световые. В… … Физическая энциклопедия

Лётное училище — Лётное училище высшее или средне техническое учебное заведение, производящее подготовку лётчиков (пилотов). Лётные училища в СССР делились на: гражданские готовящие пилотов для гражданской авиации средние (лётное училище… … Википедия

Источник

Четные и нечетные числа

Задолго до нашей эры древнегреческий ученый, занимаясь музыкой установил связь между длинной струны музыкального инструмента и издаваемым звуком. Это наблюдение позволило Пифагору сделать вывод, что не только законы музыки, но и все на свете можно выразить с помощью чисел. «Числа правят миром!» — провозгласил великий ученый.

Числа стали для Пифагора всем. Именно он впервые разделил все числа на четные и нечетные. Исследования Пифагора и его учеников положили начало важнейшей области математики — теории чисел.

Современные ученые доказали важность этой теории. Разделение всех чисел на четные и нечетные нашло свое подтверждение в структуре вирусов и ДНК, в знаменитых опытах Пастера с поляризацией винной кислоты, в нарушении четности элементарных частиц и других теориях.

Кстати сказать, что четные числа пифагорейцы считали женскими, а нечетные — мужскими. Символом брака у древних греков было число пять, которая состоит из суммы нечетной тройки и четной двойки.

Кроме математики Пифагор страстно любил музыку. Пифагор связал науку и искусство с помощью чисел. Первые четыре числа задают все известные консонантные интервалы в музыке: октаву (1:2), квинту (2:3) и кварту (3:4).

Четные и нечетные числа стали неотъемлемой частью нашей жизни. В теории числе четность определяется как характеристика целого числа, определяющая его способность делиться на два без остатка. То есть, если целое число делится без остатка на два, оно является чётным (2, 28, −8, 40), если нет — нечётным (1, 3, 75, −19).

Интересно узнать, что нуль считается чётным числом.

К основным признакам четности относятся следующие:

В том случае, если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число является чётным, в противном случае — нечётным.

Например, 42, 104, 11110, 9115817342 — чётные числа.

31, 703, 78527, 2356895125 — нечётные числа.

Так же были выделены закономерности получения четных и нечетные чисел при выполнении основным арифметический действий:

При сложении и вычитании:

Чётное ± Чётное = Чётное
Чётное ± Нечётное = Нечётное
Нечётное ± Чётное = Нечётное
Нечётное ± Нечётное = Чётное
При умножение:

Чётное × Чётное = Чётное
Чётное × Нечётное = Чётное
Нечётное × Нечётное = Нечётное
При делении:

Чётное / Чётное — не дает однозначного ответа о чётности результата, поскольку, если результат целое число, то оно может быть как чётным, так и нечётным;
Чётное / Нечётное = четное, если результат целое число;
Нечётное / Чётное — результат не может быть целым числом, следовательно у него отсутствуют показатели четности;
Нечётное / Нечётное = нечетное, если результат целое число.

Источник

Четные цифры

Средняя оценка: 4.6

Всего получено оценок: 513.

Средняя оценка: 4.6

Всего получено оценок: 513.

Четные числа – достаточно интересная и простая тема в курсе математики. Многие ученики не задумываясь, пользуются основными свойствами четных чисел, что иногда вызывает ошибки. Чтобы разобраться в вопросе раз и навсегда – разберем тему четных чисел во всех подробностях.

Что такое четное число?

Четным числом называют любое целое число, которое делиться на два нацело. Для того, чтобы лучше понять, какие числа относятся к четным, вспомним классификацию чисел по множествам.

Ноль в натуральные числа не входит, а потому первое множество чисел, где встречается ноль – целые числа.

Формула четного числа

Существует формула четного числа, она выглядит так:

k=2m – где k – четное число, m – любое целое число. Если любое целое число подставить в формулу, то результатом будет всегда четное значение.

Можно обратить внимание на число 2 в формуле, именно это значение делает любой конечный результат формулы четным. Так же есть формула нечетного числа: k=2m+1.

Сколько всего четных чисел?

Полного списка четных чисел нет и никогда не будет. Как мы помним, чисел – бесконечное множество. Это значит, что четных чисел так же бесконечно много. Но часто у учеников возникает вопрос: сколько существует четных цифр. Список четных цифр привести можно: 0,2,4,6,8 – всего пять значений.

Четные числа на числовой прямой

Еще один интересный вопрос в изучении темы, это четные числа на числовой прямой. Интересно посмотреть, являются ли отрицательные числа и ноль – четными. Ответ прост – да, являются. Исходя из определения, мы знаем, что четным числом может быть только целое значение. Попробуем подставить в формулу четных чисел 0:

Значение нуля сохранилось, а значит ноль – число четное.

Теперь подставим в формулу целое отрицательное число:

k=2*(-5)=-10 – получилось отрицательное число, то есть отрицательные числа так же могут быть четными. Это значит, что на числовой прямой, четные числа расходятся в обе стороны от нуля, а так же число ноль является четным числом.

Что мы узнали?

Мы поговорили о четных числах. Разобрались, сколько четных чисел существует в математике. Привели формулу четного числа.

Источник

Чётные и нечётные числа

Материалы к уроку

7. Чётные и нечётные числа.doc

7. Чётные и нечётные числа.ppt

Конспект урока

7. Чётные и нечётные числа

Организационный этап

Посмотрите друг на друга. Улыбнитесь соседу справа, а теперь соседу слева. Улыбка творит чудеса и поднимает настроение. Но не только улыбка творит чудеса, а и дружба. Дружные Смешарики пришли к нам на урок.

Сегодня мы повторим таблицу умножения и деления на 2. Узнаем, какие числа называются чётными, а какие – нечётными.

Этап подготовки учащихся к активному сознательному усвоению знаний

Устный счёт

Ну-ка в сторону карандаши.
Ни счетных палочек. Ни ручек. Ни мела.
Устный счёт! Мы творим это дело
Только силой ума и души!

Задание 1

Нюша расставила банки с вареньем в погребе на 2 полки. Она поставила по 5 банок на каждую полку. Сколько банок с вареньем заготовила Нюша?

Задание 2

Ёжик любит яблоки. Он приносил себе 2 дня по 8 яблок. Сколько яблок он принёс?

Этап усвоения новых знаний

Задание 3

Бараш положил в погреб на зиму 8 штук свёклы. Всю свёклу он разложил в 2 корзины поровну. Сколько штук свёклы лежит в каждой корзине?

Мы видим, что в каждую корзину положили по 4 свёклы. Значит 8 делится на 2 без остатка.

Решите еще одну задачу.

Бараш положил в погреб на зиму 11 штук тыквы.

Всю тыкву он разложил на 2 полки поровну. Сколько штук тыквы лежит на каждой полке?

Мы видим, что 11 не можем разделить на 2, т. к. на каждую полку можно положить по 5 тыкв, и одна еще останется.

Значит, есть числа, которые мы можем разделить на 2 без остатка, и числа, которые без остатка на 2 не делятся.

Числа, которые делятся на 2 без остатка, называются чётными.

2, 4, 6, 8, 10…- четные числа

Числа, которые не делятся на 2 без остатка, называются нечётными.

1, 3, 5, 7, 9…- нечетные числа

Этап закрепления новых знаний

Задание

1 3 _ _ 9 нечётные

2 _ _ 8 _ чётные

Четные номера домов: 2, 4, 6, 8, 10.

Нечетные номера домов: 1, 3, 5, 7, 9

Задание

На улице Смешариков 8 домов с чётными номерами, а с нечётными на 1 дом больше. Сколько всего домов на улице Смешариков?

В первом действии найдем, сколько домов с нечетными номерами:

1) 8 + 1 = 9 домов

Во втором действии ответим на вопрос задачи: сложим количество домов с чётными номерами и количество домов с нечётными номерами:

2) 8 + 9 = 17 домов

Запишем ответ: 17 домов на улице Смешариков.

Задание

Определите, какой номер дома последний?

Последний дом номер 17.
Это чётный или нечётный номер?

17 разделим на 2. Получится по 8 и остается еще 1. Так как 17 нельзя разделить на 2 без остатка, значит это число нечётное

Двузначное чётное число можно отличить от нечётного по последней цифре. Если последняя цифра в записи числа делится на 2, то всё число делится на 2, значит, оно чётное

Задание

Решите числовые выражения.

57-13=44 60-32=28 33+16=49

Найдите среди результатов нечётные числа и подчеркните их.

Нечётные числа – 49, 69, 15.

Самостоятельная работа

Задание

Запишите числа по порядку от 10 до 19.

Обведите кружками четные числа – красным карандашом, а нечетные – синим.

Проверьте себя и оцените свои успехи.

Нечетные числа – 11, 13, 15, 17, 19

Мы сегодня вместе со Смешариками познакомились с чётными и нечётными числами.

Какие числа называются чётными?

Числа, которые делятся на 2 без остатка, называются чётными.

2, 4, 6, 8, 10…- чётные числа

Какие числа называются нечётными?

Числа, которые не делятся на 2 без остатка, называются нечётными.

1, 3, 5, 7, 9…- нечётные числа

Выберите смайлик, который более всего соответствует вашему пониманию изученных сегодня на уроке правил и нарисуйте его у себя в тетради.

Спасибо за работу!

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовим к ЕГЭ, ОГЭ и другим экзаменам

Найдём слабые места по предмету и разберём ошибки

Повысим успеваемость по школьным предметам

Поможем подготовиться к поступлению в любой ВУЗ

Источник

Четные числа

Что такое четные числа и чем они отличаются от нечетных?

Четные числа — это числа, запись которых заканчивается цифрой 0, 2, 4, 6 или 8.

12; 406; 928; 1370; 11 754 — четные числа.

Нечетные числа — это числа, запись которых оканчивается цифрой 1, 3, 5, 7 или 9.

23; 105; 6801; 3297; 3829 — нечетные числа.

В школьном курсе сначала изучают натуральные четные и нечетные числа. Позже, после изучения отрицательных чисел, четные и нечетные числа дополняются целыми.

После этого определение четного и нечетного числа несколько меняется.

Четное число — это целое число, делящееся без остатка на 2.

Любое четное число можно представить в виде 2n, где n — целое число.

Нечетное число — это целое число, не делящееся на 2 без остатка.

Любое нечетное число можно представить в виде 2n+1 или 2n-1, где n — целое число.

Не существует ни наименьшего, ни наибольшего четного или нечетного числа.

Однако, можно говорить о наименьшем натуральном четном числе и наименьшем натуральном нечетном числе.

Наименьшее четное натуральное число — 2 (0 не является натуральным числом), наименьшее нечетное натуральное число — 1.

Источник

Чётные и нечётные числа в нумерологии

Что означают чётные и нечётные числа в духовной нумерологии. В изучении языка чисел это очень важная тема! Чем по своей сути чётные числа отличаются от нечётных чисел?
Нечётные числа в нумерологии — солнечные, мужской природы, кислотные, электрические, динамичные. При группировании нечётных чисел, одно число останется без своей пары (1 и 3; 5 и 7; 9). Эти числа являются слагаемые (их складывают с чем-либо).
Чётные числа — лунные, женской природы, щелочные, магнетические, статичные. Числа данной группы вычитаемые или уменьшаемые. Они статичны и остаются без движения, потому что имеют чётные группы пар (2 и 4; 6 и 8).

Чётные числа
Общеизвестно, что чётные числа — те числа которые делятся на два. А что означают чётные числа относительно духовной нумерологии? Какова нумерологическая суть «деления на два»? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У цифры 2 несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе. надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

Нечётные числа
Нечётными называют числа, которые не делятся на два. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное. Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел, никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера число 3 — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них.
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.

В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел.
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь.

Источник

Что такое нечетные числа и как их узнать?

Прежде чем говорить про четные и нечетные числа, стоит уяснить несколько моментов о том, какие вообще группы чисел бывают. Это необходимо для того, чтобы не пытаться выяснять четность дроби.

С каких чисел начинается изучение в основной школе?

Первыми идут натуральные. Они также сначала появились исторически. Человечеству было необходимо подсчитывать предметы. Причем при счете ноль не используется, поэтому он не входит в группу натуральных чисел. Здесь все целые, которые больше единицы.

Именно для них впервые дается определение четности. Чтобы понять, какое число нечетное, нужно запомнить признак четного. Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.

Какие числа идут дальше?

Целые. В их множество входит уже ноль и все отрицательные числа. Цепочка натуральных чисел была ограничена слева, а вправо продолжалась бесконечно. С целыми оказывается бесконечное количество чисел и слева от нуля.

В этот момент немного меняется определение четности. Оно теперь должно делиться на два без остатка. Значит, нечетные числа при делении на два дают ответ с остатком.

Причем даже вводится общая запись: для четных — 2n, нечетные — (2n+1). Если для натуральных не существует только максимального четного или нечетного, то у целых нет и минимального.

А что потом?

Кстати, для них не вводится понятие четности. Поэтому нечетные числа, записанные в виде дроби, не существуют вовсе.

Какие результаты дают действия с четными и нечетными числами?

Их можно рассмотреть в порядке усложнения арифметического действия. Тогда первым и вторым пойдут сложение и вычитание. Неважно, какое из них выполняется, ответ будет зависеть только от начальной пары чисел. К примеру, если исходные числа четные, то результат действия будет делиться на два. Такой же итог будет, если стоит разность или сумма нечетных чисел. Чтобы получить нечетное число, придется складывать или вычитать четное с нечетным.

Это легко можно проверить, используя их общую запись. Например, сложение двух четных чисел: 2n+2n = 4n = 2*2n. Здесь 2n — четное число, которое еще умножается на два. Значит, оно точно будет делиться нацело на двойку. То есть ответ — четный.

При сложении четного с нечетным имеем такую запись: 2n + (2n + 1) = 4n + 1. Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.

Третье действие — умножение. При его выполнении всегда будет четный ответ, если есть хотя бы один множитель четный. В ситуации, когда перемножаются два нечетных числа, результатом окажется нечетное.

Для иллюстрации последнего потребуется сделать такую запись: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Опять первое слагаемое представляет собой четное число, а единица сделает его нечетным.

Если делится нечетное число на четное, то ответ оказывается всегда дробным. Значит, его четность не определяется.

Когда в делении участвуют нечетные числа, то результатом также может оказаться дробь. Но если ответ целый, то он обязательно будет нечетным.

При делении четного на нечетное, как в предыдущей ситуации, возможно два варианта: дробь или целое число. Во втором случае оно всегда будет четным.

Источник

Нечётное число — целое число, которое не делится на 2 без остатка.
Сумма нечётных чисел от 0 до 100 равна 2500.

В таблице приведены нечётные числа от 0 до 100

№	число
1	1
2	3
3	5
4	7
5	9
6	11
7	13
8	15
9	17
10	19
11	21
12	23
13	25
14	27
15	29
16	31
17	33
18	35
19	37
20	39
21	41
22	43
23	45
24	47
25	49
26	51
27	53
28	55
29	57
30	59
31	61
32	63
33	65
34	67
35	69
36	71
37	73
38	75
39	77
40	79
41	81
42	83
43	85
44	87
45	89
46	91
47	93
48	95
49	97
50	99

Ряд нечётных чисел от 0 до 100:

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99

Источник

В мире чисел. Чётные и нечётные

Чёт счастливым
И красивым,
Слабым только лишь нечёт!
Но, редея,
Холодея
Чёт в нечёт перетечёт!

Если вы ещё не знаете, то я открою вам большой секрет – мы живём в МИРЕ ЧИСЕЛ. Они сопровождают нас до нашего появления на свет, и продолжают оставаться с нами, когда мы перебираемся в мир иной. Одна из книг Библии так и называется: «Числа».

Наука доказала, что считать умеют многие животные, начиная с мелких пташек до человекообразных обезьян. И только человек может уловить то общее, что объединяет разные предметы, к примеру, три камня, три пальмы или трёх слонов. За ними стоит общее число. Этот факт дал толчок человеку к росткам абстрактного мышления, что в дальнейшем породило математику, заслуженно названную царицей наук.

Самая распространённая система исчислений – десятичная, по числу пальцев рук, но есть и множество других. Всё началось с целых чисел. Если расположить числа в ряд: 1, 2, 3, 4…, и так далее, то его можно продолжать до бесконечности. Учитывая природный характер чисел, ряд назвали натуральным. Помимо целых чисел, в него входят и рациональные числа в виде дробей с конечным значением. Но есть и иррациональные числа, которые не имеют конечного точного значения. Если представить натуральный ряд в виде линейки, то она будет ещё и сплошной от чисел, без малейших зазоров.

Со временем открыли и «ноль», когда число не имеет значения. Он является истинным началом натурального ряда. А затем поняли, что числа бывают не только положительными, но и отрицательными. Воображаемая линейка будет бесконечной в обе стороны с нулём посередине.

На этом картина чисел не остановилась, когда обнаружили так называемые мнимые числа, то есть такие, которые есть, но каких будто нет. Если от воображаемой линейки провести вертикальную линию, то она будет до бесконечности заполнена мнимыми числами. Но и это ещё не всё, когда открыли комплексные числа, состоящие из действительных и мнимых чисел, а они заполнят всё поле чисел между их рядами. И это только в двух измерениях! А их множество!

Если я вас не утомил, то продолжим двигаться дальше, оставив математикам пользоваться всем множеством названных чисел.

А пока рассмотрим чётные и нечётные числа. Конечно, это относится только к целым числам, поскольку частично чётных не бывает. Чётные числа составляют половину всех натуральных чисел и также бесконечны.

В большинстве стран номера домов на обеих сторонах улицы чётные либо нечётные. Чтобы разгрузить улицы от автотранспорта, в некоторых городах в отдельные дни разрешено ездить машинам с чётными или нечётными номерами.

Живым дарят нечётное число цветов, а мёртвым – чётное. Алла Пугачёва пела, как художник один подарил актрисе миллион роз, то есть чётное число. Естественно, что после этого она дала дёру.

Однако у других народов, к примеру, китайского, отношение к нечётным числам как к дурным.

Вопросы для любителей математики. Испытайте себя:

Источник

Четные и нечетные числа в нумерологии

Кулинарный гороскоп по знакам Зодиака

Опасный тест. Узнай, какой у тебя характер

Четные и нечетные числа в нумерологии

О таинственном влиянии чисел, которые нас окружают, известно с древнейших времен. Каждая цифра имеет свое особое значение и обладает своим воздействием. И деление чисел на четные и нечетные является очень важным для определения нашей дальнейшей судьбы.

Чет и нечет

В нумерологии (науке о связях чисел с жизнью людей) нечетные числа (1, 3, 5, 7, 9, 11 и так далее) считаются выразителями мужского начала, которое в восточной философии называется — ян. Их также называют солнечными, потому что они несут энергию нашего светила. Такие цифры отражают поиск, стремление к чему-то новому.

Четные же числа (которые без остатка делятся на 2) говорят о женской природе (в восточной философии — инь) и энергетике Луны. Их суть в том, что они изначально тяготеют к двойке, поскольку делятся на нее. Эти цифры говорят о стремлении к логическим правилам отображения действительности и нежелании выйти за их пределы.

Другими словами: четные цифры более правильны, но в то же время более ограничены и прямолинейны. А нечетные способны помочь выбраться из скучного и серого бытия.

Нечетных чисел больше (ноль в нумерологии имеет собственное значение и не считается четным числом) — пять (1, 3, 5, 7, 9) против четырех (2,4,6, 8). Их более сильная энергия выражается в том, что при их сложении с четными числами снова получается нечетное число.

Таким образом, всякое нечетное число обладает мужскими характеристиками: властностью, резкостью, способностью к восприятию чего-то нового, а любое четное наделено женскими свойствами: пассивностью, стремлением сгладить любой конфликт.

Значения цифр

Как видим, нечетные цифры обладают гораздо более яркими свойствами. Согласно учению знаменитого древнегреческого математика Пифагора, именно они являлись олицетворением добра, жизни и света, а также символизировали правую от человека сторону — сторону удачи.

Четные же цифры ассоциировались с неудачной левой стороной, злом, тьмой и смертью. Эти взгляды пифагорейцев позже отразились в некоторых приметах (например, что нельзя живому человеку дарить четное количество цветов или что встать с левой ноги — к неудачному дню), хотя у разных народов они могут быть разными.

Влияние четных и нечетных чисел на нашу жизнь

Со времен Пифагора было принято считать, что «женские» четные числа ассоциируются со злом потому, что легко расщепляются на две половины — и значит, можно говорить, что внутри них пустое пространство, первобытный хаос. А нечетное число расщепить на равные части без остатка не получится, следовательно, оно содержит внутри себя нечто цельное и даже священное (в Средние века некоторые философы-теологи утверждали, что внутри нечетных чисел живет Бог).

В современной нумерологии принято учитывать многие окружающие нас цифры — например, номера телефонов или квартир, даты рождения и знаменательных событий, числа имени и фамилии и т.п.

Наибольшее значение для нашей жизни имеет так называемое число судьбы, которое высчитывается по дате рождения. Нужно сложить все цифры этой даты и «свернуть» их до простого числа.

Точно так же можно проанализировать даты важных для вас событий. В этом отношении очень показательна судьба знаменитого Наполеона. Он родился 15 августа 1769 года (15.08.1769), следовательно, его число судьбы равно единице:

1 + 5 + 0 + 8 + 1 + 7 + 6 + 9 = 37; 3 + 7 = 10; 1 + 0 = 1.

Древние люди не зря говорили, что цифры правят миром. Пользуясь знаниями нумерологии, вы легко можете подсчитать, какие события сулит та или иная дата — и в каких случаях следует воздержаться от ненужных действий.

Источник

Чётные и нечётные числа

Содержание

Определения

Арифметика

Признак чётности

В десятичной системе счисления

Если в десятичной форме записи числа последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления

История и культура

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

Практика

В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)

В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.

С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.

Согласно Правилам дорожного движения, в зависимости от чётности или нечётности числа месяца может быть разрешена стоянка под знаками 3.29, 3.30.

Напишите отзыв о статье «Чётные и нечётные числа»

Примечания

Ссылки

Отрывок, характеризующий Чётные и нечётные числа

– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.

От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.

Источник

Четные и нечетные дни недели какие

ПОДСКАЖИТЕ ПРАВИЛЬНО ЛИ Я ПОНИМАЮ, МОЙ ГИНЕК. РАБОТАЕТ

приём только беременных, 2 смена, чётные дни. Я ТАК ПОНИМАЮ ЧТО ЗАВТРА ВО ВТОРНИК ОНА БУДЕТ ПРИНИМАТЬ, ЗВОНЮ В ПОЛИКЛИНИКУ ЧТО БЫ УДОСТОВЕРИТСЯ МНЕ ГОВОРЯТ ЧЕТНЫЕ ЧИСЛА ТОЕСТЬ СЕГОДНЯ. СЕЙЧАС НА САЙТЕ ЗАДАЛА ВОПРОС — ОТВЕТ КАК ЖЕ ВСЕ ТАКИ ОНА РАБОТАЕТ. ПОКА НЕТ ОТВЕТА. ИЗДЕВАЮТСЯ НАД БЕРЕМЕННЫМИ

Вопрос решен и закрыт.

Лучший ответ

Married 6 (6044) 2 4 7 6 лет

Ответы

mark.vudu (34) 7 (49967) 7 15 131 6 лет

вторник, четверг, суббота

Енот 8 (337614) 6 26 633 6 лет

Пн, Ср, Пт, Вс – нечётные. Вт, Чт, Сб – чётные. В английской раскладке понедельник начинается в воскресенье – поэтому всё наоборот.

Козерожка 7 (95626) 12 28 106 6 лет

это те,которые делятся на два

Notebook_service 8 (159089) 11 35 254 6 лет

Нуууу. это такие дни, когда месячных нет, кажется.

Mruta_ 7 (21254) 7 79 213 6 лет

ПРОЖЕКТОР 6 (9169) 3 13 45 6 лет

Четные —это которые делятся без остатка на 2.

eXtrra (28) 7 (22822) 2 12 56 6 лет

Те, что делятся на 2

буква «т» с буквой «р» находяться рядом друг с другом на клаве, возвожно речь идёт про «чёрные дни»?

Tezija 1 (156) 1 10 6 лет

Чётные числа делятся а два

fefa 3 (763) 6 12 6 лет

KVAZI 4 (1599) 2 6 6 лет

Это те дни, когда четко соображаеш.

афмгеть сколько тебе лет что такого незнать вторник, четверг, суббота

jaguar 5 (4060) 4 5 6 лет

Чётные дни – это какие7

Первый вариант ответа.
Если речь идёт о календарных днях месяца, то:
ЧЁТНЫЕ ДНИ (числа) – это 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30.

_K0wKA_ 7 (30541) 5 59 169 6 лет

Стою в поликлинике в очереди на получение страховой карточки. Рядом регистратура. Подходит туда пожилой мужчина – вроде без налета маразма на лице. Спрашивает у тетки в регистратуре: «Скажите, а у вас там расписание врачей по четным и нечетным. Это четные и нечетные дни месяца или четные нечетные дни недели»?

Тетка явно была закаленная годами работы в поликлинике, но и она сразу не нашла, что ответить.

Комменты неиллюзорно доставили.

Пережив пароксизм первичного отвращения ко всему новому, непривычному, все больше и больше ощущаю приятственное отношение к новому дизайну.

Олег Петрович Желнов: Славься великая математизация русского языка!

Да здравствуют чётные и нечётные времена года, знаки Зодиака и цвета радуги!

Т.к. цвета радуги переходят друг в друга нечетко, то предлагаю ввести дроби!)

Так все-таки, в поликлинике какие дни имелись в виду – недели или месяца?

Ни фига не понятно. И в чем прикол – тоже.

У нас в поликлинике пишут четко расписание: по горизонтали дни недели, по вертикали врачи. И все.

На мой пофигистический взгляд, Экслер прав в случае с поликлиникой.

Поликлиника открыта для посещения каждый день месяца, включая выходные и праздники, когда работает дежурный врач. Поэтому надо принимать во внимание месячный период.
Кроме того, использование недельного чета-нечета вторично по отношению к месячному и явной необходимости в первом нет.

Представьте, если бы вас поставили работать по нечетным дням недели, а напарника – по четным.

1. Врач может работать на неполную ставку.

2. Врач может работать в двух поликлиниках – по четным здесь, по нечетным там.

3. Врач просто может в другие дни не принимать больных, а заниматься другими делами.

И это только то, что сразу пришло в голову, а жизнь как правило гораздо сложнее.

Malysh: И в неделях и в месяцах нечётных дней существенно больше чётных.

Полагаю, речь шла о чётных и нечётных днях от Р.Х.

Goodviper:
Моя женская логика говорит, что вопрос мужчины правомерный. Я редко хожу в поликлиники(ттт), и тоже теряюсь, когда читаю расписание врачей, иногда такое наворотят, мама не горюй! И тоже считала, пн, ср, пт нечетными днями недели.

Гм. Нобелевкой попахивает:) «Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.» (с) Википедия – более авторитетный источник чем я.

PS: А то что вы назвали называется как-то подругому!

[QUOTE]Goodviper:
Моя женская логика говорит, что вопрос мужчины правомерный. Я редко хожу в поликлиники(ттт), и тоже теряюсь, когда читаю расписание врачей, иногда такое наворотят, мама не горюй! И тоже считала, пн, ср, пт нечетными днями недели.

Гм. Нобелевкой попахивает «Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.» (с) Википедия – более авторитетный источник чем я.

PS: А то что вы назвали называется как-то подругому!

Не, ну можно очень глубоко копать, и докопаться до высшей математики! 😄

Следуя вашей теории, как тогда должны называться дни недели? Понедельник-«первый нечетный день», среда-«второй нечетный день» 😄

А если разделить четверг на два, то получится вторник?! 😄

Источник