Что идет после триллиона таблица
Что идет после триллиона таблица
Названия больших чисел.
Построение названия большого числа начинается с добавления суффикса «-иллион» к латинскому числительному. Название числа в 1 000 раз большего предыдущего формируется из того же латинского числительного, но в этом случае берется суффикс «-иллиард». Т.е. после триллиона в длинной системе наименования чисел следует триллиард, а вот после него квадриллион, далее квадриллиард и так далее.
Количество нулей в числе, которое записано в длинной системе и которое оканчивается суффиксом «-иллион», вычисляется при помощи формулы 6·x (где x — латинское числительное) и по формуле 6·x+3 для чисел, которые оканчиваются на «-иллиард».
Именные названия степеней тысячи.
Название числа
Значение числа
мириада или десять тысяч
10 18 [экса] тера
10 24 [иотта] пета
Произношение больших чисел большего порядка зачастую отличается.
Названия еще больших чисел получаем прямым или обратным порядком латинских числительных (правильные достоверно не известны):
Второй вариант больше соответствует построению чисел в латинском языке и не в таком случае не возникают двусмысленности (например, число трецентиллион по первому написанию является и 10 903 и 10 312 ), поэтому мы считаем второй вариант более правильным.
Следующие числа:
Что идет после миллиарда?
Один, сто, тысяча, миллион, миллиард.
А что дальше? Продолжите цепочку.
После миллиарда ( 9 нулей) идет биллион (12 нулей).
Прежде всего следует определить по какой системе исчисления вы хотите знать, что идет после миллиарда. Есть Европейская система и Американская. В России все гораздо более запутано и в обычном обиходе миллиард считают по Европейской системе, а следом за ней триллион уже по Американской системе. Поэтому по Американской системе за пресловутым миллиардом идет триллион, а по Европейской системе идет биллион.
Это число настолько велико, что практически. не имеет никакого смысла. Это число больше, чем число атомов во Вселенной.
Один из персонажей Достоевского (выдуманный Иваном Карамазовым) ради того, чтобы попасть в рай должен был пройти квадрильон километров. Сперва он отказывался делать это, но, так как перед ним была целая вечность, а делать все равно было нечего, все же прошел. А, пройдя, почувствовал себя так:
Названия больших чисел
Существует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Числа состоят из цифр. Число 52 состоит из двух цифр: 5 и 2. Числа с 1 впереди и последующими нулями имеют названия.
Так как большие числа с большим числом нулей записывать неудобно, используют сокращения в виде степеней: запись 10 11 означает число с 11-ю нулями, запись 10 52 означает число с 52-мя нулями и т.д. Приведем названия чисел с десятками и сотнями нулей.
Таблица больших чисел с указанием количества нулей и названиями на русском и английском
Названия «круглых» чисел, которые можно встретить в школьной программе:
Еще некоторые примеры интересных названий:
Самого большого числа в мире не существует, так как любое большое число всегда можно увеличить, умножить, возвести в степень, и получится другое большее число. Бесконечность не является числом.
Из известных самых больших чисел, имеющих название (математическое доказательство) можно выделить: число TREE(3), число SCG(13), число Лоудера, число Мозера, число Скьюза, число Райо, число Грэма, инфитеиплеон.
Таблица больших чисел с указанием количества нулей и названиями на русском и английском.
| Число нулей | Краткая запись | Название | Название на английском |
|---|---|---|---|
| 3 | 10 3 | тысяча | thousand |
| 6 | 10 6 | миллион | million |
| 9 | 10 9 | миллиард (биллион) | billion |
| 12 | 10 12 | триллион | trillion |
| 15 | 10 15 | квадриллион | quadrillion |
| 18 | 10 18 | квинтиллион | quintillion |
| 21 | 10 21 | секстиллион | sextillion |
| 24 | 10 24 | септиллион | septillion |
| 27 | 10 27 | октиллион | octillion |
| 30 | 10 30 | нониллион | nonillion |
| 33 | 10 33 | дециллион | decillion |
| 36 | 10 36 | ундециллион | undecillion |
| 39 | 10 39 | дуодециллион | duodecillion |
| 42 | 10 42 | тредециллион | tredecillion |
| 45 | 10 45 | кватуордециллион | quattuordecillion |
| 48 | 10 48 | квиндециллион | quindecillion |
| 51 | 10 51 | сексдециллион | sexdecillion |
| 54 | 10 54 | септендециллион | septendecillion |
| 57 | 10 57 | октодециллион | octodecillion |
| 60 | 10 60 | новемдециллион | novemdecillion |
| 63 | 10 63 | вигинтиллион | vigintillion |
| 66 | 10 66 | унвигинтиллион | unvigintillion |
| 69 | 10 69 | дуовигинтиллион | duovigintillion |
| 72 | 10 72 | тревигинтиллион | trevigintillion |
| 75 | 10 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | 10 78 | квинвигинтиллион | quinvigintillion |
| 81 | 10 81 | сексвигинтиллион | sexvigintillion |
| 84 | 10 84 | септенвигинтиллион | septenvigintillion |
| 87 | 10 87 | октовигинтиллион | octovigintillion |
| 90 | 10 90 | новемвигинтиллион | novemvigintillion |
| 93 | 10 93 | тригинтиллион | trigintillion |
| 96 | 10 96 | унтригинтиллион | untrigintillion |
| 99 | 10 99 | дуотригинтиллион | duotrigintillion |
| 102 | 10 102 | третригинтиллион | trestrigintillion |
| 105 | 10 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | 10 108 | квинтригинтиллион | quintrigintillion |
| 111 | 10 111 | секстригинтиллион | sextrigintillion |
| 114 | 10 114 | септентригинтиллион | septentrigintillion |
| 117 | 10 117 | октотригинтиллион | octotrigintillion |
| 120 | 10 120 | новемтригинтиллион | novemtrigintillion |
| 123 | 10 123 | квадрагинтиллион | quadragintillion |
| 126 | 10 126 | унквадрагинтиллион | unquadragintillion |
| 129 | 10 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | 10 132 | треквадрагинтиллион | trequadragintillion |
| 135 | 10 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | 10 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | 10 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | 10 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | 10 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | 10 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | 10 153 | квинквагинтиллион | quinquagintillion |
| 156 | 10 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | 10 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | 10 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | 10 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | 10 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | 10 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | 10 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | 10 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | 10 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | 10 183 | сексагинтиллион | sexagintillion |
| 186 | 10 186 | унсексагинтиллион | unsexagintillion |
| 189 | 10 189 | дуосексагинтиллион | duosexagintillion |
| 192 | 10 192 | тресексагинтиллион | tresexagintillion |
| 195 | 10 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | 10 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | 10 201 | секссексагинтиллион | sexsexagintillion |
| 204 | 10 204 | септенсексагинтиллион | septensexagintillion |
| 207 | 10 207 | октосексагинтиллион | octosexagintillion |
| 210 | 10 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | 10 213 | септагинтиллион | septuagintillion |
| 216 | 10 216 | унсептагинтиллион | unseptuagintillion |
| 219 | 10 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | 10 222 | тресептагинтиллион | treseptuagintillion |
| 225 | 10 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | 10 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | 10 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | 10 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | 10 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | 10 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | 10 243 | октогинтиллион | octogintillion |
| 246 | 10 246 | уноктогинтиллион | unoctogintillion |
| 249 | 10 249 | дуооктогинтиллион | duooctogintillion |
| 252 | 10 252 | треоктогинтиллион | treoctogintillion |
| 255 | 10 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | 10 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | 10 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | 10 264 | септоктогинтиллион | septoctogintillion |
| 267 | 10 267 | октооктогинтиллион | octooctogintillion |
| 270 | 10 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | 10 273 | нонагинтиллион | nonagintillion |
| 276 | 10 276 | уннонагинтиллион | unnonagintillion |
| 279 | 10 279 | дуононагинтиллион | duononagintillion |
| 282 | 10 282 | тренонагинтиллион | trenonagintillion |
| 285 | 10 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | 10 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | 10 291 | секснонагинтиллион | sexnonagintillion |
| 294 | 10 294 | септеннонагинтиллион | septennonagintillion |
| 297 | 10 297 | октононагинтиллион | octononagintillion |
| 300 | 10 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | 10 303 | центиллион | centillion |
Как называется самое большое простое число
Принципы построения названий и список больших чисел
Общий список чисел используемых в России:
| Число | Название | Латинское числительное | Увеличивающая приставка СИ | Уменьшаяющая приставка СИ | Практическое значение |
| 10 1 | десять | дека- | деци- | Число пальцев на 2 руках | |
| 10 2 | сто | гекто- | санти- | Примерно половина числа всех государств на Земле | |
| 10 3 | тысяча | кило- | милли- | Примерное число дней в 3 годах | |
| 10 6 | миллион | unus (I) | мега- | микро- | В 5 раз больше числа капель в 10-литровом ведере воды |
| 10 9 | миллиард (биллион) | duo (II) | гига- | нано- | Примерная численность населения Индии |
| 10 12 | триллион | tres (III) | тера- | пико- | 1/13 внутреннего валового продукта России в рублях за 2003 год |
| 10 15 | квадриллион | quattor (IV) | пета- | фемто- | 1/30 длины парсека в метрах |
| 10 18 | квинтиллион | quinque (V) | экса- | атто- | 1/18 числа зерен из легендарной награды изобретателю шахмат |
| 10 21 | секстиллион | sex (VI) | зетта- | цепто- | 1/6 массы планеты Земля в тоннах |
| 10 24 | септиллион | septem (VII) | йотта- | йокто- | Число молекул в 37,2 л воздуха |
| 10 27 | октиллион | octo (VIII) | неа- | сито- | Половина массы Юпитера в килограммах |
| 10 30 | нониллион | novem (IX) | деа- | тредо- | 1/5 числа всех микроорганизмов на планете |
| 10 33 | дециллион | decem (X) | уна- | рево- | Половина массы Солнца в граммах |
Произношение чисел, идущих далее, часто различается.
Дальнейшие названия могут быть получены либо прямым, либо обратным порядком латинских числительных (как правильно, не известно):
Английская система наименования чисел распространена в большей степени.
Формулы для подсчета количества нулей, таковы:
В России принята американская система наименования чисел.
Пользуясь латинскими наименованиями чисел и американской системой назовем числа:
Но и это, оказывается, не все. Есть еще числа внесистемные.
Таблица с названиями больших чисел по порядку
Бесконечность счетных чисел
Казалось бы, ответ на вопрос о том, каково самое большое число в математике — очень прост. Бесконечность, верно? Но это не совсем правильно. Ведь бесконечность — вовсе не число, а концепция. Идея.
Бесконечность (infinitum) — это понятие, которое в переводе с латинского означает «без границ». Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире. Можно лишь назвать наибольшее число, которому дали конкретное название.
Вот некоторые наиболее известные названия больших чисел:
| Число нулей | Название | Название на английском |
|---|---|---|
| 3 | тясяча | thousand |
| 6 | миллион | million |
| 9 | миллиард (биллион) | billion |
| 12 | триллион | trillion |
| 15 | квадриллион | quadrillion |
| 18 | квинтиллион | quintillion |
| 21 | секстиллион | sextillion |
| 24 | септиллион | septillion |
| 27 | октиллион | octillion |
| 30 | нониллион | nonillion |
| 33 | дециллион | decillion |
| 36 | ундециллион | undecillion |
| 39 | дуодециллион | duodecillion |
| 42 | тредециллион | tredecillion |
| 45 | кватуордециллион | quattuordecillion |
| 48 | квиндециллион | quindecillion |
| 51 | сексдециллион | sexdecillion |
| 54 | септендециллион | septendecillion |
| 57 | октодециллион | octodecillion |
| 60 | новемдециллион | novemdecillion |
| 63 | вигинтиллион | vigintillion |
| 66 | унвигинтиллион | unvigintillion |
| 69 | дуовигинтиллион | duovigintillion |
| 72 | тревигинтиллион | trevigintillion |
| 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | квинвигинтиллион | quinvigintillion |
| 81 | сексвигинтиллион | sexvigintillion |
| 84 | септенвигинтиллион | septenvigintillion |
| 87 | октовигинтиллион | octovigintillion |
| 90 | новемвигинтиллион | novemvigintillion |
| 93 | тригинтиллион | trigintillion |
| 96 | унтригинтиллион | untrigintillion |
| 99 | дуотригинтиллион | duotrigintillion |
| 102 | третригинтиллион | trestrigintillion |
| 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | квинтригинтиллион | quintrigintillion |
| 111 | секстригинтиллион | sextrigintillion |
| 114 | септентригинтиллион | septentrigintillion |
| 117 | октотригинтиллион | octotrigintillion |
| 120 | новемтригинтиллион | novemtrigintillion |
| 123 | квадрагинтиллион | quadragintillion |
| 126 | унквадрагинтиллион | unquadragintillion |
| 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | треквадрагинтиллион | trequadragintillion |
| 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | квинквагинтиллион | quinquagintillion |
| 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | сексагинтиллион | sexagintillion |
| 186 | унсексагинтиллион | unsexagintillion |
| 189 | дуосексагинтиллион | duosexagintillion |
| 192 | тресексагинтиллион | tresexagintillion |
| 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | секссексагинтиллион | sexsexagintillion |
| 204 | септенсексагинтиллион | septensexagintillion |
| 207 | октосексагинтиллион | octosexagintillion |
| 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | септагинтиллион | septuagintillion |
| 216 | унсептагинтиллион | unseptuagintillion |
| 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | тресептагинтиллион | treseptuagintillion |
| 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | октогинтиллион | octogintillion |
| 246 | уноктогинтиллион | unoctogintillion |
| 249 | дуооктогинтиллион | duooctogintillion |
| 252 | треоктогинтиллион | treoctogintillion |
| 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | септоктогинтиллион | septoctogintillion |
| 267 | октооктогинтиллион | octooctogintillion |
| 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | нонагинтиллион | nonagintillion |
| 276 | уннонагинтиллион | unnonagintillion |
| 279 | дуононагинтиллион | duononagintillion |
| 282 | тренонагинтиллион | trenonagintillion |
| 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | секснонагинтиллион | sexnonagintillion |
| 294 | септеннонагинтиллион | septennonagintillion |
| 297 | октононагинтиллион | octononagintillion |
| 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | центиллион | centillion |
Знакомимся ближе с большими цифрами
Сложного, впрочем, ничего нет, главное – понять систему образования больших чисел и принцип наименования. Как уже говорилось, каждое следующее число превосходит предыдущее в тысячу раз. Это значит, что для того чтобы правильно написать следующее в порядке возрастания число, нужно к предыдущему приписать еще три нуля. То есть, у миллиона 6 нулей, у миллиарда их 9, у триллиона – 12, у квадрильона – 15, а у квинтиллиона – уже 18.
С названиями тоже можно разобраться, если есть желание. Слово «миллион» произошло от латинского «mille», которое означает «больше тысячи». Следующие числа были образованы путем приставления латинских слов «би» (два), «три» (три), «квадро» (четыре) и т.д.
Теперь попробуем представить себе эти цифры наглядно. Большинство довольно хорошо представляют себе разницу между тысячью и миллионом. Каждый понимает, что миллион рублей – это хорошо, но миллиард – больше. Гораздо больше. Также у всех есть представление о том, что триллион – это что-то абсолютно необъятное. Но насколько триллион больше миллиарда? Насколько он громаден?
Для многих дальше миллиарда начинается понятие «уму непостижимо». Действительно, миллиард километров или триллион – разница не очень большая в том смысле, что такое расстояние все равно не пройти за всю жизнь. Миллиард рублей или триллион тоже не особо отличается, потому что таких денег все равно не заработать за всю жизнь. Но давайте немного посчитаем, подключив фантазию.
Видео
Какое самое большое число в мире

Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Время возвращения Пуанкаре
Это очень сложная вещь, но основная концепция относительно проста: при наличии достаточного времени, все возможно. Теорема Пуанкаре о возвращении предполагает количество времени, которого было бы достаточно для того, чтобы однажды вся Вселенная вернулась в свое нынешнее состояние, вызванное случайными квантовыми флуктуациями. Короче, «история повторится». Предполагается, что это займет 10^10^10^10^10^1,1 лет.
Гуголплекс
Вы наверняка слышали это слово, хотя бы в фильме «Назад в будущее», когда доктор Эммет Браун бормотал «она одна на миллион, одна на миллиард, одна на гуголплекс». Что такое гуголплекс? Помните длину гугола? Единица и сто нулей. А гуголплекс — это десять в степени гугол. Это больше, чем число всех частиц в известной нам части вселенной.
Вы можете отметить, что можно возводить десять в степень гуголплекс и будет еще больше, и так далее, и окажетесь совершенно правы.
Досчитаем до дециллиона
Давайте посчитаем еще. Например, спичечный коробок, увеличенный в тысячу раз, будет размером с шестнадцатиэтажный дом. Увеличение в миллион раз даст «коробок», который по площади больше Санкт-Петербурга. Увеличенный в миллиард раз, коробок не поместится на нашей планете. Наоборот, Земля поместится в такой «коробок» 25 раз!
Если считать дальше, то масштабы Земли окажутся уже недостаточными. Увеличенный в триллион раз коробок мог бы вместить в себя все планеты Солнечной системы вместе с их спутниками, а также астероиды и кометы. В коробке, который увеличен в квадриллион раз, Солнечная система могла бы поместиться полностью.
Увеличение коробка дает увеличение его объема. Вообразить себе такие объемы при дальнейшем увеличении будет уже почти невозможно. Для простоты восприятия попробуем увеличивать не сам предмет, а его количество, и расположим спичечные коробки в пространстве. Так будет легче ориентироваться. Квинтиллион коробков выложенных в один ряд, протянулись бы дальше звезды α Центавра на 9 триллионов километров.
Еще одно тысячекратное увеличение (секстиллион) позволит спичечным коробкам, выстроенным в линию, перегородить всю нашу галактику Млечный путь в поперечном направлении. Септиллион спичечных коробков растянулись бы на 50 квинтиллионов километров. Такое расстояние свет сможет пролететь за 5 миллионов 260 тысяч лет. А выложенные в два ряда коробки протянулись бы до галактики Андромеды.
Осталось только три числа: октиллион, нониллион и дециллион. Придется напрячь воображение. Октиллион коробков образует непрерывную линию в 50 секстиллионов километров. Это боле пяти миллиардов световых лет. Не каждый телескоп, установленный на одном краю такого объекта, мог бы разглядеть его противоположный край.
Считаем дальше? Нониллион спичечных коробков заполнил бы собой все пространство известной человечеству части Вселенной со средней плотностью 6 штук на кубический метр. По земным меркам вроде бы не очень-то и много – 36 спичечных коробков в кузове стандартной «Газели». Но нониллион спичечных коробков будет иметь массу в миллиарды раз больше чем масса всех материальных объектов известной Вселенной вместе взятых.
Дециллион. Величину, а скорее даже величественность этого исполина из мира чисел трудно себе вообразить. Только один пример – шесть дециллионов коробков уже не поместились бы во всей доступной человечеству для наблюдения части Вселенной.
Еще более поразительно величественность этого числа видна, если не умножать количество коробков, а увеличить сам предмет. Спичечный коробок, увеличенный в дециллион раз, вместил бы в себя всю известную человечеству часть Вселенной 20 триллионов раз. Невозможно такое себе даже просто представить.
Небольшие подсчеты показали, насколько огромны числа, известные человечеству уже несколько веков. В современной математике известны числа во много раз превосходящие дециллион, но применяются они только в сложных математических вычислениях. Сталкиваться с подобными числами приходится только профессиональным математикам.
Самым известным (и самым маленьким) из таких чисел является гугол, обозначаемый единицей со ста нулями. Гугол больше чем общее число элементарных частиц в видимой нам части Вселенной. Это делает гугол абстрактным числом, которое не имеет большого практического применения.
Сколько нулей в миллиард? Миллион? Триллион?
Видео: Сколько нулей в миллиард? Миллион? Триллион?
Содержание:
Хотите знать, сколько нулей в миллиард? Триллион? Нониллион?
Если вы недавно выиграли в лотерею и пытаетесь убедиться, что на вашем банковском счете правильное количество нулей, или вы просто пытаетесь найти простой способ понять, сколько нулей в большом количестве (более миллиона), это эта статья для вас.
Мы расскажем, как легко вычислить, сколько нулей в больших числах. и предоставьте удобную диаграмму для удобства.
Сколько нулей в триллионе? Как делаются большие числа
Цифра ноль (0) важна для счета больших чисел. Чем больше число, тем больше в нем нулей.
Начиная с 1000, большие числа содержат группы нулей. Каждый раз, когда вы переходите на следующий уровень числа, добавляется еще 0.
Число одна тысяча состоит из трех нулей (1000). В числе 10 000 четыре нуля (10 000). В числе ста тысяч пять нулей (100 000). Число один миллион состоит из шести нулей (1 000 000).
Каждый раз, когда у вас есть полная группа из трех нулей, например, один миллион (1000000), вы разделяете их запятыми.
Сколько нулей в миллионе? Сколько нулей в миллиард? Справочная таблица
Вот как выглядят числа от 100 000 до 1 000 000 000 000 000 000 000 000 000 000 (нониллион), записанные с правильными группами из трех нулей.
| Имя | Количество нулей | Написано |
| Одна тысяча | 3 | 1,000 |
| Десять тысяч | 4 | 10,000 |
| Сто тысяч | 5 | 100,000 |
| Один миллион | 6 | 1,000,000 |
| Миллиард | 9 | 1,000,000,000 |
| Триллион | 12 | 1,000,000,000,000 |
| Квадриллион | 15 | 1,000,000,000,000,000 |
| Квинтиллион | 18 | 1,000,000,000,000,000,000 |
| Секстиллион | 21 | 1,000,000,000,000,000,000,000 |
| Септиллион | 24 | 1,000,000,000,000,000,000,000,000 |
| Октиллион | 27 | 1,000,000,000,000,000,000,000,000,000 |
| Нониллион | 30 | 1,000,000,000,000,000,000,000,000,000,000 |
Как вычислить, сколько нулей в миллионе
Пытаетесь понять, сколько нулей должно быть в большом количестве?
Каждое большое число всегда добавляет ноль к непосредственно предшествующему числу, начиная с 1000.
1000 имеет три нуля. Это означает, что следующее большое число, десять тысяч (10 000), имеет четыре нуля.
То же самое и с миллионами. Один миллион имеет шесть нулей (1 000 000).У десяти миллионов семь нулей (10 000 000). У ста миллионов восемь нулей (100000000).
Резюме: сколько нулей в миллиард?
Обнулите самую важную цифру для создания больших чисел. Большие числа выше 100 000 имеют группы из трех нулей, разделенных запятыми.
У миллиона шесть нулей, у миллиарда девять, а у триллиона 12.
Что дальше?
Пишете исследовательскую работу для школы, но не знаете, о чем писать? В нашем справочнике по темам исследовательских работ более 100 тем в десяти категориях, так что вы можете быть уверены, что найдете для себя идеальную тему.
Узнаешь о натуральном бревне? Ознакомьтесь с нашим руководством по 11 правилам естественного журнала, которые вы должны знать, чтобы преуспеть в этом предмете.
Что такое динамическое равновесие и какое отношение оно имеет к ржавым автомобилям? Узнайте, прочитав наше полное руководство по динамическому равновесию.
Что будет после триллиона? Имена больших чисел
Видео: Что будет после триллиона? Имена больших чисел
Содержание:
Не знаете, какое число следует за триллионом? Интересуют названия других очень больших чисел? Что такое гугол? Читайте дальше, чтобы узнать, что следует за триллионом, название каждого важного числа, превышающего триллион, и некоторые способы помочь вам осмыслить чрезвычайно большие значения.
Что будет после триллиона?
Конечно, существует множество чисел от триллиона до квадриллиона, но только после квадриллиона это числовое значение получает новое имя. Числа между ними всегда будут включать слово «триллион»: два триллиона, сто триллионов и т. Д.
Как видно из диаграммы в следующем разделе, новое имя появляется каждый раз, когда степень большого числа увеличивается на 3.
Имена больших чисел
Числа написаны в научных обозначениях, чтобы их было легче читать и понимать.
| Имя | Число |
| Миллион | 1 х 10 6 |
| Миллиард | 1 х 10 9 |
| Триллион | 1 х 10 12 |
| Квадриллион | 1 х 10 15 |
| Квинтиллион | 1 х 10 18 |
| Секстиллион | 1 х 10 21 |
| Септиллион | 1 х 10 24 |
| Октиллион | 1 х 10 27 |
| Нониллион | 1 х 10 30 |
| Дециллион | 1 х 10 33 |
| Undecillion | 1 х 10 36 |
| Дуодециллион | 1 х 10 39 |
| Tredecillion | 1 х 10 42 |
| Quattuordecillion | 1 х 10 45 |
| Квиндециллион | 1 х 10 48 |
| Сексдециллион | 1 х 10 51 |
| Септендециллион | 1 х 10 54 |
| Октодециллион | 1 х 10 57 |
| Novemdecillion | 1 х 10 60 |
| Вигинтиллион | 1 х 10 63 |
| Унвигинтиллион | 1 х 10 66 |
| Дуовигинтиллион | 1 х 10 69 |
| Тревигинтиллион | 1 х 10 72 |
| Quattuorvigintillion | 1 х 10 75 |
| Квинвигинтиллион | 1 х 10 78 |
| Сексвигинтиллион | 1 х 10 81 |
| Септенвигинтиллион | 1 х 10 84 |
| Октовигинтиллион | 1 х 10 87 |
| Nonvigintillion | 1 х 10 90 |
| Тригинтиллион | 1 х 10 93 |
| Унтригинтиллион | 1 х 10 96 |
| Дуотригинтиллион | 1 х 10 99 |
| Десять-дуотригинтиллион (или гугол) | 1 х 10 100 |
| Номер вертела | 1 х 10 130 |
| Сентиллион | 1 х 10 303 |
| Гуголплекс | 1 х 10 10 100 |
| Число Скьюза |
Этот шаблон продолжается, пока вы не дойдете до Ten-duotrigintillion, более известного как Googol (да, именно отсюда поисковая система Google и получила свое название). Нет названий для чисел между Googol, Skewer’s Number, Centillion или Googolplex.
Возможно, вы заметили, что «zillion» здесь нет. Зиллион на самом деле не является действительным числом; это просто термин, используемый для обозначения неопределенного, но чрезвычайно большого количества.
Понимание больших чисел
Гугол, или 1 со ста нулями после него, в записанном виде выглядит так: 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000. Написание такого большого числа иногда может дать лучшее представление о том, насколько оно на самом деле велико, по сравнению с использованием научных обозначений.
Но есть числа даже больше, чем гуголплекс. Число Скьюза, разработанное математиком Стэнли Скьюсом, составляет от 10 до 10-го, от 10-го до 34-го. Скьюза особенно интересовали простые числа, и когда его число было введено в 1933 году, его коллега описал его как «наибольшее число, которое когда-либо служило какой-либо определенной цели в математике».
Однако с тех пор число Скьюза утратило это различие. Число Грэма, которое в настоящее время считается самым большим числом в мире. Число Грэма, которое нельзя записать в обычных обозначениях, было разработано математиком Р.Л.Грэмом. Оно настолько велико, что даже если бы всю материю во Вселенной превратить в ручки и чернила, этого все равно было бы недостаточно, чтобы полностью записать это число.
Резюме: Что будет после триллиона?
Что дальше?
Пишете исследовательскую работу для школы, но не знаете, о чем писать? В нашем справочнике по темам исследовательских работ более 100 тем в десяти категориях, так что вы можете быть уверены, что найдете для себя идеальную тему.
Что такое динамическое равновесие и какое отношение оно имеет к ржавым автомобилям? Узнайте, прочитав наши полное руководство по динамическому равновесию.
Системы наименования чисел
В европейской традиции исторически сложились два варианта построения системы наименования чисел.
Содержание
Краткая история
Термин «миллион» итальянского происхождения и встречается уже в первой печатной арифметике (анонимной), вышедшей в итальянском городе Тревизо в 1478 году, и ещё ранее в нематематической книге путешественника Марко Поло (умер в 1324 году), а в форме «миллио» — уже в рукописи 1250 года.
Для чтения многозначных чисел анонимная рукопись 1200 года впервые рекомендует разбить цифры на группы по 3 или отмечать группы точками вверху или дугами; это же затем рекомендует Леонардо Пизанский (1228). К этой системе приходят и последующие авторы.
Использование систем наименования чисел в мире:
| короткая шкала длинная шкала | обе шкалы другие системы |
В России первоначально была введена система наименования чисел с длинной шкалой, и, по-видимому, в печатном виде впервые в 1703 году в «Арифметике» Л. Ф. Магницкого. Однако в конце XVIII века, в царствование императора Павла I, вслед за Францией произошёл переход на короткую шкалу. Так, в опубликованном в 1798 году переводе части первой — «Арифметика» — «Курса математики» Этьенна Безу введена система наименования чисел с короткой шкалой, при том, что ещё в опубликованной в 1791 году книге «Арифметика или числовник» Н. Г. Курганова (1725 или 1726—1796) используется длинная шкала.
В дальнейшем выбор системы наименования чисел в России — СССР — РФ не менялся. Однако Франция в 1948 году вернулась к системе с длинной шкалой, поэтому сейчас используемая в России система отличается от французской, хотя и заимствовалась во Франции.
Короткая шкала
Длинная шкала
Названия чисел в этой системе строятся так: к латинскому числительному [1] добавляют суффикс «-иллион», название следующего числа (в 1000 раз большего) образуется из того же самого латинского числительного, но с суффиксом «-иллиард». То есть после триллиона в этой системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т. д. Количество нулей в числе, записанном по этой системе и оканчивающегося суффиксом «-иллион», определяется по формуле 6·x (где x — латинское числительное) и по формуле 6·x+3 для чисел, оканчивающихся на «-иллиард».
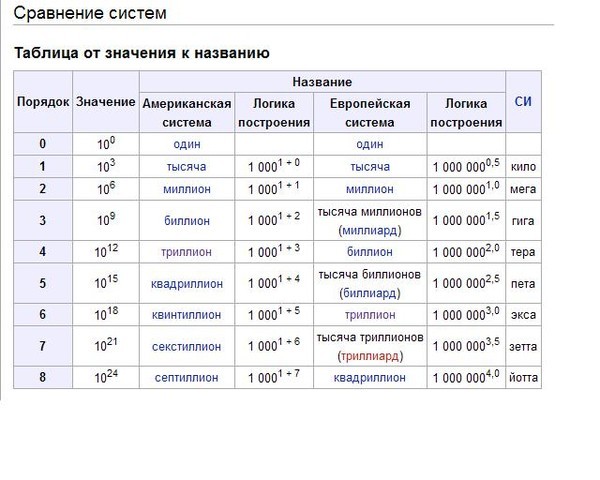
Сравнение систем
Таблица от значения к названию
| Порядок | Значение | Короткая шкала | Длинная шкала | СИ | ||
|---|---|---|---|---|---|---|
| Название | Логика построения | Название | Логика построения | |||
| 0 | 10 0 | один | один | |||
| 1 | 10³ | тысяча | 1000 1 + 0 | тысяча | 1 000 000 0,5 | кило- |
| 2 | 10 6 | миллион | 1000 1 + 1 | миллион | 1 000 000 1,0 | мега- |
| 3 | 10 9 | биллион (миллиард) [2] | 1000 1 + 2 | тысяча миллионов (миллиард) | 1 000 000 1,5 | гига- |
| 4 | 10 12 | триллион | 1000 1 + 3 | биллион | 1 000 000 2,0 | тера- |
| 5 | 10 15 | квадриллион | 1000 1 + 4 | тысяча биллионов (биллиард) | 1 000 000 2,5 | пета- |
| 6 | 10 18 | квинтиллион | 1000 1 + 5 | триллион | 1 000 000 3,0 | экса- |
| 7 | 10 21 | секстиллион | 1000 1 + 6 | тысяча триллионов (триллиард) | 1 000 000 3,5 | зетта- |
| 8 | 10 24 | септиллион | 1000 1 + 7 | квадриллион | 1 000 000 4,0 | йотта- |
| 9 | 10 27 | октиллион | 1000 1 + 8 | тысяча квадриллионов (квадриллиард) | 1 000 000 4,5 | |
| 10 | 10 30 | нониллион | 1000 1 + 9 | квинтиллион | 1 000 000 5,0 | |
| 11 | 10 33 | дециллион | 1000 1 + 10 | тысяча квинтиллионов (квинтиллиард) | 1 000 000 5,5 | |
Таблица от названия к значению
Примечания
Литература
Полезное
Смотреть что такое «Системы наименования чисел» в других словарях:
Число — У этого термина существуют и другие значения, см. Число (значения). Число основное понятие математики[1], используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей… … Википедия
Число (матем.) — см. также: Число (лингвистика) Число абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое … Википедия
Зиллион — (англ. zillion) общее название для очень больших чисел. Этот термин не имеет строгого математического определения. В 1996 году Конвей (англ. J. H. Conway) и Гай (англ. R. K. Guy) в своей книге англ. The Book of Numbers… … Википедия
Лимард — Миллиард (млрд) в европейской системе наименования чисел тысяча миллионов, число, изображаемое единицей с девятью нулями (1 000 000 000), 109. Приставки СИ: для миллиарда гига (109), для одной миллиардной нано (10−9). В американской системе… … Википедия
Млрд — Миллиард (млрд) в европейской системе наименования чисел тысяча миллионов, число, изображаемое единицей с девятью нулями (1 000 000 000), 109. Приставки СИ: для миллиарда гига (109), для одной миллиардной нано (10−9). В американской системе… … Википедия
Именные названия степеней тысячи — Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. Дополнительные сведения могут быть на странице обсуждения. (13 мая 2011) … Википедия
Дециллион — Именные названия степеней тысячи в порядке возрастания Название Значение Американская система Европейская система тысяча 10³ 10³ миллион 106 106 миллиард 109 109 биллион 109 1012 триллион 1012 … Википедия
Додециллион — Именные названия степеней тысячи в порядке возрастания Название Значение Американская система Европейская система тысяча 10³ 10³ миллион 106 106 миллиард 109 109 биллион 109 1012 триллион 1012 … Википедия
Квинтиллион — Именные названия степеней тысячи в порядке возрастания Название Значение Американская система Европейская система тысяча 10³ 10³ миллион 106 106 миллиард 109 109 биллион 109 1012 триллион 1012 … Википедия
Не вошедшее в сборник сочинений
Аркадий Сладков




Какое самое большое число вы знаете?
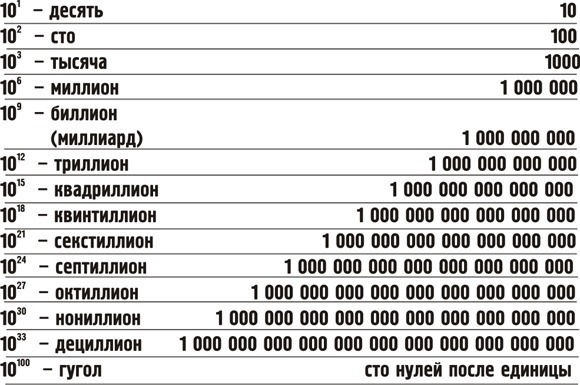
Но вернемся к нашей родной шкале. Хотите знать, что идет после триллиона? Пожалуста:
10 3 тысяча
10 6 миллион
10 9 миллиард
10 12 триллион
10 15 квадриллион
10 18 квинтиллион
10 21 секстиллион
10 24 септиллион
10 27 октиллион
10 30 нониллион
10 33 дециллион
10 36 ундециллион
10 39 додециллион
10 42 тредециллион
10 45 кваттуордециллион
10 48 квиндециллион
10 51 cедециллион
10 54 септдециллион
10 57 дуодевигинтиллион
10 60 ундевигинтиллион
10 63 вигинтиллион
10 66 анвигинтиллион
10 69 дуовигинтиллион
10 72 тревигинтиллион
10 75 кватторвигинтиллион
10 78 квинвигинтиллион
10 81 сексвигинтиллион
10 84 септемвигинтиллион
10 87 октовигинтиллион
10 90 новемвигинтиллион
10 93 тригинтиллион
10 96 антригинтиллион
На этом числе наша короткая шкала не выдерживает, и в дальшейшем мантиса увеличивается прогрессивно.
10 100 гугол
10 123 квадрагинтиллион
10 153 квинквагинтиллион
10 183 сексагинтиллион
10 213 септуагинтиллион
10 243 октогинтиллион
10 273 нонагинтиллион
10 303 центиллион
10 306 центуниллион
10 309 центдуоллион
10 312 центтриллион
10 315 центквадриллион
10 402 центтретригинтиллион
10 603 дуцентиллион
10 903 трецентиллион
10 1203 квадрингентиллион
10 1503 квингентиллион
10 1803 сесцентиллион
10 2103 септингентиллион
10 2403 окстингентиллион
10 2703 нонгентиллион
10 3003 миллиллион
10 6003 дуомилиаллион
10 9003 тремиллиаллион
10 3000003 милиамилиаиллион
10 6000003 дуомилиамилиаиллион
10 10 100 гуголплекс
10 3×n+3 зиллион
Гугол (от англ. googol) — число, в десятичной системе счисления изображаемое единицей со 100 нулями:
10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
1938 году американский математик Эдвард Каснер (Edward Kasner, 1878—1955) гулял по парку с двумя своими племянниками и обсуждал с ними большие числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было собственного названия. Один из племянников, девятилетний Милтон Сиротта (Milton Sirotta), предложил назвать это число «гуголом» (googol). В 1940 году Эдвард Кэснер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение» («New Names in Mathematics»), где и рассказал любителям математики о числе гугол.
Термин «гугол» не имеет серьёзного теоретического и практического значения. Каснер предложил его для того, чтобы проиллюстрировать разницу между невообразимо большим числом и бесконечностью, и с этой целью термин иногда используется при обучении математике.
Гуголплекс (от англ. googolplex) — число, изображаемое единицей с гуголом нулей. Как и гугол, термин «гуголплекс» был придуман американским математиком Эдвардом Каснером (Edward Kasner) и его племянником Милтоном Сироттой (Milton Sirotta).
Число гугол больше числа всех частиц в известной нам части вселенной, которое составляет величину от 1079 до 1081. Таким образом, число гуголплекс, состоящее из (гугол+1) цифр, в классическом «десятичном» виде записать невозможно, даже если всю материю в известной части вселенной превратить в бумагу и чернила или в компьютерное дисковое пространство.
Зиллион (англ. zillion) — общее название для очень больших чисел.
Этот термин не имеет строгого математического определения. В 1996 году Конвей (англ. J. H. Conway) и Гай (англ. R. K. Guy) в своей книге англ. The Book of Numbers определили зиллион n-ой степени как 10 3×n+3 для системы наименования чисел с короткой шкалой.
Какое самое большое число в мире
На вопрос ребенка можно ответить миллион. А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности. А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название?
Вот на этот вопрос можно ответить. На самом деле сейчас есть две системы наименования чисел – английская и американская.
Американская – довольно простая. Названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион, что значит тысяча. Далее получаются числа: триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион.
Такую систему используют в США, Канаде, России и Франции. Английская система более распространенная в мире. Ее используют в Испании и Великобритании, а так же в ряде других стран. Здесь названия стоятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард».
То есть после триллиона идет триллиард, после квадриллион, квадриллиард и так далее. Получается, что по английской и американской системам одни и те же большие числа называются по-разному.
В русский язык из английской системы пришел только миллиард (10 9), который американцы называют биллионом. Иногда в России употребляют слово триллиард, то есть 1000 триллионов или квадриллион.
Нас окружают миллионы чисел
Кроме чисел, которые записаны при помощи английской или американской систем, известны так называемые внесистемные числа. То есть те, у которых есть свои собственные названия, в них нет латинских префиксов. Их несколько, вернемся к ним чуть позже. А пока рассмотрим запись латинскими числительными.
А что же дальше? На самом деле можно с помощью приставок и дальше рождать числа-монстры: андециллион, дуодециллион, тредециллион и так далее. Но нам нужны собственные названия чисел, а тут только составные названия.
Однако числа больше миллеиллиона есть и известны – это внесистемные числа. Самое маленькое такое число носит название мириада. Оно даже есть в словаре Даля. Означает оно сотню сотен, то есть 10 тысяч. Слово, правда, не используется по назначению. Оно употребляется как не определенное число, а бесчисленное множество чего-либо.
Далее идет гугол. Это десять в сотой степени. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский математик Эдвард Каснер сказал, что назвать большое число таким образом предложил его племянник. А популярным это название стало после того, как в честь него назвали поисковую систему «Google».
Далее встречается число асанкхейя. Это 10 140. Общепринято, что этому числу равно количество космических циклов, которые необходимы для обретения нирваны. Следом идет число гуголплекс. Его придумал тот же Каснер с племянником. Оно означает 10 10100. Или единица с гуголом нулей.
Еще больше гуглоплекса число Скьюза. Его предложил Скьюз в 1933 году во время доказательства гипотезы Риманна о простых числах. Оно означает eee79. То есть e в степени e в степени e в степени 79.
Позже Риел свел число Скьюза к ee27/4. Это приблизительно равно 8,185•10 370. Раз это число зависит от e, значит оно не целое. Следовательно, рассматривать его не будем.
Есть второе число Скьюза. Обозначается оно как Sk2. Оно вводится, если гипотеза Риманна не справедлива. Второе число Скьюза равно 1010101000. Чем больше в числе степеней, следователь тем сложнее понять, какое же из чисел больше.
Поэтому для сверхбольших чисел пользоваться степенями неудобно. Уже придуманы числа, у которых степени степеней не вылезают за страницу. Математики придумали несколько принципов для их записи.
Правда, у каждого ученого был свой принцип записи, некоторые не связаны друг с другом. Хьюго Стейнхауза предложил записывать очень большие числа внутри геометрических фигур. К примеру, — это nn. — это «n в n треугольниках». — это «n в n квадратах». Все тот же Стейнхауз придумал два новых больших числа. — мега, а число — мегистон.
Эта нотация была доработана математиком Лео Мозером. По ней можно записать числа, которые больше мегистона. Здесь не надо рисовать круги в кругах. А достаточно после квадратом рисовать не круги, а пятиугольники, затем шестиугольники.
Таким образом, Мозер записал стейнхаузовскую мегу 2[5], а мегистон 10[5]. Он же предложил называть многоугольник с количеством сторон равным меге – как мегагон. А число 2 в Мегагоне2[2[5]]. Это число получило название число Мозера. Но и это число не самое большое.
Самое больше число, которое применяется в математическом доказательстве, это Число Грэма. Его использовали впервые в 1977 году в доказательстве оценки в теории Рамсея.
Оно выражено в особой 64-уровневой системе, поскольку связано с бихроматическими гиперкубами. Вывел систему Кнут в 1976 году.
Самое большое число
Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион.
А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности.
А если же задаться вопросом: какое самое большое число существует, и какое у него собственное название? Вот на этот вопрос можно ответить. На самом деле сейчас есть две системы наименования чисел – английская и американская.
Американская – довольно простая. Названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион, что значит тысяча. Далее получаются числа: триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион. Такую систему используют в США, Канаде, России и Франции.
Английская система более распространенная в мире. Ее используют в Испании и Великобритании, а так же в ряде других стран. Здесь названия стоятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард». То есть после триллиона идет триллиард, после квадриллион, квадриллиард и так далее. Получается, что по английской и американской системам одни и те же большие числа называются по-разному.
В русский язык из английской системы пришел только миллиард (10 9), который американцы называют биллионом. Иногда в России употребляют слово триллиард, то есть 1000 триллионов или квадриллион.
Кроме чисел, которые записаны при помощи английской или американской систем, известны так называемые внесистемные числа. То есть те, у которых есть свои собственные названия, в них нет латинских префиксов. Их несколько, вернемся к ним чуть позже.
Поэтому, по этой системе числа с собственным, а не составным названием больше 10 3003 получить невозможно. Однако числа больше миллеиллиона есть и известны – это внесистемные числа.
Самое маленькое такое число носит название мириада. Оно даже есть в словаре Даля. Означает оно сотню сотен, то есть 10 тысяч. Слово, правда, не используется по назначению. Оно употребляется как не определенное число, а бесчисленное множество чего-либо.
Далее идет гугол. Это десять в сотой степени. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский математик Эдвард Каснер сказал, что назвать большое число таким образом предложил его племянник. А популярным это название стало после того, как в честь него назвали поисковую систему «Google». Далее встречается число асанкхейя. Это 10 140. Общепринято, что этому числу равно количество космических циклов, которые необходимы для обретения нирваны. Следом идет число гуголплекс. Его придумал тот же Каснер с племянником. Оно означает 10 10100. Или единица с гуголом нулей.
Еще больше гуглоплекса число Скьюза. Его предложил Скьюз в 1933 году во время доказательства гипотезы Риманна о простых числах. Оно означает eee79. То есть e в степени e в степени e в степени 79. Позже Риел свел число Скьюза к ee27/4. Это приблизительно равно 8,185•10 370. Раз это число зависит от e, значит оно не целое. Следовательно, рассматривать его не будем.
Есть второе число Скьюза. Обозначается оно как Sk2. Оно вводится, если гипотеза Риманна не справедлива. Второе число Скьюза равно 1010101000. Чем больше в числе степеней, следователь тем сложнее понять, какое же из чисел больше. Поэтому для сверхбольших чисел пользоваться степенями неудобно. Уже придуманы числа, у которых степени степеней не вылезают за страницу. Математики придумали несколько принципов для их записи. Правда, у каждого ученого был свой принцип записи, некоторые не связаны друг с другом. Хьюго Стейнхауза предложил записывать очень большие числа внутри геометрических фигур. К примеру, — это nn. — это «n в n треугольниках». — это «n в n квадратах». Все тот же Стейнхауз придумал два новых больших числа. — мега, а число — мегистон.
Эта нотация была доработана математиком Лео Мозером. По ней можно записать числа, которые больше мегистона. Здесь не надо рисовать круги в кругах. А достаточно после квадратов рисовать не круги, а пятиугольники, затем шестиугольники. Таким образом, Мозер записал стейнхаузовскую мегу 2[5], а мегистон 10[5]. Он же предложил называть многоугольник с количеством сторон равным меге – как мегагон. А число 2 в Мегагоне2[2[5]]. Это число получило название число Мозера.
Но и это число не самое большое. Самое большое число, которое применяется в математическом доказательстве, это Число Грэма. Его использовали впервые в 1977 году в доказательстве оценки в теории Рамсея.
В повседневной жизни большинство людей оперируют достаточно небольшими числами. Десятки, сотни, тысячи, очень редко – миллионы, почти никогда – миллиарды. Примерно такими числами ограничено обычное представление человека о количестве или величине. Про триллионы приходилось слышать почти всем, но употреблять их, в каких-либо подсчетах, мало кому доводилось.
Какие они, числа-гиганты?
Между тем, числа обозначающие степени тысячи известны людям давно. В России и многих других странах используется простая и логичная система обозначений:
• Тысяча;
• Миллион;
• Биллион;
• Триллион;
• Квадриллион;
• Квинтиллион;
• Секстиллион;
• Септиллион;
• Октиллион;
• Нониллион;
• Дециллион.
В этой системе каждое следующее число получается умножением предыдущего на тысячу. Биллион обычно называют миллиардом.
Многие взрослые могут безошибочно написать такие числа как миллион – 1 000 000 и миллиард – 1 000 000 000. С триллионом уже сложнее, но почти все справятся – 1 000 000 000 000. А дальше начинается неведомая многим территория.
Знакомимся ближе с большими цифрами
Сложного, впрочем, ничего нет, главное – понять систему образования больших чисел и принцип наименования. Как уже говорилось, каждое следующее число превосходит предыдущее в тысячу раз. Это значит, что для того чтобы правильно написать следующее в порядке возрастания число, нужно к предыдущему приписать еще три нуля. То есть, у миллиона 6 нулей, у миллиарда их 9, у триллиона – 12, у квадрильона – 15, а у квинтиллиона – уже 18.
С названиями тоже можно разобраться, если есть желание. Слово «миллион» произошло от латинского «mille», которое означает «больше тысячи». Следующие числа были образованы путем приставления латинских слов «би» (два), «три» (три), «квадро» (четыре) и т.д.
Теперь попробуем представить себе эти цифры наглядно. Большинство довольно хорошо представляют себе разницу между тысячью и миллионом. Каждый понимает, что миллион рублей – это хорошо, но миллиард – больше. Гораздо больше. Также у всех есть представление о том, что триллион – это что-то абсолютно необъятное. Но насколько триллион больше миллиарда? Насколько он громаден?
Для многих дальше миллиарда начинается понятие «уму непостижимо». Действительно, миллиард километров или триллион – разница не очень большая в том смысле, что такое расстояние все равно не пройти за всю жизнь. Миллиард рублей или триллион тоже не особо отличается, потому что таких денег все равно не заработать за всю жизнь. Но давайте немного посчитаем, подключив фантазию.
Жилой фонд России и четыре футбольных поля как примеры
На каждого человека на земле приходится площадь суши размером 100х200 метров. Это примерно четыре футбольных поля. Но если людей будет не 7 миллиардов, а семь триллионов, то каждому достанется только кусочек суши 4х5 метров. Четыре футбольных поля против площади палисадника перед подъездом – таково соотношение миллиарда к триллиону.
В абсолютных значениях картина также впечатляет.
Если взять триллион кирпичей, то можно построить более 30 миллионов одноэтажных домов площадью по 100 квадратных метров. То есть около 3 миллиардов квадратных метров частной застройки. Это сопоставимо с общим жилым фондом РФ.
Если строить десятиэтажные дома, то получится примерно 2,5 миллиона домов, то есть 100 миллионов двух- трехкомнатных квартир, около 7 миллиардов квадратных метров жилья. Это в 2,5 раза больше всего жилого фонда России.
Одним словом, во всей России не наберется триллион кирпичей.
Один квадриллион ученических тетрадей покроет всю территорию России двойным слоем. А один квинтиллион тех же тетрадей накроет всю сушу слоем толщиной в 40 сантиметров. Если же удастся раздобыть секстиллион тетрадей, то вся планета, включая океаны, окажется под слоем толщиной в 100 метров.
Досчитаем до дециллиона
Давайте посчитаем еще. Например, спичечный коробок, увеличенный в тысячу раз, будет размером с шестнадцатиэтажный дом. Увеличение в миллион раз даст «коробок», который по площади больше Санкт-Петербурга. Увеличенный в миллиард раз, коробок не поместится на нашей планете. Наоборот, Земля поместится в такой «коробок» 25 раз!
Если считать дальше, то масштабы Земли окажутся уже недостаточными. Увеличенный в триллион раз коробок мог бы вместить в себя все планеты Солнечной системы вместе с их спутниками, а также астероиды и кометы. В коробке, который увеличен в квадриллион раз, Солнечная система могла бы поместиться полностью.
Увеличение коробка дает увеличение его объема. Вообразить себе такие объемы при дальнейшем увеличении будет уже почти невозможно. Для простоты восприятия попробуем увеличивать не сам предмет, а его количество, и расположим спичечные коробки в пространстве. Так будет легче ориентироваться. Квинтиллион коробков выложенных в один ряд, протянулись бы дальше звезды α Центавра на 9 триллионов километров.
Еще одно тысячекратное увеличение (секстиллион) позволит спичечным коробкам, выстроенным в линию, перегородить всю нашу галактику Млечный путь в поперечном направлении. Септиллион спичечных коробков растянулись бы на 50 квинтиллионов километров. Такое расстояние свет сможет пролететь за 5 миллионов 260 тысяч лет. А выложенные в два ряда коробки протянулись бы до галактики Андромеды.
Осталось только три числа: октиллион, нониллион и дециллион. Придется напрячь воображение. Октиллион коробков образует непрерывную линию в 50 секстиллионов километров. Это боле пяти миллиардов световых лет. Не каждый телескоп, установленный на одном краю такого объекта, мог бы разглядеть его противоположный край.
Считаем дальше? Нониллион спичечных коробков заполнил бы собой все пространство известной человечеству части Вселенной со средней плотностью 6 штук на кубический метр. По земным меркам вроде бы не очень-то и много – 36 спичечных коробков в кузове стандартной «Газели». Но нониллион спичечных коробков будет иметь массу в миллиарды раз больше чем масса всех материальных объектов известной Вселенной вместе взятых.
Дециллион. Величину, а скорее даже величественность этого исполина из мира чисел трудно себе вообразить. Только один пример – шесть дециллионов коробков уже не поместились бы во всей доступной человечеству для наблюдения части Вселенной.
Еще более поразительно величественность этого числа видна, если не умножать количество коробков, а увеличить сам предмет. Спичечный коробок, увеличенный в дециллион раз, вместил бы в себя всю известную человечеству часть Вселенной 20 триллионов раз. Невозможно такое себе даже просто представить.
Небольшие подсчеты показали, насколько огромны числа, известные человечеству уже несколько веков. В современной математике известны числа во много раз превосходящие дециллион, но применяются они только в сложных математических вычислениях. Сталкиваться с подобными числами приходится только профессиональным математикам.
Самым известным (и самым маленьким) из таких чисел является гугол, обозначаемый единицей со ста нулями. Гугол больше чем общее число элементарных частиц в видимой нам части Вселенной. Это делает гугол абстрактным числом, которое не имеет большого практического применения.
Числа великаны
Один из первых, кто научился называть большие числа, был древнегреческий математик Архимед. Названия были, но обозначать он их не мог. Архимед один из гениальнейших математиков не додумался до нуля. Впервые нуль был придуман вавилонянами примерно 2 тысячи лет назад. Однако, открытие писать нули в конце числа, было сделано в Индии полторы тысячи лет назад. Нуль был присоединен к девяти цифрам, и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было.
В истории математики сложилось так, что числа-великаны имеют свои названия и записи в двух вариантах. Их называют «длинная шкала» и «короткая шкала».
Количество нулей в числе, записанном по этой системе, определяется по формуле3·x+3 (где x — латинское числительное).
Система названий чисел-великанов по короткой шкале используется всего лишь в нескольких странах: США, Великобритании, Канаде, России, Украине, Турции и Греции. В некоторых странах вместо слова «биллион» используется слово «миллиард»
Построение ряда чисел-великанов
1000 единиц – просто тысяча
1000 тысяч – 1 миллион
1000 миллионов – 1 биллион (или миллиард)
1000 биллионов – 1 триллион
1000 триллионов – 1 квадриллион
1000 квинтиллионов – 1секстиллион
1000 секстиллионов – 1 септиллион
1000 септиллионов – 1октиллион
1000 октиллионов – 1 нониллион
Гугол число содержащее единицу и сто нулей.
Гуголплекс — число, изображаемое единицей с гуголом нулей.
Числа гугол, гуголплекс были придуманы американским математиком Эдвардом Каснером (Edward Kasner) и его племянником Милтоном Сиротта (Milton Sirotta).
В 1938 году американский математик Эдвард Каснер (Edward Kasner, 1878—1955) гулял по парку с двумя своими племянниками и обсуждал с ними большие числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было собственного названия. Один из племянников, девятилетний Милтон Сиротта (Milton Sirotta), предложил назвать это число «гуголом» (googol). В 1940 году Эдвард Кэснер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение» («New Names in Mathematics»), где и рассказал любителям математики о числе гугол.
Термин «гугол» не имеет серьёзного теоретического и практического значения. Каснер предложил его для того, чтобы проиллюстрировать разницу между невообразимо большим числом и бесконечностью, и с этой целью термин иногда используется при обучении математике.
Число гугол больше числа всех частиц в известной нам части вселенной. Таким образом, число гуголплекс в классическом десятичном виде записать невозможно, даже если всю материю в известной части вселенной превратить в бумагу и чернила или в компьютерное дисковое пространство.
Но эти названия почти не используются. Астрономы и физики, имеющие дело с большими числами, предпочитают записывать числа с помощью степени числа десять.
В заключение приведу таблицу существующих чисел-великанов для нашей шкалы:
Миллион, миллиард, триллион, триллиард, а что дальше, до бесконечности
Обозначения крупных чисел – что идёт после триллиарда и дальше?
Известно, что чисел бесконечное множество и лишь у немногих есть собственные названия, ведь большинство чисел получили имена, состоящие из малых чисел. Наибольшие числа необходимо каким-то образом обозначать.
«Короткая» и «длинная» шкала
Используемые сегодня имена числа начали получать в пятнадцатом столетии, тогда итальянцы впервые использовали слово миллион, имеющее значение «большой тысячи», бимиллион (миллиона в квадрате) и тримиллион (миллиона в кубе).
Данную систему описал в своей монографии француз Николя Шюке, он рекомендовал употреблять числительные латинского языка, добавив к ним флексию «-иллион», таким образом бимиллион стал биллионом, а тримиллион – триллионом и так далее.
Но согласно предложенной системе числа между миллионом и биллионом он называл «тысячей миллионов». С подобной градацией было не комфортно работать и в 1549 году француз Жак Пелетье советовал числа, находящиеся в указанном промежутке, называть опять же используя латинские приставки, при этом введя другое окончание — «-иллиард».
Так 109 получило название миллиард, 1015 — биллиард, 1021 — триллиард.
Постепенно эту систему стали использовать в Европе. Но некоторые ученые путали наименования чисел, это создало парадокс, когда слова биллион и миллиард стали синонимичными. Впоследствии в США был создан свой порядок именования больших чисел. Согласно ему построение названий осуществляется аналогично, но только числа разнятся.
Прежняя система продолжала применяться в Великобритании, потому и была названа британской, хотя изначально создавалась французами. Но уже с семидесятых годов прошлого века Великобритания также начала применять систему американскую.
Поэтому, чтобы избежать путаницы, созданную американскими учеными концепцию, принято именовать короткой шкалой, в то время как изначальную французско-британскую – длинной шкалой.
Короткая шкала нашла активное применение в США, Канаде, Великобритании, Греции, Румынии, Бразилии. В России она тоже в ходу, только с одним отличием – число 109 традиционно именуют миллиардом. А вот французско-британскому варианту отдали предпочтение во множестве других стран.
С целью обозначить числа, большие нежели дециллион, ученые решили объединять несколько латинских приставок, так были названы ундециллион, кваттордециллион и прочие. Если воспользоваться системой Шюке, то согласно ей гигантские числа обретут имена«вигинтиллион», «центиллион» и «миллеиллион» (103003), соответственно согласно длинной шкале такое число получит имя «миллеиллиард» (106003).
Числа с уникальными именами
Многие числа получили наименование без привязки к различным системам и частям слов. Этих чисел немало, например, это число «пи», дюжина, а также числа более миллиона.
В Древней Руси издавна использовалась своя числовая система. Сотни тысяч обозначали словом легион, миллион – называли леодром, десятки миллионов были воронами, сотни миллионов именовались колодой. Это был «малый счет», а вот «великий счет» применял те же слова, вот только смысл в них вкладывали иной, например леодр мог означать легион легионов (1024), а колода — уже десять воронов (1096).
Бывало, что названия числам придумывали дети, так, математику Эдварду Кэснеру подал идею юный Милтон Сиротта, предложивший дать имя числу с сотней нулей (10100) просто «гугол» (googol). Это число получило наибольшую огласку в девяностых годах двадцатого века, когда в его честь получил название поисковик Google. Также мальчик предложил наименование «гуглоплекс», число имеющее гугол нолей.
А вот Клод Шеннон в средине двадцатого века, оценивая ходы в шахматной игры, подсчитал, что таковых существует 10118, теперь это «число Шеннона».
В старинном труде буддистов «Джайна-сутры», написанном почти двадцать два века назад, отмечается число «асанкхейя» (10140), именно столько космических циклов, по мнению буддистов, необходимо, чтобы обрести нирвану.
Стэнли Скьюзом были описаны большие величины, так «первое число Скьюза», равное 10108,85.1033, а «второе число Скьюза» еще внушительней и равняется 1010101000.
Нотации
Разумеется, в зависимости от количества степеней содержащихся в числе, поялвяется проблематичность в фиксировании его на письме, да и чтении, баз ошибок. некоторые числа невозможно поместить на нескольких страницах, поэтому математики придумали нотации для фиксации крупных чисел.
Стоит учесть, все они отличаются, в основе каждой свой принцип фиксации. Среди таковых стоит упомянуть нотации Штейнггауза, Кнута.
Однако наиболее крупное число — «число Грэма», применялось Рональдом Грэмом в 1977 году при проведении математических расчетов, и это число G64.
Сколько нулей в миллиарде, триллионе, биллионе?
Краткий список чисел и их количественное обозначение
И так далее, вплоть до 100 нулей.
Числа с очень большим количеством нулей
Из больших чисел наиболее популярными являются миллион и миллиард (1000000000). Как называется число, имеющее 100 нулей? Это цифра googol, называнная так еще Милтоном Сироттой. Это дико огромное количество. Считаете ли вы, что это число большое? Тогда как насчет googolplex, единицы, за которой следует googol нулей? Эта цифра настолько велика, что и смысл для нее придумать сложно. По сути, необходимости в таких гигантах нет, разве что подсчитывать число атомов в бесконечной Вселенной.
Видео
Знакомимся ближе с большими цифрами
Сложного, впрочем, ничего нет, главное – понять систему образования больших чисел и принцип наименования. Как уже говорилось, каждое следующее число превосходит предыдущее в тысячу раз. Это значит, что для того чтобы правильно написать следующее в порядке возрастания число, нужно к предыдущему приписать еще три нуля. То есть, у миллиона 6 нулей, у миллиарда их 9, у триллиона – 12, у квадрильона – 15, а у квинтиллиона – уже 18.
С названиями тоже можно разобраться, если есть желание. Слово «миллион» произошло от латинского «mille», которое означает «больше тысячи». Следующие числа были образованы путем приставления латинских слов «би» (два), «три» (три), «квадро» (четыре) и т.д.
Теперь попробуем представить себе эти цифры наглядно. Большинство довольно хорошо представляют себе разницу между тысячью и миллионом. Каждый понимает, что миллион рублей – это хорошо, но миллиард – больше. Гораздо больше. Также у всех есть представление о том, что триллион – это что-то абсолютно необъятное. Но насколько триллион больше миллиарда? Насколько он громаден?
Для многих дальше миллиарда начинается понятие «уму непостижимо». Действительно, миллиард километров или триллион – разница не очень большая в том смысле, что такое расстояние все равно не пройти за всю жизнь. Миллиард рублей или триллион тоже не особо отличается, потому что таких денег все равно не заработать за всю жизнь. Но давайте немного посчитаем, подключив фантазию.
Какая цифра самая большая?
В начале двадцатого столетия математик из США Каснер прогуливался, по парку с племянниками. Разговор зашел о больших цифрах. В процессе беседы возникла дискуссия он названии числа со ста нулями. Выяснилось, что на тот момент его не существовало. Один из мальчиков придумал свое обозначение для этой цифры — гугол.
Цифра не имеет серьезного практического значения, но прочно вошло в обиход. Гугол используют для демонстрации разницы между невероятно большим числом и понятием бесконечность во время обучения.
Вскоре тот же математик предложил имя для цифры с гуголом нулей. Термин получил название гуголплекс. Эта цифра значительно превышает количество элементарных частиц в космосе.
Посмотрите видео о самых больших цифрах:
Самые большие числа и какое число идет после гугла
Знаете, какое число идет после гугла? Слово «гугол» получило широкое распространение благодаря всем известной компании и одноименной поисковой системе. Однако в названии поисковика это слово используется в немного измененной форме.
Какие интересные числа есть до гугла
Далее можно приводить еще много чисел, но их все сложнее и сложнее представить, потому что сложно найти пример, который бы их описывал. Но все же такие числа люди еще «слышат» раз через раз, например:
квадриллион — 10 в 15-й степени;
квинтиллион — 10 в 18-й степени;
секстиллион — 10 в 21-й степени;
септиллион — 10 в 24-й степени;
октиллион — 10 в 27-й степени;
нониллион — 10 в 30-й степени;
Какое число идет после гугла
Гуголплекс. Это число обозначает 10, возведенн ое в степень гугол, то есть 10, возведенное в число степен и со 100 знаками. Это число является попыткой измерить количество частиц во всей Вселенной.
Число Скьюза. Это число показывает верхний предел для математических вычислений. Считается, что числа больше числа Скьюза нарушают многие математические правила и ведут себя по-другому. Даже самое меньшее число Скьюза будет намного больше г у голплекса и обозначается как: 10˄10˄10˄36, где ˄ — это возведение в степень.
Заключение
Мы будем очень благодарны
если под понравившемся материалом Вы нажмёте одну из кнопок социальных сетей и поделитесь с друзьями.
Миллион, миллиард, триллион, триллиард, а что дальше, до бесконечности
Известно, что чисел бесконечное множество и лишь у немногих есть собственные названия, ведь большинство чисел получили имена, состоящие из малых чисел. Наибольшие числа необходимо каким-то образом обозначать.
«Короткая» и «длинная» шкала
Используемые сегодня имена числа начали получать в пятнадцатом столетии, тогда итальянцы впервые использовали слово миллион, имеющее значение «большой тысячи», бимиллион (миллиона в квадрате) и тримиллион (миллиона в кубе).
Данную систему описал в своей монографии француз Николя Шюке, он рекомендовал употреблять числительные латинского языка, добавив к ним флексию «-иллион», таким образом бимиллион стал биллионом, а тримиллион – триллионом и так далее.
Но согласно предложенной системе числа между миллионом и биллионом он называл «тысячей миллионов». С подобной градацией было не комфортно работать и в 1549 году француз Жак Пелетье советовал числа, находящиеся в указанном промежутке, называть опять же используя латинские приставки, при этом введя другое окончание — «-иллиард».
Так 109 получило название миллиард, 1015 — биллиард, 1021 — триллиард.
Постепенно эту систему стали использовать в Европе. Но некоторые ученые путали наименования чисел, это создало парадокс, когда слова биллион и миллиард стали синонимичными.
Впоследствии в США был создан свой порядок именования больших чисел. Согласно ему построение названий осуществляется аналогично, но только числа разнятся.
Прежняя система продолжала применяться в Великобритании, потому и была названа британской, хотя изначально создавалась французами. Но уже с семидесятых годов прошлого века Великобритания также начала применять систему американскую.
Поэтому, чтобы избежать путаницы, созданную американскими учеными концепцию, принято именовать короткой шкалой, в то время как изначальную французско-британскую – длинной шкалой.
Короткая шкала нашла активное применение в США, Канаде, Великобритании, Греции, Румынии, Бразилии. В России она тоже в ходу, только с одним отличием – число 109 традиционно именуют миллиардом. А вот французско-британскому варианту отдали предпочтение во множестве других стран.
С целью обозначить числа, большие нежели дециллион, ученые решили объединять несколько латинских приставок, так были названы ундециллион, кваттордециллион и прочие. Если воспользоваться системой Шюке, то согласно ей гигантские числа обретут имена«вигинтиллион», «центиллион» и «миллеиллион» (103003), соответственно согласно длинной шкале такое число получит имя «миллеиллиард» (106003).
Числа с уникальными именами
Многие числа получили наименование без привязки к различным системам и частям слов. Этих чисел немало, например, это число «пи», дюжина, а также числа более миллиона.
В Древней Руси издавна использовалась своя числовая система. Сотни тысяч обозначали словом легион, миллион – называли леодром, десятки миллионов были воронами, сотни миллионов именовались колодой. Это был «малый счет», а вот «великий счет» применял те же слова, вот только смысл в них вкладывали иной, например леодр мог означать легион легионов (1024), а колода — уже десять воронов (1096).
Бывало, что названия числам придумывали дети, так, математику Эдварду Кэснеру подал идею юный Милтон Сиротта, предложивший дать имя числу с сотней нулей (10100) просто «гугол» (googol). Это число получило наибольшую огласку в девяностых годах двадцатого века, когда в его честь получил название поисковик Google. Также мальчик предложил наименование «гуглоплекс», число имеющее гугол нолей.
А вот Клод Шеннон в средине двадцатого века, оценивая ходы в шахматной игры, подсчитал, что таковых существует 10118, теперь это «число Шеннона».
В старинном труде буддистов «Джайна-сутры», написанном почти двадцать два века назад, отмечается число «асанкхейя» (10140), именно столько космических циклов, по мнению буддистов, необходимо, чтобы обрести нирвану.
Стэнли Скьюзом были описаны большие величины, так «первое число Скьюза», равное 10108,85.1033, а «второе число Скьюза» еще внушительней и равняется 1010101000.
Нотации
Разумеется, в зависимости от количества степеней содержащихся в числе, поялвяется проблематичность в фиксировании его на письме, да и чтении, баз ошибок. некоторые числа невозможно поместить на нескольких страницах, поэтому математики придумали нотации для фиксации крупных чисел.
Стоит учесть, все они отличаются, в основе каждой свой принцип фиксации. Среди таковых стоит упомянуть нотации Штейнггауза, Кнута.
Однако наиболее крупное число — «число Грэма», применялось Рональдом Грэмом в 1977 году при проведении математических расчетов, и это число G64.
Понравилась статья? Подпишитесь на канал, чтобы быть в курсе самых интересных материалов
Что идёт после триллиона?
В европейской системе названия иные:
— тысяча
— миллион
— тысяча миллионов (миллиард)
— биллион
— тысяча биллионов (биллиард)
— триллион
— тысяча триллионов (триллиард)
— квадриллион
То есть квинтиллиону американской системы соответствует триллион европейской системы.
Названия создаются так:
В американской системе: в начале идет латинское порядковое числительное, а в конце к нему добавляется суффикс «-иллион». Исключение составляет название «миллион», которое является названием числа тысяча (лат. mille) и увеличительного суффикса «-иллион». Так получаются числа — биллион, триллион, квадриллион, квинтиллион, секстиллион и т. д. Американская система используется в США, Канаде, Великобритании, Греции и Турции. Количество нулей в числе, записанном по американской системе, определяется по формуле 3·x+3 (где x — латинское числительное). В некоторых странах, в том числе и в России, вместо слова «биллион» используется слово «миллиард».
В европейской системе: к латинскому числительному добавляют суффикс «-иллион», название следующего числа (в 1 000 раз большего) образуется из того же самого латинского числительного, но с суффиксом «-иллиард». То есть после триллиона в этой системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т. д. Количество нулей в числе, записанном по европейской системе и оканчивающегося суффиксом «-иллион», определяется по формуле 6·x (где x — латинское числительное) и по формуле 6·x+3 для чисел, оканчивающихся на «-иллиард».
Европейская (английская) система наименования наиболее распространена в мире.
Что идет после миллиарда?
Один, сто, тысяча, миллион, миллиард.
А что дальше? Продолжите цепочку.
Прежде всего следует определить по какой системе исчисления вы хотите знать, что идет после миллиарда. Есть Европейская система и Американская. В России все гораздо более запутано и в обычном обиходе миллиард считают по Европейской системе, а следом за ней триллион уже по Американской системе. Поэтому по Американской системе за пресловутым миллиардом идет триллион, а по Европейской системе идет биллион.
Если уж прибавлять по одному нолику, то получится вот что.
десять миллионов 1*10 в седьмой степени,
миллиард десять в 9 степени.
А вот дальше по мелочам не размениваются.
Это число настолько велико, что практически. не имеет никакого смысла. Это число больше, чем число атомов во Вселенной.
Один из персонажей Достоевского (выдуманный Иваном Карамазовым) ради того, чтобы попасть в рай должен был пройти квадрильон километров. Сперва он отказывался делать это, но, так как перед ним была целая вечность, а делать все равно было нечего, все же прошел. А, пройдя, почувствовал себя так:
а потом начинается самое интересное
десять миллиардов =10е10
сто миллиардов =10е11
тысяча миллиардов, триллион =10е12
Дальше такими названиями уже не оперируют, пишут просто степени десятки.
После миллиарда ( 9 нулей) идет биллион (12 нулей).
Далее идет уже пятнадцать нулей и такая цифра называется квадрильон.
После миллиарда идет биллион, биллиард, триллион, триллиард, квадриллион, квадриллиард, квинтиллион, квинтиллиард и ещё дальше просто страшно писать следующее: секстиллион и секстиллиард, септиллион и септиллиард, октиллион и октиллиард,нониллион и нонниллиард,дециллион и дециллиард. Вот такие бывают в нашей жизни цифры, которые применяются наверное для исчисления чего то глобального или космического, а может у кого то есть такие деньги или богатства.
После миллиарда идёт триллион.
Вот вам таблицы, что бы не забывали)
В обычной жизни мало кто пользуется числами больше чем миллиард, но каждый человек хоть раз задумывался о том, что же идёт дальше, как называются эти громадные числа. А названия у них такие (в скобках количество нулей):
По американской системе:
По европейской системе:
В повседневной жизни мы не используем числа более миллиона, но для ученых нужны гораздо большие числа. Даже миллиарда мало для изучения космоса, подводного мира и мира бактерий. Поэтому была придумана достаточно продолжительная система исчисления, где после единицы идет сразу 100 нулей. Такая единица исчисления называется «гугол».
Последний свой матч группового этапа отбора на чемпионат мира 2019-го года провели российские гандболисты. Игра с финнами уже не имела никакого турнирного значения, подопечные Кокшарова досрочно заняли первое место в группе и теперь сыграют в стыках за право поездки на ЧМ. Сборная Финляндии не оказала достойного сопротивления нашим спортсменам, к перерыву отрыв составлял пять мячей, а к финальной сирене увеличился ещё вдвое. Итоговый счет матча 36:26 (16:11), россияне одерживают шестую победу в шести играх и будут ждать окончания чемпионата Европы (куда они, к сожалению, не попали), тогда и определится их соперник по матчам плей-офф. Ну а сами стыки пройдут летом.
Центральный матч этой игровой недели в лиги ВТБ проходил на паркете «СК Юбилейный», куда в гости к местному «Зениту» прибыл ЦСКА. Началась встреча с оглушительного рывка армейцев, спустя четыре минуты после стартового спорного они вели плюс 13, но за оставшиеся до перерыва время питерцы все отыграли. Дальше команды не позволяли себе таких отрывов, игра шла практически очко в очко. Ну а решилось все на последних минутах, за три минуты до сирены хозяева вышли вперед на одно очко, вскоре прибавив к этому ещё три. Подопечные Итудиса толком так и не смогли организовать ответ, а на выходе оказалось 87:83 (22:22, 18:23, 23:22, 24:16) в пользу «Зенита». Для ЦСКА это второе поражение в сезоне и они скатываются на третье место регулярки, у питерцев также два проигрыша, они идут следом.
Какое число стоит после миллиарда?
Какое число стоит после миллиарда?
Что идёт после миллиарда таблица?
Таблица от значения к названию
| Порядок | Значение | Короткая шкала |
|---|---|---|
| Название | ||
| 3 | 109 | биллион (миллиард) |
| 4 | 1012 | триллион |
| 5 | 1015 | квадриллион |
Сколько миллионов в 1 млрд?
Миллиа́рд (сокращённо млрд) — натуральное число, изображаемое в десятичной системе счисления единицей с 9 нулями ( 1 = 109, тысяча миллионов) в системе наименования чисел с длинной шкалой.
Сколько миллионов в 1 Биллионе?
billion) — слово, не использующееся в российской системе наименования чисел, в других системах наименования чисел соответствует числу, изображаемому как единица с: 9 нулями ( 1 109, тысяча миллионов) в системе наименования чисел с короткой шкалой; 12 нулями (
Что идет после миллиарда и дальше?
Именные названия степеней тысячи
| Название | Значение | |
|---|---|---|
| Русское | Латинское | Короткая шкала |
| миллион (млн) | million | 106 |
| миллиард (млрд) | milliard | 109 |
| биллион | billion | 109 |
Как называется это число с 15 нулями?
Так, единица с пятнадцатью нулями называется квадриллион, единица с восемнадцатью нулями — квинтиллион, единица с двадцатью одним нулём — секстиллион, единица с двадцатью четырьмя нулями — септиллион, единица с двадцатью семью нулями — октиллион…
Что за число с 22 нулями?
Квадриллион // Большая советская энциклопедия : [в 30 т.] / гл. ред.
Что за число с 20 нулями?
, миллион в пятой степени) в системе наименования чисел с длинной шкалой.
Что за число с 18 нулями?
| Короткая шкала | Длинная шкала | |
|---|---|---|
| 1012 | триллион | биллион |
| 1015 | квадриллион | биллиард |
| 1018 | квинтиллион | триллион |
Как называется цифра с 1000 нулями?
Сколько нулей в 50 млн?
Вопрос: 50 миллионов это сколько нулей? Ответ: Согласно десятичной системе счисления в одном миллионе шесть нулей.
Сколько нулей в 300 млн?
Ответ: Согласно десятичной системе счисления в одном миллионе шесть нулей. Смотрите также — калькулятор чисел.
Как пишется 10 млн?
10 миллионов = 10 000 000; 1 млрд 10 миллионов 9000 = 1
Как написать цифрами 1 миллион?
Сколько тысяч в 1 млн?
Ответ, проверенный экспертом Для того что бы узнать, сколько тысяч в каком либо числе, нам надо, это число поделить на тысячу. Следовательно, в миллионе, тысяча тысяч.
Как правильно написать один миллион?
Числительное «миллион» является словарным словом, поэтому требуется запомнить его написание. Оно произошло от итальянского “mille” – “тысяча”. Слово «миллион» пишется с непроверяемой гласной в корне «и» и удвоенной «л».
Как написать один миллион сто тысяч рублей?
Число 1100000 прописью: один миллион сто тысяч.
Как написать миллион в тысячах рублей?
Число — это базовое понятие в математике, используемое для количественного сравнения или нумерации объектов или их частей.
Как правильно пишется три миллиона?
Одно из исключений — когда речь идет о тысячах, миллионах и проч. Например: 3 тысячи человек, 5 млн долларов. Числительные от 10 до 999 000 – цифрами.
Как пишется 300 000?
Число 3000000 прописью: три миллиона.
Как правильно писать сокращенно миллион?
Допустимые к использованию сокращения
| Сокращение | Значение | Примечание |
|---|---|---|
| букв. | буквально | |
| тыс. | тысяча | Точка обязательна. |
| млн | миллион | Пишется без точки. |
| млрд | миллиард |
Откуда взялось слово миллион?
milione, увелич. от mille «тысяча»; далее от лат. Слово «миллион», обозначающее тысячу тысяч, придумал путешественник Марко Поло. Оно, таким образом, соответствует несуществующему русскому слову «тысячища».
Как будет миллион на чеченском?
миллионаш, й] миллион.
Почему млн пишется без точки?
Правило гласит, что, если сокращение образовано отсечением части слова, точка ставится (тыс., г., стр.). Если же сокращение состоит из согласных, а гласные при этом опущены, причем последняя согласная является последней буквой полного слова, точка не ставится (млн, млрд, трлн).
Как сократить миллиарды?
Лучше всё же освоить правильное сокращение данных слов. Слово миллион сокращается так: млн, а слово миллиард так: млрд. После сокращения точка не ставится.
Как правильно читать миллиарды?
Число читают так: 23 миллиона 501 тысяча 890. Если в числе 10, 11 или 12 цифр, то появляется четвёртый класс — миллиарды. В классе миллиардов три разряда: единицы миллиардов, десятки миллиардов, сотни миллиардов. 1 — один миллиард (девять нулей).














.902ed1934b981fb8c2e33de3741ee9ec.jpg)