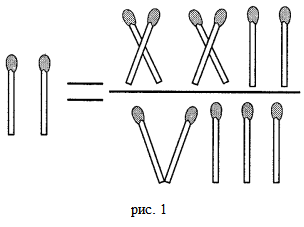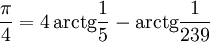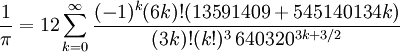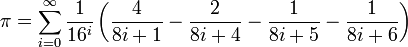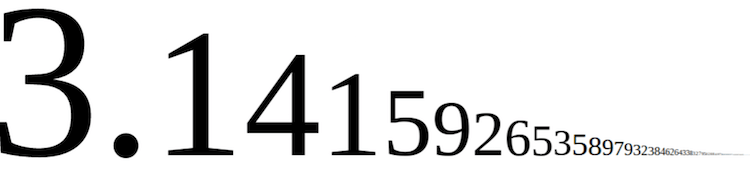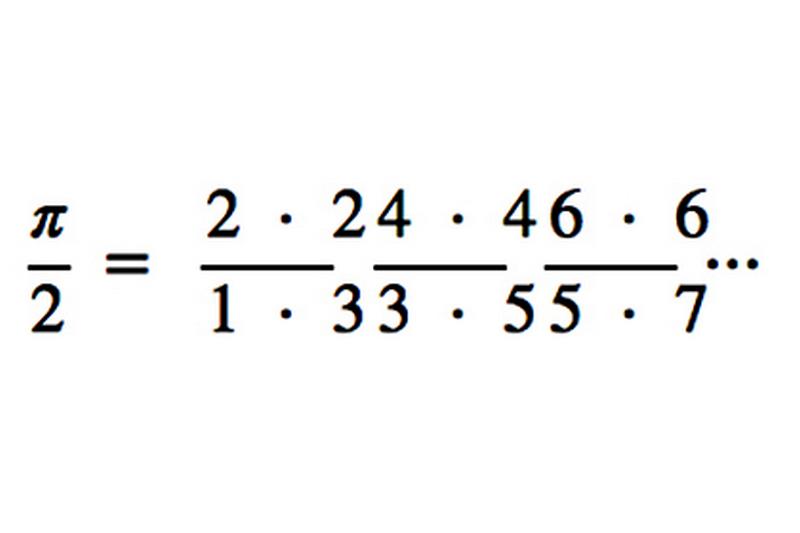Что такое число пи простыми словами
Что такое число пи простыми словами
Некоторые могут подумать, раз это отношение обозначается греческой буквой, стало быть, его вывел некий греческий математик. На самом деле об этом история умалчивает. Зато имеются данные о том, кто впервые использовал в своих работах это обозначение.
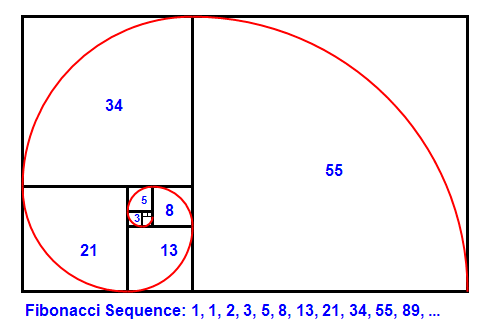
Все окружности похожи
Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:
| C1 | C2 | |
| = | ||
| d1 | d2 | (1) |
Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:
Как раз эта формула и является проводником в мир окружностей для семиклассников.
Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:
| C 2 | ||
| S | = | , |
| 12 |
где S – площадь круга, C – длина окружности (круга). Если в эту формулу подставить уже знакомые школьнику выражения площади круга S = π r 2 и длины окружности С = 2 π R, то мы получим:
| (2 π R) 2 | |
| π R 2 | = |
| 12 |
В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:
| 8 | 2 | |||
| S | = | ( | d | ) |
| 9 |
Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
По стопам Архимеда
Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: «переложите одну спичку так, чтобы равенство стало верным».
| 10 | 6336 | 14688 | 1 | ||
| 3 | π | ||||
| 71 | 1 | 1 | 7 | ||
| 2017 | 4673 | ||||
| 4 | 2 | ||||
можно записать проще: 3,140 909 π π за 3,14 для удобства подсчета.
| π D 2 |
| S= π R 2 = |
| 4 |
где S – площадь окружности, R – ее радиус, D – диаметр окружности.
Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:
где C – длина окружности, R – радиус, d – диаметр окружности.
Понятно, что диаметр d равен двум радиусам R.
Из формулы длины окружности можно легко найти радиус окружности:
| C | C |
| R= | = |
| 2 π | d |
Обозначения для этих формул остаются те же.
Диаметр окружности можно найти по формуле:
| C | |
| D= | =2R |
| π |
где D – диаметр, С – длина окружности, R – радиус окружности.
Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:
| α | ||
| S | = | π R 2 |
| 360˚ |
где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.
Такое загадочное 3,14
И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.
Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием «Пи». Фильм получил множество наград.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа Пи». К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Вниманием это удивительное число не обошли и поэты, неизвестный написал:
Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.
Давайте развлечемся!
Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.
Число пи
Число π (произносится «пи») — математическая константа, выражающая отношение длины окружности к длине её диаметра. Обозначается буквой греческого алфавита «пи».
Содержание
История
Впервые обозначением этого числа греческой буквой 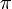
Оценки
Свойства
Соотношения
Известно много формул с числом π :
Трансцендентность и иррациональность
Нерешенные проблемы
История вычисления
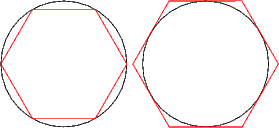
Архимед, возможно, первым предложил способ вычисления π математическим способом. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Так, для шестиугольника (см. рисунок) получается 
Рассматривая правильный 96-угольник, Архимед получил оценку 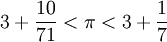
В древнекитайских трудах попадаются самые разные оценки, из которых самая точная — это известное китайское число 355/113. Цзу Чунчжи (V век) даже считал это значение точным.
В Индии Арьябхата и Бхаскара использовали приближение 3,1416
Заслуживает упоминания результат арабского математика Гиясэддина Джемшид ибн Масуд ал-Каши, завершившего в 1424 году труд под названием «Трактат об окружности», в котором он приводит 17 цифр числа π (из них 16 верных).
В Новое время для вычисления π используются аналитические методы, основанные на тождествах. Перечисленные выше формулы малопригодны для вычислительных целей, поскольку либо используют медленно сходящиеся ряды, либо требуют сложной операции извлечения квадратного корня.
Первую эффективную формулу нашёл в 1706 Джон Мэчин (John Machin):
Очень быстро работают вычислительные алгоритмы, основанные на формулах Рамануджана
В 1997 году Дэйвид Х. Бэйли, Питер Боруэйн и Саймон Плуфф открыли способ быстрого вычисления произвольной двоичной цифры числа π без вычисления предыдущих цифр, основанный на формуле
Метод иглы Бюффона
На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к 
Мнемонические правила
Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Надо только постараться И запомнить всё как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься, Это каждый должен знать. Можно просто постараться И почаще повторять: «Три, четырнадцать, пятнадцать, Девять, двадцать шесть и пять.»
2. Подсчитайте количество букв в каждом слове в нижеприведенных фразах (без учета знаков препинания) и запишите эти цифры подряд — не забывая про десятичную запятую после первой цифры «3», разумеется. Получится приближенное число Пи.
Это я знаю и помню прекрасно: Пи многие знаки мне лишни, напрасны.
Кто и шутя, и скоро пожелаетъ Пи узнать число — ужъ знаетъ!
Вот и Миша и Анюта прибежали Пи узнать число они желали.
(Вторая мнемоническая запись верна (с округлением последнего разряда) только при использовании дореформенной орфографии: при подсчете количества букв в словах необходимо учитывать твердые знаки!)
Еще один вариант этой мнемонической записи:
Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.
Раз у Коли и Арины Распороли мы перины. Белый пух летал, кружился, Куражился, замирал, Ублажился, Нам же дал Головную боль старух. Ух, опасен пуха дух!
Если соблюдать стихотворный размер, можно довольно быстро запомнить:
Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один
Число Пи — это математическая постоянная
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы подробно расскажем, что такое число «пи», которое частенько используется в математике.
На самом деле, это постоянная величина, которая помогала еще древним Египтянам проводить расчеты при проектировании. Она, например, позволяла, зная диаметр окружности, легко рассчитать ее длину (периметр).
Но вот только значение этой постоянной в те времена точно рассчитать не получалось. Сегодня же мы можем узнать чему равно число ПИ вплоть до триллионного знака после запятой.
Что такое число Пи
Впервые школьники сталкиваются с этим понятием еще в 3-м классе, когда начинают изучать окружность (что это?).
Им просто говорят, что какую бы окружность они не нарисовали, если поделить ее длину на диаметр, то получится одно и то же число. И называется это число «пи», обозначается латинской буквой «π» и равно 3,14.
Кстати, именно так и звучит официальное определение числа «пи»:
Пи – это математическая константа (постоянная), которая равна отношению длины окружности к ее диаметру.
А вот в 6-м классе школьников ближе знакомят с этим числом. Именно тогда начинают изучать формулы длины и площади окружности. А в них без «пи» не обойтись:
История возникновения числа «пи»
Ученые считают, что еще в Древнем Египте знали о существовании некой математической постоянной. Этот вывод сделали на основании папирусов, на которых расписаны вычисления площади круга. И в ней фигурировало некое число, которое равнялось 3,160.
Но число, напоминающее «пи» встречается и в других странах:
Эта греческая буква взята неслучайно, она первая в словах «περιφέρεια» (окружность) и «περίμετρος» (периметр).
И наконец, общепринятым понятие «математической постоянной» стало в 1737 году после публикации научных работ Леонардо Эйлера.
Чему равно число Пи
Количество знаков после запятой у числа «пи» бесконечно.
Во всяком случае, ни один компьютер (это что?) до сих пор так и не смог вычислить их до конца. Самая современная вычислительная машина смогла показать лишь 10 триллионов цифр.
И что наиболее любопытно, в этом огромном количестве цифр нет никакой зависимости или тенденции. Математики очень любят разбивать знаки после запятой на группы по 10 цифр. И вот среди этих групп у числа «пи» невозможно найти две одинаковые.
На рисунке ниже приведено значение числа Пи с точностью до 1000 знаков после запятой:
Число «пи» в фольклоре
Чтобы запомнить побольше знаков числа «пи» люди пользуются разными приемами мнемотехники.
Например, есть такие стихотворения:
Чтобы нам не ошибиться,
Надо правильно прочесть.
Три, четырнадцать, пятнадцать.
Девяносто два и шесть.
А есть специальные стихи, в которых числа определяются по количеству букв в словах:
Это(3) я(1) знаю(4) и(1) помню(5) прекрасно(9).
Пи(2) многие(6) знаки(5) мне(3) лишни(5), напрасны(8).
Доверимся(9) знаньям(7) громадным(9)
Тех(3), пи(2) кто(3) сосчитал(8), цифр(4) армаду(6).
Называние «пи» присутствует и в нескольких фильмах. Например, в 1998 году режиссер Даррен Аронофски снял картину «Пи». Это психологический триллер, в котором главный герой считает, что все в жизни можно описать с помощью чисел. Но в результате он чуть не сошел с ума.
А в 2012 году на экраны вышел фильм «Жизнь Пи». Он, правда, не имеет ничего общего с математикой. Это приключенческая лента о путешествиях индийского юноши по имени Пи.
С 1987 году математики даже отмечают День числа «пи». Происходит это 14 марта, так энтузиасты обыграли первые цифры (3,14). А начало торжеств приходится на определенное время – 01:59. Это также дань цифрам, которые идут после запятой.
Празднования проходят, как правило, скромно. Люди просто готовят круглый торт, садятся за круглый стол и делятся забавными историями, связанными с числом «пи» и математическими задачками в целом.
И наконец, есть даже анекдоты на тему числа «пи». Один из таких звучит так:
Один ученый спрашивает другого:
— Скажи, а почему рельсы прямые, колеса круглые, а когда поезд едет, то они стучат?
— Ну, это просто. Колеса же круглые. А значит, их площадь равна «пи эр квадрат». Вот тот самый квадрат и стучит.
Вот и все, что мы хотели рассказать о числе «пи». До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (3)
Приведенное выше число пи не точное (приближенное)
ТОчное значение этого числа 3,14269680. Это доказано в статье «Через центр масс квадранта к числу пи» см. в Инете
Самое забавное, что мы не можем вычислить точную площадь круга, именно потому что число Пи бесконечно.
Вроде бы Архимед нашел свое число Пи следующим образом, он брал два многоугольника, один был вписан в окружность, а сама окружность была вписана во второй многоугольник, затем он находил периметры этих двух многоугольников и брал их отношение, потом он увеличивал количество сторон этих многоугольников и они все больше становились похожи на окружность, так он и получил наиболее точное значение своего числа.
Да зачем нужны эти триллионы после запятой? Вот учёным делать нечего, всё равно погрешность изготовления окружности будет выше этой точности.
Что такое Число Пи
Число π (Пи) является математической константой, первоначально было определено как отношение длины окружности к её диаметру, является иррациональным числом и примерно равно 3.1415926535.
С помощью Пи мы ищем периметр окружности, а Пи называется именно так из-за того, что греческое слово περιμετρο («периметр») начинается именно с этой буквы.
Число Пи используют многие специалисты в своих профессиях, такие как: архитекторы, астрономы, физики, химики и другие.
Число Пи используется не только в математике (периметр), но и в строительстве башен, плотин и мостов, в астрономии — для вычислений орбиты спутника. Также в преобразованиях Фурье (применяется во многих областях науки), для вычисления общей теории относительности и для множества вычислений в статистике и квантовой механике.
Число пи полностью
Пи является иррациональным числом и поэтому имеет бесконечное количество знаков после запятой. С каждым годом разные страны устанавливают новые рекорды по вычислению количества знаков после запятой.
На данный момент науке уже известны более чем 2 триллиона знака после запятой. Неполное число Пи, с одной сотней знаков после запятой представлено далее:
Как получить число π
Разделить длину окружности на её диаметр ( C/d=π )
Для этого возьмите любую окружность (подойдёт любая тарелка или крышка), измерьте длину её окружности (C) и диаметр (d), а затем разделите первое на второе.
Вычисление Цзу Чунчжи (математик и астроном)
Этот способ очень простой, но даёт только 6 верных цифр после запятой. Вы можете разделить 355 на 113 (Пи≈355/113), это равно 3,1415929204 (а Пи ≈ 3,1415926535. ).
Формула Лейбница для вычисления π
Возьмите 4 («разделённое на 1», что даёт 4) и вычтите 4, разделённое на 3. Затем добавьте 4, разделённое на 5. Затем вычтите 4, разделённое на 7.
Продолжайте чередовать сложение и вычитание дробей с числителем 4 и знаменателем каждого последующего нечётного числа.
Чем больше раз вы это сделаете, тем более точное у вас будет значение пи.
История числа Пи
Число Пи известно уже почти 4000 лет. Одна вавилонская табличка (около 1900–1680 гг. до н. э.) указывает, что они обозначали это число как π = 3,125, что уже достаточно точное приближение к современному.
«Папирус Ахмеса» (папирус Ринда или папирус Райнда, около 1650 г. до н. э.) даёт нам представление о математике древнего Египта. Египтяне рассчитывали площадь круга по формуле, по которой приблизительное значение для Пи было 3,1605.
Первое вычисление числа Пи было сделано Архимедом (287–212 гг. до н. э.). Он определил, что истинное значение Пи находится между 

На протяжении почти тысячи лет самым близким значением числа Пи было вычисление китайского математика и астронома Цзу Чунчжи (429—500 гг.), сделанное в 480-х годах. Он вывел следующее: 3,1415926 

На данный момент используется алгоритм Чудновских — это быстрый алгоритм, изобретённый братьями Чудновскими, для вычисления числа π. Он показывает более триллиона знаков после запятой.
В 1700-х годах математики начали использовать греческую букву π, введённую Уильямом Джонсом в 1706 году. Использование символа было популяризировано Леонардом Эйлером, который принял его в 1737 году.
А если бы мы не знали Пи?
Путешествия на автомобиле
Для начала пи позволяет нам точно рассчитывать и создавать окружности. Представьте, что колёса вашей машины немного отличаются друг от друга, каждое слегка смещено от центра. Вы не только будете постоянно тратить кучу денег на механика, но и поездки у вас также будут менее удобными.
Путешествия по воздуху
Пи играет важную роль в расчёте времени и расстояния путешествия на самолёте. Когда самолёты летают на большие расстояния, они летят по округлой дуге потому что, Земля круглая.
Ни телевизора, ни радио, ни телефонов
Инженеры используют пи для расчёта и оптимизации звуковых волн.
Казино
Всеми любимая формула нормального распределения (также называемая распределением Гаусса) считается с помощью пи. Проще говоря: пи играет ключевую роль в формулах по теории вероятности и статистике — поэтому с пи азартные игры становятся намного более предсказуемыми. И с этими расчётами люди открывают казино, зная наверняка, какой процент их клиентов будет выигрывать и проигрывать.
Не было бы многих игр, ведь футбольные, баскетбольные, теннисные и другие мячи должны быть абсолютно круглыми.
Число Пи интересные факты
Число π по-английски произносится «пай» — это означает пирог, а слово пирог по-русски начинается с «пи».
Число Пи имеет два неофициальных праздника в году: первый — 14 марта (в США эта дата записывается как 3.14), вторая — 22 июля (22/7 : деление 22 на 7 является приблизительным результатом Пи).
Станислав Улам, польский и американский математик, в 1965 году, написал на бумаге в клетку цифры, входящие в число пи. Он поставил в центре 3 и двигался по спирали против часовой стрелки, записывая числа после запятой, при этом он обводил все простые числа кружками.
Он пришёл одновременно в удивление и ужас, заметив, что кружки выстраивались вдоль прямых. После, с помощью специального алгоритма, математик сделал на основе этого рисунка цветовую картину, которую называют «Скатерть Улама».
Число Пи можно даже играть на музыкальном инструменте поставив ноты в его порядке.
Числу «Пи» поставили несколько памятников по всему миру.
Существует стиль письма, который называется «пилиш» (от «пи», английский «pilish»), в котором длина последовательных слов соответствует цифрам числа πи. В первом слове произведения должно быть 3 буквы, во втором — одна, потом — четыре, следом — опять одна, затем пять, и так далее по цифрам π.
Например, такая поэма на английском языке:
Delicious (9) pi (2),
Как запомнить число π
Один из самых популярных способов — это запомнить фразу, а затем посчитать количество букв в каждом слове.
Например, такие фразы:
Для того чтобы запомнить число Пи, также можно выучить небольшое стихотворение из книги Сергея Боброва «Волшебный двурог»:
“Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим —
Это будет пять, три, пять,
Восемь, девять, восемь”.
Кому число Пи, а кому неравенство «ХУ»
Я не люблю писать, я не люблю бюрократические замашки, я не могу высказывать с поэтическим вдохновением мысли, которые предназначены и дают урок для многих читающих.
Хотелось бы с Вами порассуждать в начале что такое число ПИ.

Что такое число Пи? Число ПИ — математическая «константа», выражающая отношение длины окружности к длине её диаметра. Сначала по невежеству его (это отношение) считали равным трем, что было грубо приближенно, но им хватало. Но когда времена доисторические сменились временами древними (т.е. уже историческими), то удивлению пытливых умов не было предела: оказалось, что число три весьма неточно выражает это соотношение. С течением времени и развитием наук это число стали полагать равным двадцати двум седьмым. Английский математик Август де Морган назвал как-то число ПИ “…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу”. Неутомимые ученые продолжали и продолжали вычислять десятичные знаки числа Пи, что является на самом деле дико нетривиальной задачей, потому что просто так в столбик его не вычислить: число это не только иррациональное, но и трансцендентное (это вот как раз такие числа, которые не вычисляются путем простых уравнений).
В процессе вычислений этих самых знаков было открыто множество разных научных методов и целых наук. Но самое главное – в десятичной части числа пи нет повторений, как в обычной периодической дроби, а число знаков после запятой у него – бесконечно. На сегодняшний день проверено, что в 500 млрд. знаков числа пи повторений действительно нет. Есть основания полагать, что их нет вообще.
Поскольку в последовательности знаков числа пи нет повторений – это значит, что последовательность знаков числа пи подчиняется теории хаоса, точнее, число пи – это и есть хаос, записанный цифрами. Более того, при желании, можно этот хаос представить графически, и есть предположение, что этот Хаос разумен. В 1965-м году американский математик М. Улэм, сидя на одном скучном собрании, от нечего делать начал писать на клетчатой бумаге цифры, входящие в число пи. Поставив в центре 3 и двигаясь по спирали против часовой стрелки, он выписывал 1, 4, 1, 5, 9, 2, 6, 5 и прочие цифры после запятой. Попутно он обводил все простые числа кружками. Каково же было его удивление и ужас, когда кружки стали выстраиваться вдоль прямых!
В десятичном хвосте числа пи можно отыскать любую задуманную последовательность цифр. Любая последовательность цифр в десятичных знаках числа пи рано или поздно найдется. Любая!
Ну и что? – спросите вы. А то. Прикиньте: если там есть ваш телефон (а он есть), то ведь там же есть и телефон той девушки, которая не захотела дать вам свой номер. Более того, там есть и номера кредиток, и даже все значения выигрышных номеров завтрашнего тиража лотереи. Да что там, вообще всех лотерей на много тысячелетий вперед. Вопрос в том, как их там отыскать…
Если зашифровать все буквы цифрами, то в десятичном разложении числа пи можно найти всю мировую литературу и науку, и рецепт изготовления соуса бешамель, и все священные книги всех религий. Это строгий научный факт. Ведь последовательность БЕСКОНЕЧНА и сочетания в числе ПИ не повторяются, следовательно она содержит ВСЕ сочетания цифр, и это уже доказано. А раз все, то ВСЕ. В том числе и такие, которые соответствуют выбранной вами книге.
А это опять-таки означает, что там содержится не только вся мировая литература, которая уже написана (в частности и те книги, которые сгорели и т.д.), но и все книги, которые еще БУДУТ написаны. В том числе и Ваши статьи на сайтах. Получается, что это число (единственное разумное число во Вселенной!) и управляет нашим миром. Надо только рассмотреть побольше знаков, найти нужный участок и расшифровать его. Это чем-то сродни парадоксу со стадом шимпанзе, долбящем по клавиатуре. При достаточно долгом (можно даже оценить это время) эксперименте они напечатают все пьесы Шекспира.
Тут же напрашивается аналогия с периодически появляющимися сообщениями о том, что в Ветхом Завете, якобы, закодированы послания потомкам, поддающиеся прочтению с помощью хитроумных программ. Отметать сходу такую экзотическую особенность Библии не совсем мудро, кабаллисты веками занимаются поиском таких пророчеств, но хотелось бы привести сообщение одного исследователя, который с помощью компьютера нашел в Ветхом завете слова о том, что в Ветхом Завете нет никаких пророчеств. Скорее всего, в очень большом тексте, так же, как и в бесконечных цифрах числа ПИ, можно не только закодировать любую информацию, но и “найти” фразы, изначально не заложенные туда.
Для практики, в пределах Земли достаточно 11 знаков после точки. Тогда, зная, что радиус Земли равен 6400 км или 6,4*10 12 миллиметров, получится, что мы, отбросив двенадцатую цифру в числе ПИ после точки при вычислении длины меридиана, ошибемся на несколько миллиметров. А при расчете длины Земной орбиты при вращении вокруг Солнца (как известно, R=150*10 6 км = 1,5*10 14 мм) для такой же точности достаточно использовать число ПИ с четырнадцатью знаками после точки, да что уж там мелочиться — диаметр нашей Галактики около 100.000 световых лет (1 световой год примерно равен 10 13 км) или 10 18 км или 10 30 мм., а еще в XVII веке были получены 34 знака числа ПИ, избыточные для таких расстояний, а их на данный момент вычислено до 12411-триллионного знака.
Отсутствие периодически повторяющихся цифр, а именно, исходя их формулы Длина окружности=Пи*D окружность не замыкается, так как нет конечного числа. Этот факт также может тесно быть связан с спиральным проявлением в нашей жизни …
Есть еще гипотеза о том, что все (или некоторые) универсальные постоянные (постоянная Планка, число Эйлера, универсальная гравитационная постоянная, заряд электрона и т.д.) со временем меняют свои значения, так как меняется кривизна пространства из-за перераспределения материи или по другим, не известным нам причинам. Рискуя навлечь гнев просвещенного сообщества, можем предположить, что и рассматриваемое сегодня число ПИ, отражающее свойства Вселенной, может со временем меняться. Во всяком случае, никто не может нам запретить заново найти значение числа ПИ, подтвердив (или не подтвердив) имеющиеся значения.
Наглядное отображение как понять, что такое число ПИ
Вот такая Вот …ПИ… ребята!
In Love, Rostislav!
p.s. Вы можете скачать первый миллион знаков после запятой в числе ПИ. скачать
Рекомендуем к прочтению
Конец времен! Сейчас!
43 комментария
СПИРАЛИ НЕТ. Как быть в такой ситуации, получается где то не увязка, где то не стыкуется окончательная точка сращения?
в том то и дело, что если число пи не является конечным, то нет замыкания круга. Получается, что нет начала и нет конца?! при всем том, что мы можем назначить условно начало и оно будет опять же условно концом.
как же нарисованная окружность на бумаге, это ведь окончательное завершение движения точки в пространстве и времени, СПИРАЛИ НЕТ. Как быть в такой ситуации, получается где то не увязка, где то не стыкуется окончательная точка сращения?
Это образ на плоскости.
Если представить, что лист бумаги «оживает», начинает бугриться,
т.е. проявляет качества НЕ плоского Мира. Тогда получается процесс движения на приближении к идеальному числу ПИ – проявление хвостика цифр после запятой.
Ростислав!
когда кружки стали выстраиваться вдоль прямых!
Явная связь между последовательностью и свойствами пространства.
В десятичном хвосте числа ПИ можно отыскать любую задуманную последовательность цифр.
Почему-то возникает ощущение разворачивающейся точки.
Вообще, по восприятию законов Мироздания, цифры относятся к Первообразам.
А из сочетаний можно получить всю картину Мира явного и не явного.
Возможно в том “мире” число пи – вообще конечное, точное и натуральное.
Математика для того и была сделана чтобы быть точным, а то что основные расчеты делаются на основе этого знака и смотря какое ты возмешь приближение такова точность и будет. Пока нет конца … и даже повторений нет, а может это та цифра которой подчиненны все законы? Или мы просто не умеем их расшифровывать или читать.
может это та цифра которой подчиненны все законы? Или мы просто не умеем их расшифровывать или читать.
Интересная статья! Никогда не задумывался над этим числом,вероятно тут такое же образное значение в цифровых конфегурациях(если брать определённую цекличность цифр за шифр), как в рунических песьминах — плюс — минус.
Вся прелесть в том, что цикличности нет, если была бы цикличность то загадки бы это число не вызывало. А преставить себе огромное количество цифр в комбинации которых присутсвует буквально любая последовательность это весьма и весьма удивительно, кстати я в первом миллионе не нашел своего телефона и свою дату рождения, наверное глубже надо проникать к истокам 🙂
РО твоя Пи мне покоя не даёт, засела в голове, и вроде нет цикла. душой принимаю, но с листом бумаги Людмила объяснила, не ровность поверхности объясняет незаконченность окружности, вроде с одной точки начал, как с одного бугорка, на другом бугорке или впадине закончил,с виду плоскость в микрообъёме далеко не ровная поверхность.
А как тогда быть с завершённым кругом тарелки, стакана.
Но есть ещё одна мысль, в том-же микрообъёме поверхность тарелки по окружности далеко не ровная, значит точность длинны окружности относительная, как и диаметр, посему и тут Пи работает.
Видимо никогда не будет абсолютно ровной длины окружности и диаметра точного тоже нет. Во как!!
Серж тут немного не так, да, ты можешь взять ниточку и измерить, но когда ты измерениями своими будешь получать дробь, то ты получишь Пи с нескончаемым числом знаков. А ты посмотри что достаточно 34 знака после запятой чтобы произвести точные вычисления в пределах нашей Галлактике, а знаков больше Триллиона.
И еще один момент насчет начала, ты мне покажешь на круге одно начало, а я покажу тебе другое начало
Мне тоже сегодян Пи-шная тематика ночью снилась
РОСТИСЛАВ Я ПРО ЭТО: Поставив в центре 3 и двигаясь по спирали против часовой стрелки, он выписывал 1, 4, 1, 5, 9, 2, 6, 5 и прочие цифры после запятой…или спираль не имеет циклов?!)
Топаз, не буду лукавить я не проводил этот эксперимент, в источнике сказано что он это сделал и был удивлен и цифры выстроились каким то удивительным образом, пока не проверишь это — получается баян, ну а красоту в принципе можно найти в любой последовательности, возможно что то там красивое и вырисовалось 🙂 Надо будет попробовать на какой нибудь скучной конференции этим заняться 🙂
Очень интересная тема! Получается число Пи – символ проявления Бесконечности через неповторимые вариации «конечных» величин. Тут и можно увидеть и развертывание спирали в пространстве, и формирование пространства через спираль и многое другое.
Ростислав, статья правда интересная. Молодец:)
Только один нюанс вызывает вопросы.
Отсутствие периодически повторяющихся цифр, а именно, исходя их формулы Длина окружности=Пи*D окружность не замыкается, так как нет конечного числа.
Кто тебе сказал, что его нет? Вспомни, откуда появляется ПИ? Диаметр изначально конечен, длина окружности тоже. Деля конечное на конечное, получаем только конечное. То что число не обладает конечным нобором цифр, не говорит о том, что оно не обладает конечностью. Пи это определённое число и оно одно такое. Его не может быть два или три, сегодня одно, завтра другое. Поэтому окружность замыкается.
Совсем другое будет если мы к твоему кругу добавим палочку, простимулировав рост круга, от центра вверх. Тогда-то и появляется спираль, во взаимодействии круга и палочки, инь и янь, женского и мужского. Тогда-то и появляется развитие и рост.
Тома, я с Тобой согласен в плане рассуждений с математической точки зрения, в том то и дело, что величие числа пи в том, что последовательности нет, и в этом случае как и следует в большинстве случаях с точными науками учитывать мнение с философским уклоном. Нет четкого окончания числа, оно в себе содержит всю информацию, о точности знаком мы делаем свои выводы для последующих решений, если смотреть на спираль сверху — мы увидим тот же круг, но это не означает что он замкнут.
Николай, судя по комментарию и тому что вы «так внимательно» читали, сомневаюсь что вы вообще что то поняли ввиду своего ограниченного сознания. Вы даже не попытались понять почему так, на самом деле все просто и мне реально впадло объяснять ошибку. Гипотеза одна — вы слишком в своем мире, расширяйте свои границы.
300000х60х60х24х365=9,4608×10^12 что приблизительно равно 10^13 он вообще-то прав
Николай вы повторяете «ошибку» предыдущего комментатора … в тексте статьи все было уже исправлено, но вы почему то также не прочитали статью, а прочитали только комментарий и да =10^13
p.s. ошибка в статье (отсутствие надиндекса 13) появилась случайно при переносе сайта … а вдруг и не случайность … я не знаю 🙂
Не понял про повторения, в первом миллионе цифр 31415 повторяется 3 раза, один из которых дает 314159…
Подразумевается повторение — это когда последовательность повторяется полностью (цикличность), а не выборочно, да частичные повторения конечно же будут, но сама последовательность полностью не повторяется.
Про повторения есть одна идея… Посмотрю источники и поделюсь. Вот все же еще с Уламом: сам он говорил, что по спирали расставлял последовательность целых чисел: 1, 2, 3, 4,…. Другого я не видел. Если результат получается и с числом Пи, то это очень круто и совершенно не понятно — настоящая эзотерика. Хотя, может быть все дело в той же 6N+-1 и похожести Пи на натуральный ряд.
А и Б сидели на трубе, А упала Б пропала кто остался на трубе?
Какой то странный у вас вопрос. «И» осталась, что дальше?
ОЧЕНЬ ЗАМЕЧАТЕЛЬНО. СКОРОСТЬ СВЕТА И ЧИСЛО ПИ — ОДНО И ТО ЖЕ — ВОИНСТВО АЛЬЯНСА ЛОГОСА ПРОТИВ СИЛ ЗЛА… ПРЕДЕЛ РИТМА И ПРЕВРАЩЕНИЕ КВАДРАТА В КРУГ….
Рекомендую вам почитать Блаватскую, там как раз она красиво объясняет понятие круга и квадрата в нашем естестве и вообще в понимании (доступности) многих вещей
ваще! крутоооо! единственный нужный сайт1
это все рассуждения о возможном физическом смысле числа пи или есть продолжение
Ну смотря что вы подразумеваете под собой «возможные физические смыслы» … некоторые домыслы не лишены здравого смысла, как например все книги зашифрованные числами … оно бесконечно и это не лишено смысла. Если знакомы с теорией вероятности то это весьма и весьма вероятно там найти все что вам необходимо.
Правильно в XVII — 17 веке, а не в XXVII — 26 веке.
Простите, виноват, стыдно … исправил на правильный век — 17 (XVII)
в смысле 27 веке))))
Ермаков О.В. – Число Пи: Огонь и Очи. Суть главной константы Земли
Yermakov O.V. – The number Pi: Fire and Eyes. Heart of the Earth’s main constant
Первое в истории мирской (Аристотелевой) науки определение подлинной сути ее основания — числа Пи.
The first definition in the history of secular (Aristotelian) science of the true essence of its foundation — the number Pi.
Ключевые слова: Бог, Вселенная, Мир, Луна, Любовь, Аполлон, число Пи, врата, Огонь, глаз, созерцание, Гераклит, константа, Земля, познание, Единая теория Поля, Теория Всего, физика, квантовая физика, философия, метафизика, космизм, эзотерика, космогония, астрономия, космонавтика, НАСА, Сократ, Платон, Аристотель, Эйнштейн, Вернадский, филология, лингвистика, Париж
С таким успехом всю эту теорию можно применить и к числу е=2,718…., — оно также трансцендентно. А так как множество трансцендентных чисел бесконечно, то смысл конкретной составляющей вселенной размывается. То есть вселенную можно «вопхнуть» не только в число пи, но и в «е», ln2, 2^(2^0,5), т.
К примеру, если стадо овец помещается в моем дворе, то они мои. С таким же успехом стадо помещается и у соседа. Они его? Оказывается, оно помещается и у большинства жителей села, района, области. Квалифицировать принадлежность овец к кому бы то ни было по принципу «у кого поместится», — неверно в корне.
Отсюда,- любое трансцендентное число может описать вселенную. И не нужно заморачиваться только на числе пи.
Даже бесконечные множества трансцендентных чисел — малая толика в сонме иррациональных чисел.
Теория чисел сама по себе занимательная наука. Она абсолютная.
А вот нумерологию можно применить к любому процессу, она относительная,так как не имеет постянной точки отсчета.
Пример:
Астрологи просчитывают жизненные циклы человека, опираясь на первоначальную точку отсчета — день рождения. Но плод также жил 9 месяцев, и у него также были и физические циклы, и эмоциональные. И поэтому в день рождения циклы не сходятся в 0. Так что принять за 0? Момент зачатия? Также глупо. Органы формируются постепенно. Если нет начала, все расчеты — блеф.
Нумерология, положенная в основу астрологии, превращает ее в шарлатанство.
Отсюда: не ведитесь на софистику чисел. Суть всех чисел — расположить их в порядке возрастания. И, как следствие, определить сколько раз одно число вместится в другое.
Поверьте, вокруг любого числа можно создать такую тайну, насколько хватит воображения.
Я создала на Facebook страницу b назвала ее «Язык как философия жизни». Вообще-то мне хотелось назвать ее «Записки из сумасшедшего дома», ибо что иное, как не сумасшедший дом представляет собой наша современная жизнь? Нет, я не собираюсь говорить о том, что все куда-то бегут, что-то не успевают сделать, чего-то вечно не хватает: времени, денег, и т.д. Что нас захлестнула волна непонимания того, что происходит вокруг, куда катится мир…
Крутимся, как белки в колесе. Ощущаем, что бежим по замкнутому кругу. Теряем круг друзей, попадаем в порочный круг… Знакомо? А утро-день-вечер-ночь, и снова по кругу. Весна-лето-осень-зима, и опять по кругу.
Кстати, кто может точно сказать в какое конкретно время утро сменят ночь, зима, весну? Можно ли вообще проводить четкую разделительную грань между курицей и яйцом, и разделимы ли они? Может лучше признать, что яйцо – это потенциальная курица, курица – это потенциальное яйцо, и они не разделимы. Где кончаюсь я и начинаются мои проблемы, проблемы моих детей, друзей и пр., становящихся моими, просто потому, что мы живем в одной квартире, доме, городе, мире? Разве Господь-Бог сказал нам, что ноль часов нужно определять по Гринвичу, что меня нужно назвать Татьяной, а стул стулом? Где кончается мир реальный (вещественный), и начинается мир, выдуманный нами?
Земля вращается вокруг оси и по орбите (кругу, эллипсу – какая разница?). Галактики вращаются. Ученые открыли торсионные поля, доказали, что … «согласно теории относительности Альберта Эйнштейна, мир устроен не совсем так [как нас учили и учат в школе]), в нём наблюдается искривление пространства, так что две прямые, которые на данном участке пространства параллельны, на каком-то отрезке своей протяжённости, могут пересекаться. Недавно предположение Эйнштейна об искривлении пространства было подтверждено экспериментально» (Александр Бабицкий).
А мы все движемся из пункта А в пункт В, полагая, что они находятся на прямой линии.
И чего это меня, лингвиста, занесло в физику, спросите вы? Да потому что все вокруг нас, и в нас самих и есть физика. Язык есть физика. Разве звук не относится к области физики? А теперь скажите мне, что такое гласный звук? Я вам предлагаю «милое» для 21 века определение звуков: «Звуки мы произносим и слышим, а буквы пишем и видим. При произнесении гласного звука воздух не встречает преград: [а], [о], [у], [и], [ы], [э]. При произнесении согласного звука воздух встречает преграду: губы, зубы, язык. Согласный звук произносится с голосом и шумом или только с шумом.»
В принципе, все верно. Вы можете просто мычать «гласным звуком», не размыкая губ. Мычите на здоровье. А вот если, вы губы разомкнули, то у вас получаются знакомые нам всем звуке, «а», «э», которые различаются лишь степенью округленности, растягивания или вытягивания в трубочку губ. Согласны? Это как арбуз, который можно нарезать ломтиками, кубиками, фигурками, но он ведь не перестает оставаться арбузом. И в какой момент звук «а» превращается в «о»? Разве есть четкая граница? Конечно, на качество гласного звука может повлиять положение языка (задние звуки), опускание челюсти, опять же с соответствующим положением языка, но это все тот же арбуз, нарезанный фигурками.
Согласный звук есть барьер на пути гласного звука. Чем можно создать такой барьер? Читайте выше: губами, зубами, языком. Другими словами, инструментарий речи довольно ограничен, но какое обилие языков. (А как вам нравятся 7 нот и такое обилие музыки?)
Теперь давайте задумаемся, у кошки этот инструментарий есть, и у собаки, и у дельфина, да и вообще рыб, и т.д.…
«Ну и заехала», — скажете вы. Да, заехала! А разве не было времени, когда Землю считали блином? А разве электричество не существует просто потому, что мы его не видим и не слышим? Если доказано, что вакуума нет, значит есть все, но это все может быть различимо, опять же, в зависимости от инструментария, который мы используем для рассмотрения и изучения объекта. По мере его совершенствования, мы узнаем все больше нового, чего раньше даже и помыслить не могли.
Язык есть формализация мысли. А где формализуется мысль? Что мы знаем о нашем мире, о самих себе? Мы ищем иные миры, не зная собственного! В этом-то и заключается проблема!
Что мы знаем о языке, кроме того, что он формализуется в звуках. Пожалуйста, формализуйте – куммммарама. Что это? Ничего, потому что гласный звук может «нести на себе» лишь определенное количество согласных звуков, также как я, при моем весе в 50 кг не смогу поднять груз в 150 кг. Физика, понимаете ли!
Теперь обратимся к кривизне пространства и кругу, с которых мы начали. Допустим, мы усомнились в том, что язык развивается не по спирали (в плане контекста), а прямолинейно, и я сообщаю вам, что «в нашем большом городе есть главная улица пересекающая весь город на которой растет много деревьев ходит много людей…». Дурость, скажите вы, где здесь знаки препинания? Где запятые и точки?
Но что есть знаки препинания? Они и есть знаки разделения между подлежащим-сказуемым дополнением (с относящимися к ним определениями) одного предложения и начала другого. Причастие есть ни что иное, как умножение: которая проходит = проходящая, в то время как разворачивание «проходящая» на «которая проходит» – это уже деление. А это уже математика! Ничего удивительного. Мир неделим. Это целостность. Язык тоже – целостность. Нам просто пора взглянуть на все по-новому. Проснуться и оглядеться. Учить детей не правилам, наподобие «Существует отдельная группа слов — предикативы (или категория состояния). Это слова, обозначающие нединамическое состояние и выступающие в функции главного члена (сказуемого, предиката) односоставного безличного предложения. Учёные до сих пор не определились относительно статуса слов категории состояния. Так вот слово НАДО наряду с другими словами (жаль, охота, недосуг, пора и др. ) входит в эту группу слов.»
Вы поняли, о чем это? Я нет! Для кого это написано? Наверное, для учеников. Бедные ученики! Если даже ученые до сих пор чего-то там не поняли, то как это должны понимать дети? Интересно, учителя, хотя бы, выучили наизусть такое определение?
Вот для этого я и создала свой канал на YouTube, чтобы просто (человеческим языком) рассказать о главном – о языке.
Если по прочтению, вам все это (написанное, кстати наспех), покажется бредом, не спешите сообщать мне о том, что я ненормальная. Я ведь и назвала это записками и сумасшедшего дома. Если вам это кажется ненормальным, значит вы живете в доме – напротив. Я его определять не собираюсь. Живем в стране победившей демократии и … ценностей. Каждый имеет право на свое мнение.
3 мнения и 14 фактов о загадочном числе π
Сегодня, 14 марта (в некоторых странах дата пишется именно так 3.14), отмечается Международный день числа π. Личности особо скрупулезные, дабы соблюсти максимальное соответствие, начинают официально праздновать в 1:59 после полудня (3.14.1:59). Для нас же, политехников, 14-й день 3-го месяца особенный еще и потому, что число π вот уже два года является главным символом нашего университета.
Почему, спросите вы? Чтобы узнать это, сегодня на официальной страничке Политеха в соцсети объявлен конкурс, организаторы которого предлагают выложить фотографии, где обязательно должен присутствовать логотип Политеха, а в подписи к фото предложить свою версию, почему же именно число π стало элементом нового бренда Политеха. А может, потому, что заново изобретать колесо – ни к чему, всё гениальное – просто, а Политех – начинается с буквы П? Но пока идет конкурс и мы ищем ответ на этот вопрос, расскажем о секрете популярности числа π – немного истории, а также 3 мнения от ученых Политеха и 14 фактов о самой знаменитой и самой загадочной математической константе.
Со школьной скамьи все помнят о числе Пи, которое обозначается греческой буквой π и используется в геометрических формулах – например для вычисления длины окружности. Число π – самая часто используемая постоянная величина в мире, обозначающая отношение длины круга к длине его диаметра. И для абсолютно всех окружностей в мире это соотношение одинаково и равно примерно 3,14.
Это удивительное свойство окружностей люди отметили еще в глубокой древности – значение π было известно математикам в Индии, Греции, Вавилоне и Египте. Со временем ученые всего мира получали все более точные оценки, использовали все более оригинальные методы, и после запятой открывалось все больше новых цифр. С появлением компьютеров наука шагнула далеко вперед, и к 2011 году ученые смогли вычислить значение числа π с точностью в 10 триллионов цифр после запятой!
Возникает вопрос: зачем нужна такая точность и почему люди продолжают вычислять знаки после запятой числа π? Например, в строительстве и архитектуре хватит точности примерно в 10-15 знаков, около 39-ти знаков достаточно для вычисления длины окружности, опоясывающей известные космические объекты во Вселенной, с погрешностью не более чем радиус атома водорода. Однако пока неизвестно, с какими величинами придется столкнуться в дальнейшем при изучении космоса. Быть может, там понадобятся уже более точные оценки.
Действительно, число π является самой таинственной математической константой, и загадочность ей придает именно этот бесконечный цифровой ряд после запятой. Ученые полагают, что количество знаков в числе π не имеет конца, и их последовательность никогда не повторяется. Из-за того, что число бесконечно и имеет все возможные комбинации, оно может заключать в себе все что угодно – номер вашего телефона, «Войну и Мир» Толстого, симфонию Бетховена. «Дата вашего рождения, код шкафчика, ваш номер социального страхования – все они находятся где-то в этом ряду. А если вы превратите эти цифры в буквы, получите каждое существующее слово, встретите его в любой возможной комбинации», – поясняет Гарольд Финч, главный герой научно-фантастического телесериала «В поле зрения».
Использование числа π настолько широко, что трудно даже назвать такую область, в которой без него можно обойтись. Но мы пошли от обратного и решили поинтересоваться у ученых нашего университета о том, а что было бы, не открой человечество эту загадочную константу?
«Колеса были бы квадратными» (Лев Владимирович УТКИН, профессор кафедры «Телематика» (при ЦНИИ РТК)):
«Если бы не было числа π, то колеса были бы квадратными. Длина окружности и площадь круга определяются через эту константу, а если бы числа π не было, мы все мерили бы …квадратами! πR² – это площадь круга, а без π остается только площадь квадрата. С этой точки зрения все круглое было бы квадратным».
«Не было бы современной математики» (Валерий Иванович АНТОНОВ, заведующий кафедрой «Высшая математика» ИПММ):
«Наша Вселенная построена по законам, до сих пор нам до конца не известным. Мир существует на уровне атомов, молекул и так далее. Но, кроме прочего, существует информационное поле, в котором записаны некие истины нашей Вселенной. Число π – одна из таких истин. И если бы ее не было, мы бы не понимали, например, что такое рациональные числа, не было бы современной математики в общем».
«Вы не задумались бы о связи между числом π и …метанием дротика в мишень» (С.В. ХЛОПИН, доцент Высшей школы киберфизических систем и управления ИКНТ):
И напоследок – еще 14 интересных и познавательных фактов о загадочном числе π:
Материал подготовлен Медиа-центром СПбПУ по информации, предоставленной Информационно-аналитическим центром
Что такое число Пи?
Число Пи (π) — это константа, описывающая отношение длины окружности к ее диаметру. Это иррациональное число, которое обычно сводится к двум десятичным знакам как 3,14.
Греческая буква P была выбрана учителем математики из Уэльса 18 века Уильямом Джонсом, скорее всего, для обозначения «периферия».
Символически термин «Пи» был выбран для обозначения чего-то большего, чем простое число. Величина была представлена дробными числами, ни одно из которых не отражало непостижимую бесконечно длинную последовательность неповторяющихся десятичных знаков.
Джонс мог подозревать, что «точное соотношение между диаметром и окружностью никогда не может быть выражено в числах», но только в 1760-х годах швейцарский математик Иоганн Ламберт представил доказательство иррациональности числа Пи.
Когда было впервые вычислено число Пи?
Есть свидетельства этого соотношения в математике древних вавилонян около 4000 лет назад, которые считали, что периметр шестиугольника, аккуратно помещенного внутри круга, равен его шести радиусам, что дает нам значение 3,125.
Папирус Ринда (ниже), написанный примерно в 1650 г. до н.э. в Древнем Египте, утверждал, что если вы удалите «1/9 диаметра и построите квадрат на оставшейся части; он имеет ту же площадь, что и круг», что приравнивается к значению 3,16049.
(British Museum Department of Ancient Egypt and Sudan/PD)
Архимед Сиракузский также хорошо разбирался в этой проблеме. Используя многоугольники так же, как вавилоняне, умножая стороны, он придумал теоретическое значение между 3 и 1/7 и 3 и 10/71.
Почему число Пи так популярно?
Как константа для всех кругов, Пи является аксиомой — фундаментальным принципом, который можно использовать для описания широкого спектра явлений и концепций в физике и геометрии.
Это делает его применимым в огромном диапазоне приложений для анализа и описания природного мира, от извилистых рек до построения атомов.
Даже там, где круги не используются, Пи может быть задействовано. Например, вероятность того, что любые два целых числа не будут иметь общих положительных множителей — которые описываются как взаимно простые — равна 6/π^2.
Помимо практических и математических приложений, пи привлекло внимание публики исключительно из-за поэзии и эстетики. Физик из Сан-Франциско по имени Ларри Шоу заметил на выездном семинаре в 1988 году, как дата 14 марта отражает первые три знака числа Пи, 3,14.
Отсюда и родился день празднования науки и математики: День числа Пи.
Текст и изображения могут быть изменены, удалены или добавлены по решению редакции, чтобы информация оставалась актуальной.
Источники: Фото: (ScienceAlert)
15 интересных фактов о числе Пи, о которых вы, возможно, не знали
Пи считается хлебом с маслом для математиков и инженеров. Это буквально круто, немного странно, но круто. Число Пи является математической константой, и оно определяет отношение между окружностью круга и его диаметром. С начала 19-го века (наиболее вероятно с середины 18-го века), это было обозначено греческой буквой «π». Это некоторые известные вещи о пи, но как насчет вещей, которые ты не знаешь? Хотите узнать некоторые неизвестные факты об этом интересном номере? Давайте наполним вас некоторыми интересными фактами о числе Пи.
11. Ваши банковские реквизиты можно найти в пи
Что ж, мы знаем, что число Пи является иррациональным числом, то есть его десятичное представление может длиться вечно. Технически, каждое возможное число, которое вы можете придумать, находится где-то в нем. Это включает в себя ваш контактный номер, дату рождения, номер вашего шкафчика и даже ваши банковские реквизиты. Более того, если у нас будет достаточно цифр, использование алгоритма, который может преобразовывать числа в буквы, позволит нам найти Библию, полное собрание сочинений Шекспира и Чосера или любую книгу, когда-либо написанную.
10. Использует в навигации
Пи играет важную роль в системах наведения, установленных на спутниках и космических станциях. Из всего, навигация в космосе на самом деле требует высокой точности. Для каждой вычисляемой десятичной цифры мы получаем большую точность. Но насколько мы должны быть точными, чтобы все работало правильно? Сьюзан Гомез из НАСА, управляющего Международной космической станцией по навигации, навигации и управлению (GNC), сообщает, что в большинстве расчетов с использованием Пи используются 15 цифр для GNC и 16 цифр для космической интегрированной системы глобального позиционирования / инерциальной навигационной системы (SIGI).
9. Истинная площадь круга никогда не может быть известна
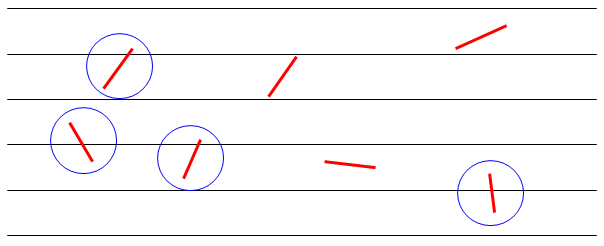
8. Игла Буффона
Игла Буффона или просто проблема с иглой в вероятности была впервые указана Жоржем-Луи Леклерком, графом де Буффоном, в 18-м веке, когда падение иглы на лист, отмеченный линиями, определит вероятность того, что игла пересечет линию на странице. Важно отметить, что вероятность результата эквивалентна значению числа Пи.
Давайте разберемся с этим. В этом случае на самом деле есть две переменные: угол наклона иглы, давайте присвоим ему символ тета (θ) и расстояние между ближайшей линией и центральной точкой иглы. Тета может варьироваться от 0 ° до 180 °, который измеряется параллельно нарисованным линиям.
Выяснилось, что вероятность того, что игла прорежет линию при посадке, составляет ровно 2 / Пи или почти 64%. Это означает, что число Пи можно как-то рассчитать, используя технику Буффона, если у кого-то будет достаточно времени и терпения, чтобы пройти все симуляции. Чтобы понять это намного лучше, вы можете попробовать это.
7. Отношения между извилистыми реками и Пи
У Пи неожиданные отношения со многими явлениями в этом мире, включая извилистые реки. Как? Что ж, путь любой реки в основном описывается ее извилистостью, способностью изгибаться, перемещаться назад и вперед по ее пойме. Математически говоря, это длина извилистого пути, деленная на длину реки от начала до конца. Оказывается, что средняя река имеет извилистость числа Пи независимо от ее длины или количества поворотов на своем пути.
6. Преобразование Фурье и обработка сигналов
Пи играет еще одну очень важную роль в области «обработки сигналов». Это просто анализ, синтез и модификация сигналов. Но здесь действует сложная система. Эта сложная система представляет собой «преобразование Фурье», которое преобразует сигналы в частотный спектр. Мобильный телефон каждого, будь то его андроид или iPhone, выполняет преобразование Фурье, когда он связывается с местной сотовой вышкой.
Кроме того, формула оценивается вашим мобильным телефоном в цифровом виде с помощью определенного алгоритма, известного как «быстрое преобразование Фурье» или «БПФ», который был открыт математиками в 1950-х годах. Важно отметить, что каждый процесс включает в себя число π. Так что технически, есть определенное значение Пи где-то в вашем телефоне, будь то простой или смартфон.
5. Распределение вероятностей
Пи также играет важную роль в нормальном распределении вероятностей. Без сомнения, вы сталкивались с таким распределением вероятностей не один, а много раз. Они важны и часто используются в различных областях исследований, включая математику, физику и общественные науки. Это то, что вам нужно, от прогнозирования результатов теста ученика до измерения отдаленных сверхновых звезд.
Это правило большого пальца: всякий раз, когда вы видите, как Пи подкрадывается где-то в любом уравнении, убедитесь, что где-то в этом спрятан круг. В этом случае Пи вводится через интеграл Эйлера – Пуассона, который содержит квадратный корень из Пи.
4. Проблема с лентой
Предположим, вы хотите обернуть вокруг Земли ленту на экваторе, длина окружности которого составляет 24 900 миль (идеальная сфера). Теперь попытайтесь выяснить, сколько потребуется ленты, которая могла бы окружить Землю на расстоянии одного дюйма над ее поверхностью. Можно легко подумать, что для этого потребуется огромное количество ленты. Но на самом деле это не так. Мы расскажем вам, как.
Еще раз предположив, что Земля является идеальной сферой, у нас будет круг с окружностью 24 900 миль (на экваторе). Это означает, что радиус будет 24 900 / (2 * пи) или примерно 3963 миль. Теперь вторая лента, на дюйм выше поверхности Земли, будет иметь радиус на один дюйм больше радиуса Земли, что дает нам уравнение C = 2 Пи (r + 1) или C = 2 Пи (r) + 2 Пи.
Отсюда можно сказать, что окружность второй ленты увеличится на 2Пи. Фактически, независимо от того, какой первоначальный радиус увеличивает радиус, всегда будет 2Пи.
3. Последовательность Фибоначчи и вычисление числа Пи
Долгое время вычисления числа Пи основывались на двух методах: первый был разработан Архимедом, а второй был разработан Джеймсом Грегори, шотландским математиком в 1671 году. Однако оказывается, что последовательность Фибоначчи также может быть эффективно использована для вычисления значение Пи.
2. Самый первый расчет
Считается, что Пи был первоначально открыт древними вавилонянами около 4000 лет назад. Согласно Rhind Papyrus, древние египтяне вычислили значение Пи как приблизительно 3.1605. Но первый зарегистрированный метод для вычисления значения числа Пи был разработан греческим математиком Архимедом Сиракузским в 250 году до нашей эры.
Архимед знал о том факте, что он не обнаружил фактическое значение Пи, а лишь приблизительное значение в этих пределах. Таким образом, Архимед показал, что число Пи между 3 1/7 и 3 10/71. Этот алгоритм строго использовался учеными и инженерами на протяжении 1000 лет, из-за чего даже сегодня его иногда называют «постоянной Архимеда».
1. Скрытая связь между квантовой механикой и Пи
Физики недавно обнаружили связь между многовековой известной математической формулой Пи и квантовой механики, которая скрывалась годами. Это было в 1665 году, когда известный британский математик Джон Уоллис представил свою собственную версию формулы вычисления Пи. Исследователи из Университета Рочестера считают, что они нашли ту же формулу, скрывающуюся при расчете энергетических уровней атома водорода.
Краткие факты
С 1998 года, каждый год 14 марта, научное сообщество празднует день Пи. Этот конкретный день был выбран из-за его соответствия с 3.14, который является пи значение. Первое широко посещаемое празднование дня пи было организовано физиком Ларри Шоу. Интересно, что Альберт Эйнштейн родился 14 марта 1879 года.
В 2002 году группа японских исследователей из Токийского университета вычислила 1,24 триллиона цифр числа пи, используя мощный суперкомпьютер Hitachi SR 8000, побив все предыдущие рекорды.
По мнению некоторых математиков, вместо того чтобы называть его Безугловым, гораздо правильнее сказать, что круг имеет бесконечное число углов.
ЧЕМУ РАВНО ЧИСЛО ПИ?
Что общего между колесом от Лады Приоры, обручальным кольцом и блюдцем вашего кота? Вы, конечно, скажете красота и стиль! Но я осмелюсь с вами поспорить. Число Пи! Это число, объединяющее все окружности, круги и округлости, к коим в частности можно отнести и мамино кольцо, и колесо от любимой папиной машины и даже блюдце любимого кота Мурзика. Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.
Что же такое число «Пи» и откуда оно взялось?
Современное обозначение числа π (Пи) появилось благодаря английскому математику Джонсу в 1706 году. Это первая буква греческого слова περιφέρεια (периферия, или окружность).
Для тех, кто проходил математику давно, да и к тому же мимо, напомним, что число Пи — это отношение длины окружности к её диаметру. Величина является константой, то есть постоянна для любой окружности, независимо от её радиуса. Люди знали об этом еще в древности. Так в древнем Египте число Пи принимали равным отношению 256 /81, а в ведических текстах приводится значение 339 /108, Архимед же предлагал соотношение 22 /7. Но ни эти, ни многие другие способы выражения числа Пи не давали точный результат.
Оказалось, что число Пи трансцендентное, соответственно, и иррациональное. А это значит, его нельзя представить в виде простой дроби. Если же его выразить через десятичную, то последовательность цифр после запятой устремятся в бесконечность, к тому же периодически не повторяясь. Что все это значит? Очень просто. Хотите узнать номер телефона понравившейся девушки? Его наверняка можно найти в последовательности цифр после запятой числа Пи.
Телефон можно посмотреть здесь ↓
Не нашли? Тогда посмотрите здесь.
Все в числе «Пи»
Вообще это может быть не только номер телефона, а любая информация, закодированная с помощью цифр. К примеру, если представить все произведения Александра Сергеевича Пушкина в цифровом виде, то они хранились в числе Пи еще до того, как он их написал, даже до того, как он родился. В принципе, они хранятся там до сих пор. Кстати, ругательства математиков в π тоже присутствуют, да и не только математиков.
Словом, в числе Пи есть всё, даже мысли, которые посетят вашу светлую голову завтра, послезавтра, через год, а может, через два. В это очень трудно поверить, но даже если мы представим, что поверили, еще труднее будет получить оттуда информацию и расшифровать её. Так что вместо того, чтобы копаться в этих цифрах, может проще подойти к понравившейся девушке и спросить у неё номер. Но для тех, кто не ищет легких путей, ну или просто интересующихся, чему же равно число Пи, предлагаю несколько способов его вычисления. Считайте на здоровье.
Чему равно число Пи? Методы его вычисления:
Экспериментальный метод.
Если число Пи это отношение длины окружности к её диаметру, то первый, пожалуй, самый очевидный способ нахождения нашей загадочной константы будет вручную произвести все измерения и вычислить число Пи по формуле π=l/d. Где l — длина окружности, а d — её диаметр. Все очень просто, необходимо лишь вооружится ниткой для определения длины окружности, линейкой для нахождения диаметра, и, собственно, длины самой нитки, ну и калькулятором, если у вас проблемы с делением в столбик. В роли измеряемого образца может выступить кастрюля или банка из под огурцов, неважно, главное? чтоб в основании была окружность.
Рассмотренный способ вычисления самый простой, но, к сожалению, имеет два существенных недостатка, отражающихся на точности полученного числа Пи. Во-первых, погрешность измерительных приборов (в нашем случае это линейка с ниткой), а во-вторых, нет никакой гарантии, что измеряемая нами окружность будет иметь правильную форму. Поэтому не удивительно, что математика подарила нам множество других методов вычисления π, где нет нужды производить точные измерения.
Ряд Лейбница.
Существует несколько бесконечных рядов, позволяющих точно вычислять число Пи до большого количества знаков после запятой. Одним из самых простых рядов является ряд Лейбница. π = (4/1) — (4/3) + (4/5) — (4/7) + (4/9) — (4/11) + (4/13) — (4/15) …
Все просто: берем дроби с 4 в числителе (это то что сверху) и одним числом из последовательности нечетных чисел в знаменателе (это то что снизу), последовательно складываем и вычитаем их друг с другом и получаем число Пи. Чем больше итераций или повторений наших нехитрых действий, тем точнее результат. Просто, но не эффективно, к слову, необходимо 500000 итераций чтоб получить точное значение числа Пи с десятью знаками после запятой. То есть, нам придется несчастную четверку разделить аж 500000 раз, а помимо этого полученные результаты мы должны будем 500000 раз вычитать и складывать. Хотите попробовать?
Ряд Нилаканта
Нет времени возится с рядом Лейбница? Есть альтернатива. Ряд Нилаканта, хотя он немного сложнее, но позволяет быстрее получить нам искомый результат. π = 3 + 4/(2*3*4) — 4/(4*5*6) + 4/(6*7*8) — 4/(8*9*10) + 4/(10*11*12) — (4/(12*13*14) … Думаю, если внимательно посмотреть на приведенный начальный фрагмент ряда, все становится ясным, и комментарии излишни. По этому идем дальше.
Метод «Монте-Карло»
Довольно интересным методом вычисления числа Пи является метод Монте Карло. Столь экстравагантное название ему досталось в честь одноименного города в королевстве Монако. И причина тому случайность. Нет, его не назвали случайно, просто в основе метода лежат случайные числа, а что может быть случайней чисел, выпадающих на рулетках казино Монте Карло? Вычисление числа Пи не единственное применение этого метода, так в пятидесятых годах его использовали при расчетах водородной бомбы. Но не будем отвлекаться.
Возьмем квадрат со стороной, равной 2r, и впишем в него круг радиусом r. Если наугад ставить точки в квадрате, то вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=Sкр/Sкв=πr 2 /(2r) 2 =π/4.
Теперь отсюда выразим число Пи π=4P. Остается только получить экспериментальные данные и найти вероятность Р как отношение попаданий в круг Nкр к попаданиям в квадрат Nкв. В общем виде расчетная формула будет выглядеть следующим образом: π=4Nкр / Nкв.
Хочется отметить, что для того, чтобы реализовать этот метод, в казино идти необязательно, достаточно воспользоваться любым более или менее приличным языком программирования. Ну а точность полученных результатов будет зависеть от количества поставленных точек, соответственно, чем больше, тем точнее. Желаю удачи 😉
Число Тау(Вместо заключения).
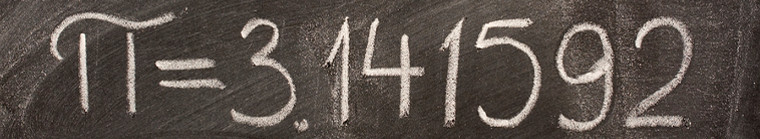
Число Пи.
Значение числа 
длины окружности к длине её диаметра, оно выражается бесконечной десятичной дробью.
Обозначается буквой греческого алфавита «пи». Старое название — лудольфово число.
Чему равно число пи? В простых случаях хватает знать первые 3 знака (3,14). Но для более
сложных случаев и там, где нужна бОльшая точность необходимо знать больше, чем 3 цифры.
Какое число пи? Первые 1000 знаков числа пи после запятой:
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989.
В обычных условиях приблизительное значение числа пи можно вычислить следуя пунктам,
Свойства числа Пи.
дроби m/n, где m и n являются целыми числами. Из этого видно, что десятичное представление
числа пи никогда не заканчивается и оно не является периодическим.
коэффициентами. В 1882 году профессор Кёнигсбергский доказал трансцендентность числа пи, а
позднее, профессором Мюнхенского университета Линдеманом. Доказательство упростил
Феликс Клейн в 1894 году.
то доказательство трансцендентности пи дало конец спору о квадратуре круга, длившемуся более
Но никто не знает, принадлежит ли 
Формула числа пи.
Пи (число)
Из Википедии — свободной энциклопедии
(Эта непрерывная дробь не периодическая. Записана в линейной нотации)
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
…
ЧИСЛО ПИ
Полезное
Смотреть что такое «ЧИСЛО ПИ» в других словарях:
число — Прие моч ное Источник: ГОСТ 111 90: Стекло листовое. Технические условия оригинал документа Смотри также родственные термины: 109. Число бетатронных колебаний … Словарь-справочник терминов нормативно-технической документации
число — сущ., с., употр. очень часто Морфология: (нет) чего? числа, чему? числу, (вижу) что? число, чем? числом, о чём? о числе; мн. что? числа, (нет) чего? чисел, чему? числам, (вижу) что? числа, чем? числами, о чём? о числах математика 1. Числом… … Толковый словарь Дмитриева
ЧИСЛО — ЧИСЛО, числа, мн. числа, чисел, числам, ср. 1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 знач.).… … Толковый словарь Ушакова
ЧИСЛО — абстрактное, лишенное особенного содержания обозначение какоголибо члена некоторого ряда, в котором этому члену предшествует или следует за ним какой нибудь др. определенный член; абстрактный индивидуальный признак, отличающий одно множество от… … Философская энциклопедия
Число — Число грамматическая категория, выражающая количественные характеристики предметов мысли. Грамматическое число одно из проявлений более обшей языковой категории количества (см. Категория языковая) наряду с лексическим проявлением («лексическое… … Лингвистический энциклопедический словарь
ЧИСЛО e — Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e kt, где k число,… … Энциклопедия Кольера
число — а; мн. числа, сел, слам; ср. 1. Единица счёта, выражающая то или иное количество. Дробное, целое, простое ч. Чётное, нечётное ч. Считать круглыми числами (приблизительно, считая целыми единицами или десятками). Натуральное ч. (целое положительное … Энциклопедический словарь
ЧИСЛО — ср. количество, счетом, на вопрос: сколько? и самый знак, выражающий количество, цифра. Без числа; нет числа, без счету, многое множество. Поставь приборы, по числу гостей. Числа римские, арабские или церковные. Целое число, ·противоп. дробь.… … Толковый словарь Даля
ЧИСЛО — ЧИСЛО, а, мн. числа, сел, слам, ср. 1. Основное понятие математики величина, при помощи к рой производится счёт. Целое ч. Дробное ч. Действительное ч. Комплексное ч. Натуральное ч. (целое положительное число). Простое ч. (натуральное число, не… … Толковый словарь Ожегова
ЧИСЛО Е — ЧИСЛО «Е» (ЕХР), иррациональное число, служащее основанием натуральных ЛОГАРИФМОВ. Это действительное десятичное число, бесконечная дробь, равная 2,7182818284590. является пределом выражения (1/ ) при п, стремящемся к бесконечности. По сути,… … Научно-технический энциклопедический словарь
Что особенного в числе Пи?
Буквально через 2 недели дату своего рождения празднует знаменитое число Пи. Про него говорят ученые, продолжают снимать фильмы и безудержно используют в высшей математике. Праздник для универсального числа пройдёт 14 марта в 1.59.26 ночи. Знатокам математики не трудно разгадать, почему именно этот весенний день считается именитым. А тем, кто не знают, но хочет получить ответ на загадку, узнать особенности числа Пи – наша статья в помощь.
Перед тем, как перейти к основным вопросам давайте ознакомимся с самым длинным числом. В 2011 году американскому учёному удалось вновь установить мировой рекорд и вычислить количество знаков числа Пи до 10 триллионов. Прежний рекорд был установлен тем же американским и японским экспертами, но количество знаков составляло 5 триллионов. Конечно ни один математик не сможет запомнить последовательность 10 триллионов цифр. Да и необходимости в этом нет. Для вычисления окружности с диаметром достаточно знать 39 цифр.
Число Пи история.
Знак Пи интересные особенности.
Интересный факт:
В марте 2011 года американский музыкант Майкл Блэйк решил создать из числа Пи мелодию. Он положил его на музыку. Чтобы эксперимент прошёл успешно, композитор взял 31 цифру после запятой. Распределил ноты для каждой, правда пришлось залезть в соседнюю октаву. С помощью квинтового круга назначил каждой цифре собственный аккорд. Провёл аранжировку мелодии в темпе 157 ударов в минуту. Получилась весьма интересная и бурная мелодия. Найти ее можно в любом интернет источнике.
Число Пи, что такое? Его краткая история
Число Пи знак математической константы. Он приравнивает отношение длины окружности к длине ее диаметра. Обозначать данное число названием «Пи» предложил британский математик Джонс в 1706 году. А уже в 1737 году число Пи приняло форму официального названия благодаря учёному математику Леонарду Эйлеру.
Но на самом деле значение существует уже больше 4000 лет. Ведь древнеегипетские математики подтвердили, что длина окружности к диаметру одинаковые для любой окружности. Значение равно чуть больше трёх.
Архимед, Хэн, Ариабхата – математические эксперты, которые на протяжение многих лет приближали число Пи к точному значению. Но самую приближённую цифру открыл китайский математик Цзу Чунчжи в 480-ых годах. На тот период число имело около 10 символов после запятой. Голландцу Людольфу удалось назвать ещё 20 знаков. Он потратил на это 20 лет жизни. Позже археологи нашли его дневник, в котором было указано следующие 15 чисел. На 1500 год значение Пи имело уже 35 цифр.
Как только в мире появились компьютерные системы, значение резко стало увеличиваться. Количество символов после запятой доросло до триллионов.
Число Пи, особенности и факты
Часто задаваемые вопросы про Пи значение
Чему равно число пи в математике
Чтобы ответить на вопрос, чему равно число пи, необходимо вспомнить некоторые его свойства:
Несмотря на всё вышеперечисленное учёные издревле пытались вычислить значение этой константы.
История вычисления константы пи
Ещё в третьем тысячелетии до нашей эры учёные из Древнего Египта, Месопатамии, Индии и Греции замечали, что соотношение длины и диаметра окружности всегда чуть больше трёх независимо от размеров окружности.
Изучение пи в древней Европе
Увеличивая количество углов в многоугольниках, Архимед повышал точность своей оценки. Когда он дошёл до 96 углов в многоугольнике, расчётное значение длины окружности оказалось больше, чем 3+10/71, но меньше, чем 3+1/7. Тогда Архимед выбрал верхнюю границу в качестве приблизительного значения константы пи. Согласно этому предположению, число пи равно 22/7 или 3,142857, если представить его в виде десятичной дроби. То есть, Архимед приблизился к числу пи с точностью до второго знака.
Во втором веке нашей эры дело Архимеда продолжил Клавдий Птолемей. Он довёл количество углов в многоугольнике до 720 и получил приблизительное значение числа пи 377/120 или 3,14166667. Клавдию Птолемею удалось высчитать константу пи с точностью до третьей цифры после запятой.
В шестнадцатом веке нашей эры математик из Голландии Лудольф ван Цейлен потратил десять лет на удваивание углов многоугольника и высчитал константу пи с точностью до двадцати знаков после запятой. Он завещал, чтобы найденные им цифры были выбиты на его надгробной плите. А саму константу стали называть числом Лудольфа.
Изучение числа пи в древнем Китае
Наряду с европейскими математиками, число пи пытались рассчитать и в Поднебесной. В третьем веке нашей эры математик из Китая Лю Хуэй вывел алгоритм, для расчёта константы пи с любой возможной степенью точности. В основу алгоритма легла всё та же идея Архимеда. По такому алгоритму самим Лю Хуэем было высчитано приближение пи для многоугольника с 3072 углами. Оно получилось равным 3,14159. Точность возросла до пятого знака после запятой. В пятом веке нашей эры математик Цзу Чунчжи Вычислил пи с точностью до семи цифр после запятой, расположив эту константу между 3,1415926 и 3,1415927.
Число пи: от средневековья до наших дней
В связи с развитием математического анализа во втором тысячелетии нашей эры для нахождения значения числа пи стали использоваться математические ряды:
Теория вероятностей тоже внесла свой вклад в вычисление пи с помощью метода Монте-Карло и Иглы Бюффона. Но с появлением компьютеров, а также открытием преобразования Фурье, использование рядов для вычисления значения пи позволило достигать астрономической точности.
Чему равно число пи?

Последнее зарегистрированное открытие, связанное с числом пи, было сделано в 2016 году. Американец Йи на пару с японцем Кондо высчитал десять триллионов цифр константы. Выучить их все, скорее всего, не удастся. Мировой рекорд по запоминанию цифр константы пи принадлежит индийскому студенту, запомнившему всего семьдесят тысяч знаков.
Сколько цифр из числа пи нужно знать зависит от требуемой точности вычислений. Держать в голове несколько сотен знаков константы пи имеет смысл только для тренировки памяти. Есть он-лайн калькуляторы, позволяющие высчитать пи с любой заданной точностью.
Как запомнить число пи?
Если же хочется держать в памяти более точное значение пи, чем выученные в школе 3,14, то на помощь придут мнемонические правила запоминания. Стишок С. Боброва из произведения «Волшебный двурог» позволяет запомнить число пи с точностью до тринадцати знаков после запятой:
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Другая разновидность мнемонических правил предлагает запоминать цифры из числа пи, сопоставляя их с количеством букв в каждом из слов стихотворения. Например:
Но многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.
Это маленькое четверостишие позволяет вспомнить до двадцати цифр числа пи после запятой.
Видео
Что такое число Пи?
Чему равно число Пи
Пи — это иррациональное число, то есть, его нельзя выразить простой дробью. Все дело в том, что число Пи, как его называют математики, является «бесконечной десятичной дробью», которое никогда не закончится.
Но к счастью, в использовании всех цифр π нет необходимости — его сокращают до 3,14 или до 3,14159. Но если вам интересно, на сайте piday.org содержатся цифры числа Пи до первого миллиона.
Как вычислили значение Пи
Число Пи известно уже почти 4000 лет — впервые его стали использовать древние вавилоняне. До нас дошли древние таблички примерно 1900-1680-х годов до н.э., на которых написано, что Пи равно 3,125. Древние египтяне тоже делали подобные открытия, о чем свидетельствует папирус Ринда 1650 года до н. э. В этом документе египтяне рассчитали площадь круга по формуле, которая также присваивает числу Пи приблизительное значение 3,1605.
Что такое число пи
Пи («π») представляет из себя математическую константу, полученную довольно интересным путем. Допустим, что диаметр окружность равен 1 условной единице. Тогда число π — это длина данной окружности, которая приблизительно равна 3,14 условных единиц. Говоря другими словами, число «пи» выражает соотношение между длиной окружности и ее диаметром. Это соотношение будет всегда постоянным.
Пи обладает рядом свойств.
Во-первых, число π иррационально, это означает, что его нельзя представить в виде правильной дроби. Значение 3,14 является достаточно приблизительным, доподлинно не известно, сколько же знаков после запятой у этой константы.
Во-вторых, число π — трансцендентное. Это означает, что оно никогда не может быть степенью какого-либо корня из другого числа. Говоря иначе, число π не является алгебраическим. Более того, если какое-либо число возвести в степень π, то опять же получится трансцендентное число.
Стоит отметить, что древние математики Египта, Греции, Рима, Сирии и Ирана уже знали, что соотношение между диаметром окружности и ее длиной является постоянной величиной. К примеру, в Вавилоне это соотношение оценивалось как 25/8, а в Египте как 256/81. Но наибольших успехов в вычислении значения числа π добился Архимед, который путем многократного описывания вокруг окружности и вписывания в нее правильных многоугольников добился довольно точных результатов. Периметр вписанного многоугольника Архимед принял за минимальное значение числа π, а описанного — за максимальное. Таким образом, Архимед вывел значение константы π, равное 3.142857142857143.
Забавно отметить, что существует праздник «День числа π», который празднуется 14 марта. Это происходит потому, что если записать числами день и дату праздника, то получится 3.14 — приблизительное значение данной константы. По другой версии, этот праздник надо отмечать 22 июля, так как 22/7 тоже является одним из первых соотношений, приблизительно равным 3.14
Новое в блогах
Почему число «Пи» так называется?
Тот факт, что отношение длины окружности к её диаметру является постоянной величиной (независимо от размеров окружности) заметили ещё в далекой древности. В Древнем Вавилоне при строительстве Вавилонской башни уже использовали значение Пи, округленное до 3-х целых. Математики древней Греции применяли уже более точное значение Пи (а именно 3.16). Но первым, кто серьезно занялся вычислением Пи, был Архимед. Он заменил длину окружности периметром вписанного в неё 96-угольника и, вычислив отношение, получил дробь «22/7» назвав его «архимедовым числом», которая в десятичном эквиваленте составляла 3,14286.
Тем не менее, до XVIII века число Пи не имело унифицированного названия. Одни говорили о нём, как о «числе, которое при умножении на диаметр дает длину окружности», другие называли «архимедовым числом» или «людольфовым числом» (в честь ученого Людольфа ван Цейлена, сумевшего вычислить число Пи до 20-го знака после запятой). Но в 1706 году математик из Англии Уильям Джонс выпустил книгу «Обозрение достижений математики», где впервые использовал букву греческого алфавита π (с буквы «пи» начинается слово περιμετρέ, что означает «измеряю вокруг»).
PS. На данный момент число π вычислено с точностью 31,4 триллионов десятичных знаков.
28 фактов о числе пи
Международный день знаменитой константы отмечается 14 марта
Почему именно 14 марта? Потому что 3-й месяц, 14 число. С константой пи знакомо большинство людей — отношение длины окружности к ее диаметру. Но что еще вы знаете о числе пи? Ниже 28 фактов, которые, возможно, будут любопытными.
.jpg) |
| Пай, посвященный числу пи. Источник: Wikipedia |
Пи в обществе
Пи и компьютеры
Случайные факты о пи
Шутки о пи
Пи в кино и телевидении
Пи в числах
Пи как число
Знак пи
У пи есть соперники
Эволюция пи
Число пи применение в жизни
Почти все мы узнали об этом загадочном числе, когда проходили обучение в школе. Но далеко не все из нас понимают его суть и силу. Ведь это необыкновенное число, которое люди изучают уже на протяжении 4000 лет. В нашей действительности оно используется практически везде — от расчётов прогноза погоды до больших данных по мировой статистике.


Число Пи обозначается символом греческой буквы П, который используется в математических формулах, вот уже на протяжении 250 лет. Букву греческого алфавита Пи для обозначения отношения длины окружности к её диаметру, самым первым использовал английский математик, Уильям Джонс, в 1706 году. Позднее, это обозначение было распространено в математическом сообществе с подачи Леонарда Эйлера.
Последовательность цифр, входящих в состав числа Пи, не повторяется и не оканчивается. Нельзя узнать абсолютно точного значения этого числа — ведь Пи иррациональное число, то есть, его цифры можно представить лишь в форме бесконечной непериодической десятичной дроби.
Также число Пи является трансцендентным числом. То есть, нет такого ряда из суммы дробей с рациональными числами которым бы равнялось число Пи.
Так как последовательность цифр числа Пи не имеет определённого порядка повторения, значит данная последовательность подчиняется теории хаоса, точнее, само число является выражением хаоса, записанным в виде цифровой записи.
Одно из первых упоминаний о числе Пи находится в математических текстах на папирусе древнеегипетского писца по имени Ахмес (около 1650 года до н. э.), известных сейчас, как папирус Ахмеса (Ринда). В нём содержится первая попытка вычисления числа Пи по «квадратуре круга», которая заключалась в измерении диаметра круга по созданным внутри квадратам.
Геометрически, число Пи находится как отношение длины окружности к длине её диаметра.
На пути вычисления числа Пи
Приближенное значение числа Пи знали несколько тысячелетий назад в Древнем Вавилоне и Египте.
Вычисление значения числа Пи математиками древности было основано на вписывании геометрических полигонов с большим количеством сторон, которые в зависимости от количества углов всё теснее вписывались в площадь круга. Для этих целей Архимед использовал 96-угольник.
Китайская цивилизация получила точное значение числа Пи намного раньше, чем западная. Ведь у китайцев было два преимущества: они применяли десятичную систему счисления и символ нуля. Так, китайский математик Лю Хуэй сумел вписать в окружность 192-угольник, а чуть позже — 3072-угольник.
Китайским математиком Цзу Чунчжи В 480-х годах н. э. было вычислено, что значением Пи примерно равно дроби 355/113. Используя алгоритм Лю Хуэя, применительно к 12288-угольнику он также он показал, что значение этого числа лежит в промежутке 3,1415926
14 сентября 2005 года, Николаем Скрипкой из Краснодара, был установлен рекорд России по запоминанию 6006 знаков числа «Пи». Свои необыкновенные способности он приписывает упорному труду и изучению всевозможных систем тренировки памяти.
В 1995 году, в Токийском радиовещательном центре был зафиксирован рекорд, установленный японцем Хирюоки Гото, который сумел воспроизвести по памяти 42 195 знаков числа Пи после запятой.
Житель Китая, Лю Чао, в 2006 году, в течение 1444 минут (без перерывов на пищу и посещение уборной) без ошибок воспроизвёл 67 890 знаков после запятой (со скоростью – 47 цифр/мин). Конечно, в его планы входило назвать 93 тыс. цифр, но он допустил ошибку на 67891 позиции.
Однако, другой японец Акира Харагучи, в 2005 году, сумел воспроизвести 83 431 цифры после запятой. Перечислять цифры он начал днём в пятницу, а закончил только к утру в субботу. Как утверждает Харагучи, он остановился на этом знаке только лишь потому, что его попросили покинуть заведение, которое закрывалось в 8 часов вечера.
Прочие факты о числе Пи
У числа Пи имеется два неофициальных праздника. Первый из них, отмечается в день 14 марта, в связи с тем, что дата этого дня в США записывается, как 3.14. Второй праздник отмечается 22 июля, дата которого записывается в европейском формате дат, как 22/7, что в результате деления этой дроби является приближённым значением числа Пи.
Использование числа Пи, с точностью до девятого знака, при расчётах длины экватора Земли даёт погрешность около 6 миллиметров.
На полях в Великобритании, в 2008 году, появились таинственные круги, в которых учёные сумели определить зашифрованную последовательность первых 10 цифр числа Пи.
Число Пи также было найдено в квантовой механике. Физик Карл Хаген и математик Тамар Фридман из Рочестерского университета в штате Нью-Йорк вывели формулу для числа Пи из квантовой механики. Они использовали вариационный принцип для определения энергетических уровней атома водорода.
В данном случае траектория электрона в атоме водорода описывается методами классической физики и расположена на сфере. Из конечного выражения для подобного энергетического уровня ученым удалось найти формулу для вычисления числа Пи.
Это выражение исследователями было записано в виде формулы Валлиса, представляющей собой произведение бесконечного числа множителей и была получена ещё в 1655 году английским математиком Джоном Валлисом.
В начале 2000-х годов немецкий математик Герард Штеффенс выяснил, что для доменного имени существует предел в 63 символа, и определил, какие длинные имена уже были разобраны. Свой домен 3.141592653589793238462643383279502884197169399375105820974944592.com он приобрел у индийца, который хвастался тем, что адрес его домена стал первым из самых длинных имён.
При этом, учёный способен по памяти воспроизвести все цифры доменного имени сайта, которым он владеет. Однако, самым интересным фактом, является то, что на сайте есть предложение автора отыскать или угадать страницу, на которой по его заверениям отображается 1 миллион знаков числа Пи. При этом, какой-либо конкретной ссылки на эту страницу вы не найдете.
Кстати существует сайт pi.com, на котором вы найдете лишь запись из нескольких знаков числа Пи. Обратиться к автору можно только перечислив любым из предлагаемых способов 3 доллара.
1 апреля 1998 года учеными из организации «New Mexicans for Science and Reason» была опубликована заметка о том, что законодательными органами власти штата Алабама было принято постановление об изменении значения числа «Пи» с 3,1415 на 3,0. Статья была подхвачена интернет-сообществом и получила большую огласку в сети. Люди начали тревожить настойчивыми звонками алабамских чиновников, высказывая протесты против этих нововведений.
Число Пи в искусстве
В фантастическом романе «Связь» Карла Франсуа Сагана учеными предпринимается попытка определить более точное значение числа Пи, чтобы найти скрытые сообщения от создателей человеческой расы и открыть миру доступ к «более глубоким уровням вселенских знаний».
В 1998 году художественный фильм «Пи: Вера в хаос» режиссера Даррена Аронофски получил премию за лучшую режиссуру драматического фильма на кинофестивале Сандэнс. По сюжету, главный герой ищет простые ответы на вопросы, связанные с числом Пи, что сводит его с ума.
Вместе с увеличением диаметра окружности, увеличивается и сама окружность – звучит просто. Но их связь гораздо теснее. Если длину разных окружностей разделить на их диаметр, то мы будем получать постоянное значение – число Пи. «Пи» происходит от греческого слова «периферия», окружность.
Историки все еще не знают, когда и как люди получили пи, но то что отношение длины к окружности – постоянное число, равное чуть больше трех, было известно на протяжении нескольких тысячелетий. Не совсем точные расчеты числа пи можно обнаружить в работах египетских, вавилонских, индийских, китайских и древнегреческих геометров. По легенде Вавилонскую башню строили, используя число пи. И виной ее обрушения стал не гнев божий, а неправильные вычисления. Первым, кто попытался вычислить пи математическим способом, был Архимед. Для этого он использовал 96-угольник.
Когда же подсчитают точное число пи вместо того, чтобы использовать приблизительное?
Никогда. Поскольку число Пи иррационально, оно не может быть записано в виде дроби. Даже если подсчитать его с максимальной точностью, всегда будет небольшой остаток.
Люди даже проводят соревнования в способности запомнить как можно больше чисел после запятой. Согласно книге рекордов Гиннеса, 21 марта 2015 года индийский студент Раджвир Мина за девять часов воспроизвел около 70000 знаков. Для запоминания числа пи разработано много техник: например, написание текстов, в которых слова имеют такое же количество букв, что и соответствующая цифра после запятой.
Но, чтобы использовать пи в науке, достаточно знать первые 40 чисел.
Использование числа пи в науке
В любых математических расчетах есть окружности: начиная от предметов на нашем рабочем столе и заканчивая орбитами космических спутников. Также пи используют при описании гармонических колебаний (начальная фаза, период и т.д.).
Число Пи помогает статистам подсчитать площадь ниже кривой нормального распределения – на ее основе создаются финансовые модели и измеряется погрешности в научных расчетах.
По-настоящему удивляет тот факт, что пи использовали для подсчета плотности целой Вселенной, в которой, к слову, неизмеримо меньше материи, чем цифр в числе пи.
В математике существует бесконечное множество различных чисел. Большинство из них совершенно не привлекает внимания. Однако некоторые, на первый взгляд, абсолютно неинтересные числа известны настолько, что имеют даже свои имена. К одной из таких констант относится и иррациональное число Пи, изучаемое ещё в школе и используемое для расчёта площади или периметра окружности по заданному радиусу.
Из истории константы
Интересные факты о числе Пи — история изучения. Существование постоянной рассчитывает около 4 тысячелетий. Иными словами, она немного моложе самой математической науки.
Первое свидетельство того, что число Пи было известно ещё в Древнем Египте, заключается в папирусе Ахмеса, одном из старейших найденных задачников. Документ датируется приблизительно 1650 г. до н. э. В папирусе константа принималась равной 3,1605. Это достаточно точное значение, если учесть, что другие народы использовали 3 для вычисления длины окружности по её диаметру.
Немного более точно число Пи рассчитал Архимед, древнегреческий математик. Ему удалось приближённо представить значение в виде обыкновенных дробей 22/7 и 223/71. Известно предание, что он был настолько занят расчётами константы, что не обратил внимания на то, как римляне захватили его город. В тот момент, когда воин подошёл к учёному, Архимед крикнул ему, чтобы тот не трогал его чертежи. Эти слова математика стали последними.
Над расчётами постоянной работал основатель алгебры Аль-Хорезми, живший в VIII-IX вв. С небольшой погрешностью он получил число Пи, равное 3,1416.
Спустя 8 веков математиком Людольфом ван Цейленом были правильно определены 36 символов после запятой. За это достижение число Пи иногда называют людольфовой постоянной (другие известные наименования – архимедова константа или круговая постоянная), а полученные учёным цифры были выбиты на его могильной плите.
Примерно в это же время постоянную начали применять не только для окружности, но и для вычисления сложных кривых – арки и гипоциклоида.
Лишь в начале XVIII века константу начали называть числом Пи. Обозначение в виде буквы π выбрано неслучайно – именно с неё начинаются 2 греческих слова, означающих окружность и периметр. Название было предложено учёным Джонсом в 1706 году, и уже спустя 30 лет изображение этой греческой буквы прочно использоваться среди других математических обозначений.
В XIX веке Уильям Шенкс работал над вычислением первых 707 символов константы. Ему не удалось полностью добиться поставленной задачи – в расчёты закралась ошибка, и 527 цифра оказалось неверной. Однако даже полученный результат был неплохим достижением для науки того времени.
В конце XIX века неправильное значение числа, равное 3,2, чуть было не приняли на уровне государства в штате Индиана. К счастью, математики успели выступить против законопроекта и предотвратить ошибку.
В XX-XXI вв. с применением вычислительной техники точность и скорость расчёта константы повысилась в тысячи раз. К 2002 году в Японии при помощи компьютера было определено свыше 1 триллиона цифр постоянной. Спустя 9 лет точность вычисления составила уже 10 триллионов символов после запятой.
В искусстве и маркетинге
Несмотря на то, что Пи – это математическая константа, на протяжении многих лет люди пытались использовать иррациональное и загадочное значение и в других сферах жизни, в том числе в произведениях искусства.
Самые первые признаки постоянной были найдены в памятнике архитектуры в Гизе. При определении размеров Великой пирамиды выяснилось, что отношение периметра её основания к высоте равно π. Неизвестно только, хотел ли использовать архитектор свои знания об этом числе, или такое соотношение вышло случайно.
В настоящее время число Пи также не обделено вниманием в творчестве. К примеру, если обозначить каждую ноту минорной гаммы цифрой от 0 до 9, а затем наиграть полученную последовательность в виде числа Пи на музыкальном инструменте, можно насладиться необычной мелодией с интересным звучанием.
Постоянная также не обошла стороной кинематограф. Драматический фильм под названием «Пи: вера в хаос» получил награду за лучшую режиссуру на фестивале кино Санденс. По сюжету главный герой находится в поисках простых и понятных ответах на вопросы о константе, что в результате почти довело его до сумасшествия. Упоминания числа встречаются также в других кинофильмах и сериалах.
Своё применение число нашло даже в такой неожиданной области, как маркетинг. Так, компанией Гивенчи был выпущен одеколон под названием «Пи».
Константа и общество
Некоторые особенностей числа:
С целью обмена информацией об открытиях был учреждён Пи-клуб. Желающим вступить в него приходится выдерживать нелёгкий экзамен: будущий член математического сообщества должен верно назвать на память как можно больше знаков постоянной.
Конечно, заучивание длинной числовой последовательности, не имеющей закономерностей и повторений — занятие достаточно трудное. Чтобы облегчить задачу, придумываются различные тексты и стихотворения, в которых количество букв в слове соответствует определённой цифре константы. Этот способ запоминания популярен у членов Пи-клуба. Один из самых длинных рассказов содержал 3834 первых знаков числа.
Однако признанные рекордсмены по заучиванию – это, конечно же, жители Китая и Японии. Так, японец Акира Харагути смог выучить свыше 83 тысяч цифр после запятой. А китаец Лю Чао прославился как человек, который смог назвать 67890 символов числа Пи за рекордное время – 24 часа. При этом средняя скорость составила 47 знаков за 1 минуту. Изначально его цель была назвать 93 тысячи цифр, однако им была допущена ошибка, после которой он не стал продолжать.
Чтобы подчеркнуть значение константы, в Сиэтле перед Музеем искусств был воздвигнут памятник в виде огромной греческой буквы π.
Кроме того, с 1988 года каждое 14 марта отмечается день числа Пи. Дата совпадает с первыми знаками постоянной – 3,14. Празднуют его после 1:59. В этот день заинтересованные люди угощаются тортами и печеньем с символом Пи, после чего проводят различные математические конкурсы и викторины. Кстати, именно в этот день родились А.Эйнштейн, астроном Скиапарелли и космонавт Сернан.
Число Пи – удивительная константа, которая нашла своё применения в самых разных областях, начиная от техники и строительства и заканчивая сферами искусства. Как и любая другая величина, которая применяется часто и которую невозможно вычислить полностью, она всегда будет привлекать к себе внимание математиков, физиков и других учёных.