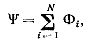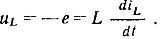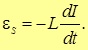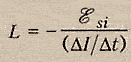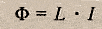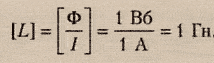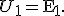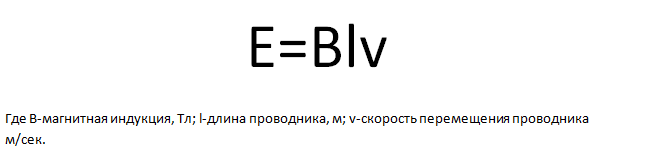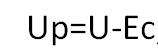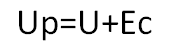Что такое индуктивность
Что такое индуктивность
Что такое индуктивность

В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электрического поля и преобразование электрической энергии в другие виды энергии, в частности в тепловую.
Количественно способность реального и идеализированного элементов электрической цепи запасать энергию магнитного поля характеризуется параметром, называемым индуктивностью.
Таким образом термин «индуктивность» применяется как название идеализированного элемента электрической цепи, как название параметра, количественно характеризующего свойства этого элемента, и как название основного параметра индуктивной катушки.
Рис. 1. Условное графическое обозначение индуктивности
Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости изменения потокосцепления катушки ψ и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:
Потокосцепление катушки равно алгебраической сумме магнитных потоков пронизывающих ее отдельные витки:
где N — число витков катушки.

Первая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, вторая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и постоянных магнитов. Если вторая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее называют магнитным потоком взаимоиндукции.

здесь еси — ЭДС самоиндукции, евп — ЭДС внешних полей.
Если магнитные потоки внешних по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.
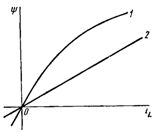
В частном случае, например для катушки без магнитного сердечника, эта зависимость может быть линейной (рис. 2, кривая 2).
В системе единиц СИ индуктивность выражают в генри (Гн).
При анализе цепей обычно рассматривают не значение ЭДС, наведенной в катушке, а напряжением на ее зажимах, положительное направление которого выбирают совпадающим с положительным направлением тока:
Для линейной индуктивности напряжение на ее зажимах пропорционально скорости изменения тока. При протекании через индуктивность постоянного тока напряжение на ее зажимах равно нулю, следовательно, сопротивление индуктивности постоянному току равно нулю.
Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Катушка индуктивности
Что такое катушка индуктивности
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
В — магнитное поле, Вб
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
U — напряжение в катушке, В
R — сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
1 — это каркас катушки
2 — это витки катушки
3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Отдалим витки катушки друг от друга
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Индуктивность
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.
Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.
Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
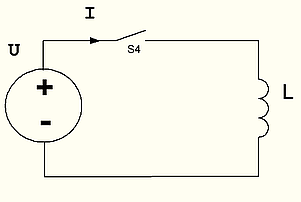
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.
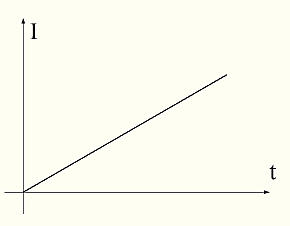
При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?
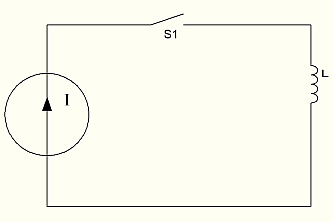
Ну тут из серии «кто кого заборет — слон или кит».
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16

Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.
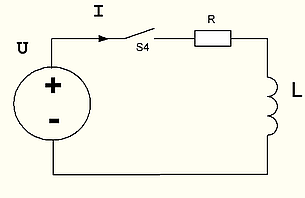
На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.
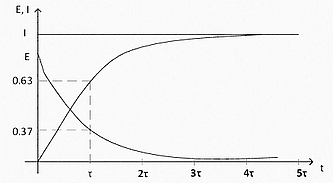
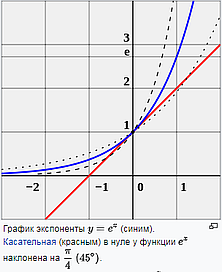
зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.
Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.
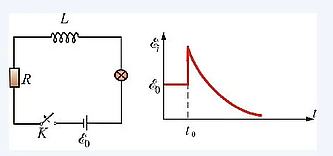
Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь
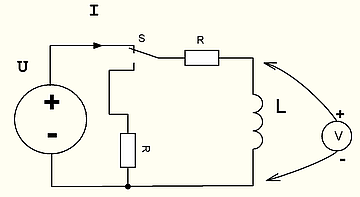
Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.
Что такое индуктивность
Индуктивность – это элемент цепи, где происходит накопление энергии от магнитного поля. Так происходит запас поля или его преобразование в иные виды энергий. Самым идеальным примером служит катушка индуктивности. В ней происходит запасание поля и его дальнейшее преобразование в энергию других видов, в том числе и тепловую. Способность накапливать магнитное поле и является индуктивностью. Индуктивность напрямую связана с электромагнитной индукцией, статья о которой, также есть на нашем сайте. В данной статье будет описано данное физическое явление, как оно происходит, а также как используется на практике, в чем измеряется и как можно рассчитать физические характеристики. Дополнениями служат два ролика и одна статья, по выбранной теме.
Индуктивность в цепи переменного тока
Прохождение электрического тока по проводнику или катушке сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока, в которую включена катушка индуктивности, имеющая небольшое количество витков проволоки сравнительно большого сечения, активное сопротивление которой можно считать практически равным нулю. Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
Электродвижущая сила самоиндукции, согласно правилу Ленца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э. д. с. генератора, то она препятствует прохождению переменного тока. При расчетах это учитывается по индуктивному сопротивлению, которое обозначается XL и измеряется в омах.
Таким образом, индуктивное сопротивление катушки XL, зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ω) и от индуктивности катушки L
Так как угловая частота переменного тока ω = 2πf, то индуктивное сопротивление
где f — частота переменного тока, гц.
Индуктивностью называется идеализированный элемент электрической цепи, в котором происходит запасание энергии магнитного поля. Запасания энергии электрического поля или преобразования электрической энергии в другие виды энергии в ней не происходит.
Пример. Катушка, обладающая индуктивностью L = 0,5 гн, присоединена к источнику переменного тока, частота которого f = 50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f = 50 гц;
2) индуктивное сопротивление этой катушки переменному току, частота которого f = 800 гц.
Решение. Индуктивное сопротивление переменному току при f = 50 гц
При частоте тока f = 800 гц
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивление катушки XL равно нуло. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется з. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток. Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д. с. самоиндукции изменяет свое направление и увеличивается, препятствуя убыванию силы тока. В третью четверть периода ток изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
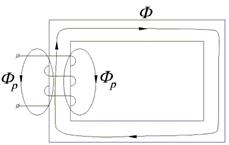
Из сказанного следует, что ток в цепи и э. д. с. самоиндукции не совпадают по фазе. Ток опережает э. д. с. самоиндукции по фазе на четверть периода или на угол φ = 90°. Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U. В связи с этим напряжение и э. д. с. самоиндукции ес также сдвинуты по фазе друг относительно друга на 180°.
Из изложенного следует, что в цепи переменного тока, содержащей только индуктивность, ток отстает от напряжения, вырабатываемого генератором, на угол φ = 90° (на четверть периода) и опережает э. д. с. самоиндукции на 90°. Можно также сказать, что в индуктивной цепи напряжение опережает по фазе ток на 90°. Построим векторную диаграмму тока и напряжения для цепи переменного тока с индуктивным сопротивлением. Для этого отложим вектор тока I по горизонтали в выбранном нами масштабе.
Чтобы на векторной диаграмме показать, что напряжение опережает по фазе ток на угол φ = 90°, откладываем вектор напряжения U вверх под углом 90°. Закон Ома для цепи с индуктивностью можно выразить так:
[stextbox подчеркнуть, что имеется существенное отличие между индуктивным и активным сопротивлением переменному току. Когда к генератору переменного тока подключена активная нагрузка, то энергия безвозвратно потребляется активным сопротивлением.[/stextbox]
Если же к источнику переменного тока присоединено индуктивное сопротивление r = 0, то его энергия, пока сила тока возрастает, расходуется на возбуждение магнитного поля. Изменение этого поля вызывает возникновение э. д. с. самоиндукции. При уменьшении силы тока энергия, запасенная в магнитном поле, вследствие возникающей при этом э. д. с. самоиндукции возвращается обратно генератору.
Таким образом, в первую и третью четверть каждого периода генератор переменного тока расходует свою энергию в цепи с индуктивностью на создание магнитного поля, а во вторую и четвертую четверть каждого периода энергия, запасенная в магнитном поле катушки в результате возникающей э. д. с. самоиндукции, возвращается обратно генератору.
Из этого следует, что индуктивная нагрузка в отличие от активной в среднем не потребляет энергию, которую вырабатывает генератор, а в цепи с индуктивностью происходит «перекачивание» энергии от генератора в индуктивную нагрузку и обратно, т. е. возникают колебания энергии. Из сказанного следует, что индуктивное сопротивление является реактивным. В цепи, содержащей реактивное сопротивление, происходят колебания энергии от генератора к нагрузке и обратно.
Индуктивность и емкость в цепи переменного тока
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:
u = Uм sin (ϕ + ωt),
e = Ɛm sin (ψ + ωt).
Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:
В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X L, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:
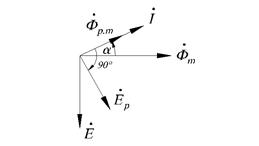
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;
Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное X L и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:
и имеет индуктивный характер при X L > Хс и емкостный характер при X L 2 R
Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при X L=X C.)
Устройство катушки
Более близким к идеализированному элементу — индуктивности — является реальный элемент электронной цепи — индуктивная катушка. В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электронного поля и преобразование электронной энергии в другие виды энергии, а именно в термическую. Количественно способность реального и идеализированного частей электронной цепи припасать энергию магнитного поля характеризуется параметром, именуемым индуктивностью.
Таким макаром термин «индуктивность» применяется как заглавие идеализированного элемента электронной цепи, как заглавие параметра, количественно характеризующего характеристики этого элемента, и как заглавие основного параметра индуктивной катушки.
Связь меж напряжением и током в индуктивной катушке определяется законом электрической индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости конфигурации потокосцепления катушки ψ и направленная таким макаром, чтоб вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:
В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).
Магнитный поток Ф, пронизывающий любой из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции Фси и магнитный поток наружных полей Фвп: Ф — Фси + Фвп.
1-ая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, 2-ая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и неизменных магнитов. Если 2-ая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее именуют магнитным потоком взаимоиндукции.
Потокосцепление катушки ψ, так же как и магнитный поток Ф, может быть представлено в виде суммы 2-ух составляющих: потокосцепления самоиндукции ψси, и потокосцепления наружных полей ψвп
Наведенная в индуктивной катушке ЭДС е, в свою очередь, может быть представлена в виде суммы ЭДС самоиндукции, которая вызвана конфигурацией магнитного потока самоиндукции, и ЭДС, вызванной конфигурацией магнитного потока наружных по отношению к катушке полей:
тут еси — ЭДС самоиндукции, евп — ЭДС наружных полей.
Если магнитные потоки наружных по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.
Индуктивность
Полезное
Смотреть что такое «Индуктивность» в других словарях:
Индуктивность — Размерность L2MT−2I−2 Единицы измерения СИ Гн СГС … Википедия
ИНДУКТИВНОСТЬ — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия
ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ… … Современная энциклопедия
индуктивность — индуктивность; статическая индуктивность; отрасл. коэффициент самоиндукции Скалярная величина, характеризующая связь потокосцепления самоиндукции с током в рассматриваемой электрической цепи, равная отношению потокосцепления самоиндукции этой… … Политехнический терминологический толковый словарь
индуктивность — Скалярная величина, равная отношению потокосцепления самоиндукции элемента электрической цепи к электрическому току в нем. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия Синонимы собственная индуктивность … Справочник технического переводчика
Индуктивность — ИНДУКТИВНОСТЬ, физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ… … Иллюстрированный энциклопедический словарь
ИНДУКТИВНОСТЬ — физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ измеряется в… … Большой Энциклопедический словарь
ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, свойство электрической цепи или элемента цепи, создающий ЭЛЕКТРОДВИЖУЩУЮ СИЛУ (ЭДС) при изменении электрического тока. В системе СИ единицей измерения служит ГЕНРИ. Самоиндукция (обозначение L) имеет место при протекании тока по… … Научно-технический энциклопедический словарь
ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, индуктивности, мн. нет, жен. (книжн. спец.). отвлеч. сущ. к индуктивный. Ииндуктивность доказательств. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ИНДУКТИВНОСТЬ — мера магнитной энергии, возникающей вокруг данной цепи, когда через нее проходит определенный электрический ток. Наличие индуктивности всегда тормозит процесс изменений тока. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское… … Морской словарь
ИНДУКТИВНОСТЬ — свойство магнитного поля, создаваемого током проводника, при изменениях величины этого тока возбуждать в проводнике так наз. электродвижущую силу самоиндукции. Энергия возникающих при этом в проводнике индукционных токов образуется за счет… … Технический железнодорожный словарь
ИНДУКТИВНОСТЬ



Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф
B), индукция пропорциональна силе тока в проводнике
(B
I), следовательно магнитный поток пропорционален силе тока (Ф
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Также индуктивность можно рассчитать по формуле:
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды
Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:
Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.
Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E1 и с действующим значением напряжения U1. На вторичной обмотке ЭДС E2 и напряжение U2.
Из законов Ома 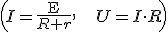
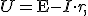
где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r1 делают очень малым, поэтому часто им можно пренебречь. Тогда
Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e1, как и ЭДС индукции e2 в каждом витке первичной обмотки, т.е. e1 = e2. Следовательно, отношение ЭДС в первичной E1 и вторичной E2 обмотках равно отношению числа витков в них:
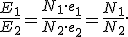
Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I1/I2 приблиз = w1/w2 = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником
часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Фр (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен
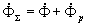 . . | (1.14) |
На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:
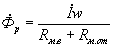 . . |
Так как 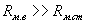
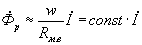
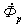
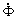
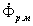
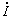
Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником
Индуктивность и дроссели
Что такое индуктивность
Что такое индуктивность — это физическая величина, которая рассказывает нам о магнитных свойствах электрической цепи. Индуктивность измеряют в Гн (Генри).
Если вы вообще не понимаете о чём речь, то советую ознакомиться сначала с вот с этой статьей.
В электрических схемах например, нам встречаются какие-то непонятные катушки, дроссели и многие даже не знают их функциональную роль. В этой статье я постараюсь доступным языком рассказать, что такое индуктивность и как это явление применить на своей любимой работе.
Давайте посмотрим на рисунок
Давайте начнём движение проводника в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, то тогда в нашем проводнике появляется электродвижущая сила (ЭДС). Или наоборот проводник остаётся на месте, а магнит передвигают таким образом, чтобы силовые линии магнита пересекали проводник. Сейчас был пример электромагнитной индукции. Значение индуцированной электродвижущей силы в проводнике прямо пропорциональна магнитной индукции поля, скорости перемещения и длине проводника
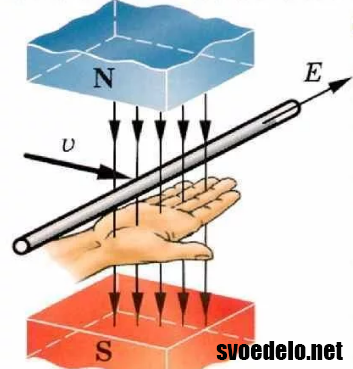
Направление возникшей электродвижущей силы в проводнике определяют через правило правой руки.
Правая рука находится в таком положении чтобы силовые линии магнита заходили в ладонь. Следовательно, большой палец показывает нам направление перемещения проводника, а остальные пальцы покажут нам направление возникшей электродвижущей силы.
Для усиления электродвижущей силы индукции применяют электрические катушки
А если подать напряжение на катушку, то по её виткам потечёт ток, который создаёт своё магнитное поле.
Закон Ленца
Закон Ленца говорит нам, что индуцированный ток направлен так, чтобы препятствовать той причине, которая его вызвала. Например, подаём мы на катушку напряжение. В катушке образуется магнитное поле которое в момент включения пересекает витки катушки и наводит там электродвижущую силу самоиндукции. По закону Ленца индуцированная ЭДС самоиндукции будет направлена навстречу току который её вызвал.
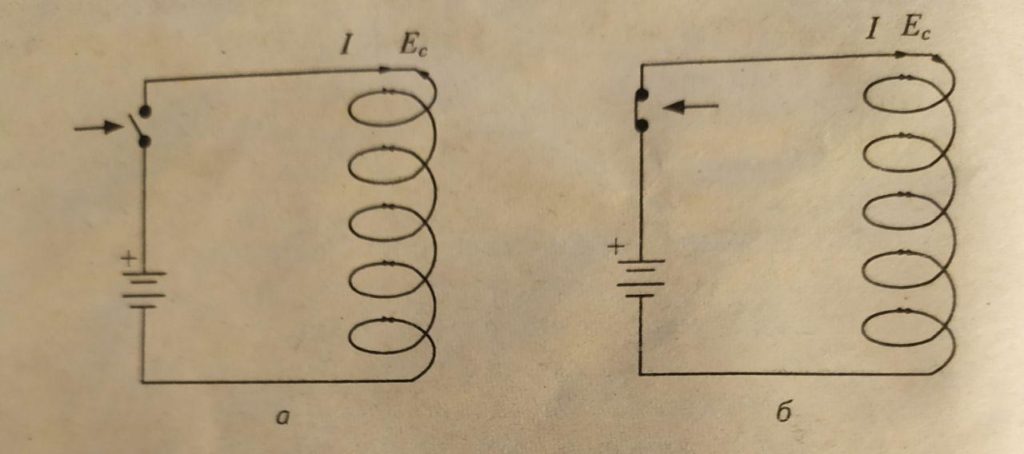
Если подавать (а) и снимать (б) напряжение с катушки, то произойдёт следующее. Магнитное поле будет то появляться, то исчезать. В результате изменяющееся магнитное поле будет пересекать витки катушки и индуцировать в ней ЭДС.
Новое понятие ЭДС самоиндукции. Давайте рассмотрим её поподробнее.
ЭДС самоиндукции
Если подавать и снимать напряжение с электрической катушки, то магнитное поле будет появляться, исчезать, появляться, исчезать… В итоге получаем магнитное поле, которое постоянно меняется. Проходя через витки катушки магнитное поле будет индуцировать в ней электродвижущую силу, которая называется ЭДС самоиндукции.
Коэффициент самоиндукции – это величина ЭДС самоиндукции, возникающей при изменении тока в единицу времени. Коэффициент самоиндукции измеряется в Генри (Гн).
Индуктивностью в 1 Генри обладает катушка. В которой при изменении тока на 1 Ампер в 1 секунду возникает ЭДС самоиндукции в 1 Вольт.
Давайте напряжение цепи катушки обозначим через U, результирующее напряжение Uр, а ЭДС самоиндукции Ес, тогда получим следующие формулы:
В момент замыкания цепи результирующее напряжение будет следующим:
А в момент размыкания цепи:
Величина ЭДС самоиндукции может многократно превышать напряжение источника тока. Поэтому при размыкании цепей с большой индуктивностью появляется дуга, и соответственно обгорают контакты.
Что такое дроссель
Дроссель — это вид катушки индуктивности, которая оказывает высокое сопротивление переменному току и малое постоянному.
Применяется дроссель в следующих случаях:
И это только перечислена маленькая часть того где применяются дроссели.
Давайте представим, что у нас стоит дроссель перед электродвигателем. И в какой-то момент происходит скачок тока, что происходит: Мы знаем, что в момент пропускания тока через дроссель, формируется электромагнитное поле вокруг катушки. А для формирования поля нам нужна энергия, поэтому в самом начале протекания тока он тратится на формирование электромагнитного поля. По закону Ленца, мы знаем, что ток в катушке не может измениться мгновенно. А явление самоиндукции при изменении тока, направлено навстречу основному току. Таким образом дроссель просто скушает скачок тока в сети.
Индуктивность и явление самоиндукции
Люди, чья профессия или хобби связано с электрическим током, должны знать и разбираться в таких понятиях, как индуктивность и самоиндукция. Ведь подобные явления довольно часто используются в современном мире.
Что такое самоиндукция — для чайников
Любой электронный проводник имеет переменное магнитное поле, которое порождает дополнительный, так называемый индукционный ток. И если рассматривать в качестве проводника – электрическую цепь, то при изменении силы тока в ней изменится и магнитное поле, которое спровоцирует возникновение вихревого электрического поля.
Подобные явления станут причиной появления электродвижущей силы (ЭДС) в той же самой цепи, что и является самоиндукцией. Таким образом, самоиндукцией считается явление, во время которого в электрическом проводнике возникает ЭДС из-за изменения тока в самом проводнике. Именно самоиндукция мешает току приобрести определенное значение при резком замыкании или размыкании электрической цепи, так как ЭДС в проводнике во время нарастания тока направлена в противоположную сторону относительно источника питания и наоборот во время его уменьшения.
Явление самоиндукции можно наглядно увидеть при включении или выключении 2 одинаковых ламп, которые соединены параллельно.
При этом ЭДС самоиндукции можно рассчитать по формуле:
ЭДС измеряется в вольтах, когда единицей измерения магнитного поля является вебер.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Польза и вред
Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.
Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.
Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.
Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.
Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.
Что такое индуктивность, в чём измеряется, основные формулы
Индуктивность характеризует свойства элементов электрической цепи накапливать энергию магнитного поля. Также это мера связи между током и магнитным полем. Ещё её сравнивают с инерцией электричества – также, как массу с мерой инерции механических тел.
Явление самоиндукции
Если ток, идущий через проводящий контур, изменяется по величине, то возникает явление самоиндукции. В этом случае изменяется магнитный поток через контур, и на выводах рамки с током возникает ЭДС, называемая ЭДС самоиндукции. Эта ЭДС противоположна направлению тока и равна:
Очевидно, что ЭДС самоиндукции равна скорости изменения магнитного потока, вызванного изменением протекающего по контуру тока, а также пропорциональна скорости изменения тока. Коэффициент пропорциональности между ЭДС самоиндукции и скоростью изменения тока называется индуктивностью и обозначается L. Эта величина всегда положительна, и имеет единицу измерения в СИ 1 Генри (1 Гн). Также используются дробные доли – миллигенри и микрогенри. Об индуктивности в 1 Генри можно говорить, если изменение тока на 1 ампер вызывает ЭДС самоиндукции в 1 Вольт. Индуктивностью обладает не только контур, но и отдельный проводник, а также катушка, которую можно представить как множество последовательно включенных контуров.
В индуктивности запасается энергия, которую можно вычислить, как W=L*I 2 /2, где:
И здесь энергия прямо пропорциональна индуктивности катушки.
Важно! В технике индуктивностью также называется устройство, в котором происходит запасание электрического поля. Реальный элемент, наиболее близкий к такому определению – катушка индуктивности.
Общая формула для расчета индуктивности физической катушки имеет сложный вид и для практических вычислений неудобна. Полезно запомнить, что индуктивность пропорциональна количеству витков, диаметру катушки и зависит от геометрической формы. Также на индуктивность влияет магнитная проницаемость сердечника, на котором расположена обмотка, но не влияет ток, протекающий по виткам. Для вычисления индуктивности каждый раз надо обращаться к приведенным формулам для конкретной конструкции. Так, для цилиндрической катушки её основная характеристика вычисляется по формуле:
Для вычисления индуктивности для цилиндрической катушки и катушек других форм лучше воспользоваться программами-калькуляторами, в том числе онлайн-калькуляторами.
Последовательное и параллельное соединение индуктивностей
Индуктивности можно соединять последовательно или параллельно, получая набор с новыми характеристиками.
Параллельное соединение
При параллельном соединении катушек напряжение на всех элементах равны, а токи (переменные) распределяются обратно пропорционально индуктивностям элементов.
Общая индуктивность цепи определяется, как 1/L=1/L1+1/L2+1/L3. Формула справедлива для любого количества элементов, а для двух катушек упрощается до вида L=L1*L2/(L1+L2). Очевидно, что итоговая индуктивность меньше индуктивности элемента с наименьшим значен
Последовательное соединение
При таком виде соединения через цепь, составленную из катушек, течёт один и тот же ток, а напряжение (переменное!) на каждом компоненте цепи распределяется пропорционально индуктивности каждого элемента:
Суммарная индуктивность равна сумме всех индуктивностей, и будет больше индуктивности элемента с наибольшим значением. Поэтому такое соединение используют при необходимости получить увеличение индуктивности.
Важно! При соединении катушек в последовательную или параллельную батарею формулы расчёта верны только для случаев, когда исключено взаимное влияние магнитных полей элементов друг на друга (экранировкой, большим расстоянием и т.д.). Если влияние существует, то общее значение индуктивности будет зависеть от взаимного расположения катушек.
Некоторые практические вопросы и конструкции катушек индуктивности
На практике применяют различные конструкции катушек индуктивности. В зависимости от назначения и области применения устройства можно выполнить различным способом, но надо учитывать эффекты, возникающие в реальных катушках.
Добротность катушки индуктивности
У реальной катушки, кроме индуктивности, есть ещё несколько параметров, и один из самых важных – добротность. Эта величина определяет потери в катушке и зависит от:
Все эти величины определяют сопротивление потерь, а добротностью называют безразмерную величину, равную Q=ωL/Rпотерь, где:
Можно приближённо говорить о том, что добротность равна отношению реактивного (индуктивного) сопротивления к активному. С одной стороны, с ростом частоты растёт числитель, но в то же время за счет скин-эффекта растёт и сопротивление потерь за счет уменьшения полезного сечения провода.
Экранный эффект
Для уменьшения влияния посторонних предметов, а также электрических и магнитных полей и взаимного влияния элементов посредством этих полей, катушки (особенно высокочастотные) часто помещают в экран. Кроме полезного эффекта, экранирование вызывает снижение добротности катушки, снижение её индуктивности и повышение паразитной ёмкости. Причём чем ближе стенки экрана к виткам катушки, тем выше вредное влияние. Поэтому экранированные катушки практически всегда выполняют с возможностью подстройки параметров.
Подстроечная индуктивность
В некоторых случаях требуется точно установить значение индуктивности на месте после подключения катушки к другим элементам цепи, компенсируя отклонение параметров при настройке. Для этого применяются разные способы (переключения отводов витков и т.п.), но наиболее точный и плавный метод – подстройка с помощью сердечника. Он выполняется в виде стержня с резьбой, который можно вворачивать и выворачивать внутри каркаса, настраивая индуктивность катушки.
Переменная индуктивность (вариометр)
Там, где требуется оперативная регулировка индуктивности или индуктивной связи, применяются катушки другой конструкции. Они содержат две обмотки – подвижную и неподвижную. Общая индуктивность равна сумме индуктивностей двух катушек и взаимной индуктивности между ними.
Изменением относительного положения одной катушки к другой, регулируется общее значение индуктивности. Такое устройство называется вариометром и часто применяется в связной аппаратуре для настройки резонансных контуров в тех случаях, когда применение конденсаторов переменной ёмкости по каким-то причинам невозможно. Конструкция вариометра довольно громоздкая, что ограничивает область его применения.
Индуктивность в виде печатной спирали
Катушки с небольшой индуктивностью можно выполнять в виде спирали из печатных проводников. Достоинством такой конструкции являются:
К недостаткам относят невозможность точной подстройки при регулировке и сложность получения больших значений индуктивности – чем выше индуктивность, тем больше катушка занимает места на плате.
Катушка с секционной намоткой
Индуктивность без ёмкости бывает только на бумаге. При любой физической реализации катушки сразу же возникает паразитная межвитковая ёмкость. Это во многих случаях вредное явление. Паразитная ёмкость складывается с ёмкостью LC-контура, снижая резонансную частоту и добротность колебательной системы. Также у катушки возникает собственная резонансная частота, которая провоцирует нежелательные явления.
Для снижения паразитной ёмкости применяют различные способы, самый простой из которых – намотка индуктивности в виде нескольких последовательно включенных секций. При таком включении индуктивности складываются, а суммарная ёмкость снижается.
Катушка индуктивности на тороидальном сердечнике
Линии магнитного поля цилиндрической катушки индуктивности проводят через внутреннюю часть обмотки (если там сердечник – то через него) и замыкаются снаружи через воздух. Этот факт влечёт за собой несколько недостатков:
От этих недостатков во многом свободны катушки, намотанные на тороидальных сердечниках (в виде кольца или «бублика»). Магнитные линии проходят внутри сердечника в виде замкнутых петель. Это означает, что внешние предметы практически не оказывают влияние на параметры намотанной на таком сердечнике катушки, и экранировка для такой конструкции не нужна. Также увеличивается индуктивность при прочих равных параметрах, а характеристики проще рассчитать.
К недостаткам катушек, намотанных на торах, относят невозможность плавной подстройки индуктивности на месте. Другая проблема – высокая трудоёмкость и низкая технологичность намотки. Впрочем, это относится ко всем индуктивным элементам в целом, в большей или меньшей степени.
Также общим недостатком физической реализации индуктивности являются высокие массогабаритные показатели, относительно невысокая надежность и низкая ремонтопригодность.
Электрическая индуктивность
Индуктивностью называется свойство проводника препятствовать изменениям проходящего через него тока. Индуктивность измеряется в генри(Гн).
Индуктивностью в 1 Гн обладает электрическая цепь, в которой возникает ЭДС самоиндукции в 1 Вольт при равномерном изменении тока в этой цепи, со скоростью 1 Ампер в секунду.
Сопротивление, которое преобразует электрическую энергию в тепловую, называется активным сопротивлением. Активным сопротивлением индуктивности является электрическое сопротивление провода её обмотки при прохождении через неё постоянного тока. При этом на обмотке выделяется тепловая мощность.
Реактивным сопротивлением индуктивности является сопротивление, оказываемое катушкой при прохождении через нее переменного тока. Добротностью называется отношение реактивного сопротивления индуктивности к её активному сопротивлению.
Индуктивности находят широкое применение в РЭА в составе колебательных контуров и различных фильтрах.
Индуктивности различных типов в нашем каталоге
Значение слова «индуктивность»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
— сила тока в контуре,
Нередко говорят об индуктивности прямого длинного провода (см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведённое выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции (в вольтах), возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током:
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников.
Для имитации индуктивности, то есть ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
ИНДУКТИ’ВНОСТЬ, и, мн. нет, ж. (книжн. спец.). Отвлеч. сущ. к индуктивный. И. доказательств.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
Что такое индуктивность, её определение и единица измерения

Человеческий мозг предположил следующее: поле должно протекать вокруг проводников не по воздуху, а по железу, сопротивляемость которого магнитному полю намного меньше. Такие катушки являются индуктивными.
Свойства
Коэффициент самоиндукции — это есть индуктивность. Иными словами: величина, которая характеризует связь между находящимся в проводнике электрическим током и магнитным полем, создаваемым при протекании. Эта мера представляет сумму потока индукции. Прямая зависимость её от конфигурации проводника и от проницаемости доказана.
При подаче на катушку электрического тока постоянного напряжения, в катушке возникает напряжение, противоположное напряжению электрического тока (Е =U), которое исчезает через некоторое время. Это противоположное напряжение называется ЭДС (электродвижущей силой самоиндукции). Параметр зависит от индуктивности катушки.
Как найти индуктивность
Формулы индуктивности будут выглядеть следующим образом:
ЭДС определяет энергию магнитного поля, от этой величины зависит противодействие системы при изменении тока. При этом ЭДС самоиндукции направлена противоположно последнему.
Перевод слова «индукция» с латинского языка (induct) — побуждение, наведение. Исходя из сказанного, понятно, что это величина, которая характеризует магнитные свойства электрической цепи. Ток проводящего контура создаёт в окружающем его пространстве магнитное поле. При этом, возникающий в контуре поток Ф, имеет прямую ему пропорциональность. Формально записывается это так: Ф=LI, где L — коэффициент пропорциональности или коэффициент самоиндукции контура. Его определяют размеры и формы контура, а также, магнитная проницаемость среды.
Энергия W магнитного поля тока I определяется по формуле: W =LI2/2. При проведении аналогии между электрическим и механическими явлениями, энергия сопоставима с кинетической энергией тела T=mv2/2, где m — масса, v — скорость. Тогда индуктивность подобна массе, а ток — скорости. Это наглядное сравнение помогает лучше понять суть. Эта интересная характеристика определяет инерционные свойства электрического тока.
На практике для увеличения её значения применяют катушки с сердечниками из ферромагнетиков, их свойства имеют зависимость от напряжённости магнитного поля и, следовательно, I. В основном это ферритовые пластины из электротехнической стали. Эффективность применения сердечников довольно значительна: индуктивность катушки возрастает в несколько раз. Помимо цилиндрических, распространены тороидальные варианты, они позволяют достичь большей индуктивности, из-за наличия замкнутого магнитного потока.
Индуктивность соленоида определённой длины, имеющего N витков и площадь поперечного сечения S в среде, имеющей проницаемость m равна:
где m0— магнитная проницаемость вакуума.
Определение индуктивности

Для того, чтобы её определить, нужно измерить действующее значение переменного тока и его частоту, а также, напряжение на катушке и её активное сопротивление:
Применение катушек в технике
Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:
Как работает катушка индуктивности: ЛикБез
В радиоэлектронике частенько встречается такая штука, как катушка индуктивности. Ещё её называют индуктивным элементом. Эта деталь довольно важна и понимание принципа её функционирования важно для каждого грамотного человека, поэтому, давайте вместе разбираться для чего она нужна и как работает.
Что такое индуктивность «на пальцах»
Прежде, чем вникать в принцип работы катушки индуктивности, давайте вспомним, что вообще такое индуктивность в курсе физики и для чего она нужна или из-за чего появляется. Несмотря на то, что словом «индуктивность» часто упрощенно называют соответствующую радиодеталь, у термина есть и прототип в виде физического понятия. Вы наверняка помните, что если пропускать через провод электрический ток, то вокруг провода появляется магнитное поле.
Вокруг проводника с током появляется магнитное полеЕсли же согнуть этот проводник в бараний рог, то и линии магнитной индукции согнутся вместе с этим проводником. Получится довольно занятная картинка.
Магнитное поле вокруг согнутого проводника с токомСиловые линии магнитного поля от каждого витка проводника будто круги на воде объединяются и формируют внутри такой нехитрой конструкции почти прямые линии магнитной индукции. Полученная котовасия внутри пружины носит название «магнитный поток» и обозначается буквой Ф.
Ну и. Напрашивается сама катушка индуктивности
Собственно, логично предположить,что если скрутить такую пружинку особым образом, то можно получить разные индуктивности. Сделали пружинку и получили деталь с некоторой индуктивностью. Ну а если внутри такой детали разместить ещё и сердечник из определенного материала, то индуктивность тоже будет меняться.
Страшная самоиндукция
Есть у катушек индуктивности и ещё одно важное свойство, про которое просто необходимо знать! Это самоиндукция. Благодаря самоиндукции, сила тока в катушке индуктивности не может моментально увеличиваться или моментально падать. Она постепенно нарастает и постепенно уменьшается. Эффект по логике напоминает инертность в механике.Происходит это из-за того, что сформированный в катушке ток будет направлен против тока от источника питания и тем самым окажет ему сопротивление.Причиной порождения электрического тока в катушке является переменное магнитное поле. Мы ведь помним, что там, где магнитное поле, там и электрический ток. И наоборот.Вечная связка.
Вот и получается, что изменение магнитного поля катушки является причиной появления в ней нового электрического тока (или правильнее, но не понятнее говорить ЭДС самоиндукции), который препятствует прохождению основного тока. И пока он «раскочегарится» на максимальные значения выйти не получится. Как не получится и мгновенно всё отключить. А определяется всё это индуктивностью катушки или её способностью превращать электрический ток в магнитное поле. Ситуация очень запутанная и довольно сложная. Да и наука не до конца может объяснить каждый процесс. Поэтому, мы пользуемся стандартным определением и просто принимаем как факт, что есть такая закономерность. Ну и теперь логично предположить, что все эти фишки катушки индуктивности можно было бы удобно применить на практике. А как?
Для чего нужны катушки индуктивности?
Специфическая особенность этой детали позволяет делать весьма интересные схемы и получать самые разные результаты. Давайте перечислим только некоторые из них:
Смотрите мой проект на YouTube и подписывайтесь на телеграм!
Индуктивность: формула
Если существует замкнутый контур, в котором протекает ток, создающий магнитное поле (магнитный поток), то между током и потоком существует взаимосвязь. Коэффициент пропорциональностями между этими величинами является определением индуктивности.
Также эту пропорциональность можно назвать характеристикой инерционности электрической цепи, которая напрямую связана с понятием ЭДС самоиндукции, которая возникает в цепи, когда изменяется сила тока.
Электрическая цепь и индуктивность
Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.
Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.
Самоиндукция и измерение индуктивности
При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.
Напряжение ЭДС определяется формулой расчета индукции:
То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».
Обозначение и единицы измерения
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
Теоретическое обоснование
Ток, протекающий в замкнутом контуре, создает магнитное поле, при этом величина вектора магнитного поля пропорциональна протекающему току. Таким образом, магнитный поток также пропорционален току.
Коэффициент пропорциональности между магнитным потоком и порождающим его током равен индуктивности рассматриваемого контура.
Свойства
Имеет следующие свойства:
Схемы соединения катушек
Как радиотехнический элемент, катушки индуктивностей обладают свойствами соединений, полностью идентичными соединениям резисторов.
Параллельное соединение
Параллельное соединение:
Для двух элементов формула упрощается:
Последовательное соединение
Общее значение последовательного соединения равняется сумме индуктивностей:
Добротность катушки
Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.
Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:
где:
Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает.
Одновитковой контур и катушка
Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.
Соленоид
Соленоид отличается от обычной катушки по двум признакам:
Параметры соленоида можно узнать из такого выражения:
где:
Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника.
Обратите внимание! Используя подвижный сердечник, можно производить оперативное изменение параметров соленоида.
Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.
Тороидальная катушка (катушка с кольцевым сердечником)
Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:
где r – усредненный радиус тороидального сердечника.
Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:
где:
r – внутренний радиус сердечника;
R – внешний радиус;
Важно! Вторая формула позволяет узнавать результат с большей точностью.
Длинный прямой проводник
Как найти индуктивность прямого проводника? Существует формула, дающая точное значение при условии, что проводник имеет длину, значительно превышающую толщину:
где:
Какой магнитной проницаемостью обладает проводник, можно узнать из справочных материалов.
Применение катушек индуктивности
Рассматриваемые элементы широко применяются в радио,- и электротехники:
Колебательный контур
Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.
Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.
Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.
Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.
Видео
Индуктивность
Из Википедии — свободной энциклопедии
Индуктивность является электрической инерцией, подобной механической инерции тел. А вот мерой этой электрической инерции как свойством проводника может служить ЭДС самоиндукции. Характеризуется свойством проводника противодействовать появлению, прекращению и всякому изменению электрического тока в нём.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :
E i = − d Φ d t = − L d I d t <\displaystyle <\mathcal
 .
.При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :
Для имитации индуктивности, то есть ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются [6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
В электромагнетизм и электроника, индуктивность это тенденция электрический проводник противодействовать изменению электрический ток протекает через него. Поток электрического тока создает магнитное поле вокруг проводника. Напряженность поля зависит от величины тока и следует за любыми изменениями тока. От Закон индукции Фарадея, любое изменение магнитного поля в цепи вызывает электродвижущая сила (ЭДС) (Напряжение ) в проводниках процесс, известный как электромагнитная индукция. Это индуцированное напряжение, создаваемое изменяющимся током, имеет эффект противодействия изменению тока. Об этом заявляет Закон Ленца, а напряжение называется обратная ЭДС.
Индуктивность определяется как отношение индуцированного напряжения к скорости изменения вызывающего его тока. Это коэффициент пропорциональности, который зависит от геометрии проводников цепи и магнитная проницаемость близлежащих материалов. [1] An электронный компонент предназначен для добавления индуктивности в цепь, называется индуктор. Обычно он состоит из катушка или спираль из проволоки.
Содержание
История
История электромагнитной индукции, аспекта электромагнетизма, началась с наблюдений древних: электрического заряда или статического электричества (натирание шелка о янтарь ), электрический ток (молния ) и магнитное притяжение (магнит ). Понимание единства этих сил природы и научная теория электромагнетизма началась в конце 18 века.
Электромагнитная индукция была впервые описана Майкл Фарадей в 1831 г. [6] [7] В эксперименте Фарадей намотал два провода на противоположные стороны железного кольца. Он ожидал, что, когда ток начнет течь по одному проводу, через кольцо пройдет своего рода волна и вызовет электрический эффект на противоположной стороне. С помощью гальванометр, он наблюдал переходный ток во второй катушке провода каждый раз, когда батарея была подключена или отключена от первой катушки. [8] Этот ток был вызван изменением магнитный поток это произошло при подключении и отключении аккумулятора. [9] Фарадей обнаружил несколько других проявлений электромагнитной индукции. Например, он видел переходные токи, когда быстро вставлял стержневой магнит в катушку с проводами и из нее и создавал устойчивый (ОКРУГ КОЛУМБИЯ ) ток путем вращения медного диска возле стержневого магнита с помощью скользящего электрического провода («Диск Фарадея «). [10]
Источник индуктивности
Все проводники имеют некоторую индуктивность, которая может иметь как желательные, так и вредные эффекты в практических электрических устройствах. Индуктивность цепи зависит от геометрии пути тока и от магнитная проницаемость из близлежащих материалов; ферромагнитный материалы с более высокой проницаемостью, такие как утюг вблизи проводника увеличиваются магнитное поле и индуктивность. Любое изменение в цепи, которое увеличивает поток (общее магнитное поле) через цепь, создаваемую заданным током, увеличивает индуктивность, потому что индуктивность также равна отношению магнитный поток к текущему [11] [12] [13] [14]
An индуктор является электрический компонент состоит из проводника, форма которого увеличивает магнитный поток и увеличивает индуктивность цепи. Обычно он состоит из проволоки, намотанной на катушка или спираль. Спиральный провод имеет более высокую индуктивность, чем прямой провод такой же длины, потому что силовые линии магнитного поля проходят через цепь несколько раз, и у него несколько потокосоединения. Индуктивность пропорциональна квадрату количества витков в катушке, предполагая, что потокосцепление полное.
Индуктивность катушки можно увеличить, поместив магнитный сердечник из ферромагнитный материал в отверстие в центре. Магнитное поле катушки намагничивает материал сердечника, выравнивая его магнитные домены, и магнитное поле сердечника добавляется к полю катушки, увеличивая поток через катушку. Это называется индуктор с ферромагнитным сердечником. Магнитопровод может увеличить индуктивность катушки в тысячи раз.
Самоиндукция и магнитная энергия
Следовательно, индуктивность также пропорциональна энергии, запасенной в магнитном поле для данного тока. Эта энергия сохраняется, пока ток остается постоянным. Если ток уменьшается, магнитное поле уменьшается, вызывая напряжение в проводнике в противоположном направлении, отрицательное на конце, через которое ток входит, и положительное на конце, через которое он выходит. Это возвращает накопленную магнитную энергию во внешнюю цепь.
Если ферромагнитный материалы расположены рядом с проводником, например, в индукторе с магнитный сердечник, приведенное выше уравнение постоянной индуктивности справедливо только для линейный области магнитного потока при токах ниже уровня, на котором ферромагнитный материал насыщает, где индуктивность примерно постоянна. Если магнитное поле в индукторе приближается к уровню, при котором сердечник насыщается, индуктивность начинает изменяться с током, и необходимо использовать интегральное уравнение.
Индуктивное реактивное сопротивление
Когда синусоидальный переменный ток (AC) проходит через линейную индуктивность, индуцированная противо-ЭДС также синусоидальный. Если ток через индуктивность равен я ( т ) = я пик грех ( ω т ) < Displaystyle я (т) = я _ < текст <пик>> грех влево ( омега т вправо)> 
Таким образом, амплитуда (пиковое значение) напряжения на индуктивности равна
Индуктивный реактивное сопротивление это противодействие катушки индуктивности переменному току. [19] Он определяется аналогично электрическое сопротивление в резисторе, как отношение амплитуда (пиковое значение) зависимости переменного напряжения от тока в компоненте
Расчет индуктивности
В самом общем случае индуктивность может быть вычислена из уравнений Максвелла. Многие важные случаи можно решить с помощью упрощений. Если учитываются токи высокой частоты, при скин эффект, плотности поверхностного тока и магнитное поле могут быть получены путем решения Уравнение лапласа. Если проводники представляют собой тонкие проволоки, самоиндукция по-прежнему зависит от радиуса проволоки и распределения тока в проволоке. Это распределение тока примерно постоянное (на поверхности или в объеме провода) для радиуса провода, намного меньшего, чем для других масштабов длины.
Индуктивность прямого одиночного провода
Отделение провода от других частей схемы вносит некоторую неизбежную ошибку в результаты любых формул. Эти индуктивности часто называют «частичными индуктивностями», отчасти для того, чтобы стимулировать рассмотрение других вкладов в индуктивность всей цепи, которые не учитываются.
Практические формулы
Для вывода приведенных ниже формул см. Rosa (1908). [20] Общая низкочастотная индуктивность (внутренняя и внешняя) прямого провода составляет:
Для достаточно высоких частот скин-эффекты вызывают исчезновение внутренних токов, оставляя только токи на поверхности проводника; индуктивность по переменному току, L AC < displaystyle L _ < text 
В примере из повседневного опыта, только один из проводников шнура лампы длиной 10 м, сделанный из провода калибра 18, имел бы индуктивность только около 19 мкГн, если бы он был вытянут прямо.
Взаимная индуктивность двух параллельных прямых проводов
Следует рассмотреть два случая:
Взаимная индуктивность двух проводных шлейфов
Вывод
Теорема Стокса был использован для третьего шага равенства.
Для последнего шага равенства мы использовали Запаздывающий потенциал выражение для А j < displaystyle A_ 
Самоиндукция проволочной петли
Индуктивность соленоида
Следовательно, для катушек с воздушным сердечником индуктивность зависит от геометрии катушки и количества витков и не зависит от тока.
Индуктивность коаксиального кабеля
Пусть внутренний проводник имеет радиус р я < displaystyle r_ > 





L ′ = d L d ℓ ≈ μ d 2 π пер р о 1 р я < displaystyle L '= < frac << text
Индуктивность многослойных катушек
Наиболее практичные индукторы с воздушным сердечником представляют собой многослойные цилиндрические катушки с квадратным поперечным сечением, чтобы минимизировать среднее расстояние между витками (круглое поперечное сечение было бы лучше, но сложнее сформировать).
Магнитные сердечники
Многие индукторы включают магнитный сердечник в центре обмотки или частично вокруг нее. В достаточно большом диапазоне они демонстрируют нелинейную проницаемость с такими эффектами, как магнитное насыщение. Насыщение делает результирующую индуктивность функцией приложенного тока.
Секущая индуктивность или индуктивность большого сигнала используется в расчетах потока. Это определяется как:
С другой стороны, дифференциальная или малосигнальная индуктивность используется при расчете напряжения. Это определяется как:
Напряжение цепи для нелинейного индуктора получается через дифференциальную индуктивность, как показано законом Фарадея и Правило цепи исчисления.
v ( т ) = d Λ d т = d Λ d я d я d т = L d ( я ) d я d т < displaystyle v (t) = < frac << text
Аналогичные определения могут быть получены для нелинейной взаимной индуктивности.
Взаимная индуктивность
Вывод взаимной индуктивности
Приведенные выше уравнения индуктивности являются следствием Уравнения Максвелла. Для важного случая электрических цепей, состоящих из тонких проводов, вывод прост.
Взаимная индуктивность и энергия магнитного поля
Умножая уравнение на vм выше с ямdt и подводя итог м дает энергию, передаваемую системе за промежуток времени dt,
Это должно согласовываться с изменением энергии магнитного поля, W, вызванные токами. [24] В условие интегрируемости
Взаимная индуктивность возникает, когда изменение тока в одной катушке индуктивности индуцирует напряжение в другой соседней катушке индуктивности. Это важно как механизм, с помощью которого трансформаторы работают, но это также может вызвать нежелательное соединение между проводниками в цепи.
Между взаимной индуктивностью также существует соотношение:
M 21 < displaystyle M_ <21>> 



Коэффициент связи
в то время как отношение, если весь поток связан, является отношением витков, следовательно, отношение квадратного корня из индуктивностей
Матричное представление
Взаимосвязанные катушки индуктивности могут быть описаны любым из двухпортовая сеть представления матрицы параметров. Самыми прямыми являются z параметры, которые даются
[ z ] = s [ L 1 M M L 2 ] < displaystyle [ mathbf
Эквивалентные схемы
Т-образный контур
Взаимосвязанные индукторы могут быть эквивалентно представлены Т-образной цепью индукторов, как показано. Если связь сильная и индукторы имеют неодинаковые значения, тогда последовательная индуктивность на понижающей стороне может принимать отрицательное значение.
которое не зависит от импеданса нагрузки. Если индукторы намотаны на один и тот же сердечник и с одинаковой геометрией, то это выражение равно отношению витков двух индукторов, потому что индуктивность пропорциональна квадрату отношения витков.
Входное сопротивление сети определяется выражением
Таким образом, текущий прирост, А я < displaystyle A_ > 
выполняется, и в этом случае
Z я п ≈ L 1 L 2 Z < displaystyle Z _ < mathrm
А я ≈ L 1 L 2 = 1 А v < displaystyle A _ < mathrm > приблизительно < sqrt
π-схема
В качестве альтернативы, две связанные индукторы можно смоделировать с помощью π эквивалентная схема с дополнительными идеальными трансформаторами на каждом порте. Хотя схема более сложная, чем Т-образная схема, ее можно обобщить [28] к цепям, состоящим из более чем двух связанных индукторов. Эквивалентные элементы схемы L s < displaystyle L _ < text >> 
>> 
Значения эквивалентных элементов схемы могут быть рассчитаны из коэффициентов связи с
L S я j = Det ( K ) − C я j < Displaystyle L_ 
где матрица коэффициентов связи и ее кофакторы определены как
Для двух связанных индукторов эти формулы упрощаются до
и для трех связанных индукторов (для краткости показаны только для L s12 < displaystyle L _ < text 

Резонансный трансформатор
Идеальные трансформаторы
V s = N s N п V п < displaystyle V _ < text >> я s = N п N s я п < displaystyle I _ < text >> Мощность через одну катушку индуктивности такая же, как и через другую. В этих уравнениях не учитывается воздействие источников тока или напряжения.> = < frac > = < frac Самоиндукция тонкой проволоки
Самоиндукция тонкой проволоки
Тип Индуктивность Комментарий Одиночный слой
соленоидИзвестная аппроксимационная формула Уиллера
для катушки с воздушным сердечником модели токового листа: [29] [30]