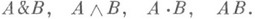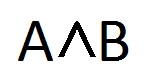Что такое конъюнкция

29.08.202229.08.2022 admin 0 Комментариев

Что такое конъюнкция

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

1. Логические выражения и логические операции

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.

Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.

Существуют разные варианты обозначения истинности и ложности логических переменных:

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Введем перечисленные логические операции.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Источник

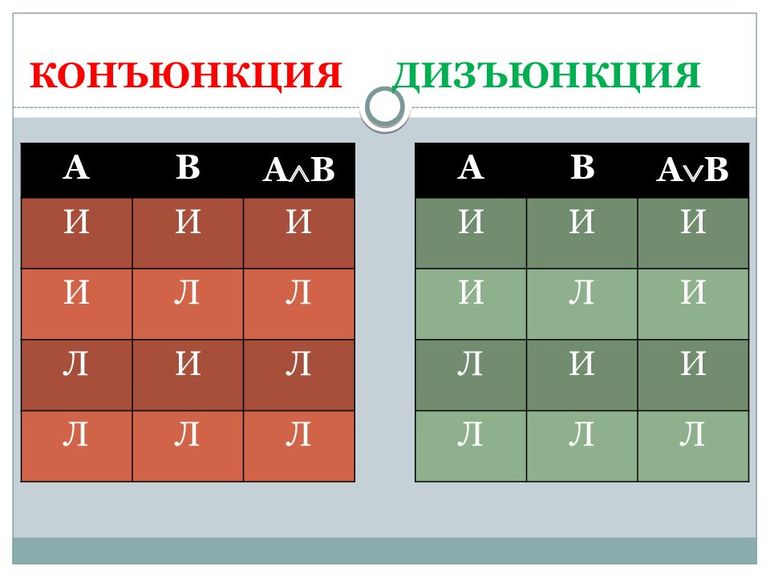
Конъюнкция

Конъюнкция — это логическая операция, принятая в формализованных языках (см. Язык формализованный) для образования сложных высказываний (формул) из элементарных (простых) высказываний (см. Высказывание) и по смыслу эквивалентная соединительному союзу «и» в естественном языке (см. Язык). Другое название конъюнкции: логическое умножение.

Конъюнкция читается: «A и B»; записывается: A ⋀ B, другие обозначения конъюнкции: A & B, A × B (здесь A и B называются конъюнктивными членами высказывания A ⋀ B, а знак ⋀, или &, или × — знаком конъюнкции). Употреблению конъюнкции в математической логике соответствует истинностная таблица:

A	B	A ⋀ B
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Из таблицы видно, что высказывание A ⋀ B истинно только при истинности обоих высказываний A и B.

Конъюнкция может быть бинарной операцией (иметь два операнда), тернарной операцией (иметь три операнда), или n-арной операцией (иметь n операндов), но на практике операции более, чем бинарные, используются очень редко.

Понятие конъюнкции сформировалось в процессе обособления языка логики и его последующей символизации (см. Логика символическая). В классической логике (см. Логика), формальной логике (см. Логика формальная), языках формальных теорий (см. Формализация) и языках программирования конъюнкция составляет одну из пяти наиболее распространённых логических связок, или логических операций (см. Логические операции), наряду с дизъюнкцией (см. Дизъюнкция), импликацией (см. Импликация), эквиваленцией (см. Эквиваленция) и отрицанием (см. Отрицание).

Источник

конъюнкция

Смотреть что такое «конъюнкция» в других словарях:

КОНЪЮНКЦИЯ — КОНЪЮНКЦИЯ, логическое высказывание, которое получается путем объединения двух простых утверждений союзом «и». Например, утверждение «В доме есть свет и в доме есть вода» верно лишь в том случае, если обе составляющие его части верны по… … Научно-технический энциклопедический словарь

КОНЪЮНКЦИЯ — (от лат. conjunctio союз, связь), в широком смысле сложное высказывание, образованное с помощью союза «и». В принципе можно говорить о К. бесконечного числа высказываний (напр., о К. всех истинных предложений математики). В логике К. наз … Философская энциклопедия

конъюнкция — логическое произведение; операция. Ant. дизъюнкция Словарь русских синонимов. конъюнкция сущ., кол во синонимов: 1 • операция (457) Словарь синонимов ASIS. В.Н … Словарь синонимов

Конъюнкция — Конъюнкция ♦ Conjonction Соединение или связь. В логике конъюнкцией называют высказывание, состоящее из двух или более высказываний, связанных соединительным союзом «и»: «p и q» – пример конъюнкции. Конъюнкция истинна только при том условии … Философский словарь Спонвиля

КОНЪЮНКЦИЯ — (от лат. conjunctio союз связь), логический эквивалент союза и ; операция, формализующая логические свойства этого союза … Большой Энциклопедический словарь

конъюнкция — логическое умножение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы логическое умножение EN conjunction … Справочник технического переводчика

КОНЪЮНКЦИЯ — логическая операция, образующая сложное высказывание из двух высказываний, объединённых с помощью логического союза «И». Логический переключательный элемент, реализующий функцию К., называется схемой совпадения или вентилем. С помощью этой… … Большая политехническая энциклопедия

КОНЪЮНКЦИЯ — (Coniunctio лат.) в буквальном смысле термин «конъюнкция» используется в алхимии для обозначения химических комбинаций, рождения нового элемента, психологически он указывает на союз противоположностей и на появление новых возможностей. Юнг… … Словарь по аналитической психологии

Источник

Конъюнкция

Логическая операция конъюнкция — бинарная операция над высказываниями, результатом которой является истинное высказывание только в случае, когда исходные высказывания истинны.

Другие названия конъюнкции — логическое умножение, логическое И или просто И.

Конъюнкция изучается в информатике при рассмотрении раздела алгебра логики.

В естественных языках конъюнкцию заменяют союзом «и».

В языках программирования для конъюнкции используют обозначение ‘ and ‘ или знак амперсанд ‘ & ‘ (либо ‘ && ‘) (например, x>0 and x или a>=10 & a ).

Как набрать знак конъюнкции на клавиатуре

Таблица истинности для конъюнкции

Истинность конъюнкции определяется ее таблицей истинности.

A	B	A /\ B
0	0	0
0	1	0
1	0	0
1	1	1

Конъюнкция и круги Эйлера

Результатом конъюнкции является область пересечения высказываний.

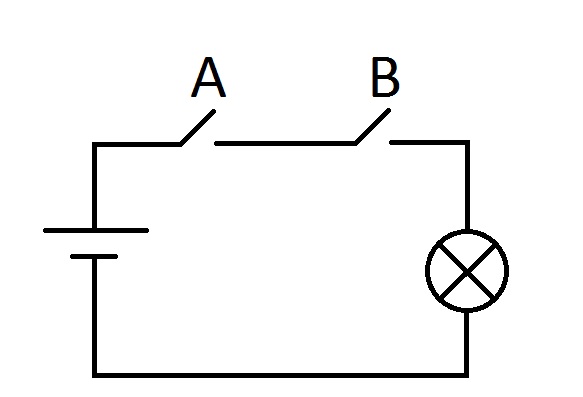
Электрический аналог конъюнкции

Представим, что выключатели A и B — это высказывания, причем 0 — выключатель разомкнут, 1 — выключатель замкнут. Лампа символизирует конъюнкцию. Когда она не горит — 0, горящая лампа — 1. Тогда становится очевидным, что лампа будет гореть только когда оба выключателя будут замкнуты, что полностью соотносится с таблицей истинности для конъюнкции.

Источник

КОНЪЮНКЦИЯ

Полезное

Смотреть что такое «КОНЪЮНКЦИЯ» в других словарях:

Источник

Логические операции. ➞ Что такое конъюнкция, дизъюнкция, импликация

Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.

Основные положения

Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.

Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).

Примером таким высказываний будут являться:

Логические высказывания делятся на два типа — простые и сложные.

В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.

Булево выражение – это символическое (знаковое) описание высказывания.

Операции

Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.

Конъюнкция

Конъюнкция (булево умножение) — функция, по своему смыслу приближенная к союзу «И». При выполнении конъюнкции результат истинен (равен 1) тогда и только тогда, когда истинны ВСЕ переменные. Если хотя бы одно из высказываний ложно, то ложно и всё выражение (равно 0).

Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков $ \wedge $ и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:

Дизъюнкция

Дизъюнкцией называется функция булева сложения. По смыслу дизъюнкция приближена к союзу «ИЛИ». В результате выполнения данной функции результирующие выражение является истинным, когда хотя бы одно из высказываний в этом выражении тоже истинно.

Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.

Инверсия

Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.

Импликация

Также называется булевым следованием. В русском языке данной функции соответствует оборот «Если …, то …». Например, если на улице гремит гром, то стоит пасмурная погода.

Эквивалентность

Булева тождественность или равенство. На простом языке будет обозначено как «… эквивалентно (равно) …». Результат будет истинным тогда, когда все значения в выражении будут иметь одинаковую истинность.

Обозначается с помощью трех черточек или ⟺.

Порядок выполнения операций

Логические операции выполняются в следующем порядке:

Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.

Пример

Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула $ ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) $ истинна при любом значении z. Варианты ответа:

Решение: Подставим в уравнение $ ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) $ =1 значения B и C и составим таблицу истинности:

Получившаяся формула $ ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 $. По условию $ z \in A $=1.

Таблица истинности для всех отрезков:

Ответ: A = [3,11].

Видео

Заключение

Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.

Источник

КОНЪЮНКЦИЯ

— логическая oперация, служащая для образования высказывания «A и В» из высказываний А и В. В формализованных языках К. высказываний А и В обозначается посредством

Высказывания Аи Вназ. конъюнктивными членами высказывания АaВ. Употреблению К. в математической логике соответствует следующая истинностная таблица (см. выше).

Смотреть что такое «КОНЪЮНКЦИЯ» в других словарях:

Источник

КОНЪЮНКЦИЯ

Смотреть что такое «КОНЪЮНКЦИЯ» в других словарях:

Источник

Конъюнкция

Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Связанные понятия

В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.

Упоминания в литературе

Связанные понятия (продолжение)

В математике (особенно в теории категорий), коммутативная диаграмма — изображаемая в наглядном виде структура наподобие графа, вершинами которой служат объекты определённой категории, а рёбрами — морфизмы. Коммутативность означает, что для любых выбранных начального и конечного объекта для соединяющих их ориентированных путей композиция соответствующих пути морфизмов не будет зависеть от выбора пути.

В теории категорий есте́ственное преобразова́ние предоставляет способ перевести один функтор в другой, сохраняя внутреннюю структуру (например, композиции морфизмов). Поэтому естественное преобразование можно понимать как «морфизм функторов». Эта интуиция может быть строго формализована в определении категории функторов. Естественные преобразования — наиболее базовое определение в теории категорий наряду с функторами, поэтому оно появляется в большинстве её приложений.

Источник

КОНЪЮНКЦИЯ (от лат. conjunctio – союз, связь)

– логическая операция, с помощью которой два или более высказываний объединяются в новое сложное высказывание. Это новое высказывание называется конъюнктивным высказыванием или просто К.

Символически конъюнктивная связка обозначается знаками « • », «&», «U». Если А, В, С. представляют простые высказывания, то конъюнктивное высказывание выглядит следующим образом: А&В или А&В&С и т. п. В обыденной речи К. соответствует союз «и», поэтому К. читается так: А и В. Напр.: «Пассажиры заняли свои места, и поезд тронулся».

Значение истинности сложного конъюнктивного высказывания зависит от истинностных значений входящих в него простых высказываний и определяется на основе следующей таблицы истинности:

Эта таблица говорит о том, что конъюнктивное высказывание истинно только в одном случае, когда все входящие в него простые высказывания истинны. Напр., высказывание «Киев стоит на Днепре, и Киев – столица Украины» истинно, а высказывание «Киев стоит на Днепре, и Киев – столица Белоруссии» ложно. Следует иметь в виду, что К. учитывает только истинностные значения простых высказываний и не учитывает смысловые связи между ними. Поэтому К. может соединять высказывания, между которыми нет никакой содержательной связи. Напр., «Дважды два четыре, и снег бел» и т. п. Для К. справедлив закон коммутативности: А&В эквивалентно В&А, хотя в высказываниях с союзом «и» этот закон действует далеко не всегда. Напр., если в высказывании «Подул ветер, и деревья закачались» поменять местами члены К., высказывание станет бессмысленным с точки зрения здравого смысла.

Поделиться ссылкой на выделенное

Нажмите правой клавишей мыши и выберите «Копировать ссылку»

Источник

Значение слова «конъюнкция»

конъю́нкция

1. матем. лог. логическое высказывание, получаемое путём объединения двух простых утверждений союзом «и»

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: подкрашенный — это что-то нейтральное, положительное или отрицательное?

Синонимы к слову «конъюнкция&raquo

Предложения со словом «конъюнкция&raquo

Понятия со словом «конъюнкция»

Отправить комментарий

Дополнительно

Предложения со словом «конъюнкция&raquo

Строгая дизъюнкция эксплицируется просто как отрицание конъюнкции.

Под p понимается любое высказывание, под \ p – отрицание высказывания, знак \ перед формулой – отрицание двух высказываний, ал – знак конъюнкции.

Сложное высказывание, полученное с помощью двух (или более) высказываний при помощи слова «и», называется конъюнкцией.

Синонимы к слову «конъюнкция&raquo

Морфология

Правописание

Карта слов и выражений русского языка

Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.

Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.

Сайт оснащён мощной системой поиска с поддержкой русской морфологии.

Источник

конъюнкция

Смотреть что такое «конъюнкция» в других словарях:

Источник

конъюнкция

Смотреть что такое «конъюнкция» в других словарях:

Источник

Конъюнкция

Смотреть что такое «Конъюнкция» в других словарях:

Источник

Основы логики

1. Основные понятия логики

Понятие

Понятие — форма мышления, в которой отражаются существенные отличительные признаки предметов.

Понятие имеет две основные логические характеристики: содержание и объем.

Содержанием понятия называется совокупность существенных признаков, отраженных в этом понятии.

Объем понятия — это множество предметов, каждому из которых принадлежат признаки, относящиеся к содержанию понятия.

Совместимые и несовместимые понятия

По объему понятия могут быть совместимыми или несовместимыми. Объемы совместимых понятий совпадают полностью или частично (т.е. существуют объекты, имеющие признаки обоих понятий). Объемы несовместимых понятий не включают ни одного общего элемента.

Отношения совместимых понятий:

l пересечение (часть элементов объема каждого понятия входит в объем другого понятия); например, «мальчик»–«болельщик»;

l тождество (полное совпадение объемов понятий);

l подчинение (объем одного понятия полностью входит в объем другого); например, «акула»–«рыба».

Отношения несовместимых понятий:

l соподчинение; например, «рыба»–«птица» (соподчинены понятию «животное»);

l противоположность (объект, не попадающий под одно понятие, может не попадать и под другое); например, «черный»–«белый»;

l противоречие (объект принадлеит объему либо одного, либо другого понятия); например, «светящийся объект»–«несветящийся объект».

Высказывание

Высказывание (суждение) — форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах, или отношениях.

Высказывание характеризуется своим содержанием и формой.

Умозаключение

Умозаключение — форма мышления, посредством которой из одного или нескольких высказываний, называемых посылками, мы по определенным правилам вывода получаем заключение.

С точки зрения содержания мышление может давать истинное или ложное отражение мира, формально же оно может быть логически правильным или неправильным.

Логические операции

Высказывание, включающее другие высказывания, называют сложным. Для образования сложных высказываний используют логические операции (связки). Рассмотрим некоторые из них (в порядке приоритета при вычислении логических выражений).

Инверсия (отрицание)

Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.

В выражениях обозначается ¬A или Ā.

Читается «НЕ» (например, «не А»).

Конъюнкция (логическое умножение)

Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.

В выражениях обозначается AÙ B или A&B (знак может не указываться — AB).

Читается «И» (например, «А и Б»)

Дизъюнкция (логическое сложение)

Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.

В выражениях обозначается AÚ B, иногда A+B.

Читается «ИЛИ» (например, «А или Б»)

Импликация (следование)

Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.

В выражениях обозначается A Þ B или A ® B.

Читается «ЕСЛИ. ТО» (например, «если А, то Б»)

Эквивалентность (равнозначность)

Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.

В выражениях обозначается A Û B или A º B.

Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)

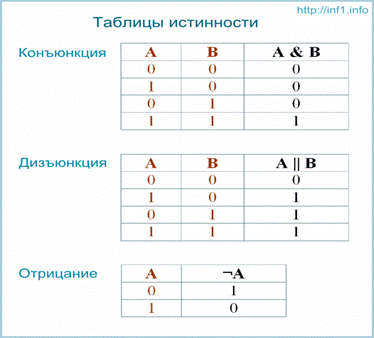
Таблицы истинности логических операций

Таблица истинности — таблица, в которой указаны значения логической функции для всех возможных комбинаций значений ее аргументов.

Источник

Общие сведения

Булева алгебра — раздел математического анализа, изучающий истинность логических утверждений. Ее открыл Д. Буль в ХIХ веке. Алгебра логики получила практическое применение только в ХХ веке при проектировании различных элементов персонального компьютера. Дисциплина доказывает истинность или ложность тождеств логического типа математическим путем с применением специальных таблиц.

Следует отметить, что логическое тождество является определенной функцией, принимающей значения 0 или 1 в зависимости от ее элементов. В алгебре логики значения имеют следующие названия: 0 — ЛОЖЬ (FALSE) и 1 — ИСТИНА (TRUE).

Операторы сравнения

Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t 0). При использовании логического отрицания условие выглядит короче: t=!0.

Приоритеты вычислений

При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:

Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:

Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.

Примеры решений

В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).

Решать задание нужно по такому алгоритму:

Следующий пример будет сложнее, поскольку выражение ¬ < ¬[ ¬((S|0)&¬(T|S)& ¬(S&(T&S)) ]& ¬(S&S) >следует упростить, а затем составить таблицу. Задача решается по такой методике:

Следует отметить, что исходное логическое выражение необходимо на начальном этапе решения упростить, а затем строить таблицу. В этом возможно убедиться на основании приведенного примера, в котором сокращается одна переменная.

Таким образом, для решения выражения, содержащего логические операции конъюнкции, дизъюнкции и инверсии, необходимо его упростить, а затем разбить на простые элементы.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 1.3. Элементы алгебры логики

Информатика. 8 класса. Босова Л.Л. Оглавление

Ключевые слова:

1.3.1. Высказывание

Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.

Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.

В русском языке высказывания выражаются повествовательными предложениями. Но не всякое повествовательное предложение является высказыванием.

Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.

Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.

Побудительные и вопросительные предложения высказываниями не являются.

Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».

Высказывания могут строиться с использованием знаков различных формальных языков — математики, физики, химии и т. п.

Примерами высказываний могут служить:

Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:

Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X

1.3.2. Логические операции

Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций.

Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.

Конъюнкция

Рассмотрим два высказывания: А = «Основоположником алгебры логики является Джордж Буль», В = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.

Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.

Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы А и В), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.

Конъюнкцию также называют логическим умножением.

Дизъюнкция. Инверсия

Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использова ния в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.

Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Дизъюнкция определяется следующей таблицей истинности:

Дизъюнкцию также называют логическим сложением. Подумайте почему.

Инверсия

Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Инверсия определяется следующей таблицей истинности:

Инверсию также называют логическим отрицанием.

Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке одно и то же, «Я знаю китайский язык». Отрицанием высказывания «Все юноши 8-х классов — отличники» является высказывание «Неверно, что все юноши 8-х классов — отличники», другими словами, «Не все юноши 8-х классов — отличники».

Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».

Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.

Логические операции при выполнении имеют следующий приоритет: ин версия, конъюнкция, дизъюнкция.

1.3.2. Логические операции

Решение. Изобразим множество всех web-страниц рассматриваемого сектора сети Интернет кругом, внутри которого разместим два круга: одному из них соответствует множество web-страниц, где истинно высказывание А, второму — где истинно высказывание В (рис. 1.3).

Изобразим графически множества web-страниц, для которых истинны выражения и высказывание а) — в) (рис. 1.4).

Построенные схемы помогут нам ответить на вопросы, содержащиеся в задании.

Выражение А ИЛИ В истинно для 7000 web-страниц, а всего страниц 5 000 000. Следовательно, выражение А ИЛИ В ложно для 4 993 000 web-страниц. Иначе говоря, для 4 993 000 web-страниц истинно выражение НЕ (А ИЛИ В).

Чтобы выяснить, для скольких web-страниц истинно высказывание А и одновременно ложно высказывание В, следует из 4800 вычесть 2300. Таким образом, высказывание «На web-странице встречается слово «крейсер” И не встречается слово «линкор»» истинно на 2500 web-страницах.

Самостоятельно запишите логическое выражение, соответствующее рассмотренному выше высказыванию.

На сайте Федерального центра информационно-образовательных ресурсов (http://fcoir.edu.ru/) размещён информационный модуль «Высказывание. Простые и сложные высказывания. Основные логические операции». Знакомство с этим ресурсом позволит вам расширить представления по изучаемой теме.

1.3.3. Построение таблиц истинности для логических выражений

Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:

Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.

Заполненная таблица истинности имеет вид:

1.3.4. Свойства логических операций

Рассмотрим основные свойства логических операций, называемых также законами алгебры логики.

1. Переместительный (коммутативный) закон:

2. Сочетательный (ассоциативный) закон:

При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.

3. Распределительный (дистрибутивный) закон:

4. Закон двойного отрицания:

Двойное отрицание исключает отрицание.

5. Закон исключённого третьего:

Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

6. Закон повторения:

7. Законы операций с 0 и 1:

8. Законы общей инверсии:

Законы алгебры логики могут быть доказаны с помощью таблиц истинности.

Докажем распределительный закон для логического сложения:

Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.

Пример 2. Найдём значение логического выражения

Решение. При X = 0 получаем следующее логическое выражение:

Так как логические выражения 0

Элементы алгебры логики. Решение логических задач

Рассмотрим несколько способов решения логических задач.

Задача 1. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. На вопрос, кто разбил вазу, они дали такие ответы:

Бабушка знала, что один из её внуков, назовём его правдивым, оба раза сказал правду; второй, назовём его шутником, оба раза сказал неправду; третий, назовём его хитрецом, один раз сказал правду, а другой раз — неправду. Назовите имена правдивого, шутника и хитреца. Кто из внуков разбил вазу?

Решение. Пусть К = «Коля разбил вазу», В = «Вася разбил вазу», С — «Серёжа разбил вазу». Для решения задачи можно составить таблицу истинности, в которой представить высказывания каждого мальчика. Так как ваза разбита одним внуком, то чтобы выяснить, кто именно это сделал, достаточно фрагмента таблицы истинности, содержащего наборы значений входных переменных: 001, 010, 100.

Исходя из того, что знает о внуках бабушка, следует искать в таблице строку, содержащую в каком-либо порядке три комбинации значений: 00 (слова шутника), 11 (слова правдивого внука), 01 или 10 (слова хитреца). Такая строка отмечена галочкой. Согласно этой строке, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.

Задача 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:

По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах? Решение. Рассмотрим простые высказывания:

Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:

Логическое произведение истинных высказываний будет истинным:

На основании распределительного закона преобразуем левую часть этого выражения:

Высказывание C₁ • С₂ означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В₂ • С₂. Учитывая закон операций с константой 0, запишем:

Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:

Из последнего равенства следует, что С₁ = 1, Д₃ = 1, А₂ = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.

Познакомиться с другими способами решения логических задач, принять участие в интернет-олимпиадах и конкурсах по их решению вы сможете на российской странице международного математического конкурса «Кенгуру» (http://mathkang.ru/).

На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.

Логические элементы

Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.

Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.

На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.

Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.

Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.

Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента 0, то на выходе 1 и наоборот.

Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.

Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе F при каждом возможном наборе сигналов A и B на входах.

Решение. Все возможные комбинации сигналов А и Б на входах внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную 4 схему.

Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа А и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,

Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov.narod.ru/prog/logic.htm).

Элементы алгебры логики. Самое главное

Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.

Таблицы истинности для основных логических операций:

При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:

§ 1.3. Элементы алгебры логики

§ 2.1. Алгоритмы и исполнители

Источник

Логические операции. Дизъюнкция, конъюнкция и отрицание

Логические основы ЭВМ

Алгебра логики и логические основы компьютера

Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.

Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.

Логические операции. Дизъюнкция, конъюнкция и отрицание

Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6».

Как мы решаем, что нам сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае правдивости обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным.

Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.

При конъюнкции@/a> истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.

При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.

Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.

Для логических величин обычно используются три операции:

Конъюнкция – логическое умножение (И) – and, &, ∧.

Дизъюнкция – логическое сложение (ИЛИ) – or, |, v.

Логическое отрицание (НЕ) – not,.

Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).

Логические основы компьютера

В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.

Переключательные схемы

В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.

Вентили, триггеры и сумматоры

Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.

Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.

Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.

Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.

Информация и информационные процессы. Виды информации, её двоичное кодирование. Количество информации, подходы к определению понятия «количество информации», единицы измерения информации. Двоичное кодирование числовой, текстовой, графической, звуковой информации

Информация (от лат. informatio — «разъяснение, изложение, осведомлённость») — сведения о чём-либо, независимо от формы их представления.

В настоящее время не существует единого определения информации как научного термина. С точки зрения различных областей знания данное понятие описывается своим специфическим набором признаков. Понятие «информация» является базовым в курсе информатики, где невозможно дать его определение через другие, более «простые» понятия.

Свойства информации:

— Объективность (информация объективна, если она не зависит от чьего-либо мнения, суждения);

— Достоверность (информация достоверна, если она отражает истинное положение дел);

— Полнота (информация полна, если ее достаточно для понимания и принятия решения);

— Актуальность (информация актуальна, своевременна, если она важна, существенна для настоящего времени);

— Полезность (оценивается по тем задачам, которые мы можем решить с ее помощью);

— Понятность (информация понятна, если она выражена на языке, доступном для получателя);

— Доступность (информация доступна, если мы можем её получить).

Информация проявляется именно в информационных процессах. Информационные процессы всегда протекают в каких-либо системах (социальных, социотехнических, биологических и пр.).

Наиболее обобщенными информационными процессами являются сбор, преобразование, использование информации.

К основным информационным процессам, изучаемым в курсе информатики, относятся: поиск, отбор, хранение, передача, кодирование, обработка, защита информации.

Информационные процессы, осуществляемые по определенным информационным технологиям, составляет основу информационной деятельности человека.

Компьютер является универсальным устройством для автоматизированного выполнения информационных процессов.

Люди имеют дело со многими видами информации. Общение людей друг с другом дома и в школе, на работе и на улице – это передача информации. Учительский рассказ или рассказ товарища, телевизионная передача, телеграмма, письмо, устное сообщение и т.д. – все это примеры передачи информации.

И мы уже говорили о том, что одну и ту же информацию можно передать и получить различными путями. Так, чтобы найти дорогу в музей в незнакомом городе, можно спросить прохожего, получить справку в справочном бюро, попытаться разобраться самому с помощью плана города или обратиться к путеводителю. Когда мы слушаем объяснение учителя, читаем книги или газеты, смотрим новости ТВ, посещаем музеи и выставки – в это время мы получаем информацию.

Человек хранит полученную информацию в голове. Мозг человека – огромное хранилище информации. Блокнот или записная книжка, ваш дневник, школьные тетрадки, библиотека, музей, кассета с записями любимых мелодий, видеокассеты – все это примеры хранения информации.

Информацию можно обрабатывать: перевод текста с английского языка на русский и наоборот, вычисление суммы по заданным слагаемым, решение задачи, раскрашивание картинок или контурных карт – все это примеры обработки информации. Все вы любили в свое время раскрашивать книжки-раскраски. Оказывается, в это время вы занимались важным процессом – обработкой информации, черно-белый рисунок превращали в цветной.

Информацию можно даже терять. Допустим, Иванов Дима забыл дневник дома и поэтому записал домашнее задание на листочке. Но, играя на перемене, он сделал из него самолетик и запустил его. Придя домой, Дима не смог сделать домашнюю работу, он потерял информацию. Теперь ему нужно или попытаться вспомнить, что же ему задали, или позвонить однокласснику, чтобы получить нужную информацию, или идти в школу с невыполненным домашним заданием.

Двоичное кодирование – один из распространенных способов представления информации. В вычислительных машинах, в роботах и станках с числовым программным управлением, как правило, вся информация, с которой имеет дело устройство, кодируется в виде слов двоичного алфавита.

Двоичный алфавит состоит из двух цифр 0 и 1.

Цифровые ЭВМ (персональные компьютеры относятся к классу цифровых) используют двоичное кодирование любой информации. В основном это объясняется тем, что построить техническое устройство, безошибочно различающее 2 разных состояния сигнала, технически оказалось проще, чем то, которое бы безошибочно различало 5 или 10 различных состояний.

К недостаткам двоичного кодирования относят очень длинные записи двоичных кодов, что затрудняет работу с ними.

Источник

Конъюнкция и дизъюнкция — правила и примеры решения в математике

В информатике существует специальная дисциплина, рассматривающая логические операции отрицания, конъюнкции и дизъюнкции. В математике это направление называется булевой алгеброй и применяется для построения алгоритмов, проверяющих различные условия и соответствия. Специалисты в области информационных технологий рекомендуют перед практическим решением примеров получить теоретические знания.

Общие сведения

Следует отметить, что логическое тождество является определенной функцией, принимающей значения 0 или 1 в зависимости от ее элементов. В алгебре логики значения имеют следующие названия: 0 — ЛОЖЬ (FALSE) и 1 — ИСТИНА (TRUE).

Операторы сравнения

Следует отметить, что в этих примерах получается истинное значение, поскольку условие выполняется. Однако в информатике при построении алгоритмов используются методы ветвления. Они представляют собой такую конструкцию: ЕСЛИ (a>b), ТО a+b. ИНАЧЕ (a*b). Читается запись следующим образом: в том случае, когда значение а больше b, нужно сложить оба числа, а иначе (a Логические операции

Операции логического типа очень часто применяются при построении выражений, используемых в программировании. К ним относятся следующие:

Однако булева алгебра не ограничивается только ими, поскольку существуют и другие их производные. Для каждой из трех составляются определенные таблицы истинности, которые каждый раз необходимо строить для получения результата вычисления логических выражений. Специалисты рекомендуют отдельно на листе картона перечертить таблицы всех логических операций.

Функция конъюнкции

Конъюнкция — операция логического умножения, которая будет истинным при достоверности каждого выражения. Ее обозначение — символ конъюнктора «&». Записывается следующим образом: S&T, где S и T — логические тождества или конкретные значения. Операция имеет такие особенности: только при равенстве всех элементов 1 значение выражения является истинным, а в других случаях — ложью. Для проверки необходимо составить таблицу значений логического тождества:

S	T	S&T
0	0	F
0	1	F
1	0	F
1	1	T

Таблица 1. Значение функции в зависимости от логических переменных.

Из таблицы 1 видно, что выражение S&T принимает только TRUE при всех истинных значениях переменных. Если рассматривать алгебру, то можно провести аналогию между логическим и обыкновенным умножениями. Например, произведение двух чисел S*T, которые для удобства сравнения принимают значения 0 или 1.

Если сравнивать два результата, то они будут идентичны. Следовательно, для правильного построения таблицы для конъюнкции нужно руководствоваться аналогичной операцией умножения.

Информация о дизъюнкции

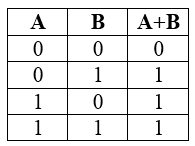
В булевой алгебре операция логического сложения называется дизъюнкцией. Обозначается она символом, который называется дизъюнктором (V или I). Логическое тождество, содержащее два элемента, имеет такой вид: SVT. Операция имеет только ложное значение при равенстве S и T нулю. Для нее нужно также строить специальную таблицу:

Таблица 2. Истинность операции дизъюнкции SVT.

Операция аналогична сложению в алгебре, хотя имеются некоторые отличия. Чтобы убедиться в этом, требуется выполнить определенное действие — построить специальную таблицу результатов для алгебраического сложения нулей и единиц.

Если рассмотреть результаты в последнем случае, то можно сделать вывод о схожести сложения и дизъюнкции. Однако в последней строке алгебраической суммы есть некоторое несоответствие — 2. Это показывает, какое переполнение разряда происходит в булевой алгебре. В последней происходит переход с одного разряда в другой.

Булево отрицание

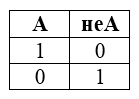
В алгебре логики применяется также операция отрицания, которую также называют инверсией. Суть ее заключается в том, что при истинном значении выражения под знаком инверсии получается ложный результат, а при ложном — истина. Обозначается она символом инверсии «¬», а записывается в таком виде ¬(S). Для демонстрации операции необходимо ознакомиться с таблицей:

Исходное выражение, S	Результат, ¬(S)
0	T
1	F

Таблица 3. Истинность ¬(S).

Приоритеты вычислений

Примеры решений

В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).

Решать задание нужно по такому алгоритму:

Источник

Логические операции и их свойства

Вы будете перенаправлены на Автор24

Конъюнкция или логическое умножение (в теории множеств – это пересечение)

Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.

Таблица истинности для конъюнкции

Дизъюнкция или логическое сложение (в теории множеств это объединение)

Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.

Таблица истинности для дизъюнкции

Готовые работы на аналогичную тему

Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)

Таблица истинности для инверсии

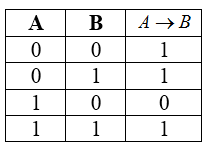
Импликация или логическое следование

Таблица истинности для импликации

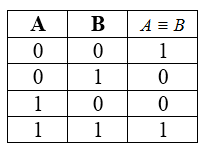
Эквивалентность или логическая равнозначность

Таблица истинности для эквивалентности

Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)

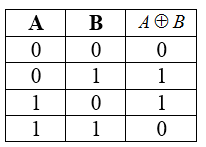
Строгая дизъюнкция истинна, если значения аргументов не равны.

Таблица истинности для операции сложения по модулю два

Свойства строгой дизъюнкции:

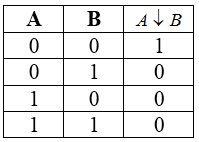
Стрелка Пирса

Таблица истинности для стрелки Пирса

Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:

$X \downarrow X = ¬X$— отрицание

$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция

$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция

$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация

В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).

Штрих Шеффера

Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.

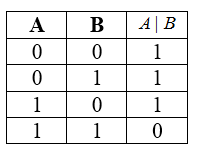
Таблицей истинности для функции штрих Шеффера

Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,

$X \mid X = ¬X$ — отрицание

$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция

$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция

Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).

Порядок выполнения логических операций в сложном логическом выражении

Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.

Общие свойства

Нужны еще материалы по теме статьи?

Воспользуйся новым поиском!

Найди больше статей и в один клик создай свой список литературы по ГОСТу

Автор этой статьи Дата написания статьи: 24.03.2016

Источник

конъюнкция

Смотреть что такое «конъюнкция» в других словарях:

Источник

Урок на тему «Логические операции. Конъюнкция»

В предыдущем уроке мы рассмотрели логическую операцию отрицание. Сегодня поговорим о конъюнкции. Конъюнкцию также называют «логическое умножение» или «логическое И«, а часто просто «И«.

В естественном языке конъюнкцию заменяют союзом И.

Конъюнкция — бинарная операция, т. е. для нее необходимо два операнда.

Для обозначения конъюнкции применяют различные символы. Это может быть знак &, AND. Но чаще всего для обозначения конъюнкции используют символ

Рассмотрим пример. Пусть есть два высказывания: A = «Москва — столица России» и B = «Сегодня солнечно«. Тогда конъюнкция этих высказываний будет выглядеть так «Москва — столица России И сегодня солнечно«, а обозначаться так:

Так как на клавиатуре нет символа конъюнкции, его можно набрать из слэша ( / ) и бэкслэша ( \ ) — получится /\ — похоже на обозначение конъюнкции.

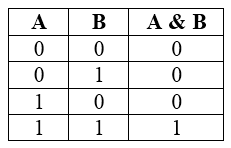
Таблица истинности для конъюнкции выглядит так:

A	B	A /\ B
0	0	0
0	1	0
1	0	0
1	1	1

Запомнить довольно просто — конъюнкция истинна только в одном случае — когда оба исходных высказывания истинны. А еще проще запомнить таблицу истинности для конъюнкции, если представить ее электрический аналог — два последовательно включенных выключателя:

Электрический аналог конъюнкции

И теперь сразу понятно, что лампочка будет гореть только тогда, когда оба выключателя включены — цепь замкнута. Все также как и у конъюнкции.

Автор: Александр Чернышов

Оцените статью, это очень поможет развитию сайта.

Источник

конъюнкция

Смотреть что такое «конъюнкция» в других словарях:

Источник

КОНЪЮНКЦИЯ

Смотреть что такое «КОНЪЮНКЦИЯ» в других словарях:

Источник

КОНЪЮНКЦИЯ

КОНЪЮНКЦИЯ — логическая операция, образующая сложное высказывание из двух высказываний, объединённых с помощью логического союза «И». Логический переключательный элемент, реализующий функцию К., называется схемой совпадения или вентилем. С помощью этой операции легко проверяется, установлен данный бит (см.) или нет.

Смотреть что такое «КОНЪЮНКЦИЯ» в других словарях:

Источник

Конъюнкция

Смотреть что такое «Конъюнкция» в других словарях:

Источник

КОНЪЮНКЦИЯ

Смотреть что такое «КОНЪЮНКЦИЯ» в других словарях:

Источник

Конъюнкция

Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Содержание

Обозначения

Наиболее часто встречаются следующие обозначения для операции конъюнкции:

Булева алгебра

Определение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).

Правило: результат равен наименьшему операнду.

Таблицы истинности:
для бинарной конъюнкции

для тернарной конъюнкции

Многозначная логика

Следует отметить, что название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.

Классическая логика

С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Схемотехника

Теория множеств

С точки зрения теории множеств, конъюнкция аналогична операции пересечения.

Программирование

В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:

Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.

подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.

Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	01100101 2 <\displaystyle 01100101_<2>>
b =	00101001 2 <\displaystyle 00101001_<2>>
то
a И b =	00100001 2 <\displaystyle 00100001_<2>>

Связь с естественным языком

Источник