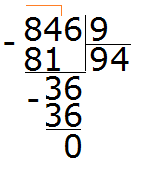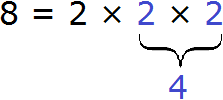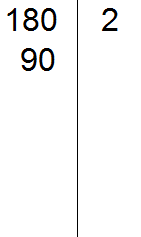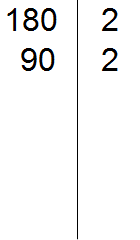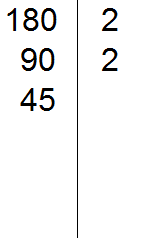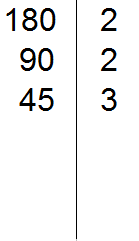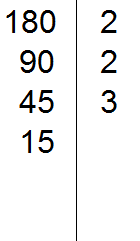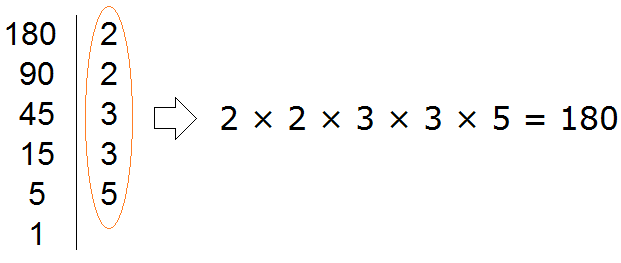Что такое кратное число

29.08.202229.08.2022 admin 0 Комментариев

Что такое кратное число

Кратное и делитель

Если одно натуральное число делится без остатка на другое натуральное число, то первое называется кратным второго, а второе — делителем первого.

Кратное числа — это делимое, которое делится на данный делитель без остатка.

Делитель числа — это делитель, на который делимое делится без остатка.

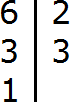
Пример. Возьмём, например, такое деление:

Число 6 делится на число 3 без остатка. Следовательно, число 6 — кратное числа 3, а число 3 — делитель числа 6.

Пусть m и n — натуральные числа, если число m является кратным числа n, то говорят: m кратно n или m делится на n

Пример. 6 кратно 3 (шесть кратно трём) или 6 делится на 3 (шесть делится на три).

Самым маленьким кратным любого натурального числа является само это число, так как любое натуральное число можно разделить само на себя без остатка (в частном всегда будет единица).

Пример. Для числа 7 наименьшим кратным является число 7, для числа 2 — число 2:

7 : 7 = 1 (семь кратно семи);

2 : 2 = 1 (два кратно двум).

Для любого натурального числа существует бесконечно много кратных. Получить кратное для данного числа достаточно легко, можно просто умножить его на любое натуральное число, полученное произведение и будет его кратным.

Пример. Получим кратное числа 5, умножив его, например, на 2:

Число 10 — кратное числа 5:

Так как на единицу делится любое натуральное число, то число 1 является делителем любого натурального числа.

Источник

кратное

Смотреть что такое «кратное» в других словарях:

КРАТНОЕ — число, делящееся на данное целое число без остатка, напр. 12 кратно 3. Общее кратное нескольких целых чисел число, делящееся на каждое из них в отдельности, напр. 180 общее кратное чисел 30, 18, 2. При арифметических действиях особое значение… … Большой Энциклопедический словарь

кратное (число) — кратный многократный множественный составной параллельный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы… … Справочник технического переводчика

кратное число — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN multiple … Справочник технического переводчика

Кратное — натурального (целого положительного) числа а, натуральное число, делящееся на а без остатка. Так, 156 есть К. 13, тогда как 108 не является К. 13. Число n, которое делится на каждое из чисел а, b. m, называется общим К. этих чисел. Из … Большая советская энциклопедия

Кратное — ср. Целое число, делящееся на какое либо число без остатка. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

КРАТНОЕ — число, делящееся на данное целое число без остатка, напр. 12 кратно 3. Общее К. неск. целых чисел число, делящееся на каждое из них в отдельности, напр. 180 общее К. чисел 30, 18, 2. При арифметич. действиях особое значение имеет наименьшее общее … Естествознание. Энциклопедический словарь

Кратное — Делимость одно из основных понятий арифметики и теории чисел, связаное с операцией деления. Содержание 1 Определение 2 Обозначения 3 Связанные определения … Википедия

кратное — кр атное, ого … Русский орфографический словарь

кратное — ого; ср. Целое число, делящееся на данное без остатка. Шесть кра/тное чисел два и три. Наименьшее общее кра/тное нескольких чисел … Словарь многих выражений

Источник

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

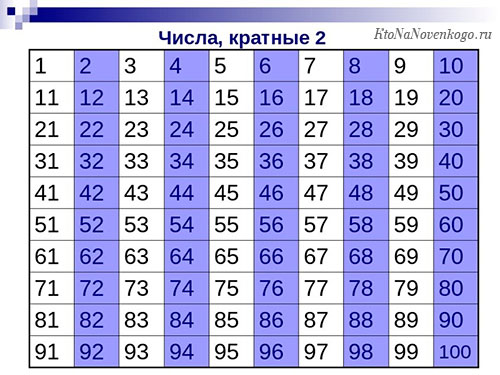
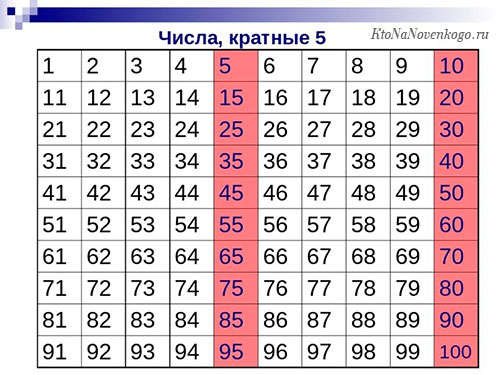
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

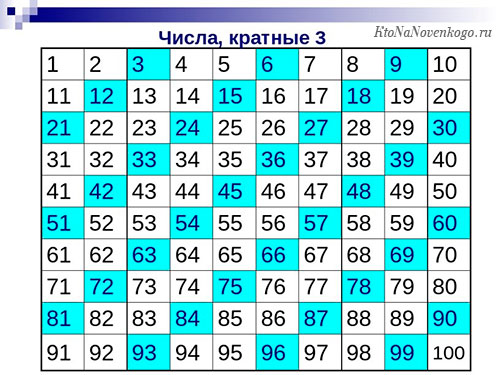
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

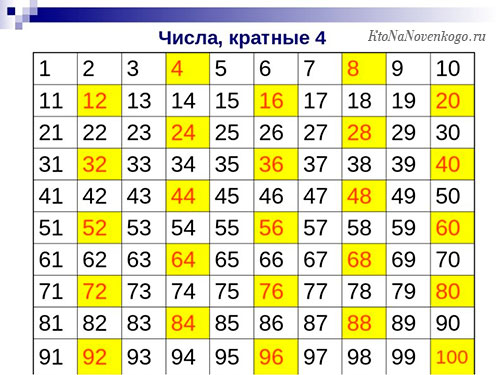
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

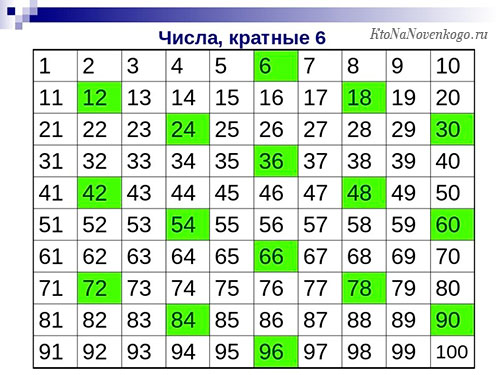
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

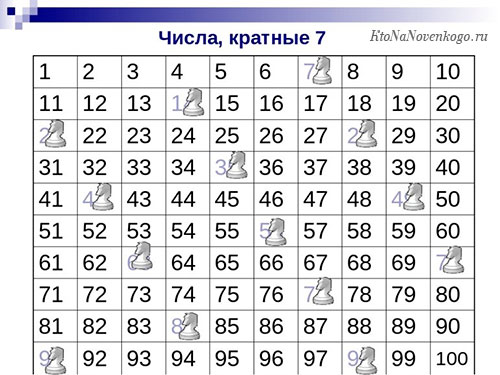
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Числа, кратные 9	27	198	5 877	3 816	117	72
Сумма	9	18	27	18	9	9

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Делитель и кратное в математике

Что такое делители и кратные числа

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

Делимое — число, которое делят на несколько частей.

Делитель — число, которое показывает, на сколько частей нужно разделить делимое.

Частное — число, которое является результатом деления.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е

Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.

16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.

Делителем числа a называется такое число b, на которое a делится нацело.

Например, 9 : 4 = 2 (остаток 5 ).

В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.

Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.

Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.

Тогда представим решение данной задачи в виде уравнения:

72 — целое число, без остатка.

Произведение делителей должно дать в результате 144:

72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.

Ответ: числа 2 и 72 — делители 144.

Число называют кратным, если оно делится на данное число нацело, без остатка.

Например, 15:3 нацело.

Тогда число 15 является кратным 3.

Пишут: 15 кратно 3.

Слово «кратно» синонимично слову «делится».

Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Основные понятия и определения

Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.

Делится нацело = без остатка.

Наименьшим делителем любого числа является единица.

Наибольшим делителем числа является само число.

Делителем нуля будет любое число, но сам 0 делителем не будет.

При делении нуля на любое число получаем 0. А делить на ноль нельзя.

У единицы только один делитель — единица.

Другие числа, кроме 1, имеют не меньше двух делителей.

Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.

Наименьшее кратное числа является равным самому числу.

Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.

Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.

Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.

Чем отличаются друг от друга, как найти

Делитель отличается от кратного тем, что:

Чтобы найти делители числа, нужно данное число разложить на множители.

Разложить на множители — представить число в виде произведения целых чисел.

Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.

Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.

Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.

Примеры решения задач

Необходимо найти делители числа 14.

Решить задание можно двумя способами.

Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.

Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.

Ответ: делители числа 14: 1, 2, 7, 14.

Представим 14 в виде произведения чисел:

14 = 14 * 1 = 2 * 7

Делителями будут множители, так как можем разделить 14 нацело на каждый из них.

Ответ: делители 14: 1, 2, 7, 14.

Найдите три числа, кратных 7.

Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.

7 * 1 = 7 — семь кратно семи;

7 * 2 = 14 — 14 кратно 7;

7 * 3 = 21 — 21 кратно 7.

Ответ: числа, кратные 7: 7, 14, 21.

Самостоятельно проверьте, 225 кратно 3 или нет.

Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.

75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Найдите любое число, делителями которого являются числа 7 и 8.

Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:

Источник

Что значит кратно числу? Как это понять?

В заданиях по математике можно встретить фразы: «найдите число, кратное. » Иногда эта формулировка может вызвать непонимание. Что значит кратно? Это значит, что одно число делится на другое целиком, без остатка. Приведем пример: Найти число, кратное 2. Это значит, что число должно без остатка делиться на 2. Ответом может быть любое четное число.

Приведем еще пример: Число, кратное 5. Что это за число? Например, 10, 35, 55, 60 и все другие, которые делятся на 5 без остатка.

Кратность в математике означает делимость.

12 кратно числу 3, то есть 12 можно сократить на 3, разделить на 3 без остатка.

20 кратно числу 5, то есть 20 можно сократить на 5, разделить на 5 без остатка.

Кратно какому-либо числу может быть только другое определённое (меньшее первому) число, обладающее соответствующими свойствами: кратное число должно быть ровно во сколько-то крат (раз) больше другого. Это арифметическое понятие.

десять кратно двум = десять делится на два

восемь кратно четырем = восемь делится на четыре

Иногда слово «кратное» применяют не только в учебниках математики, но в разговорах, касающихся экономических или других показателей.

Источник

Делители и кратные числа: определения и примеры

Основные определения

Для начала сформулируем определения для целого числа.

Если вспомнить такое понятие, как делимость, то данную формулировку можно слегка изменить.

Остановимся на делителях таких чисел, как нуль, единица и минус единица. Поскольку нам знакомы свойства делимости, то мы можем заключить, что делителем 0 может стать любое целое число (включая сам 0 ), а единица и минус единица имеют только делители, равные 1 и − 1 соответственно.

Какие еще можно привести примеры делителей в случае с целыми числами?

Далее мы будем говорить лишь о положительных делителях целых положительных (натуральных) чисел.

У единицы есть только один положительный делитель – сама единица. Этим 1 отличается от остальных натуральных чисел, поскольку другие имеют не меньше 2 делителей: кроме единицы их можно разделить на числа, равные им самим. В зависимости от того, имеются ли делители, отличные от самого числа и единицы, различают числа простые и составные.

Понятие кратных чисел

Начнем, как всегда, с определения.

Возьмем несколько примеров кратных чисел.

Наименьшее положительное кратное положительного числа есть само это число. Обратите внимание, что наименьшее кратное в этом случае не нужно путать с наименьшим общим кратным для нескольких чисел (НОК).

Далее будут рассмотрены другие случаи с натуральными кратными целых положительных чисел.

Источник

Что такое кратное число

Определение кратного числа

Некоторые признаки делимости натуральных чисел

Признак делимости на 2.

Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.

Признак делимости на 3.

Число делится на 3, если сумма его цифр делится на 3.

Признак делимости на 4.

Признак делимости на 5.

Число делится на 5, если оно заканчивается либо на 0, либо на 5.

Признак делимости на 8.

Признак делимости на 9.

Число делится на 9, если сумма его цифр делится на 9.

Признак делимости на 11.

Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11.

Признак делимости на 25.

Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:

$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$

Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:

; ;

;

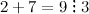
Таким образом, на 3 делятся числа:

$$27 ; 36 ; 1119: 12354$$

Наименьшее общее кратное (НОК)

Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).

Алгоритм нахождения наименьшего общего кратного нескольких чисел:

Источник

Делители и кратные

В данном уроке мы рассмотрим такие понятия как делители и кратные.

Что такое делитель?

Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.

Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:

Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:

Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:

10 : 4 = 2 (2 в остатке)

Определение. Делителем числа а называется число, на которое число а делится без остатка.

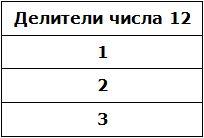
Делителем числа 12 называется число, на которое 12 делится без остатка.

Попробуем перечислить эти числа:

Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:

12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:

Чётные и нечётные числа

Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:

Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:

21 : 2 = 10 (1 в остатке)

Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.

Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Простые и составные числа

Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:

Значит, число 5 является простым числом.

Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1

Значит, число 4 является составным числом.

Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.

Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.

Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4

Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6

Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.

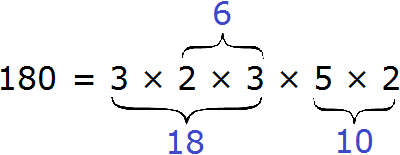
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10

Теперь раскладываем множители 18 и 10 на другие множители:

Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:

Теперь собираем все простые множители вместе:

На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.

Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.

При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.

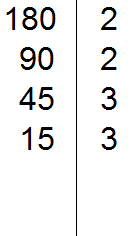
Например, разложим предыдущее число 180 этим способом.

Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.

180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:

Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.

90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.

45 на 2 не делится. Тогда проверяем делится ли 45 на 3.

45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:

Теперь делим 15. Проверяем делится ли 15 на 2.

15 не делится на 2. Тогда проверяем делится ли 15 на 3.

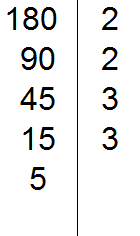
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:

Теперь делим 5. Проверяем делится ли 5 на 2.

5 не делится на 2. Тогда проверяем делится ли 5 на 3.

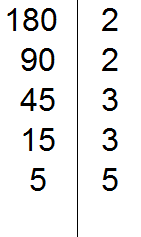
5 не делится на 3. Тогда проверяем делится ли 5 на 5.

5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:

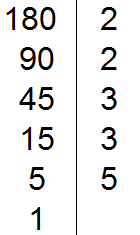
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.

Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:

Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

Пример 1. Найти делители числа 12

Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

1, 2, 3, 6

Источник

Кратное

Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.

Содержание

Определение

Обозначения

Связанные определения

Свойства

Число делителей

Обобщения

Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.

См. также

Полезное

Смотреть что такое «Кратное» в других словарях:

кратное — ого; ср. Целое число, делящееся на данное без остатка. Шесть к. чисел два и три. Наименьшее общее к. нескольких чисел. * * * кратное число, делящееся на данное целое число без остатка, например 12 кратно 3. Общее кратное нескольких целых чисел … … Энциклопедический словарь

кратное — кр атное, ого … Русский орфографический словарь

Источник

Урок 1 Бесплатно Делители и кратные

Операция деления известна с давних времен.

Привычные нам сегодня обозначения операции деления появлялись постепенно, в более древние времена люди использовали другие знаки.

Первый из символов ( / ), в обиходе косая черта, впервые был применен в 1631 году в одной из работ англичанина Уильяма Отреда.

Со временем в математике стали использовать и знак ( : ). Его в своих работах использовал немецкий математик Готфрид Вильгельм Лейбниц (1646—1716)

При выполнении операции деления используют три математических составляющих:

Сегодня мы познакомимся с делителями и со связанными с ними понятиями кратных.

Делители и кратные

Допустим, у вас есть 30 конфет и их надо разделить поровну шести друзьям.

В этом случае 6 друзей получат по 5 конфет, потому что 30 : 6 = 5

Если натуральное число делится без остатка на второе натуральное число, то первое называется кратным, а второе называют делителем.

Другими словами, 30 кратно 6, а 6 это делитель 30.

Могут быть и другие варианты решения задачи, которые зависят от данного нам условия.

Если друзей будет 7, тогда раздать всем равное количество конфет не получится, так как 30 без остатка на 7 не делится.

Значит, 30 не кратно 7, и 7 не является делителем 30

Натуральное число, на которое делится без остатка другое число, называется его делителем.

Само число 15 имеет четыре делителя: 1; 3; 5; 15, так как на каждое из этих чисел оно делится без остатка.

Натуральное число, которое делится на другое без остатка, называется его кратным.

Любое натуральное число имеет бесконечно много кратных.

Наименьшим из кратных натурального числа является само это число.

Например, кратными 4 будут числа: 4; 8; 12; 16; 20 и т.д.

У меня есть дополнительная информация к этой части урока!

Существуют числа, равные сумме всех их делителей, не считая самого числа.

Например, число 6.

Его делители 1, 2, 3.

Само число 6 не учитываем.

Сложив их, получим в сумме 6

К числам с таким свойством можно отнести еще 28 или 496

Пройти тест и получить оценку можно после входа или регистрации

Использование понятий делителя и кратного при решении примеров и задач

Любые математические понятия используются при решении примеров и задач, ответах на вопросы из жизни.

Разберем некоторые из них подробнее.

Пример 1

На сколько равных кучек можно разделить 24 ореха?

Решение:

Нужно выяснить все делители числа 24

Такими будут числа: 1; 2; 3; 4; 6; 8; 12; 24

Каждое из этих чисел будет являться ответом на поставленный вопрос, таким образом:

1 кучка из 24 орехов

2 кучки по 12 орехов

3 кучки по 8 орехов и т.д.

Пример 2

Напишите все двузначные числа, кратные 44

Решение:

Еще нам дано условие, что такие числа должны быть двузначными.

Значит, это два числа 44 и 88.

Оба они делятся на 44 без остатка, в чем можно легко убедиться: 44 : 44 = 1; 88 : 44 = 2

Пример 3

Какое число и кратно 15, и является делителем 15?

Решение:

Оно кратно самому себе и является для себя делителем.

Пример 4

В строю 300 солдат. Можно ли их разделить на 7 равных групп для проведения физической подготовки?

Решение:

Чтобы проверить, можно ли разделить 300 солдат на 7 равных групп, поделим число 300 на 7.

Имеем: 300 : 7 = 42 и в остатке 6. То есть 300 не делится нацело на 7.

Значит, разбить 300 солдат на 7 равных групп не получится.

Пример 5

Докажите, что число 70525 кратно числу 217.

Доказательство:

Выполним деление 70525 на 217 уголком.

Видим, что деление выполнено без остатка, значит, число 70525 кратно числу 217.

У меня есть дополнительная информация к этой части урока!

Делителем любого натурального числа является единица.

И правда, ведь на единицу делится любое натуральное число без остатка

Пройти тест и получить оценку можно после входа или регистрации

Интересная информация

Раньше алгоритм деления в России выглядел совершенно иначе и не имел ничего общего с современным видом.

Например, деление могло получиться в виде полумесяца или по форме напоминать геометрическую фигуру- ромб.

Пусть требуется разделить 598432 на 678

Вот как выглядела запись деления:

436

1792

5603

5984/

882

678

5424

1356

436

598432 верно разделено

Или разделить 9649378 на 5634:

259

59417

4015530

9649378

5634444

56333

566

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник

Кратное число

Средняя оценка: 4.1

Всего получено оценок: 203.

Средняя оценка: 4.1

Всего получено оценок: 203.

Математика имеет много специфических понятий, среди которых кратное число и делимость чисел. Сегодня мы разберем понятие кратности, а так же все понятия из математики 6 класса, которые связаны с кратностью.

Деление

Операция деления является обратной для операции умножения. Деление показывает, сколько раз одно число умножили на другое, чтобы получить изначальный результат. Для нахождения результата простейших операций деления пользуются таблицей умножения.

Для более сложных примеров пользуются деление в столбик. Так же различают деление с остатком, нацело и деление с дробным остатком:

Так же вместо деления всегда можно записать обычную или неправильную дробь, но в качестве ответа такая запись не подойдет.

Отрицательные числа так же можно поделить нацело. Так же, как и в делении отрицательных чисел на положительные и положительные на отрицательные. Нельзя так же забывать, что на деление действует правило знаков. То есть деление отрицательного числа на положительное дает отрицательный результат. Деление отрицательного числа на отрицательное – положительный результат.

Кратность и делимость

Разберем эти понятия на числе 9. Так для числа 9 кратными будут 18, 27, 36 и так далее. То есть кратными называют числа, которые можно поделить на заданное число нацело.

Делимостью же называют способность самого числа поделиться нацело. То есть для 9 делителями будут числа 9,3,1. Число делителей – ограниченно, число кратных – нет.

Бывают числа кратные для нескольких значений одновременно.

Для нескольких чисел существует два понятия, связанных с делимостью и кратностью:

Иногда ученики пытаются найти таблицу кратных чисел. Но такого материала просто не существует. Нельзя свести в одну таблицу все числа. А для наиболее простых от 1 до 10 существует таблица умножения.

Что мы узнали?

Мы вспомнили, что такое операция деления. Рассказали, что такое кратность и делимость чисел. Разделили два этих понятия. Сказали о том, что таблицы кратности в математике пока не изобрели. Рассказали, в каких математических показателях используются понятия кратности и делимости.

Источник

Что такое кратное число? Ответ на

Что такое делители и кратные числа

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

Делимое — число, которое делят на несколько частей. Делитель — число, которое показывает, на сколько частей нужно разделить делимое. Частное — число, которое является результатом деления.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Делителем числа a называется такое число b, на которое a делится нацело.

Например, 9:4=2(остаток5). В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток. Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9:4=2(остаток5) — число 4 не является делителем числа 9.

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2. Объяснение: Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель. Тогда представим решение данной задачи в виде уравнения: 144:x=2;x=144:2;x=72. 72 — целое число, без остатка. Проверка: Произведение делителей должно дать в результате 144: 72*2=144 — верно, значит, 72 — корень уравнения и делитель 144. Ответ: числа 2 и 72 — делители 144.

Число называют кратным, если оно делится на данное число нацело, без остатка.

Например, 15:3 нацело. 15:3=5. Тогда число 15 является кратным 3. Пишут: 15 кратно 3. Слово «кратно» синонимично слову «делится». Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Видео

Кратные числа

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

5 : 5 = 1 10 : 5 = 2 15 : 5 = 3 20 : 5 = 4 25 : 5 = 5

Чётные и нечётные числа

21 : 2 = 10 (1 в остатке)

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Примеры решения задач

Необходимо найти делители числа 14. Решить задание можно двумя способами. Способ 1: Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу. 14:1=14;14:2=7;14:3=4(остаток2);14:4=3(остаток2);14:5=2(остаток4);14:6=2(остаток2);14:7=2;14:8=1(остаток6);14:9=1(остаток5);14:10=1(остаток4;)14:11=1(остаток3);14:12=1(остаток2);14:13=1(остаток1);14:14=1. Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14. Ответ: делители числа 14: 1, 2, 7, 14. Способ 2: Представим 14 в виде произведения чисел: 14=14*1=2*7 Делителями будут множители, так как можем разделить 14 нацело на каждый из них. Ответ: делители 14: 1, 2, 7, 14.

Найдите три числа, кратных 7. Решение: Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число. 7*1=7 — семь кратно семи; 7*2=14— 14 кратно 7; 7*3=21 — 21 кратно 7. Ответ: числа, кратные 7: 7, 14, 21.

Самостоятельно проверьте, 225 кратно 3 или нет. Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга. 225:3=75. 75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Найдите любое число, делителями которого являются числа 7 и 8. Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители: 7*8=56. Ответ: 56.

Источник

Словари

Делящийся без остатка на какое-либо число (в математике).

КРА́ТНЫЙ, кратная, кратное; кратен, кратна, кратно (мат.).

1. Делящийся без остатка на какое-нибудь число. Число десять кратно пяти и двум.

1. Делящийся без остатка на какое-л. число.

Целое число, делящееся на данное без остатка.

Вторая составная часть сложных слов, обозначающая: повторяющийся столько-то раз, больший во столько-то раз (сколько указано в первой части), например: пятикратный, двукратный, многократный.

кра́тный, кра́тен, кра́тна, кра́тно, кра́тны

кра́тный, кратк. ф. кра́тен, кра́тна (неправильно кратна́), кра́тно, кра́тны.

кра́тный, кра́тная, кра́тное, кра́тные, кра́тного, кра́тной, кра́тных, кра́тному, кра́тным, кра́тную, кра́тною, кра́тными, кра́тном, кра́тен, кра́тна, кра́тно, кра́тны, кра́тнее, покра́тнее, кра́тней, покра́тней

прил., кол-во синонимов: 2

сложный, составной; кратен. Ant. простой

Syn: сложный, составной

делимость (признаки делимости).

составное число. простое число.

каждый энный (каждый третий голосовал против).

разбить на (# пары).

двукратный. троекратный. пятикратный. семикратный.

к (один к трем). на (один на три).

из расчета (# три к одному).

сколько раз на протяжении чего, ↓ половина

Источник

КРАТНОЕ

Смотреть что такое «КРАТНОЕ» в других словарях:

кратное — кр атное, ого … Русский орфографический словарь

Источник

Признаки делимости чисел

О чем эта статья:

Понятие делимости

Признаки делимости чисел — это особенности чисел, которые позволяют определить, кратно число делителю или нет.

Все целые числа делятся на единицу.

Каждое целое число, не равное нулю, делится на натуральное число, равное модулю от данного целого.

Все натуральные числа являются делителями нуля.

Если целое число a делится на натуральное число b и модуль числа a меньше b, то a равно нулю.

Если целое число a отлично от нуля и делится на натуральное число b, то модуль числа a не меньше числа b.

Единственный делитель единицы — сама единица.

Чтобы целое число a делилось на натуральное число b, необходимо и достаточно, чтобы модуль числа a делился на b.

Если натуральные числа делятся друг на друга без остатка, то они равны.

Свойства делимости можно использовать при решении задач и доказательстве теорем.

Четные числа — это числа, которые делятся на два: 0, 2, 4, 6, 8, 10, 12 и т. д. Ноль тоже относится к четным числам.

Нечетные числа — это числа, которые на два не делятся: 1, 3, 5, 7, 9, 11, 13 и т. д.

Признаки делимости

Рассмотрим признаки делимости на 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Признак делимости на 1

Каждое целое число делится на 1.

Признаки делимости на 2

Число делится на 2, если его последняя цифра четная.

Пример: число 2164 делится на 2, так как последняя цифра (6) — четная.

Признаки делимости на 3

На 3 делятся только те числа, у которых сумма цифр делится на 3.

Пример: число 81 300 делится на 3, так как сумма его цифр 8 + 1 + 3 + 0 + 0 = 12 делится на 3.

Признаки делимости на 4

Число делится на 4, если две последние его цифры — нули или образуют число, которое делится на 4.

число 37 100 делится на 4, так как оно оканчивается двумя нулями;

число 7524 делятся на 4, так как две последние цифры (24) делятся на 4.

Признаки делимости на 5

На 5 делятся те числа, которые оканчиваются на 0 или 5.

Пример: число 450 делится на 5, так как последняя цифра 0.

Признаки делимости на 6

Число делится на 6, если оно делится одновременно на 2 и на 3.

число 912 делится на 6, так как оно делится и на 2 и на 3;

число 861 не делится на 6, так как оно делится на 3, но не делится на 2.

Признаки делимости на 7

Делимость на число 7 можно проверить так:

Последнюю цифру числа умножить на два.

Полученное произведение вычесть от оставшегося числа (без последней цифры).

Полученная разность должна быть кратна 7.

Пример: число 343 делится на 7, так как 34 − (2 · 3) = 28, и 28 делится на 7.

Признаки делимости на 8

На 8 делятся те числа, у которых три последние цифры являются нулями или образуют число, которое делится на 8.

число 11 000 делится на 8, так как оно оканчивается тремя нулями;

число 12 128 делится на 8, так как три последние цифры образуют число (128), которое делится на 8.

Признаки делимости на 9

На 9 делятся только те числа, у которых сумма цифр делится на 9.

Пример: число 2637 делится на 9, так как сумма его цифр 2 + 6 + 3 + 7 = 18 делится на 9.

Признаки делимости на 10

На 10 делятся те числа, которые оканчиваются на ноль или несколько нулей.

число 980 делится на 10;

число 462 не делится на 10 — последняя цифра 2.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Источник

Как найти кратность числа

Содержание статьи

Нахождение наименьшего общего кратного: основные понятия

Чтобы понять, как вычислять НОК, следует определиться в первую очередь со значением термина «кратное».

Кратным числу А называют такое натуральное число, которое без остатка делится на А. Так, числами кратными 5 можно считать 15, 20, 25 и так далее.

Делителей конкретного числа может быть ограниченное количество, а вот кратных бесконечное множество.

Общее кратное натуральных чисел – это такое число, которое делится на них без остатка.

Как найти наименьшее общее кратное чисел

Наименьшее общее кратное (НОК) чисел (двух, трех или больше) – это самое маленькое натурально число, которое делится на все эти числа нацело.

Чтобы найти НОК, можно использовать несколько способов.

Для небольших чисел удобно выписать в строчку все кратные этих чисел до тех пор, пока среди них не найдется общее. Кратные обозначают в записи заглавной буквой К.

Например, кратные числа 4 можно записать так:

Так, можно увидеть, что наименьшим общим кратным чисел 4 и 6 является число 24. Эту запись выполняют следующим образом:

Если числа большие, или нужно найти наименьшее общее кратное трех и более чисел, то лучше использовать другой способ вычисления НОК.

Для выполнения задания необходимо разложить предложенные числа на простые множители.

Сначала нужно выписать в строчку разложение наибольшего из чисел, а под ним – остальных.

В разложении каждого числа может присутствовать различное количество множителей.

Например, разложим на простые множители числа 50 и 20.

В разложении меньшего числа следует подчеркнуть множители, которые отсутствуют в разложении первого самого большого числа, а затем их добавить к нему. В представленном примере не хватает двойки.

Теперь можно вычислить наименьшее общее кратное 20 и 50.

НОК (20, 50) = 2 * 5 * 5 * 2 = 100

Так, произведение простых множителей большего числа и множителей второго числа, которые не вошли в разложение большего, будет наименьшим общим кратным.

Чтобы найти НОК трех чисел и более, следует их все разложить на простые множители, как и в предыдущем случае.

В качестве примера можно найти наименьшее общее кратное чисел 16, 24, 36.

Так, в разложение большего числа на множители не вошли только две двойки из разложения шестнадцати (одна есть в разложении двадцати четырех).

Таким образом, их нужно добавить к разложению большего числа.

НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9

Существуют частные случаи определения наименьшего общего кратного. Так, если одно из чисел можно поделить без остатка на другое, то большее из этих чисел и будет наименьшим общим кратным.

Например, НОК двенадцати и двадцати четырех будет двадцать четыре.

Если необходимо найти наименьшее общее кратное взаимно простых чисел, не имеющих одинаковых делителей, то их НОК будет равняться их произведению.

Основные определения

Для начала сформулируем определения для целого числа.

Если вспомнить такое понятие, как делимость, то данную формулировку можно слегка изменить.

Какие еще можно привести примеры делителей в случае с целыми числами?

Далее мы будем говорить лишь о положительных делителях целых положительных (натуральных) чисел.

Понятие кратных чисел

Начнем, как всегда, с определения.

Возьмем несколько примеров кратных чисел.

Далее будут рассмотрены другие случаи с натуральными кратными целых положительных чисел.

Онлайн-калькулятор «Нахождение НОД и НОК чисел«. Наш калькулятор поможет вам найти наибольший общий делить (НОД) и наименьшее общее кратное (НОК) чисел. Особенностью данного калькулятора является то, что он может находить НОК и НОД не только двух чисел, но и трех или четырех чисел. Введите натуральные числа и нажмите кнопку «Вычислить» и наш калькулятор не просто выдаст ответ, но и представит подробное решение, где последовательно будет изложен порядок нахождения НОД и НОК чисел.

Первое число

Второе число

Третье число

Четвертое число

Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое эти числа делятся без остатка. Наибольший общий делитель обозначается следующим образом: НОД (18; 48) = 6

Наименьшее общее кратно нескольких чисел – это самое меньшее число, которое делится на каждое из этих чисел без остатка. Например: НОК (18; 48) = 144

Это следует знать! Как определить, что число делится на 3 без остатка? Очень просто – на 3 делятся только те числа, сумма цифр которых делится на 3. Например: число 795 делится на 3, так как сумма его цифр 7 + 9 + 5 = 21 делится на 3.
21 : 3 = 7

Источник

кратное

Наименьшее общее кра́тное нескольких чисел.

Смотреть что такое «кратное» в других словарях:

кратное — кр атное, ого … Русский орфографический словарь

Источник

Что такое кратное число

Здравствуйте!
Пытаюсь разобраться – что такое кратное число? Где используется? Примеры?
Спасибо!

Число k называют кратным относительно натурального числа r, если его можно нацело разделить на r. Принято говорить «k кратно r».
Существуют признаки делимости на некоторые из натуральных чисел.
Делимость на 2:
Число делится на 2, если последняя цифра в его записи 0 или тоже делится на 2.
Например, число 17864 делится на 2, т.к. последняя цифра записи данного числа 4 делится на 2.

Делимость на 3:
Число делится на 3, если результат сложения его цифр делится на 3.
Например, число 1734 делится на 3, потому что 1+7+3+4=15 делится на 3.
Делимость на 4:
Число делится на 4, если две последние цифры в его записи являются нулями или число из этих цифр делится на 4.
Например, число 123476 делится на 4, потому что 76 делится на 4.
Делимость на 5:
Число делится на 5, если его запись заканчивается цифрой 0 или 5.
Например, числа 10, 378585, 1317230 делятся на 5.
Делимость на 8:
Число делится на 8, если три последние цифры в его записи являются нулями или число, составленное из этих цифр, делится на 8.
Например, 1234888 делится на 8, потому что число 888 делится на 8.
Делимость на 9:
Число делится на 9, если результат сложения его цифр делится на 9.
Например, число 93312723618 делится на 9, потому что 9+3+3+1+2+7+2+3+6+1+8=45 делится на 9.
Делимость на 11:
Число делится на 11, если результат сложения цифр, которые стоят на четных местах, равен сумме цифр, которые стоят на нечетных местах, или отличается от этого значения на число, которое делится на 11.
Например, число 616 делится на 11, потому что 6+6–1=11 делится на 11.

Источник

Признаки делимости чисел

В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.

Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.

Примеры:

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.

Примеры:

Признак делимости на 4

Двузначное число

Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.

Число разрядов больше 2

Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.

Примечание:

Число делится на 4 без остатка, если:

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.

Примеры:

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).

Примеры:

Признак делимости на 7

Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.

Признак делимости на 8

Трехзначное число

Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.

Число разрядов больше 3

Число делится на 8, когда три последние цифры образуют число, делящееся на 8.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.

Примеры:

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Примеры:

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.

Примеры:

Источник

Найти кратные числа онлайн

Нахождение кратных чисел с калькулятором онлайн. Просто введите любое целое число, а калькулятор быстро посчитает и выдаст результат.

Калькулятор

Инструкция

Шаг 1. Введите число.

Шаг 2. Нажмите кнопку “Найти”.

Шаг 3. Получите результат.

Шаг 4. Нажмите кнопку “More”, чтобы увидеть больше кратных чисел.

Например, ищете кратные числа к цифре 6. Вводите цифру “6” в поле “Введите число” и высветятся: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60. Это и есть числа, кратные “6”.

Что такое кратные числа

Кратные числа – это такие числа, которые делятся на любое заданное целое число без какого-либо остатка. То есть, в итоге должно получится целое число.

Например: число 12 делится без остатка на 3, 4 и 6. Это означает, что 12 является кратным числам 3, 4, 6, так как существуют натуральные числа 4, 3 и 2. Это легко проверить на примерах ниже:

Источник

КРАТНОЕ

Смотреть что такое «КРАТНОЕ» в других словарях:

кратное — кр атное, ого … Русский орфографический словарь

Источник

Какие числа кратны 10

Содержание статьи

Термин «кратность» относится к области математики: с точки зрения этой науки, он означает количество раз, которое определенное число входит в состав другого числа.

Понятие кратности

Второе важное свойство касается определения наименьшего целого числа, являющегося кратным рассматриваемому. Так, наименьшим кратным по отношению к любому числу является само это число. Это связано с тем, что наименьшим целым результатом деления одного числа на другое является единица, а именно деление числа само на себя и обеспечивает этот результат. Соответственно, число, кратное рассматриваемому, не может быть меньше, чем само это число. Например, для числа 3 наименьшим кратным числом будет 3. При этом определить наибольшее число, кратное рассматриваемому, фактически невозможно.

Числа, кратные 10

Числа, кратные 10, обладают всеми перечисленными свойствами наравне с другими кратными числами. Так, из перечисленных свойств следует, что наименьшим числом, кратным 10, является само число 10. При этом, поскольку число 10 является двузначным, можно сделать вывод, что кратным числу 10 могут быть только числа, состоящие не менее чем из двух знаков.

Для того чтобы получить другие числа, кратные 10, необходимо число 10 умножить на любое целое положительное число. Таким образом, в перечень чисел, кратных 10, войдут числа 20, 30, 40, 50 и так далее. Следует обратить внимание, что все полученные числа должны без остатка делиться на 10. При этом определить наибольшее число, кратное 10, как и в случаях с другими числами, невозможно.

Кроме того, обратите внимание, что существует простой практический способ определить, является ли конкретное рассматриваемое число кратным 10. Для этого следует выяснить, какова его последняя цифра. Так, если она равна 0, рассматриваемое число будет кратным 10, то есть может быть без остатка разделено на 10. В противном случае число не является кратным 10.

Источник

Делители и кратные числа. Определения и примеры

Если одно натуральное число нацело делится на другое натуральное число, то первое число называют кратным второму числу, а второе число называют делителем первого числа.

Делитель числа

Делителем натурального числа a называют число b, на которое a делится без остатка.

Пример: найдите все делители числа 18.
Это означает, что нужно найти все числа, на которые 18 делится без остатка.
Число всегда можно поделить на 1 и на само себя без остатка. Записываем делители 1 и 18. Подбираем остальные числа. Примерим в качестве делителя 2. 18 : 2 = 9, 18 : 9 = 2, значит нам стали известны еще 2 делителя: 2 и 9. 18 : 3 = 6, 18 : 6 = 3, пишем 6 и 3.
Ответ: 18, 9, 6, 3, 2, 1.

Число 1 является делителем любого натурального числа.

Любое целое число делится на себя и на единицу, так как a=a·1 и a=1·a. На основании свойств умножения целых чисел можно записать равенства a=(−a)·(−1) и a=(−1)·(−a), из которых следует, что числа −a и −1 также являются делителями целого числа a. Таким образом, числа a, −a, 1 и −1 всегда являются делителями целого числа a. Например, делителями числа 15 являются числа 15, −15, 1 и −1.

Отдельно нужно сказать о делителях целых чисел 0, 1 и −1. Вспомнив свойства делимости, заключаем, что делителем нуля является любое целое число, в том числе и нуль, а делителями единицы и минус единицы являются только числа 1 и −1.

Итак, целое число 0 имеет бесконечно много делителей, ими являются любые целые числа, числа 1 и −1 имеют только два делителя – единицу и минус единицу, а любое другое целое число a (кроме −1, 0 и 1) имеет, по крайней мере, четыре делителя: a, −a, 1 и −1.

Приведем еще примеры делителей целых чисел. Число −2 является делителем числа 8, так как верно равенство 8=(−2)·(−4). Делителями целого числа 8 являются также числа −8, −4, −1, 1, 2, 4, 8. А вот число −3 не является делителем числа 8, так как не существует целого числа q такого, чтобы выполнялось условие 8=(−3)·k. Иными словами, возможно только деление с остатком целых чисел 8 и −3. Вообще, ни одно целое число, кроме −8, −4, −2, −1, 1, 2, 4, 8, не является делителем 8.

Из рассмотренных примеров отчетливо видно, что делителями целого числа могут быть как целые положительные, так и целые отрицательные числа. Это утверждение обосновывается следующим свойством делимости: если целое число b является делителем целого числа a, то −b (b и −b – противоположные числа) также является делителем числа a. Таким образом, мы можем рассматривать лишь положительные делители чисел, но при этом помнить, что все целые числа, противоположные положительным делителям данного числа, также являются делителями этого числа.

Напомним еще одно свойство делимости: если целое число b является делителем целого числа a, то b также является делителем целого числа −a. Из него следует, что множества делителей чисел a и −a совпадают.

Поэтому, отдавая дань краткости и простоте, в школьных учебниках рассматривают лишь делители целых положительных чисел.

Учитывая информацию двух предыдущих абзацев, дальше можно рассматривать лишь положительные делители целых положительных чисел (натуральных чисел).

Натуральное число 1 имеет единственный положительный делитель – это число 1. Этот факт отличает единицу от других натуральных чисел, так как натуральные числа, отличные от единицы, имеют не менее двух делителей, а именно себя самого и 1. В зависимости от отсутствия или наличия делителей, отличных от самого натурального числа и от единицы, различают простые и составные числа.

Здесь же заметим, что особую роль в математике имеет наибольший общий делитель – НОД.

Кратное чисел

Кратным натуральному числу b называют число а, которое делится без остатка на b.

Любое натуральное число имеет бесконечно много кратных.

Мы можем умножать число 16 из предыдущего примера на 5, 120, 15678, 999 765 433 и так до бесконечности, получая бесконечное количество чисел, кратных 16-ти.

Наименьшим из кратных натурального числа является само это число.

Почему? Чтобы получить кратное числа а, можно умножить число а на 1, при этом всегда получится само число а.

Общее кратное нескольких целых чисел — число, делящееся на каждое из них в отдельности.

Если a является кратным целого числа b, то говорят, что a кратно b.

Определение кратного и делимого явно указывает на существующую между ними связь. Действительно, по определению если a – кратное числа b, то b – делитель числа a, и наоборот, если b – делитель числа a, то a – кратное числа b.

Приведем примеры кратных. Например, целое число −12 есть кратное числа 3, так как −12=3·(−4). Другими кратными числа 3 являются целые числа 0, 3, −3, 6, −6, 9, −9 и так далее. А вот число 7 не является кратным целого числа 3, так как 7 не делится на 3 без остатка, то есть, не существует такого целого числа q, чтобы выполнялось равенство 7=3·q.

Из определения кратного числа понятно, что нуль является кратным любого целого числа b, в том числе и нуля. Равенство 0=b·0 в этом случае выглядит очень доказательно.

Отметим, что существует бесконечно много кратных любого целого числа b, так как целых чисел бесконечно много, и любое целое число, равное произведению b·q, где q – произвольное целое число, является кратным числа b.

Наименьшим положительным кратным данного положительного числа a является само это число a. Здесь же стоит обратить внимание на то, что наименьшее положительное кратное не стоит путать с наименьшим общим кратным (НОК) нескольких чисел.

Дальше мы можем рассматривать лишь натуральные кратные целых положительных чисел. Это мы можем делать в силу тех же причин, которые были упомянуты в первом пункте этой статьи, при этом общность изложения не будет нарушена.

Источник

кратное число

кратное число
—
[[http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=23]]

Тематики

Смотреть что такое «кратное число» в других словарях:

ЧИСЛО — Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете (положительным целым числам 1, 2, 3 и т.д.), числам, являющимся возможными результатами (идеализированных) измерений (это такие… … Энциклопедия Кольера

Источник

Значение слова «кратный»

1. Делящийся без остатка на какое-л. число. Кратные числа.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Число десять кратно пяти и двум. 2. в знач. сущ. кра́тное, ого, ср. Целое число, делящееся на данное. Десять — кратное двух. Общее наименьшее кратное нескольких чисел (наименьшее из целых чисел, делящихся на любое из данных чисел).

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

кра́тный

1. матем. делящийся без остатка на какое-либо число ◆ Чётными называются целые числа, кратные двум.

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: струящийся — это что-то нейтральное, положительное или отрицательное?

Источник

Делители и кратные натуральных чисел

В статье рассмотрим делители и кратные натуральных чисел:
➤ понятие делителей и кратных чисел;
➤ простые и составные числа, признаки делимости;
➤ разложение составного числа на множители;
➤ нахождение делителей числа;
➤ НОД (наибольший общий делитель) и НОК (наименьшее общее кратное).

➤ Понятие: делители и кратные чисел

Делитель — это число, на которое нужно разделить.
Пример 1. В выражении 21 : 7 = 3, делителем является число 7, потому что число 21 делится на число 7 без остатка).
Пример 2. Число 12 делится без остатка на числа 1, 2, 3, 4, 6, 12. Поэтому все эти числа являются делителями числа 12.

Кратное — это число, которое без остатка делится на другое число.
Пример 1. Число 6 делится на 3 без остатка. Поэтому 6 является кратным числа 3.
Пример 2. Кратными числа 5 являются числа 5, 10, 15, 20, 25 и т.д.. Все они кратны 5, поскольку делятся на 5 без остатка. У любого числа бесконечно много кратных.

➤ Простые и составные числа

Последовательность простых чисел начинается так : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Составным называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него более 2 делителей: 1, 2 и 4. Значит, число 4 является составным числом.

➤ Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Рассмотрим наиболее популярные из них.

Признак делимости на 2
Любое четное число делится на 2.

Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10.

Признак делимости на 5
Любое число, которое оканчивается на 0 или 5, делится на 5.

Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27. Сумма его цифр равна 9 (2 + 7 = 9). Девять делится на 3, значит 27 делится на 3.

Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр равна 9 (1 + 8 = 9). Девять делится на девять, значит 18 делится на 9.

➤ Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители, то есть представить это число в виде произведения нескольких простых множителей.
Например: 18 = 2 × 3 × 3, 210 = 2 × 3 × 5 × 7
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
Например: 180 = 18 × 10 = 3×6 × 5×2 = 3 × 2×3 × 5×2.

Удобно раскладывать составное число на простые множители по схеме: проводится вертикальная линия. Слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители. При разложении числа этим способом, используют признаки делимости.

180
90
45
15
5
1

2
2
3
3
5

Когда в итоге получена единица, деление завершается. При этом нужно проверить, чтобы делители, записанные справа от вертикальной линии, были простыми числами.

➤ Нахождение делителей числа

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим пример.

Пример 1. Найти делители числа 12.
Чтобы понять, как эти получаются делители, разложим число 12 на простые множители: 12=2×2×3.
Таким образом, мы получили делители числа 12: 1, 2, 3 и 12.
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой: 2×2=4, 2×3=6.
Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании примера можно сформировать правило для нахождения делителей числа:

➤ НОД — наибольший общий делитель.

Наибольший общий делитель (НОД) чисел a и b — это наибольшее число, на которое a и b делятся без остатка.

Пример. Найдем НОД для чисел 18 и 24.
Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка. Причем делитель является наибольшим из всех существующих делителей.
Чтобы найти НОД, нужно разложить оба числа на простые множители и перемножить общие из них:
1) 18 = 2 × 3 × 3
2) 24 = 2 × 2 × 2 × 3
Перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить: 2 × 3 = 6
Получаем: НОД (24, 18) = 6

Наибольший общий делитель можно также находить для нескольких чисел, а не только для двух. Для этого все числа раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например. Найдём НОД для чисел 18, 24 и 36
1) 18 = 2 × 3 × 3
2) 24 = 2 × 2 × 2 × 3
3) 36 = 2 × 2 × 3 × 3
Общие множители для чисел 18, 24 и 36 — это 2 и 3. Эти множители входят во все три разложения.
Получаем: НОД (24, 18, 36) = 6

➤ НОК — наименьшее общее кратное.

Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это самое маленькое число, которое делится без остатка на число a и число b.

Пример. Найдем НОК для чисел 9 и 12.
Наименьшее общее кратное (НОК) для чисел 9 и 12 — это наименьшее число, которое делится на 9 и 12.
Чтобы найти НОК, нужно разложить оба числа на простые множители.
1) 9 = 3 × 3
2) 12=2 × 2 × 3
Затем выписываются все множители, входящие в первое разложение ( 3 × 3) и добавляют недостающие множители из второго разложения (2 × 2). Полученные множители перемножают и получают НОК.
Получаем: 3 × 3 × 2 × 2 = 36 ➤ НОК (9, 12) = 36

На сайте также есть калькулятор для нахождения НОД и НОК (для самоконтроля).

Источник

Значение слова кратное

Кратное в словаре кроссвордиста

кратное

ср.Целое число, делящееся на какое-либо число без остатка.

Большой современный толковый словарь русского языка

ср. Целое число, делящееся на какое-л. число без остатка.

Новый толково-словообразовательный словарь русского языка Ефремовой

Словарь русского языка Лопатина

число, делящееся на данное целое число без остатка, напр. 12 кратно

2. При арифметических действиях особое значение имеет наименьшее общее кратное: для чисел 30, 18, 2 им будет

Современный толковый словарь, БСЭ

кратное ср. Целое число, делящееся на какое-л. число без остатка.

Толковый словарь Ефремовой

Большая советская энциклопедия, БСЭ

Полный орфографический словарь русского языка

на эту разность между положением Солнца в эфемеридах и положением Солнца в карте рождения, что даст нам дневное, кратное число /в математике кратными величинами числа называются делители этого числа/, но гораздо проще обратиться к помощи специальных таблиц.

Все это наложи- лось на ставшее хроническими сетованиями руководства на то, что издание убыточно (и это при снижении объемов гонораров в 2 раза, 4-5 кратное снижение количества цветных полос и двукратное увеличение тиража, вызванное значительным ростом качества публикаций!!) и наезды в журналистском непрофессионализме.

Не то, чтобы Жан-Луи целенаправленно искал цыпочку, похожую на Франсуаз Фабиан, таких Франсуаз – девять на десяток, ладно – пусть три, кратное девяти, но все же имеются.

Если снежинку повернуть вокруг оси, проходящей через ее центр перпендикулярно к плоскости, на шестьдесят градусов, или на число градусов, кратное шестидесяти, то ее вид в целом останется неизменным, даже если какая-нибудь вершина и изменила свое положение.

представляет собой наименьшее кратное трёх циклов: 28-летнего солнечного, приводящего дни недели на те же числа месяцев; 19-летнего лунного (цикл метона), приводящего фазы Луны на те же даты; 15-летнего, т.

Число 9 интересно тем, что любое кратное ей число при суммировании его составляющих дает в сумме девятку (18, 27, 36, и т. д.), то есть опять становится самим собой.

Однажды на математике мы проходили округление – когда цифра меняется на ближайшее, кратное 10 число.

Что, в сущности, мешало передвинуть его и на двенадцать, и на двадцать четыре, да и на любое число, кратное двадцати четырем?

Источник

КРАТНЫЙ

Смотреть что такое «КРАТНЫЙ» в других словарях:

кратный — сложный, составной; кратен. Ant. простой Словарь русских синонимов. кратный прил., кол во синонимов: 2 • аликвотный (1) • … Словарь синонимов

КРАТНЫЙ — КРАТНЫЙ, кратная, кратное; кратен, кратна, кратно (мат.). 1. Делящийся без остатка на какое нибудь число. Число десять кратно пяти и двум. 2. в знач. сущ. кратное, кратного, ср. Целое число, делящееся на данное. Десять кратное двух. Общее… … Толковый словарь Ушакова

кратный — КРАТНЫЙ, кратная, кратное; кратен, кратна, кратно (мат.). 1. Делящийся без остатка на какое нибудь число. Число десять кратно пяти и двум. 2. в знач. сущ. кратное, кратного, ср. Целое число, делящееся на данное. Десять кратное двух. Общее… … Толковый словарь Ушакова

. кратный — …КРАТНЫЙ, кратная, кратное. Вторая часть сложных прил. в знач. повторяющийся столько то раз, больший во столько то раз (сколько указывает первая часть), напр. семикратный, многократный. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

КРАТНЫЙ — КРАТНЫЙ, ая, ое; тен, тна. В математике: делящийся без остатка на какое н. число. Девятьчисло, кратное трём. Девятькратное (сущ.) трёх. | сущ. кратность, и, жен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

кратный — кратный, кратк. ф. кратен, кратна (неправильно кратна), кратно, кратны … Словарь трудностей произношения и ударения в современном русском языке

кратный — свернутый — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы свернутый EN fold … Справочник технического переводчика

кратный — ▲ целый ↑ соотношение кратность целое соотношение. деление нацело. делимость (признаки делимости). делитель (# числа). составное число. < > простое число. кратное число число, которое делится без остатка на другое число. четный кратный двум … Идеографический словарь русского языка

кратный ложный сигнал акустоэлектронного изделия — кратный ложный сигнал Ложный сигнал акустоэлектронного изделия, время задержки которого кратно времени задержки основного сигнала акустоэлектронного изделия. [ГОСТ 28170 89] Тематики изделия акустоэлектронные Обобщающие термины функциональные… … Справочник технического переводчика

Источник