Что такое криптография
Что такое криптография
Что такое криптография?
Это может быть не очевидно, но мы сталкиваемся с криптографией каждый день. Например, когда мы оплачиваем покупки картой, смотрим видео на YouTube или заправляем машину, криптография защищает нашу информацию. Может показаться, что криптография – это удел разработчиков, хакеров и корпораций, а простому пользователю знать о ней вовсе не обязательно. Однако это полезно не только узким специалистам, но и всем, кто заботится о собственной безопасности. Этот гайд поможет разобраться, что такое криптография и какое применение она находит в повседневной жизни.
Как появилась криптография?
С момента зарождения человеческой цивилизации информация была одним из наших самых ценных активов. Уже много тысячелетий назад наши предки столкнулись с необходимостью передавать информацию в пространстве (из точки А в точку Б) или во времени (например, от учителя к ученикам). Письменность помогла решить эту задачу, однако следом возникла следующая: как сохранить передаваемую информацию от глаз тех, к кому она попасть не должна?
Примерно 3500 лет назад гончары в Месопотамии защищали секреты своего мастерства от конкурентов с помощью шифрования на глиняных табличках. Политики шифровали свои послания, чтобы сохранить их в тайне.
Как выглядел этот шифр? Разберем на примере:
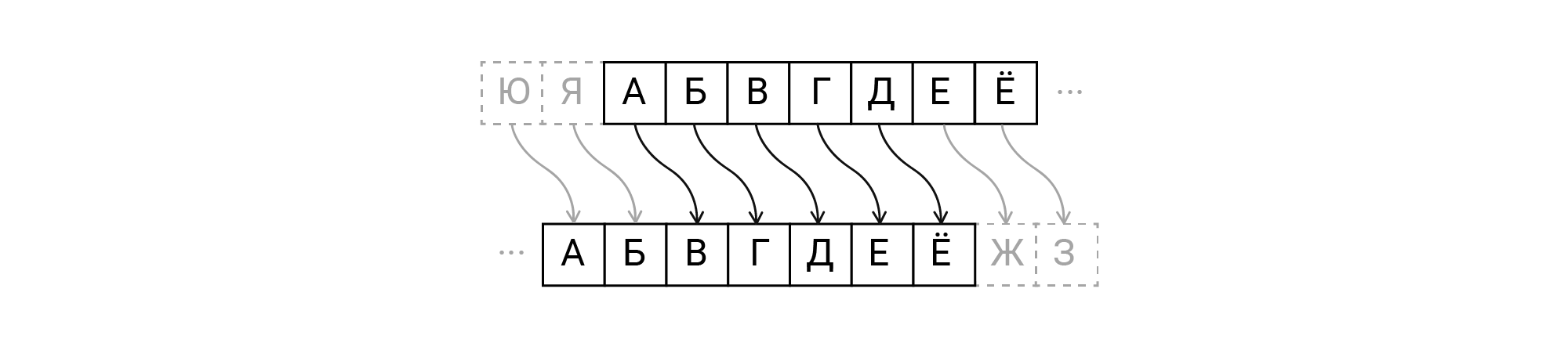
Допустим, нам нужно зашифровать сообщение «Привет». Один из путей — сдвигать буквы алфавита на фиксированное число позиций. Такой метод называется шифр сдвига или шифр Цезаря.
На рисунке ниже показан сдвиг на две буквы вперд.
Сдвиг на две буквы означает, что:
Сообщение «Привет» превращается в «Сткджб».
Шифр можно улучшить, применив более продвинутый метод. Представим, что после каждого использования алгоритм шифрования меняется, то есть повторное сообщение с такой же информацией будет выглядеть совершенно по-другому. Проще говоря, если в первом случае мы получили «Сткджб», то следом то же слово будет зашифровано как «Опздбдс»: теперь сдвиг произошел на одну букву назад.
Современные методы криптографии
Современная криптография совсем не похожа на перестановку букв. Для шифрования и безопасной передачи данных используются алгоритмы, которые невозможно «разгадать». Речь идет об алгоритмах, основанных на математических преобразованиях — работать с ними способен только компьютер. Карандашом и листком бумаги уже не обойтись. Чаще всего используются три криптографических метода, каждый из которых имеет преимущества и недостатки. Рассмотрим каждый из них.
Симметричная криптография
Один из самых простых типов шифрования. Симметричная криптография использует секретный ключ, который может быть числом, словом или строкой случайных символов для шифрования и расшифровки данных. Единственный ключ известен как отправителю, так и получателю. Это один из старейших и наиболее распространенных методов шифрования.
Этот метод обычно не используется для передачи сообщений через интернет, так как ключ необходимо передавать отдельно. Если третья сторона каким-то образом получит ключ, она сможет просмотреть зашифрованные данные.
Получается уловка-22: если вы хотите отправить зашифрованное сообщение, чтобы его содержимое было скрыто от посторонних глаз, вам придется сначала отправить незашифрованное сообщение, которое будет полностью видно. Это делает данный метод крайне небезопасным.
Именно поэтому симметричная криптография обычно используется для шифрования локальных баз данных, например, на жестком диске сервера или данных в вашем iPhone.
Асимметричное шифрование
Метод шифрования данных, в котором используются два ключа — открытый и закрытый. Открытый или «публичный» ключ используется для шифрования информации и может передаваться по незащищенным каналам. Закрытый или «приватный» ключ используется для расшифровки данных, зашифрованных с помощью открытого ключа. Открытый и закрытый ключи — это очень большие числа, связанные определенной функцией, но таким образом, что если вы знаете один ключ, то вычислить другой крайне сложно.
Асимметричное шифрование решает основную проблему безопасности симметричного шифрования, когда для шифрования и получения данных используется один и тот же ключ. С другой стороны, асимметричные алгоритмы намного медленнее симметричных, поэтому часто используются оба метода.
Хеширование
Отдельно выделим метод, который преобразовывает информацию в уникальный набор символов, но не шифрует данные. По сути, хеширование — это изменение сообщения в нечитаемую строку не для того, чтобы скрыть сообщение, а для проверки его содержимого. Чаще всего он используется при передаче больших файлов.
Допустим, нам нужно обновить программное обеспечение на компьютере. Хеширование — хороший способ проверки загружаемых файлов, файлов Windows (.ISO) или Mac (.DMG). Когда мы скачиваем обновление, вместе с файлом мы получаем хеш от этого файла. Наш компьютер хеширует скачанный файл еще раз и сравнивает хеши (полученный и скачанный): если они совпадают, значит, мы получили неповрежденный файл. Даже самое незначительное изменение загруженного файла, вызванное повреждением или намеренным вмешательством, резко изменит полученный хеш. Только после проверки целостности компьютер может продолжить работу с файлом.
Принципы криптографии
Задача криптографии — обеспечить защиту информации. Она основана на четырех принципах:
Аутентификация
Проще говоря, — это процесс, обеспечивающий уверенность в том, что стороны на обоих концах соединения действительно являются теми, за кого себя выдают.
По крайней мере один тип аутентификации используется в интернете всякий раз, когда вы пользуетесь защищенным веб-сайтом. Например, внутренним сайтом вашей компании или, например, сайтом Hexlet.
В зависимости от используемого браузера пользователь в увидит закрытый замок или зеленый URL (или и то, и другое), указывающий на то, что сайт, к которому он подключен, является тем сайтом, за который себя выдает.
Это особенно важно, когда мы совершаем покупки в Интернете, делаем банковские операции или оплачиваем счета через Интернет. Это гарантирует, что мы не передадим хакерам информацию о своих банковских счетах или кредитных картах.
Другим примером использования криптографии для аутентификации является Pretty Good Privacy — пакет бесплатного программного обеспечения. Он используется для шифрования и аутентификации сообщений, цифровых подписей, сжатия данных, а также электронных писем и их вложений.
Неотказуемость (от англ. non-repudiation)
Эта концепция особенно важна для тех, кто использует или разрабатывает финансовые приложения или приложения для электронной коммерции.
На заре развития финансовых операций и электронной коммерции в интернете одной из серьезных проблем была повсеместная распространенность пользователей, которые могли опровергнуть транзакции после того, как совершали ее. Например, клиент банка просит перевести деньги на другой счет. Позже он заявляет, что никогда не делал этого запроса, и требует вернуть всю сумму на его счет.
Однако если банк принял меры по обеспечению безопасности с помощью криптографии, он может доказать, что данная транзакция действительно была инициирована пользователем.
Целостность
Криптография помогает убедиться, что данные не были просмотрены или изменены во время передачи или хранения.
Например, использование криптографической системы для обеспечения целостности данных гарантирует, что конкурирующие компании не смогут подделать внутреннюю переписку и конфиденциальные данные конкурента.
Наиболее распространенным способом обеспечения целостности данных с помощью криптографии является использование криптографических хешей, о которых говорилось выше.
Конфиденциальность
В условиях постоянных утечек информации и бесконечного числа скандалов, связанных с конфиденциальностью, сохранение частной информации является одной из главных задач для криптографии. Именно с целью защиты информации и были изначально разработаны криптографические системы.
С помощью правильных инструментов шифрования пользователи могут защитить конфиденциальные данные компании, личные переписки или просто заблокировать свой компьютер простым паролем.
Однако в современных условиях такие методы не смогут обеспечить безопасность огромных систем электронных коммуникаций или торговли. Теперь приходится работать не только с частными случаями хранения или передачи информации, но и с огромными объемами данных.
Как обычным пользователям использовать криптографию?
Как говорилось в начале статьи, криптография — часть повседневной жизни. Оплата покупки картой или простое подключение к Wi-Fi требуют использования криптографии.
Хотя большинство операций в повседневной жизни уже защищены криптографией, существуют области, в которых можно сравнительно легко докупить еще один уровень безопасности к повседневным действиям.
Виртуальная частная сеть (VPN) шифрует интернет-соединение, не позволяя посторонним следить за вашей деятельностью в Интернете.
VPN заключает интернет-соединение в «туннель» шифрования, который действует подобно туннелю метро. Хотя мы можем знать, что в туннеле есть поезда, мы не сможем определить, где они находятся, сколько вагонов в составе и куда он направляется.
Виртуальная – означает, что VPN создаётся программным способом в виде отдельной прослойки поверх другой сети. Для передачи данных используется туннелирование — трафик заворачивается в отдельный туннель, который проходит по более низкоуровневому каналу связи. Информация в VPN-туннеле надёжно зашифрована. Частная – VPN – внутренняя сеть, в которой находятся только доверенные устройства. Сеть – соединение происходит между двумя устройствами — клиентом и VPN-сервером, образующими единую сеть.
VPN обеспечивает защиту — никто не сможет узнать, какие сайты посещает пользователь или какие файлы скачивает.
В последнее время VPN стали популярным инструментом для пользователей, которые хотят защитить свои действия в интернете от постороннего наблюдения.
HTTPS
Страницы HTTPS обычно используют протокол SSL (Secure Sockets Layer) или TLS (Transport Layer Security) для повышения безопасности страниц, которые просматривает пользователь, с помощью открытых ключей.
Этот тип соединения шифрует сообщения, отправляемые между вашим компьютером и просматриваемым сайтом, чтобы защитить данные пользователя от хищения. Это очень важно, когда вы передаете важную личную информацию или финансовые данные.
HTTPS — это расширение браузера с открытым исходным кодом, совместимое с Chrome, Firefox и Opera. С помощью этого расширения любой сайт, который вы посещаете, будет вынужден использовать соединение HTTPS вместо менее безопасного соединения HTTP.
BitLocker (for Windows) or FileVault2 (for Mac)
Дополнительный шаг (помимо пароля для входа в систему) для обеспечения безопасности личной информации на компьютере или ноутбуке — это установка BitLocker или FileVault2.
Эти программы шифрования дисков защищают данные с помощью криптографического алгоритма AES, обеспечивая шифрование целых томов. Если выбирать это программное обеспечение, обязательно нужно записать свои учетные данные и храните их в надежном месте. Если эти учетные данные будут утеряны, то почти наверняка навсегда будет утерян и доступ ко всей зашифрованной информации.
Криптография не совершенна
Мы разобрались, как работает криптология и как она защищает данные. Хотя криптография, безусловно, может обеспечить защиту информации, она не может обеспечить полную безопасность. Даже самые лучшие криптографические алгоритмы несовершенны.
Поэтому стоит осознавать, что «более безопасно» не означает «абсолютно безопасно».
Заключение
Благодаря более глубокому пониманию распространенных методов шифрования и криптографических алгоритмов, используемых сегодня, мы сможем лучше защитить себя от потенциальных кибератак.
Существует множество способов использования криптографии и, возможно, лучшим способом обеспечить надежный уровень шифрования для действий в интернете является использование качественного VPN.
Хотя криптография не совершенна, она необходима для обеспечения безопасности личной информации.
Криптография: будущее децентрализованных вычислений
Хотя технологии на основе блокчейна обладают многими качествами, которые отличают их от других вычислительных парадигм, их основным ценностным предложением является генерация криптографической истины. В самом простом смысле, криптографическая истина — это форма вычислений и ведения учета, которая является более точной, доступной, проверяемой и защищенной от взлома, чем существующие альтернативы.
В данной статье мы рассмотрим, как криптография и децентрализованный консенсус сочетаются в блокчейн для создания криптографической истины, а затем обсудим, как оракулы расширяют криптографическую истину для проверки любого типа событий или вычислений, недоступных в блокчейн.
Чтобы полностью понять криптографическую истину и ее роль в блокчейн, важно сначала ознакомиться с терминологией и общими принципами работы современной криптографии.
Криптография — это наука о безопасном общении в присутствии враждебного поведения. Хотя большинство людей понимает роль криптографии в сохранении конфиденциальности коммуникации (например, приложения для обмена сообщениями с шифрованием), она также используется для аутентификации происхождения, проверки целостности и установления безответности коммуникации; т.е. для определения того, что сообщение пришло от конкретного человека и не было подделано, и что эти свойства не могут быть опровергнуты отправителем.
Криптография используется для преобразования оригинального сообщения в неразборчивое сообщение, которое может интерпретировать только тот, кто в курсе. Шифрование — это двусторонняя функция, которая шифрует исходное сообщение (т.е. открытый текст) в неразборчивое сообщение (т.е. шифротекст), которое может расшифровать только получатель, чтобы извлечь открытый текст. Другие криптографические функции являются односторонними и направлены только на доказательство какого-либо знания или свойства данных, а не на то, чтобы сделать исходные данные известными.
Алгоритм шифрования называется шифром, а ключ — это секрет, обычно строка символов, которая позволяет кому-то понять шифр. В шифрах используются два основных типа техник: подстановка и перестановка (также называемая транспортировкой). Шифры подстановки заменяют буквы, цифры и символы открытого текста другими буквами, цифрами или символами. Шифры перестановки используют буквы открытого текста, но меняют их порядок. Для создания сложности эти методы часто комбинируются, наслаиваются друг на друга, подвергаются влиянию внешних данных и изменяются с течением времени.
Первые шифры были аппаратными, то есть они запоминались, писались от руки или создавались с помощью нецифровых машин. Однако с появлением компьютеров алгоритмы шифрования на основе программного обеспечения стали доминирующей формой шифрования.
Существует три общих класса современной криптографии на основе программного обеспечения: хэш-функции, симметричное шифрование и асимметричное шифрование.
Хэш-функции преобразуют данные любой длины в фиксированную битовую длину, называемую хэшем. Хэш — это уникальный идентификатор данных, сродни отпечатку пальца, по сути, проверяющий исходный набор данных. Хеширование данных широко используется для индексации данных и эффективного извлечения их из базы данных. Оно также используется для безопасного хранения данных, например, в случае веб-сайтов, которые хранят только соленый хэш паролей пользователей, чтобы предотвратить утечку паролей в случае взлома базы данных.
Самым популярным безопасным алгоритмом хэширования на сегодняшний день является SHA-256, который создает строки длиной 256 бит (т.е. 256 последовательных 1 и 0). 256-битные хэши часто представляются в шестнадцатеричном формате строк, поэтому их длина может составлять 32 или 64 символа. SHA-256 существует в рамках набора хэш-функций SHA-2, пришедшего на смену взломанному SHA-1. SHA-3 также был представлен в 2015 году на основе криптографического примитива Keccak.
Симметричное шифрование (оно же шифрование с использованием секретных ключей) предполагает использование общего секретного ключа, который отправитель и получатель используют для шифрования и расшифровки сообщений. Симметричное шифрование является быстрым и эффективным, но при этом возникает проблема безопасного обмена секретным ключом через Интернет. Хотя обмен можно осуществлять лично, этот метод не является глобально масштабируемым, поскольку требует формальных отношений с каждым контрагентом. Другая проблема заключается в том, что если секретный ключ скомпрометирован, то любой, кто его использует, рискует расшифровать все предыдущие и будущие сообщения. Именно поэтому многие интернет-протоколы, использующие симметричное шифрование, такие как TLS, также используют протоколы обмена ключами для безопасного создания общего секретного ключа без его передачи через интернет.
Асимметричное шифрование (оно же криптография с открытым ключом) дает каждому пользователю пару открытого и закрытого ключей. Открытый ключ виден всем, в то время как закрытый ключ известен только его владельцу. Пользователи могут шифровать сообщения с помощью своего закрытого ключа, который может расшифровать любой человек с открытым ключом. Это известно как цифровая подпись, поскольку она доказывает знание секрета без раскрытия самого секрета (т.е. у пользователя есть закрытый ключ к адресу открытого ключа). Пользователи также могут шифровать сообщения с помощью чужого открытого ключа, который может расшифровать только человек с закрытым ключом (т.е. отправка конфиденциальной информации).
Блокчейн использует две основные формы криптографии: криптографию с открытым ключом и хэш-функции. Однако все чаще используются и другие криптографические методы для обеспечения масштабирования, конфиденциальности и внешних подключений к блокчейну. Ниже перечислены некоторые способы использования криптографических функций в блокчейн.
При отправке транзакций пользователь посылает в сеть сообщение со своего адреса в блокчейне, содержащее данные о транзакции и цифровую подпись. Данные транзакции описывают действие, которое пользователь хочет совершить в сети, а цифровая подпись подтверждает подлинность этого действия. Цифровая подпись генерируется из двух входных данных: хэша данных транзакции пользователя и его закрытого ключа. Затем цифровая подпись присоединяется к данным транзакции, образуя транзакцию с цифровой подписью.
Майнеры/валидаторы и полные узлы, которые управляют блокчейном, запускают протокол проверки цифровой подписи, чтобы проверить действительность транзакции. Протокол проверки берет исходные данные транзакции и хэширует их. Он также расшифровывает цифровую подпись с помощью открытого ключа пользователя, чтобы получить хэш. Если эти два хэша совпадают, то транзакция считается действительной. Благодаря сочетанию хэширования и криптографии с открытым ключом для поддержки цифровых подписей блокчейн гарантирует, что только владелец закрытого ключа может получить доступ к средствам, хранящимся на соответствующем адресе блокчейна.
Производство блоков — это процесс, в ходе которого майнеры/валидаторы объединяют ожидающие транзакции в структуры данных, называемые блоками, и предлагают их в сети. Блок обычно состоит из списка всех транзакций, включенных в блок, и заголовка блока, содержащего метаданные блока. Чтобы создать блок, майнер/валидатор должен сгенерировать правильный хэш блока, иначе блок будет отклонен.
Блокчейн Proof-of-Stake (PoS), такой как Ethereum 2.0, также генерирует хэши при производстве блоков, но этот процесс специально разработан таким образом, чтобы быть легким, поскольку нет конкуренции между валидаторами. Вместо этого валидаторы PoS обычно выбираются в качестве авторов блоков случайным образом, часто на основе веса их доли. Блокчейн PoS создает устойчивость к атаке Сивиллы, требуя от валидаторов внесения криптовалюты (т.е. ставки) для участия в производстве блоков. Таким образом, валидаторы PoS должны вкладывать финансовые ресурсы, чтобы увеличить свои шансы быть выбранными в качестве автора блока. Зачастую их доля подлежит сокращению (т.е. конфискации), если они нарушают определенные правила протокола, например, включают в свой блок недействительные транзакции или подписывают два блока на одной высоте.
Как правило, правильный хэш блока должен иметь следующие исходные данные:
Блоки включают хэш-значение предыдущего блока, чтобы криптографически связать их вместе в цепочку, сохраняя хронологический порядок реестра. Именно поэтому блокчейн считается неизменяемым, так как для отмены ранее подтвержденных блоков, называемых реорганизацией блоков или просто реорганизацией, потребовалось бы много вычислительной мощности и/или финансовых рисков. Даже если изменяется только одна транзакция в блоке, меняется весь хэш этого блока, и, таким образом, другие узлы могут легко заметить его. Обратите внимание, что не все перерегистрации являются злонамеренными; например, перерегистрации 1 блока на вершине цепочки более распространены из-за асинхронных сетевых условий. Однако глубокие перерегистрации могут быть более спорными, и их значительно сложнее осуществить, чем дальше назад они происходят.
В блокчейне PoW майнерам приходится заново генерировать достоверные хэши для всех заменяемых блоков, чтобы провести атаку на перестройку, а в это время другие майнеры тратят вычислительные ресурсы на добавление новых блоков к последнему блоку. Именно здесь вступает в игру логика консенсуса Накамото, согласно которой «самая длинная цепочка с наибольшим количеством работы является действительной», поскольку она предоставляет майнерам простой способ определения действительной версии реестра.
В сетях PoS всем или части валидаторов, не производящих в данный момент блоки, часто поручается подтвердить достоверность новых блоков с помощью механизма голосования. Валидатор, пытающийся провести перегруппировку, должен подвергнуть риску свою финансовую долю, причем штраф за нарушение децентрализованного консенсуса (обычно >2/3 валидаторов) увеличивается тем больше, чем глубже атака. Эта обобщенная модель PoS придает криптоэкономические свойства таким алгоритмам консенсуса, как Practical Byzantine Fault Tolerance, Tendermint, Casper и HotStuff.
Некоторые блокчейны PoS также имеют ограничение на то, как далеко назад может быть изменена главная книга блокчейна, по существу устанавливая контрольную точку, в которой каждая транзакция до нее имеет явную окончательность. Например, при объединении цепочки маяков PoS в текущую сеть Ethereum производство и проверка блоков будут разделены на эпохи, причем каждая эпоха имеет 32 слота длиной 12 секунд каждый. В течение каждой эпохи все валидаторы случайным образом делятся на комитеты размером не менее 128, при этом валидаторы в каждую эпоху перемешиваются. Во время каждого слота валидатор предлагает блок, а валидаторы из одного или нескольких комитетов подтверждают этот блок. Это сделано так, чтобы валидаторы подтверждали один предложенный блок за эпоху.
В конце каждой эпохи блоки в рамках предыдущей эпохи считаются обоснованными, если их обоснованность подтверждают не менее двух третей всех валидаторов (т.е. супербольшинство). Если две предыдущие эпохи подряд оправданы, то первая эпоха становится завершенной. При идеальных условиях сети и участии валидаторов завершение транзакции происходит в среднем около 14 минут. После того как эпоха завершена, правила протокола не позволяют отменить ее без внешнего социального консенсуса.
Блокчейн — это реестр, содержащий все транзакции, которые когда-либо происходили в сети блокчейн в хронологическом порядке (хотя некоторые блокчейны изучают возможность обрезки исторических данных после определенной контрольной точки). Чем дольше работает блокчейн, тем больше становится реестр и тем дороже узлам обходится ее хранение и синхронизация. Чрезмерные требования к хранению и пропускной способности ставят под угрозу децентрализацию сети блокчейн, поскольку увеличивают аппаратные требования к работе всего узла, что потенциально позволяет небольшой группе субъектов нарушить работу сети.
Для эффективного и безопасного кодирования данных реестра блокчейн использует структуры данных, называемые деревьями Меркла. В дереве Меркла каждая транзакция пользователя хэшируется, затем сопоставляется с другой хэшированной транзакцией и снова хэшируется. Хеши постоянно сопоставляются и хешируются вверх по дереву, пока не образуется единый хеш всех хешей, называемый корнем Меркла.
Биткойн использует дерево Меркла для транзакций на основе модели «Неизрасходованный выход транзакции» (UTXO), а Ethereum использует деревья Меркла для транзакций, состояния и квитанций (например, журналов и событий) в так называемой модели учётной записи с обобщенной поддержкой смарт-контрактов.
Деревья Меркла полезны, поскольку занимают меньше дискового пространства по сравнению с другими структурами данных и способствуют эффективной проверке целостности данных и включению данных в распределённый реестр. Кроме того, поскольку корни Меркла включаются в заголовки блоков, они позволяют легким клиентам, подключенным к доверенному полному узлу, быстро и безопасно проверить, что конкретная транзакция была включена в блок, не загружая весь блокчейн.
Некоторые из других криптографических примитивов, используемых в блокчейн, включают:
Теория игр — это математический подход к стратегии, основанный на предсказании действий рациональных участников в определенном соревновании. В рамках теории игр разработка механизмов — это искусство использования стимулов для достижения желаемых результатов в рамках стратегических взаимодействий.
Давайте рассмотрим, как блокчейн структурирован и стимулирован для достижения истины через результат честного большинства.
Блокчейн — это прозрачный реестр с открытым исходным кодом, то есть все участники могут просматривать всю историю реестра и проверять, как функционирует код. Участники сети блокчейн делятся на пять основных групп:
Пользователи совершают транзакции в сети либо по личным причинам, либо для размещения приложений. В блокчейн-цепочках без разрешений любому человеку разрешается отправлять транзакции в сеть в любое время.
Майнеры/валидаторы расширяют реестр, создавая новые блоки из транзакций пользователей. В некоторых блокчейнах майнером/валидатором может стать любой желающий, в то время как в других блокчейнах количество участников ограничено. Некоторые компенсируют это ограничение, позволяя пользователям голосовать или делегировать долю валидаторам.
Полные узлы выполняют несколько функций в сетях блокчейн. Во-первых, полные узлы предоставляют конечные точки RPC, которые позволяют пользователям читать из блокчейна и писать в него. Конечные точки RPC могут быть созданы на самостоятельно размещенных узлах или доступны через сторонних поставщиков (например, Infura). При записи данных в блокчейн (т.е. отправке транзакций) полные узлы либо передают их в публичный мемпул, либо хранят в частных пулах транзакций. Это связано с тем, что в одноранговой децентрализованной сети не существует единого пула транзакций, а каждый полный узел имеет свой собственный пул транзакций.
Поставщики услуг — это внешние организации, которые предоставляют услуги блокчейн или создают услуги на основе содержимого блокчейн. К ним относятся оракулы, протоколы индексирования, централизованные биржи, легкие клиенты, архивные узлы, исследователи блоков и многие другие. Эти организации обычно имеют бизнес-модели, которые требуют взаимодействия с блокчейном. Например, централизованные биржи обеспечивают переход между криптовалютами и традиционной финансовой системой, легкие клиенты позволяют пользователям проверять информацию, отправленную с полных узлов, без необходимости иметь полную копию реестра, а оракулы предоставляют ключевые внешние ресурсы для приложений смарт-контрактов.
MEV-боты — это субъекты, которые стремятся повлиять на то, как упорядочиваются транзакции во время добычи блоков, в частности майнеры и разработчики MEV. Извлекаемая майнерами стоимость (MEV), также называемая максимальной извлекаемой стоимостью, основана на способности майнеров/валидаторов выбирать, какие транзакции будут включены в блок и как эти транзакции будут упорядочены. Затем они могут использовать эту привилегию в своих интересах для извлечения стоимости, например, опережая или атакуя пользователей и используя возможности ликвидации и арбитража. MEV-боты обычно работают через частные пулы транзакций и офф-чейн аукционы в блокчейне, хотя могут действовать и самостоятельно.
Стимулы делятся на две большие категории: неявные и явные. Явные стимулы — это прямые вознаграждения или наказания за действия, совершенные в игре, например, обязательный платеж за доступ к услуге или жестко закодированный штраф за нарушение правил протокола. Неявные стимулы — это косвенные вознаграждения и наказания, вытекающие из игры, например, упущенные участниками возможности получения будущих доходов или затраты труда без гарантированной компенсации.
Наиболее очевидными стимулами в блокчейн являются вознаграждение за блок и плата за транзакции, выплачиваемая майнерам/валидаторам за создание одобренных блоков. Вознаграждение за блок обычно стандартизировано по количеству, в то время как плата за транзакции может колебаться в большую или меньшую сторону в зависимости от текущего спроса на ограниченное пространство блока. В процессе производства блоков также существуют стимулы для заказа транзакций определенным образом, которыми MEV-боты пытаются воспользоваться для получения финансовой выгоды.
Блокчейн также использует финансовые санкции через механизмы, устойчивые к атаке Сивиллы, такие как PoW и PoS; т.е. майнеры/валидаторы должны сделать вычислительную или финансовую ставку, чтобы получить шанс заработать вознаграждение, которое может быть потрачено впустую или сокращено, если они идут против консенсуса сети. Еще одним преимуществом требования к производителям блоков делать вычислительную или финансовую ставку является то, что это стимулирует децентрализацию. В частности, потому, что майнеру/валидатору становится все дороже получать больший контроль над хэш-мощностью сети или долей.
Блокчейн также платит майнерам/валидаторам в их собственной криптовалюте. Это создает неявный стимул для майнеров/валидаторов честно участвовать в работе сети, поскольку безопасная и надежная сеть, скорее всего, привлечет больше пользователей. Большее количество пользователей ведет к увеличению комиссий за транзакции, а также к потенциально более высокой цене на зарабатываемую ими криптовалюту. Более высокая цена криптовалюты может означать больший доход от каждого блока и увеличение личных средств.
Хотя явного стимула для запуска полного узла в протоколе обычно нет, существует множество неявных стимулов для этого. Для начала, полные узлы необходимы для работы сети, поэтому, как минимум, майнеры должны их запускать. Пользователи, приложения и поставщики услуг также должны запускать полные узлы или иметь к ним доступ, чтобы отправлять и проверять статус ожидающих транзакций. Таким образом, для поддержки экосистемы существует несколько моделей бесплатных узлов и узлов как услуги.
Помимо финансовых стимулов, полные узлы критически важны для целостности реестра, поскольку отсутствие децентрализации дает меньшей группе участников контроль над сетью. Скомпрометированный реестр повлияет на поставщиков услуг и децентрализованные приложения, бизнес-модели которых зависят исключительно от предположения о честном большинстве в блокчейн.
Децентрализованная сеть с полным узлом также помогает отделить генерацию блока от его верификации, обеспечивая подотчетность майнеров/валидаторов за счет снижения их способности произвольно изменять правила протокола. Кроме того, организации, управляющие собственным полным узлом, имеют наибольшую степень устойчивости к цензуре и гарантии безопасности, поскольку им не нужно доверять третьим лицам для чтения или записи в блокчейн. Эти неявные стимулы побуждают пользователей и ключевых экономических субъектов запускать полные узлы.
Внедрение этих стимулов в рамках заявленной структуры игры приводит к желаемым результатам блокчейн:
Благодаря этим желаемым свойствам у пользователей появляется больше стимулов для взаимодействия с сетью блокчейн. Не только использование сети может возрасти, но и пользователям станет удобнее хранить на блокчейне большие суммы ценностей и использовать свои активы на сети в приложениях смарт-контрактов.
С учетом вышесказанного, блокчейн, вероятно, является наиболее эффективной сетью для защиты от нежелательных атак и изменений, которые идут вразрез с большинством общественного консенсуса, особенно с помощью криптографических и экономических механизмов.
Например, Chainlink — это децентрализованная сеть оракулов, предназначенная для генерирования истины о внешних данных и вычислениях вне блокчейна. В этом смысле сеть оракулов генерирует истину из в значительной степени недетерминированной среды. Детерминизм — это свойство вычислений, при котором конкретный вход всегда приводит к конкретному выходу, то есть код будет выполняться точно так, как написано. Децентрализованные блокчейны считаются детерминированными, поскольку в них используются методы минимизации доверия, которые устраняют или снижают до почти статистической невозможности любые переменные, которые могут препятствовать внутренней подаче, выполнению и проверке транзакций.
Проблема недетерминированных сред заключается в том, что истина может быть субъективной, труднодоступной или дорогостоящей для проверки. Например, какова цена биткойна? Ответ заключается в том, что универсальной цены биткойна не существует, поскольку она варьируется на разных биржах, каждая из которых находится в состоянии постоянного изменения. Более того, все ли пользователи согласятся с ценой, которую они готовы заплатить за истину и степенью уверенности, которую дает конкретная методика ее получения? Например, сеть из множества высокопроизводительных IoT-устройств позволит получить более точные показания погоды, чем один низкокачественный датчик, но при этом будет дороже в установке и эксплуатации. Эти ситуации подчеркивают реальность того, что методология получения внешней правды и стоимость, которую люди готовы за нее заплатить, будут отличаться от человека к человеку и от компании к компании.
В этом смысле окончательная истина — это определяемый пользователем механизм консенсуса для децентрализованных сетей оракулов, которые привязываются к блокчейну, чтобы работать в более доверительной манере. Некоторые из параметров консенсуса, которые пользователи могут определить, включают инфраструктуру сети оракулов, конкретные используемые источники данных, точные выполняемые вычисления, получаемые награды/штрафы и то, как сеть оракулов будет доказывать блокчейну целостность своей работы. И хотя эти параметры могут быть настроены в соответствии с различными бюджетами, требованиями к производительности и предположениями о доверии, отраслевые стандарты также укоренятся, и целые рынки или крупные сегменты рынков придут к согласию в качестве общего источника истины.
С точки зрения минимизации доверия сеть оракулов использует многие из тех же методов, что и блокчейн, например:
В итоге получается минимизированная с точки зрения доверия структура для выполнения вычислений вне цепочки в соответствии с любыми заданными пользователем параметрами, а результаты вместе с подписями передаются в блокчейн, где они могут быть проверены. Эти новые гибридные приложения «on-chain/off-chain» значительно расширяют возможности блокчейн, поскольку позволяют коду смарт-контракта на блокчейн реагировать на данные и вычисления из внешней среды, такие как поставщики данных, веб-интерфейсы API, сети IoT, другие блокчейн, унаследованные бэкенды, платежные системы или любые другие внешние ресурсы, и напрямую влиять на них.
Например, Price Feeds — это децентрализованные сети оракулов, которые используют многоуровневую архитектуру агрегации для создания отраслевого стандарта криптографической истины в отношении цен на активы и информации о финансовых рынках в режиме реального времени.
В Price Feeds данные агрегируются профессиональными компаниями-агрегаторами данных, которые генерируют средневзвешенные по объему цены (VWAPs) из необработанных данных сотен бирж. Затем каждый узел оракулов получает VWAP от нескольких агрегаторов данных и берет медиану. Наконец, медианные значения каждого узла далее объединяются в медиану для создания единого достоверного значения, которое хранится в блокчейн. Значения, представленные каждым узлом и сетью оракулов в целом, могут быть проверены любым человеком с помощью данных на цепочке.
Традиционные и децентрализованные финансовые приложения используют эти цены для выполнения важнейших операций, таких как выдача и ликвидация кредитов, расчеты по контрактам с деривативами и установление обменных курсов.
Телеграм канал про web3 разработку, смарт-контракты и оракулы.
Криптография
Kласс: Это незавершённая статья по ивентологии и её применениям
Криптогра́фия (от греч. κρυπτός — скрытый и γράφω — пишу) — наука о математических методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации.
Криптография — одна из старейших наук, ее насчитывает несколько тысяч лет. Более того, первоначально письменность сама по себе была криптографической системой, так как в древних обществах ею владели только избранные. Священные книги Древнего Египта, Древней Индии тому примеры.
С широким распространением письменности криптография стала формироваться как самостоятельная наука. Первые криптосистемы встречаются уже в начале нашей эры. Бурное развитие криптографические системы получили в годы первой и второй мировых войн. Начиная с послевоенного времени и по нынешний день, появление вычислительных средств ускорило разработку и совершенствование криптографических методов.
Почему проблема использования криптографических методов в информационных системах стала в настоящий момент особо актуальна?
С одной стороны, расширилось использование компьютерных сетей, в частности глобальной сети Интернет, по которым передаются большие объемы информации государственного, военного, коммерческого и частного характера, не допускающего возможность доступа к ней посторонних лиц.
С другой стороны, появление новых мощных компьютеров, технологий сетевых и нейронных вычислений сделало возможным дискредитацию криптографических систем еще недавно считавшихся практически не раскрываемыми. Проблемой защиты информации путем ее преобразования занимаеся криптология (греч. kryptos — тайный, logos — наука).
Криптология разделяется на два направления — криптографию и криптоанализ. Цели этих направлений прямо противоположны.
Криптография занимается поиском и исследованием математических методов преобразования информации. Сфера интересов криптоанализа — исследование возможности расшифровывания информации без знания ключей.
Содержание
Основные понятия
Для удобства дальнейшего изложения введем следующие обозначения: M – открытый текст, C – шифротекст, E – функция шифрования, D – обратная функция функции E.
Таким образом процесс кодирования будет представлен в виде формул:
E(M) = C – шифрование открытого текста М по алгоритму Е
D(C) = M – дешифрование шифртекста С по алгоритму D
Используя понятие ключа, процесс зашифрования можно описать в виде соотношения, где K – ключ:


Все многообразие существующих криптографических методов можно свести к следующим классам преобразований:
Моно- и многоалфавитные подстановки Наиболее простой вид преобразований, заключающийся в замене символов исходного текста на другие (того же алфавита) по более или менее сложному правилу. Для обеспечения высокой криптостойкости требуется использование больших ключей.
Перестановки Также несложный метод криптографического преобразования. Используется, как правило, в сочетании с другими методами.
Гаммирование Этот метод заключается в наложении на исходный текст некоторой псевдослучайной последовательности, генерируемой на основе ключа.
Блочные шифры Представляют собой последовательность (с возможным повторением и чередованием) основных методов преобразования, применяемую к блоку (части) шифруемого текста. Блочные шифры на практике встречаются чаще, чем “чистые” преобразования того или иного класса в силу их более высокой криптостойкости. Российский и американский стандарты шифрования основаны именно на этом классе шифров.
Шифр замены
Шифр Цезаря
Историческим примером шифра замены является шифр Цезаря (I век до н.э.), описанный историком Древнего Рима Светонием. Гай Юлий Цезарь в своей переписке использовал шифр собственного изобретения. Применительно к русскому языку он состоял в следующем: каждая буква алфавита заменялась другой буквой, из этого алфавита, идущей за первой через некоторый интервал.
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ю Я
И запишем под ним тот же алфавит, но с циклическим сдвигом
Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ю Я А Б В
При шифровании буква А заменялась буквой Г, Б заменялась на Д, и так далее. Так, например, слово «Империя» превращалось в слово «Лптзулв». Получатель сообщения искал буквы, из которых написано послание, и заменял их на буквы из верхней строки – в этом заключался способ декодирования.
Естественное развитие шифра Цезаря очевидно: нижняя строка двустрочной записи букв алфавита может быть произвольным расположением этих букв. Если в алфавитном расположении букв существует всего 32 варианта (для русского языка, без буквы «ё»), то при произвольном расположении число ключей становиться 33!≈10^35.
Квадрат Полибия
Одним из криптографических изобретений древних греков является так называемы квадрат Полибия (Полибий – греческий государственный деятель, полководец, историк, III век до н.э.). Другое название этого шифра – шифр Плайфера, используемый применительно к английскому языку, мы же будем пользоваться именем Полибия.
Применительно к современному латинскому алфавиту из 26 букв, шифрование заключалось в следующем. В квадрат размером 5×5 клеток выписываются все буквы алфавита, при этом буквы I, J не различаются.
| A | B | C | D | E | |
| A | A | B | C | D | E |
| B | F | G | H | I | K |
| C | L | M | N | O | P |
| D | Q | R | S | T | U |
| E | V | W | X | Y | Z |
Шифруемая буква заменялась на координаты квадрата, в котором она записана. Так, B заменялась на AB, F заменялась на BA, R на DB, и т.д. При расшифровании каждая такая пара определяла соответствующую букву сообщения.
Сообщение «ТНЕ ТABLE», будет иметь вид: DD BC AE DD AA AB CA AE
Заметим, что секретом в данном случае является сам способ замены букв. Ключом является порядок следования букв.
К примеру, квадрат вида
| A | B | C | D | E | |
| A | T | H | E | A | B |
| B | L | C | D | F | G |
| C | I | K | M | N | O |
| D | P | Q | R | S | U |
| E | V | W | X | Y | Z |
зашифрует послание «ТНЕ ТABLE» следующим образом: AA AB AC AA AD AE BA AC.
Шифр перестановки
Вторым примером исторического шифра является шифр перестановки.
Этот метод заключается в том, что символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока символов. Рассмотрим некоторые разновидности этого метода, которые могут быть использованы в автоматизированных системах.
Самая простая перестановка — написать исходный текст задом наперед и одновременно разбить шифрограмму на группы из нескольких букв. Пусть группа состоит из пяти букв. Например, из фразы
ПУСТЬ БУДЕТ ТАК, КАК МЫ ХОТЕЛИ.
получится такой шифротекст:
ИЛЕТО ХЫМКА ККАТТ ЕДУБЪ ТСУП
В последней группе (пятерке) не хватает одной буквы. Значит, прежде чем шифровать исходное выражение, следует его дополнить незначащей буквой (например, О) до числа, кратного пяти:
Тогда шифрограмма, несмотря на столь незначительные изменения, будет выглядеть по-другому:
ОИЛЕТ ОХЫМК АККАТ ТЕДУБ ЬТСУП
Кажется, ничего сложного, но при расшифровке проявляются серьезные неудобства.
Во время Гражданской войны в США в ходу был такой шифр: исходную фразу писали в несколько строк. Например, по пятнадцать букв в каждой (с заполнением последней строки незначащими буквами).
П У С Т Ь Б У Д Е Т Т А К К А
К М Ы Х О Т Е Л И К Л М Н О П
После этого вертикальные столбцы по порядку писали в строку с разбивкой на пятерки букв:
ПКУМС ЫТХЬО БТУЕД ЛЕИТК ТЛАМК НКОАП
Если строки укоротить, а количество строк увеличить, то получится прямоугольник-решетка, в который можно записывать исходный текст. Но тут уже потребуется предварительная договоренность между адресатом и отправителем посланий, поскольку сама решетка может быть различной длины-высоты, записывать к нее можно по строкам, по столбцам, по спирали туда или по спирали обратно, можно писать и подиагоналями, а для шифрования можно брать тоже различные направления. В общем, здесь масса вариантов.
Гаммирование
Пусть нам дано некоторое сообщение, состоящее из n символов, включая пробел. Ключом является последовательность из некоторого числа i символов. Под открытый текст подписывается ключ
Если длина ключа меньше длины сообщения, то ключ периодически повторяется. Каждому знаку открытого текста и ключа ставится в соответствие некоторый вычет по модулю n.
Ключом является символы последовательности 



Гаммирование чаще осуществляется:
• по модулю 2, если открытый текст представляется в виде бинарной последовательности;
• по модулю 256, если открытый текст представляется в виде последовательности байтов;
• по модулю 10, если открытый текст последовательность цифр.
Какие же требования должны быть предъявлены, чтобы обеспечить достаточное качество шифра?
1. Необходимо, чтобы период повторения генерируемой гаммы был достаточно большим, лучше – максимально возможным. По крайней мере, он должен превосходить наибольшее возможное количество символов в шифруемом сообщении.
2. Необходимо, чтобы соседние или близкие по расположению элементы последовательности <
Смысл в том, что метод гаммирования по своей сути требует одноразовой гаммы, иначе он легко вскрывается по алгоритмической линии. Если же период повторения вырабатываемой гаммы недостаточно велик, различные части одного и того же длинного сообщения могут оказаться зашифрованными с помощью одинаковых участков гаммы. Второе требование является менее очевидным, и, вообще говоря, имеет место только для шифров вполне определенных архитектур, в которых шаг шифрования является комбинацией нескольких сравнительно простых преобразований, в ходе каждого из которых различия в шифруемых блоках данных увеличиваются весьма незначительно.
Блочные шифры
Исходное сообщение разбивается на блоки длины n, и с каждым блоком производятся операции шифрования, после чего блоки объединяют в один – шифртекст. Таким образом, криптостойкость блочного шифра есть произведение криптостойкости шифров входящих в алгоритм кодирования блока.
Алгоритм блочного шифрования
Блочные шифры на практике встречаются чаще, чем «чистые»преобразования того или иного класса в силу их более высокойкриптостойкости. Еще важной особенностью блочных шифров является параллельная обработка данных, что дает более высокую скорость шифрования. Российский и американский стандарты шифрования основаны именно на этом классе шифров.
Машинные методы шифрования
В криптографии, всегда использовались всевозможные устройства, как для облегчения кодирования сообщения, так и повышения стойкости шифра.
Одним из самых известных устройств являются роторные машины.
Самым известным роторным устройством является «Энигма» (Enigma). Энигма использовалась немцами во Второй Мировой Войне. Сама идея пришла в голову Артуру Шербиусу (Arthur Scherbius) и Арвиду Даму (Arvid Gerhard Damm) в Европе. В США она была запатентована Артуром Шербиусом. Немцы значительное усовершенствовали базовый проект для использования во время войны [3].
Рассмотрим работу 4-роторной «Энигмы». 4 ротора – 4 вращающихся на одной оси барабана – диска.
На каждой стороне диска по окружности располагалось 25 электрических контактов, столько же, сколько букв в латинском алфавите. Контакты с обеих сторон соединялись в нутрии диска, достаточно случайным образом, 25 проводами, формировавшими замену символов. Диски складывались вместе и их контакты, касаясь друг друга, обеспечивали прохождение электрических импульсов через весь пакет дисков на регулирующее устройство. На боковой поверхности дисков был нанесен алфавит. Перед началом работы диски поворачивались так, чтобы установить кодовое слово. При нажатии клавиши и кодировании левый барабан поворачивался на один шаг. После того как диск делал полный оборот, поворачивался следующий барабан.
В процессе шифрования на один из контактов левого диска поступал электрический импульс. Так как барабаны соприкасались контактами, то электрический импульс попадал на выход, проходя четыре диска и претерпевая четыре простые замены. Исполняющее устройство (пишущая машинка или перфоратор) фиксировало знак шифрованного текста в соответствии с тем, на какой контакт выходного диска поступал электрический импульс. Поскольку в каждый такт шифрования сдвигался на один шаг хотя бы один диск, подстановка – простая замена, по которой осуществлялось шифрование, менялась для каждого символа открытого текста. Ключом шифратора, который сменялся каждый сеанс, являлся набор начальных угловых положений дисков. Долговременным ключом, он менялся очень редко, служили коммутации дисков – соединения проводов внутри дисков. Для затруднения расшифрования диски выбирались из комплекта, состоящего из 10-20 дисков [1].
Несмотря на сложность Энигмы, она была взломана в течении Второй Мировой войны. Сначала группа польских криптографов взломала немецкую Энигму, а англичане продолжали криптоанализ новых версий. Несмотря на то, что немцы изменили способ передачи и дополнительно усложнили саму машину, англичанам неизменно удавалось проникать в немецкие шифры. Для ускорения процесса расшифровки англичане создали ряд вспомогательных технических приспособлений. Помимо шифров Энигмы, немцы использовали и некоторые другие шифровальные машины дальнего действия, обеспечивавшие высокий уровень связи. Эти машины, имевшие широкое обозначение Geheimschreiber (тайнописные машины), были способны порождать чрезвычайно сложные шифры. Для анализа этих шифров англичане сконструировали целый ряд «протокомпьютеров», с помощью которых они часто успешно взламывали немецкие машинные шифры. Полученные при этом сведения были широко известны под обозначением ULTRA.
Тем временем американцы успешно раскалывали японские шифры. Полученные ими данные были известны широкой публике под кодовым обозначением MAGIC. Вслед за машинами RED и PURPLE криптоаналитики раскрыли устройство японских шифровальных машин JADE и CORAL.
Компьютерная криптография (с 70-х годов XX века) обязана своим появлением вычислительным средствам с производительностью, достаточной для реализации криптосистем, обеспечивающих при большой скорости шифрования на несколько порядков более высокую защищенность, чем при «ручных» или «механических» [2].
Первым классом криптосистем, практическое применение которых стало возможно с появлением мощных и компактных вычислительных средств, стали блочные шифры. В 70-е годы был разработан американский стандарт шифрования DES (принят в 1978 году). Один из его авторов, Хорст Фейстел (сотрудник IBM), описал модель блочных шифров, на основе которой были построены другие, более стойкие симметричные криптосистемы, в том числе отечественный стандарт шифрования ГОСТ 28147-89.
С появлением DES обогатился и криптоанализ, для атак на американский алгоритм был создано несколько новых видов криптоанализа, практическая реализация которых опять же была возможна только с появлением мощных вычислительных систем.
Принципы стойкости шифра
Принципы Керкхоффса
Основное назначение криптографии – это защита информации. Другими словами построение такого шифра, который способен сохранить информацию при разнообразных атаках на сообщению. Август Керкхоффс (Kerckhoffs), известный голландский лингвист 19 в., сформулировал несколько общих принципов, которым должен удовлетворять любой хороший шифр.
Большинство любительских систем не удовлетворяют как минимум одному из принципов Керкхоффса. Эти принципы заключаются в следующем. Во-первых, шифр должен обеспечивать достаточную стойкость к взлому. Несмотря на то, что одиночное шифрованное сообщение может быть в принципе невзламываемым, часто бывает необходимо переслать сотни сообщений, зашифрованных в одной и той же системе. И хотя одиночное сообщение может быть трудно или невозможно расшифровать, большое число одинаково зашифрованных сообщений взломать куда проще. «Достаточная» стойкость ко взлому означает также, что разработчику шифра необходимо учитывать фактор времени: на взлом шифра должно требоваться время, достаточное для того, чтобы сообщения успевали потерять ценность для криптоаналитика.
Обеспечение абсолютной стойкости шифра редко необходимо, и даже если оно, возможно, обычно требует неоправданных затрат. Во-вторых, шифр должен быть прост в использовании.
Опыт показывает, что пользователи избегают пользоваться сложными и громоздкими шифросистемами либо пользуются ими с ошибками. В-третьих, стойкость шифра ко взлому должна полностью зависеть от обеспечения секретности ключа, а не алгоритма. Опять-таки из опыта известно, что алгоритм, которым пользуется много людей, не может долго оставаться в секрете. Ключ же, напротив, гораздо проще как изменить, так и сохранить в тайне.
«Невзламываемые» шифры
«Невзламываемые» шифры – это целый класс систем, широко известных под названием «одноразовые вкладыши». Соответствующий принцип был, по-видимому, впервые отчетливо сформулирован американским ученым Гилбертом Вернамом примерно в 1917. Вернам занимался разработкой криптографических методов для использования в телетайпных машинах. В этой связи он предложил комбинировать открытый текст, представленный в виде отверстий в бумажной перфоленте, с данными, нанесенными на другую перфоленту и являющимися ключом к шифру. Ключ должен был состоять из отверстий, перфорированных в ленте случайным образом. Комбинация этих двух лент и составляла шифротекст.
Шифрование по принципу Вермана
| Ключ | EVTIQWXQVVOPMCXREPYZ |
| Открытый текст | ALLSWELLTHATENDSWELL |
| Шифротекст | EGEAMAIBOCOIQPAJATJK |
| Шифрограмма | EGEAM AIBOC OIQPA JATJK |
Без знания ключа зашифрованное сообщение не поддается анализу. Даже если бы можно было перепробовать все ключи, в качестве результата мы получили бы все возможные сообщения данной длины плюс колоссальное количество бессмысленных дешифровок, выглядящих как беспорядочное нагромождение букв. Но и среди осмысленных дешифровок не было бы никакой возможности выбрать искомую.
Когда случайная последовательность (ключ) сочетается с неслучайной (открытым текстом), результат этого (шифротекст) оказывается совершенно случайным и, следовательно, лишенным тех статистических особенностей, которые могли бы быть использованы для анализа шифра.
Но невзламываемые шифры не употребляется повсеместно. Дело в том, что порождение «случайного» ключа – процесс весьма непростой. С помощью математических алгоритмов можно получать последовательности, обладающие многими свойствами, которые присущи «случайности»; однако эти последовательности не являются истинно случайными. Для порождения шифровальных ключей, представляющих собой случайную последовательность, можно использовать также естественные процессы – такие, как радиоактивный распад и электронный шум (статический), причем результаты обычно получаются лучшие, чем в случае с математическими формулами, но необходимость задания производящим перфоленты машинам отборочных уровней – это еще один источник неслучайного отбора.
Легкость порождения ключа – решающий фактор в том, что касается практической применимости шифров типа «одноразовых вкладышей». Ведь ключ должен быть точно такой же длины, что и шифруемое. Более того, никакой ключ нельзя использовать повторно, потому что данный факт часто может быть обнаружен с помощью статистических тестов и тогда те куски сообщения (или сообщений), в которых был использован тот же самый ключ, будут расшифрованы. То обстоятельство, что ключ может быть использован только один раз, и определяет «одноразовость» таких шифров.
Прежде чем пересылать невзламываемую шифрограмму, необходимо передать получателю копию ключа. Поскольку ключ имеет ту же длину, что и открытый текст, одна проблема (надежно засекреченная передача сообщения) оказывается просто замененной на другую такую же (надежно засекреченное распространение ключа). Однако у такого шифра есть и преимущество, которое состоит в том, что ключ может быть распространен заранее, а также по более медленным и надежным каналам связи, после чего шифрограмму можно совершенно безбоязненно пересылать по обычным каналам. В результате появления микропроцессоров и дискет для хранения и распространения компьютерных данных практическая значимость «одноразовых» шифров возросла, потому что порождение и сверка относительно большого числа ключей может теперь производиться автоматически. Еще одной проблемой, связанной с использованием шифров «одноразового вкладыша», является то, что под рукой всегда необходимо иметь достаточное количество ключей, которые могут понадобиться в дальнейшем для шифрования больших объемов открытого текста. Реальный же объем текста зачастую трудно оценить заранее, в особенности это касается дипломатической и военной сферы, где ситуация способна меняться быстро и непредсказуемо. Это может приводить к нехватке ключей, что может заставить шифровальщика либо использовать ключ(и) повторно, либо полностью прервать шифрованную связь.
Литература
1. Бабаш А.В., Шанкин Г.П. Криптография: аспекты защиты. М.: Солон – Р, 2002.
2. Баричев С.Г. Основы современной криптографии. М.: Горячая Линия – Телеком, 2001. 175 стр.
3. Шнайер Б. Прикладная криптография (Schneier B. Applied Cryptography. N. Y.: John Wiley & Sons Inc., 1996)
Криптография: что это такое и сферы применения
Криптография – это то, что позволяет вам безбоязненно проводить оплату за покупки в Интернете. Это то, что помогает авторизоваться на сайте или же использовать электронную подпись для документов. То есть благодаря криптографии наши персональные данные защищены от возможной кражи и могут участвовать в безопасной передаче информации в Интернете.
Даже если вы ранее не сталкивались с понятием криптографии, вы все равно уже знакомы с ее работой. Она лежит в основе и банковских транзакций, и передачи интернет-трафика, и даже в обеспечении связи для вашего смартфона. Получается, что криптография гарантирует конфиденциальность, но как она это делает?
Что такое криптография простыми словами
Определение понятия криптография может звучать так: криптография – это наука, изучающая разные способы и методы шифрования данных. Для защиты передаваемой информации при этом служат специальные алгоритмы, протестированные в открытых средах и дающие возможность находить и ликвидировать уязвимые места.

Вот основные принципы, по которым работает любая криптографическая система:
Далее – об основных терминах в криптографии:
Задачи криптографии
Типичная схема обмена данными, к которым нельзя допускать посторонних, выглядит примерно так:
Можно сказать, что криптография – это особая тайнопись, защищающая информацию от мошенников.
Вот какие задачи выполняет криптография:
Сферы применения криптографии
Современная криптография применяется сейчас всюду, ведь информационные технологии и всякие гаджеты плотно внедрились в самые разные сферы жизнедеятельности человека.
Вот где криптография используется активнее всего:
Получается, что всюду, где речь идет об информационных и цифровых технологиях, есть место и криптографии. Так что в качестве профессии это направление весьма перспективно.
Криптография активно применяется в программировании, информатике, сфере информационной безопасности, особенно если речь идет о крупных проектах. Над чем бы вы ни работали (будь то новое приложение, мессенджер или сервер), всегда есть риск перехвата данных. Не допустить утечек помогает криптография, здесь для каждой операции есть свой протокол защиты, поэтому у мошенников нет шанса завладеть вашей информацией.
Разновидности методов криптографии
Существующие методы криптографии классифицируются разными способами, но чаще всего – с учетом количества используемых ключей.
С данной точки зрения различают:
Скачивайте и используйте уже сегодня:
Топ-30 самых востребованных и высокооплачиваемых профессий 2022
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Алгоритмы шифрования данных
Сейчас существует очень много алгоритмов шифрования с высокой криптографической стойкостью, то есть, устойчивых перед криптоанализом (криптография и криптоанализ – это противоположные направления, а именно – шифровка и дешифровка, соответственно). Всего выделяют три основные группы алгоритмов шифрования:
Симметричные алгоритмы
Тут и шифрование, и расшифровка выполняется одним и тем же ключом. Алгоритмы данного типа должны отвечать двум основным требованиям: удалять из объекта все статистические закономерности и не допускать линейности. Среди симметричных систем выделяют блочные и поточные.
Вообще, симметричная криптография – это сложный многоступенчатый процесс подстановок и перестановок подлежащих шифрованию данных. Ступеней, называемых проходами, тут может быть очень много, и каждая – со своим «ключом прохода».

И у симметричных, и у асимметричных алгоритмов есть свои плюсы, и свои минусы. У симметричных, в частности, больше скорость шифрования, ключи могут быть короче (и они при этом не теряют своей стойкости). Такие системы в целом лучше изучены и проще в использовании. Что касается минусов, то здесь процесс обмена ключами (а он нужен обязательно) довольно сложен из-за того, что в ходе обмена ключи могут утратить свою секретность. А еще если сеть крупная, то ключами становится тяжело управлять.
Далее перечислим несколько примеров симметричных шифров:
Асимметричные алгоритмы
В данном виде алгоритмов задействуется криптография с открытым ключом. Этот ключ передается в открытую, и с его помощью выполняется шифрование исходной информации и проверка электронной подписи. А вот расшифровка уже делается посредством другого, секретного ключа.
В асимметричных алгоритмах всё устроено по аналогии с односторонними функциями ƒ(х). То есть, когда сам х находить легко (при известном значении функции), но если наоборот, известен х, то искать ƒ(х) очень-очень трудно. Нагляднее будет видно на примере: представьте себе телефонный справочник огромного мегаполиса. По фамилии и инициалам вы запросто отыщете номер человека, а вот по номеру найти владельца – задача почти невыполнимая.
Введение в криптографию и шифрование, часть первая. Лекция в Яндексе
Чтобы сходу понимать материалы об инфраструктуре открытых ключей, сетевой безопасности и HTTPS, нужно знать основы криптографической теории. Один из самых быстрых способов изучить их — посмотреть или прочитать лекцию Владимира ivlad Иванова. Владимир — известный специалист по сетям и системам их защиты. Он долгое время работал в Яндексе, был одним из руководителей нашего департамента эксплуатации.
Мы впервые публикуем эту лекцию вместе с расшифровкой. Начнём с первой части. Под катом вы найдёте текст и часть слайдов.
Я когда-то читал в МГУ лекции по крипте, и они занимали у меня по полгода. Я попытаюсь вам всё рассказать за два с половиной часа. Никогда этого не делал. Вот и попробуем.
Кто понимает, что такое DES? AES? TLS? Биноминальное отображение?
Говорить постараемся в общих терминах, потому что сложно и глубоко разбирать не получится: мало времени и базовая подготовка должна быть довольно большой. Будем оперировать общими концепциями, довольно поверхностно.
Мы поговорим о том, что такое криптографические примитивы, простые штучки, из которых впоследствии можно строить более сложные вещи, протоколы.
Мы будем говорить о трех примитивах: симметричном шифровании, аутентификации сообщений и асимметричном шифровании. Из них вырастает очень много протоколов.
Сегодня мы попробуем чуть-чуть поговорить про то, как вырабатываются ключи. В общем виде поговорим о том, как отправить защищенное сообщение, используя криптопримитивы, которые у нас есть, от одного пользователя другому.
Когда люди говорят про крипту вообще, есть несколько фундаментальных принципов. Один из них — принцип Керкгоффса, который говорит, что open source в криптографии очень важен. Если точнее, он дает общее знание об устройстве протоколов. Смысл очень простой: криптографические алгоритмы, которые используются в той или иной системе, не должны быть секретом, обеспечивающим ее устойчивость. В идеале необходимо строить системы так, чтобы их криптографическая сторона была полностью известна атакующему и единственным секретом являлся криптографический ключ, который в данной системе используется.
Современные и коммерчески доступные системы шифрования — все или почти все или лучшие из них — построены из компонент, устройство и принцип работы которых хорошо известны. Единственная секретная вещь в них — ключ шифрования. Есть только одно известное мне значимое исключение — набор секретных криптографических протоколов для всевозможных государственных организаций. В США это называется NSA suite B, а в России это всякие странные секретные алгоритмы шифрования, которые до определенной степени используются военными и государственными органами.
Не сказал бы, что такие алгоритмы приносят им большую пользу, за исключением того, что это примерно как атомная физика. Можно попытаться по пониманию дизайна протокола понять направление мысли людей, которые его разработали, и неким образом обогнать другую сторону. Не знаю, насколько такой принцип актуален по нынешним меркам, но люди, знающие про это больше меня, поступают именно так.
В каждом коммерческом протоколе, с которым вы столкнетесь, ситуация обстоит иначе. Там везде используется открытая система, все придерживаются этого принципа.
Первый криптографический примитив — симметричные шифры. 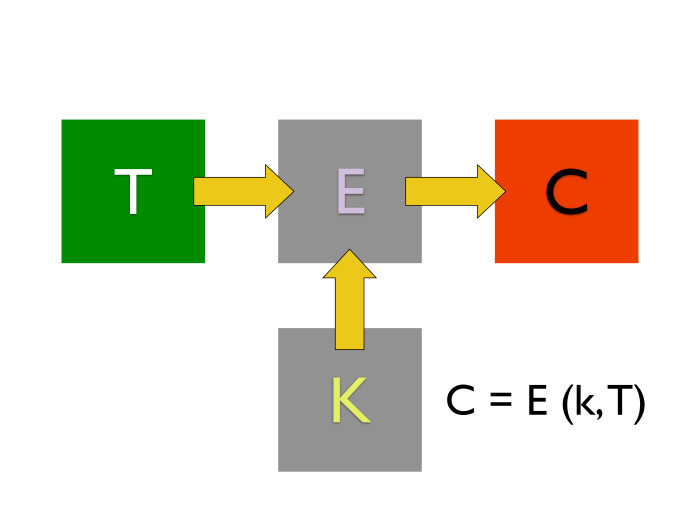
Они очень простые. У нас есть какой-то алгоритм, на вход которого поступает открытый текст и нечто, называемое ключом, какое-то значение. На выходе получается зашифрованное сообщение. Когда мы хотим его дешифровать, важно, чтобы мы брали тот же самый ключ шифрования. И, применяя его к другому алгоритму, алгоритму расшифровки, мы из шифротекста получаем наш открытый текст назад. 
Какие здесь важные нюансы? В большинстве распространенных алгоритмов симметричного шифрования, с которыми можно столкнуться, размер шифротекста всегда равен размеру открытого текста. Современные алгоритмы шифрования оперируют размерами ключей. Размер ключей измеряется в битах. Современный размер — от 128 до 256 бит для алгоритмов симметричного шифрования. Об остальном, в том числе о размере блока, мы поговорим позже. 
Исторически, в условном IV веке до нашей эры, существовало два метода дизайна шифров: шифры подстановки и перестановки. Шифры подстановки — алгоритм, где в те времена заменяли одну букву сообщения на другую по какому-то принципу. Простой шифр подстановки — по таблице: берем таблицу, где написано, что А меняем на Я, Б на Ю и т. д. Дальше по этой таблице шифруем, по ней же дешифруем.
Как вы считаете, с точки зрения размера ключа насколько это сложный алгоритм? Сколько вариантов ключей существует? Порядок факториала длины алфавита. Мы берем таблицу. Как мы ее строим? Допустим, есть таблица на 26 символов. Букву А можем заменить на любой из них, букву Б — на любой из оставшихся 25, С — на любой из оставшихся 24… Получаем 26*25*24*… — то есть факториал от 26. Факториал размерности алфавита.
Если взять log226!, это будет очень много. Думаю, вы точно получите в районе 100 бит длины ключа, а то и поболее. Оказалось, что с точки зрения формального представления стойкости указанный алгоритм шифрования — довольно неплохой. 100 бит — приемлемо. При этом все, наверное, в детстве или юности, когда сталкивались с кодировками, видели, что такие алгоритмы дешифруются тривиально. Проблем с расшифровкой нет.
Долго существовали всякие алгоритмы подстановки в разных конструкциях. Одним из них, еще более примитивным, является шифр Цезаря, где таблица формируется не случайной перестановкой символов, а сдвигом на три символа: А меняется на D, B на Е и т. д. Понятно, что шифр Цезаря вместе со всеми его вариантами перебрать очень легко: в отличие от табличной подстановки, в ключе Цезаря всего 25 вариантов при 26 буквах в алфавите — не считая тривиального шифрования самого в себя. И его как раз можно перебрать полным перебором. Здесь есть некоторая сложность.
Почему шифр табличной подстановки такой простой? Откуда возникает проблема, при которой мы можем легко, даже не зная ничего про криптографию, расшифровать табличную подстановку? Дело в частотном анализе. Есть самые распространенные буквы — какая-нибудь И или Е. Их распространенность велика, гласные встречаются намного чаще, чем согласные, и существуют негативные пары, никогда не встречающиеся в естественных языках, — что-то вроде ЬЪ. Я даже давал студентам задание сделать автоматический дешифратор шифра подстановки, и, в принципе, многие справлялись.
В чем проблема? Надо статистику распределения букв исказить, чтобы распространенные буквы не так светились в зашифрованном тексте. Очевидный способ: давайте будем шифровать самые часто встречающиеся буквы не в один символ, а в пять разных, например. Если буква встречается в среднем в пять раз чаще, то давайте по очереди — сначала в первый символ будем зашифровывать, потом во второй, в третий и т. д. Далее у нас получится маппинг букв не 1 к 1, а, условно, 26 к 50. Статистика, таким образом, нарушится. Перед нами первый пример полиалфавитного шифра, который как-то работал. Однако с ним есть довольно много проблем, а главное, очень неудобно работать с таблицей.
Дальше придумали: давайте не будем шифровать такими таблицами, а попробуем брать шифр Цезаря и для каждой следующей буквы изменять сдвиг. Результат — шифр Виженера.
Берем в качестве ключа слово ВАСЯ. Берем сообщение МАША. Задействуем шифр Цезаря, но отсчитывая от этих букв. Например, В — третья буква в алфавите. Мы должны сдвинуть на три буквы соответствующую букву в открытом тексте. М сдвигается в П. А в А. Ш — на 16, перескочим букву А, получим, условно, Д. Я сдвинет А в Я. ПАДЯ.
Что удобно в получившемся шифре? Здесь было две одинаковых буквы, но в результате они зашифровались в разные. Это классно, потому что размывает статистику. Метод хорошо работал, пока где-то в XIX веке, буквально недавно на фоне истории криптографии, не придумали, как его ломать. Если посмотреть на сообщение из нескольких десятков слов, а ключ довольно короткий, то вся конструкция выглядит как несколько шифров Цезаря. Мы говорим: окей, давайте каждую четвертую букву — первую, пятую, девятую — рассматривать как шифр Цезаря. И поищем среди них статистические закономерности. Мы обязательно их найдем. Потом возьмем вторую, шестую, десятую и так далее. Опять найдем. Тем самым мы восстановим ключ. Единственная проблема — понять, какой он длины. Это не очень сложно, ну какой он может быть длины? Ну 4, ну 10 символов. Перебрать 6 вариантов от 4 до 10 не очень сложно. Простая атака — она была доступна и без компьютеров, просто за счет ручки и листа бумаги.
Как из этой штуки сделать невзламываемый шифр? Взять ключ размера текста. Персонаж по имени Клод Шэннон в ХХ веке, в 1946 году, написал классическую первую работу по криптографии как по разделу математики, где сформулировал теорему. Длина ключа равна длине сообщения — он использовал XOR вместо сложения по модулю, равному длине алфавита, но в данной ситуации это не очень принципиально. Ключ сгенерирован случайным образом, является последовательностью случайных бит, и на выходе тоже получится случайная последовательность бит. Теорема: если у нас есть такой ключ, то подобная конструкция является абсолютно стойкой. Доказательство не очень сложное, но сейчас не буду про него говорить.
Важно, что можно создать невзламываемый шифр, но у него есть недостатки. Во-первых, ключ должен быть абсолютно случайным. Во-вторых, он никогда не должен использоваться повторно. В-третьих, длина ключа должна быть равна длине сообщения. Почему нельзя использовать один и тот же ключ для шифровки разных сообщений? Потому что, перехватив этот ключ в следующий раз, можно будет расшифровать все сообщения? Нет. В первых символах будет виден шифр Цезаря? Не очень понял. Кажется, нет.
Возьмем два сообщения: МАША, зашифрованная ключом ВАСЯ, и другое слово, у которого ключ тоже был ВАСЯ, — ВЕРА. Получим примерно следующее: ЗЕШЯ. Сложим два полученных сообщения, причем так, чтобы два ключа взаимно удалились. В итоге получим лишь разницу между осмысленным шифротекстом и осмысленным шифротекстом. На XOR это делается удобнее, чем на сложении по длине алфавита, но разницы практически никакой.
Если мы получили разницу между двумя осмысленными шифротекстами, то дальше, как правило, становится намного легче, поскольку у текстов на естественном языке высокая избыточность. Зачастую мы можем догадаться, что происходит, делая разные предположения, гипотезы. А главное, что каждая верная гипотеза будет раскрывать нам кусочек ключа, а значит и кусочки двух шифротекстов. Как-то так. Поэтому плохо.
Помимо шифров подстановки, были еще шифры перестановки. С ними тоже все довольно просто. Берем сообщение ВАСЯИ, записываем его в блок какой-то длины, например в ДИДОМ, и считываем результат так же.
Не бог весть какая штука. Как ее ломать, тоже понятно — переберем все возможные варианты перестановок. Тут их не очень много. Берем длину блока, подбираем и восстанавливаем.
В качестве следующей итерации был выбран такой способ: возьмем все то же самое, а сверху напишем какой-нибудь ключ — СИМОН. Переставим столбцы так, чтобы буквы оказались в алфавитном порядке. В итоге получим новую перестановку по ключу. Она уже намного лучше старой, поскольку количество перестановок намного больше и подобрать ее не всегда легко.
Каждый современный шифр тем или иным способом базируется на этих двух принципах — подстановки и перестановки. Сейчас их использование намного более сложное, но сами базовые принципы остались прежними. 
Если говорить про современные шифры, они делятся на две категории: поточные и блочные. Поточный шифр устроен так, что фактически представляет собой генератор случайных чисел, выход которого мы складываем по модулю 2, «ксорим», с нашим шифротекстом, как видно у меня на слайде. Ранее я сказал: если длина получившегося ключевого потока — она же ключ — абсолютно случайная, никогда повторно не используется и ее длина равна длине сообщения, то у нас получился абсолютно стойкий шифр, невзламываемый.
Возникает вопрос: как сгенерировать на такой шифр случайный, длинный и вечный Ключ? Как вообще работают поточные шифры? По сути, они представляют собой генератор случайного числа на основе какого-то начального значения. Начальное значение и является ключом шифра, ответом.
Из этой истории есть одно занятное исключение — шифроблокноты. Речь идет о настоящей шпионской истории про настоящий шпионаж. Некие люди, которым нужна абсолютно устойчивая коммуникация, генерируют случайные числа — например, буквальным бросанием кубика или буквальным выниманием шаров из барабана, как в лото. Создают два листа, где печатают эти случайные числа. Один лист отдают получателю, а второй оставляют у отправителя. При желании пообщаться они используют этот поток случайных чисел в качестве ключевого потока. Нет, история взята не из совсем далекого прошлого. У меня есть настоящий радиоперехват от 15 октября 2014 года: 7 2 6, 7 2 6, 7 2 6. Это позывной. 4 8 3, 4 8 3, 4 8 3. Это номер шифроблокнота. 5 0, 5 0, 5 0. Это количество слов. 8 4 4 7 9 8 4 4 7 9 2 0 5 1 4 2 0 5 1 4 и т. д. 50 таких числовых групп. Не знаю где, где-то не в России сидел какой-нибудь человек с ручкой и карандашом у обычного радиоприемника и записывал эти цифры. Записав их, он достал похожую штуку, сложил их по модулю 10 и получил свое сообщение. Другими словами, это реально работает, и подобное сообщение нельзя взломать. Если действительно были сгенерированы хорошие случайные числа и он впоследстии сжег бумажку с ключом, то осуществить взлом нельзя никак, совсем.
Но тут есть довольно много проблем. Первая — как нагенерировать по-настоящему хорошие случайные числа. Мир вокруг нас детерминирован, и если мы говорим про компьютеры, они детерминированы полностью.
Во-вторых, доставлять ключи такого размера… если мы говорим про передачу сообщений из 55 цифровых групп, то проделать подобное не очень сложно, а вот передать несколько гигабайт текста — уже серьезная проблема. Следовательно, нужны какие-нибудь алгоритмы, которые, по сути, генерируют псевдослучайные числа на основе какого-нибудь небольшого начального значения и которые могли бы использоваться в качестве таких потоковых алгоритмов. 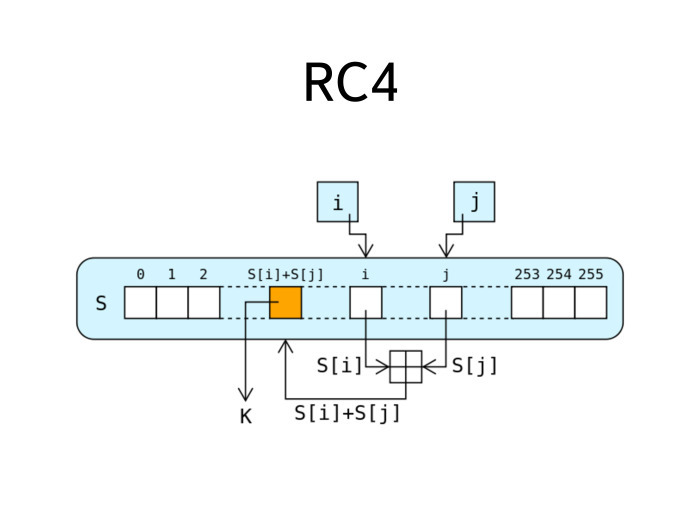
Самый исторически распространенный алгоритм подобного рода называется RC4. Он был разработан Роном Ривестом лет 25 назад и активно использовался очень долго, был самым распространенным алгоритмом для TLS, всех его различных вариантов, включая HTTPS. Но в последнее время RC4 начал показывать свой возраст. Для него существует некоторое количество атак. Он активно используется в WEP. Была одна хорошая лекция Антона, история, которая показывает: плохое применение пристойного даже по нынешним меркам алгоритма шифрования приводит к тому, что компрометируется вся система.
RC4 устроен несложно. На слайде целиком описана его работа. Есть внутренний байтовый стейт из 256 байт. На каждом шаге этого стейта есть два числа, два указателя на разные байты в стейте. И на каждом шаге происходит сложение между этими числами — они помещаются в некоторое место стейта. Полученный оттуда байт является следующим байтом в числовой последовательности. Вращая эту ручку таким образом, выполняя подобное действие на каждом шаге, мы получаем каждый следующий байт. Мы можем получать следующий байт числовой последовательности вечно, потоком.
Большое достоинство RC4 — в том, что он целиком внутрибайтовый, а значит, его программная реализация работает довольно быстро — сильно быстрее, в разы, если не в десятки раз быстрее, чем сравнимый и существовавший примерно в одно время с ним шифр DES. Поэтому RC4 и получил такое распространение. Он долго был коммерческим секретом компании RSA, но потом, где-то в районе 90-х годов, некие люди анонимно опубликовали исходники его устройства в списке рассылки cypherpunks. В результате возникло много драмы, были крики, мол, как же так, какие-то неприличные люди украли интеллектуальную собственность компании RSA и опубликовали ее. RSA начала грозить всем патентами, всевозможными юридическими преследованиями. Чтобы их избежать, все реализации алгоритма, которые находятся в опенсорсе, называются не RC4, а ARC4 или ARCFOUR. А — alleged. Речь идет о шифре, который на всех тестовых кейсах совпадает с RC4, но технически вроде как им не является.
Если вы конфигурируете какой-нибудь SSH или OpenSSL, вы в нем не найдете упоминания RC4, а найдете ARC4 или что-то подобное. Несложная конструкция, он уже старенький, на него сейчас есть атаки, и он не очень рекомендуется к использованию. 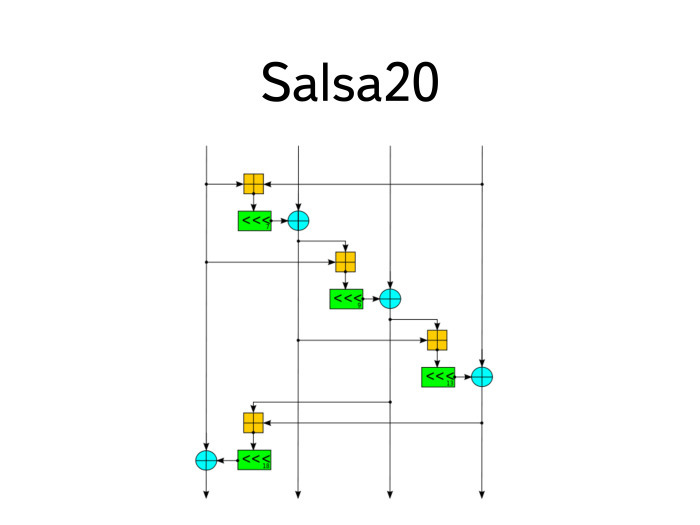
Было несколько попыток его заменить. Наверное, на мой предвзятый взгляд самым успешным стал шифр Salsa20 и несколько его последователей от широко известного в узких кругах персонажа Дэна Берштайна. Линуксоидам он обычно известен как автор qmail.
Salsa20 устроен сложнее, чем DES. Его блок-схема сложная, но он обладает несколькими интересными и классными свойствами. Для начала, он всегда выполняется за конечное время, каждый его раунд, что немаловажно для защиты от тайминг-атак. Это такие атаки, где атакующий наблюдает поведение системы шифрования, скармливая ей разные шифротексты или разные ключи за этим черным ящиком. И, понимая изменения во времени ответа или в энергопотреблении системы, он может делать выводы о том, какие именно процессы произошли внутри. Если вы думаете, что атака сильно надуманная, это не так. Очень широко распространены атаки подобного рода на смарт-карты — очень удобные, поскольку у атакующего есть полный доступ к коробке. Единственное, что он, как правило, не может в ней сделать, — прочитать сам ключ. Это сложно, а делать все остальное он может — подавать туда разные сообщения и пытаться их расшифровать.
Salsa20 устроен так, чтобы он всегда выполнялся за константное одинаковое время. Внутри он состоит всего из трех примитивов: это сдвиг на константное время, а также сложение по модулю 2 и по модулю 32, 32-битных слов. Скорость Salsa20 еще выше, чем у RC4. Он пока что не получил такого широкого распространения в общепринятой криптографии — у нас нет cipher suite для TLS, использующих Salsa20, — но все равно потихоньку становится мейнстримом. Указанный шифр стал одним из победителей конкурса eSTREAM по выбору лучшего поточного шифра. Их там было четыре, и Salsa — один из них. Он потихоньку начинает появляться во всяких опенсорс-продуктах. Возможно, скоро — может, через пару лет — появятся даже cipher suite в TLS с Salsa20. Мне он очень нравится.
Какая проблема с поточными шифрами? Если у вас есть поток данных, передаваемый по сети, поточный шифр для него удобен. К вам влетел пакет, вы его зашифровали и передали. Влетел следующий — приложили эту гамму и передали. Первый байт, второй, третий по сети идут. Удобно.
Если данные, например гигабайтный файл целиком, зашифрованы на диске поточным шифром, то чтобы прочитать последние 10 байт, вам нужно будет сначала сгенерировать гаммы потока шифра на 1 гигабайт, и уже из него взять последние 10 байт. Очень неудобно.
В Salsa указанная проблема решена, поскольку в нем на вход поступает в том числе и номер блока, который надо сгенерировать. Дальше к номеру блока 20 раз применяется алгоритм. 20 раундов — и мы получаем 512 бит выходного потока.
Самая успешная атака — в 8 раундов. Сам он 256-битный, а сложность атаки в 8 раундов — 250 или 251 бит. Считается, что он очень устойчивый, хороший. Публичный криптоанализ на него есть. Несмотря на всю одиозность личности Берштайна в этом аспекте, мне кажется, что штука хорошая и у нее большее будущее.
Исторически поточных шифров было много. Они первые не только в коммерческом шифровании, но и в военном. Там использовалось то, что называлось линейными регистрами сдвига.
Какие тут проблемы? Первая: в классических поточных шифрах, не в Salsa, чтобы расшифровать последнее значение гигабайтного файла, последний байт, вам нужно сначала сгенерировать последовательность на гигабайт. От нее вы задействуете только последний байт. Очень неудобно.
Поточные шифры плохо пригодны для систем с непоследовательным доступом, самый распространенный пример которых — жесткий диск.
Есть и еще одна проблема, о ней мы поговорим дальше. Она очень ярко проявляется в поточных шифрах. Две проблемы в совокупности привели к тому, что здорово было бы использовать какой-нибудь другой механизм.
Другой механизм для симметричного шифрования называется блочным шифром. Он устроен чуть по-другому. Он не генерирует этот ключевой поток, который надо ксорить с нашим шифротекстом, а работает похоже — как таблица подстановок. Берет блок текста фиксированной длины, на выходе дает такой же длины блок текста, и всё.
Размер блока в современных шифрах — как правило, 128 бит. Бывают разные вариации, но как правило, речь идет про 128 или 256 бит, не больше и не меньше. Размер ключа — точно такой же, как для поточных алгоритмов: 128 или 256 бит в современных реализациях, от и до.
Из всех широко распространенных блочных шифров сейчас можно назвать два — DES и AES. DES очень старый шифр, ровесник RC4. У DES сейчас размер блока — 64 бита, а размер ключа — 56 бит. Создан он был в компании IBM под именем Люцифер. Когда в IBM его дизайном занимался Хорст Фейстель, они предложили выбрать 128 бит в качестве размера блока. А размер ключа был изменяемый, от 124 до 192 бит.
Когда DES начал проходит стандартизацию, его подали на проверку в том числе и в АНБ. Оттуда он вернулся с уменьшенным до 64 бит размером блока и уменьшенным до 56 бит размером ключа. 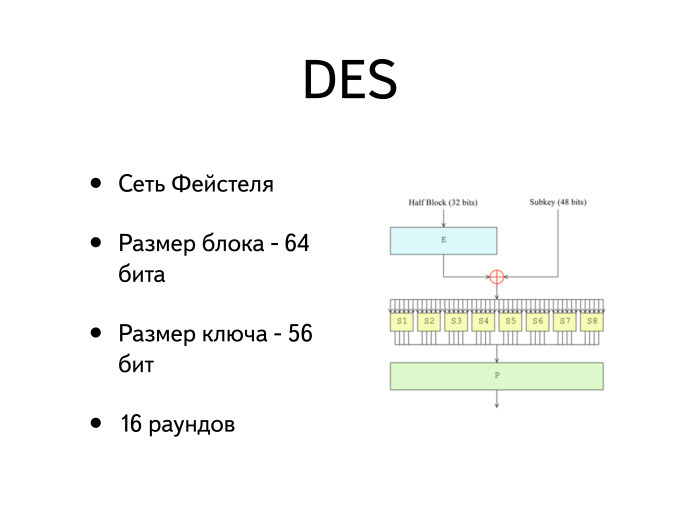
20 лет назад вся эта история наделала много шума. Все говорили — наверняка они туда встроили закладку, ужасно, подобрали такой размер блока, чтобы получить возможность атаковать. Однако большое достоинство DES в том, что это первый шифр, который был стандартизован и стал тогда основой коммерческой криптографии.
Его очень много атаковали и очень много исследовали. Есть большое количество всевозможных атак. Но ни одной практически реализуемой атаки до сих пор нет, несмотря на его довольно почтенный возраст. Единственное, размер ключа в 56 бит сейчас просто неприемлемый и можно атаковать полным перебором.
Как устроен DES? Фейстель сделал классную штуку, которую называют сетью Фейстеля. Она оперирует блоками. Каждый блок, попадающий на вход, делится на две части: левую и правую. Левая часть становится правой без изменений. Правая часть ксорится с результатом вычисления некой функции, на вход которой подается левая часть и ключ. После данного преобразования правая часть становится левой. 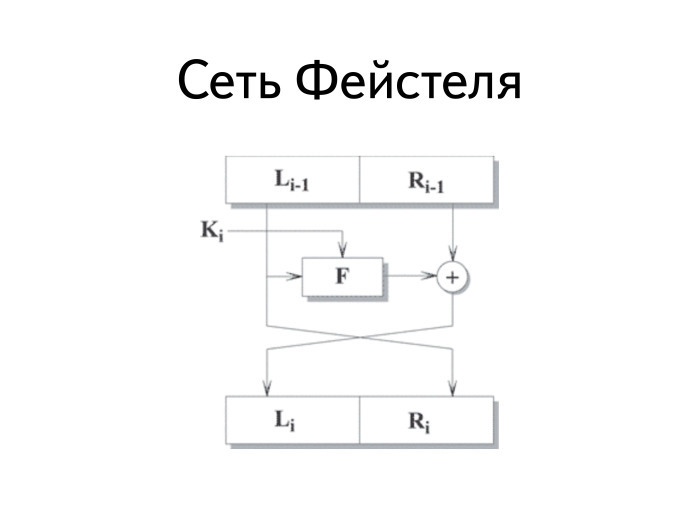
У нее есть несколько интересных достоинств. Первое важное достоинство: функция F может быть любой. Она не должна обладать свойствами обратимости, она может и не быть линейной или нелинейной. Все равно шифр остается симметричным.
Второе очень удобное свойство: расшифровка устроена так же, как шифрование. Если нужно расшифровать данную сеть, вы в прежний механизм вместо открытого текста засовываете шифротекст и на выходе вновь получаете открытый текст.
Почему это удобно? 30 лет назад удобство являлось следствием того, что шифраторы были аппаратными и заниматься дизайном отдельного набора микросхем для шифрования и для расшифровки было трудоемко. А в такой конструкции все очень здорово, фактически мы можем один блок использовать для разных задач.
В реальной ситуации такая конструкция — один раунд блочного шифра, то есть в реальном шифре она выполняется 16 раз с разными ключами. На каждом 16 раунде генерируется отдельный ключ и 16 раундовых подключей, каждый из которых применяется на каждом раунде для функции F.
Раунд тоже выглядит довольно несложно — он состоит всего из двух-трех операций. Первая операция: размер попавшегося полублока становится равен 32 бита, полубок проходит функцию расширения, на вход попадает 32 бита. Дальше мы по специальной несекретной таблице немного добавляем к 32 битам, превращая их в 48: некоторые биты дублируются и переставляются, такая гребеночка.
Потом мы его ксорим с раундовым ключом, размер которого — тоже 48 бит, и получаем 48-битное значение.
Затем оно попадает в набор функций, которые называются S-боксы и преобразуют каждый бит входа в четыре бита выхода. Следовательно, на выходе мы из 48 бит снова получаем 32 бита.
И наконец, окончательная перестановка P. Она опять перемешивает 32 бита между собой. Все очень несложно, раундовая функция максимально простая.
Самое интересное ее свойство заключается в указанных S-боксах: задумано очень сложное превращение 6 бит в 4. Если посмотреть на всю конструкцию, видно, что она состоит из XOR и пары перестановок. Если бы S-боксы были простыми, весь DES фактически представлял бы собой некоторый набор линейных преобразований. Его можно было бы представить как матрицу, на которую мы умножаем наш открытый текст, получая шифротекст. И тогда атака на DES была бы тривиальной: требовалось бы просто подобрать матрицу.
Вся нелинейность сосредоточена в S-боксах, подобранных специальным образом. Существуют разные анекдоты о том, как именно они подбирались. В частности, примерно через 10 лет после того, как DES был опубликован и стандартизован, криптографы нашли новый тип атак — дифференциальный криптоанализ. Суть атаки очень простая: мы делаем мелкие изменения в открытом тексте — меняя, к примеру, значение одного бита с 0 на 1 — и смотрим, что происходит с шифротекстом. Выяснилось, что в идеальном шифре изменение одного бита с 0 на 1 должно приводить к изменению ровно половины бит шифротекста. Выяснилось, что DES, хоть он и был сделан перед тем, как открыли дифференциальный криптоанализ, оказался устойчивым к этому типу атак. В итоге в свое время возникла очередная волна паранойи: мол, АНБ еще за 10 лет до открытых криптографов знало про существование дифференциального криптоанализа, и вы представляете себе, что оно может знать сейчас.
Анализу устройства S-боксов посвящена не одна сотня статей. Есть классные статьи, которые называются примерно так: особенности статистического распределения выходных бит в четвертом S-боксе. Потому что шифру много лет, он досконально исследован в разных местах и остается достаточно устойчивым даже по нынешним меркам.
56 бит сейчас уже можно просто перебрать на кластере машин общего назначения — может, даже на одном. И это плохо. Что можно предпринять?
Просто сдвинуть размер ключа нельзя: вся конструкция завязана на его длину. Triple DES. Очевидный ответ был таким: давайте мы будем шифровать наш блок несколько раз, устроим несколько последовательных шифрований. И здесь всё не слишком тривиально.
Допустим, мы берем и шифруем два раза. Для начала нужно доказать, что для шифрований k1 и k2 на двух разных ключах не существует такого шифрования на ключе k3, что выполнение двух указанных функций окажется одинаковым. Здесь вступает в силу свойство, что DES не является группой. Тому существует доказательство, пусть и не очень тривиальное.
Окей, 56 бит. Давайте возьмем два — k1 и k2. 56 + 56 = 112 бит. 112 бит даже по нынешним меркам — вполне приемлемая длина ключа. Можно считать нормальным всё, что превышает 100 бит. Так почему нельзя использовать два шифрования, 112 бит?
Одно шифрование DES состоит из 16 раундов. Сеть применяется 16 раз. Изменения слева направо происходят 16 раз. И он — не группа. Есть доказательство того, что не существует такого ключа k3, которым мы могли бы расшифровать текст, последовательно зашифрованный выбранными нами ключами k1 и k2.
Есть атака. Давайте зашифруем все возможные тексты на каком-нибудь ключе, возьмем шифротекст и попытаемся его расшифровать на всех произвольных ключах. И здесь, и здесь получим 2 56 вариантов. И где-то они сойдутся. То есть за два раза по 2 56 вариантов — плюс память для хранения всех расшифровок — мы найдем такую комбинацию k1 и k2, при которых атака окажется осуществимой.
Эффективная стойкость алгоритма — не 112 бит, а 57, если у нас достаточно памяти. Нужно довольно много памяти, но тем не менее. Поэтому решили — так работать нельзя, давайте будем шифровать три раза: k1, k2, k3. Конструкция называется Triple DES. Технически она может быть устроена по-разному. Поскольку в DES шифрование и дешифрование — одно и то же, реальные алгоритмы иногда выглядят так: зашифровать, расшифровать и снова расшифровать — чтобы выполнять операции в аппаратных реализациях было проще.
Наша обратная реализация Triple DES превратится в аппаратную реализацию DES. Это может быть очень удобно в разных ситуациях для задачи обратной совместимости.
Где применялся DES? Вообще везде. Его до сих пор иногда можно пронаблюдать для TLS, существуют cipher suite для TLS, использующие Triple DES и DES. Но там он активно отмирает, поскольку речь идет про софт. Софт легко апдейтится.
А вот в банкоматах он отмирал очень долго, и я не уверен, что окончательно умер. Не знаю, нужна ли отдельная лекция о том, как указанная конструкция устроена в банкоматах. Если коротко, клавиатура, где вы вводите PIN, — самодостаточная вещь в себе. В нее загружены ключи, и наружу она выдает не PIN, а конструкцию PIN-блок. Конструкция зашифрована — например, через DES. Поскольку банкоматов огромное количество, то среди них много старых и до сих пор можно встретить банкомат, где внутри коробки реализован даже не Triple DES, а обычный DES.
Однажды DES стал показывать свой возраст, с ним стало тяжело, и люди решили придумать нечто поновее. Американская контора по стандартизации, которая называется NIST, сказала: давайте проведем конкурс и выберем новый классный шифр. Им стал AES.
DES расшифровывается как digital encrypted standard. AES — advanced encrypted standard. Размер блока в AES — 128 бит, а не 64. Это важно с точки зрения криптографии. Размер ключа у AES — 128, 192 или 256 бит. В AES не используется сеть Фейстеля, но он тоже многораундовый, в нем тоже несколько раз повторяются относительно примитивные операции. Для 128 бит используется 10 раундов, для 256 — 14.
Сейчас покажу, как устроен каждый раунд. Первый и последний раунды чуть отличаются от стандартной схемы — тому есть причины.
Как и в DES, в каждом раунде AES есть свои раундовые ключи. Все они генерируются из ключа шифрования для алгоритма. В этом месте AES работает так же, как DES. Берется 128-битный ключ, из него генерируется 10 подключей для 10 раундов. Каждый подключ, как и в DES, применяется на каждом конкретном раунде.
Каждый раунд состоит из четырех довольно простых операций. Первый раунд — подстановка по специальной таблице.
В AES мы строим байтовую матрицу размером 4 на 4. Каждый элемент матрицы — байт. Всего получается 16 байт или 128 бит. Они и составляют блок AES целиком.
Вторая операция — побайтовый сдвиг.
Устроен он несложно, примитивно. Мы берем матрицу 4 на 4. Первый ряд остается без изменений, второй ряд сдвигается на 1 байт влево, третий — на 2 байта, четвертый — на 3, циклично.
Далее мы производим перемешивание внутри колонок. Это тоже очень несложная операция. Она фактически переставляет биты внутри каждой колонки, больше ничего не происходит. Можно считать ее умножением на специальную функцию.
Четвертая, вновь очень простая операция — XOR каждого байта в каждой колонке с соответствующим байтом ключа. Получается результат.
В первом раунде лишь складываются ключи, а три других операции не используются. В последнем раунде не происходит подобного перемешивания столбцов:
Дело в том, что это не добавило бы никакой криптографической стойкости и мы всегда можем обратить последний раунд. Решили не тормозить конструкцию лишней операцией.
Мы повторяем 4 описанных шага 10 раз, и на выходе из 128-битного блока снова получаем 128-битный блок.
Какие достоинства у AES? Он оперирует байтами, а не битами, как DES. AES намного быстрее в софтовых реализациях. Если сравнить скорость выполнения AES и DES на современной машине, AES окажется в разы быстрее, даже если говорить о реализации исключительно в программном коде.
Производители современных процессоров, Intel и AMD, уже разработали ассемблерные инструкции для реализации AES внутри чипа, потому что стандарт довольно несложный. Как итог — AES еще быстрее. Если через DES на современной машинке мы можем зашифровать, например, 1-2 гигабита, то 10-гигабитный AES-шифратор находится рядом и коммерчески доступен обычным компаниям.
Блочный алгоритм шифрует блок в блок. Он берет блок на 128 или 64 бита и превращает его в блок на 128 или 64 бита.
А что мы будем делать, если потребуется больше, чем 16 байт?
Первое, что приходит в голову, — попытаться разбить исходное сообщение на блоки, а блок, который останется неполным, дополнить стандартной, известной и фиксированной последовательностью данных.
Да, очевидно, побьем всё на блоки по 16 байт и зашифруем. Такое шифрование называется ECB — electronic code boot, когда каждый из блоков по 16 байт в случае AES или по 8 байт в случае DES шифруется независимо. 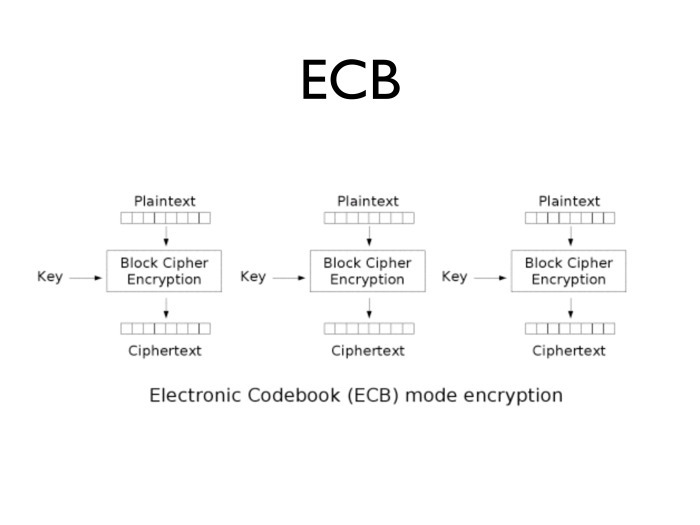
Шифруем каждый блок, получаем шифротекст, складываем шифротексты и получаем полный результат. 
Примерно так выглядит картинка, зашифрованная в режиме ECB. Даже если мы представим себе, что шифр полностью надежен, кажется, что результат менее чем удовлетворительный. В чем проблема? В том, что это биективное отображение. Для одинакового входа всегда получится одинаковый выход, и наоборот — для одинакового шифротекста всегда получится одинаковый открытый текст.
Надо бы как-нибудь исхитриться и сделать так, чтобы результат на выходе все время получался разным, в зависимости от местонахождения блока — несмотря на то, что на вход подаются одинаковые блоки шифротекста. Первым способом решения стал режим CBC. 
Мы не только берем ключ и открытый текст, но и генерируем случайное число, которое не является секретным. Оно размером с блок. Называется оно инициализационным вектором.
При шифровании первого блока мы берем инициализационный вектор, складываем его по модулю 2 с открытым текстом и шифруем. На выходе — шифротекст. Дальше складываем полученный шифротекст по модулю 2 со вторым блоком и шифруем. На выходе — второй блок шифротекста. Складываем его по модулю 2 с третьим блоком открытого текста и шифруем. На выходе получаем третий блок шифротекста. Здесь видно сцепление: мы каждый следующий блок сцепляем с предыдущим.
В результате получится картинка, где всё, начиная со второго блока, равномерно размазано, а первый блок каждый раз зависит от инициализационного вектора. И она будет абсолютно перемешана. Здесь все неплохо.
Однако у CBC есть несколько проблем.
О размере блока. Представьте: мы начали шифровать и, допустим, у нас DES. Если бы DES был идеальным алгоритмом шифрования, выход DES выглядел бы как равномерно распределенные случайные числа длиной 64 бита. Какова вероятность, что в выборке из равномерно распределенных случайных чисел длиной 64 бита два числа совпадут для одной операции? 1/(2 64 ). А если мы сравниваем три числа? Давайте пока прервемся.