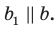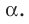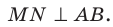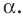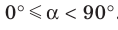Что такое перпендикулярно

29.08.202229.08.2022 admin 0 Комментариев

Что такое перпендикулярно

Значение слова «перпендикулярный»

1. Мат. Являющийся перпендикуляром. Перпендикулярная линия.

2. Расположенный, направленный под прямым углом к чему-л. [Игнат] свернул на другую дорогу, перпендикулярную той, на какой их обогнали вражеские танки. Б. Полевой, Золото.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

перпендикуля́рный

1. геометр. являющийся перпендикуляром ◆ Прямая бывает перпендикулярна к основанию, когда соединяет вершину равнобедренного треугольника с серединой основания. Н. И. Лобачевский, «Новые начала Геометрии с полной теорией параллельных», 1835–1838 г. (цитата из НКРЯ)

2. расположенный под прямым углом к чему-либо ◆ Ежели середи магнита положишь иглу так, чтобы она с его осью, то есть с линеею, от одного полюса до другого проведенною, была перпендикулярна, тогда повернётся она концами к полюсам и станет с осью параллельно, равно таким же образом, как палка по реке вдоль простирается. М. В. Ломоносов, «Волфианская экспериментальная физика, с немецкого подлинника на латинском языке сокращенная», 1745 г. (цитата из НКРЯ) ◆ Верстах в двух от оврага дорогу перерезывал, почти в перпендикулярном направлении, довольно значительной высоты холм. Е. Саранчов, «Хивинская экспедиция 1873 года», 1874 г. (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: докосить — это что-то нейтральное, положительное или отрицательное?

Источник

Значение слова «перпендикуляр»

[От лат. perpendicularis — отвесный]

ПЕРПЕНДИКУЛЯ’Р, а, м. [латин. perpendicularis — отвесный] (мат.). Прямая линия, составляющая прямой угол с данной прямой. Опустить из какой-н. точки п. на линию, на плоскость. Восставить п. какой-н. линии из какой-н. точки ее. П. к линии. П. к плоскости.

перпендикуля́р

1. геометр. прямая линия, пересекающая какую-либо прямую под прямым углом (в 90 градусов)

Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова выбраненный (прилагательное):

Ассоциации к слову «перпендикуляр&raquo

Синонимы к слову «перпендикуляр&raquo

Предложения со словом «перпендикуляр&raquo

Понятия, связанные со словом «перпендикуляр»

Отправить комментарий

Дополнительно

Предложения со словом «перпендикуляр&raquo

Затем к этой линии проведите перпендикуляр от самой отдалённой части углубления стопы, как показано на следующей странице.

Для определения суточных потребностей в воде и электролитах восстанавливают перпендикуляр от показателя возраста или массы больного до пересечения с неправильной кривой в средней части номограммы.

Это разметочный инструмент, который применяют для измерения длины на чертежах, деления углов, прямых линий для вычерчивания окружностей, построения перпендикуляров.

Источник

Перпендикулярность

Смотреть что такое «Перпендикулярность» в других словарях:

ПЕРПЕНДИКУЛЯРНОСТЬ — (от сл. перпендикуляр). Отвесность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕРПЕНДИКУЛЯРНОСТЬ от слова перпендикуляр. Отвесность. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык,… … Словарь иностранных слов русского языка

перпендикулярность — вертикальность, нормальность, ортогональность Словарь русских синонимов. перпендикулярность сущ., кол во синонимов: 4 • вертикальность (3) • … Словарь синонимов

ПЕРПЕНДИКУЛЯРНОСТЬ — ПЕРПЕНДИКУЛЯРНОСТЬ, перпендикулярности, мн. нет, жен. (мат.). Перпендикулярное положение. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

перпендикулярность — ПЕРПЕНДИКУЛЯРНЫЙ, ая, ое; рен, рна. Являющийся перпендикуляром. Перпендикулярные линии. Расположить перпендикулярно (нареч.) к чему н. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Перпендикулярность — 4.16 Перпендикулярность: а) поверхности 6 к поверхностям 7 и 9; Источник: ГОСТ 2110 93: Станки расточные горизонтальные с крестовым столом. Нормы точности оригинал документа … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случай ортогональности. Содержание 1 На плоскости 1.1 Перпендикулярные … Википедия

Перпендикулярность оси шпинделя к плоскости крепления привода — 2.9. Перпендикулярность оси шпинделя к плоскости крепления привода Черт. 8 Таблица 8 Ширина В бабок, мм Допуск, мкм, для класса точности Н П В 125, 160 20 12 8 200, 250 25 16 10 320, 400 … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность поверхности пропила базовой поверхности образца — 3.4. Перпендикулярность поверхности пропила базовой поверхности образца Допуск перпендикулярности ± 2 мм на длине 100 мм. Проверка проводится в соответствии со схемой, указанной на черт. 6в. Перпендикулярность поверхностей пропила проверяют… … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность боковой поверхности Д к верхней поверхности А — 2.3.4. Перпендикулярность боковой поверхности Д к верхней поверхности А Измерения по ГОСТ 25889.3 83, метод 2, на поверочной плите или на столе станка, в незажатом положении образца изделия (черт. 34). Черт. 34 Таблица 12 Размер образца изделия h … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность боковых поверхностей повернутого параллелепипеда — 2.11. Перпендикулярность боковых поверхностей повернутого параллелепипеда 16 Источник: ГОСТ 26016 83: Станки фрезерные широкоуниверсальные инструментальные. Нормы точности … Словарь-справочник терминов нормативно-технической документации

Перпендикулярность вертикального перемещения траверсы к рабочей поверхности стола в продольной плоскости — 2.17. Перпендикулярность вертикального перемещения траверсы к рабочей поверхности стола в продольной плоскости (для продольно шлифовальных станков двухстоечных) Черт. 34 Таблица 16 Длина перемещения траверсы, мм Допуск, мкм, для станков классов… … Словарь-справочник терминов нормативно-технической документации

Источник

Значение слова «перпендикулярно»

ПЕРПЕНДИКУЛЯ́РНО. Нареч. к перпендикулярный (во 2 знач.). Когда большая стрелка [часов] станет прямо вверх, а маленькая почти перпендикулярно к ней вправо, то тогда надо ему сменяться. Куприн, Ночная смена.

перпендикулярно

1. геометр. составляя прямой угол с какой-либо прямой или плоскостью ◆ У большинства планет, включая Землю, ось вращения расположена почти вертикально, то есть перпендикулярно к плоскости орбиты планеты. Георгий Бурба, «Открытый дважды», 15 июня 2004 г. // «Вокруг света» (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: юбочник — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «перпендикулярно&raquo

Синонимы к слову «перпендикулярно&raquo

Предложения со словом «перпендикулярно&raquo

Цитаты из русской классики со словом «перпендикулярно»

Понятия, связанные со словом «перпендикулярно»

Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).

Отправить комментарий

Дополнительно

Предложения со словом «перпендикулярно&raquo

Ход ствольной коробки ограничивается ствольной задержкой, кривошип поворачивается до своего крайнего заднего положения – почти перпендикулярно оси канала ствола.

Гиподерма состоит из соединительных перегородок жировой ткани, расположенных перпендикулярно к дерме.

При вертикальной проводке провода располагаются строго перпендикулярно к полу или потолку, при горизонтальной – только параллельно линиям потолка и стен.

Синонимы к слову «перпендикулярно&raquo

Ассоциации к слову «перпендикулярно&raquo

Карта слов и выражений русского языка

Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.

Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.

Сайт оснащён мощной системой поиска с поддержкой русской морфологии.

Источник

Что такое перпендикулярно

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

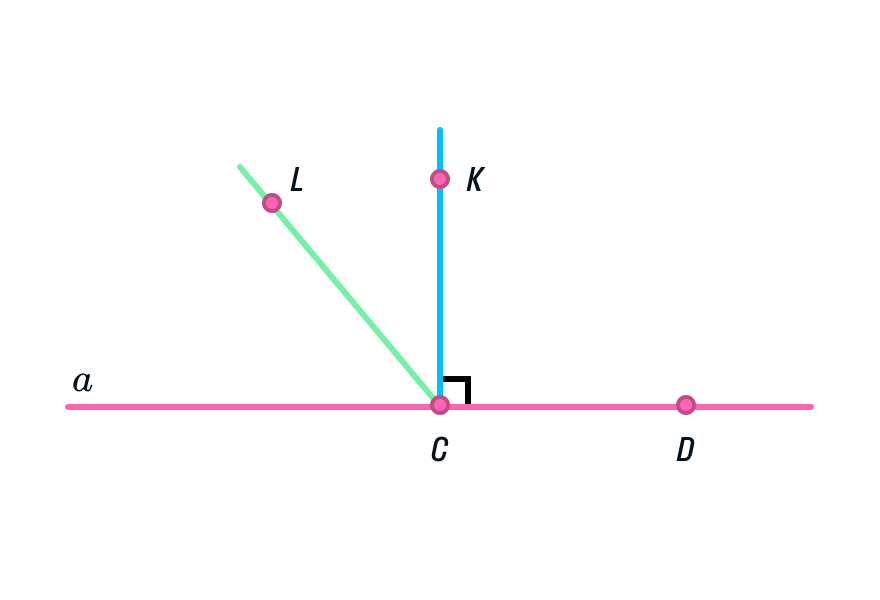
Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Источник

Перпендикулярность

Содержание

На плоскости

Перпендикулярные прямые

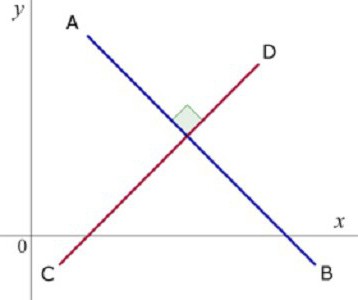
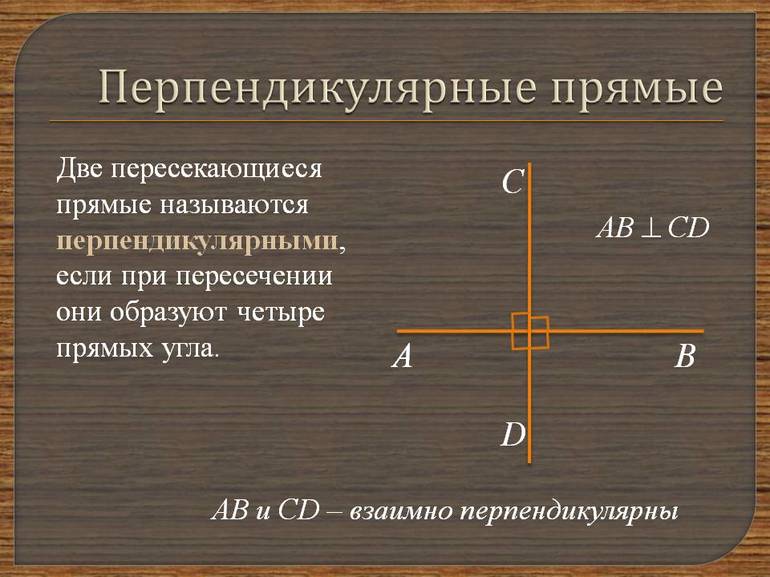
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

В аналитическом выражении прямые, заданные линейными функциями и будут перпендикулярны, если выполнено условие . Эти же прямые будут перпендикулярны, если . (Здесь — углы наклона прямой к горизонтали)

Для обозначения перпендикулярности имеется общепринятый символ: , предложенный в 1634 году французским математиком Пьером Эригоном.

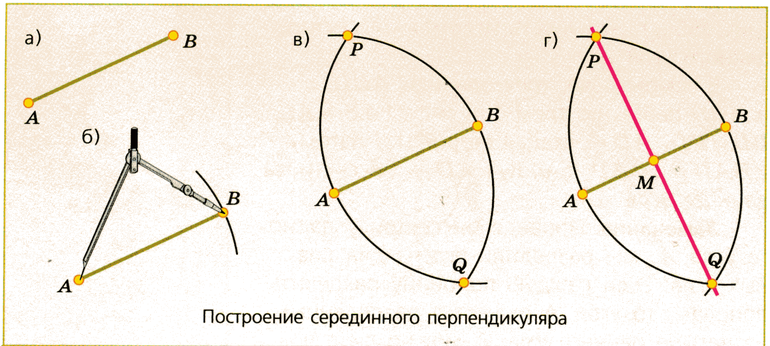
Построение перпендикуляра

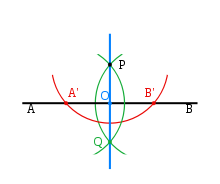
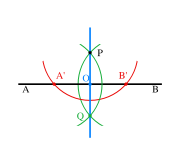
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Координаты точки основания перпендикуляра к прямой

A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).

Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.

Во всех остальных случаях

xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.

В трёхмерном пространстве

Перпендикулярные прямые

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

Перпендикулярность прямой и плоскости

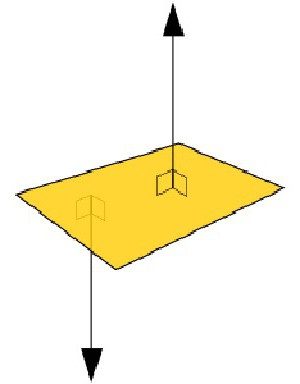
Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости

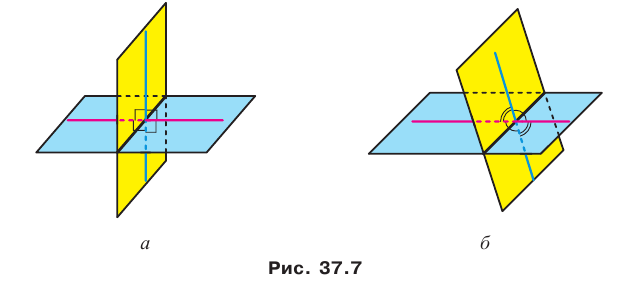
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство , а прямая l с направляющим векторным пространством и гиперплоскость с направляющим векторным пространством (где , ) принадлежат пространству .

Прямая l называется перпендикулярной гиперплоскости , если подпространство ортогонально подпространству , то есть

Источник

Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

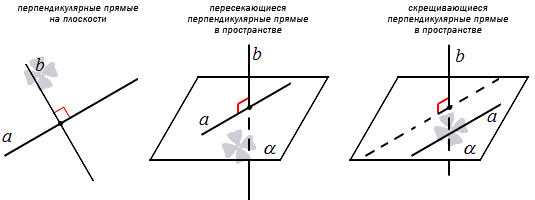
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Решение

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Источник

ПЕРПЕНДИКУЛЯР

Полезное

Смотреть что такое «ПЕРПЕНДИКУЛЯР» в других словарях:

перпендикуляр — нормаль, отвес Словарь русских синонимов. перпендикуляр сущ., кол во синонимов: 4 • апотема (2) • апофе … Словарь синонимов

ПЕРПЕНДИКУЛЯР — (от латинского perpendicularis отвесный), прямая (или ее отрезок), пересекающая данную прямую (плоскость) под прямым углом. В этом случае обе прямые (соответственно прямая и плоскость) называются взаимно перпендикулярными … Современная энциклопедия

ПЕРПЕНДИКУЛЯР — (от лат. perpendicularis отвесный) к данной прямой (плоскости) прямая, пересекающая данную прямую (плоскость) под прямым углом. В этом случае обе прямые (соответственно прямая и плоскость) называют взаимно перпендикулярными. Две плоскости… … Большой Энциклопедический словарь

ПЕРПЕНДИКУЛЯР — ПЕРПЕНДИКУЛЯР, а, муж. В математике: прямая, составляющая прямой угол с другой прямой или плоскостью. Опустить п. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ПЕРПЕНДИКУЛЯР — муж. черта под прямым углом, под углом в 90°, отвесная, отвес; ный, отвесный; ность жен. состоянье это, отвесность. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

Перпендикуляр — Перпендикуляр, восстановленный из какой либо точки прямой линии илиплоскости прямая линия, составляющая прямой угол с данною прямою илисоставляющая прямые углы с всякою прямою, проведенною в плоскости черезту точку, из которой П. восстановлен.… … Энциклопедия Брокгауза и Ефрона

перпендикуляр — ПЕРПЕНДИКУЛЯР, а, м. Что л. непонятное, смутное, сложное … Словарь русского арго

перпендикуляр — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN cross track … Справочник технического переводчика

Перпендикуляр — (от латинского perpendicularis отвесный), прямая (или ее отрезок), пересекающая данную прямую (плоскость) под прямым углом. В этом случае обе прямые (соответственно прямая и плоскость) называются взаимно перпендикулярными. … Иллюстрированный энциклопедический словарь

ПЕРПЕНДИКУЛЯР — (1) к плоскости прямая, пересекающая под прямым углом любую прямую, лежащую в данной плоскости и проходящую через точку пересечения; (2) к прямой прямая, пересекающая под прямым углом данную прямую … Большая политехническая энциклопедия

Источник

Что значит «перпендикулярно»? Происхождение и значение термина

Слово «перпендикулярно» часто встречается в учебниках геометрии. А вот каково происхождение этого понятия? Что значит «перпендикулярно», откуда появилось это слово? Об этом и рассказывается в данной статье.

Происхождение слова

Наречие «перпендикулярно» происходит от существительного «перпендикуляр». Это слово пришло в русский язык из латыни. Там per и pendere означало «перед» и «висеть», а сочетание этих двух слов можно перевести как «отвес». Словосочетание показалось очень удобным, и его стали применять в геометрии.

Перпендикуляром можно назвать прямую. Но не каждую, а лишь ту, которая находится под прямым углом. Поэтому ответ на вопрос о том, что значит перпендикулярно, обязательно должен содержать упоминание прямого угла. Прямая может быть перпендикулярна другой прямой, лучу, вектору, стороне геометрической фигуры и даже плоскости.

Свойства перпендикулярности

Несколько свойств делают перпендикулярность довольно интересным геометрическим явлением. По умолчанию, если первая линия расположена под углом 90° ко второй, то и вторая перпендикулярна первой. Поэтому в условии задачи нет смысла обсуждать, какая из линий перпендикулярна другой.

При изучении высшей математики объяснить, что значит перпендикулярно, будет сложнее. Для математика перпендикулярность – всего лишь частный случай общей математической концепции ортогональности. В понятие перпендикулярности также входит описание многомерных геометрических объектов и их свойств.

Обозначение

На вопрос о том, что значит перпендикулярно, можно ответить и графически. Все математики мира придерживаются определенный условных обозначений, понятных даже тем, кто не знает иностранных языков.

Обозначение перпендикуляра впервые появилось на свет в 1634 году. Оно было опубликовано в работах французского астронома и математика Пьера Эригона. В своем многотомном труде он обобщил все математические знания, известные в то время, и изложил их на французском и латинском языках. Его труды не утратили своего значения много лет спустя – так, Эригона цитировали в своих работах Лейбниц и Паскаль. Он был автором нескольких математических обозначений, наиболее долгоживущим из них оказался знак перпендикулярности. На языке математики «перпендикулярно» выглядит вот так:

Как видно, ничего сложного в обозначении перпендикуляра нет. Просто нужно дорисовать маленький квадратик в углу пересекающихся линий. Иногда перпендикуляр рисуют в виде угла с обозначением в 90°.

Теперь вы тоже знаете о том, что значит слово «перпендикулярно» и кто придумал такое удачное обозначение геометрического понятия.

Источник

Перпендикуляр

Содержание

Перпендикулярность прямых на плоскости

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

В аналитическом выражении прямые, заданные линейными функциями 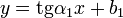и будут перпендикулярны, если выполнено условие . (Здесь α₁,α₂ — углы наклона прямой к горизонтали)

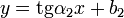
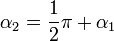
Перпендикулярность прямых в пространстве

Построение перпендикуляра на плоскости

Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Перпендикулярность прямой и плоскости

Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.

Перпендикулярность плоскостей в 3-мерном пространстве

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90 градусам.

Перпендикулярность плоскостей в 4-мерном пространстве

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Таких пар 6 (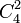): xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Источник

ПЕРПЕНДИКУЛЯР

Смотреть что такое «ПЕРПЕНДИКУЛЯР» в других словарях:

ПЕРПЕНДИКУЛЯР — (лат., от per, и pendere висеть). Отвес, прямая, встречающая другую прямую, так что образует с нею прямые углы. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕРПЕНДИКУЛЯР линия, пересекающая другую под прямым… … Словарь иностранных слов русского языка

перпендикуляр — ПЕРПЕНДИКУЛЯР, а, м. Что л. непонятное, смутное, сложное … Словарь русского арго

Источник

перпендикулярный

Смотреть что такое «перпендикулярный» в других словарях:

ПЕРПЕНДИКУЛЯРНЫЙ — (этим. см. пред. слово). Отвесный. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕРПЕНДИКУЛЯРНЫЙ этимологию см. Перпендикуляр. Отвесный. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык … Словарь иностранных слов русского языка

перпендикулярный — поперечный, пересекающийся, пересекающий, ортогональный; нормальный, отвесный, вертикальный. Ant. параллельный Словарь русских синонимов. перпендикулярный прил., кол во синонимов: 4 • вертикальный (5) … Словарь синонимов

ПЕРПЕНДИКУЛЯРНЫЙ — ПЕРПЕНДИКУЛЯРНЫЙ, перпендикулярная, перпендикулярное; перпендикулярен, перпендикулярна, перпендикулярно, к чему (мат.). прил. к перпендикуляр; являющийся перпендикуляром. Перпендикулярная линия. Одна дорожка перпендикулярна другой. Одна дорожка… … Толковый словарь Ушакова

ПЕРПЕНДИКУЛЯРНЫЙ — ПЕРПЕНДИКУЛЯРНЫЙ, ая, ое; рен, рна. Являющийся перпендикуляром. Перпендикулярные линии. Расположить перпендикулярно (нареч.) к чему н. | сущ. перпендикулярность, и, жен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

перпендикулярный — (перпендикулярно) чему и к чему. Перпендикулярный плоскости (к плоскости). Проснувшись, он подымал ноги перпендикулярно туловищу вверх, потом быстро опускал их вниз (Короленко). Когда большая стрелка станет прямо вверх, а маленькая почти… … Словарь управления

Перпендикулярный спрэд — опционная стратегия, использующая опционы с близкими датами исполнения, но разными ценами. По английски: Perpendicular spread См. также: Вертикальные спрэды Финансовый словарь Финам … Финансовый словарь

перпендикулярный спред — Стратегия в операциях с опционами, при которой используются опционы, имеющие одну и ту же дату истечения и различные цены страйк (цены, по которым опцион может быть исполнен). Перпендикулярный спред может использоваться как в расчете на подъем… … Финансово-инвестиционный толковый словарь

Перпендикулярный — прил. 1. соотн. с сущ. перпендикуляр, связанный с ним 2. Свойственный перпендикуляру, характерный для него. отт. Расположенный под прямым углом к чему либо. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

перпендикулярный — перпендикулярный, перпендикулярная, перпендикулярное, перпендикулярные, перпендикулярного, перпендикулярной, перпендикулярного, перпендикулярных, перпендикулярному, перпендикулярной, перпендикулярному, перпендикулярным, перпендикулярный,… … Формы слов

перпендикулярный — перпендикул ярный; кратк. форма рен, рна … Русский орфографический словарь

перпендикулярный — кр.ф. перпендикуля/рен, перпендикуля/рна, рно, рны … Орфографический словарь русского языка

Источник

перпендикулярно

Смотреть что такое «перпендикулярно» в других словарях:

перпендикулярно — перпендикулярно … Орфографический словарь-справочник

перпендикулярно — под прямым углом Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011. перпендикулярно нареч, кол во синонимов: 5 • вертикально … Словарь синонимов

перпендикулярно расположенный — перпендикулярно расположенный … Орфографический словарь-справочник

перпендикулярно смонтированный — перпендикулярно смонтированный … Орфографический словарь-справочник

перпендикулярно-отвесный — перпендикулярно отвесный … Орфографический словарь-справочник

перпендикулярно-поперечный — перпендикулярно поперечный … Орфографический словарь-справочник

перпендикулярно-продольный — перпендикулярно продольный … Орфографический словарь-справочник

перпендикулярно к грани — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN normal to the face … Справочник технического переводчика

перпендикулярно к плоскости — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN normal to the plane … Справочник технического переводчика

перпендикулярно к удлинению — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN normal to elongation … Справочник технического переводчика

Перпендикулярно — нареч. качеств. обстоят. Располагаясь под прямым углом к чему либо. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

Источник

ПЕРПЕНДИКУЛЯРНЫЙ

Смотреть что такое «ПЕРПЕНДИКУЛЯРНЫЙ» в других словарях:

перпендикулярный — перпендикул ярный; кратк. форма рен, рна … Русский орфографический словарь

Источник

Значение слова «перпендикулярность»

Для обозначения перпендикулярности имеется общепринятый символ:

, предложенный в 1634 году французским математиком Пьером Эригоном. Например, перпендикулярность прямых

ПЕРПЕНДИКУЛЯ’РНОСТЬ, и, мн. нет, ж. (мат.). Перпендикулярное положение.

перпендикуля́рность

1. бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве

Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова борщок (существительное):

Синонимы к слову «перпендикулярность&raquo

Предложения со словом «перпендикулярность&raquo

Понятия, связанные со словом «перпендикулярность»

Отправить комментарий

Дополнительно

Предложения со словом «перпендикулярность&raquo

Здесь главное – соблюдать перпендикулярность карандаша относительно проводимых прямых независимо от их наклона.

Чем длиннее ножка угольника, тем точнее определяется перпендикулярность плоскостей.

Условие параллельности двух прямых: m1 / m2 =p1/ p2 =q1 / q2. Условие перпендикулярности двух прямых: m1m2 +p1p2 +q1q2 = 0.

Источник

Перпендикулярно

Смотреть что такое «Перпендикулярно» в других словарях:

перпендикулярно — перпендикулярно … Орфографический словарь-справочник

перпендикулярно расположенный — перпендикулярно расположенный … Орфографический словарь-справочник

перпендикулярно смонтированный — перпендикулярно смонтированный … Орфографический словарь-справочник

перпендикулярно-отвесный — перпендикулярно отвесный … Орфографический словарь-справочник

перпендикулярно-поперечный — перпендикулярно поперечный … Орфографический словарь-справочник

перпендикулярно-продольный — перпендикулярно продольный … Орфографический словарь-справочник

Источник

Что такое перпендикуляр?

Перпендикуля́рность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д. ) в евклидовом пространстве. Частный случай ортогональности.

Содержание [убрать]
1 На плоскости
1.1 Перпендикулярные прямые
1.2 Построение перпендикуляра
2 В трёхмерном пространстве
2.1 Перпендикулярные прямые
2.2 Перпендикулярность прямой и плоскости
2.3 Перпендикулярные плоскости
3 В многомерных пространствах
3.1 Перпендикулярность плоскостей в 4-мерном пространстве
3.2 Перпендикулярность прямой и гиперплоскости
3.3 Перпендикулярные гиперплоскости
4 См. также

[править] На плоскости
[править] Перпендикулярные прямые
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

[править] Построение перпендикуляра

Построение перпендикуляраШаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

[править] В трёхмерном пространстве
[править] Перпендикулярные прямые
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

[править] Перпендикулярность прямой и плоскости
Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой в этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

[править] Перпендикулярные плоскости
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90 градусам.

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
[править] В многомерных пространствах

Источник

Перпендикуляр, что это такое?

Перпендикуляр это отрезок, опущенный на прямую под углом 90 градусов (или иначе называемым «прямым углом»)

На данном рисунке, перпендикуляр В, опущен на прямую А.

Если же, отрезок опускается на прямую под углом не равным 90 градусам, такой отрезок называется «наклонной»

Перпенликуляр представляет собой прямую линию, которая пересекается с ещё одной прямой линией под углом в девяносто градусов. Таким образом, в прямоугольном треугольнике катеты являются перпендикулярными линиями.

Все помнят как учили в школу, что перпендикуляр это прямая или отрезок, которая или который пересекает другую плоскость или прямую под прямым углом (угол 90 градусов). До сих пор со страхом вспоминаю эти теоремы и их доказательства.

Также перпендикуляр называют «нормалью».

Хотя нормаль-более широкое название, чем перпендикуляр и распространяется на нелинейные кривые и поверхности не являющиеся плоскостями.

Источник

Перпендикулярные прямые

О чем эта статья:

Скорее всего, вы смогли бы отыскать три варианта:

Прямые параллельны друг другу;

Прямые совпадают, накладываются друг на друга;

Что это означает? Рассмотрим определение перпендикулярных прямых.

Основные определения

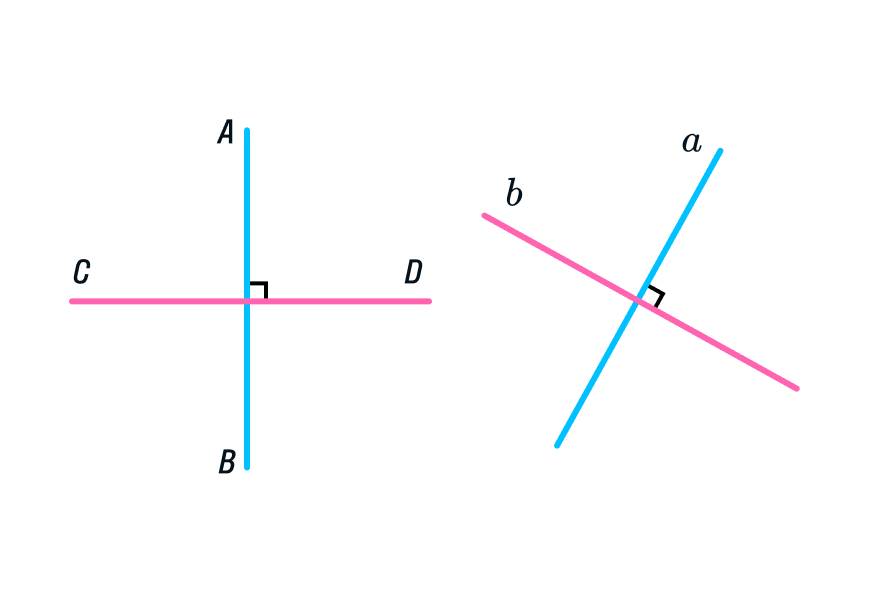
Перпендикулярные прямые — это прямые, которые пересекаются друг с другом под углом 90 градусов. Обозначение перпендикулярных прямых: а ┴ b.

Угол, равный 90 градусам, в математике называют прямым и помечают на чертеже квадратиком.

Еще один интересный факт из мира геометрии: если при пересечении двух прямых один из образовавшихся углов равен 90°, то и все остальные углы — прямые, а их сумма будет равна 360°.

Перпендикулярные отрезки — это отрезки, лежащие на перпендикулярных прямых.

Чтобы называться перпендикулярными, отрезкам не обязательно пересекаться самим. Достаточно, чтобы угол между прямыми, на которых они лежат, был равен 90°.

В качестве задачки со звездочкой давайте вспомним, в каких фигурах могут встречаться перпендикулярные отрезки (стороны)? Наверняка вы сразу назовете квадрат и прямоугольник, но также подходит прямоугольный треугольник и даже прямоугольная трапеция — с ней вы познакомитесь на уроках геометрии в 8-м классе.

Также перпендикулярно к стороне могут располагаться различные элементы внутри фигуры. Попробуйте расположить перпендикулярно друг другу диаметр и радиус окружности, две хорды, биссектрису угла треугольника (кстати, последнее задание получится выполнить только в случае, если проводить биссектрису угла к основанию равнобедренного треугольника).

Как мы видим, прямые очень часто пересекаются под углом 90 градусов. Можно сказать, это своего рода обычное, будничное поведение прямых. Прямые углы окружают нас повсюду: в комнате, на оживленных улицах города, в бассейне и даже в любимой книге.

Способы построения перпендикулярных прямых

Но как можно построить перпендикулярные прямые? Что для этого может понадобиться? Давайте разберем все доступные нам способы.

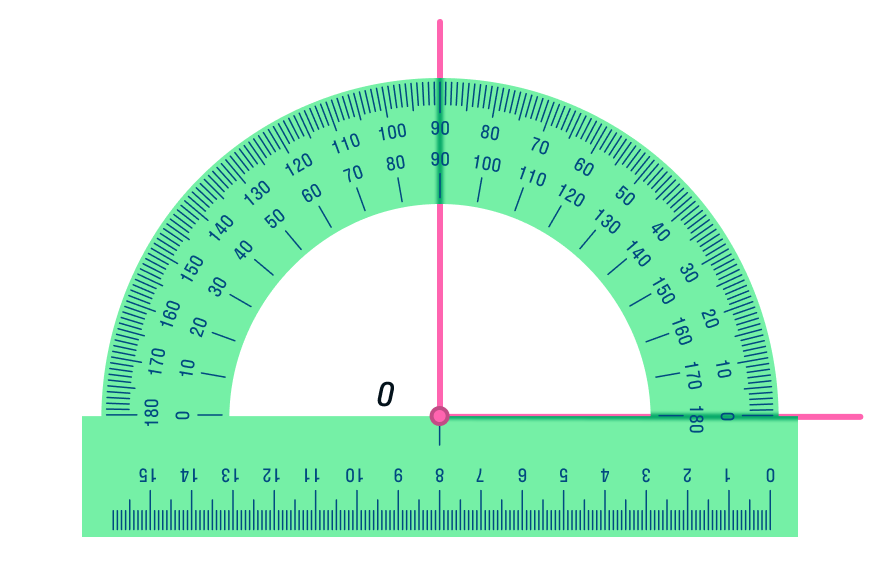
Самый легкий — воспользоваться транспортиром. Построим прямую а и точку А, не лежащую на этой прямой. Совместим значение 90 градусов с точкой таким образом, чтобы нижняя часть транспортира в виде линейки полностью совпала с прямой, и сделаем засечку в отверстии транспортира. Соединим точку А с поставленной засечкой до пересечения с прямой.

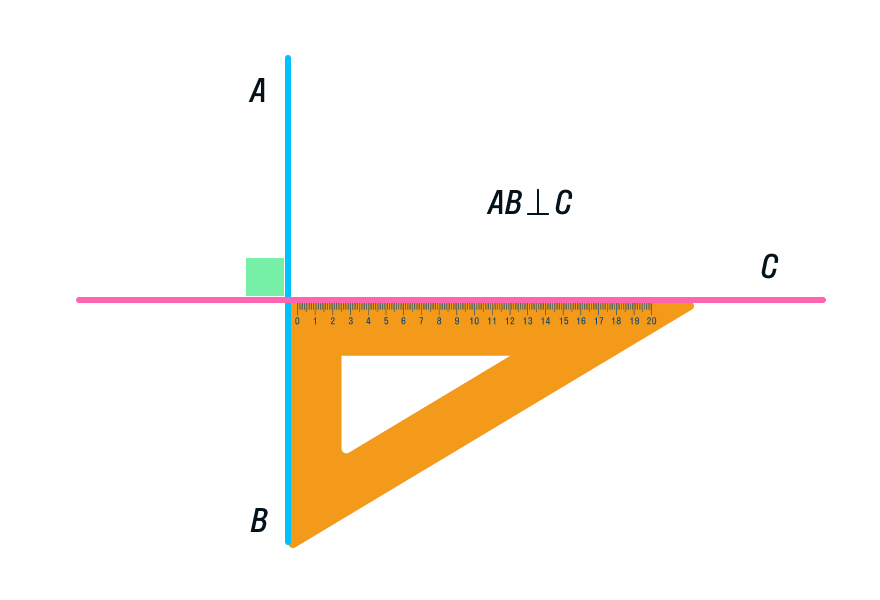
Но что делать, если транспортир благополучно забыт дома и у нас есть только линейка и угольник? Внимательно рассмотрите рисунок и попрактикуйтесь в построении дома.

Теорема о перпендикулярных прямых и ее доказательство

«Кто это вообще придумал?», — можете возразить вы. «Почему мы должны этому верить? Вдруг все иначе, а нас обманывают». Если это так, то ваши опасения — показатель пытливости ума!

Что такое теорема? Это утверждение, нуждающееся в доказательстве. Это означает, что его не принимает на веру никто: ни вы, ни учитель, ни самый великий ученый. Есть много способов доказательства теорем, один из которых — метод от противного. Используя его, мы будто соглашаемся с противоположным заявлением и рассуждаем, что из этого последует.

Например, попробуем доказать утверждение «осенью грачи улетают на юг» методом от противного. Предположим, что грачи остаются зимовать в наших городах. Тогда мы должны видеть их осенью и зимой повсеместно, а в небе не должно быть видно признаков масштабного перелета. Так ли это на самом деле? Конечно же, нет.

Теперь с помощью этого метода попробуем доказать теорему о перпендикулярных прямых.

Предположим, что теорема ложна, а значит, через точку, лежащую на прямой, можно провести несколько перпендикулярных прямых.

Возьмем линейку и проведем прямую а, отметив на ней точки С и D.

Далее построим перпендикулярную прямую из точки С. Угол КСD равен 90°.

Отрезок КС находится на прямой, перпендикулярной а.

Предположим, что есть еще одна прямая, перпендикулярная а. Проведем ее через точку С и отметим на ней точку L.

Тогда угол LCD равен 90° и угол КСD равен 90°.

Пункт номер 5 невозможен: от отрезка CD можно отложить только один прямой угол в данной плоскости.

А значит, через точку С можно провести только одну прямую, перпендикулярную прямой а.

Что и требовалось доказать: вы — молодцы!

Свойства перпендикулярных прямых

Перпендикулярные прямые обладают свойствами, которые можно использовать при решении геометрических задач. Давайте изучим их и приведем доказательство каждого.

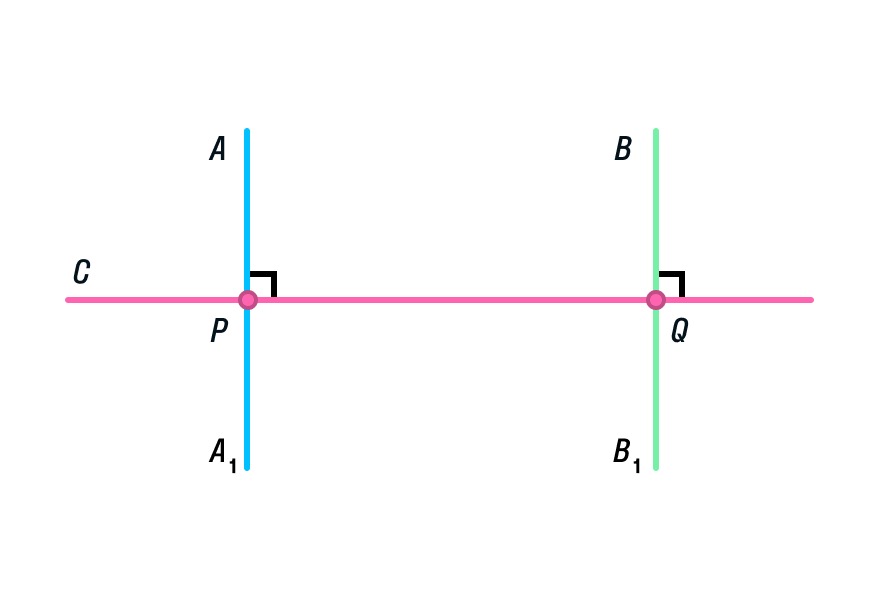
Две прямые, перпендикулярные к третьей, не пересекаются

Конечно же, это свойство хорошо просматривается при построении. Но как мы уже выяснили, математики — народ сомневающийся, поэтому попробуем обосновать, почему это так.

Предположим, что прямые АА₁ и ВВ₁ все же пересекутся в точке К. Что бы это значило? Что мы совершили невероятное и опровергли теорему о перпендикулярных прямых! Ведь тогда получается, что через точку К проходит несколько перпендикулярных прямых, которые в свою очередь пересекают прямую а под углом 90 градусов! Как было сказано выше, это невозможно, а значит и прямые АА₁ и ВВ₁ не пересекаются.

Перпендикуляр, проведенный из точки к прямой, называется расстоянием от прямой до этой точки

Интересно, что такое расстояние является кратчайшим.

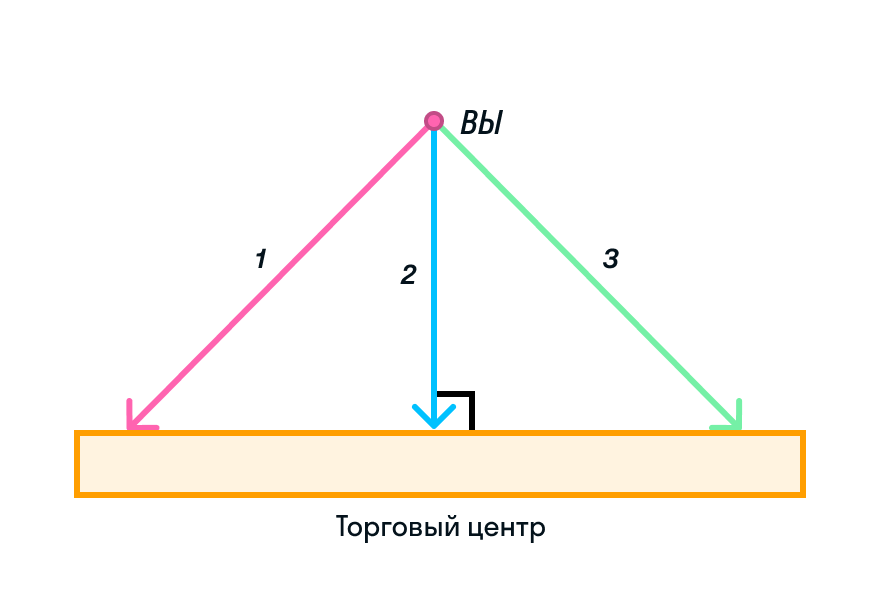
Представьте, что вам необходимо проложить путь от вас до огромного торгового центра, состоящего из множества магазинчиков. Вам не важно, в какой из них заглянуть, вы просто хотите потратить на дорогу как можно меньше времени. Какой путь вы выберете?

Конечно же, путь номер 2! Но есть ли этому научное объяснение?

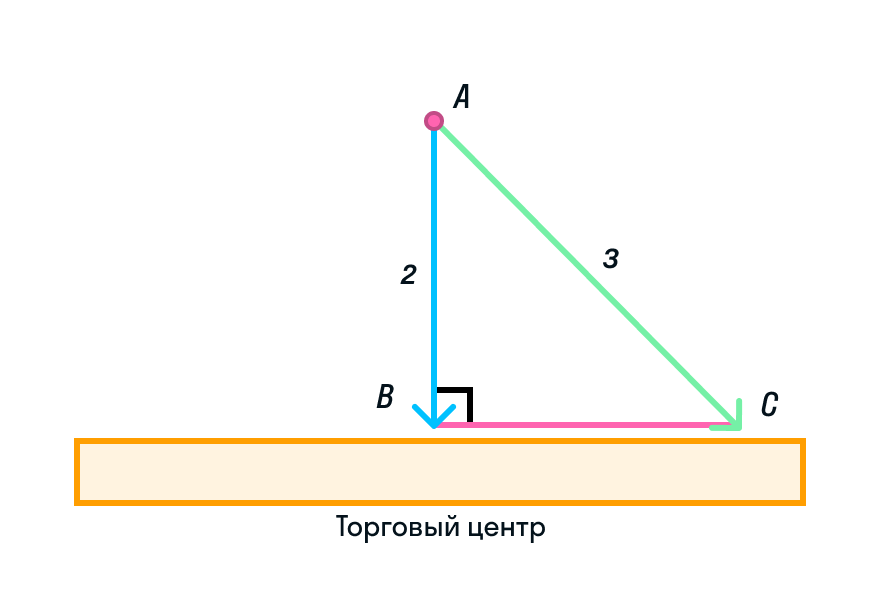
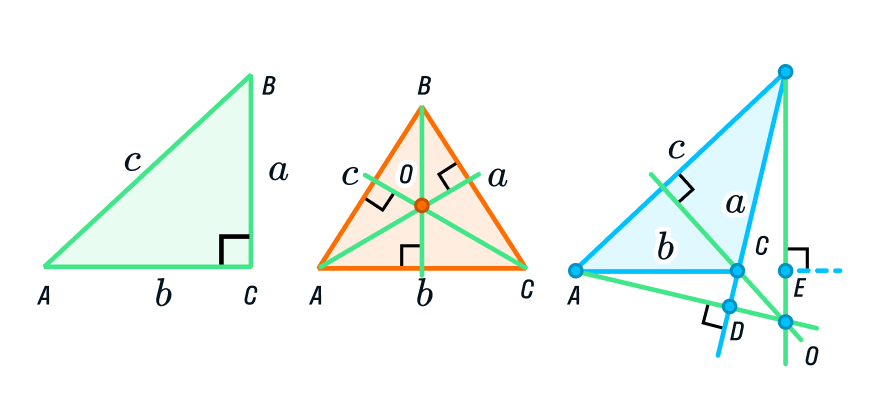
Треугольник АВС прямоугольный, АВ и ВС— катеты, АС — гипотенуза. Согласно соответствию углов и сторон, в треугольнике наибольшая сторона лежит напротив наибольшего угла. Таким углом является прямой угол В, а наибольшая сторона — гипотенуза АС. Под каким бы углом мы ни расположили гипотенузу, она всегда будет больше остальных сторон.

Кстати, перпендикуляр, проведенный из вершины угла фигуры на прямую, содержащую противоположную сторону, известен под именем высота. С высотами связано множество теорем и свойств, которые вы будете изучать немного позже. В качестве интриги оставим вам пример того, где находится точка пересечения высот в треугольниках разного типа. Заметили что-то необычное?

Применение знания о перпендикулярных прямых

Напоследок ответим на вопрос, который мог возникнуть у некоторых из вас: «А как в древности люди решали вопрос с построением перпендикулярных прямых, прямых углов в частности? Были ли у них приспособления для этого?»

Построение прямых углов было важным умением даже в древности, так как от этого зависела крепость и устойчивость возведенных стен зданий, мостов, механизмов для строительства. Один лишний градус — и целый город мог оказаться в опасности из-за обрушившегося дворца или башни.

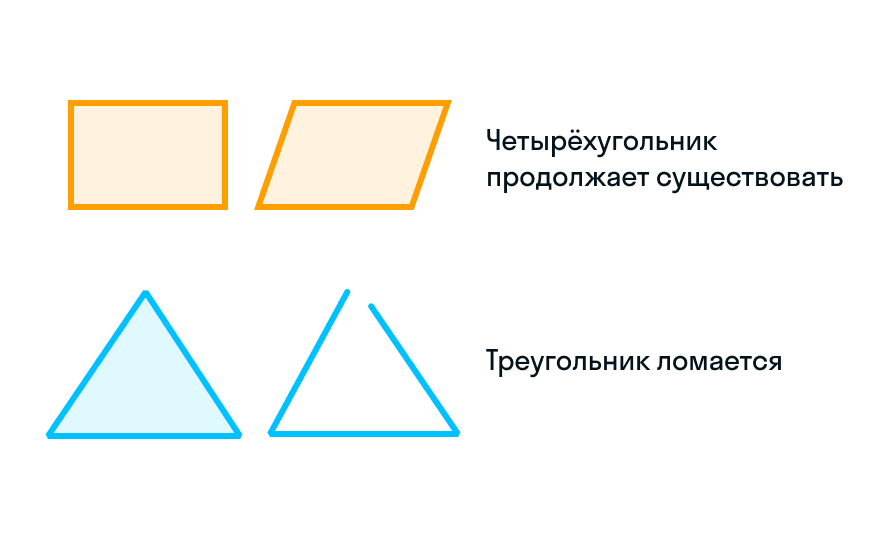
Древние зодчие поняли, что возлагать все надежды на четырехугольники не стоит, потому что квадраты и прямоугольники легко превращаются в параллелограммы, меняя величину углов и оставляя неизменными длины сторон. Стоит только немного потянуть за «ушки» квадрата, как он начинает беспощадно ломать прямые углы, а ведь в условиях строительства многое может пойти не так и искривить конструкцию: ветер, изменение температуры, неточность мастера.

Хорошо, что есть более стабильная фигура — треугольник. Все дело в соотношении его сторон и углов, а еще в невозможности создать несколько треугольников из сторон заданной длины. Если у вас есть отрезки длиной 6, 8 и 10 сантиметров, из них можно составить только один треугольник. В случае, если одна сторона растянется под действием нагрузки или сожмется из-за понижения температуры — треугольник просто перестанет существовать.

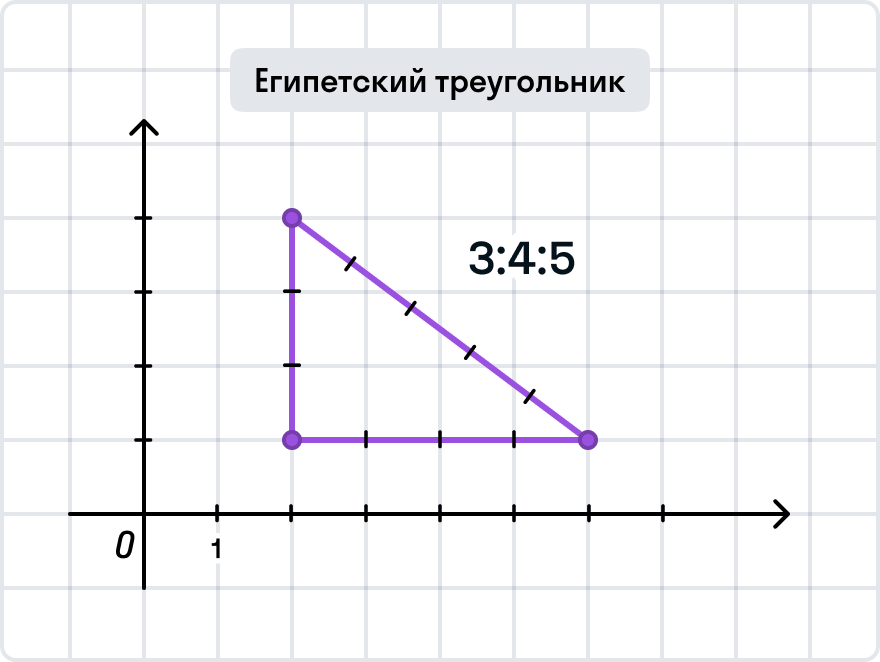
С этой точки зрения прямоугольные треугольники — лучшие друзья архитекторов, которые хотят строить ровные и красивые здания. Зодчие Древнего Египта использовали шнур или веревку, на которых через равные расстояния были завязаны 12 узлов. Строители натягивали такой шнур, создавая прямоугольный треугольник со сторонами 3, 4 и 5 единиц. Такой метод получения угла, равного 90 градусам, был сверхточным, а по сторонам-катетам-шнурам можно было выкладывать кирпичи или камни.

Удивлены? Еще больше поразительных фактов и, самое главное, помощь в понимании алгебры и геометрии вы получите на курсах профильной математики в онлайн-школе Skysmart. Секреты древних архитекторов, бытовые задачки и подготовка к экзаменам — все на удобной платформе с опытными учителями. Ждем вас!

Источник

ПЕРПЕНДИКУЛЯРНЫЙ

Смотреть что такое «ПЕРПЕНДИКУЛЯРНЫЙ» в других словарях:

перпендикулярный — перпендикул ярный; кратк. форма рен, рна … Русский орфографический словарь

Источник

ПЕРПЕНДИКУЛЯРНЫЙ

Смотреть что такое «ПЕРПЕНДИКУЛЯРНЫЙ» в других словарях:

перпендикулярный — перпендикул ярный; кратк. форма рен, рна … Русский орфографический словарь

Источник

перпендикулярный

Свернуть на перпендикулярную улицу.

Перпендикуля́рный взмах рук.

П-ое положение ног.

Смотреть что такое «перпендикулярный» в других словарях:

перпендикулярный — перпендикул ярный; кратк. форма рен, рна … Русский орфографический словарь

Источник

Основные свойства

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.

Определение перпендикулярности прямой и плоскости

Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.

Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:

В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.

Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:

В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.

Четырехмерная система координат и лемма

Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:

Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.

Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

Применение термина

Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.

В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.

Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.

Источник

перпендикулярно

Смотреть что такое «перпендикулярно» в других словарях:

перпендикулярно расположенный — перпендикулярно расположенный … Орфографический словарь-справочник

перпендикулярно смонтированный — перпендикулярно смонтированный … Орфографический словарь-справочник

перпендикулярно-отвесный — перпендикулярно отвесный … Орфографический словарь-справочник

перпендикулярно-поперечный — перпендикулярно поперечный … Орфографический словарь-справочник

перпендикулярно-продольный — перпендикулярно продольный … Орфографический словарь-справочник

Источник

Перпендикулярность

Содержание

На плоскости

Перпендикулярные прямые

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

Построение перпендикуляра

Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Координаты точки основания перпендикуляра к прямой

A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).

Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.

Во всех остальных случаях

xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.

В трёхмерном пространстве

Перпендикулярные прямые

Перпендикулярность прямой и плоскости

Перпендикулярные плоскости

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность прямой и гиперплоскости

Источник

Значение слова перпендикулярно

нареч. качеств.-обстоят.Располагаясь под прямым углом к чему-либо.

Большой современный толковый словарь русского языка

нареч. Соотносится по знач. с прил.: перпендикулярный (
2).

Новый толково-словообразовательный словарь русского языка Ефремовой

перпендикулярно нареч. Соотносится по знач. с прил.: перпендикулярный (
2).

Толковый словарь Ефремовой

составляя прямой угол с какой-либо прямой или плоскостью

Разговор шел о таких непонятных мне материях, как переход Сатурна в положение, перпендикулярное Луне, что сулило подлог и обман, и о чем свидетельствует нахождение уязвленного Нептуна в седьмом доме, а Марса опять-таки перпендикулярно его родному Меркурию в созвездии Девы.

Выберем начало координат в каком-либо узле и проведем оси координат – одну перпендикулярно к оси кристалла, по которой период равен a, вторую перпендикулярно к оси с периодом b.

На горизонтальной плоскости (рис. 16) она принимает вертикальное положение ( перпендикулярно оси х), а на профильной плоскости – горизонтальное ( перпендикулярно оси z).

Плазменный объект летел параллельно линиям механических напряжении отрыва и перпендикулярно линиям сжатия.

Поворотом своего мощного тела на девяносто градусов корабль становится к берегу перпендикулярно ; таким образом он фасом своим, взятым с носа, попадает точно против расщелины окружающих скал и рисуется во всю ширину своих боков ва чистом небесном фоне!

Виктор Степанович Черномырдин

Транслитерация: perpendikulyarno
Задом наперед читается как: онрялукиднепреп
Перпендикулярно состоит из 15 букв

Источник

Перпендикулярность в пространстве с примерами решения

Содержание:

Перпендикулярность в пространстве

В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свойство ортогональной проекции многоугольника.

Угол между прямыми в пространстве

Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает (рис. 33.1).

Угол между двумя параллельными прямыми считают равным 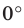Следовательно, если — угол между двумя прямыми, лежащими в одной плоскости, то .

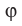
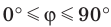
Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

Пусть прямые 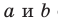скрещивающиеся. Через точку М пространства проведем прямые так, что (рис. 33.2). По определению угол между скрещивающимися прямыми равен углу между пересекающимися прямыми .

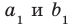
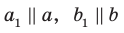
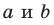
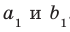
Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.

Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми 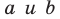равен углу между пересекающимися прямыми , где

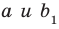
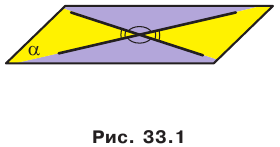
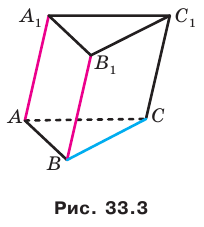
Например, на рисунке 33.3 изображена треугольная призма 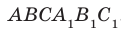. Угол между скрещивающимися прямыми и ВС равен углу между пересекающимися прямыми и ВС.

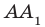
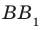
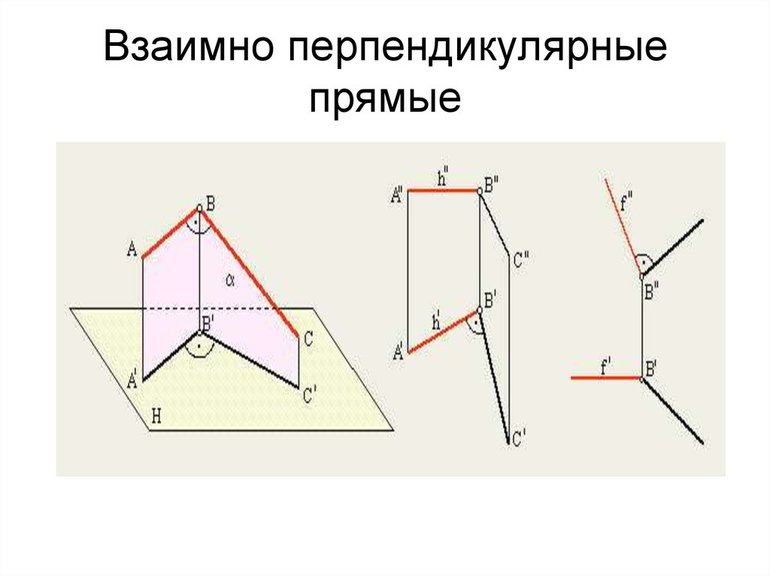
Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.

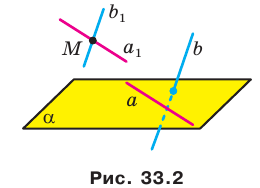
Если прямые 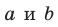перпендикулярны, то записывают: Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.

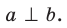
Например, ребра AD и 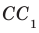куба перпендикулярны (рис. 33.4). Действительно, поскольку то угол между прямыми AD и равен углу между прямыми AD и . Но , поэтому .

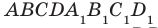
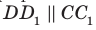
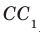
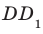
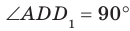
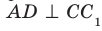
Пример:

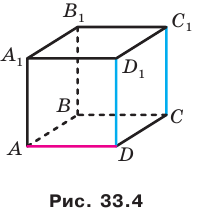
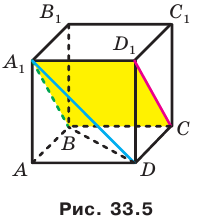
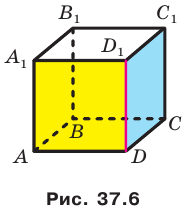
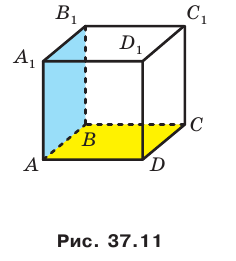
На рисунке 33.5 изображен куб 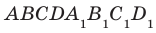. Найдите угол между прямыми и .

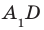
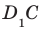
Решение:

Соединим точки 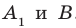. Поскольку , то точки лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости по параллельным прямым . Следовательно, угол между прямыми равен углу . Соединим точки В и D. Отрезки равны как диагонали равных квадратов. Следовательно, треугольник равносторонний. Тогда . Ответ : 60°.

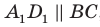
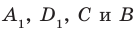
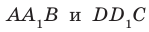
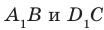
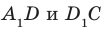
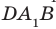
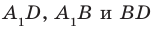
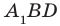
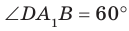
Перпендикулярность прямой и плоскости

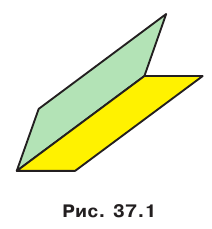
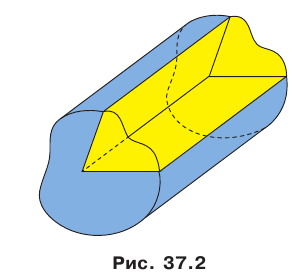
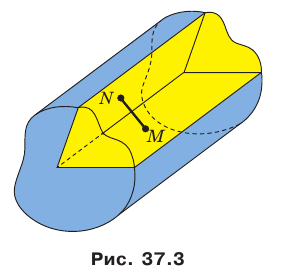
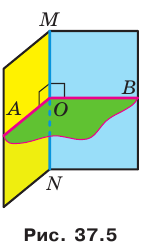
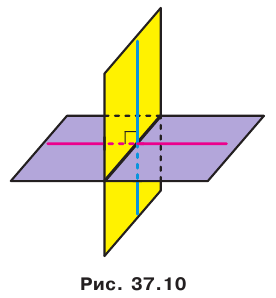
В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.

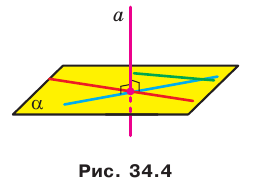
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).

Если прямая 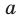перпендикулярна плоскости то записывают: Также принято говорить, что плоскость перпендикулярна прямой или прямая и плоскость перпендикулярны.

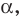
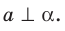
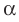
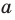
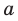
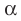
Из определения следует, что если прямая 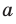перпендикулярна плоскости то она пересекает эту плоскость.

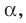
Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.

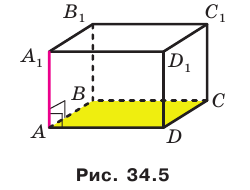
Например, интуитивно понятно, что ребро 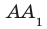прямоугольного параллелепипеда перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.

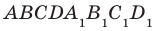
Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.

На рисунке 34.5 прямая 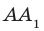перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпендикулярности прямой и плоскости а значит, и ребро также перпендикулярно плоскости АВС.

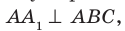
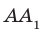
Приведем теорему, которую можно рассматривать как еще один признак перпендикулярности прямой и плоскости.

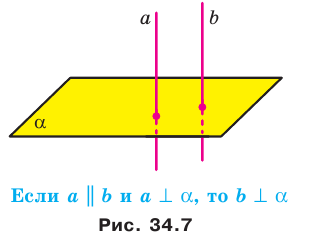
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).

Например, на рисунке 34.5 прямая 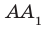перпендикулярна плоскости АВС, а прямая параллельна прямой . Следовательно, по теореме 34.2 прямая также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.

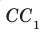
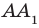
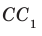
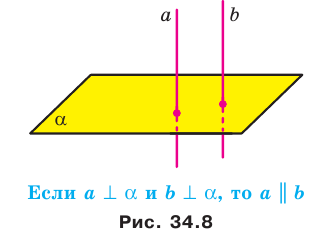
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.

Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Пример:

Плоскость 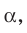перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а гипотенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.

Решение:

Поскольку прямая АС перпендикулярна плоскости 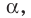то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому . Из этого следует, что треугольники AEF и подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.

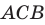
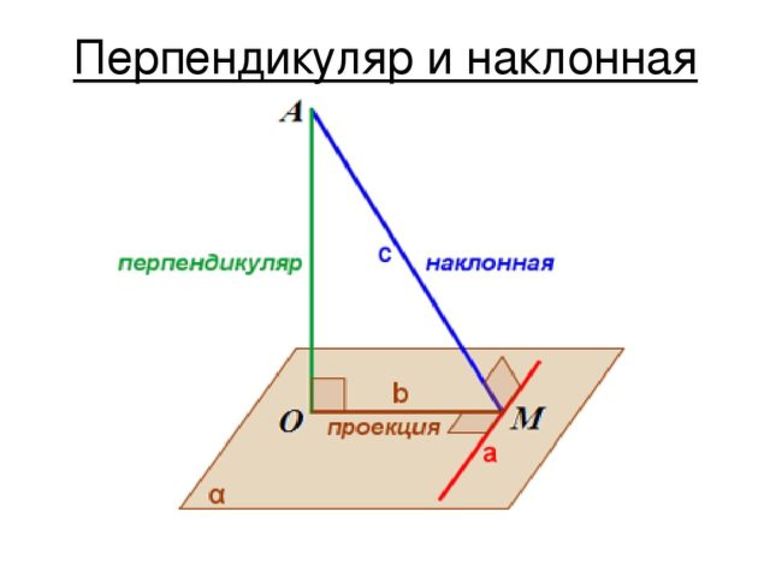
Перпендикуляр и наклонная

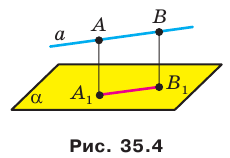
Пусть фигура 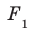— параллельная проекция фигуры F на плоскость в направлении прямой Если , то фигуру называют ортогональной проекцией фигуры F на плоскость

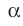
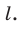
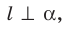
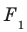
Например, основание ABCD прямоугольного параллелепипеда 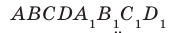является ортогональной проекцией основания на плоскость АВС в направлении прямой (рис. 35.1).

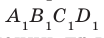
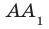
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.

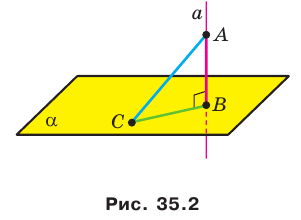
Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость .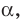

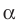
Отметим на плоскости 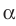какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.

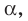
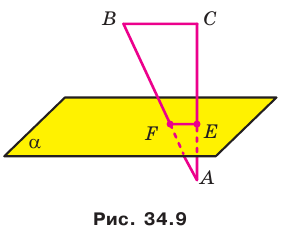
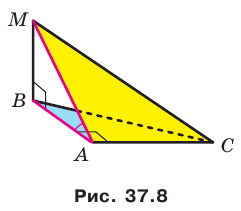
Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.

Пример:

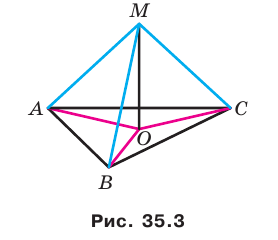
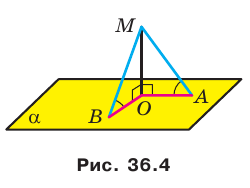
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.

Решение:

Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку 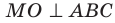, то . В прямоугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.

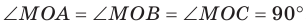
Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.

Определение. Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Пример:

Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.

Решение:

Пусть А и В — две произвольные точки прямой 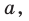параллельной плоскости Точки — основания перпендикуляров, опущенных соответственно из точек А и В на плоскость (рис. 35.4). Докажем, что .

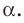
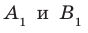
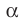
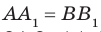
По теореме 34.3 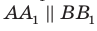. Следовательно, точки лежат в одной плоскости. Плоскость проходит через прямую параллельную плоскости и пересекает плоскость по прямой . Тогда по теореме 30.2 получаем: . Таким образом, в четырехугольнике каждые две противолежащие стороны параллельны. Следовательно, четырехугольник — параллелограмм. Отсюда Так как точки А и В выбраны на прямой произвольно, то утверждение задачи доказано.

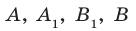
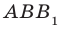
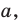
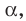
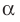
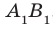
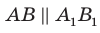
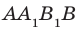
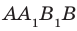
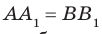
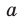
Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.

Пример:

Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.

Результаты, полученные в ключевых задачах 2 и 3, часто используют в практической деятельности, например в строительстве (рис. 35.5).

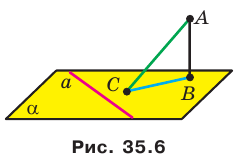
Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

Доказательство. Докажем первую часть теоремы.Пусть прямая 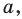принадлежащая плоскости перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что . Имеем: следовательно, . Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,. Поскольку то Доказательство второй части теоремы аналогично доказательству первой части.

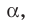
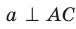
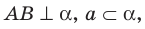
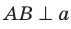
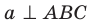
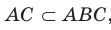
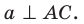
Пример:

Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.

Решение:

Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.

Отрезок ON является проекцией наклонной MN на плоскость АВС. По построению 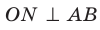. Тогда по теореме о трех перпендикулярах получаем:

Аналогично можно доказать, что 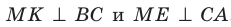. Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ.

В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.

Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.

Угол между прямой и плоскостью

Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.

Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.

Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.

Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен .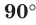

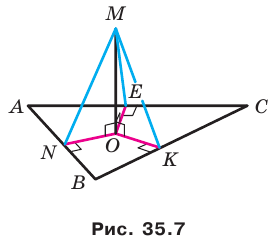
Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).

Из определения следует, что если 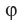— угол между прямой и плоскостью, то .

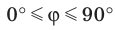
Также принято говорить, что прямая образует угол 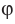с плоскостью.

Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.

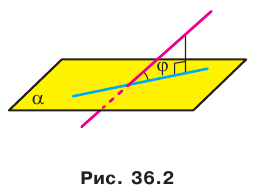
Например, рассмотрим куб 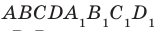(рис. 36.3). Угол между диагональю грани и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой на плоскость АВС. Тогда угол между прямой и плоскостью АВС равен величине угла . Поскольку четырехугольник — квадрат, то .

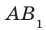
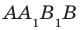
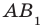
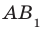
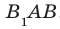
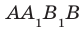
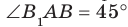
Пример:

Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.

Решение:

Пусть МЛ и М В — наклонные, образующие с плоскостью 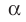равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.

Прямая ОА является проекцией прямой МА на плоскость 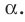Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью . Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью По условию .

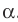
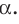
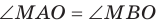
Поскольку 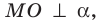то . Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда .

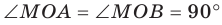
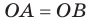
Двугранный угол. Угол между плоскостями

На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугранным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).

Отрезок MN принадлежит «желтому» двугранному углу, а «синему» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).

Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).

Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.

Отметим на ребре MN двугранного угла произвольную точку О. Через точку О в гранях двугранного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугранного угла. Поскольку 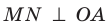и , то . Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.

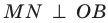
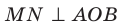
Определение. Величиной двугранного угла называют величину его линейного угла.

Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.

Например, рассмотрим куб 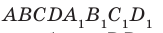(рис. 37.6). Двугранный угол с ребром , грани которого принадлежат плоскостям и является прямым. Действительно, поскольку и , то угол ADC — линейный угол двугранного угла с ребром .

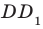
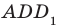
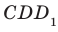
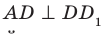
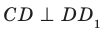
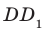
Угол ADC прямой.

При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:

В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.

Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.

Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.

Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.

Пример:

Прямоугольные треугольники 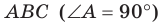и АВМ имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.

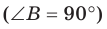
Решение:

Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как 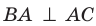, то по теореме о трех перпендикулярах . Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.

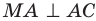
Для стороны AM прямоугольного треугольника АМС можно записать: 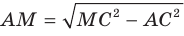. Отсюда . Для угла МАВ прямоугольного треугольника МАВ запишем: . Отсюда и . Ответ: 30°.

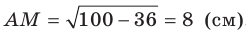
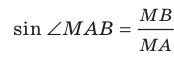
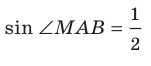
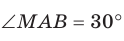
Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.

Теорема 37.1 (площадь ортогональной проекции многоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где .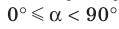

Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.

Если плоскости 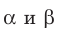перпендикулярны, то записывают: . Также принято говорить, что плоскость перпендикулярна плоскости или плоскость перпендикулярна плоскости .

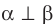
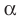
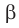
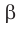
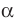
Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).

Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).

Теорема 37.2 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Например, плоскость грани 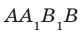прямоугольного параллелепипеда , (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость проходит через прямую , перпендикулярную плоскости АВС.

ГЛАВНОЕ В ПАРАГРАФЕ 5

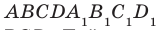
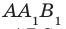
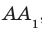
Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Перпендикулярность прямой и плоскости

Ортогональная проекция фигуры

Пусть фигура 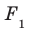— параллельная проекция фигуры F на плоскость в направлении прямой . Если , то фигуру называют ортогональной проекцией фигуры F на плоскость

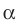
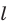
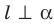
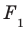
Расстояние от точки до плоскости

Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Расстояние от прямой до параллельной ей плоскости

Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.

Расстояние между двумя параллельными плоскостями

Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.

Теорема о трех перпендикулярах

Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

Угол между прямой и плоскостью

Величина двугранного угла

Величиной двугранного угла называют величину его линейного угла.

Угол между двумя пересекающимися плоскостями

Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.

Площадь ортогональной проекции многоугольника

Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где

Перпендикулярные плоскости

Две плоскости называют перпендикулярными, если угол между ними равен 90°.

Признак перпендикулярности плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник