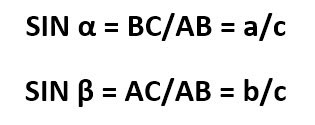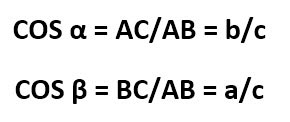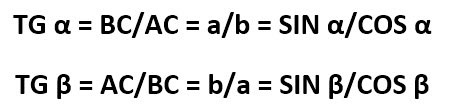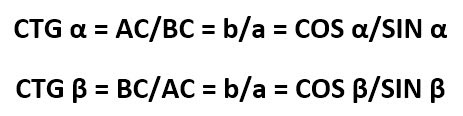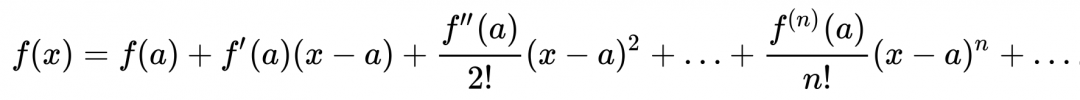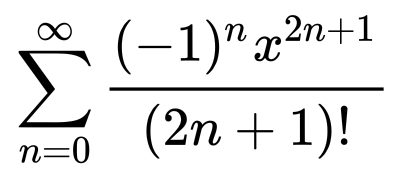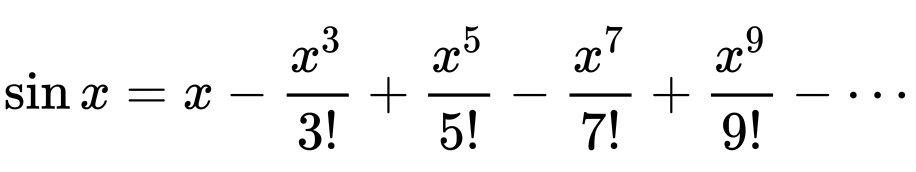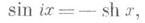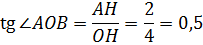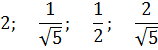Что такое синус угла

Что такое синус

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такие СИНУС.

Наверняка многие знают, что это понятие относится к математике. Все мы учились в школе и проходили тригонометрию.

С понятиями СИНУС, КОСИНУС, ТАНГЕНС и КОТАНГЕНС школьники знакомятся в 8 классе.

И сейчас без этих знаний не обойтись на ЕГЭ. И задачки по тригонометрии обязательно входят в программу тестов единого государственного экзамена.

Так что эта статья будет в первую очередь полезна старшеклассникам. А читателям более старшего возраста будет полезно лишний раз освежить давно забытые знания.

Что такое тригонометрия

Но давайте начнем совсем с азов. Раз уж мы сказали, что СИНУС – это некая тригонометрическая функция, давайте расскажем и что такое тригонометрия.

Тригонометрия – это раздел математики, который был основан еще в Древней Греции. Само слово состоит из двух половин «τρίγωνον» и «μετρέω», что можно дословно перевести как «изучение треугольников».

Впервые нечто похожее на тригонометрические функции появилось в Древней Греции. Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.

Хотя ученые не исключают, что похожими вычислениями пользовались и при строительстве Египетских пирамид. А это уже 2-2,5 тысячи лет до нашей эры.

И опять же, пирамиды ведь имеют треугольную форму (в плоскости). И тригонометрия связана напрямую с треугольниками. Возможно совпадение, а возможно и нет.

Правда, в тригонометрии рассматривают конкретные треугольники – прямоугольные. Напомним, это такие фигуры, у которых две стороны из трех пересекаются друг с другом под углом 90 градусов.

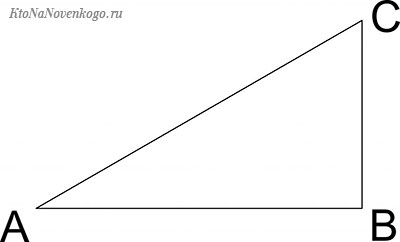
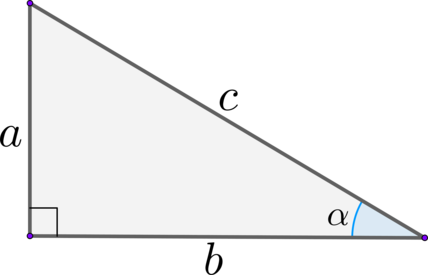
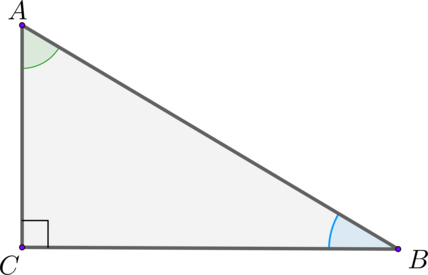
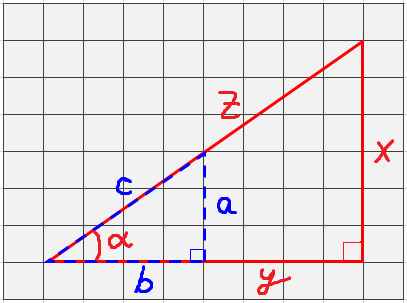
Выглядит такой треугольник вот так:

У такого треугольника стороны имеют определенные названия:

КАТЕТЫ – это стороны, которые пересекаются под прямым углом.

В нашем случае это стороны АВ и ВС. Это название также имеет древнегреческие корни. Так, слово «káthetos» переводится как «перпендикуляр, опущенный, ответственный».

ГИПОТЕНУЗА – сторона, которая идет под наклоном и соединяет между собой два катета.

В нашем случае это отрезок АС. Слово также родом из Древней Греции, «ὑποτείνουσα» означает «натянутая». И это очень хорошо характеризует этот отрезок, ведь он действительно выглядит как натянутая струна между двух опор. И даже если перевернуть треугольник, это ощущение не изменится.

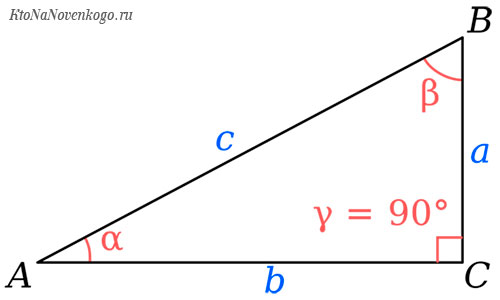
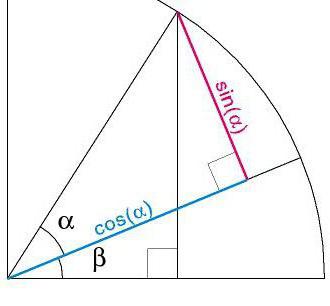
А вот теперь мы подобрались к самому главному, определению СИНУСА. Это величина не существует сама по себе. Она имеет отношение к какому-то углу треугольника. А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.

А вот теперь долгожданное определение:

СИНУС угла – это отношение противолежащего катета к гипотенузе.

Чтобы было понятно, о чем речь, взгляните еще раз на наш рисунок прямоугольного треугольника. В данном случае, противолежащим катетом к углу α будет сторона ВС. А противолежащим катетом к углу β будет сторона АС.

Соответственно, катет ВС для угла α будет прилежащим. И точно таким же будет катет ВС для угла β.

Конкретные формулы синусов будут такими:

Значения синусов

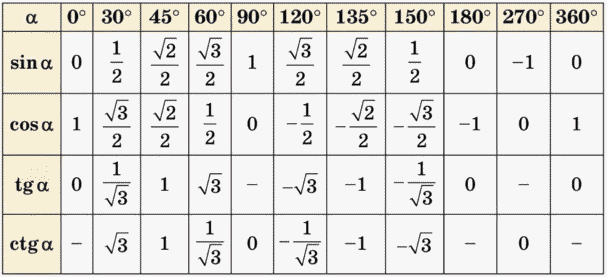
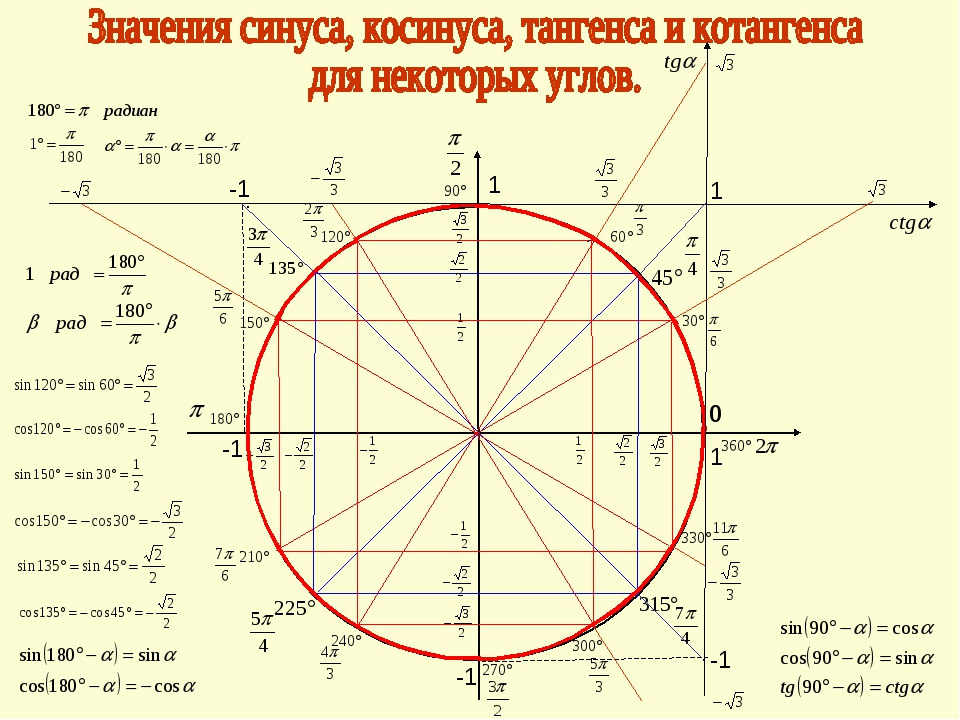
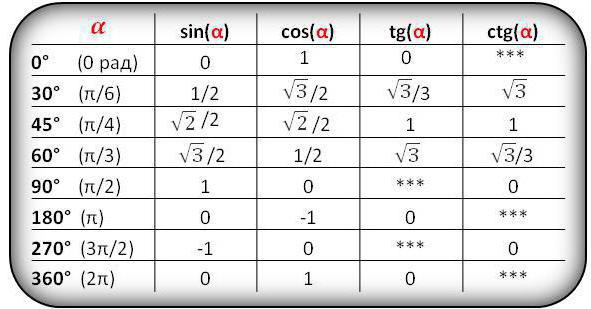
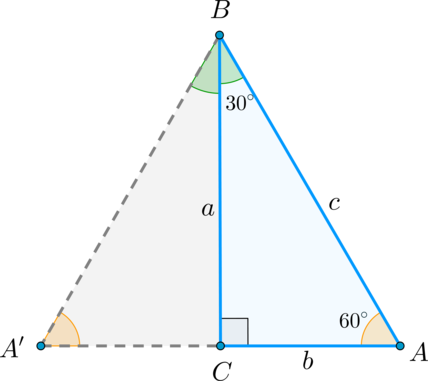
Чаще всего школьники имеют дело с определенными углами. Например, 30, 45, 60, 90 градусов и так далее. И чтобы не высчитывать каждый раз значение тригонометрических функций через стороны треугольника, есть уже готовые таблицы:

Вместо заключения

СИНУС – это не единственная тригонометрическая функция, которую проходят в школе. Есть еще и другие, и все они также связаны с прямоугольным треугольником.

А называются они вот так:

Вот и все, что мы хотели рассказать о тригонометрической функции СИНУС.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

Вот я вроде школу давно окончил, а вот все равно помню все. Потому что учили нас на совесть, а не спустя рукава. Вот скажите мне, а где в школах есть такое, что если ученик не понял, то учитель был готов потратить на него субботу и воскресенье чтобы объяснить дополнительно? Именно поэтому даже ярые троешники что-то знали.

Сейчас если ты в школе не понял, то все. Я дочери сам объяснял все по синусам, хотя и не учитель вообще. И кстати в современных учебниках материал очень плохо подан. Качаю старые советские, там куда понятнее. У вас кстати в статье хорошо рассказано. Я кстати в свое время так и запоминал, что это противоположный катет к гипотенузе.

Вспомнить никогда не будет лишним. Согласна с вами, Владимир, учили нам на совесть, спасибо нашим учителям.

«Соответственно, катет ВС для угла α будет прилежащим.»

Ошибка, для угла α прилежащим будет катет AC!

Источник

Что такое «Синус»? Определение слова «Синус» и его смысл

Синус (ударение на «и») это тригонометрическая функция, которая для острого угла в прямоугольном треугольнике определена как отношение противоилежащего катета к гипотенузе. Синус — родной брат косинуса и троюродный дядя тангенса.

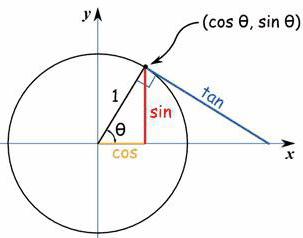
На системе с единичной окружностью синус центрального угла является ординатой (координатой y) точки на окружности, соответствующей этому углу. Синус обозначается латинскими буквами sin.

Синус острого угла в прямоугольном треугольнике принимает значения от 0 до 1, а на единичной окружности — от (-1) до 1. Аргумент синуса в прямоугольном треугольнике принимает значения от 0 до (π/2), а в случае с единичной окружностью он может быть любым рациональным числом, в том числе и отрицательным.

Синус и косинус связаны через теорему Пифагора следующей формулой. Для любого угла α выполняется:

sin 2 (α) + cos 2 (α) = 1

Примеры значений синуса для некоторых «знаменитых» углов:

Источник

Синус, косинус и тангенс острого угла прямоугольного треугольника

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы затронем изучение одного из важнейших разделов математики – тригонометрии. Тригонометрия является своеобразным мостиком между алгеброй и геометрией, поскольку в одинаковой степени важна и там, и там. На этом уроке мы начнём «строительство» этого мостика со стороны геометрии, то есть именно из того раздела математики, где впервые возникла задача, которая и привела к появлению тригонометрии. Чуть позже мы расширим понятие тригонометрических функций, а в старших классах узнаем об их «алгебраических корнях». Мы введём понятия синуса, косинуса и тангенса острого угла, изучим связь между этими величинами и докажем основное тригонометрическое тождество.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть уроки:

Источник

Как компьютер считает синусы

Два способа: готовые таблицы и точный расчёт

Это текст про математику и компьютеры. Если тема интересна, посмотрите также на математический тренажёр Практикума — он бесплатный и интерактивный.

А сейчас — про синусы.

Что такое синус и зачем он нужен?

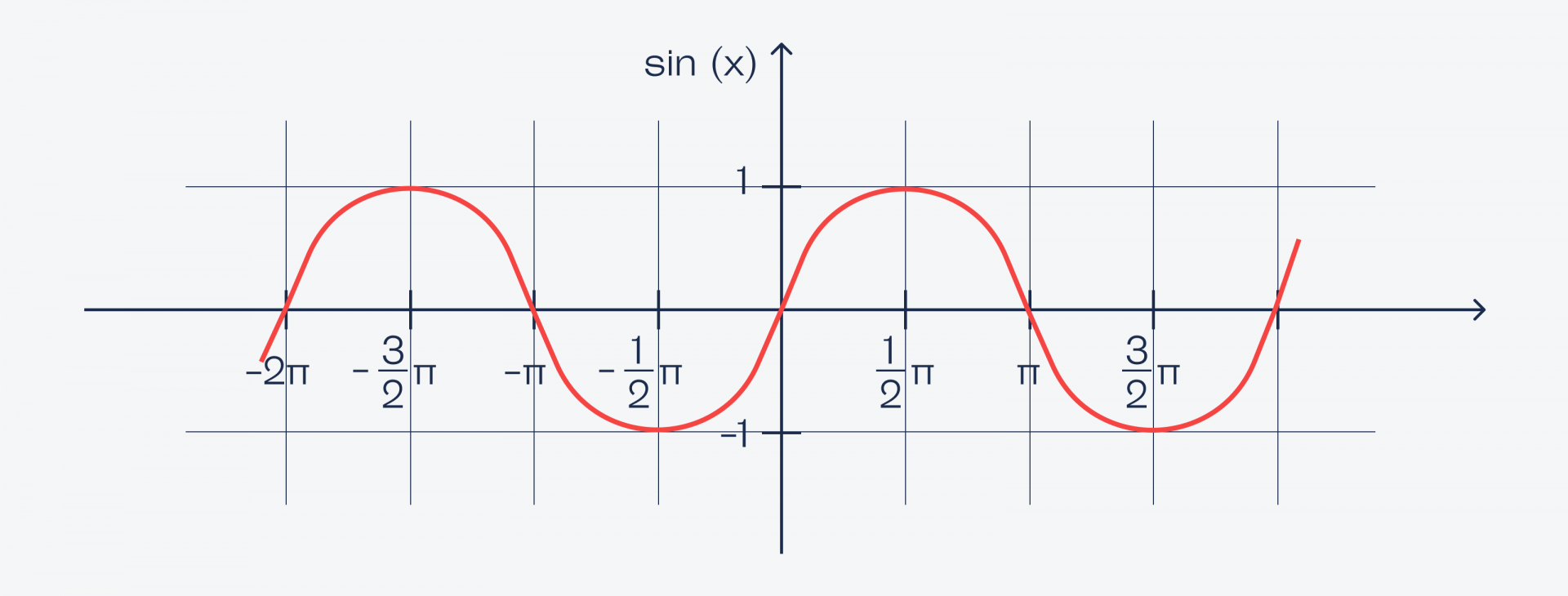
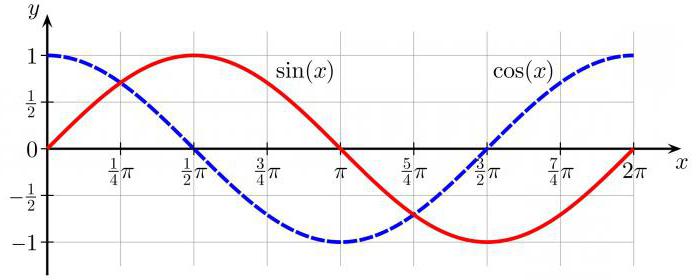
Вульгарное объяснение: синус — это математическая коробка, в которую засовывают любое число, а она в ответ выдаёт числа от −1 до 1. Если эти числа выстроить подряд на некой оси, то получится кривая вот такого вида:

Как читать эту кривую: если затолкать в коробку «sin» число, примерно равное 1,57, то коробка выдаст число, близкое к единице. Если затолкать число 2, на выходе будет примерно 0,909. Если затолкать примерно 3,14 — вернёт примерно 0. Синус от 4,712 даст примерно −0,999. И так дальше: число может быть сколько угодно большим, а синус всегда будет возвращать какие-то дробные значения от −1 до 1.

Это число взято из тригонометрии — то есть из науки, которая занимается углами и сторонами треугольника. В частности, синус описывает отношение сторон прямоугольного треугольника: насколько один из катетов (короткая сторона треугольника) короче, чем гипотенуза (длинная сторона треугольника). Но чаще всего мы знаем не длины сторон, а угол между ними, поэтому в синусы всегда запихивают значения углов.

Грубо говоря, вы говорите коробке: «Коробка, у меня тут прямоугольный треугольник. Я смотрю на его острый угол, он равен 30º. Что ты мне на это скажешь»? А коробка отвечает: «Если у тебя угол 30º, то короткая сторона твоего треугольника вдвое короче, чем длинная гипотенуза. Так что sin(30º) = ½».

Это число нужно много где в математике и компьютерах. Например, без синуса невозможно соединить две точки прямой линией на плоскости. Люди это делают без труда с помощью линейки, а компьютеру нужно очень чётко считать, куда поставить пиксель, и для этого нужен синус.

Помимо синуса есть ещё три аналогичные функции — косинус, тангенс и котангенс. Они такие же по принципу работы, но описывают отношения других сторон.

Во многих языках программирования есть встроенная команда нахождения синуса угла — sin(). Внутри этой функции зашита какая-то логика для нахождения этого числа.

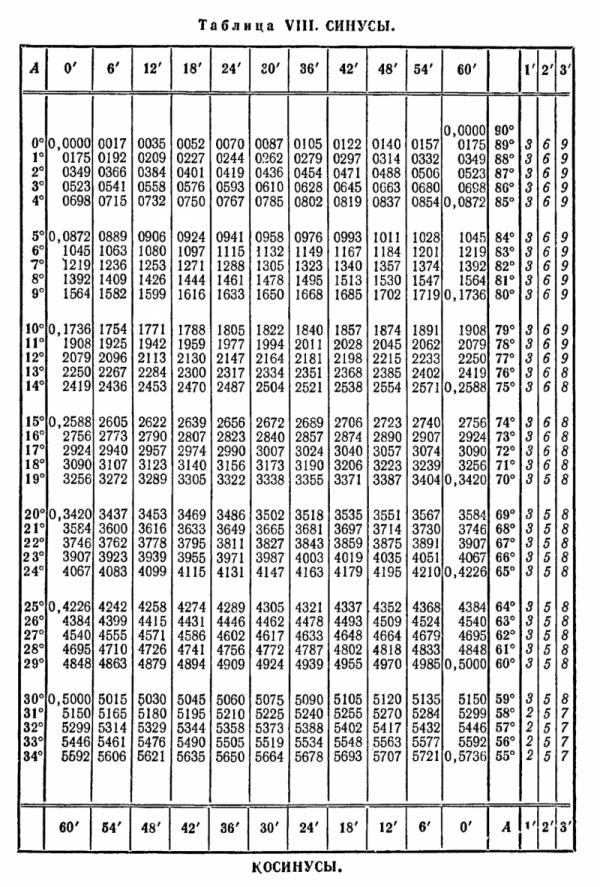
Чаще всего, когда не нужна высокая точность, компьютер берёт значения синуса из готовых таблиц — он находит там нужный угол и возвращает значение, ничего не вычисляя. Это быстро и достаточно точно для бытовых вычислений. Вы наверняка использовали его в школе, когда считали синусы по таблице Брадиса.

Но когда нужна высокая точность вычислений (например, 20 знаков после запятой), то синусы и другие тригонометрические функции высчитывают каждый раз с нуля. Для этого используют много разных алгоритмов, и самый простой из них — использование рядов Тейлора.

Таблица Брадиса, по которой компьютер находит значения синусов с точностью 4 знака после запятой

Что такое ряд Тейлора

Брук Тейлор — это английский математик из 17-го века, в честь которого назвали формулу, связывающую значение функции и значение всех её производных в выбранной точке. Если сильно упростить и перевести на понятный язык, то формула будет звучать так:

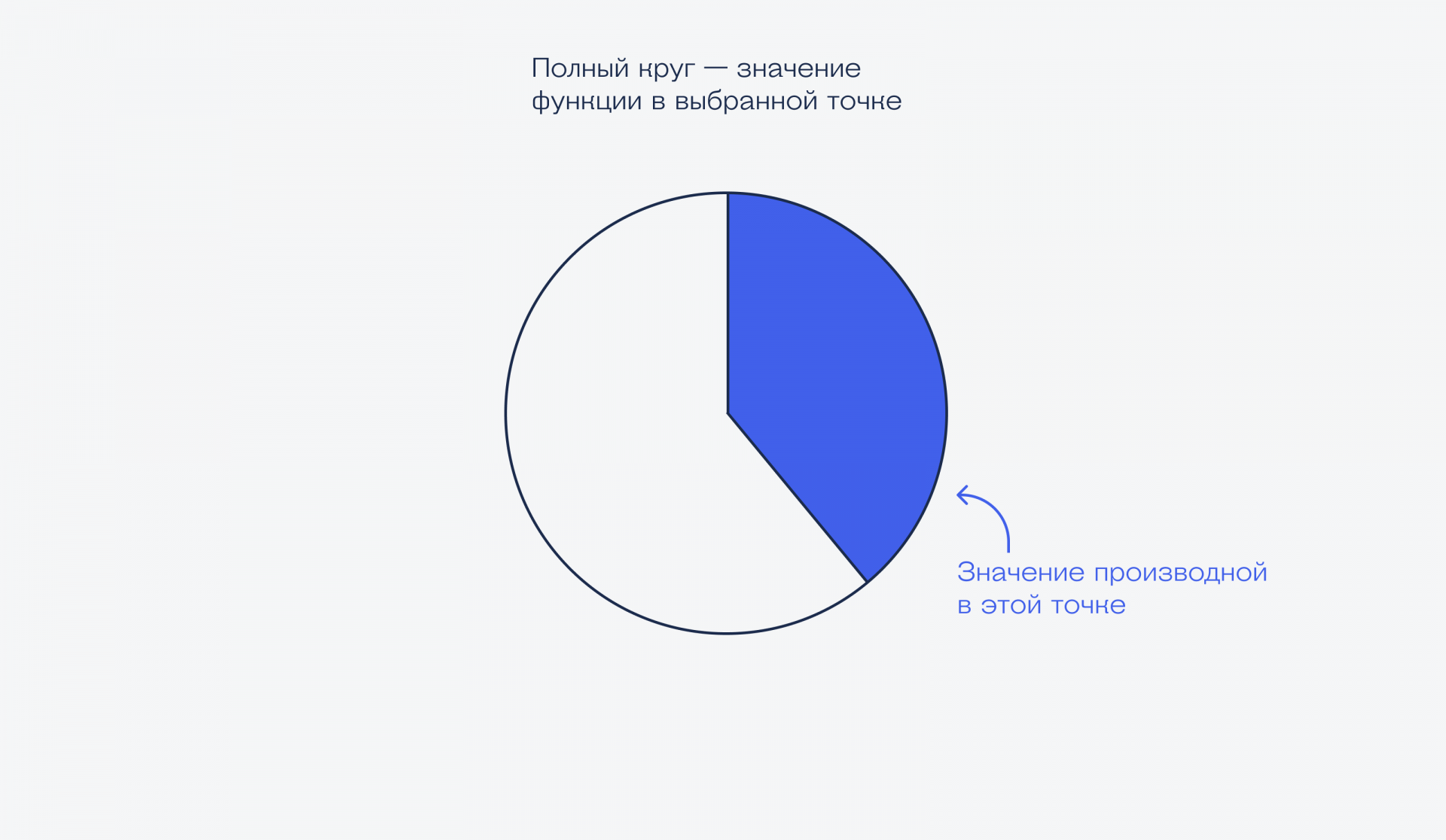
Представим, что значение функции, например, синуса — это круг, заполненный на 100%. Производная функции в этой точке — это часть круга:

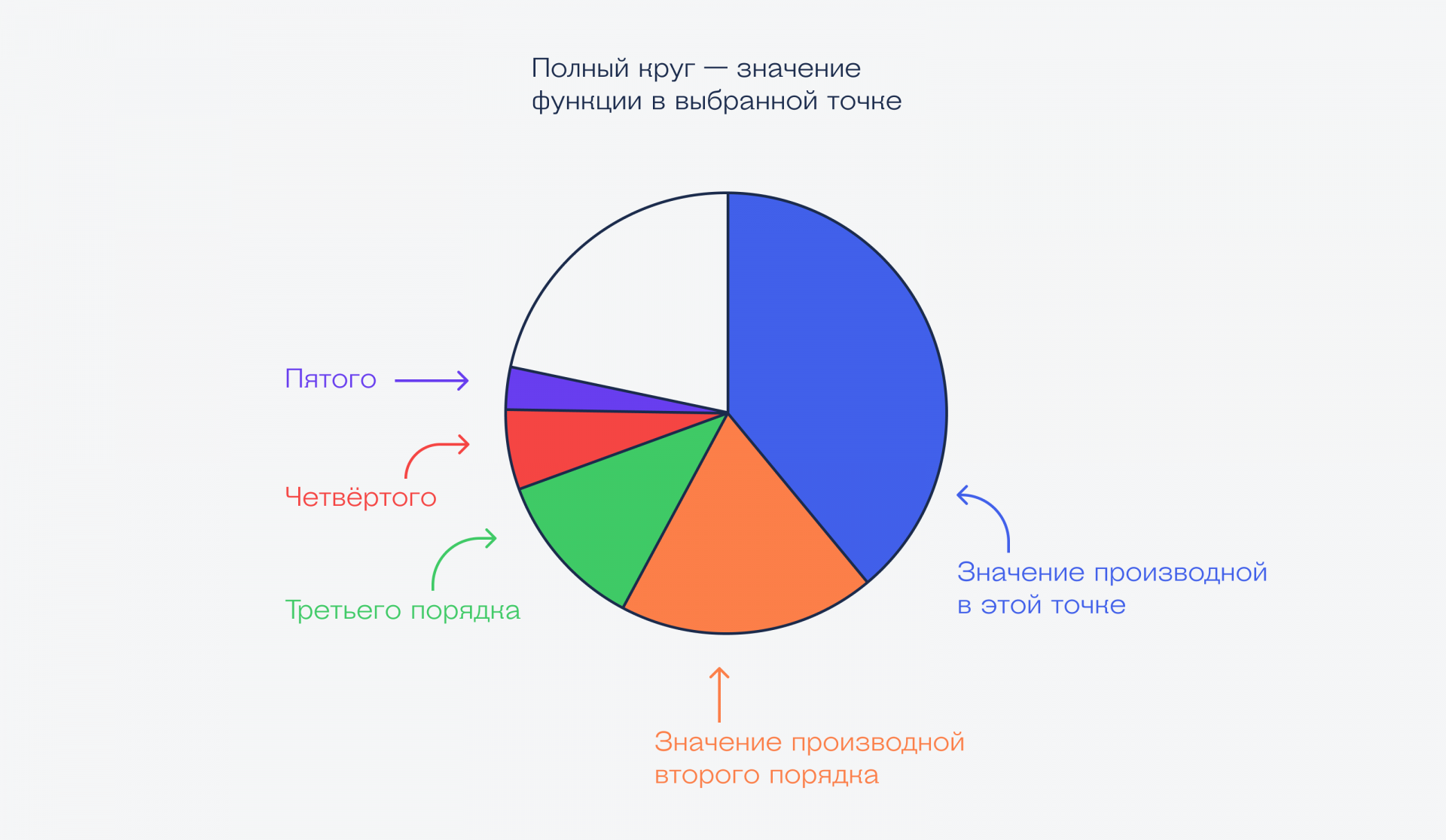
Есть производные первого порядка в этой точке, второго, третьего и так до бесконечности. Каждая производная следующего порядка добавляет в круг сектор поменьше:

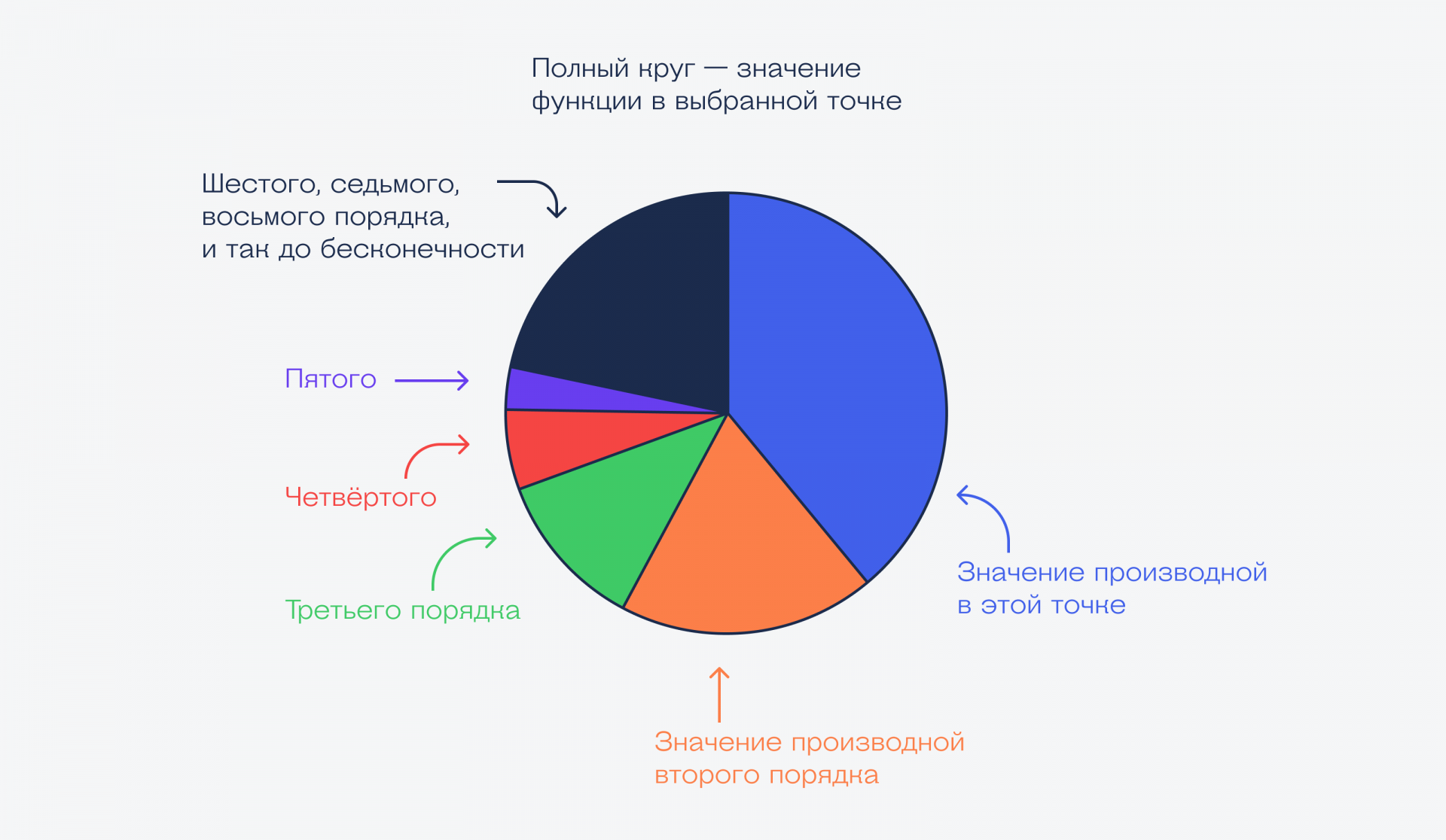
Если сложить все производные до бесконечности, то получим полный круг — это и будет значение синуса:

В общем виде ряд Тейлора функции выглядит так:

Для каждой функции ряд Тейлора выглядит по-своему. Для синуса он выглядит так:

Выглядит сложно. Но если разложить эту формулу сумму в понятный вид, она будет выглядеть так:

Восклицательный знак — это факториал. Это просто произведение всех целых чисел до этого числа. Например: 5! = 1 × 2 × 3 × 4 × 5 = 120.

Получается, что компьютеру для нахождения синуса достаточно использовать умножение — и для факториала, и для возведения в степень. Зная это, можно написать простой алгоритм.

Точность расчётов

Особенность ряда Тейлора в том, что это бесконечный ряд — а значит, и вычисления тоже придётся делать бесконечно. Чтобы обойти это ограничение, используют погрешность — с какой точностью нам нужно посчитать значение формулы. Для этого делают так:

С таким подходом можно найти синус любого угла с любой точностью, главное, чтобы у компьютера хватило памяти на все эти вычисления.

Радианы

Чтобы использовать ряд Тейлора для вычисления синуса, нам нужно перевести градусы в радианы. Радиан — это мера измерения углов в тригонометрии, которая привязана к числу π.

Радианы с углами связаны так:

1 радиан = 180/π градусов

Получается, что для того, чтобы перевести углы в градусах в радианы, нам нужно градусы разделить на 180 и умножить на π.

Теперь мы знаем всё, чтобы написать код вычисления синуса на Python

Пишем код

Логика алгоритма будет такая:

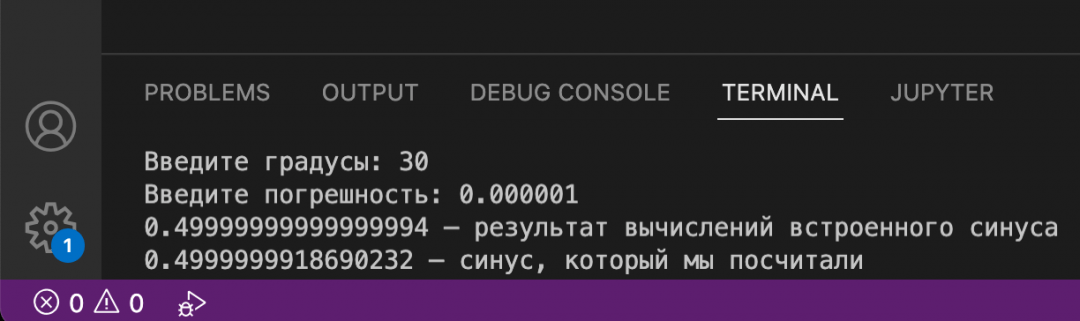
Читайте комментарии, чтобы разобраться в коде, а потом запустите его у себя, чтобы проверить результаты:

Что дальше

В следующий раз попробуем сделать то же самое с квадратным корнем — посмотрим, как компьютер сможет посчитать его без таблиц.

Источник

Тригонометрия

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Эта тема доставляет массу проблем ученикам. Считается одной из самых суровых. Что такое синус и косинус? Что такое тангенс и котангенс? Что такое числовая окружность? Стоит задать эти безобидные вопросы, как человек бледнеет и пытается увести разговор в сторону… А зря. Это простые понятия. И ничем эта тема не сложнее других. Просто нужно с самого начала чётко уяснить ответы на эти самые вопросы. Это очень важно. Если уяснили – тригонометрия вам понравится. Итак,

Что такое синус и косинус? Что такое тангенс и котангенс?

Начнём с глубокой древности. Не волнуйтесь, все 20 веков тригонометрии мы пройдём минут за 15. И, незаметно для себя, повторим кусочек геометрии из 8 класса.

Нарисуем прямоугольный треугольник со сторонами а, в, с и углом х. Вот такой.

Напомню, что стороны, которые образуют прямой угол, называются катетами. а и в – катеты. Их два. Оставшаяся сторона называется гипотенузой. с – гипотенуза.

Треугольник и треугольник, подумаешь! Что с ним делать? А вот древние люди знали, что делать! Повторим их действия. Измерим сторону в. На рисунке специально клеточки нарисованы, как в заданиях ЕГЭ бывает. Сторона в равна четырём клеточкам. Ладно. Измерим сторону а. Три клеточки.

А теперь поделим длину стороны а на длину стороны в. Или, как ещё говорят, возьмём отношение а к в. а/в = 3/4.

Можно наоборот, поделить в на а. Получим 4/3. Можно в поделить на с. Гипотенузу с по клеточкам не посчитать, но она равна 5. Получим в/с = 4/5. Короче, можно делить длины сторон друг на друга и получать какие-то числа.

Ну и что? Какой смысл в этом интересном занятии? Пока никакого. Бестолковое занятие, прямо скажем.)

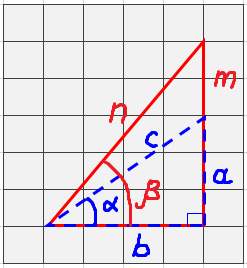
А вот их отношения – нет!

Отношение а/в было: а/в = 3/4, стало m/n = 6/8 = 3/4. Отношения других соответствующих сторон также не изменятся. Можно как угодно менять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, не меняя угла х – отношения соответствующих сторон не изменятся. Можно проверить, а можно поверить древним людям на слово.

А вот это уже очень важно! Отношения сторон в прямоугольном треугольнике никак не зависят от длин сторон (при одном и том же угле). Это настолько важно, что отношения сторон заслужили свои специальные названия. Свои имена, так сказать.) Знакомьтесь.

Что такое синус угла х? Это отношение противолежащего катета к гипотенузе:

Что такое косинус угла х? Это отношение прилежащего катета к гипотенузе:

Что такое тангенс угла х? Это отношение противолежащего катета к прилежащему:

Что такое котангенс угла х? Это отношение прилежащего катета к противолежащему:

Всё очень просто. Синус, косинус, тангенс и котангенс – это некоторые числа. Безразмерные. Просто числа. Для каждого угла – свои.

Зачем я так занудно всё повторяю? Затем, что это надо запомнить. Железно запомнить. Запоминание можно облегчить. Фраза «Начнём издалека…» знакома? Вот и начинайте издалека.

Синус угла – это отношение дальнего от угла катета к гипотенузе. Косинус – отношение ближнего к гипотенузе.

Тангенс угла – это отношение дальнего от угла катета к ближнему. Котангенс – наоборот.

Уже проще, правда?

Ну а если запомнить, что в тангенсе и котангенсе сидят только катеты, а в синусе и косинусе гипотенуза появляется, то всё станет совсем просто.

Можно ещё посчитать отношения гипотенузы к катетам. Эти отношения называются секанс и косеканс. Но они в школьном курсе не рассматриваются. И мы не будем. На радость ученикам.)

Всю эту славную семейку – синус, косинус, тангенс и котангенс называют ещё тригонометрическими функциями.

А теперь вопрос на соображение.

Почему мы говорим синус, косинус, тангенс и котангенс угла? Речь-то идёт об отношениях сторон, вроде. При чём здесь угол?

Смотрим на вторую картинку. Точно такую же, как и первая.

Наведите мышку на картинку. Я изменил угол х. Увеличил его с х до Х. Все отношения поменялись! Отношение а/в было 3/4, а соответствующее отношение t/в стало 6/4.

И все остальные отношения стали другими!

Существуют специальные таблицы, где для каждого угла расписаны его тригонометрические функции. Таблицы Брадиса называются. Они очень давно составлены. Когда ещё не было ни калькуляторов, ни компьютеров.

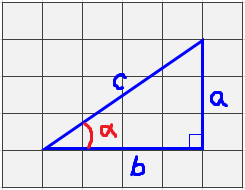
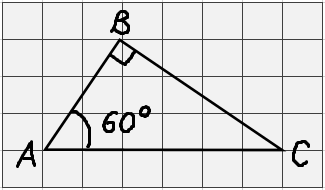
Вот мы и повторили кусочек геометрии из 8-го класса. Оно нам надо для ЕГЭ? Надо. Вот вам типичная задачка из ЕГЭ. Для решения которой достаточно 8-го класса. Дана картинка:

Всё. Больше никаких данных нет. Надо найти длину катета ВС.

Клеточки слабо помогают, треугольник как-то неправильно расположен. Специально, поди… Из информации есть длина гипотенузы. 8 клеток. Ещё зачем-то дан угол.

Вот здесь надо сразу вспоминать про тригонометрию. Есть угол, значит, мы знаем все его тригонометрические функции. Какую функцию из четырёх в дело пустить? А посмотрим-ка, что нам известно? Нам известны гипотенуза, угол, а найти надо прилежащий к этому углу катет! Ясно дело, косинус нужно в дело запускать! Вот и запускаем. Просто пишем, по определению косинуса (отношение прилежащего катета к гипотенузе):

Угол С у нас 60 градусов, его косинус равен 1/2. Это знать надо, безо всяких таблиц! Стало быть:

Элементарное линейное уравнение. Неизвестное – ВС. Кто подзабыл, как решать уравнения, прогуляйтесь по ссылке, остальные решают:

Это и есть верный ответ.

Когда древние люди поняли, что у каждого угла имеется свой комплект тригонометрических функций, у них возник резонный вопрос. А не связаны ли как-нибудь синус, косинус, тангенс и котангенс между собой? Так, чтобы зная одну функцию угла, можно было найти остальные? Не вычисляя сам угол?

Вот такие они были неугомонные. )

Связь между тригонометрическими функциями одного угла.

Эти формулы надо знать железно. Без них вообще в тригонометрии делать нечего. Из этих основных тождеств вытекают ещё три вспомогательных тождества:

Сразу предупреждаю, что три последние формулы быстро выпадают из памяти. Почему-то.) Можно, конечно, вывести эти формулы из первых трёх. Но, в трудную минуту. Сами понимаете.)

Задачка почти элементарная. Ищем формулу, где имеются синус и косинус. Вот она эта формула:

sin 2 x + cos 2 x = 1

Подставляем сюда известную величину, а именно, 0,8 вместо косинуса:

sin 2 x + 0,8 2 = 1

Ну и считаем, как обычно:

sin 2 x + 0,64 = 1

Вот, практически и всё. Мы вычислили квадрат синуса, осталось извлечь квадратный корень и ответ готов! Корень из 0,36 будет 0,6.

Собственно, восьмиклассникам такие тонкости не нужны. Они работают только с прямоугольными треугольниками, где углы могут быть только острые. И не знают, счастливые, что бывают и отрицательные углы, и углы в 1000°. И у всех этих кошмарных углов есть свои тригонометрические функции и с плюсом, и с минусом.

Или как-нибудь иначе. В примерах ниже увидите.) Для решения таких примеров нужно знать, в какую четверть попадает заданный угол х и какой знак имеет нужная тригонометрическая функция в этой четверти.

Итак, отметим самое главное:

1. Запомните определения синуса, косинуса, тангенса и котангенса. Очень пригодится.

А теперь порешаем, как водится. Сначала задания в объёме 8-го класса. Но и старшеклассникам тоже можно. )

1. Вычислить значение tgА, если ctgА = 0,4.

3. Определить синус острого угла х, если tgх = 4/3.

4. Найти значение выражения:

5. Найти значение выражения:

(1-cosx)(1+cosx), если sinх = 0,3

Ответы (через точку с запятой, в беспорядке):

Получилось? Отлично! Восьмиклассники могут уже пройти за своими пятёрками.)

Не всё получилось? Задания 2 и 3 как-то не очень. Не беда! Есть один красивый приём для подобных заданий. Всё решается, практически, вообще без формул! Ну и, следовательно, без ошибок. Этот приём в уроке: «Связь между тригонометрическими функциями одного угла» в Разделе 555 описан. Там же разобраны и все остальные задания.

6. Найти значение tgβ, если sinβ = 12/13, а

8. Найти значение выражения sinβ·cosβ, если ctgβ = 1.

Ответы (в беспорядке):

А если не решили? Гм. Ну, тут Раздел 555 поможет. Там решения всех этих заданий подробно расписаны, трудно не разобраться.

В этом уроке дано очень ограниченное понятие тригонометрических функций. В пределах 8-го класса. А у старших остаются вопросы.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Что такое синус?

Тригонометрия является разделом математики, изучающим тригонометрические функции, а также их использование на практике. К таким функциям относятся синус, косинус, тангенс и котангенс.

Синус – это тригонометрическая функция, отношение величины противолежащего катета к величине гипотенузы.

Синус в тригонометрии.

Как уже сказано выше, синус имеет непосредственное отношение к тригонометрии и тригонометрическим функциям. Его функция определяется тем, чтобы

Необходимо помнить, что величина синуса будет всегда одинакова для любых размеров треугольника, поскольку синус – это не измерение, а соотношение.

Следовательно, для того чтобы не высчитывать эту постоянную величину при каждом решении той или иной задачи, были созданы специальные тригонометрические таблицы. В них величины синусов, косинусов, тангенсов и котангенсов уже просчитаны и закреплены. Обычно эти таблицы приводятся на форзаце учебников по алгебре и геометрии. Также их можно найти в Интернете.

Синус в геометрии.

Геометрия требует наглядности, поэтому, чтобы понять на практике, что такое синус угла, нужно нарисовать треугольник с прямым углом.

Допустим, что стороны, образующие прямой угол, названы а, в, противоположный им угол – х.

Обычно в заданиях указана длина сторон. Допустим, а=3, в=4. В таком случае соотношение сторон будет выглядеть как ¾. При этом если удлинить стороны треугольника, прилегающие к острому углу х, то увеличатся и стороны а и в, и гипотенуза – третья сторона прямоугольного треугольника, лежащая не под прямым углом к основанию. Теперь стороны треугольника можно назвать иначе, допустим: m, n, k.

При этом видоизменении сработал закон тригонометрии: длины сторон треугольника изменились, а их отношение – нет.

Тот факт, что при изменении длины сторон треугольника во сколько угодно раз и при сохранении величины угла х, соотношение между его сторонами всё равно останется неизменным, заметили ещё древние ученые. В нашем случае длина сторон могла измениться так: а/в = ¾, при удлинении стороны а до 6 см, а в – до 8 см получаем: m/n = 6/8 = 3/4.

Соотношения сторон в прямоугольном треугольнике в связи с этим получили названия:

Источник

Что такое синус?

Тригонометрия является разделом математики, изучающим тригонометрические функции, а также их использование на практике.

К таким функциям относятся синус, косинус, тангенс и котангенс.

Синус – это тригонометрическая функция, отношение величины противолежащего катета к величине гипотенузы. Синус в тригонометрии.

Как уже сказано выше, синус имеет непосредственное отношение к тригонометрии и тригонометрическим функциям. Его функция определяется тем, чтобы помогать высчитать угол, при условии известности величин сторон треугольника; помогать высчитать величины стороны треугольника, при условии известности угла. Необходимо помнить, что величина синуса будет всегда одинакова для любых размеров треугольника, поскольку синус – это не измерение, а соотношение.

Следовательно, для того чтобы не высчитывать эту постоянную величину при каждом решении той или иной задачи, были созданы специальные тригонометрические таблицы. В них величины синусов, косинусов, тангенсов и котангенсов уже просчитаны и закреплены. Обычно эти таблицы приводятся на форзаце учебников по алгебре и геометрии.

Синус в геометрии.

Геометрия требует наглядности, поэтому, чтобы понять на практике, что такое синус угла, нужно нарисовать треугольник с прямым углом. Допустим, что стороны, образующие прямой угол, названы а, в, противоположный им угол – х.

Обычно в заданиях указана длина сторон. Допустим, а=3, в=4. В таком случае соотношение сторон будет выглядеть как ¾. При этом если удлинить стороны треугольника, прилегающие к острому углу х, то увеличатся и стороны а и в, и гипотенуза – третья сторона прямоугольного треугольника, лежащая не под прямым углом к основанию.

Теперь стороны треугольника можно назвать иначе, допустим: m, n, k.

При этом видоизменении сработал закон тригонометрии: длины сторон треугольника изменились, а их отношение – нет. Тот факт, что при изменении длины сторон треугольника во сколько угодно раз и при сохранении величины угла х, соотношение между его сторонами всё равно останется неизменным, заметили ещё древние ученые.

В нашем случае длина сторон могла измениться так: а/в = ¾, при удлинении стороны а до 6 см, а в – до 8 см получаем: m/n = 6/8 = 3/4.

Соотношения сторон в прямоугольном треугольнике в связи с этим получили названия:

синус угла х – это отношение противолежащего катета к гипотенузе: sinx = а/с;

косинус угла х – это отношение прилежащего катета к гипотенузе: сosx = в/с;

тангенс угла х – это отношение противолежащего катета к прилежащему: tgx = а/в;

котангенс угла х – это отношение прилежащего катета к противолежащему: ctgx = в/а.

Источник

СИНУС

(sin x)’ = cos x. Интеграл от С.:

С. разлагается в степенной ряд:

Функция, обратная С., наз. арксинусом. С. и косинус комплексного аргумента z связаны с показательной функцией формулами Эйлера

Смотреть что такое «СИНУС» в других словарях:

СИНУС — (лат.). Тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СИНУС в тригонометрии… … Словарь иностранных слов русского языка

СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь

СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов

СИНУС — (sine) Соотношение в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой. Синус угла х пишется как sin x. Если описывается круг единичного радиуса, измерение углов начинается с востока против часовой стрелки; sin x –… … Экономический словарь

СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Синус, косинус, тангенс и котангенс в тригонометрии: определения, примеры

В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии. Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.

Навигация по странице.

Определение синуса, косинуса, тангенса и котангенса

Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.

Острого угла в прямоугольном треугольнике

Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.

Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.

Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.

Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.

Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.

Угла поворота

В заключение этого пункта стоит заметить, что в разговоре про синус, косинус, тангенс и котангенс угла поворота часто опускают словосочетание «угол поворота» или слово «поворота». То есть, вместо фразы «синус угла поворота альфа» обычно используют фразу «синус угла альфа» или еще короче – «синус альфа». Это же касается и косинуса, и тангенса, и котангенса.

Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0 до 90 градусов. Это мы обоснуем в последнем пункте этой статьи.

Числа

Дальше возникает потребность отвязаться от углов и дать определения синуса, косинуса, тангенса и котангенса числа, а не угла.

Синусом, косинусом, тангенсом и котангенсом числа t называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t радианов соответственно.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки. Остановимся на этом подробнее.

Покажем, как устанавливается соответствие между действительными числами и точками окружности:

Тригонометрические функции углового и числового аргумента

Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями.

Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла (угловым аргументом), так и числовым аргументом.

Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов.

Связь определений из геометрии и тригонометрии

Если рассматривать угол поворота α величиной от 0 до 90 градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии. Обоснуем это.

Источник

Что такое синус, косинус, тангенс, котангенс

Рассмотрим окружность, центр которой совпадает с центром координат, а радиус равен ОА:

Повернув радиус ОА против часовой стрелки, получим некий угол АОВ. Такой угол называется положительным (на рисунке выделен синим цветом).

Повернув радиус ОА по часовой стрелке, получим угол АОК. Такой угол называется отрицательным (на рисунке выделен желтым цветом).

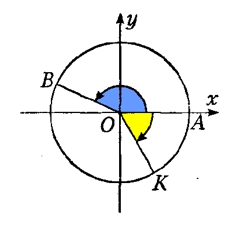
Теперь возьмем некий положительный угол АОВ, полученный поворотом радиуса ОА против часовой стрелки на некоторый угол α (закрашен желтым цветом):

Синусом угла AOB (или α) называют отношение ординаты точки В (отрезок ОК=ВС) к длине радиуса ОВ:

Косинусом угла AOB (или α) называют отношение абсциссы точки В (отрезок ОС) к длине радиуса ОВ:

Тангенсом угла АОВ называют отношение синуса этого угла к его косинусу:

Котангенсом угла АОВ называют отношение косинуса этого угла к его синусу:

Поскольку, в формулах тангенса и котангенса присутствует деление, то тангенс и котангенс не всегда можно определить, поскольку на ноль делить нельзя.

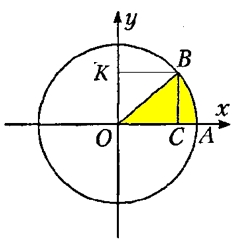
Учитывая изложенное обстоятельство, определения синуса, косинуса, тангенса и котангенса угла α прямоугольного треугольника СОВ будут формулироваться следующим образом:

В таком случае, для вершины В, расположенной на окружности с единичным радиусом, можно сказать, что:

Следует запомнить значения синуса, косинуса, тангенса и котангенса для «стандартных» углов, которые будут встречаться наиболее часто в дальнейшем:

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

Синус

Смотреть что такое «Синус» в других словарях:

СИНУС — (лат.). Тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СИНУС в тригонометрии… … Словарь иностранных слов русского языка

СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь

СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов

СИНУС — (sine) Соотношение в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой. Синус угла х пишется как sin x. Если описывается круг единичного радиуса, измерение углов начинается с востока против часовой стрелки; sin x –… … Экономический словарь

СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Значение слова «синус»

1. Мат. Одна из тригонометрических функций угла в прямоугольном треугольнике, равная отношению катета противолежащего угла к гипотенузе.

2. Анат. Полость, пазуха. Синусы лимфатических сосудов. Синусы мозга.

[От лат. sinus — изгиб, кривизна]

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

си́нус

1. матем. тригонометрическая функция угла, равная соотношению в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой ◆ Синус и косинус 45 градусов равны.

2. анат. полость в некоторых органах тела ◆ Синусит — это воспаление лобных синусов.

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова сагитированный (прилагательное):

Источник

Как пишется синус угла

Таблица синусов и как ей пользоваться – с примерами решения задач

Одной из самых часто используемых из всех тригонометрических таблиц Брадиса, является таблица синусов. В этой статье мы разберемся с таким понятием, как синус (sin), научимся находить значения синуса для различных углов (0, 30, 45, 60, 90), и поймем, для чего нужна таблица синусов.

Таблица синусов и её применение

Для начала нужно напомнить, что означает такое понятие, как синус угла.

Синус – это отношение противолежащего этому углу катета к гипотенузе.

Это справедливо в случае, если треугольник прямоугольный.

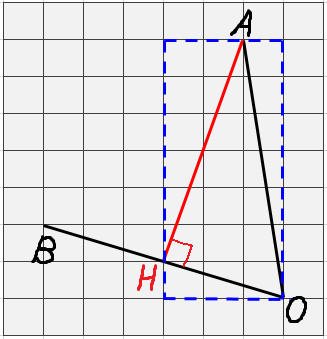
Пример: найдем синус угла ⍺ и угла β
sin ⍺ = а/с или отношение стороны ВС к стороне АВ. Если брать угол β, то противостоящим будет считаться сторона b или АС. Гипотенуза в данном случае та же – AB. Тогда:
sin β = b/с или АС отношение АВ.

В прямоугольном треугольнике всегда 2 катета и только одна гипотенуза

Как известно, целых значений угла – 360. Но часто нужно рассчитать значения для самых популярных углов, таких как: синус 0°, синус 30°, синус 45°, синус 60°, синус 90°. Эти значения можно найти в таблицах Брадиса.

Несмотря на то, что в 2021 году она отмечает свой столетний юбилей, свою актуальность таблица Брадиса не утратила. В частности ее применяют архитекторы, проектанты, конструктора для проведения быстрых промежуточных расчетов. Таблицы Брадиса разрешены к использованию в школах при сдаче ЕГЭ, в отличие от калькуляторов.

Как рассчитать синус угла

Некоторые значения синуса угла можно рассчитать достаточно просто, воспользовавшись таблицей синусов угла π (пи) в радианах.

Но часто нужно решить задачу для каких то либо целей, при котором значения углов будут другими. Посмотрим пример решения такой задачи.

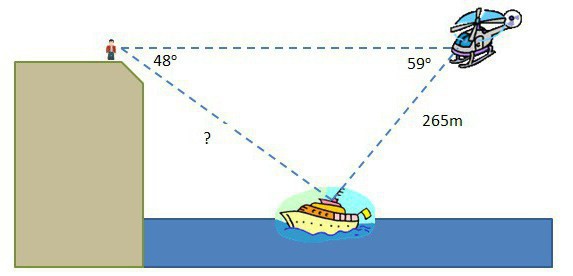
Её можно использовать в случае, если у нас известна гипотенуза треугольника и два угла или один из катетов. Тогда в соответствии с правилами пропорции находим:

Что найти синус угла, к примеру: α = 42°, угол β =48 °, открываем таблицу Брадиса. Так как у нас углы без минут, находим значение синуса угла по первой колонке. Sin α = 0,6691, sin β = 0,7431. Пусть в условии сторона с = 9 см, Синус 90° = 1. Подставляем значение и получаем: а = 9 х (0,6691: 1) = 6, 0219 (см).

Что такое таблица синусов π и таблица Брадиса

В таблице синусов значение угла α дается в:

Это таблица не только для синусов, но и для других тригонометрических знаков.

Как пользоваться таблицей Брадиса для синусов

Если у вас стоит вопрос, как пользоваться таблицей Брадиса, для нахождения синуса угла, рассмотрим такой пример.

Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Синус, косинус и тангенс острого угла прямоугольного треугольника.
Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Это тема не сложная, главное это запомнить правила. И так начнем:
Вспомним, что такое прямоугольный треугольник?
Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.

Определение:
Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;

Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;
Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;
tg(a)=sin(a)/cos(a)
Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;
ctg(a)=cos(a)/sin(a)
Рассмотрим на примере:
Пусть дан прямоугольный треугольник ABC с прямым углом C.
sin(a)=BC/AB
cos(a)=AC/AB
tg(a)=BC/AC
ctg(a)=AC/BC

Таблица СИНУСОВ для углов от 0° до 360° градусов

СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.

Малая таблица значений тригонометрических функций (в радианах и градусах)α (радианы)0π/6π/4π/3π/2π√3π/22πα (градусы)0°30°45°60°90°180°270°360°SIN α (СИНУС)01/2√ 2/2√3 /210-10Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°Угол в градусахSin (Синус)0°01°0.01752°0.03493°0.05234°0.06985°0.08726°0.10457°0.12198°0.13929°0.156410°0.173611°0.190812°0.207913°0.22514°0.241915°0.258816°0.275617°0.292418°0.30919°0.325620°0.34221°0.358422°0.374623°0.390724°0.406725°0.422626°0.438427°0.45428°0.469529°0.484830°0.531°0.51532°0.529933°0.544634°0.559235°0.573636°0.587837°0.601838°0.615739°0.629340°0.642841°0.656142°0.669143°0.68244°0.694745°0.707146°0.719347°0.731448°0.743149°0.754750°0.76651°0.777152°0.78853°0.798654°0.80955°0.819256°0.82957°0.838758°0.84859°0.857260°0.86661°0.874662°0.882963°0.89164°0.898865°0.906366°0.913567°0.920568°0.927269°0.933670°0.939771°0.945572°0.951173°0.956374°0.961375°0.965976°0.970377°0.974478°0.978179°0.981680°0.984881°0.987782°0.990383°0.992584°0.994585°0.996286°0.997687°0.998688°0.999489°0.999890°1Угол в градусахSin (Синус)91°0.999892°0.999493°0.998694°0.997695°0.996296°0.994597°0.992598°0.990399°0.9877100°0.9848101°0.9816102°0.9781103°0.9744104°0.9703105°0.9659106°0.9613107°0.9563108°0.9511109°0.9455110°0.9397111°0.9336112°0.9272113°0.9205114°0.9135115°0.9063116°0.8988117°0.891118°0.8829119°0.8746120°0.866121°0.8572122°0.848123°0.8387124°0.829125°0.8192126°0.809127°0.7986128°0.788129°0.7771130°0.766131°0.7547132°0.7431133°0.7314134°0.7193135°0.7071136°0.6947137°0.682138°0.6691139°0.6561140°0.6428141°0.6293142°0.6157143°0.6018144°0.5878145°0.5736146°0.5592147°0.5446148°0.5299149°0.515150°0.5151°0.4848152°0.4695153°0.454154°0.4384155°0.4226156°0.4067157°0.3907158°0.3746159°0.3584160°0.342161°0.3256162°0.309163°0.2924164°0.2756165°0.2588166°0.2419167°0.225168°0.2079169°0.1908170°0.1736171°0.1564172°0.1392173°0.1219174°0.1045175°0.0872176°0.0698177°0.0523178°0.0349179°0.0175180°0УголSin (Синус)181°-0.0175182°-0.0349183°-0.0523184°-0.0698185°-0.0872186°-0.1045187°-0.1219188°-0.1392189°-0.1564190°-0.1736191°-0.1908192°-0.2079193°-0.225194°-0.2419195°-0.2588196°-0.2756197°-0.2924198°-0.309199°-0.3256200°-0.342201°-0.3584202°-0.3746203°-0.3907204°-0.4067205°-0.4226206°-0.4384207°-0.454208°-0.4695209°-0.4848210°-0.5211°-0.515212°-0.5299213°-0.5446214°-0.5592215°-0.5736216°-0.5878217°-0.6018218°-0.6157219°-0.6293220°-0.6428221°-0.6561222°-0.6691223°-0.682224°-0.6947225°-0.7071226°-0.7193227°-0.7314228°-0.7431229°-0.7547230°-0.766231°-0.7771232°-0.788233°-0.7986234°-0.809235°-0.8192236°-0.829237°-0.8387238°-0.848239°-0.8572240°-0.866241°-0.8746242°-0.8829243°-0.891244°-0.8988245°-0.9063246°-0.9135247°-0.9205248°-0.9272249°-0.9336250°-0.9397251°-0.9455252°-0.9511253°-0.9563254°-0.9613255°-0.9659256°-0.9703257°-0.9744258°-0.9781259°-0.9816260°-0.9848261°-0.9877262°-0.9903263°-0.9925264°-0.9945265°-0.9962266°-0.9976267°-0.9986268°-0.9994269°-0.9998270°-1УголSin (Синус)271°-0.9998272°-0.9994273°-0.9986274°-0.9976275°-0.9962276°-0.9945277°-0.9925278°-0.9903279°-0.9877280°-0.9848281°-0.9816282°-0.9781283°-0.9744284°-0.9703285°-0.9659286°-0.9613287°-0.9563288°-0.9511289°-0.9455290°-0.9397291°-0.9336292°-0.9272293°-0.9205294°-0.9135295°-0.9063296°-0.8988297°-0.891298°-0.8829299°-0.8746300°-0.866301°-0.8572302°-0.848303°-0.8387304°-0.829305°-0.8192306°-0.809307°-0.7986308°-0.788309°-0.7771310°-0.766311°-0.7547312°-0.7431313°-0.7314314°-0.7193315°-0.7071316°-0.6947317°-0.682318°-0.6691319°-0.6561320°-0.6428321°-0.6293322°-0.6157323°-0.6018324°-0.5878325°-0.5736326°-0.5592327°-0.5446328°-0.5299329°-0.515330°-0.5331°-0.4848332°-0.4695333°-0.454334°-0.4384335°-0.4226336°-0.4067337°-0.3907338°-0.3746339°-0.3584340°-0.342341°-0.3256342°-0.309343°-0.2924344°-0.2756345°-0.2588346°-0.2419347°-0.225348°-0.2079349°-0.1908350°-0.1736351°-0.1564352°-0.1392353°-0.1219354°-0.1045355°-0.0872356°-0.0698357°-0.0523358°-0.0349359°-0.0175360°0

Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.

Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».

Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.

Чему равен синус 45? …

– А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071

Источник

Синус

Смотреть что такое «Синус» в других словарях:

СИНУС — (лат.). Тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СИНУС в тригонометрии… … Словарь иностранных слов русского языка

СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь

СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов

СИНУС — (sine) Соотношение в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой. Синус угла х пишется как sin x. Если описывается круг единичного радиуса, измерение углов начинается с востока против часовой стрелки; sin x –… … Экономический словарь

СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

СИНУС

Полезное

Смотреть что такое «СИНУС» в других словарях:

СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь

СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов

СИНУС — (sine) Соотношение в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой. Синус угла х пишется как sin x. Если описывается круг единичного радиуса, измерение углов начинается с востока против часовой стрелки; sin x –… … Экономический словарь

СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Что такое синус и косинус в тригонометрии?

Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.

Школьный предмет

Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.

Использование

Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?

Определения

Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус – прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?

Что нужно запомнить

Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.

Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов. Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.

Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.

Теоремы

В базовой тригонометрии существует две основные теоремы: синусов и косинусов.

Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая – что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.

Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать – две рассмотренные теоремы существенно упростят решение задачи.

Цели и задачи

Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации – это может быть величина одного угла и длины двух сторон или, например, три стороны.

Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.

Нестыковки при изучении тригонометрии

Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.

Единицы измерения

Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга – 2 сантиметра, длина окружности составит 3,14*2, или 6,28.

Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.

Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева – «Пи». Это угловая величина, измеренная в радианах, ведь полукруг – это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.

Заглянем в будущее

Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая – это прямая.

Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.

Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.

Тригонометрические функции в жизни

Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь – здесь приходится использовать более сложные формулы.

Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.

В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.

Заключение

Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться – стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия – это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.

Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.

В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.

Источник

Свойства синуса, косинуса, тангенса и котангенса

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

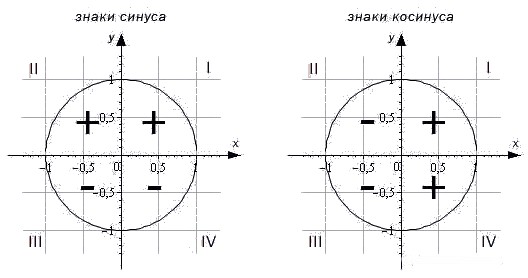
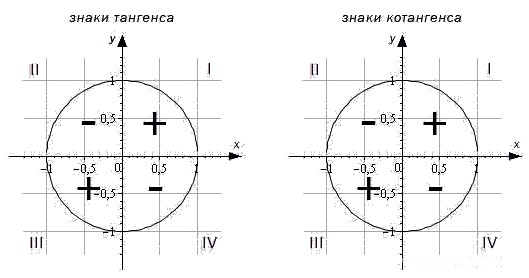
Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Для наглядности приведем иллюстрацию.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Свойство периодичности

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.

Математически данное свойство записывается так:

sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.

sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5

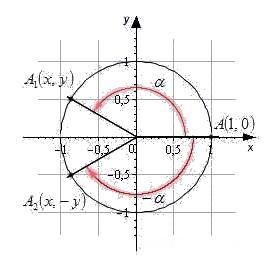
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

Вновь обратимся к единичной окружности.

Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов

Согласно этому свойству, справедливы равенства

Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.

Источник

Начальные сведения о синусе, косинусе, тангенсе и котангенсе

Определения

Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: \(\sin \alpha=\dfrac ac\)

Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: \(\cos \alpha=\dfrac bc\)

Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: \(\mathrm\,\alpha=\dfrac ab\)

Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: \(\mathrm\,\alpha=\dfrac ba\)

Утверждение

Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.

Теорема

Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:

Утверждение

В прямоугольном треугольнике \(ABC\) с прямым углом \(\angle C\) :

\(\sin \angle A=\cos \angle B\)

Доказательство

Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.

Теорема

Для углов \(30^\circ, 45^\circ, 60^\circ\) верна следующая таблица:

\[<\large<\begin <|c|c|c|c|>\hline & \phantom<000>30^\circ \phantom <000>& \phantom <000>45^\circ \phantom <000>& \phantom <000>60^\circ \phantom <000>\\[2pt] \hline &&&\\ \sin &\frac12&\frac<\sqrt2>2&\frac<\sqrt3>2\\[4pt] \cos &\frac<\sqrt3>2&\frac<\sqrt2>2&\frac12\\[4pt] \mathrm &\frac<\sqrt3>3&1&\sqrt3\\[4pt] \mathrm&\sqrt3&1&\frac<\sqrt3>3\\[4pt] \hline \end>>\]

Доказательство

Теперь по определению \(\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac<\sqrt3>2\)

Замечание

Для простоты запоминания таблицы можно записать ее в следующем виде:

Теорема

Справедливы следующие формулы приведения:

\[\begin \sin(180^\circ-\alpha)&=\sin\alpha\\ \cos(180^\circ-\alpha)&=-\cos\alpha\\ \mathrm\,(180^\circ-\alpha)&=-\mathrm\,\alpha\\ \mathrm\,(180^\circ-\alpha)&=-\mathrm\,\alpha \end\]

Пример

Учащиеся, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение конкурентных баллов по итогам его прохождения, непременно должны повторить теорию о синусе, косинусе, тангенсе и котангенсе. Как показывает практика, задания по данной тематике ежегодно встречаются в аттестационном испытании. Таким образом, если одним из ваших слабых мест являются формулы и теоремы синусов, косинусов, тангенсов и котангенсов, рекомендуем освежить в памяти базовую теорию. В этом вам поможет образовательный портал «Школково». В соответствующем разделе представлена теория о синусах, косинусах, тангенсах и котангенсах, которая позволит вам подготовиться к сдаче экзамена. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Ознакомившись с теорией, выпускник сможет грамотно объяснять решение задач ЕГЭ на синусы, косинусы, тангенсы и котангенсы. В этом состоит половина успеха при прохождении аттестационного испытания.

Для того чтобы учащиеся из Москвы или другого населенного пункта России, посетившие наш ресурс, смогли легко и качественно подготовиться к ЕГЭ, мы не только в понятной форме изложили теорию косинусов, синусов, тангенсов и котангенсов, но и подобрали соответствующие упражнения. Для каждого из них наши специалисты прописали подробный алгоритм решения и правильный ответ. Выполняя такие задачи при подготовке к ЕГЭ по математике, выпускники смогут лучше закрепить изученную теорию синусов и косинусов в треугольнике. Выбрать простые и более сложные упражнения вы можете в разделе «Каталог».

Изучив теорию о синусах, косинусах, тангенсах и котангенсах и попрактиковавшись в решении задач по данной теме при подготовке к ЕГЭ, учащиеся имеют возможность сохранить любое задание в «Избранное», чтобы при необходимости обсудить его с преподавателем.

Источник

Что такое синус и косинус? Что такое тангенс и котангенс?

Откуда появилась тригонометрия?

Знакомство наше начнём с глубокой древности. С древнего Египта, Вавилона и Китая. Не переживайте, все 20 веков тригонометрии мы с вами освоим всего за 20 минут. Можете засекать время.)

Итак, откуда же и как появилась тригонометрия?

Первоначально, на заре своего становления, тригонометрия не являлась самостоятельным разделом математики. Она, скорее, была частью астрономии. Дело всё в том, что древним астрономам, которые интересовались нашими главными небесными телами (Луной и Солнцем) и вовсю изучали их поведение, постоянно приходилось просчитывать и расстояния до них. С достаточной точностью для того далёкого времени, между прочим.) Скажем, чтобы предсказывать затмения. Или приливы/отливы. Просчитывать эти самые расстояния древним людям приходилось с помощью обыкновенного… треугольника.) Да-да! Просчитывать — значит, искать какие-то неизвестные элементы треугольника по известным другим. Это могут быть стороны (т.е. расстояния), а могут быть и какие-то углы. Всё зависело от того, какую именно задачу решали древние люди. И тот факт, что между сторонами и углами треугольника существует взаимосвязь, уже тогда у древних людей не вызывал сомнений.

Чуть позже, по мере развития цивилизации, большинство учёных стало осознавать чрезвычайную важность тригонометрии не только в астрономии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика, навигация в дальних морских походах, геодезия и картография… Слово «триангуляция» (разбиение местности на треугольники) вам знакомо? Нет? А тригонометрическая вышка или тригонометрический знак? Тоже нет? Что ж, если попутешествуете по нашей необъятной Родине, то на открытых местах (на вершинах холмов, в полях и т.п.) вы можете заметить небольшие пирамидки или башенки. Эти пирамидки — и есть тригонометрические знаки. Или геодезические пункты. Они служили верой и правдой геодезистам и картографам тех далёких времён для составления карт местности.) Этих знаков сохранилось по России очень много.)

Короче, в любых областях, где приходилось сталкиваться с обычным треугольником и вычислением его элементов (сторон и углов) через другие его элементы, людям неизбежно приходилось сталкиваться с тригонометрией.

А дальше — теория колебаний, электричество, акустика, радиосвязь… И в основе всего этого богатства — тоже тригонометрия, да…)

И не было бы у нас сегодня ни мобильников, ни телевизоров, ни микроволновок, ни спутниковых навигаторов, ни многих других современных атрибутов комфортной жизни, кажущихся нам обыденностью…

Итак, в основе всей тригонометрии лежит обыкновенный треугольник! Да-да! Именно так.

Почему именно треугольник и откуда собственно взялось это красивое слово «тригонометрия» — об этом далее.)

Синус, косинус, тангенс и котангенс… Что за звери?

Вот такая картинка у нас получится:

На всякий случай, напомню, что стороны, образующие прямой угол, называются катетами (a и b — катеты), а третья сторона, лежащая напротив прямого угла, называется гипотенузой (c — гипотенуза).

Казалось бы, треугольник и треугольник, эка невидаль! Что с ним делать-то? Спокойствие. Сейчас всё узнаете.)

Сейчас, как и древние люди, мы будем наш треугольник измерять. Да-да! Кстати, страшное слово «тригонометрия» с древнегреческого языка на русский так и переводится — измерение треугольников. Намёк понятен?)

Вот и измеряем. На рисунке специально клеточки нарисованы, как и в заданиях ЕГЭ или ОГЭ бывает. Чему равен катет a? Трём клеточкам (a = 3). А катет b? Не вопрос! Четырём клеточкам он равен (b = 4). А гипотенуза? Гипотенузу, конечно, по клеточкам не посчитаешь, но, воспользовавшись великой и могучей теоремой Пифагора, легко можно получить, что гипотенуза равна пяти (c = 5).

Кстати сказать, прямоугольный треугольник со сторонами 3, 4, 5 — весьма интересная фигура! Он известен ещё с античных времён и называется египетским треугольником. Ибо активно применялся для построения прямых углов египетскими землемерами и архитекторами. В том числе и при построении пирамид, между прочим.)

А вообще, целые числа a, b, c, которые могут быть длинами сторон прямоугольного треугольника, т.е. для которых выполняется теорема Пифагора

А мы продолжим. Теперь сделаем следующее. Поделим длину катета a на длину катета b. Или, как принято говорить в математике, возьмём отношение a к b.

Можно наоборот, поделить b на a. Получим 4/3. Или, скажем, поделить a на c. Получим 3/5. Иными словами, можно брать любые стороны прямоугольного треугольника, делить их длины друг на друга и получать какие-то числа. Безразмерные.

И что из этого? Согласен, пока ничего особенного. Бессмысленное занятие, одним словом.)

А теперь я поступлю следующим образом. Увеличу треугольник, продлив стороны b и c, но не как попало, а так, чтобы наш треугольник остался прямоугольным. Это важно. На картинке я для удобства увеличил все стороны треугольника в два раза.

А вот отношения новых длин сторон — не изменились!

Стало: x/y = 6/8 = 3/4.

Вот такая вот весёлая семейка. Возможно, особо внимательные и любознательные ученики заметили, что я ничего не сказал здесь про отношения гипотенузы к катетам c/a и с/b. Они имеют какие-то свои специальные названия? Конечно! Секанс и косеканс.)

Но эти соотношения никакого практического смысла не имеют и в школе не рассматриваются. И мы тоже не будем.)

Вся эта великолепная четвёрка (синус, косинус, тангенс и котангенс) называется тригонометрическими функциями.

Зачем я всё это так занудно повторяю и некоторые слова выделяю жирным шрифтом? Да затем, что это надо запомнить! Причём запомнить железно. Улавливаете?

Процесс запоминания можно существенно облегчить, если для начала запомнить, что в тангенсе и котангенсе сидят только катеты, а в синусе и косинусе гипотенуза появляется. Кроме того, ещё могут нахлынуть сомнения, какой из катетов, противолежащий или прилежащий, сидит соответственно у синуса/косинуса. Да и у тангенса/котангенса тоже. Здесь работает принцип под условным названием «дальше/ближе».

Например: синус угла — это отношения дальнего от угла (т.е. противолежащего) катета к гипотенузе, а косинус — отношение ближнего (т.е. прилежащего) катета к гипотенузе.

Тангенс — отношение дальнего от угла катета к ближнему. А котангенс — наоборот.

Подведём предварительный итог. Как вы видите, всё просто. Синус, косинус, тангенс и котангенс — это просто какие-то числа. Безразмерные. Ни больше ни меньше. Для каждого конкретного угла — свои персональные.

А теперь давайте поразмышляем вот над чем. Как вы думаете, почему мы всегда говорим синус, косинус, тангенс и котангенс угла? Вроде бы мы отношения сторон считаем. Угол-то тут при чём? Догадались? Если нет, то тогда смотрим на следующую картинку:

Что здесь нового? Я изменил (увеличил) угол с α до β («бета»). При этом все отношения сторон стали другими!

Скажем, было a/b = 3/4, а стало m/b = 5/4. И все остальные отношения сторон также поменялись. Какой вывод можно сделать? Да! При одном и том же угле α отношения длин сторон никак не зависят от их длин. Но при этом колоссально зависят от этого самого угла! И только от него. Именно поэтому тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к углу. И говорить, скажем, о тангенсе, без конкретного угла — бессмысленно. Угол — ключевая действующая фигура в тригонометрии.

Отсюда можно сделать важный вывод: если нам известен некий угол, то мы автоматически знаем и все его тригонометрические функции. Это неразрывная связь, которую надо уяснить железно.

Стало быть, если нам дан угол, то считается, что все его тригонометрические функции нам тоже известны. Полностью весь комплект, от синуса до котангенса. И наоборот, если нам дана какая-то из тригонометрических функций угла (скажем, косинус), то автоматически нам известен и сам угол.

Запоминаем: если нам известен угол, то нам автоматически известны и ВСЕ его тригонометрические функции. И наоборот — известна какая-то из тригонометрических функций (хотя бы одна), то известен и сам угол.

У каждого угла есть свои персональные синус и косинус. И почти у каждого — свои тангенс и котангенс.

Слово «почти» для тангенса и котангенса стоит не случайно. Об этом узнаете дальше.)

Сейчас, в век калькуляторов и компьютеров, найти тригонометрическую функцию какого-либо угла — не проблема. И наоборот, по функции найти угол. Нажал нужную кнопочку и — ответ готов.) А вот раньше, во времена отсутствия вычислительной техники, для тригонометрических функций углов существовали свои специальные таблицы. Таблицы Брадиса назывались. Они, конечно же, существуют и поныне, но, благодаря техническому прогрессу, давно отошли на задний план и пылятся на полках. Но знать об их существовании и уметь ими пользоваться — очень и очень полезно.

Конечно же, запомнить все-все значения тригонометрических функций всех-всех углов нереально. И не нужно.) Но среди всего многообразия углов есть некоторые углы, про которые вы обязаны знать всё. Об этом в следующих уроках будет. Но общий принцип «знаю угол — знаю его тригонометрические функции» срабатывает всегда! Безотказно.)

А зачем нам вообще нужны все эти синусы, косинусы, тангенсы и котангенсы — спросите вы? Вопрос резонный.

Пожалуйста! Вот вам типичная задачка из ЕГЭ:

Всё. Никаких данных, кроме тех, что на картинке, больше нет. Нужно найти длину катета AB.

Что делать будем? Клеточки не спасают: треугольник как-то неправильно ориентирован. Специально, похоже.) Известна длина гипотенузы (6 клеток). Зачем-то дан ещё и угол…

Вот тут самое время вспомнить про тригонометрию. Раз нам дан угол, то вспоминаем заклинание: «знаю угол — знаю и его тригонометрические функции!» И какую же из функций в дело пускать? А что нам дано в задачке? Нам дана гипотенуза AB, дан угол А, а найти просят прилежащий к этому углу катет.

Понятное дело, что надо косинус в дело пускать. Вот и действуем. Прямо по определению косинуса (отношение прилежащего катета к гипотенузе) пишем:

Гипотенуза AC равна 6 клеток, угол А у нас 60 градусов. Про этот угол известно, что его косинус равен 1/2. Это одно из тех значений, которое ученик знать обязан. Безо всяких таблиц и безо всяких калькуляторов!

Подставляем наши данные и получаем:

Простенькое линейное уравнение с величиной АВ в качестве неизвестного. Решаем и получаем:

Что и является верным ответом.

В этой задачке нам, конечно, пришлось вспомнить, чему равен косинус угла в 60 градусов. Для знающих учеников никаких проблем. А вот у новичков, ещё не знакомых с тригонометрическими функциями популярных углов, пока остаются вопросы… Откуда и почему именно 1/2? А не 1? Или, может быть, 2/3…

Ответы на эти вопросы будут позже. В соответствующем уроке.)

Ещё из той же оперы, ближе к нашей теме. Уже чисто на определение и понимание смысла тригонометрических функций. Никаких конкретных табличных значений знать не требуется.

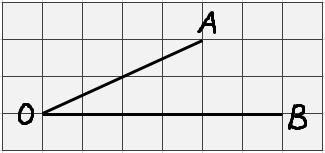
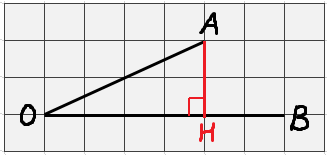
На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите тангенс этого угла.

Внушает? Вспоминаем определение тангенса — отношение противолежащего катета к прилежащему. Но… где здесь катеты? Дан просто угол, а для тангенса нам позарез нужен прямоугольный треугольник. Где его взять?!

Не беда! Раз надо, значит… сделаем!) Привяжем наш угол к некоторому прямоугольному треугольнику, про который мы точно знаем всё что нам нужно. А именно — катеты. Первое что напрашивается — опустить перпендикуляр из точки А на сторону ОВ.

Ну и как? Осеняет? Вот вам и прямоугольный треугольник и катеты! Противолежащий катет AH = 2, а прилежащий OH = 4.

Прямо по определению тангенса записываем и считаем:

И все дела.) Это правильный ответ.

А теперь задачка для самостоятельного решения.

На клетчатой бумаге с размером клетки 1х1 изображён угол. Найдите все тригонометрические функции этого угла.

Что, круто, да? Да-да, надо найти полный набор функций — от синуса до котангенса включительно. Тренироваться так тренироваться.)

Но где здесь прямоугольный треугольник? Нету его! Да и угол как-то совсем уж скверно расположен. Ни одну из сторон напрямую по клеточкам не посчитать, да…

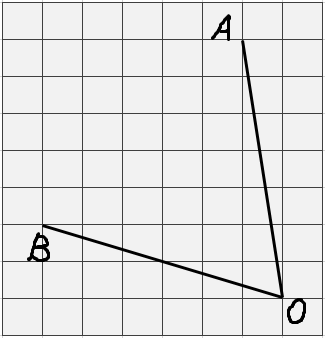
Что ж, подскажу немного, что именно надо дополнительно построить, чтобы не надорваться. Снова, как и в предыдущей задаче, опускаем перпендикуляр из точки А на сторону OB. Получим прямоугольный треугольник AHO.

А теперь внимание! Клеточки, конечно, дело хорошее, удобное и красивое. Но… Кто гарантировал, что основание перпендикуляра (точка Н) уляжется ровно на середину отрезка OB (т.е. строго в один из узлов сетки)? Интуиция? Интуиция в математике — штука опасная. Особенно при рисовании картинок, да…

Поэтому, прежде чем что-то решать, что-то считать, делаем задание по элементарной геометрии. На доказательство. А именно — докажите, что отрезок AH, проведённый так, как показано на картинке, действительно будет перпендикулярен отрезку OB. Или, что то же самое, треугольник AHO — действительно прямоугольный. И да помогут вам вспомогательные синие пунктирные линии и теорема Пифагора (это подсказка)! Ну и клеточки спасут, само собой.:)

Без доказательства этого важного факта и без прямоугольного треугольника говорить о каких-либо тригонометрических функциях бессмысленно. Пока что… Придёт время — и мы с вами научимся считать любые тригонометрические функции любых углов без прямоугольного треугольника. Вообще. Как? Совсем скоро узнаете. Всему своё время.)

А пока — доказываем перпендикулярность отрезков, а затем считаем синус, косинус, тангенс и котангенс угла. После доказательства все необходимые данные для расчёта тригонометрических функций у вас уже будут. Обязательно.)

Ответы (в беспорядке):

А где какая функция — это уж вы сами как-нибудь.)

Итак, вот мы с вами и освоили синус, косинус, тангенс и котангенс на самом примитивном уровне. С помощью обычного прямоугольного треугольника. Но это пока только первый шаг.

Когда древние люди поняли, что у каждого угла имеется свой набор тригонометрических функций, они озадачились вполне логичным вопросом — а не связаны ли как-нибудь синус, косинус, тангенс и котангенс между собой? Чтобы, зная какую-то одну из функций, можно было бы отыскать и все остальные? Не вычисляя сам угол.

Источник