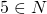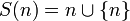Что значит натуральное число
Что значит натуральное число
Что такое натуральное число
Определение натурального числа
Натуральными числами называются числа, которые используются при счете или для указания порядкового номера предмета среди однородных предметов.
Задание. Какие из следующих чисел являются натуральными?
$$-89 ; 7 ; \frac<4> <3>; 34 ; 2 ; 11 ; 3,2 ; \sqrt[3] <129>; \sqrt<5>$$
Сложение натуральных чисел
Подробнее о сложении чисел читайте по ссылке.
Задание. Найти сумму чисел:
Для вычисления второй суммы, для упрощения вычислений, применим к ней вначале свойство ассоциативности сложения:
Умножение натуральных чисел
Операция умножения натуральных чисел обладает следующими свойствами:
Подробнее о умножении чисел читайте по ссылке.
Задание. Найти произведение чисел:
Решение. По определению операции умножения:
$$12 \cdot 3=12+12+12=36$$
Ко второму произведению применим свойство ассоциативности умножения:
$$7 \cdot 25 \cdot 4=7 \cdot(25 \cdot 4)=7 \cdot 100=700$$
Операция сложения и умножения натуральных чисел связаны законом дистрибутивности умножения относительно сложения:
$$(n+m) \cdot k=n \cdot k+m \cdot k$$
Сумма и произведение любых двух натуральных чисел всегда есть число натуральное, поэтому множество всех натуральных чисел замкнуто относительно операций сложения и умножения.
Так же на множестве натуральных чисел можно ввести операции вычитания и деления, как операции обратные к операциям сложения и умножения соответственно. Но эти операции не будут однозначно определенны для любой пары натуральных чисел.
Решение. По определению натуральной степени натурального числа это выражение можно записать следующим образом
$$2^<5>=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2=32$$
Значение словосочетания «натуральное число»
Существуют два подхода к определению натуральных чисел:
натуральные числа — числа, возникающие при подсчёте (нумерации) предметов (первый, второй, третий, четвёртый, пятый»…);
натуральные числа — числа, возникающие при обозначении количества предметов (0 предметов, 1 предмет, 2 предмета, 3 предмета, 4 предмета, 5 предметов»…).
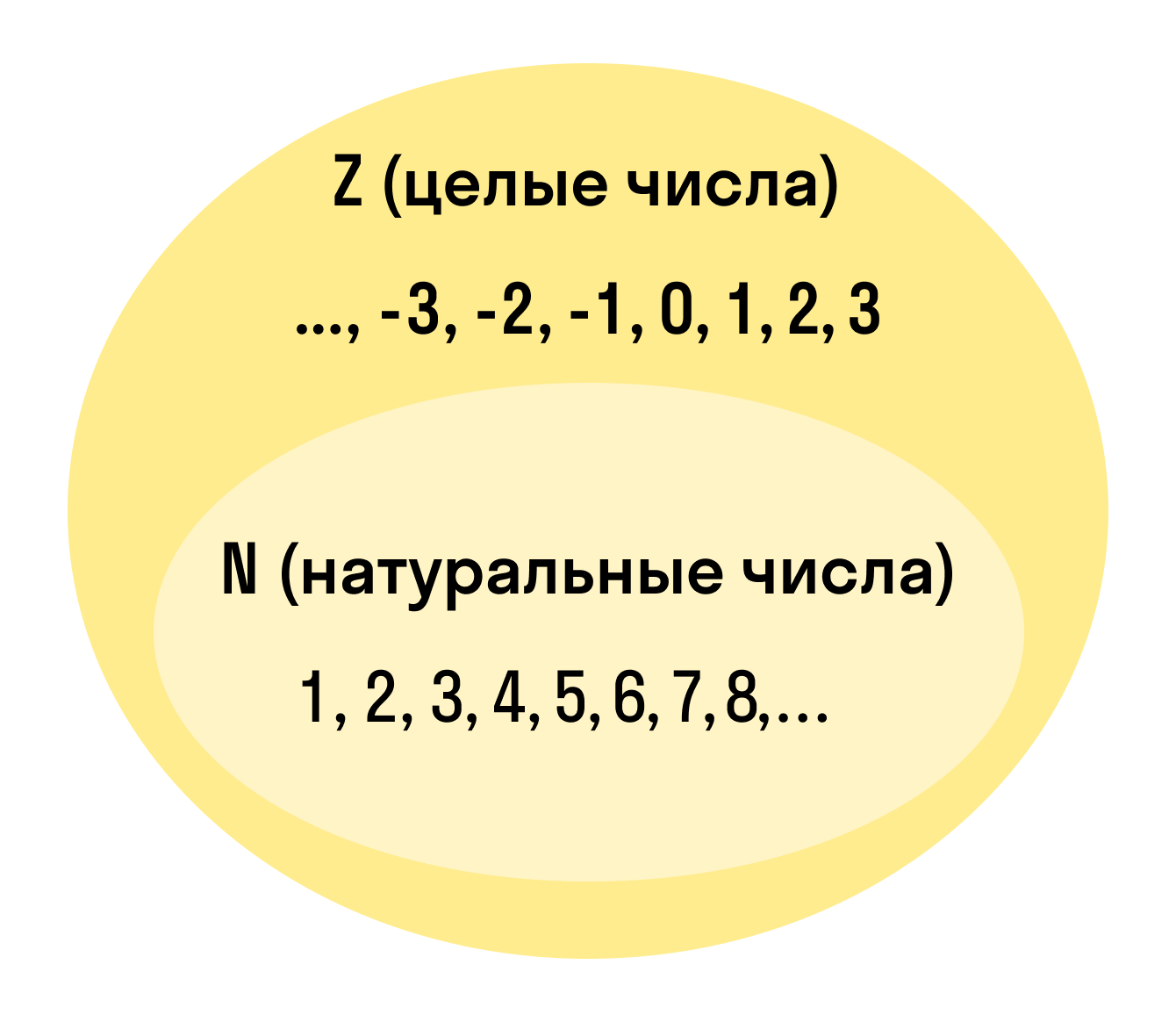
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли нуль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход. Второй подход, например, применяется в трудах Николя Бурбаки, где натуральные числа определяются как мощности конечных множеств.
Отрицательные и нецелые (рациональные, вещественные, …) числа к натуральным не относятся.
Множество всех натуральных чисел принято обозначать символом
(от лат. naturalis — естественный). Множество натуральных чисел является бесконечным, так как для любого натурального числа
найдётся натуральное число, большее чем
Наличие нуля облегчает формулировку и доказательство многих теорем арифметики натуральных чисел, поэтому при первом подходе вводится полезное понятие расширенного натурального ряда, включающего нуль. Расширенный ряд обозначается
Значение слова «натуральное число»
Натура́льные чи́сла (от лат. naturalis — естественный; естественные числа) — числа, возникающие естественным образом при счёте (например, 1, 2, 3, 4, 5…). Последовательность всех натуральных чисел, расположенных в порядке возрастания, называется натуральным рядом.
Существуют два подхода к определению натуральных чисел:
натуральные числа — числа, возникающие при подсчёте (нумерации) предметов (первый, второй, третий, четвёртый, пятый»…);
натуральные числа — числа, возникающие при обозначении количества предметов (0 предметов, 1 предмет, 2 предмета, 3 предмета, 4 предмета, 5 предметов»…).
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли нуль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход. Второй подход, например, применяется в трудах Николя Бурбаки, где натуральные числа определяются как мощности конечных множеств.
Отрицательные и нецелые (рациональные, вещественные, …) числа к натуральным не относятся.
Множество всех натуральных чисел принято обозначать символом
(от лат. naturalis — естественный). Множество натуральных чисел является бесконечным, так как для любого натурального числа
найдётся натуральное число, большее чем
Наличие нуля облегчает формулировку и доказательство многих теорем арифметики натуральных чисел, поэтому при первом подходе вводится полезное понятие расширенного натурального ряда, включающего нуль. Расширенный ряд обозначается
натуральное число
1. матем. целое положительное число; одно из чисел, возникающих естественным образом при счёте, подсчёте (нумерации) предметов; член арифметической прогрессии, где первый член и шаг прогрессии равны единице
Натуральные числа
Вы будете перенаправлены на Автор24
История
Натуральные числа и различные системы для их обозначения использовались еще в древних цивилизациях: Древнем Междуречье, Древнем Египте, Древнем Китае, в племенах Майя. Понятие числа «ноль», по видимому, появилось позже понятия натуральных чисел в позднем Вавилоне и у Майя.
В самые древние времена для счета использовали палочки. Такой способ записи сохранился в римском исчислении. Число при такой записи представляло собой сумму или разность палочек, которая была записана без каких-либо знаков.
С развитием систем счисления определенные числа стали обозначать буквами алфавита. В современных системах счисления значение каждой цифры числа определяет ее место в записи числа. Первой такой системой счисления была вавилонская (шестидесятеричная) и индийская (десятичная).
В работах математика Пьера де Ферма были положены основы теории чисел или высшей арифметики как отдельной науки, которая изучает чистые, формальные свойства натуральных чисел.
Натуральные числа. Множество натуральных чисел
Готовые работы на аналогичную тему
Если выстроить все натуральные числа в порядке их возрастания, то получим натуральный ряд.
Для определения натуральных чисел существует два подхода:
Числа, которые возникают при подсчете (нумерации) предметов (например, первый, второй и т.д.).
Числа, которые используют для обозначения количества предметов (нет стула, один стул, два стула и т.д.).
Математики не пришли к единому выводу считать ли ноль натуральным числом. В большинстве российских источников традиционным является первый подход. Второй подход широко используется в программировании (например, при индексации массивов, нумерации битов машинного кода и т.д.).
К натуральным числам не относятся ни отрицательные, ни нецелые числа.
Какие из чисел являются натуральными?
Ноль как натуральное число
Чтобы прочитать натуральное число, нужно выполнить следующие действия:
Название класса пропускают, если в группе цифр все нули.
Каждую цифру класса называют разрядом класса.
Аксиомы Пеано для натуральных чисел
$1\in N$: единица является натуральным числом.
$\nexists x\in N\ \left(S\left(x\right)=1\right)$: Не существует натурального числа, которое находится перед единицей>.
Все аксиомы отражают представление о натуральном ряде и числовой линии.
Теоретико-множественное определение натуральных чисел (определение Фреге—Рассела)
По теории множеств единственным объектом конструирования любых математических систем является множество.
Таким образом, исходя из понятия множества натуральные числа вводятся по двум правилам:
Заданные таким образом числа называются порядковыми или ординальными.
Описываются первые порядковые числа и натуральные числа, которые им соответствуют, следующим образом:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 23.05.2022
Алгебра
План урока:
Натуральные числа
Ещё в далекие доисторические времена человек освоил такую математическую операцию, как счет. Можно было подсчитать количество соплеменников в племени или животных в стае, на которых велась охота. При этом человек ещё не осознавал понятие числа как некое отвлеченное понятие. Анализ языков народов, находящихся на самых низких стадиях развития, показывает, что они в словосочетаниях «три змеи», «три палки», «три камня» используют разные слова для числа 3. Однако со временем человек осознал, что количество предметов можно определять числом, которое не будет зависеть от природы подсчитываемых объектов. Числа, используемые для счета, сегодня называют натуральными числами. Долгое время человечество не знало никаких других чисел.
В качестве примера можно привести следующие натуральные числа: 1, 8, 10, 1000, 64141 и т.п. Если можно представить, что в каком-то множестве содержится N элементов, то N будет натуральным числом.
Вообще все натуральные числа являются частью так называемого натурального ряда чисел. Начинается этот ряд с единицы, а каждое следующее число больше предыдущего на 1.
Таким образом, можно дать ещё одно определение натуральных чисел – это числа, входящие в натуральный ряд. Традиционно ноль не является натуральным числом, ведь при подсчете предметов счет начинают с единицы. Такой подход используется в большинстве российских источников. Однако стоит отметить, что иногда в зарубежной литературе всё же предпочитают начинать натуральный ряд не с единицы, а с нуля. В этом случае 0 становится натуральным числом. Это деление весьма условно. Для обозначения множества натуральных чисел используется буква N. Очевидно, что натуральных чисел существует бесконечно много, а потому не существует наибольшего натурального числа.
Любые два натуральных числа можно складывать друг с другом и перемножать, при этом в результате будет снова получаться натуральное число. При вычитании может получиться ноль или отрицательное число, а при делении – дробное.
Простые и составные числа
Все натуральные числа можно разбить на три группы:
Единицу традиционно не считают ни простым, ни составным числом. Составным же называют натуральное число, делящееся не только на единицу и себя. Можно дать и другие определения, основанные на количестве делителей у числа. Так, единица имеет ровно 1 делитель. У простого числа всегда ровно 2 делителя, а у составного – 3 и более.
В качестве примера простых чисел можно привести: 2, 3, 5, 7, 31, 101, 163. Примерами составных чисел являются:
Среди делителей составного числа могут быть как другие составные, так и простые числа. Например, 50 имеет простые делители 2 и 5 и составные 10 и 25.
Заметим, что если число n делится на m, а m в свою очередь делится на k, то и n делится на k. Так, 45 делится на 9, а 9 делится на 3. Значит, и 45 делится на 3. Из этого свойства чисел вытекает следующее утверждение:
Любое составное число имеет хотя бы один простой делитель, причем им обязательно будет наименьший из всех делителей числа. Докажем это. Пусть число H – составное, и имеет наименьший делитель F. Предположим, что F – составное число. Тогда у него есть делитель L, который меньше его. Но тогда L должен быть делителем и для H. Так как L 1 1
Натуральные числа
Натуральные числа проще всего определить их перечислением: 
Третий пункт требуется для порядка, чтобы никакие другие числа (не натуральные) не затесались в наш натуральный ряд. Так называется множество натуральных чисел выписанных в порядке возрастания: 
Если число 



Простым числом называется натуральное число, которое делится без остатка только на само себя и на единицу.
Если число не простое, оно называется составным.
Одной из задач, которые ставятся для натуральных чисел, есть разложение их на множители. Интерес вызывает такое разложение, в котором все сомножители есть простые числа.
Пример 1 Разложение числа
на множители может быть таким:

Последнее разложение на простые множители однозначно с точностью до перестановки множителей. Этот факт представляет собой содержание основной теоремы арифметики:
Основная теорема арифметики. Любое натуральное число однозначно представляется в виде произведения своих простых сомножителей (с точностью до перестановки сомножителей).
В число простых чисел не входит единица. Это сделано для удобства, иначе в большинстве вопросов о разложениях пришлось бы оговаривать: не включая единицу и т.д.
Простые числа не всегда легко определить. Конечно, опытный математик сразу скажет простое число или составное, если само число в пределах сотни. Для больших чисел нужно уже делать анализ. Дадим еще несколько определений.
Здесь следует также записать разложение на простые множители всех трех чисел:
Поступаем наоборот: берем простые множители в наибольшей степени: 

В заключение приведем еще несколько примеров.
Для решения используем свойства числовых неравенств и запишем очевидную цепочку:

Пример 6 Доказать, что для любого натурального число делится на
.
Из двух подряд идущих натуральных чисел (у нас это и ) одно делится на 
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
Что называют натуральным числом
Натуральными числами называют целые положительные числа.
Для записи натуральных чисел используют следующие цифры (графические символы):
В свою очередь, цифры также являются натуральными числами: например, цифра 3 является натуральным числом 3, которое состоит из одной цифры 3.
Отрицательные и дробные числа не являются натуральными.
Среди ученых давно ведутся споры на тему, считать ли 0 натуральным числом. Единого мнения среди специалистов нет, но обычно 0 не считают натуральным числом.
Чтение натуральных чисел
Число, которое состоит из одной цифры, называют однозначным.
В многозначном числе каждая цифра занимает строго определенную позицию, которую называют разрядом числа.
Разряды чисел отсчитывают с его конца.
Разряды идут в следующем порядке:
Любое натуральное число всегда закачивается разрядом единиц. В случае, если какой-либо разряд в числе отсутствует, на его месте пишется цифра 0 (ноль).
Если натуральное число небольшое, проичитать его не составит большого труда.
Правила чтения натуральных чисел:
Правило на первый взгляд достаточно путаное и непонятное, но, если разобрать его на примерах, то оно достаточно простое.
Примеры (для удобства чтения мы будем отделять классы пробелом):
Запись натуральных чисел
Правило записи натуральных чисел еще более запутано и непонятно, чем правило чтения. Поэтому, разберем его на примерах.
Мы не рассматривали классы чисел, старше триллионов. В программе средней школы в этом нет необходимости.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Натуральные числа
Простейшие числа — это числа натуральные. Мы пользуемся ими в повседневной жизни для счета предметов, то есть для определения их количества и порядка.
Для записи чисел в настоящее время используется позиционная десятичная система счисления (для записи любого числа используются 10 цифр — 0,1, 2, 3, 4, 5, 6, 7, 8, 9; при этом значение каждой цифры определяется ее местом в записи числа).
Определение. — это числа, используемые для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
Например: 3, 132, 68, 126, 548, 10050.
Натуральные числа, расположенные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурального числа — 1. Наибольшего натурального числа нет, так как ряд натуральных чисел бесконечен. Если к любому натуральному числу прибавить единицу, то получаем число, следующее за данным числом.
Число 0 натуральным числом не является, так как означает полное отсутствие чего бы то ни было, значит, счет предметов тоже отсутствует.
Например, первые члены ряда: 1, 2,3,4
В древнейшие времена для записи чисел и счета использовались палочки, этот способ счисления сохранился в римских цифрах. При этом число представляло собой сумму или разность палочек, записанную без каких-либо знаков.
Следующим этапом развития систем счисления стало обозначение определенных чисел буквами алфавита. Наконец, современные системы счисления являются поместными: значение каждой цифры числа определяется ее местом в записи числа. Первыми из таких систем счислений были вавилонская (шестидесятеричная) и индийская (десятичная).
Современная система счисления, которая называется арабской, является одним из вариантов индийской. Однако в индийской системе счисления отсутствовала цифра 0. Эту цифру изобрели арабы, после чего система счисления приняла современный вид.
Десятичная система счисления основана на разрядности и десятичности.
Материалом для построения числа являются цифры от 0 до 9.
Для исчисления времени в градусной мере углов сохранилась шестидесятеричная система счисления (за основу взято число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.
Что такое натуральное число в математике?
Все дети с ранних лет изучают математику. Поначалу она позволяет узнать простые вещи, легко применимые в жизни, но с течением времени задачи постоянно усложняются. Появляется и новая терминология, по которой не всегда можно понять, что имеется в виду. Например, что такое натуральное число в математике?
В древние времена люди не пользовались цифрами так, как делают это сейчас, однако счет всё равно был им необходим. Предметы сравнивались по количеству с чем-то, например, кто-то имел столько же ягод, сколько и пальцев на одной руке. Постепенно люди изобрели систему счета, а с ней появились и новые термины.
Что такое натуральное число в математике?
Это понятие относится к одним из самых старых, так как оно родилось из-за древней необходимости научиться считать количество обычных предметов. Что значит натуральное число? Чаще всего дается следующее определение – это числа, которые возникают при подсчете, причем происходит подобное естественным образом.
Отсюда берется и второе название этого термина – естественные числа. Своей последовательностью, расположенностью по возрастанию, они образуют натуральный ряд. Иначе говоря, все цифры, начиная с единицы, которые используются для подсчета предметов, являются натуральными.
Таким образом, существует самое малое натуральное число – им является единица. Наибольшего же не бывает, так как к любой цифре можно добавить ещё один. Ноль не входит в натуральный ряд, так как с его помощью нельзя ничего посчитать, хотя далеко не все ученые с этим согласны.
Определение натуральных чисел
Подобные цифры определяются двумя главными методами. Первый из них подразумевает перечисление всего имеющегося, а второй называет итоговое количество.
В этой цифре и заключается основная разница между двумя данными методами определения. В первом случае минимальным числом является единица, а во втором возможно и использование нуля. Математики так и не смогли прийти к единогласному решению о том, какой метод лучше, и стоит ли ставить ноль в один ряд с другими натуральными числами.
Как правило, применяется всё же первый вариант, оставляющий спорную цифру в стороне. Тем не менее, в некоторых трудах, вроде Бурбаки, используется другой подход. Помимо этого, ноль является неотъемлемой и широко применяемой частью в мире программирования.
Особенности натуральных чисел
Главное, о чем нужно помнить при упоминании подобных чисел, так это об их обязанности быть естественными. Они должны быть такими, чтобы с их помощью было возможно подсчитать количество каких-то предметов. Естественные числа должны быть доступными и понятными для всех.
По этой причине к ним не относятся отрицательные показатели и различные нецелые числа. Например, рациональное, обозначающееся в виде дроби, или вещественные, представляющее собой математический объект, не смогут стать частью натурального ряда.
Что такое натуральное число в математике? Все эти цифры принято обозначать буквой N. Её выбрали потому, что на латинском языке слово естественный пишется как naturalis, то есть начинается с литеры N. Число, подразумеваемое под этим обозначением, бесконечно.
Нередко для доказательства сложных теорем полезно помнить и о нуле. Он входит в расширенный натуральный ряд, который обозначают с помощью соответствующей цифры, приписанной снизу к букве N. Иногда вместо неё применяете Z, вновь с тем же маленьким нулем рядом.
Операции с натуральными числами
В математике существует понятие замыкания. Оно обозначает минимально возможное расширение какого-то множества, операции с которым не выходят за его пределы. В отношении натуральных чисел выделяется несколько таких замкнутых операций.
Иногда в данном вопросе рассматриваются ещё две операции. Их проблема заключается в том, что они применимы не для всех случаев. Иногда подобное может существовать, а иногда нет. К этим операциям относятся:
Как правило, наука сосредотачивается на первых двух операциях – сложении и вычитании. Интересно, что именно они способствуют созданию кольца целых чисел – это происходит через бинарные сложения и умножения.
Что стоит знать о натуральных числах?
Цифры, используемые для счета, не всегда были такими, как мы их знаем сегодня. Изначально применялось относительно схематическое изображение, постепенно сформировавшееся в римские цифры.
Современный же вариант зародился в Индии, примерно полторы тысячи лет назад. Впоследствии они были привезены в европейские страны арабами, за что и получили своё известное название – арабские цифры. Несмотря на то, что натуральных чисел может быть любое количество, цифр всего десять – от нуля и до девятки.
Если рассматривать натуральный ряд, то в нем каждое число будет отличаться от предыдущего или последующего на единицу, при том, что сам ряд бесконечен. Однако, в процессе счета появляется так называемая десятичная позиционная.
Под этим словом подразумевается тот факт, что когда числа доходят до десяти, они образуют новую единицу старшего разряда. Эти разряды бывают самыми разными – в частности, к ним относятся миллионы и миллиарды. В зависимости от их количества, разряды объединяют по классам.
Например, миллиарды могут исчисляться десятками или сотнями. Это будут разряды, но все они в целом образуют класс миллиардов. То же самое происходит и с разрядами миллионов, тысяч, сотен, десяток и единиц.
Натуральные числа для нас очень привычны и естественны. И это не удивительно, так как знакомство с ними начинается с первых лет нашей жизни на интуитивно понятном уровне.
Информация этой статьи создает базовое представление о натуральных числах, раскрывает их предназначение, прививает навыки записи и чтения натуральных чисел. Для лучшего усвоения материала приведены необходимые примеры и иллюстрации.
Навигация по странице.
Натуральные числа – общее представление.
Не лишено здравой логики следующее мнение: появление задачи счета предметов (первый, второй, третий предмет и т.д.) и задачи указания количества предметов (один, два, три предмета и т.д.) обусловило создание инструмента для ее решения, этим инструментом явились натуральные числа.
Из этого предложения видно основное предназначение натуральных чисел – нести в себе информацию о количестве каких-либо предметов или порядковом номере данного предмета в рассматриваемом множестве предметов.
Чтобы человек мог использовать натуральные числа, они должны быть каким-либо образом доступны как для восприятия, так и для воспроизведения. Если озвучить каждое натуральное число, то оно станет воспринимаемым на слух, а если изобразить натуральное число, то его можно будет увидеть. Это самые естественные способы, позволяющие донести и воспринять натуральные числа.
Так приступим же к приобретению навыков изображения (записи) и навыков озвучивания (чтения) натуральных чисел, познавая при этом их смысл.
Десятичная запись натурального числа.
Сначала следует определиться с тем, от чего мы будем отталкиваться при записи натуральных чисел.
Давайте запомним изображения следующих знаков (покажем их через запятую): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Приведенные изображения представляют собой запись так называемых цифр. Давайте сразу договоримся не переворачивать, не наклонять и иным образом не искажать цифры при записи.
Теперь условимся, что в записи любого натурального числа могут присутствовать только лишь указанные цифры и не могут присутствовать никакие другие символы. Также условимся, что цифры в записи натурального числа имеют одинаковую высоту, располагаются в строчку друг за другом (с почти отсутствующими отступами) и слева находится цифра, отличная от цифры 0.
Приведем несколько примеров правильной записи натуральных чисел: 604, 777 277, 81, 4 444, 1 001 902 203, 5, 900 000 (обратите внимание: отступы между цифрами не всегда одинаковы, подробнее об этом будет сказано при рассмотрении классов натуральных чисел). Из приведенных примеров видно, что в записи натурального числа не обязательно присутствуют все из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; некоторые или все цифры, участвующие в записи натурального числа, могут повторяться.
Записи 014, 0005, 0, 0209 не являются записями натуральных чисел, так как слева находится цифра 0.
Запись натурального числа, выполненная с учетом всех требований, описанных в этом пункте, называется десятичной записью натурального числа.
Дальше мы не будем разграничивать натуральные числа и их запись. Поясним это: дальше в тексте будут использоваться фразы типа «дано натуральное число 582», которые будут означать, что дано натуральное число, запись которого имеет вид 582.
Натуральные числа в смысле количества предметов.
Пришло время разобраться с количественным смыслом, который несет в себе записанное натуральное число. Смысл натуральных чисел в плане нумерации предметов рассмотрен в статье сравнение натуральных чисел.
Начнем с натуральных чисел, записи которых совпадают с записями цифр, то есть, с чисел 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Теперь открываем глаза и видим: 
Аналогично, 






Итак, с рассмотренной позиции натуральные числа 1, 2, 3, …, 9 указывают количество предметов.
Число, запись которого совпадает с записью цифры 0, называют «нуль». Число нуль НЕ натуральное, однако, его обычно рассматривают вместе с натуральными числами. Запомним: нуль означает отсутствие чего-либо. Например, нуль предметов – это ни одного предмета.
В следующих пунктах статьи мы продолжим раскрывать смысл натуральных чисел в плане указания количества.
Однозначные натуральные числа.
Перечислим все однозначные натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего однозначных натуральных чисел девять.
Двузначные и трехзначные натуральные числа.
Сначала дадим определение двузначных натуральных чисел.
К примеру, натуральное число 45 – двузначное, числа 10, 77, 82 тоже двузначные, а 5 490, 832, 90 037 – не двузначные.
Давайте разберемся, какой смысл несут в себе двузначные числа, при этом будем отталкиваться от уже известного нам количественного смысла однозначных натуральных чисел.
Для начала введем понятие десятка.
Представим такую ситуацию – мы открыли глаза и увидели множество, состоящее из девяти предметов и еще одного предмета. В этом случае говорят об 1 десятке (одном десятке) предметов. Если рассматривают вместе один десяток и еще один десяток, то говорят о 2 десятках (двух десятках). Если к двум десяткам присоединить еще один десяток, то будем иметь три десятка. Продолжая этот процесс, будем получать четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков, и наконец, девять десятков.
Теперь мы можем перейти к сути двузначных натуральных чисел.
Для этого посмотрим на двузначное число как на два однозначных числа – одно находится слева в записи двузначного числа, другое находится справа. Число слева указывает количество десятков, а число справа – количество единиц. При этом если справа в записи двузначного числа находится цифра 0, то это означает отсутствие единиц. В этом и есть весь смысл двузначных натуральных чисел в плане указания количества.
К примеру, двузначное натуральное число 72 соответствует 7 десяткам и 2 единицам (то есть, 72 яблока – это множество из семи десятков яблок и еще двух яблок), а число 30 отвечает 3 десяткам и 0 единицам, то есть, единиц, которые не объединены в десятки, нет.
Ответим на вопрос: «Сколько всего существует двузначных натуральных чисел»? Ответ: их 90.
Переходим к определению трехзначных натуральных чисел.
Натуральные числа, запись которых состоит из 3 знаков – 3 цифр (различных или повторяющихся), называются трехзначными.
Примерами натуральных трехзначных чисел являются 372, 990, 717, 222. Натуральные числа 7 390, 10 011, 987 654 321 234 567 не являются трехзначными.
Для понимания смысла, заложенного в трехзначных натуральных числах, нам понадобится понятие сотни.
Множество из десяти десятков – это 1 сотня (одна сотня). Сотня и сотня – это 2 сотни. Две сотни и еще одна сотня – это три сотни. И так далее, имеем четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, и, наконец, девять сотен.
Теперь посмотрим на трехзначное натуральное число как на три однозначных натуральных числа, идущих друг за другом справа налево в записи трехзначного натурального числа. Число справа указывает количество единиц, следующее число указывает количество десятков, следующее число – количество сотен. Цифры 0 в записи трехзначного числа означают отсутствие десятков и (или) единиц.
Таким образом, трехзначное натуральное число 812 соответствует 8 сотням, 1 десятку и 2 единицам; число 305 – трем сотням (0 десяткам, то есть, десятков, не объединенных в сотни, нет) и 5 единицам; число 470 – четырем сотням и семи десяткам (единиц, не объединенных в десятки, нет); число 500 – пяти сотням (десятков, не объединенных в сотни, и единиц, не объединенных в десятки, нет).
Аналогичным образом можно дать определения четырехзначных, пятизначных, шестизначных и т.д. натуральных чисел.
Многозначные натуральные числа.
Итак, переходим к определению многозначных натуральных чисел.
Многозначные натуральные числа – это натуральные числа, запись которых состоит из двух или трех или четырех и т.д. знаков. Иными словами, многозначные натуральные числа – это двузначные, трехзначные, четырехзначные и т.д. числа.
Сразу скажем, что множество, состоящее из десяти сотен, – это одна тысяча, тысяча тысяч – это один миллион, тысяча миллионов – это один миллиард, тысяча миллиардов – это один триллион. Тысяче триллионов, тысяче тысяч триллионов и так далее также можно дать свои названия, но в этом нет особой надобности.
Так какой смысл скрывается за многозначными натуральными числами?
К примеру, многозначное натуральное число 7 580 521 соответствует 1 единице, 2 десяткам, 5 сотням, 0 тысячам, 8 десяткам тысяч, 5 сотням тысяч и 7 миллионам.
Таким образом, мы научились группировать единицы в десятки, десятки в сотни, сотни в тысячи, тысячи в десятки тысяч и так далее и выяснили, что цифры в записи многозначного натурального числа указывают соответствующее количество вышеперечисленных групп.
Чтение натуральных чисел, классы.
Мы уже упоминали, как читаются однозначные натуральные числа. Выучим содержимое следующих таблиц наизусть.

Чтобы научиться читать двузначные числа, придется запомнить данные следующих таблиц.

А как читаются остальные двузначные числа?
Поясним на примере. Прочитаем натуральное число 74. Как мы выяснили выше, это число соответствует 7 десяткам и 4 единицам, то есть, 70 и 4. Обращаемся к только что записанным таблицам, и число 74 читаем как: «Семьдесят четыре» (союз «и» не произносим). Если нужно прочитать число 74 в предложении: «Нет 74 яблок» (родительный падеж), то это будет звучать так: «Нет семидесяти четырех яблок». Еще пример. Число 88 – это 80 и 8, следовательно, читаем: «Восемьдесят восемь». А вот пример предложения: «Он думает о восьмидесяти восьми рублях».
Переходим к чтению трехзначных натуральных чисел.
Для этого нам придется выучить еще несколько новых слов.

Осталось показать, как читаются остальные трехзначные натуральные числа. При этом будем использовать уже полученные навыки чтения однозначных и двузначных чисел.
Разберем пример. Прочитаем число 107. Это число соответствует 1 сотне и 7 единицам, то есть, 100 и 7. Обратившись к таблицам, читаем: «Сто семь». А теперь произнесем число 217. Это число есть 200 и 17, поэтому, читаем: «Двести семнадцать». Аналогично, 888 – это 800 (восемьсот) и 88 (восемьдесят восемь), читаем: «Восемьсот восемьдесят восемь».
Переходим к чтению многозначных чисел.
Для чтения запись многозначного натурального числа разбивается, начиная справа, на группы по три цифры, при этом в самой левой такой группе может оказаться либо 1, либо 2, либо 3 цифры. Эти группы называются классами. Класс, находящийся справа, называют классом единиц. Следующий за ним (справа налево) класс называют классом тысяч, следующий класс – классом миллионов, следующий – классом миллиардов, далее идет класс триллионов. Можно дать названия и следующих классов, но натуральные числа, запись которых состоит из 16, 17, 18 и т.д. знаков, обычно не читают, так как их очень трудно воспринять на слух.
Посмотрите на примеры разбиения многозначных чисел на классы (для наглядности классы отделяют друг от друга небольшим отступом): 489 002, 10 000 501, 1 789 090 221 214.
Занесем записанные натуральные числа в таблицу, по которой легко научиться их читать.
Прочитаем число 489 002 по приведенным правилам.
Чтение ведем слева направо,
Приступаем к чтению числа 10 000 501.
Осталось прочитать натуральное число 1 789 090 221 214.
Сделаем это без подробных пояснений: 1 789 090 221 214 – «один триллион семьсот восемьдесят девять миллиардов девяноста миллионов двести двадцать одна тысяча двести четырнадцать».
Итак, в основе навыка чтения многозначных натуральных чисел лежит умение разбивать многозначные числа на классы, знание названий классов и умение читать трехзначные числа.
Рекомендуем также изучить тему из курса русского языка «склонение числительных».
Разряды натурального числа, значение разряда.
В записи натурального числа значение каждой цифры зависит от ее позиции. К примеру, натуральное число 539 соответствует 5 сотням, 3 десяткам и 9 единицам, следовательно, цифра 5 в записи числа 539 определяет количество сотен, цифра 3 – количество десятков, а цифра 9 – количество единиц. При этом говорят, что цифра 9 стоит в разряде единиц и число 9 является значением разряда единиц, цифра 3 стоит в разряде десятков и число 3 является значением разряда десятков, а цифра 5 – в разряде сотен и число 5 является значением разряда сотен.
Таким образом, разряд – это с одной стороны позиция цифры в записи натурального числа, а с другой стороны значение этой цифры, определяемое ее позицией.
Разрядам присвоены названия. Если смотреть на цифры в записи натурального числа справа налево, то им будут соответствовать следующие разряды: единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов и так далее.
Названия разрядов удобно запоминать, когда они представлены в виде таблицы. Запишем таблицу, содержащую названия 15 разрядов.
Заметим, что количество разрядов данного натурального числа равно количеству знаков, участвующих в записи этого числа. Таким образом, в записанной таблице содержатся названия разрядов всех натуральных чисел, запись которых содержит до 15 знаков. Следующие разряды также имеют свои названия, но они очень редко используются, поэтому не имеет смысла их упоминать.
С помощью таблицы разрядов удобно определять разряды данного натурального числа. Для этого нужно записать в эту таблицу данное натуральное число так, чтобы в каждом разряде оказалась одна цифра, и крайняя справа цифра оказалась в разряде единиц.
Приведем пример. Запишем натуральное число 67 922 003 942 в таблицу, при этом станут отчетливо видны разряды и значения этих разрядов.
В записи этого числа цифра 2 стоит в разряде единиц, цифра 4 – в разряде десятков, цифра 9 – в разряде сотен и т.д. Следует обратить внимание на цифры 0, находящиеся в разрядах десятков тысяч и сотен тысяч. Цифры 0 в этих разрядах означают отсутствие единиц данных разрядов.
Следует еще обмолвиться о так называемом низшем (младшем) и высшем (старшем) разряде многозначного натурального числа. Низшим (младшим) разрядом любого многозначного натурального числа является разряд единиц. Высшим (старшим) разрядом натурального числа является разряд, соответствующий крайней справа цифре в записи этого числа. Например, младшим разрядом натурального числа 23 004 является разряд единиц, а старшим – разряд десятков тысяч. Если в записи натурального числа двигаться по разрядам слева направо, то каждый следующий разряд ниже (младше) предыдущего. Например, разряд тысяч младше разряда десятков тысяч, тем более разряд тысяч младше разряда сотен тысяч, миллионов, десятков миллионов и т.д. Если же в записи натурального числа двигаться по разрядам справа налево, то каждый следующий разряд выше (старше) предыдущего. Например, разряд сотен старше разряда десятков, и тем более, старше разряда единиц.
В некоторых случаях (например, при выполнении сложения или вычитания) используется не само натуральное число, а сумма разрядных слагаемых этого натурального числа.
Вкратце о десятичной системе счисления.
Итак, мы познакомились с натуральными числами, со смыслом, заложенным в них, и способом записи натуральных чисел с помощью десяти цифр.
Вообще, метод записи чисел с помощью знаков, называют системой счисления. Значение цифры в записи числа может зависеть от ее позиции, а может и не зависеть от ее позиции. Системы счисления, в которых значение цифры в записи числа зависит от ее позиции, называют позиционными.
Таким образом, рассмотренные нами натуральные числа и метод их записи, указывает на то, что мы пользуемся позиционной системой счисления. Следует заметить, что особое место в этой системе счисления имеет число 10. Действительно, счет ведется десятками: десять единиц объединяются в десяток, десяток десятков объединяется в сотню, десяток сотен – в тысячу, и так далее. Число 10 называют основанием данной системы счисления, а саму систему счисления называют десятичной.
Помимо десятичной системы счисления существуют и другие, например, в информатике используется двоичная позиционная система счисления, а с шестидесятеричной системой мы сталкиваемся, когда речь идет об измерении времени.
Натуральные числа
Понятие натурального числа в математике — одно из основных.
Натуральные числа — первый вид чисел, который изучают в школьном курсе математики. Какие числа называются натуральными? Сколько существует натуральных чисел? Какое натуральное число является наименьшим?
Натуральные числа — это числа, которые используют при счете предметов.
Первые натуральные числа: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11 и т.д.
Все натуральные числа образуют множество натуральных чисел. Множество натуральных чисел обозначают N.
Чтобы показать, что некоторое число, например, 5, является натуральным, пишут:
Читают: «пять принадлежит множеству натуральных чисел» или просто «пять принадлежит эн».
Сколько всего существует натуральных чисел?
Множество натуральных чисел бесконечно.
Натуральные числа можно пронумеровать по порядку, но для любого натурального числа существует следующее за ним большее число.
Наименьшее натуральное число — единица. (Нуль не является натуральным числом).
Наибольшего натурального числа не существует.
Следовательно, натуральных чисел бесконечно много.
Натуральные числа и нуль
Видеоурок по этой теме можно посмотреть по ссылке: Натуральные числа и ноль.
Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!
Нас повсюду окружают предметы. Так было раньше, и так будет всегда. И очень часто необходимо знать, сколько у нас или где-то еще есть тех или иных предметов: яблок, машин, людей, денег и т.д.
Еще в очень глубокой древности, когда не было не только науки математики, но и даже такого понятия как число, древние люди проводили подсчет при помощи наиболее близких для них инструментов – собственных частей тела: «Там столько буйволов, сколько на моих руках пальцев», или: «Мы поймали рыбы столько, сколько пальцев на руках у меня и тебя».
Со временем они заметили, что десять буйволов, десять рыб, десять врагов и т.д. объединяет то, что рассказывая об этом, люди употребляют одинаковое описание: «сколько на моих руках пальцев». То есть, они обнаружили, что группы разных предметов обладают одним схожим свойством – количеством, и что удобнее назвать одинаковое количество чего-либо обобщенным названием, которое будет определять эту величину. И вместо: «Мы поймали столько рыбы, сколько пальцев на моих руках» люди начали говорить: «Мы поймали десять рыб». Так появились числа, которые впоследствии были названы натуральными. Подробнее об истории возникновения чисел можно почитать по ссылке.
Натуральные числа – это те числа, при помощи которых мы осуществляем счет предметов: 1, 2, 3, 4, 5 и т.д
Число 1 (один) имеет еще одно название: единица.
Если к единице приложить еще единицу, к получившемуся результату еще одну, потом еще, и еще и т.д., то мы получим ряд натуральных чисел или просто натуральный ряд: один, два, три, четыре, пять и т.д.
Любое натуральное число можно представить в виде единицы или собрания нескольких единиц.
Начинается натуральный ряд чисел с единицы, то есть, с числа 1 (один).
Каждое последующее число ряда отличается от предыдущего на единицу.
Любое натуральное число больше нуля.
Нуль не относится к натуральному ряду чисел. В некоторых англоязычных странах его включают в этот ряд, но в отечественной математике принято по-другому. Действительно, нуль означает отсутствие чего-либо, «ни одной единицы», «ни одного», «ничего». А поскольку ряд натуральных чисел состоит из единицы и совокупности сложений единиц, то число «ни одной единицы» не может находиться в этом ряду.
Нуль обладает такими свойствами:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.1 / 5. Количество оценок: 8
Натуральные числа
Понятие натуральные числа возникло естественным образом при счете. Перечисляя или исчисляя человек еще в древности дал определение натуральных чисел.
Надо помнить, что отрицательные и нецелые числа — натуральными числами не являются.
В бесконечном множестве натуральных чисел для любого натурального числа найдется другое натуральное число, которое больше его.
Исходя из теории множеств, единственным объектом для построения любых математических систем является множество.
Введение натуральных чисел, согласно определению множества, выполняется по двум правилам:
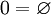
Такие числа, называются ординальными.
Над натуральными числами можно проводить ряд арифметических операций. Рассмотрим основные из них.
Операции, не выводящие результат из множества натуральных чисел, называются замкнутыми. К замкнутым арифметическим операциям относятся:
К основным свойствам сложения и умножения натуральных чисел относятся:
Результатом сложения и умножение двух натуральных чисел всегда является натуральное число.
К дополнительным арифметическим операциям над натуральными числами относятся:
Если m, n, k натуральные числа, то при m — n = k говорят, что m — уменьшаемое, n — вычитаемое, k — разность;
При m : n = k говорят, что m — делимое, n — делитель, k — частное.
К основным признакам делимости натуральных числе относятся:
Ненатуральные числа. Как отличить натуральные от ненатуральных
Что же такое натуральные и ненатуральные числа? Как объяснить ребенку, а может и не ребенку, в чем же отличия между ними? Давайте разбираться. Насколько известно, ненатуральные и натуральны числа изучают в 5 классе, и нашей целью является объяснить ученикам так, чтобы они действительно поняли и усвоили, что и как.
История
Все о натуральных числах
Такая система счисления стала современной из-за цифры 0, которую и изобрели арабы. До этого в индийской системе она отсутствовала.
Ненатуральные числа. Что это?
Ниже приведены примеры.
Ненатуральные числа бывают:
Иррациональные числ, такие, как e = 2,71828, √2 = 1,41421 и тому подобное.
Мы надеемся, что очень помогли вам разобраться с ненатуральными и натуральными числами. Теперь вам станет легче объяснить своему малышу данную тему, и он усвоит ее так же хорошо, как великие математики!
Натуральные числа и их свойства
Вы будете перенаправлены на Автор24
Натуральные числа и их свойства
Нуль не относят к натуральным числам.
Свойства отношения следования
Единица- натуральное число, которое не следует ни за каким натуральным числом.
За каждым натуральным числом следует одно и только одно число
Свойство сложения натуральных чисел
Сумма не изменяется при перестановке слагаемых
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом, к полученной сумме- второе слагаемое
От прибавления нуля число не измениться и если прибавить к нулю какое- нибудь число, то получится прибавленное число.
Свойства вычитания
Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а затем из полученной разности- второе слагаемое
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое
Если из числа вычесть нуль, то число не изменится
Если из числа вычесть его само, то получится нуль
Готовые работы на аналогичную тему
Свойства умножения
Произведение двух чисел не изменяется при перестановке множителей
Чтобы умножить число на произведение двух чисел,можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель
При умножении на нуль произведение равно нулю
Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо
Свойства умножения относительно сложения и вычитания
Распределительное свойство умножения относительно сложения
Для того чтобы умножить сумму на число,можно умножить на это число каждое слагаемое и сложить получившиеся произведения
Распределительное свойство умножение относительно вычитания
Для того,чтобы умножить разность на число,множно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе
Сравнение натуральных чисел
Меньшим считается число, которое в натуральном ряду появляется раньше, а большим, которое появляется позже. Нуль меньше любого натурального числа.
в любом подмножестве натуральных чисел, содержащем хотя бы одно число, есть наименьшее число
Подмножеством в математике называют часть множества. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества
Округление натуральных чисел
Натуральные числа округляют до десятков, сотен,тысяч и т.д
Правило округления натуральных чисел
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 27.05.2022
Сообщение по математике на тему «Натуральные числа»
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Сообщение по математике на тему « Натуральные числа»
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N. Это множество имеет начало, но не имеет конца.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания.
Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.
Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.
Особенности натуральных чисел
· Наименьшее натуральное число: единица (1).
· Наибольшее натуральное число: не существует. Натуральный ряд бесконечен.
· У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7 и т. д.
Классы натуральных чисел
Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:
1. От перестановки множителей конечное произведение не изменится.
2. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель (справедливо для всех множителей).
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Натуральные числа
Натуральные числа — это числа, которые используются при счёте или нумерации.
Натуральные числа, записанные в порядке их возрастания (начиная с 1) и без пропусков, образуют ряд натуральных чисел, или короче натуральный ряд:
В натуральном ряду есть первое число — 1 (один или единица), но нет последнего числа — за каждым натуральным числом следует ещё одно, которое больше предшествующего на единицу. Таким образом, есть наименьшее натуральное число — 1, а наибольшего натурального числа не существует. Следовательно 1 — это самое маленькое натуральное число.
Натуральный ряд бесконечен.
Все натуральные числа записать невозможно. Поэтому при записи натурального ряда выписывают подряд несколько первых чисел, следующих друг за другом в натуральном ряду, и в конце ставят многоточие (три точки).
Отсутствие предметов для счёта условились обозначать числом 0 (нуль).
Нуль не считается натуральным числом.
Чётные и нечётные натуральные числа
В натуральном ряду чередуются нечётные и чётные числа, то есть числа, которые делятся на 2 и которые на 2 не делятся. Начинается натуральный ряд с нечётного числа:
Нечётные числа обозначены чёрным цветом, а чётные — красным.
Прямой и обратный счёт
Прямой счёт — это перечисление чисел в порядке их возрастания. Под порядком возрастания, в данном случае, подразумевается что каждое последующее число больше предыдущего на единицу.
Рассмотрим прямой счёт от 1 до 10:
| 1, | 2, | 3, | 4, | 5, | 6, | 7, | 8, | 9, | 10 |
| один | два | три | четыре | пять | шесть | семь | восемь | девять | десять |
Перечисление чисел натурального ряда в порядке их возрастания называется прямым счётом.
Обратный счёт — это перечисление чисел в порядке их убывания. Под порядком убывания, в данном случае, подразумевается что каждое последующее число меньше предыдущего на единицу.
Рассмотрим обратный счёт от 10 до 1:
| 10, | 9, | 8, | 7, | 6, | 5, | 4, | 3, | 2, | 1 |
| десять | девять | восемь | семь | шесть | пять | четыре | три | два | один |
Перечисление чисел натурального ряда в порядке их убывания называется обратным счётом.
Какие числа называются целыми
О чем эта статья:
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Что нужно знать о свойствах натурального числа — основные сведения
Определение натурального числа
Натуральное число является значимым понятием современной математики. Они возникают при естественном счете.
Натуральные числа служат для счета предметов, объектов. При этом числа не связаны с их индивидуальными характеристиками.
Число — результат абстрагирования.
Но числа в сознании могут оставаться связанными с осязаемыми объектами — пальцами, узелками, камушками. В языках народов для обозначения предметов используют различные сочетания числительных.
Особенности натурального числа
Натуральными являются целые положительные числа. Любое такое число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Запись называют десятичной.
Те натуральные числа, которые формируют последовательность, образуют натуральный ряд. В натуральном ряду каждое следующее число на 1 больше предыдущего.
Единица — самое маленькое натуральное число. Самое большое число натурального ряда подобрать нельзя — он бесконечен.
К натуральным числам не относят ноль. Это число означает «ни одного».
Множество натуральных чисел обозначают буквой латинского алфавита N.
Операции над натуральными числами
К операциям над натуральными числами относят:
a, b — слагаемые, c — сумма.
Сумма всегда больше любого из слагаемых.
Когда нужно найти неизвестное слагаемое, из суммы вычитают известное слагаемое: b=c-a.
a, b — множители или множитель и сомножитель, c — их произведение.
В операции умножения натуральных чисел самым большим числом будет произведение.
Чтобы найти неизвестный множитель, произведение делят на известный множитель: b=c:a.
a — основание, b — показатель степени, a b — степень.
a — уменьшаемое, b — вычитаемое, c — разность.
Самое большое число в операции вычитания — уменьшаемое.
Вычитаемое = уменьшаемое — разность.
Уменьшаемое = вычитаемое + разность.
a — делимое, b — делитель, c — частное.
Самое большое число в делении — делимое.
Делимое = делитель * частное.
Делитель = делимое : частное.
a — делимое, b — делитель, c — неполное частное, q — остаток от деления.
Делимое = делитель * неполное частное + остаток.
Свойства натуральных чисел
Математическую теорию натуральных (то есть целых положительных) чисел называют арифметикой.
Арифметика опирается на факты: сложение и умножение целых чисел подчиняются определенным закономерностям. Чтобы описать эти законы, прибегают к использованию символов — букв a, b, c…
Это делается для того, чтобы не рассматривать частные случаи на примере определенных числовых значений, а создать универсальные правила. А для применения сформулированных законов достаточно заменить буквенные символы заданными числами и воспользоваться правилами.
Существует пять основных законов арифметики или пять основных свойств, которыми обладают натуральные числа. С их помощью упрощают выражения.
Пять законов арифметики:
Коммутативный — переместительный закон сложения: при сложении можно менять порядок чисел, над которыми совершается действие.
a+b=b+a — от перестановки слагаемых сумма не меняется.
Коммутативный — переместительный закон умножения: при умножении можно менять порядок чисел, над которыми совершается действие.
a * b = b * a — от перестановки множителей произведение не меняется.
Ассоциативный — сочетательный закон сложения: при сложении трех чисел результат не изменится, если к первому числу прибавим сумму второго и третьего, или прибавим третье к сумме второго и первого.
Ассоциативный — сочетательный закон умножения: когда умножаем три числа, то результат не изменится, если перемножать множители не по порядку.
Дистрибутивный — распределительный закон: при умножении суммы на число можно умножить число на каждый компонент суммы, а потом полученные произведения сложить.
Алгебраические операции с нулем рассмотрим без приведения доказательств:
Свойство нуля при сложении:
Свойства нуля при вычитании:
Свойство нуля при умножении:
Свойства нуля при делении:
При делении числа на само себя получаем 1.
Разряды и их значения
Значение цифры в записи числа определяется ее местом.
Место цифры в числе называется разрядом.
При записи числа выделяют три разряда:
Разряд единиц — последнее место в записи числа в соответствующем классе.
Разряд десятков — предпоследнее место.
Разряд сотен — третье место от конца записи числа.
Если в разряде стоит ноль, то говорят об отсутствии единиц данного разряда в десятичной записи числа.
Если число состоит из одного знака — цифры — его называют однозначным. Когда в числе два знака — двузначным.
Числа, которые состоят более чем из одного знака, называют многозначными.
Чтобы прочитать многозначное число, его запись разбивают на классы справа налево. В каждый класс заключают три знака — три разряда.
Разрядов только три.
Разбейте число на классы и прочитайте его: 123 456 789 098 000 321 654.
В этом числе 654 единицы в классе единиц, 321 единица в классе тысяч, ноль единиц в классе миллионов, 98 единиц в классе миллиардов, 789 единиц в классе триллионов, 456 единиц в классе квадриллионов и 123 единицы в классе квинтиллионов.
Представим решение задания в таблице:
| Классы | Квинтиллионы | Квадриллионы | Триллион | Миллиарды (биллионы) | Миллионы | Тысячи | Единицы | ||||||||||||||
| Разряды | сотни | десятки | единицы | сотни | десятки | единицы | сотни | десятки | единицы | сотни | десятки | единицы | сотни | десятки | единицы | сотни | десятки | единицы | сотни | десятки | единицы |
| Число | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 9 | 8 | 0 | 0 | 0 | 3 | 2 | 1 | 6 | 5 | 4 |
Число читается: 123 квинтиллиона 456 квадриллионов 789 триллионов 98 миллиардов 321 тысяча 654.
Десятичная система счисления
В десятичной системе счисления для записи натуральных чисел используют 10 знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — десять цифр. Из этих цифр составляют другие натуральные числа большей величины.
Смысл каждой из используемых цифр зависит от ее положения в числе — разряда. Принцип образования числа, когда в основе лежит определение позиции каждой цифры в нем, называют позиционным.
Изобретение позиционной нумерации, которая основана на поместном значении цифр, приписывают вавилонянам и шумерийцам. Такая нумерация была развита индусами. Древние системы нумерации были построены на аддитивном принципе, но с элементами позиционности. Например, римская нумерация предполагает «сложение или вычитание разрядов».
VII — пять + один + один = семь.
IV — пять – один = четыре.
Египетская, греческая системы были на том же уровне.
Главное неудобство такой системы заключалось в необходимости введения большого количества новых символов при увеличении числа. Это затрудняло арифметические вычисления.
Позиционная система, за счет небольшого количества символов для обозначения разных чисел, выгоднее в использовании.
Десятичная система счисления — позиционная.
Число 10 в десятичной системе счисления — «основание» системы.
Задания для самопроверки
Запишите решение выражения в столбик: 234+4567.
Записываем число под числом, цифра под цифрой — разряд под разрядом. Для удобства в верхней строке запишем то число, которое длиннее: 4567. Строго под ним число 234. Разряды второго располагаются строго под соответствующими разрядами первого числа.
В числе 4567 в разряде единиц класса единиц стоит 7, в числе 234 в разряде единиц класса единиц — 4. Значит, 4 пишем строго под 7.
В 4567 в разряде десятков класса единиц стоит 6, в 234 в разряде десятков класса единиц — 3. Значит, 3 пишем строго под 6.
В 4567 в разряде сотен класса единиц стоит 5, в 234 в разряде сотен класса единиц стоит 2. Значит, 2 пишем строго под 5.
В 4567 в разряде единиц класса тысяч стоит 4, в 234 в разряде единиц класса тысяч ничего не стоит. Значит, под 4 ничего не пишем.
7+4=11, 1 пишем в разряде единиц, 1 в уме добавляем в следующий разряд — разряд десятков.
3+6=9 и еще один в уме, получаем 10. Ноль пишем в разряде десятков, один запоминаем.
5+2=7 и еще 1 (запоминали), получаем 8. Пишем 8 разряд сотен.
К 4 ничего не прибавляем, просто переписываем в сумму в разряд единиц класса тысяч.
Используя свойства сложения из урока, упростите выражение: 54+(26+73).
Используем сочетательное свойство умножения для решения задачи.
Сначала сложим число и первый компонент суммы. К результату прибавим оставшееся число.
Из свойства сложения следует: 26+b+14=b+26+14=b+(26+14)=b+40. По образцу упростите выражение: 72+y+32.
Для упрощения выражения воспользуемся переместительным свойством сложения.
Самостоятельно решите тренажер, используя свойства сложения и умножения из конспекта:
Объяснение работы по алгоритму.
Используя сочетательное свойство умножения, получим:
Упростим выражение: 12(5+6).
Используя распределительный закон, получим:
Математика для блондинок
Страницы
понедельник, 1 февраля 2010 г.
 |
| Цифры, из которых состоят натуральные числа |
Для того, чтобы понимать, какие числа в математике называются натуральными, могу предложить такой вариант распознавания натуральных чисел: единица и все числа, которые можно получить в результате сложения единиц, будут натуральными числами.
Если кто-то считает, что нуль принадлежит к натуральным числам, ничего страшного. Просто выучите наизусть, что ноль является натуральным числом и всё. В разных странах этот вопрос решается по-разному. Например, в англоязычной математике ноль считается натуральным числом. Спросите у любого шпиона))) Кстати, разведчики точно также могут проколоться на этом вопросе)))
Что мы сделали? Мы счетные палочки в руке заменили единичками в математике. Теперь проверим на практике, как это работает. Рассмотрим число 2 (два):
Число 2 является натуральным числом, так как может быть представлено в виде суммы двух единиц, что соответствует двум счетным палочкам или двум другим предметам «для счета естественным образом» (цитата из классического определения натуральных чисел).
Возьмем пример посложнее. Если дробное число 7,5 разделить на другое дробное число 2,5, будет ли результат натуральным числом?
Да, в результате деления двух дробных чисел мы получили натуральное число 3, поскольку оно может быть получено в результате сложения трех единиц.
Если число рассыпается на единички без шума и пыли, такое число является натуральным. Например, число 2,5 (два с половиной) не является натуральным, так как кроме двух единичек со страшным грохотом отваливается дробная часть числа 0,5:
Еще один пример. Число -4 (минус четыре) не является натуральным, поскольку при разложении на единички отпадает знак минус и поднимает целую кучу пыли. Отрицательные числа невозможно получить сложением положительных единиц. Кстати, в пыли отрицательных чисел математики блуждали, как ежики в тумане. Вместо того, чтобы разобраться в причинах пылевой бури, они придумали модуль числа, чем еще больше всех запутали.
Надеюсь, мое пояснение поможет вам лучше ориентироваться в таких разных названиях таких одинаковых чисел.
34 комментария:
дробные числа, которые при максимальном упрощении остаются дробными несократимы
Прекрастный сайт, главное весёлый)
Не удалось найти «доступного» обьяснения о модуле. Это я чтото не правильно ищу или его здесь дейвствительно нет?
спасибо вам огромное за сайт и вашу работу!
слишком много слов. достаточно было написать что натуральные это целые неотрицательные числа и всё.
Аноним, я тоже умный и закончил физфак, но с Николаем согласен. Это математика для блондинок и должно быть а) точно, б) доступно. Здесь это удачно сочетается. Вы уверены, что Вашего определения достаточно?
Это Интернет, а не учебник. Кстати, даже в диссертациях есть требование к минимально допустимому объему )))
Спасибо огромное за определение.
Так я еще никому не объясняла.
Выведем математику на новый уровень
А что такое «сложение» в определении натурального числа? Не будет ли правильнее определить множество натуральных чисел, и только затем задать на нем операцию сложения?
Лично я вообще против определений. Всё-таки, эту статью нужно переделать, что бы не вводить народ в заблуждение.
В третьем абзаце опечатка
Попытался подправить. Теперь правильно?
Очень доступно. Школу закончила давно, но в самом начале вашего объяснени про модуль сразу поняла о чем речь. Спасибо. Простота Ваших объяснений очень поможет в занятиях математикой с внуком. Суперские шпаргалки для бабушек, не только для блонди!
Не надо изобретать велосипед, почитайте лучше арифметику Киселева. Вот выдержки по вашей теме:
«Один предмет да один предмет составляют два предмета; два предмета да один предмет составляют три предмета; три да один составляют четыре и т.д. Один, два, три, четыре и т.д. называются целыми числами. Таким образом всякое целое число есть либо единица либо собрание нескольких единиц.
Если к единице присоединить еще единицу, к полученному числу снова присоединить единицу, потом еще единицу и т.д. получится натуральный ряд чисел: один, два, три, четыре, пять, шесть и т.д. Наименьшее число в этом ряду единица, наибольшего числа нет, т.к. к любому числу как бы велико оно ни было, всегда можно присоединить еще единицу и получить число еще большее; значит, натуральный ряд можно продолжать без конца; поэтому говорят, что натуральный ряд бесконечен.»
Согласен, изобретать велосипед не стоит. Но если у изобретателя не хватает ума научить других пользоваться велосипедом? Вот и приходится таким, как я и Киселев, писать пошаговые инструкции по езде на велосипеде :)))
так что же делать с нулём?
Единственное,что я знаю точно, так это то, что нулю абсолютно всё равно, что мы с ним будем делать. Лично я противник постоянных молитв типа «знаменатель не равняется нулю». Проще усвоить, что ноль не является числом и в знаменателе его просто не может быть. Дешево и сердито )))
Я не могу решить задачу, не зная точно, принадлежит ли ноль к множеству натуральных чисел! Мне плевать на Англию с её шпионами, но в России что делать с нулём при решении задач о нескольких первых значениях множества натуральных чисел.
В России ноль обычно не входит во множество натуральный чисел, если это не оговорено отдельно. Во всезнающей Википедии по поводу нуля и теории множеств написан полный бред, что так часто встречается в математике.
Желаю успехов в обучении))))
А причём тут блондинки. Можно подумать остальные категории населения(с другим цветом волос) шибко много понимают,мужские особи точно так же пользуются помощью данного ресурса. Или это очередной способ как легально оскорбить женщин.
Отличное определение! Как и у Киселева. А с нулем нужно поконкретнее. Я бы сказал: Ноль числом не является, но если хотите, то можете пользоваться, а когда с ним возникнут проблемы, просто вспомните об этом. Хотя. может быть, здесь про ноль вообще не упоминать, есть же спецраздел про ноль. Этот ноль так часто путается под ногами, что только мешает.
Блин, с этой говорящей дрессированной обезьяной меня ещё не сравнивали. Про ноль правильно, если его отодвинуть в сторонку, он никому мешать не будет)))
Не знаю, обезьяна или нет. Я взял приписываемые ему слова чуть выше на этой странице.
Мне хоть и 8лет но я не поняла ничего
Вот что нашёл в http://www.decoder.ru
Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства
В математике существует несколько различных множеств чисел: действительные, комплексные, целые, рациональные, иррациональные, дробные… В нашей повседневной жизни мы чаще всего используем натуральные числа, так как мы сталкиваемся с ними при счете и при поиске, обозначении количества предметов.
Какие числа называются натуральными
Из десяти цифр можно записать абсолютно любую существующую сумму классов и разрядов. Натуральными значениями считаются те, которые используются:
N значения всегда целые и положительные. Наибольшего N не существует, так как множество целых значений не ограничено.
[warning]Внимание! Натуральные числа получаются при счете предметов или при обозначении их количества.[/warning]
Абсолютно любое число может быть разложено и представлено в виде разрядных слагаемых, например: 8.346.809=8 миллионов+346 тысяч+809 единиц.
Множество N
Множество N находится в множестве действительных, целых и положительных. На схеме множеств они бы находились друг в друге, так как множество натуральных является их частью.
Множество натуральных чисел обозначается буквой N. Это множество имеет начало, но не имеет конца.
Еще существует расширенное множество N, где включается нуль.
Наименьшее натуральное число

Но в иностранных математических школах, например во французской, нуль считается натуральным. Наличие в ряде нуля облегчает доказательство некоторых теорем.
Ряд значений N, включающий в себя нуль, называется расширенным и обозначается символом N0 (нулевой индекс).
Ряд натуральных чисел
N ряд – это последовательность всех N совокупностей цифр. Эта последовательность не имеет конца.
Особенность натурального ряда заключается в том, что последующее число будет отличаться на единицу от предыдущего, то есть возрастать. Но значения не могут быть отрицательными.
[warning]Внимание! Для удобства счета существуют классы и разряды:[/warning]
Все N
Все N находятся во множестве действительных, целых, неотрицательных значений. Они являются их составной частью.
Эти значения уходят в бесконечность, они могут принадлежать классам миллионов, миллиардов, квинтиллионов и т.д.
Например:
Последовательность в N

от нуля до плюс бесконечности, включая концы, и от единицы до плюс бесконечности, включая концы, то есть все положительные целые ответы.
N совокупности цифр могут быть как четными, так и не четными. Рассмотрим понятие нечетности.
Нечетные (любые нечетные оканчиваются на цифры 1, 3, 5, 7, 9.) при делении на два имеют остаток. Например, 7:2=3,5, 11:2=5,5, 23:2=11,5.
Что значит четные N
Любые четные суммы классов оканчиваются на цифры: 0, 2, 4, 6, 8. При делении четных N на 2, остатка не будет, то есть в результате получается целый ответ. Например, 50:2=25, 100:2=50, 3456:2=1728.
[stop]Важно! Числовой ряд из N не может состоять только из четных или нечетных значений, так как они должны чередоваться: за четным всегда идет нечетное, за ним снова четное и т.д.[/stop]
Свойства N
Как и все другие множества, N обладают своими собственными, особыми свойствами. Рассмотрим свойства N ряда (не расширенного).
[warning]Внимание! Все вышеперечисленные неравенства действительны и в обратном направлении.[/warning]
Как называются компоненты умножения

Для того, чтобы быстро и правильно умножать и уметь решать обратные задачи, необходимо знать компоненты умножения.
15.10=150. В данном выражении 15 и 10 являются множителями, а 150 – произведением.
Умножение обладает свойствами, которые необходимы при решении задач, уравнений и неравенств:
Например: 15.Х=150. Разделим произведение на известный множитель. 150:15=10. Сделаем проверку. 15.10=150. По такому принципу решаются даже сложные линейные уравнения (если упростить их).
[stop]Важно! Произведение может состоять не только из двух множителей. Например: 840=2.5.7.3.4[/stop]
Что такое натуральные числа в математике?
Разряды и классы натуральных чисел
Вывод
Подведем итоги. N используются при счете или обозначении количества предметов. Ряд натуральных совокупностей цифр бесконечен, но он включает в себя только целые и положительные суммы разрядов и классов. Умножение тоже необходимо для того, чтобы считать предметы, а также для решения задач, уравнений и различных неравенств.
Числа
Операции над натуральными числами
К замкнутым операциям над натуральными числами (операциям в результате, которых получается натуральных чисел) относятся следующие арифметические операции:
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как их результат не всегда будет натуральным числом.
Сколько нулей в числе
Повторяем состав чисел
Сова: Хорошо. Посмотрим, как ребята помнят состав чисел. Что такое состав чисел? Правильно. Это два числа, из которых состоит каждое число. А зачем нам нужно знать состав чисел? Чтобы быстро считать удобным способом.
Давайте вспомним, как мы это делали во втором классе. Например, нам нужно найти сумму чисел 23 и 50. Что мы с вами будем делать? Разложим число 27 на два слагаемых: 20 и 7. Теперь нам легче будет сложить десятки и к полученной сумме прибавить три единицы.
Вспомнили? Решите несколько примеров, используя свои знания о составе чисел.
Сова : Молодцы, ребята! О, черепашке Маше уже не терпится решать с вами задачи. Что ты ребятам сегодня приготовила?
Геометрические фигуры и задачи
Кошка Алиса: Мур, мур! Да, я люблю рисовать различные геометрические фигуры. А ребята помнят геометрические фигуры?
Назовите все геометрические фигуры, которые видите.
Сова: Ну что скажешь, Алиса, знают ребята геометрические фигуры?
Алиса :Мур, мур, знают. А вот,помнят они, как чертить отрезки, делить их и обозначать буквами?
Сова: А ты проверь. Дай им задачу и посмотри, помнят или забыли за лето?
Алиса: Хорошо. Вот вам геометрическая задача.
Начертите в тетради отрезок АВ длиной 1 дм 2 см. Разделите его точками на три равные части. Обозначьте буквами отмеченные точки. Запишите все полученные отрезки.
Ответ : АС, СD, DB..
Поверья разных народов
У различных древних народов есть дополнительные правила трактовки чисел. Одни уверенны, что счастливым знаком являются только нечетные. Мудрецы Востока считают девятку предвестником неудачи. Она предупреждает об изменениях в жизни, как о положительных, так и о негативных.
Считается, что гадание на время на часах предупреждает о недругах, если человеку постоянно попадаются четные комбинации. Избежать неприятностей можно, если снизить активность, занять выжидательную позицию.
Магия чисел
Каждый человек, как всем известно, является любопытным от природы существом, особенно если речь идет про его будущее. Даже те люди, которые не воспринимают эзотерику всерьез, все равно иногда невольно прислушиваются к ней. Особо восприимчивыми к таким практикам являются те люди, у которых в жизни появились некоторые проблемы.
С начала нашего рождения числа следуют за нами по пятам. Вы наверняка знаете, что дата рождения, количество букв в имени и фамилии человека имеют большое влияние на судьбу младенца. Это всё есть знаки судьбы, которые предсказывают наше будущее либо предупреждают о предстоящих опасностях.
Изучение чисел от 1 до 100
Это табличка для изучения чисел от 1 до 100. Пособие подходящее для детей старше 4 лет.
Те, кто знаком с Монтесори обучением, наверно уже такую табличку видел. У нее есть много приложений и сейчас мы с ними познакомимся.
Ребенок должен отлично знать числа до 10, прежде начать работу с таблицей, так как счет до 10 лежит в основе обучения чисел до 100 и выше.
При помощи этой таблице, ребенок выучит имена чисел до 100; считать до 100; последовательность чисел. Можно так же тренироватся считать через 2, 3, 5, и т.д.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди называть количество единиц каждого класса и добавлять название класса.
Название класса единиц не произносят, также не произносят название класса, если все три цифры в его разрядах — нули.
Числа 1, 10, 100, 1000 … называются разрядными единицами. С их помощью натуральное число записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Следующие за миллиардом классы названы в соответствии с латинскими наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее, но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества) во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого 100 нулей.
Подготовка к гаданию
Сперва вы должны решить, на кого станете гадать. Вам нужно будет представить человека в мельчайших подробностях, таких как его лицо, привычки, внешность и т. д. Проведите глубокую концентрацию на своём запросе, глубоко осознайте что вас именно интересует.
Для гадания «Сотня» вам понадобится: листок бумаги (чистый), а также пишущее средство. На листке заполняем в любом порядке цифры от 1 до 100 (цифры с нулями, как и нули, ставить не надо, а если хотите поставить цифру 30, вписываете число 3).
Прежде чем начать гадать, нужно обязательно поверить в эту практику, и тогда она приоткроет завесу в будущее.
Ряд первый заполняйте так, как вам вздумается. Доверьтесь своей судьбе и пишите любое количество цифр. В последующих рядах их должно быть то же количество символов, ни больше ни меньше. Внизу вы обязательно должны указать день, месяц, год, а также точное время ритуала.
Таблица квадратов
Случайное | рандомное число онлайн в 1 клик
Числа окружают нас с самого рождения и играют важную роль в жизни. У многих людей сама работа связана с числами, кто-то полагается на удачу, заполняя числами лотерейные билеты, а кто-то придает им и вовсе мистическое значение. Так или иначе, иногда нам не обойтись без того, чтобы воспользоваться такой программой, как генератор рандомных чисел.
К примеру, вам необходимо организовать розыгрыш призов среди подписчиков вашей группы. Быстро и честно выбрать призеров и поможет наш генератор случайных чисел онлайн. Вам просто нужно, например, задать нужное количество рандомных чисел (по числу призеров) и максимальный диапазон (по числу участников, если им присвоены номера). Подтасовка в таком случае полностью исключается.
Эта программа может также послужить как генератор случайных чисел для лото. К примеру, вы купили билет и хотите полностью полагаться на случайность и удачу в выборе чисел. Тогда наш рандомайзер чисел поможет заполнить ваш лотерейный билет.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Таблица натуральных чисел
Сравнение натуральных чисел.
Определяем верные и неверные равенства
Сова : Продолжаем работать. Вспомним, что такое равенство и неравенство?
Равенство это когда левая часть выражения (примера) равна правой. Например, 12+4 = 16. В равенстве используют знак «=»
А неравенство – левая часть выражения больше или меньше правой. Например, 12+4
Повторили? А теперь, закрепим. Вам нужно будет выписать только неверные неравенства.

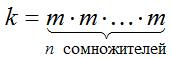



 на множители может быть таким:
на множители может быть таким: .
.