Дискретная математика что это

Дискретная математика

Дискре́тная матема́тика — область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях.

К числу таких структур могут быть отнесены конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы, машины Тьюринга и так далее. Это примеры структур конечного (финитного) характера. Раздел дискретной математики, изучающий их, называется конечной математикой. Иногда само это понятие расширяют до дискретной математики. Помимо указанных конечных структур, дискретная математика изучает некоторые алгебраические системы, бесконечные графы, вычислительные схемы определённого вида, клеточные автоматы и т. д. В качестве синонима иногда употребляется термин «дискретный анализ».

Содержание

Разделы дискретной математики

Примечания

Литература

См. также

Ссылки

Полезное

Смотреть что такое «Дискретная математика» в других словарях:

ДИСКРЕТНАЯ МАТЕМАТИКА — то же, что конечная математика … Большой Энциклопедический словарь

дискретная математика — то же, что конечная математика. * * * ДИСКРЕТНАЯ МАТЕМАТИКА ДИСКРЕТНАЯ МАТЕМАТИКА, то же, что конечная математика (см. КОНЕЧНАЯ МАТЕМАТИКА) … Энциклопедический словарь

ДИСКРЕТНАЯ МАТЕМАТИКА — конечная математика, раздел математики, занимающийся изучением св в объектов конечного характера. К их числу могут быть отнесены, напр., конечные группы, конечные графы, нек рые матем. модели преобразователей информации. Д. м. теоретич. основа… … Большой энциклопедический политехнический словарь

ДИСКРЕТНАЯ МАТЕМАТИКА — то же, что конец ноя математика … Естествознание. Энциклопедический словарь

«Дискретная математика» — научный журнал РАН, с 1989, Москва. Учредитель (1998) Отделение математики РАН. 4 номера в год … Энциклопедический словарь

Теория функциональных систем (дискретная математика) — У этого термина существуют и другие значения, см. Теория функциональных систем (значения). Теория функциональных систем раздел дискретной математики, занимающийся изучением функций, описывающих работу дискретных преобразователей. В теории… … Википедия

МАТЕМАТИКА — (греч. mathematike от mathema наука), наука, в которой изучаются пространственные формы и количественные отношения. До нач. 17 в. математика преимущественно наука о числах, скалярных величинах и сравнительно простых геометрических фигурах;… … Большой Энциклопедический словарь

Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия

математика — и; ж. [греч. mathēmatikē] 1. Наука о количественных отношениях и пространственных формах действительного мира. Высшая м. Элементарная м. Прикладная м. Законы математики. // Учебный предмет, изучающий эту науку. Экзамен по математике. Преподавать… … Энциклопедический словарь

Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия

Источник

Основы дискретной математики

Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.

Об этой статье

Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!

ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?

Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.

Мы рассмотрим пять основных разделов в следующем порядке.

ЛОГИКА

Что такое логика?

Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.

Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).

Начнем с азов. Рассмотрим следующее высказывание на естественном языке:

«Если я голоден, я ем».

Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:

A => B (то есть из A следует B)

NB. Посылка и следствие являются суждениями.

Логические выражения

Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.

Например, 10 4 — ИСТИНА.

Логические операции

Суждение P — это утверждение, которое может быть как истинным, так и ложным.

Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).

Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).

Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.

Источник

Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.

Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.

Дискретность – это …

Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.

В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.

Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.

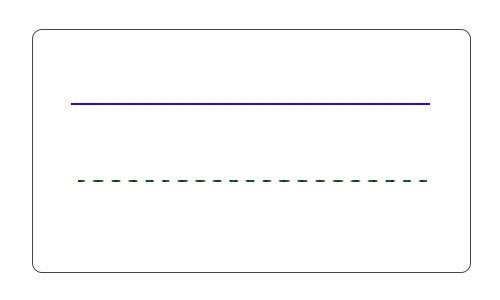
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:

Дискретность можно толковать следующим образом:

Далее проанализируем особенности применения термина в различных областях.

Дискретная математика

Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.

ДМ условно подразделяется на пять направлений:

Дискретная величина

Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.

Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.

Дискретность в информатике

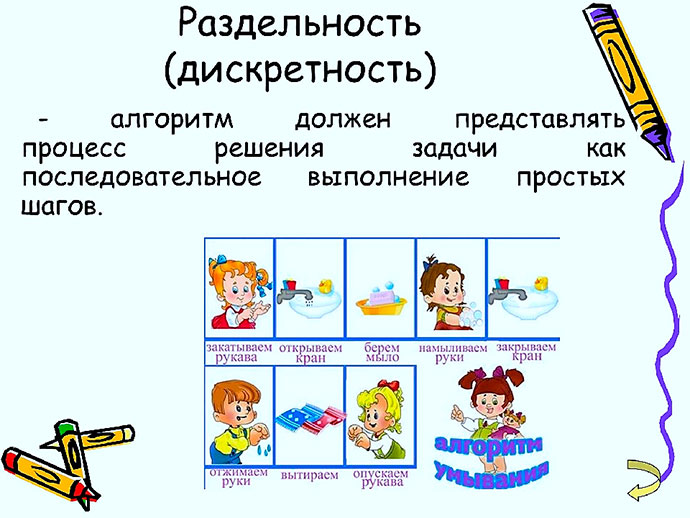
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).

Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.

Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):

Дискретная видеокарта

Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.

Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.

Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.

Дискретность в биологии

Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Благодарю за дискретное изложение материала

Источник

Дискретные структуры: матан для айтишников

Посмотришь на любую программу обучения по IT-специальности, и тут же увидишь дисциплину «Дискретная математика» (возможно, под другим названием), обычно для перво- или второкурсников. И её наличие вполне разумно, поскольку дискретная математика и непрерывная математика (представленная на первом курсе институтов с незапамятных времён математическим анализом) — две грани единой Математики, — красивой, могучей науки.

Хотя раньше такого понятия, как «дискретная математика» вовсе не было, это не значит, что не возникало дискретных задач: Абель, Дирихле, Фибоначчи, Эйлер, чьи имена возникают по ходу изучения дискретной математики, — отнюдь не наши современники! Но просто в те времена для выделения самостоятельной ветви математики ещё не сложилось критической массы задач и приёмов, не было видно взаимосвязей между ними. А большое количество плодотворных взаимосвязей между, на первый взгляд, различными понятиями, — то, что математики в своей науке очень ценят.

Ну хорошо, математикам всё математическое интересно. А зачем дискретная математика программисту?

Зачем это айтишнику

Во-первых, многие идеи, которые особенно ярко иллюстрируются на дискретных задачах, неотъемлемы и для информатики. Взять, хотя бы, фундаментальные понятия рекурсии и индукции.

Рекурсия — это, дословно, возврат, обращение к самому себе. Хорошо известные вездесущие числа Фибоначчи проще всего определяются рекурсивно: первые два числа Фибоначчи равны единице, а каждое следующее число равно сумме двух своих предшественников: 1,1,2,3,5,8,… Таким образом, для вычисления очередного числа мы обращаемся к уже рассчитанным числам такого же вида. Трудно представить, как можно изучить функциональное программирование, да и многое из других областей информатики, не освоившись хорошо с рекурсией. Очень близкий процесс к рекурсии — это индукция, способ доказательства математических утверждений, при котором в доказательстве сложных случаев мы опираемся на более простые. Параллели с рекурсией очевидны, и действительно, обычное дело, когда индуктивное доказательство существования какого-то объекта можно переформулировать в описание рекурсивного способа построения этого объекта.

Раз речь зашла о таких фундаментальных вещах, как индукция и рекурсия, не могу не сказать, что многие приёмы, которые очень хорошо видны на примерах из дискретной математики, эффективны в математике в целом. Это не только индукция, но и принцип Дирихле, принцип выбора по среднему значению и другие.

Следующий элемент, без которого информатику нельзя представить — это графы. Простейшие алгоритмы на графах обязательно входят в любой, даже самый вводный, курс по алгоритмам. Скажем, с понятием гамильтонова цикла связана одна из классических задач информатики, задача коммивояжёра.

Ещё одно архиважное умение — считать точно и оценивать приблизительно количества. Например, как вычислить количество раз, которые выполняется операция сравнения в цикле:

Или вот ещё пример. Нужно из списка из 100 товаров выбрать 20, так, чтобы их суммарная стоимость была ровно 2000 рублей («без сдачи»). Это вариант классической задачи о рюкзаке. Допустим, ваш коллега, подумав ночь, предложил решать задачу перебором: перебрать всевозможные наборы из двадцати товаров, и, как только в ходе перебора возникнет нужный набор, выдать его в качестве ответа. Между прочим, характеристика «переборный» далеко не всегда ставит клеймо на алгоритме. Всё зависит от размера входных данных. Так вот, как прикинуть, удастся ли за разумное время решить перебором эту задачу выбора 20 объектов из 100?

Наконец, для современного «дизайнера алгоритмов» обязателен к пониманию и вероятностный метод. Это общий метод, позволяющей решать многие задачи в современной комбинаторике. Очень часто наилучшие решения задач, известные на сегодняшний день, получены именно этим методом. Для практика же овладение этим методом полезно постольку, поскольку вероятностные алгоритмы прочно заняли место в современной информатике. И при анализе работы таких алгоритмов очень помогает интуиция, развитая в ходе изучения вероятностного метода.

Онлайн-курс «Дискретные структуры»

С верой в то, что перечисленные понятия из дискретной математики действительно не помешают любому программисту, а, скорее, помешает их незнание, я читаю соответствующий курс на факультете ФИВТ МФТИ. А недавно у меня появилась возможность сделать онлайн-курс, чем я с радостью воспользовался. Записаться на него можно по ссылке. Главное, чего я пожелаю всем записавшимся: не побоявшись трудностей, пройти курс до самого конца, и получить заслуженное звание Дипломированного Дискретчика. В общем, чтобы MOOC прошёл без мук и обогатил знаниями! Да и собственная корысть у меня тут тоже есть: чем больше онлайн-учеников у меня будет, тем большему я смогу научиться, читая обсуждения и наблюдая статистику решения задач. Ведь учиться учить тоже никогда не поздно!

Какие знания потребуются

Для прохождения первых двух модулей потребуются только школьные знания. Третий модуль потребует знание основ математического анализа на уровне «что такое предел» и «какая из функций x 20 или 2 x растёт быстрее (чему равны производные функций)». Для последних трёх модулей понадобится представление о том, что такое вероятность, условная вероятность, математическое ожидание, дисперсия. Также хорошо бы знать, что такое базис и размерность линейного пространства. Если с вероятностью и линейной алгеброй вы не знакомы, можно записаться заодно на эти вводные курсы. Тогда как раз, к моменту, когда нам потребуются эти знания, они у вас будут.

Post scriptum

Меня можно было бы упрекнуть в конфликте интересов, всё-таки я математик, и, естественно, хочу приобщить к своей секте как можно больше завсегдатаев Хабра. В своё оправдание могу сослаться на этот ответ на Quora. Под большей частью тем, перечисленных в этом ответе, я готов лично подписаться, в онлайн-курс многие из них вошли. Ещё сошлюсь на подборку мнений яндексоидов.

Источник

Дискретная математика

Категории Дискретная математика | Под редакцией сообщества: Математика

Важнейшие примеры дискретных математических объектов: натуральный ряд чисел; конечное множество элементов произвольной природы; функция (отображение) из конечного множества в конечное множество; слово (последовательность символов) в конечном алфавите; формальный язык (множество слов в конечном алфавите); конечный граф и другие.

Содержательно дискретный объект обычно мыслится как состоящий из строго отграниченных, отделенных друг от друга неделимых частей. Объекты рассматривают как дискретные также в тех случаях, когда по каким-либо причинам отвлекаются от присущих им свойств непрерывности.

В обычном понимании дискретность и непрерывность являются оппозитными (противоположными, взаимно дополнительными) понятиями. Следует, однако, подчеркнуть, что деление математики на «непрерывную» и «дискретную» весьма условно; математика едина: вся она пронизана глубокими аналогиями, сходные идеи и конструкции одинаково успешно работают в различных ее разделах.

Различают дискретную математику в широком и в узком смысле. Дискретная математика в наиболее широком смысле включает в себя знания о всех видах дискретных объектов из теории чисел, алгебры, геометрии, математической логики, теории вероятностей, численного анализа и других разделов математики. Дискретная математика в собственном (узком) смысле состоит из ряда специальных разделов, среди которых важнейшие: комбинаторный анализ, теория графов, теория дискретных функций, теория автоматов и алгоритмов, теория сложности, теория формальных языков, теория дискретных экстремальных задач, теория кодирования, дискретная геометрия и другие. Применения дискретной математики составляют основу современных компьютерных наук и информатики.

Содержание

↑История развития

Возникновение дискретной математики относят к глубокой древности. С незапамятных времен известны комбинаторно-логические задачи, решение которых связано с перебором комбинаций дискретных объектов и логическим анализом возникающих вариантов. Некоторые из них сохранились до нашего времени в занимательной математике в виде задач-головоломок или салонных игр (простейшие примеры: широко известные задачи о волке, козе и капусте, о Ханойской башне и другие). Когда число возникающих вариантов велико, а перебор сократить не удается, решение задачи становится затруднительным.

Такие задачи в общем виде по сию пору относятся к числу труднейших в математике. Дискретные системы с древнейших времен применяются в вычислительной практике.

Начало современного этапа в развитии дискретной математики относят к XVII веку и связывают с появлением работ Л. Эйлера в области комбинаторного анализа и теории графов, Я. Бернулли по комбинаторной теории вероятностей. Большую роль в развитии идеологии дискретной математики сыграл Г. В. Лейбниц. В XIX веке в области дискретной математики работали известные математики: Ж. Л. Лагранж, А. Кэли, Дж. Буль, К. Жордан и многие другие.

В начале XX века значительное развитие получили «предтечи» современной дискретной математики: дескриптивная теория множеств, комбинаторная топология, общая алгебра.

Большое значение для осознания роли дискретной математики в науке XX века имело возникновение и распостранение в современном естествознании представлений о дискретном характере окружающей нас реальности (атомно-молекулярная теория, квантовая и статистическая физика). Существенное влияние на развитие дискретной математики на этом этапе оказали исследования в области оснований математики, в частности, финитистские установки А. Пуанкаре и Д. Гильберта (грубо говоря, стремление считать «законными» лишь такие математические построения, которые сводятся к выполнению в конечное число шагов процедур над конечными объектами), работы Э.Л. Поста, А.М.Тьюринга и других по теории алгоритмов, исследования Э.Л.Поста в области выразимости функций алгебры логики.

Бурное развитие дискретной математики во второй половине XX века связывают с произошедшей в те годы (и продолжающейся поныне) «цифровой революцией» в телекоммуникационной и вычислительной технике. Дискретная математика стала основой проектирования и применения многочисленных цифровых электронных устройств. Первые применения дискретной математики в этой области связаны с именами В. А. Котельникова, К. Э. Шеннона, В.И. Шестакова. Возникновение в рамках кибернетики математической теории управляющих систем привело к развитию целых новых разделов дискретной математики: теории сложности, теории тестов, теории надежности схем, теории автоматов и других. Существенный вклад в дискретную математику на этом этапе был сделан Дж. фон Нейманом, А.А. Ляпуновым, С.В. Яблонским, О.Б. Лупановым.

↑Методы, задачи и разделы дискретной математики

В последние десятилетия методы дискретной математики глубоко проникли во многие отрасли науки и техники, включая физику, химию, экономику, биологию, экологию и другие. Повсеместное распостранение моделей и методов дискретной математики привело к появлению большого числа новых задач и существенно расширило содержание многих классических разделов дискретной математики.

В современном комбинаторном анализе помимо традиционных перечислительных задач большое внимание уделяется изучению комбинаторных конфигураций (дизайнов), алгоритмам решения комбинаторных задач, комбинаторной оптимизации, вероятностной комбинаторике. В теории графов развились новые разделы: экстремальная теория графов, теория матроидов, теория потоков в сетях и другие. В 1976 году К. Аппелем и В. Хакеном было предложено «машинное» решение известной проблемы четырех красок, вызвавшее ожесточенные споры о правомерности использования вычислительных машин для доказательства математических утверждений.

Одним из центральных разделов дискретной математики является теория дискретных функций, изучающая отображения дискретных множеств. Важнейшие из них: булевы функции (см.: булева функция), функции конечнозначных логик, автоматные (ограниченно-детерминированные) функции, вычислимые функции и другие. Исследования в этой области сосредоточены, главным образом, на проблемах выразимости функций (в частности, выразимости в виде суперпозиций) и на изучении метрических характеристик дискретных функций.

Возможность практического решения задач существенно зависит от их сложности. Всякий вычислительный процесс, осуществляемый в реальном устройстве, требует расхода вычислительных ресурсов, основными из которых являются время и память. Эти и другие величины, с содержательной точки зрения выражающие трудность решения задачи, называют мерами сложности. Теория сложности изучает математические модели вычислительных процессов и устройств с целью их оптимизации по отношению к различным мерам сложности и для различных классов задач.

Одним из наиболее развитых в теории сложности является раздел, изучающий сложность булевых функций. Большое значение имеют вопросы сложности двоичной арифметики, используемой практически во всех вычислительных процессах. Широко разработаны вопросы сложности алгоритмов решения разнообразных конкретных задач (в частности, задач обработки текстовой информации, сортировки и поиска, численного анализа и многие другие).

К числу наиболее известных нерешенных задач дискретной математики относится ряд проблем теории сложности, касающихся умножения двоичных чисел, умножения матриц, дискретного логарифмирования, распознавания изоморфизма графов; особо важное значение придается проблеме получения нелинейных нижних оценок сложности булевых функций и проблеме равенства классов P и NP в теории сводимости комбинаторных задач (проблема P=NP?).

Одним из наиболее развитых разделов дискретной математики является теория кодирования, изучающая математические вопросы передачи информации по зашумленным каналам связи. Основные задачи теории кодирования связаны с построением оптимальных в том или ином смысле кодов, в частности, кодов с исправлением ошибок. Построение таких кодов связано с задачами наилучшей упаковки дискретных пространств множествами заданного вида. Наиболее известными кодами с исправлением ошибок являются коды Хэмминга, исправляющие единичную ошибку, коды Боуза-Чоудхури-Хоквингема (БЧХ-коды), коды Рида-Маллера.

Значительное место в исследованиях по дискретной математике и ее приложениям занимают дискретные экстремальные задачи. Большое число работ в этой области посвящено задачам целочисленного программирования, теории расписаний, поиска и распознавания информации.

↑Рекомендуемая литература

1. Дискретная математика и математические вопросы кибернетики. Т. I. / Под общ. ред. С. В. Яблонского и О. Б. Лупанова. М.: Наука, 1974.

3. Робертс Ф. Дискретные математические модели с приложениями к социальным, биологическим и экологическим задачам. М.: Наука, 1986.

4. Саати Т. Целочисленные методы оптимизации и связанные с ними экстремальные проблемы. М.: Мир, 1973.

5. Яблонский С. В. Введение в дискретную математику. М.: Наука, 1979.

Эта статья еще не написана, но вы можете сделать это.

Источник

Дискретная математика для первокурсников: опыт преподавателя

Сегодня у меня необычный текст, совершенно не связанный с машинным обучением (для новых читателей: этот текст – часть блога компании Surfingbird, в котором я в течение последнего года рассказывал о разных аппаратах машинного обучения в приложении к рекомендательным системам). В этом посте математической части практически не будет, а будет описание очень простой программки, которую я написал для своих студентов. Вряд ли кто-то узнает для себя из этого поста много содержательно нового, но мне кажется, что некоторую ценность представляет сама идея – многие люди просто не задумываются о том, что «и так можно». Итак…

Постановка задачи

В этом семестре у меня началась несколько непривычная деятельность: я преподаю дискретную математику для первокурсников в петербургском филиале Высшей Школы Экономики; преподаю я давно, но, кажется, раньше никогда у меня не было студентов младше четвёртого-пятого курса. По ссылке можно найти краткое содержание курса, да и то неполное (курс ещё идёт), но речь не совсем об этом.

Думаю, большинство обитателей хабра хотя бы приблизительно помнят, что такое «дискретная математика для первокурсников»: пропозициональная логика, конъюнктивные и дизъюнктивные нормальные формы, базисы булевских функций, бинарные отношения, частичные порядки… В общем, ничего концептуально сложного, но это всё вещи, которыми надо овладеть очень прочно, на них держится любое математическое образование, и необходимость осознанно задумываться о них быстро станет непозволительной роскошью. Поэтому нужно много практических примеров и заданий, чтобы «набить руку».

В качестве одной из форм отчётности я выбрал «большое домашнее задание»: несколько как раз таких практических примеров, которые надо решать. У такой формы много плюсов: студенты работают в удобном им темпе, я тоже проверять могу сколько нужно, всё в письменном виде происходит, что всегда удобно. Но есть и минусы; главный минус прост – трудно сделать и проверить пятьдесят вариантов на пятьдесят студентов (на потоке их примерно столько и есть). А если дать один вариант на большую группу, понятно, что на выходе получишь красиво переписанные правильные ответы, особенно учитывая, что в такой базовой дискретной математике «ход решения» нередко просто отсутствует (как построить СДНФ – ну как, посмотреть на таблицу истинности да записать. ).

Чтобы обойти эту проблему, я решил написать простую программку, которая будет генерировать индивидуальное домашнее задание для каждого студента случайным образом. Идея чрезвычайно простая, но почему-то ни в свою бытность студентом, ни в более позднем преподавательском опыте я её ни разу не встречал – собственно, поэтому и пишу этот пост. Я приведу минимальный работающий пример, а потом покажу, что у меня в результате получилось.

Базовая технология понятна – нужно сделать LaTeX-заготовку, в которую вставлять конкретные задания для каждого студента. Совершенно всё равно, на каком языке это делать, мне исторически привычнее писать небольшие программки на C++, поэтому я и тут буду его использовать. Самый простой способ сделать это в C++, который я знаю, – это boost::format: достаточно сделать заготовки с плейсхолдерами вроде %1%, %2%, и потом можно вставлять туда что угодно (у boost::format есть и другие возможности, но нам они сейчас не понадобятся).

Итак, делаем шаблоны. Сначала общий шаблон «абстрактного LaTeX-документа»:

Потом конкретный шаблон собственно задания – его мы будем подставлять вместо %1%. Я здесь, как и обещал, привожу минимальный пример. Мы будем генерировать только одну задачку: по заданной булевской формуле перевести её в несколько других форм.

И теперь нам просто нужно сгенерировать, чем заполнить %3% (вместо %1% и %2% будут подставляться имя студента и номер группы). Для этого нужно научиться генерировать формулы. Сразу предупреждаю, что я плохой программист, и код ниже наверняка напоминает спагетти – в принципе, он работает, если кто-нибудь посоветует изящный рефакторинг, скажу спасибо.

Сначала надо завести структуру, которая будет хранить разные связки и типы узлов в формуле; для нашего минимального примера это лишнее, но мне надо было сделать ещё задачку про формулы алгебры множеств (объединения, пересечения да симметрические разности), и код про деревья формул хотелось переиспользовать. Поэтому вот глобальный объект, хранящий основную информацию:

Здесь мы создали «язык булевских формул», у которого пять бинарных связок (конъюнкция, дизъюнкция, импликация, XOR и эквивалентность) и одна унарная (отрицание). Седьмой тип узла – это переменная, у неё арность 0. В домашнем задании я ограничился формулами из четырёх переменных: меньше маловато, а больше становится слишком громоздко. Сюда же удобно записать генераторы случайного типа узла, случайной переменной, случайной бинарной связки (я пользовался распределениями из boost::random – опять же, очень удобно; хоть там и не так уж много чего реализовано, но нам сейчас много и не надо).

Такую структуру легко будет переиспользовать для формул алгебры множеств (это просто для сравнения, дальше GSet использоваться не будет):

Теперь создаём класс формулы. Булевская формула – это дерево, листьями которого служат переменные, а внутренними вершинами – логические связки. Мы хотим уметь генерировать формулы заданной глубины, поэтому в конструктор будем передавать, не пора ли сделать этот узел листом или, наоборот, обязательно бинарной связкой. Если нужно создать случайный узел, будем передавать тип g->TypesNo. Если узел оказался листом, ему нужно сгенерировать переменную (чтобы с большой вероятностью переменные попали все, мы просто берём их по кругу – формулы, конечно, не совсем случайные получаются, но это не страшно).

Теперь начинаем заполнять класс BNode. Главное для нас – чтобы формула успешно печаталась в LaTeX:

Кроме того, нужно будет уметь подсчитывать значение формулы на заданном наборе переменных:

Оставим пока класс BNode (мы к нему ещё вернёмся); теперь мы можем написать генератор случайной формулы. Будем генерировать формулу с заданной минимальной и максимальной глубиной (для поддержки минимальной глубины мы добавляли раньше в конструктор поле must_not_be_leaf):

Тут всё самоочевидно; единственное решение, которое я здесь принял – сделал унарные функции (т.е. отрицания) «бесплатными», не считающимися для глубины, иначе формулы получались бы слишком простыми. Кроме того, в булевской формуле логично запретить ставить два отрицания подряд, это бессмысленно; для этого нам и нужен был флаг must_be_binary в конструкторе.

И можно писать обработчик файла со списком студентов:

а затем и main, который читает файлы с форматами и процессит файлы со списками студентов:

Но постойте, слышу я голос внимательного читателя. Будет же ерунда получаться – небось, добрая половина так сгенерированных случайных формул окажутся тривиальными! Что верно, то верно – про половину не знаю, но даже одна случайно сгенерированная формула вида \varphi = x изрядно подмочит репутацию нашего метода. Давайте мы научимся это проверять. Для этого мы просто подсчитаем, сколько в формуле встречается связок и разных переменных, и потребуем, чтобы переменные встречались все, а связки – хотя бы две разные. Добавляем в BNode обход формулы:

и вписываем проверку формулы на разумность:

Можно ещё захотеть проверить, не является ли формула, скажем, всегда истинной, но я этого сознательно решил не делать – если сложная на вид формула вдруг окажется тождественно истинной, тем интереснее будет это задание для студента. А очевидные подформулы типа «x или не x» в нашем генераторе не будут получаться, потому что переменные перебираются по очереди, а не случайно.

Решения

Скептически настроенный читатель на этом месте разумно возразит: ну конечно, ты можешь сгенерировать over 9000 разных заданий, но ведь ты замучаешься их потом проверять! И действительно, проверять у каждого студента таблицу истинности – занятие для очень сильных духом людей, к которым я себя не отношу. Поэтому нашу программку надо будет модифицировать так, чтобы она могла облегчить и процесс проверки. Совсем автоматизировать его не получится (студенты всё равно будут сдавать работы, написанные в свободном формате от руки), поэтому достаточно будет просто сделать заранее самую противную часть этой работы.

Заводим другой LaTeX-шаблон для документа с ответами:

Я, опять же, ограничусь минимальным примером – давайте просто выведем таблицу истинности. Для этого нужно пройтись по всем возможным значениям переменных, посчитать истинностное значение формулы и красиво оформить результат в TeX’е. Добавляем два метода в класс BNode:

а затем добавляем это в process_one_student_file_boolean:

В результате в пару к файлу заданий (пример) получается соответствующий ему файл решений (тот же пример, решения), по которому проверять становится гораздо проще.

Заключение

И вот результат – полдня работы, а на выходе сколько угодно заданий с готовыми ответами, всё красиво оформлено и готово к выдаче студентам. Если интересно, каким получилось реальное задание, вот пример окончательного результата. Файл с ответами выкладывать не буду, чтобы лишний раз не подсказывать студентам – они сейчас как раз решают это домашнее задание. Думаю, если моё преподавание в ГУ-ВШЭ будет продолжаться, эта программка мне ещё не раз послужит; ближайший шанс её применить – билеты для письменного экзамена в тех же группах.

Источник

Дискретная математика

В контексте математики в целом дискретная математика часто отождествляется с конечной математикой — направлением, изучающим конечные структуры — конечные графы, конечные группы, конечные автоматы. И при этом можно выделить некоторые особенности, не присущие разделам, работающим с бесконечными и непрерывными структурами. Так, в дискретных направлениях как правило обширнее класс разрешимых задач, так как во многих случаях возможен полный перебор вариантов, тогда как в разделах, имеющих дело с бесконечными и непрерывными структурами, для разрешимости обычно требуются существенные ограничения на условия. В этой же связи в дискретной математике особо важную роль играют задачи построения конкретных алгоритмов, и в том числе, эффективных с точки зрения вычислительной сложности. Ещё одна особенность дискретной математики — невозможность применения для её экстремальных задач техник анализа, существенно использующих недоступные для дискретных структур понятия гладкости. В широком смысле, дискретной математикой могут считаться охваченными значительные части алгебры, теории чисел, математической логики.

В рамках учебных программ дискретная математика обычно рассматривается как совокупность разделов, связанных с приложениями к информатике и вычислительной технике: теория функциональных систем, теория графов, теория автоматов, теория кодирования, комбинаторика, целочисленное программирование.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Данная статья представляет собой обзор основных событий и тенденций в истории математики с древнейших времён до наших дней.

Источник

Дискретная математика простым языком

Посмотришь на любую программу обучения по IT-специальности, и тут же увидишь дисциплину «Дискретная математика» (возможно, под другим названием), обычно для перво- или второкурсников. И её наличие вполне разумно, поскольку дискретная математика и непрерывная математика (представленная на первом курсе институтов с незапамятных времён математическим анализом) — две грани единой Математики, — красивой, могучей науки.

Хотя раньше такого понятия, как «дискретная математика» вовсе не было, это не значит, что не возникало дискретных задач: Абель, Дирихле, Фибоначчи, Эйлер, чьи имена возникают по ходу изучения дискретной математики, — отнюдь не наши современники! Но просто в те времена для выделения самостоятельной ветви математики ещё не сложилось критической массы задач и приёмов, не было видно взаимосвязей между ними. А большое количество плодотворных взаимосвязей между, на первый взгляд, различными понятиями, — то, что математики в своей науке очень ценят.

Ну хорошо, математикам всё математическое интересно. А зачем дискретная математика программисту?

Зачем это айтишнику

Во-первых, многие идеи, которые особенно ярко иллюстрируются на дискретных задачах, неотъемлемы и для информатики. Взять, хотя бы, фундаментальные понятия рекурсии и индукции.

Рекурсия — это, дословно, возврат, обращение к самому себе. Хорошо известные вездесущие числа Фибоначчи проще всего определяются рекурсивно: первые два числа Фибоначчи равны единице, а каждое следующее число равно сумме двух своих предшественников: 1,1,2,3,5,8,… Таким образом, для вычисления очередного числа мы обращаемся к уже рассчитанным числам такого же вида. Трудно представить, как можно изучить функциональное программирование, да и многое из других областей информатики, не освоившись хорошо с рекурсией. Очень близкий процесс к рекурсии — это индукция, способ доказательства математических утверждений, при котором в доказательстве сложных случаев мы опираемся на более простые. Параллели с рекурсией очевидны, и действительно, обычное дело, когда индуктивное доказательство существования какого-то объекта можно переформулировать в описание рекурсивного способа построения этого объекта.

Раз речь зашла о таких фундаментальных вещах, как индукция и рекурсия, не могу не сказать, что многие приёмы, которые очень хорошо видны на примерах из дискретной математики, эффективны в математике в целом. Это не только индукция, но и принцип Дирихле, принцип выбора по среднему значению и другие.

Следующий элемент, без которого информатику нельзя представить — это графы. Простейшие алгоритмы на графах обязательно входят в любой, даже самый вводный, курс по алгоритмам. Скажем, с понятием гамильтонова цикла связана одна из классических задач информатики, задача коммивояжёра.

Ещё одно архиважное умение — считать точно и оценивать приблизительно количества. Например, как вычислить количество раз, которые выполняется операция сравнения в цикле:

Или вот ещё пример. Нужно из списка из 100 товаров выбрать 20, так, чтобы их суммарная стоимость была ровно 2000 рублей («без сдачи»). Это вариант классической задачи о рюкзаке. Допустим, ваш коллега, подумав ночь, предложил решать задачу перебором: перебрать всевозможные наборы из двадцати товаров, и, как только в ходе перебора возникнет нужный набор, выдать его в качестве ответа. Между прочим, характеристика «переборный» далеко не всегда ставит клеймо на алгоритме. Всё зависит от размера входных данных. Так вот, как прикинуть, удастся ли за разумное время решить перебором эту задачу выбора 20 объектов из 100?

Наконец, для современного «дизайнера алгоритмов» обязателен к пониманию и вероятностный метод. Это общий метод, позволяющей решать многие задачи в современной комбинаторике. Очень часто наилучшие решения задач, известные на сегодняшний день, получены именно этим методом. Для практика же овладение этим методом полезно постольку, поскольку вероятностные алгоритмы прочно заняли место в современной информатике. И при анализе работы таких алгоритмов очень помогает интуиция, развитая в ходе изучения вероятностного метода.

Онлайн-курс «Дискретные структуры»

С верой в то, что перечисленные понятия из дискретной математики действительно не помешают любому программисту, а, скорее, помешает их незнание, я читаю соответствующий курс на факультете ФИВТ МФТИ. А недавно у меня появилась возможность сделать онлайн-курс, чем я с радостью воспользовался. Записаться на него можно по ссылке. Главное, чего я пожелаю всем записавшимся: не побоявшись трудностей, пройти курс до самого конца, и получить заслуженное звание Дипломированного Дискретчика. В общем, чтобы MOOC прошёл без мук и обогатил знаниями! Да и собственная корысть у меня тут тоже есть: чем больше онлайн-учеников у меня будет, тем большему я смогу научиться, читая обсуждения и наблюдая статистику решения задач. Ведь учиться учить тоже никогда не поздно!

Какие знания потребуются

Для прохождения первых двух модулей потребуются только школьные знания. Третий модуль потребует знание основ математического анализа на уровне «что такое предел» и «какая из функций x 20 или 2 x растёт быстрее (чему равны производные функций)». Для последних трёх модулей понадобится представление о том, что такое вероятность, условная вероятность, математическое ожидание, дисперсия. Также хорошо бы знать, что такое базис и размерность линейного пространства. Если с вероятностью и линейной алгеброй вы не знакомы, можно записаться заодно на эти вводные курсы. Тогда как раз, к моменту, когда нам потребуются эти знания, они у вас будут.

Post scriptum

Меня можно было бы упрекнуть в конфликте интересов, всё-таки я математик, и, естественно, хочу приобщить к своей секте как можно больше завсегдатаев Хабра. В своё оправдание могу сослаться на этот ответ на Quora. Под большей частью тем, перечисленных в этом ответе, я готов лично подписаться, в онлайн-курс многие из них вошли. Ещё сошлюсь на подборку мнений яндексоидов.

Очень часто слышу о том, что дискретная математика крайне необходима программисту, но не увидел где бы то ни было четко аргументированного ответа с примерами, зачем она нужна и где применяется.

Посему, хочу попросить гуру программирования или просто прошаренных в этой области людей привести либо учебные материалы (можно и на русском и на английском), либо примеры из жизни, где будет желательно в деталях объясняться, как именно применяется этот раздел математики.

Убедительная просьба воздержаться от комментариев об очевидности данного вопроса, т.к. для меня он не очевиден и я бы хотел разобраться в нем.

Источник

ДИСКРЕТНАЯ МАТЕМАТИКА

Смотреть что такое «ДИСКРЕТНАЯ МАТЕМАТИКА» в других словарях:

ДИСКРЕТНАЯ МАТЕМАТИКА — то же, что конечная математика … Большой Энциклопедический словарь

Дискретная математика — Дискретная математика область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях. К числу таких структур могут быть отнесены конечные группы, конечные графы, а… … Википедия

дискретная математика — то же, что конечная математика. * * * ДИСКРЕТНАЯ МАТЕМАТИКА ДИСКРЕТНАЯ МАТЕМАТИКА, то же, что конечная математика (см. КОНЕЧНАЯ МАТЕМАТИКА) … Энциклопедический словарь

ДИСКРЕТНАЯ МАТЕМАТИКА — то же, что конец ноя математика … Естествознание. Энциклопедический словарь

«Дискретная математика» — научный журнал РАН, с 1989, Москва. Учредитель (1998) Отделение математики РАН. 4 номера в год … Энциклопедический словарь

Теория функциональных систем (дискретная математика) — У этого термина существуют и другие значения, см. Теория функциональных систем (значения). Теория функциональных систем раздел дискретной математики, занимающийся изучением функций, описывающих работу дискретных преобразователей. В теории… … Википедия

МАТЕМАТИКА — (греч. mathematike от mathema наука), наука, в которой изучаются пространственные формы и количественные отношения. До нач. 17 в. математика преимущественно наука о числах, скалярных величинах и сравнительно простых геометрических фигурах;… … Большой Энциклопедический словарь

Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия

математика — и; ж. [греч. mathēmatikē] 1. Наука о количественных отношениях и пространственных формах действительного мира. Высшая м. Элементарная м. Прикладная м. Законы математики. // Учебный предмет, изучающий эту науку. Экзамен по математике. Преподавать… … Энциклопедический словарь

Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия

Источник

Дискретная математика

Вы будете перенаправлены на Автор24

Понятие дискретной математики

В понятие «дискретная математика» объединены все разделы математики, которые основаны на дискретных структурах. Между ними существуют определенные взаимосвязи, которые зачастую ссылаются друг на друга, но в общей совокупности они составляют единую теорию, к которой относится и вся математика в целом. Однако, дискретная математика строится на самостоятельных теориях и направлениях.

Дискретная математика – это часть математики, которая построена на исследовании дискретных математических структур, к которым относятся графы и утверждения в логике.

Дискретная математика, в контексте математики как науки, отождествляется с конечной математикой (направлением, основой знаний которой является исследование конечных структур – конечных графов, конечных автоматов, конечных групп). Конечность определяет некоторые особенности, которые не характерны разделам, изучающим бесконечные и непрерывные структуры (например, для дискретных направлений характерен более широкой круг решаемых задач, потому как во многих случаях возможен перебор различных вариантов, при том, как в изучении бесконечных и непрерывных структур характерны существенные ограничения для решения задач).

В дискретной математике большое значение уделено построению определенных алгоритмов, в том числе, эффективных с точки зрения вычислений и их сложности. Еще одной отличительной особенностью дискретной математики является невозможность использования ее техник анализа при решении экстремальных задач, потому как используются недоступные для дискретных структур понятия гладкости.

Дискретная математика рассматривается как совокупность разделов, которые связаны с информатикой и вычислительной техникой, в частности, к ним относятся: теория графов, теория функциональных систем, теория автоматов, комбинаторика и теория кодирования, целочисленное программирование.

История развития

С давних времен дискретные системы применялись в вычислительной практике. В древности были широко известны различные системы счисления и связанные с ними алгоритмы выполнения различных арифметических операций, решения уравнений и пр. Распространение получили различные дискретные инструменты: различные виды счетных досок, абак.

Готовые работы на аналогичную тему

Дискретная математика развивалась параллельно с другими разделами математики, являясь составной частью единого целого.

Примерами дискретных математических объектов являются:

Дискретный объект с позиции его содержания обычно состоит из отдельно взятых элементов, отделенных друг от друга неделимых частей. Объекты рассматривают как дискретные, если по определенным причинам отвлекаются от присущих им свойств непрерывности.

Разделение математики на «дискретную» и «непрерывную» условно, потому как математика представляет собой единую систему, пронизанную аналогиями. В ее разделах развиваются различные сходные конструкции и идеи, то есть происходит обмен идеями и методами, также зачастую возникает необходимость в исследовании моделей, которые обладают как дискретными, так и непрерывными функциями.

В широком смысле дискретная математика включает в себя такие разделы математики как: теория чисел, теория множеств, алгебра, математическая логика и прочие.

Узконаправленно дискретная математика формирует ряд специализированных разделов и новые разделы, которые интенсивно развиваются с середины прошлого века, что обусловлено новыми изобретениями и их внедрением с применение вычислительной техники и цифровых технологий (теория функциональных систем, теория сетей и графов, теория алгоритмов и автоматов, комбинаторный анализ, теория кодирования, теория синтеза управляющих систем, дискретная геометрия и пр.).

Этапы развития дискретной математики связаны с исследованиями Л. Эйлера (XVII в.), который ввел комбинаторный анализ и теорию графов, и Я. Бернулли, разработавшем комбинаторную теорию вероятностей. Большой вклад в идеологию дискретной математики вложили Г.В. Лейбниц, Ж.Л. Лагранж, А. Кэли, Дж. Буль, Ж. Жордан и прочие.

Нужны еще материалы по теме статьи?

Воспользуйся новым поиском!

Найди больше статей и в один клик создай свой список литературы по ГОСТу

Источник

Почему школам важно уделять больше времени изучению дискретной математики

Автор материала приводит аргументы в пользу изучения дискретной математики на этапе школьного образования.

Большинство программ по математике [в США] для средних и старших классов следуют четко прописанной схеме:

Предалгебраические задачи → Алгебра 1 → Геометрия → Алгебра 2 → Тригонометрия/начала матанализа → Матанализ

В некоторых других школах предпочтение отдается более комплексному подходу, в рамках которого элементы алгебры, геометрии и тригонометрии подаются смешанно в течение 3-х или 4-х летнего курса. Однако обоим методикам недостает существенного акцента на дискретную математику и такие ее разделы, как комбинаторика, теория вероятности, теория чисел, теория множеств, логика, алгоритмы и теория графов. Дискретная математика очень мало фигурирует в большинстве «критически важных» промежуточных экзаменов средних и старших классов. Аналогично ситуация обстоит и с приемными экзаменами для вузов и колледжей, таких, как SAT. Из-за этого дискретной математике часто уделяется мало внимания.

Тем не менее эта область знаний в последние годы становится все более и более важным направлением. И на то есть целый ряд причин:

Дискретная математика играет существенную роль в изучении математики в колледжах, вузах и более высоких ступенях.

Дискретная математика наряду с численными методами и общей алгеброй входит в список фундаментальные компонентов математики вузовского уровня. Ученики, получившие солидный объем знаний по дискретной математике перед поступлением в колледж, получают существенное преимущество во время дальнейшей учебы.

Дискретная математика — это математика вычислительных процессов.

Все вычисления современной компьютерной науки практически полностью основаны на дискретной математике, и в частности, комбинаторике и теории графов. Это значит, что для изучения фундаментальных алгоритмов, используемых компьютерными программистами, студентам требуется иметь твердые знания в этих областях. Действительно, для получения диплома в области компьютерных наук в большинстве университетов предусмотрен соответствующий обязательный курс по дискретной математике.

Дискретная математика больше всего приближена к задачам реального мира.

Многие учащиеся часто задаются вопросами о том, где в реальной жизни им может пригодится традиционная высшая математика, то есть алгебра, геометрия, тригонометрия и другие ее направления. Часто, глядя на абстрактную природу этих предметов, они теряют к ним интерес. Дискретная математика, и в частности, комбинаторика и теория вероятности, позволяют ученикам даже уровня средней школы очень быстро прийти к изучению интересных и нетривиальных задач, имеющих прямое отношение к задачам реального мира.

Дискретная математика — популярное направление большинства математических соревнований средней и старшей школы.

Видные математические олимпиады вроде MATHCOUNTS (средняя школа) и American Mathematics Competitions (старшие классы) включают значительное количество заданий по дискретной математике. В более сложных соревнования для старшеклассников, таких, как AIME, количество задач увеличивается еще сильнее. Ученики, не имеющие соответствующей базы знаний будут иметь гораздо меньше шансов на успех в таких соревнованиях. Один известный преподаватель, занимающийся подготовкой учеников к MATHCOUNTS, даже уделяет половину времени подготовке к заданиям по комбинаторике и теории вероятности. Настолько он считает их важными.

Дискретная математика развивает логическое мышление и учит техникам доказательства.

Алгебра часто преподается в виде совокупности формул и алгоритмов, которые ученики должны запомнить. Например, формула корней квадратного уравнения, или решение систем линейных уравнений путем замены. Геометрия часто преподается как серия упражнений, доказывающих теоремы и объясняющих их суть, которые нередко предлагается заучить наизусть. Несмотря на несомненную важность изучения подобного материала, в целом он не очень хорошо способствует развитию творческого математического мышления учеников. В противовес этому, изучающие дискретную математику дети учатся мыслить гибко и творчески уже с самого начала. Количество формул, которые требуется знать наизусть, относительно невелико. В этой области знаний акцент делается скорее на потребность изучить некоторое количество фундаментальных понятий, которые впоследствие можно применять совершенно по-разному.

Дискретная математика — это весело.

Многие студенты, особенно одаренные и мотивированные находят алгебру, геометрию и даже методы матанализа скучными, не вызывающими живого интереса. Что же касается дискретной математики, то в ней такие темы встречаются редко. Когда мы интересуемся у учащихся их любимыми темами, большинство называет комбинаторику или теорию чисел. Самой непопулярной темой при этом оказывается геометрия. Иными словами, большинство студентов находят дискретную математику более интересной, чем алгебра или геометрия.

Исходя из всех этих аргументов, мы настоятельно рекомендуем строить программу так, чтобы после изучения геометрии, школы уделяли некоторое время ознакомлению учеников с элементарными идеями дискретной математики, и в частности, комбинаторики, теории вероятности и теории чисел.

Источник

Дискретная математика что это

Что же такое «Дискретная математика»? Чем она отличается от обычной математики? Почему имеет широкое применение в информатике? Будем разбираться в этих и других вопросах, касательно этой интересной и очень важной темы в современном мире [1].

Математика в переводе с греческого означает изучение, наука, исторически возникла на основе измерения формы объектов, подсчёта чего-либо и т.д. Люди считали овец в своих стадах, высчитывали сколько материала понадобится для строительства, сейчас математика используется во многих науках узкого и широкого направлениях: экономика, физика, астрономия, информатика и так далее [2].

Дискретная математика изучается столько же, сколько и обычная, частью которой и является. Термин «дискретный» означает прерывистый и имеет противоположный по свойствам термин «непрерывный».

Если открыть кран так, чтобы текла струя воды, то поток будет описывать некоторую непрерывную прямую. Если сделать так, чтобы из крана капали капли, то это будет дискретная совокупность. Причём не важно, как часто капают капли. Главное, что нас интересует, то, что через какое-то время появляется новая капля, которая не соединена с первой в пространстве. В математике нет чёткой границы между понятиями «дискретный» и «непрерывный».

Дискретная математика используется нами повседневно, мы совершаем расчёты, выводы и операции даже не подозревая, что это часть такой интересной науки. Школьные знания, которые просты и понятны нам, людям, которые уже не сидят за партой, предстают для нас с новыми названиями, описаниями с точки зрения высшей математики. Это лишний раз подтверждает, что дискретная математика позволяет решать не только простейшие задания, но и те, над которыми трудятся доктора наук [3].

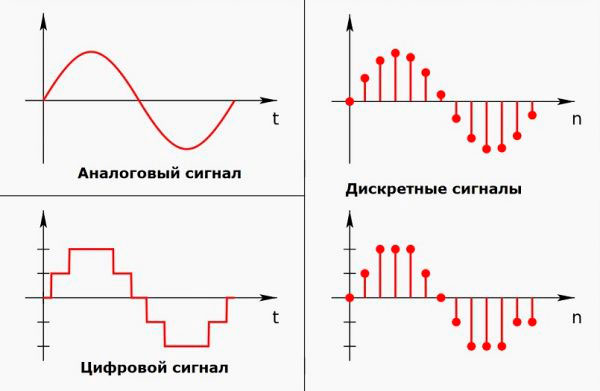
На момент появления первых компьютеров большинство электронных устройств, а именно: радио, телевизоры, магнитофоны и другие, было аналоговым. Это значит, что в данных устройствах использовались непрерывные сигналы. А при проектировании подобных устройств использовались методы непрерывной математики.

Первые ЭВМ были невероятно большого размера, они занимали целые здания, и были исключением среди электронных устройств того времени потому, что в них как раз и нужна была дискретная математика. Со временем ЭВМ превратились из больших и пугающих машин в те, что могут помещаться в отдельной комнате, затем на рабочем столе, а после в обыденные и незаменимые «Мобильники». Теперь мы чуть ли не каждый день имеем дело с электроникой, использующей достижения дискретной математики. Почти все современные устройства являются цифровыми: от фотоаппаратов и видеокамер до интернета и спутникового телевидения. Уже полвека дискретная математика является важным компонентом компьютеров. А значит, она необходима и в информатике [4–6].

Информатика – это наука, которая изучает компьютер, автоматическую переработку информации, взаимодействие человека с компьютером.

Информация – это сведения об окружающем нас мире. С разных точек зрения, может быть рассмотрена по разному. Является функциональной и абстрактной, такой же, как категория материи, энергии и пространства, следовательно, информация тоже неисчерпаемая.

Информатика использовалась людьми с древних времён. Логика мышления компьютера не стала чем-то новым. Но то, что компьютер, в отличие от человека никогда не ошибается и справляется с рутиной работой с невероятной скоростью и без малейшей усталости, является тем, что упростило нашу жизнь. Таким образом, у нас появилось свободное время на новые духовные и культурные свершения.

Информатика стала отдельной наукой относительно недавно, потому что с появлением ЭВМ необходимость в специалистах, умеющих правильно обращаться с аппаратурой, стала важным критерием для работы с передовым оборудованием. В современном мире компьютеры и программы для них стали намного проще, и теперь многие люди являются пользователями-любителями. Но есть и те компьютеры, для которых нужны узкоспециализированные работники или другими словами пользователи-профессионалы. К примеру, они нужны для правильной эксплуатации таких устройств как: сонары на подводных лодках, солнечные панели на космических кораблях и лунных базах, роботы-спасатели, супер-компьютеры, устройства для информационной и компьютерной безопасности, и так далее [7, 8].

Как и информатика, дискретная математика помогает современному человеку находить общий язык с компьютером, программами. Эти две, относительно молодые, науки позволяют создавать «Умные» дома; машины, управляемые без человека; космические корабли и оборудование, для высадки на Марс и дальнейшего создания на нём колонии.

Информатика сейчас очень актуальная тема для исследования и создания всё более умных машин, роботов, программ, различных устройств.

Дискретная математика служит необходимым инструментом для реализации идей в информатике (и не только).

Такой раздел дискретной математики как теория множеств составляет базу, основу для изучения других разделов. Научившись составлять и задавать математически множества, элементы которых обладают характерным изучаемым свойством, в дальнейшем можно устанавливать, какие есть между ними отношения, выполнять операции над ними. В более сложных случаях применяют теорию нечётких множеств, применение которой позволяет правильно сделать выбор в пользу конкурентоспособного товара или услуги методом нечеткого предпочтения, поэтому эта теория используется в маркетологии, когда нужно проанализировать рынки экономических благ.

Математическая логика, теория предикатов, теория алгоритмов позволяют алгоритмизировать знания, накопленные математикой. Причём в дискретной математике есть базовые элементы, понятные и простые в применении, но есть и более сложные структуры, позволяющие математически точно отражать явления и процессы. Математическая логика нашла своё применение в различных областях деятельности человека, даже в тех, которые кажутся далёкими от математики – биологии, медицине, лингвистике, педагогике, психологии, экономике, технике, но, конечно же, стала базовым разделом дискретной математики в развитии вычислительной техники, в разработке искусственных языков для общения с компьютером. Средства математической логики позволяют решать логические задачи, имеющих много исходных условий, которые после перевода на язык алгебры логики становятся более обозримыми и удобными для дальнейшего анализа, приводящего к верному умозаключению.

Математическая логика непосредственно используется как для создания материальной части компьютера – «железа», так и для математического – программного обеспечения, то есть к релейно-контактным (переключательным) схемам и к языкам программирования и к самому процессу программирования и получающимся в результате этого программам. Математическая логика оказалась единственной математической наукой, методы которой стали мощнейшими инструментами познания во всех разделах информатики. Поэтому сколько-нибудь серьезное изучение информатики немыслимо без освоения основ математической логики.

Теория графов, математическая логика широко применяются в таких секторах экономики как эконометрика, логистика, математическое моделирование. Так в эконометрике, например, используются булевские переменные для построения регрессионных моделей по неоднородным данным и для анализа регрессионных моделей с переменной структурой. В логистике при необходимости задать маршруты или описать потоки, удобнее применить теорию графов, с помощью которой схему дорог можно изобразить, как ориентированный граф, и далее выбрать самый короткий маршрут. Теория графов позволяет описывать сетевые взаимодействия как на примитивном, бытовом уровне, так и при сетевом планировании огромных промышленных предприятий.

А такие разделы дискретной математики как булева алгебра, комбинаторика, различные математические алгоритмы, хэш-функции и квантовые алгоритмы позволяют шифровать и дешифровать огромное количество информации. Так в криптографии с помощью средств комбинаторики чаще всего просчитывается возможное число вариантов при исходных данных, а вот использование сложных хэш-функций приводит к невозможности по конечному результату – хэшу – вычислить начальный массив данных, обработанный хеш-функцией.

Комбинаторика является неотъемлемой частью создания искусственных нейронных сетей, способствующих развитию отраслей, связанных с искусственным интеллектом. Также применяется при анализе сложности различных алгоритмов, выборе оптимальной стратегии перебора.

Дискретная математика является основой проектирования многих электронных приборов. Появление математической теории управляющих систем стало новым шагом к продвижению новых разделов дискретной математики, таких как: теория сложности; теория надёжности схем; теория автоматов. Теория сложности говорит о том, что не все алгоритмы равны с точки зрения их практической пригодности и есть некая «функция сложности», которая «измеряет» качество этих алгоритмов. На базе теории алгоритмов возникла теория автоматов, то есть математических моделей, преобразующих дискретную информацию по шагам в дискретные моменты времени и формирующих получаемые результаты по шагам заданного алгоритма.

Методы дискретной математики и информатики дают возможность анализировать, исследовать и моделировать многие экономические, технические, технологические процессы.

Человек использует нужные ему инструменты для достижения всё более грандиозных проектов. Дискретная математика и информатика, в правильных руках, являются невероятно действенными и незаменимыми инструментами [9, 10].

Таким образом, мы получили ответы на поставленные вопросы и разобрались в некоторых тонкостях данных областей. Так же становится понятно, что данные темы лишь набирают обороты в современном мире и помогают учёным совершать новые открытия в разных областях, ведь компьютеры нужны и химикам, и археологам, и историкам, и многим исследователям других областей. Человечество открывает новое (науки, знания) и это новое помогает открыть нечто большее, что будет обыденным уже для следующих поколений.

Источник

История развития дискретной математики и ее роль в обучении информатиков-экономистов

Статья просмотрена: 12355 раз

Библиографическое описание:

Фирсова, Е. В. История развития дискретной математики и ее роль в обучении информатиков-экономистов / Е. В. Фирсова. — Текст : непосредственный // Молодой ученый. — 2012. — № 2 (37). — С. 304-311. — URL: https://moluch.ru/archive/37/4204/ (дата обращения: 19.08.2022).

Математика является частью нашей культуры. Человек не может считать себя широкообразованным, не имея представления о со­временной математике, ее роли в повседневной жизни, в науке.

Математика (от греческого mathema – наука) – наука, в которой изучаются пространственные формы и количественные отношения. Математика зародилась в глубокой древности и от рождения условно делится на дис­кретную и континуальную (непрерывную) математику. К континуальной математике относится все, что содержит идеи теории пределов и непрерывности. Все остальное — это дискретная математика (discrete mathematics). Главной ее спецификой является дискретность, т.е. антипод непрерывности.

Дискретные системы с древнейших времен применяются в вычислительной практике. Широко известны изобретенные в древности различные системы представления чисел и связанные с ними алгоритмы выполнения арифметических операций, решения уравнений и т.д., повсеместно были распространены дискретные вычислительные приспособления: абак, различные виды счетов.

Развиваясь параллельно с другими разделами математики, элементы дискретной математики являлись их составной частью. Важнейшие примеры дискретных математических объектов: натуральный ряд чисел; конечное множество элементов произвольной природы; функция (отображение) из конечного множества в конечное множество; слово (последовательность символов) и формальный язык (множество слов) в конечном алфавите; конечный граф и другие. Содержательно дискретный объект обычно мыслится как состоящий из строго отделенных друг от друга неделимых частей. Объекты рассматривают как дискретные также в тех случаях, когда по каким-либо причинам отвлекаются от присущих им свойств непрерывности.

Следует подчеркнуть, что деление математики на «непрерывную» и «дискретную» весьма условно, т.к. вся математика едина и пронизана глубокими аналогиями. Сходные идеи и конструкции одинаково успешно работают в различных ее разделах. С одной стороны, происходит обмен идеями и методами между ними, а с другой – часто возникает необходимость исследования моделей, обладающих как дискретными, так и непрерывными свойствами одновременно. Например, аппарат теории множеств и теории графов используется при изучении не только дискретных, но и непрерывных объектов. Математика, изучающая количественный аспект материаль­ной действительности, отражает противоречивость реального мира. Непрерывность и однородность пространства — это предпосылки возникновения континуальных разделов математики, а разрывность и неоднородность — дискретных разделов. В то же время единство мира, тесная связь его непрерывных и дискретных свойств являют­ся основанием единства математики. Однако характер объектов, исследуемых дискретной математикой, настолько своеобразен, что методов классической математики не всегда достаточно для их изучения. Поэтому те спе­цифические методы, которые применяются для очень широкого класса конечных дискретных объектов, и были объеди­нены в общее направление — дискретную математику. Изучение элементов дискретной математики является существенной и неотъемлемой частью общемате­матического образования на всех его этапах и для всех обучаемых.

В широком смысле дискретная математика включает в себя такие давно сложившиеся разделы математики, как теория чисел, алгебра, теория множеств, математическая логика и другие. В узком смысле д искретная математика состоит из ряда специальных разделов и сравнительно новых разделов, которые интенсивно стали развиваться с середины прошлого века в связи с изобретением и постепенным внедрением во все сферы жизни ЭВМ и цифровых технологий. К таким разделам можно отнести теорию функциональных систем, теорию графов и сетей, комбинаторный анализ, теорию автоматов и алгоритмов, теорию кодирования, теорию синтеза управляющих систем, дискретную геометрию и др.

Конечная математика – «область математики, занимающаяся изучением свойств структур финитного (конечного) характера, которые возникают как внутри математики, так и в ее приложениях» [7]. К числу таких конечных структур могут быть отнесены, например, конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы и т. п. Иногда допускают расширение предмета конечной математики до произвольных дискретных структур и приходят к дискретной математике. К таким структурам могут быть отнесены некоторые алгебраические системы, бесконечные графы, определенные виды вычислительных схем, клеточные автоматы и т. д. В качестве синонима понятий «конечная математика» и «дискретная математика» иногда употребляется термин «дискретный анализ».

В статье Кудрявцев В.Б. «Конечная математика» дискретная математика про­тивопоставляется классической: «В отличие от конечной математи­ки классическая, в основном, занимается изучением свойств объ­ектов непрерывного характера» [7]. Такое противопоставле­ние не совсем точное, поскольку до определения в середине XX в. понятия «дискретная математика» к классической математике от­носилось и изучение дискретных объектов [4, с. 13].

Начало следующего этапа в развитии дискретной математики относят к XVII в. и связывают с появлением работ Л. Эйлера в области комбинаторного анализа и теории графов и Я. Бернулли по комбинаторной теории вероятностей. Большую роль в развитии идеологии дискретной математики сыграл Г. В. Лейбниц. В XIX веке в области дискретной математики работали известные математики, такие, как Ж. Л. Лагранж, А. Кэли, Дж. Буль, К. Жордан и многие другие.

Начиная с XVII века, в математике в основном занимались изучением функций непрерывно меняющегося аргумента, что являлось основой для всех ее приложений. Однако изучение моделей, имеющих принципиально дискретный характер, привело к необходимости обратить­ся к разделам математики, идущим в основном от математической логики и традиционно включающим комбинаторный ана­лиз, теорию графов, теорию алгоритмов, теорию алгебраиче­ских систем и ряд других. В современной математической науке, а также в ее приложениях, исследования в этих областях зани­мают все более заметное место.

Наряду с использованием дискретных математических ме­тодов для решения аналитических и прикладных задач в гуманитарных и естественнонаучных дисциплинах, важным аспектом их применения является также формирование методо­логических и языковых навыков, позволяющих формализовать и структурировать проблемы в соответствующей предметной области [5, с. 5].

(с XVII по XX в.)

(с XX в. по н. в.)

Элементарная математика

Высшая математика

Дискретная математика

Рис. 1. Периоды развития математики

Так же, как высшая математика опирается на элемен­тарную математику и включает ее, дискретная математика опи­рается на высшую математику и включает ее элементы. В то же время, для понимания основных разделов по дискретной математике достаточно знаний в объеме основной образовательной программы среднего (полного) общего образования.

Во взаимоотношениях математики и ее приложений с середи­ны XX века произошел существенный перелом. Математические методы, традиционно используемые в таких областях, как физика, механика, инженерные науки, стали вторгаться в самые различные сферы науки и практики — от биологии, экономики, социологии, психологии до компьютерных технологий. Эти приложения потребовали изменить представление о математике как о вычислительной теории, стали обращаться к восприятию абстракт­ной природы ее основных понятий и методов, что позволило мыслить более ясно и последовательно при решении научных проблем.

Большое значение для осознания роли дискретной математики в науке XX века имело возникновение и распостранение в современном естествознании представлений о дискретном характере окружающей нас реальности (атомно-молекулярная теория, квантовая и статистическая физика). Существенное влияние на развитие дискретной математики на этом этапе оказали исследования и работы А. Пуанкаре и Д. Гильберта, Э. Л. Поста, А. М. Тьюринга и других ученых.

Бурное развитие дискретной математики во второй половине XX века связывают с «цифровой революцией» в телекоммуникационной и вычислительной технике. Дискретная математика стала основой проектирования и применения многочисленных цифровых электронных устройств. Первые применения дискретной математики в этой области связаны с именами В. А. Котельникова, К. Э. Шеннона, В.И. Шестакова. Возникновение в рамках кибернетики математической теории управляющих систем привело к развитию целых новых разделов дискретной математики: теории сложности, теории тестов, теории надежности схем, теории автоматов и других. Существенный вклад в дискретную математику на этом этапе был сделан Дж. фон Нейманом, А.А. Ляпуновым, С.В. Яблонским, О.Б. Лупановым [10].

Начиная с середины XX в. в нашу жизнь бурно вошли и вско­ре заняли доминирующее место информационные системы раз­личного назначения. Сначала это были кибернетические систе­мы, а затем системы с интеллектуальными свойствами. Определяющими в таких системах являются информацион­но-логические, принципиально дискретные процессы решения разнообразных задач. Для этих процессов не существенны ме­сто и время их решения, они мало зависят от пре­образования энергии и вещества.

Классической высшей математики недостаточно для моделирования кибернетических и интеллектуальных систем. Для описания главных систем информационного периода и появилась новая математика, которую называют в России дискретной математикой (выделяется дискретность структуры информации, собственно информационной системы и ее функционирования); в США — Computer Science (на первое место выдвигается техническая сторона дела — компьютеры); в Западной Европе — информатикой (акцент делается на инфор­мационные процессы) [6, с. 3].

Дискретная математика ориентирована на описание и ис­следование информационных систем, функционирующих в информационной среде. Дискретная математика объединила отдельные разделы, ранее сформированные как самостоятельные теории (математическая логика, теории множеств, гра­фов, кодирования и др.)

Кибер­нетические области информатики используют в качестве аппара­та язык как фундаментальной, так и прикладной математики. Кибернетика — наука об общих принципах уп­равления в живых, неживых и искусственных системах. Решая мно­жество разнообразных задач, кибернетика имеет общий стержень, общую методологию, в основе которой лежит понятие системы, т.е. структуры, объединения некото­рого количества обособленных элементов, подчиненных единой взаимосвязи, определенным отношениям. Кибернетика является наукой об управляемых системах любого характера: биологиче­ских, социальных, технических, экономических. В связи с этим в различных системах выделяют так называемый кибернетический подход, смысл которого заключается в наличии механизма управ­ления этой системой, в существовании обратной связи [2, с. 10].

Кибернетические системы — разнообразные автоматы. Ав­томаты обрабатывают входные сигналы (входное слово) и выра­батывают выходные сигналы (выходное слово). Те входные сло­ва, которые автомат не обрабатывает, называются нештатными ситуациями. Таким образом, кибернетические системы решают только штатные для них задачи.

Интеллектуальные системы нацелены на решение не толь­ко своих штатных задач, но и некоторых нештатных для них задач. Примерами интеллектуальных систем являются следу­ющие: человек, высшее животное; сообщество людей, популяция высших животных и т. п.; автоматизированные системы с преобладанием техни­ческого фактора (самолет, автомобиль, операцион­ная система компьютера вместе с пользователем и т. п.), автоматические системы с интеллектуальными свойствами, в которых предполагается отсутствие человека (беспилотный межпланетный космический аппарат и т. п.).

В XXI веке дискретная математика является бурно развивающейся ветвью математики. Ее роль и место определяются в основном тремя факторами [3, с. 3]: 1) дискретную математику можно рассматривать как теоретические основы компьютерной математики; 2) модели и методы дискретной математики являются хорошим сред­ством и языком для построения и анализа моделей в различных науках, включая химию, биологию, генетику, физику, психологию, экологию, со­циологию и др.; 3) язык дискретной математики чрезвычайно удобен и стал фактиче­ски метаязыком всей современной математики.

Дискретной математикой также называют совокупность математиче­ских дисциплин, изучающих свойства абстрактных дискретных объектов, т.е. свойства математических моделей объектов, про­цессов, зависимостей, существующих в реальном мире, которы­ми оперируют в различных областях знаний. Ее математический аппарат можно опреде­лить как взаимосвязанную совокупность языка, моделей и мето­дов математики, ориентированную на решение различных, в том числе инженерных, задач. Использование такого аппарата связа­но с характером исследуемых моделей – отдельных элементов абстрактных множеств, отдельных чисел в различных системах счисления, отдельных значений 0 и 1 (истина и ложь), булевых функций и т.д.

В настоящее время знание дискретной математики необхо­димо специалистам в различных областях деятельности и элементы дискретной математики все чаще вводят в программы подготовки не только математиков, инженеров, программистов, но даже юристов. Ин­терес к этой дисциплине не случаен, т.к. потребность в зна­ниях этой области математики объясняется широким кругом ее применения: электроника и информатика, вопросы оптимизации и принятия решений. XXI в. называют веком информатизации, когда основной объем информации хранится в памяти ЭВМ. Применение ЭВМ для комплексной автома­тизации информационной деятельности принципиально измени­ло характер взаимоотношений человека и машины. Если раньше компьютер осваивали только те, кто непосредственно его обслу­живал: программисты, электронщики, операторы, то в XXI в. без машинной обработки информации не обойдется ни одна отрасль деятельности.

Стимулом для развития многих направлений дискретной мате­матики явились запросы теоретической кибернетики, непосред­ственно связанной с развитием ЭВМ. Теоретическая кибернетика или теоре­тическая информатика исполь­зует математические методы для построения и изучения моделей обработки, передачи и использования информации. Объекты ее изучения — дискретные множества. Теоретическая информатика является как поставщиком задач, так и потребителем методов дискретной математики.

Теоретическая кибернетика занимается изучением разнообраз­ных практических проблем средствами дискретной математики [2, с. 9]:

растущий поток информации и проблемы ее передачи, обра­ботки и хранения привели к возникновению и развитию теории кодирования;

различные экономические задачи, задачи электротехники сти­мулировали создание и развитие теории графов;

связь релейно-контактных схем с формулами алгебры логики и их использование для описания функционирования автоматов дали начало развитию и применению математической логики и теории автоматов. Математическая логика в широком смысле изучает основания математики, принципы построения матема­тических теорий.

Дискретная математика исследует объекты, которые порой не имеют ни физической, ни числовой интерпретации. В классиче­ской математике характеристики реальных объектов можно представить в виде чисел, а закономерности — в виде соотношений. В отличие от реальных характеристиками информационных объек­тов могут служить понятия «структура», «отношение», «связь». Обычно объекты информатики рассматривают как комбинации некоторых абстрактных символов, над которыми производятся некие манипуляции.

В настоящем время идет процесс информатизации общества, ин­теллектуализации организационных систем, внедрения компью­теров во все сферы жизни человека. Происходит процесс информатиза­ции разнообразных технических систем, постоянное расширение интеллектуальных возможностей динамических систем.

Методы, разрабатываемые дискретной математикой, часто ис­пользуются в различных направлениях информатики.

Достижения математической логики используются для ана­лиза процессов переработки информации с помощью ЭВМ. Тео­рия автоматов разрабатывает методы, с помощью которых мож­но на основе моделей логического типа изучать процессы, про­текающие в самой машине во время ее работы. Для работы на компьютере информацию представляют в дискретной форме, позволяющей переводить ее в программы, понятные ЭВМ.

Теория информации изучает вид тех форм, в которых инфор­мация представляется в компьютере. Формализация любой информации, реально существующей в живой и неживой природе, происходит через компьютерное моделирование. Системный ана­лиз изучает структуру реальных объектов и дает способы их фор­мализованного описания. Общая теория систем как часть систем­ного анализа изучает различные по характеру системы с общих позиций. Теория массового обслуживания изучает широкий класс моделей передачи и переработки информации в системах массо­вого обслуживания.

В настоящее время нашла широкое применение наука семи­отика, которая исследует знаковые системы самой различной природы. Четко различая понятие знака и знаковой ситуации, се­миотика включает такие разделы, как синтактика (что связывает знак), семантика (что выражает знак), сигматика (что обозначает знак) и прагматика (что дает знак) [2, с.11]. Синтактический аспект ин­формации, связанный со структурными и статистическими оцен­ками, в основном рассматривается в информатике и вычислительной технике. Сигматический аспект рассматривает теория сиг­налов и кодирования. Знаковые системы благодаря своей гибкости способны обеспечить разнообразные запросы пользователей.

Имитационное моделирование — наука, в которой создаются и используются специальные приемы воспроизведения процессов, протекающих в реальных объектах, в тех моделях этих объектов, которые реализуются в вычислительных машинах.

Теория принятия решений изучает общие схемы, используемые при выборе решения из альтернативных возможностей (в услови­ях неопределенности). Теория игр изучает модели, в которых вы­бор происходит в условиях конфликта или противоборства. Мате­матическое программирование рассматривает проблемы принятия оптимальных решений с помощью математического аппарата.

Искусственный интеллект — одно из молодых и перспектив­ных направлений информатики, появившееся во второй полови­не XX в. на базе вычислительной техники, математической логи­ки, программирования, психологии, лингвистики и других от­раслей знаний. Объектами его изучения являются межпредметные процедуры (метапроцедуры), используемые при решении интеллектуальных задач.

Информационные системы применяются для анализа и про­гнозирования потока информации, исследования способов ее представления, хранения и извлечения. Актуальным является так­же создание информационно-поисковых систем, систем хранения, обработки передачи информации, в состав которых входят информационные базы данных, терминалы, средства связи. Опе­рационные системы связаны с разработкой и производством ком­пьютеров.

Теперь уже можно осознать место дискретной математики в системе знаний, необходимых для тех, кто связал свою жизнь с компьютером. Для представителей многих специальностей, особенно для про­граммистов и информатиков-экономистов, существенное значение в будущей профессиональ­ной деятельности имеет знание классической логики, т.к. она образует математическую основу информатики. На знаниях законов логики базируются принципы алгоритми­зации, которые лежат в основе программирования. Фундаментом всей вычислительной техники и автоматики является преобразо­вание двоичных сигналов, анализ, проектирование и использова­ние логических схем. Основу современной математической логи­ки составляют исчисление высказываний и исчисление предика­тов, на которых базируется любой язык программирования. Широко применяются логические методы для построения баз дан­ных. Активно используются знания логики в развитии современ­ных направлений информационных наук. Ряд проблем искусственного интеллекта невозможно решить без знаний основ классической логики.

Часто приходится обрабатывать информацию, полученную в результате всевозможных статистических обобщений, социологи­ческих опросов и т.д., с помощью средств теории вероятностей и математической статистики. При этом понадобятся умения форму­лировать гипотезы о видах распределений, проверять их жизнеспо­собность, истинность, отражение реальности. Поэтому специалистам важно ориентироваться в различных видах индуктивных умозаключений и уметь отличать достоверные выводы от вероятно­стных, т.е. применять в работе знания классической логики.

Изучая дискретную математику, нельзя не уделять внимания людям, которым принадлежат основополагающие результаты. Поэтому, перечислим имена крупных математиков, внесших существенный вклад в современную дискретную математику: английский математик и философ Б. Рассел, английский математик А. Тьюринг, американские математики А. Чёрч, К. Гёдель, Э. Пост, С. Клини, польские математи­ки Л. Лукасевич, С. Мостовской, советские математики А. А. Марков, И. И. Жегалкин, П. С. Новиков, В. М. Глушков, российские ученые С. В. Яблонский, О. Б. Лупанов, Ю. И. Журавлев.

Обучение дискретной математике – многоцелевой, многоуровневый, многофункциональный процесс, состоящий в целенаправленном воздействии на элементы систе­мы обучения и их связи [4, с. 62].

Как было показано ранее, математика является единой научной дисциплиной, непрерывные и дискретные разделы кото­рой постоянно взаимодействуют между собой, обогащая друг друга. Этапы непрерывно­го обучения дискретной математике определяются возрастом обу­чаемых, их психологическими и физическими возможностями, раз­личными целями и задачами, достигаемыми и решаемыми при обучении. Главной целью обучения дискретной математике на всех этапах является усвоение обучаемыми знаний для продук­тивной деятельности в современном информационном мире, овла­дение ими умениями использования мощных средств исследования реальной действительности, в том числе и вычислительной техни­ки, развитие их умственных способностей для решения жизненных вопросов.

Достижение этой цели возможно, с одной стороны, при зна­комстве учащихся с необходимым комплексом знаний и обучении активным навыкам их использования, с другой стороны, при уско­рении у учащихся умственного развития, знакомстве их с различ­ными стилями мышления, обучении умению эффективно исполь­зовать эти стили в случае необходимости.

Выбор дискретной математики как составляющей при обуче­нии математике вызван широким распространением дискретных математических моделей при исследовании кибернетических си­стем, повсеместным изучением информатики, теоретической базой которой является дискретная математика. Кроме того, целью изучения дискретной математики является повышение с ее помощью интеллектуального развития человека, умственное совершенствование обучаемых, формирование у них приемов логического мышления, развитие их соображения и вооб­ражения, формирование их личности.

Основными задачами обучения дискретной математике явля­ется развитие логических и математических способностей обучае­мых, формирование умений построения и анализа математических моделей и алгоритмов их исследования, формирование представ­лений о математике как едином целом, осознание связи между математикой и другими дисциплинами, связи между математикой и информатикой.

Дисциплина «Дискретная математика» в соответствии с Государственным образовательным стандартом высшего профессионального образования по специальности 351400 «Прикладная информатика (по областям)» относится к дисциплинам федерального компонента цикла ЕН &#; общие математические и естественно-научные дисциплины: ЕН.Ф.01 Математика. Дискретная математика: логические исчисления, графы, комбинаторика [1].

Целью изучения дисциплины «Дискретная математика» является прочное усвоение студентами теоретических и практических основ дискретной математики, математической логики, комбинаторики и теории графов, составляющих фундамент ряда математических, компьютерных дисциплин и дисциплин прикладного характера, например, «Исследование операций в экономике», «Математические методы принятия решений», «Численные методы», «Эконометрика», «Информатика и программирование», «Базы данных» и т.д.

Задачами изучения данной дисциплины являются: обучение студентов теоретическим основам курса, овладение методами решения практических задач, приобретение навыков самостоятельной научной деятельности.

Требования к профессиональной подготовленности информатика-экономиста по дисциплине «Дискретная математика»[1]: должен знать и уметь использовать основные понятия и методы дискретной математики; иметь опыт употребления математической символики для выражения количественных и качественных отношений объектов; иметь представление: о математике как особом способе познания мира, общности ее понятий и представлений; дискретности и непрерывности в природе и обществе; о соотношении порядка и беспорядка в природе и обществе, упорядоченности строения объектов, переходах в неупорядоченное состояние и наоборот.

В процессе изучения данной дисциплины студенты должны

знать: базовые понятия дискретной математики; основные понятия теории множеств, алгебры высказываний, теории бинарных отношений на множествах, комбинаторики и теории графов; основные методы дискретной математики, области их применения, принципы использования языка, средств, методов и моделей дискретной математики в проблемах прикладного характера;

уметь : использовать арсенал методов дискретной математики для решения практических и прикладных задач;

иметь представление : об основных терминах, понятиях и методах дискретной математики как о языке и средствах построения моделей в прикладных исследованиях; о современном состоянии дискретной математики; об адаптации методов дискретной математики к решению конкретных задач.

Следовательно, тематический план дисциплины «Дискретная математика» для информатиков-экономистов представляет собой изучение следующих тем: Множества, Алгебра высказываний, Проблемы разрешимости, Нормальные формы, Исчисление высказываний, Логика предикатов, Комбинаторика, Графы, Экстремальные задачи на графах.

Информатик-экономист должен уметь решать задачи, соответствующие его квалификации. Он должен обладать [1]:

профессиональной компетентностью, определяемой совокупность теоретических и практических навыков, полученных при освоении профессиональной образовательной программы по специальности 351400 «Прикладная информатика (по областям)»;

специальной подготовкой в экономике и в области информационных технологий для анализа, проектирования и сопровождения профессионально-ориентированных информационных систем;

профессиональной способностью прогнозирования, моделирования и создания информационных процессов в экономике;

умением выполнять работы по развитию возможностей профессионально-ориентированных информационных систем на всех стадиях их жизненного цикла;

специализацией, определяемой перечнем специальных и информационных дисциплин;

способностью осуществлять профессиональные функции в рамках одного или более видов деятельности; пониманием основных тенденций развития информационных технологий и информационных систем в области применения;

коммуникационной готовностью выпускника, определяемой: 1) перечнем решаемых задач; 2) владением теорией в области применения; 3) умением читать и переводить профессионально ориентированные тексты на иностранном языке; 4) умением разрабатывать документацию и пользоваться ею; 5) умением профессионально использовать компьютерную технику и средства связи; 6) развитой способностью к творческим подходам в решении профессиональных задач; 7) умением ориентироваться в нестандартных условиях и ситуациях, анализировать возникающие проблемы, разрабатывать и осуществлять план действий; 8) устойчивым позитивным отношением к своей профессии, к повышению квалификации информатика в области применения; 9) стремлением к непрерывному личностному и профессиональному совершенствованию.

За последние десятилетия произошло значительное усиление роли дискретной математики в решении практических задач и интенсивное использование информатики, теоретической базой которой является дискретная математика, в науке, технике, экономике и повседневной жизни. Все это во многом связано с изучением кибернетических систем, получивших весьма широкое распространение, при моделировании которых существенно используется дискретная матема­тика. В последнее время их изучение стало более актуальным в связи с увеличением масштабов производства, расширением экономических связей, со­зданием межгосударственных объединений.

Широкое распространение ЭВМ вызвало изу­чение программирования и информатики, непосредственно связан­ной с дискретной математикой, практически во всех учебных заве­дениях. Использование для исследования сложных объектов и ситу­аций моделей дискретной математики требует глубокого ознаком­ления с методикой их построения, изучения методов дискретной математики и способов ее применения для решения практических задач студентами естественных, технических и экономических спе­циальностей. При этом необходимо обучение студентов умениям создания эффективных алгоритмов исследования моделей, оцени­вания их качества и скорости, сравнения алгоритмов с ранее су­ществующими. Кроме того, большое значение приобретает умение будущих специалистов исследовать построенные модели на компьютерах с помощью пакетов прикладных программ. Поэтому становится важным раннее пропедевтическое озна­комление с началами дискретной математики, начиная с дошколь­ных заведений и школы, и заканчивая в вузе.

Решение задач дискретной математики на начальном уровне ее изучения не требует глубоких теоретических знаний, а нуждается только в сообразительности, поэтому их можно широко использо­вать для ускорения математического развития школьников. Часто такие задачи легко представить в занимательной форме, что способствует повышению интереса к обучению. Кроме того, дискретную математику можно использовать для решения ме­тодических задач в математическом образовании. Например, с ее помощью возможно знакомство школьников с математической ин­дукцией, тяжелыми для них понятиями «необходимые и достаточ­ные условия» и т.д.

Недооценка дискретной математики в школе приводит к тому, что ее выпускник прихо­дит в вуз, не имея никаких навыков мышления, ориентированного на восприятие дискретных объектов, что затрудняет ему овладение различными дискретными математическими курсами, связанными с кибернетикой и информатикой.

Увеличение значения дискретной математики в технике и в эко­номике, новые требования к обучению информатике в школах и ву­зах должны изменить и отношение к преподаванию дискретной ма­тематики. Но в школе происходит постоянное увеличение объема знаний, предлагаемых для усвоения ученикам. К сожалению, часто это увеличение происходит за счет сокращения часов, отводимых на фундаментальные знания, в том числе и на математику, что ведет к резкому ухудшению качества обучения и появлению все новых и новых трудностей.

Необходима перестройка обучения дискретной математики и в высшей школе. Требования к подготовке молодых специалистов, высказываемые руководителями предприятий, приводят к тому, что технические и экономические вузы постепенно начинают знако­мить студентов с дискретными математическими моделями, встречающимися в соответствующих отраслях, и методами их исследо­вания, при остающейся недооценке теоретических дисциплин дис­кретной математики в целом.

Сегодня дискретная математика является не только фундаментом математической кибернетики, но и важным звеном математического образования. Она является одной из основных дисциплин в программах вузов для специальностей, имеющих отношение к математике, кибернетике, вычислительной технике и многим другим областям современной науки и техники. Применение дискретной математики составляют основу современных компьютерных наук и информатики.

Теперь для того, чтобы быть современным человеком, спо­собным существовать в «компьютерном» мире, в котором придется искать лучшие решения и кратчайшие пути в лабиринте возможно­стей, выпускник вуза должен не только знать элементы дискретной математики, но и уметь думать на языке дискретных моделей. С вы­числительной техникой практически связан любой человек XXI века: либо как создатель новых ЭВМ и их математического обеспечения, либо как разработчик алгоритмов и программ, либо как обычный пользователь стандартных пакетов на своем рабочем месте или в быту. Хорошее знание дискретной математики облегчит любому человеку освоение компьютера и применение его для решения практических задач.
Литература:

Государственный образовательный стандарт высшего профессионального образования утвержден 14 марта 2000 года, номер государственной регистрации 52 мжд/сп. Специальность 351400 «Прикладная информатика (по областям)».

Дискретная математика / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2006. – 368с.

Ерусалимский Я.М. Дискретная математика: Теория, задачи, приложения. – М. : Вузовская книга, 2005. – 268с.

Мельников О.И. Обучение дискретной математике. – М. : Издательство ЛКИ, 2008. – 224с.

Осипова В.А. Основы дискретной математики. – М. : ФОРУМ: ИНФРА-М, 2006. – 160с.

Соболева Т.С. Дискретная математика : учебник для студ. Вузов / Т. С. Соболева, А.В. Чечкин; под. ред. А.В. Чечкина. – М. : Издательский центр «Академия», 2006. – 256с.

Источник

Дискретная математика

Дискретная математика — раздел математики, занимающийся изучением дискретных структур (то есть структур, к которым не может применяться понятие непрерывности, см. Дискретность). Часть дискретной математики, изучающая конечные структуры (например, конечные группы, графы, машины Тьюринга), называется конечной математикой.

В расширенном смысле дискретная математика делится на теорию чисел, вычислительную математику, математическую логику, комбинаторный анализ, а также новые направления исследований — теорию графов, теорию кодирования, целочисленное программирование, теорию автоматов, расписаний, ЭВМ, программирование и др., в которых объекты исследований имеют дискретный характер.

[править] История

Элементы дискретной математики возникли в глубокой древности и развивались параллельно с другими разделами математики. Например, тогдашние типичные задачи, связанные со свойствами целых чисел (истоки теории чисел): поиск алгоритмов сложения и умножения натуральных чисел (Египет, 2-е тысячелетие до н. э.), задачи суммирования и делимости натуральных чисел в пифагорейской школе (6 в. до н. э.).

[править] Общие подходы

На практике чаще всего одновременно присутствуют свойства непрерывности и дискретности, конечности и бесконечности; при решении конкретных задач широко используется прием замены непрерывной модели ее дискретным аналогом. В дискретной математике вместе с построением алгоритмов решения отдельных задач выявляются вопросы алгоритмической разрешимости, оценки вычислительной сложности алгоритмов, выявление трудноразрешимых задач и др.

Источник