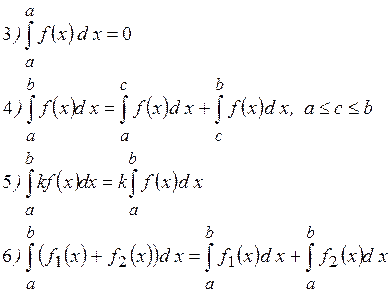интеграл и его приложения определение

Тема 1.3. Интеграл и его приложения

В рекомендуемых учебных пособиях необходимо ознакомиться со следующими краткими сведениями справочного характера по интегральному исчислению.

-понятие первообразной данной функции;

— определение неопределенного интеграла;

— основные свойства неопределенного интеграла;

— таблица основных неопределённых интегралов;

— применение основных свойств и таблицы неопределенных интегралов, непосредственное интегрирование;

— определение и свойства определенного интеграла;

— определённый интеграл как площадь криволинейной трапеции, его принципиальное отличие от неопределенного интеграла;

— вычисление определённого интеграла. Формула Ньютона-Лейбница.

— замена переменной в определенном интеграле;

— вычисление площадей плоских фигур и объёмов тел вращения;

— использование определенного интеграла при решении задач прикладного характера.

В результате изучения темы студент должен:

Уметь:

— находить неопределённые интегралы, сводящиеся к табличным, с помощью основных свойств и простых преобразований;

— восстанавливать закон движения по заданной скорости, скорость по ускорению, количество электричества по силе тока и др.;

— вычислять определённый интеграл с помощью основных его свойств и формулы Ньютона-Лейбница;

— находить площади криволинейных трапеций;

— решать простейшие прикладные задачи, сводящиеся к составлению и вычислению интеграла.

использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:

— решения прикладных задач на вычисление в простейших случаях площадей и объемов с использованием определенного интеграла;

Приведём основные свойствами неопределенного интеграла:

1) постоянный множитель (к¹0) можно выносить за знак интеграла:

.

2) интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций

.

3) или .

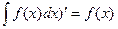
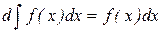
4) или .

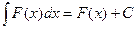
5) .

Основные формулы интегрирования

Приведем таблицу основных неопределенных интегралов:

;

;

;

;

;

;

;

;

;

;

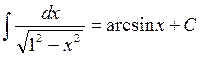
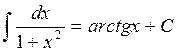
Справедливость этих формул можно проверить путем дифференцирования, т.е. легко убедиться в том, что производные от правых частей формул

будут равны соответствующим подынтегральным функциям. Интегралы таблицы называются табличными.

Основные методы интегрирования.

Непосредственное интегрирование – это такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Интегрирование методом подстановки (замены переменной).

Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае используют метод подстановки. Для интегрирования методом постановки будем использовать следующую схему:

1. Часть подынтегральной функции заменим новой переменной;

2. Найдем дифференциал от обеих частей замены;

3. Выразим подынтегральное выражение через новую переменную (после чего должен получиться табличный интеграл);

4. Найдем полученный табличный интеграл;

5. Сделаем обратную замену, вернемся к старой переменной.

Определение. Если -первообразная функция для , то приращение первообразных функций при изменении аргумента от до называется определенным интегралом и обозначается

т.е.

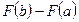
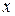
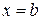
Непосредственное вычисление определенного интеграла

В отличие от неопределенного интеграла, представляющего собой совокупность всех первообразных от данной функции, определенный интеграл есть число. Для его вычисления применяют формулу Ньютона- Лейбница

где — нижний, а — верхний пределы определенного интеграла.

Т. е. значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции при нижнем и верхнем пределах интегрирования. Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов.

Если функция положительна, то определенный интеграл представляет собой площадь криволинейной трапеции (фигура, ограниченная графиком непрерывной функции , , прямыми и отрезком оси Ox). В этом заключается геометрический смысл определенного интеграла. Таким образом, площадь криволинейной трапеции можно вычислить по формуле: .

Основные свойства определенного интеграла

Вопросы для самоконтроля

1. Какая связь существует между операциями дифференцирования и интегрирования?

2. Какая функция называется первообразной для заданной функции?

3. Дайте определение неопределенного интеграла.

4. Назовите основные свойства неопределенного интеграла.

5. Перечислите основные табличные интегралы.

6. Запишите формулу Ньютона- Лейбница.

7. Объясните, почему она называется формулой, выражающей связь определённого интеграла с неопределённым? Где в ней неопределённый интеграл?

8. В чём принципиальное различие неопределённого и определённого интегралов?

9. Какую фигуру называют криволинейной трапецией?

10. Запишите формулу для вычисления площади криволинейной трапеции.

11. В чем заключается геометрический смысл определённого интеграла?

12. Запишите основные свойства определенного интеграла.

13. Какие методы вычисления определенного интеграла Вам известны?

14. Назовите несколько примеров применения определенного интеграла в геометрии и физике.

Источник

Интегралы для чайников: как решать, правила вычисления, объяснение

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Свойства определенного интеграла

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Конспект по теме: «Интеграл и его приложения»

Занятие 108. Интегральные суммы. Обозначение интеграла.

Занятие 109. Первообразная и её свойства.

Занятие 110. Вычисление первообразной

Занятие 111. Практическое занятие 40. Вычисление первообразной

Занятие 112. Практическое занятие 41. Самостоятельная работа №17.

Занятие 113. Теорема Ньютона-Лейбница.

Занятие 114. Свойства интеграла. Вычисление интеграла

Занятие 115. Практическое занятие 42. Вычисление интеграла.

Занятие 116. Практическое занятие 43. Самостоятельная работа №18.

Занятие 117. Вычисление площади с помощью интеграла.

Занятие 118. Практическое занятие 44. Решение задач на вычисление площади.

Занятие 119. Вычисление площади с помощью интеграла.

Занятие 120. Практическое занятие 45. Самостоятельная работа №19.

Занятие 121. Решение задач на применение интеграла.

Занятие 122. Решение задач на применение интеграла.

Занятие 123. Практическое занятие 46. Решение задач на применение интеграла.

Занятие 124. Практическое занятие 47. Контрольная работа № 15.

Занятие 125. Практическое занятие 48. Решение задач на применение интеграла.

Занятие 126. Практическое занятие 49. Решение задач на применение интеграла.

Операция нахождения скорости по заданному положению точки называется дифференцированием.

Обратная задача – нахождение положения точки по её скорости –решается с помощью другой математической операции – интегрирования.

Геометрический смысл интеграла.

Криволинейную трапецию, построенную с помощью графика неотрицательной функции f, будем сокращённо называть подграфиком функции f.

Пусть дана неотрицательная функция f, определённая на конечном отрезке [a; b]. Интегралом от функции f называется площадь её подграфика.

интеграл – это площадь

Занятие 108. Интегральные суммы. Обозначение интеграла.

Разделим отрезок [a; b] на n частей.

Тогда приближенно площадь каждого прямоугольника:

Составим сумму площадей

Точное значение площади получается при помощи предельного перехода.

Интеграл – это предел интегральных сумм.

Скорость роста площади.

Рассмотрим неотрицательную функцию f, заданную на отрезке [a; b].

Рассмотрим криволинейную трапецию, полученную следующим образом: закрепим левую «стенку» х ₀ =а, а правую начнём перемещать вдоль оси абсцисс. Обозначим площадь переменной трапеции ( подграфика функции

Для данной функции:

Теорема (о скорости роста площади)

Итак связь между функциями f и S такова:

Знак ∫ введен Лейбницем, это удлиненная первая буква от латинского слова

(1) т.е. интеграл – это сумма

Значения a и b – соответственно нижний и верхний пределы интегрирования. Таким образом, определенный интеграл представляет собой число, а не формулу в отличие от неопределенного интеграла.

если f(x) ≤ 0 на [a, b], то

Интегралом от функции называется сумма площадей её подграфика, взятых со знаком «+» для частей, расположенных выше оси абсцисс, и со знаком «-» ниже неё.

Занятие 109. Первообразная и её свойства.

Первообразной для функции называется такая функция F , производная которой равна данной функции.

Для обозначения первообразной используют знак «неопределённого интеграла», т. е. интеграла, без указания пределов интегрирования.

3. Первообразная суммы функций равна сумме первообразных:

4. Постоянную можно вынести за знак первообразной:

f(x) — называют подынтегральной функцией ;

f(x)dx — называют подынтегральным выражением ;

x — называют переменной интегрирования ;

F(x) — одна из первообразных функции f(x) ;

С — произвольная постоянная.

Для того, чтобы найти первообразные для простейших функций используем таблицу производных.

Давайте составим таблицу первообразных:

Д/З: Практическая работа: «Таблица первообразных»

Продолжите заполнение таблицы. Min 30 функций.

Найти все первообразные для функций:

F ( x )= Сократим и запишем ответ.

Сократим и запишем ответ.

Пример 2. Найдите первообразную, график которой проходит через точку :

Занятие 110. Вычисление первообразной

Пример 1. Выяснить, является ли функция F ( x ) = х 3 – 3 х + 1 первообразной для функции f ( x ) = 3( х 2 – 1).

Решение: F'( x ) = ( х 3 – 3 х + 1)′ = 3 х 2 – 3 = 3( х 2 – 1) = f ( x ), т.е. F'( x ) = f ( x ), следовательно, F(x) является первообразной для функции f(x).

Пример 2. Найти все первообразные функции f(x): f ( x ) = х 4 + 3 х 2 + 5

Решение: Используя таблицу и правила нахождения первообразных, получим:

Ответ:

Пример 3. Найдите первообразную, график которой проходит через точку (1;

Решение: Используя таблицу и правила нахождения первообразных, найдём все первообразные для функции:

Тема: «Вычисление первообразной»

Найдите все первообразные для функций:

Тема: «Вычисление первообразной. Самостоятельная работа № 17 »

Самостоятельная работа №17

1. Найдите все первообразные для функций:

b ) y ( x ) = 3 x 2 – 2 x 3 + 4 x – 5

2. Найдите первообразную, график которой проходит через точку (1;5)

1. Найдите все первообразные для функций:

1. Найдите все первообразные для функций:

2. Найдите первообразную, график которой проходит через точку (-3; 10)

1. Найдите все первообразные для функций:

2. Найдите первообразную, график которой проходит через точку (0;3)

Занятие 113. Теорема Ньютона-Лейбница.

Данная формула является основной формулой интегрального исчисления, и ее доказательство основано на свойствах интеграла с переменным верхним пределом.

Докажем ее. В самом деле, поскольку производная от интеграла с переменным верхним пределом по верхнему пределу равна подынтегральной функции, можно сказать, что сам интеграл с переменным верхним пределом является первообразной для подынтегральной функции.

Полученная формула сводит нахождение определенных интегралов к нахождению неопределенных интегралов. При этом приращение первообразной F(b) – F(a) принято обозначать .

Подчеркнем, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную для подынтегральной функции, например, имеющую наиболее простой вид при С = 0 (в дальнейшем не будем записывать константу при нахождении неопределенного интеграла, поскольку будем считать ее равной нулю).

Отметим, что при нахождении приращения первообразной общий сомножитель был вынесен за скобки.

Интеграл как площадь криволинейной трапеции

Понятие определённого интеграла возникает в связи с задачей о нахождении площади криволинейной трапеции, нахождении пути по известной скорости при неравномерном движении и т. п.

Определение: Определённым интегралом по отрезку [a;b]от функции f(x) называется предел интегральной суммы , если этот предел существует и не зависит ни от деления отрезка [a;b]на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆x _i ) стремится к нулю, т.е

Числа a,b называются соответственно нижним и верхним пределами интегрирования, т.е [a;b]-отрезок интегрирования.

Занятие 114. Свойства интеграла. Вычисление интеграла

Свойства определённого интеграла по [a;b].

1. Интегралы противоположны, если поменять местами пределы интегрирования:

2. Интеграл равен нулю, если верхний и нижний пределы интегрирования равны:

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b и с

4. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых):

5. Постоянный множитель можно выносить за знак интеграл a :

6. Обе части неравенства можно почленно интегрировать, т.е. если на отрезке [а, b] ( а

Следствие. Пусть на отрезке [а, b], где а

Тогда

Это вытекает из того, что , а интегралы от констант вычисляются по формулам и .

Т.е. если функция ограничена сверху и снизу некоторыми числами, то интеграл от этой функции ограничен произведениями этих чисел на длину отрезка (промежутка интегрирования).

Правила вычисления определённого интеграла для функция f(x) на [a;b]

— формула Ньютона-Лейбница, где F(x)- первообразная

2. — интегрирование по частям.

3. , где x=j(t) функция непрерывная вместе со своей производной

на [a;b]

Вычислить определённый интеграл:

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

Занятие 115. Практическое занятие 42. Вычисление интеграла.

Геометрически теорема о среднем означает, что на отрезке найдется такая точка, что площадь под кривой у = f(х) на этом отрезке будет равна площади прямоугольника со сторонами у = f(x) и b – a (см. рисунок 4.5).

Рисунок 4.5 – Теорема о среднем

Интегралом с переменным верхним пределом называют функцию Ф(х) вида , где x Î [а, b], а f(t) – функция, интегрируемая на отрезке [а, b].

Геометрический смысл интеграла с переменным верхним пределом представлен на рисунке 4.6 (этот интеграл равен площади S(x) под кривой
y =f(t) на отрезке [а, х]).

Рисунок 4.6 – Интеграл с переменным верхним пределом

Рассмотрим без доказательства свойства интеграла с переменным верхним пределом:

1. Если функция f(t) непрерывна на отрезке [а, b], то функция Ф(х) также непрерывна на [а, b].

2. Производная от интеграла с переменным верхним пределом по верхнему пределу равна подынтегральной функции:

Занятие 116. Практическое занятие 43. Самостоятельная работа №18.

Самостоятельная работа № 18

Занятие 117. Вычисление площади с помощью интеграла.

Интеграл как площадь криволинейной трапеции

Понятие определённого интеграла возникает в связи с задачей о нахождении площади криволинейной трапеции, нахождении пути по известной скорости при неравномерном движении и т. п.

Определение: Определённым интегралом по отрезку [a;b]от функции f(x) называется предел интегральной суммы , если этот предел существует и не зависит ни от деления отрезка [a;b]на части, ни от выбора точек t внутри каждой из частей при условии, что длина наибольшего из частичных отрезков (∆x _i ) стремится к нулю, т.е

Числа a,b называются соответственно нижним и верхним пределами интегрирования, т.е [a;b]-отрезок интегрирования.

Метод замены переменной

Основные понятия и теоремы

Теорема. Пусть функция x = ϕ(t) определена и дифференцируема на промежутке T, а промежуток X − множество ее значений. Пусть функция

y = f(x) определена на X и имеет на этом промежутке первообразную F(x).

Тогда на промежутке T функция F(ϕ(t)) является первообразной для функции f(ϕ(t))ϕ /(t).

Из теоремы 2 следует, что

Определение. Разность F (b)– F (a) называется интегралом от функции f (x) на отрезке [ a ; b ] и обозначается так: = F (b)– F (a) – формула Ньютона-Лейбница.

Геометрический смысл интеграла.

Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b:

.

Вычисление площадей с помощью интеграла.

1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :

2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и прямыми х=а, х= b :

3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и :

4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и осью Ох:

Методику нахождения площади рассмотрим сначала на относительно простом примере.

Найти площадь фигуры, ограниченной линиями

Вот искомая площадь:

Это общая формула. Конкретно к нашему случаю она применима так:

Пределы интегрирования .

= .

Вычислили площадь криволинейной фигуры.

Ответ: ед 2

В следующей задаче площадь искомой фигуры образовывается с помощью А именно:

Найти площадь фигуры, ограниченной линиями

Посмотрим, как выглядит фигура (рис. 4).

Рис. 4. Фигура, ограниченная линиями

Формула та же самая:

В нашем случае . Итак, надо найти определенный интеграл

=-(-1)+1=1+1=2.

Искомая площадь найдена, и ответ получен.

Найти площадь фигуры, ограниченной линиями

Рис. 5. Площадь фигуры, ограниченной линиями

Формула для площади та же самая:

В нашем случае .

Ответ : ед 2

В следующем примере ищется площадь под параболой.

Найти площадь фигуры, ограниченной линиями

Схематически изобразим параболу Корни

Рис. 6. Парабола

Применим известную формулу

И применим ее для данной функции и пределов интегрирования

Искомая площадь найдена.

Ответ: ед 2

В предыдущих задачах площадь образовывалась с помощью разных кривых, но эта площадь находилась над осью . В следующей задаче наоборот.

Рассмотрим случай, когда фигура находится под осью абсцисс.

Найти площадь фигуры, ограниченной линиями .

Посмотрим, что это за фигура. График в пределах от до расположен под осью Ox (рис. 7).

Рис. 7. График в пределах от до

Ясно, что если возьмем определенный интеграл, то мы получим отрицательное число.

1. Сначала вычисляем определенный интеграл от π до 2π от подынтегральной функции

Надо найти первообразную.

По таблице первообразных: .

Занятие 118. Практическое занятие 44. Решение задач на вычисление площади.

Общий случай для нахождения площади плоской фигуры, ограниченной двумя кривыми.

Следующее усложнение – искомая площадь расположена между двумя кривыми.

Найти площадь фигуры, ограниченной линиями (рис. 8)

Рис. 8. Площадь фигуры, ограниченной линиями

Итак, площадь образуют 2 кривые, одна из них может находиться под осью .

Каким образом мы будем решать эту задачу?

Во-первых, мы можем сдвинуть фигуру на такое положительное , что площадь находится над осью . Рис. 9.

Рис. 9. Сдвиг фигуры

Затем мы возьмем соответствующий определенный интеграл и найдем площадь. Искомая площадь равна разности двух площадей.

Площадь под верхней кривой минус площадь под нижней кривой .

Каждую из площадей мы умеем находить.

Таким образом, в общем виде была поставлена задача, в общем виде получен ответ.

Ответ:

Обсудим и постановку задачи, и полученный важный результат.

Нам надо было найти площадь фигуры, ограниченной линиями

.

Мы использовали известный прием: эту площадь подняли на некоторое , и это Так вот, эту площадь теперь можно считать без введения . Правило следующее:

Площадь фигуры, ограниченной прямыми линиями непрерывных на отрезке и таких, что для всех из отрезка вычисляется по формуле, которую мы вывели:

Рассмотрим первый конкретный пример на нахождение площади между двумя линиями.

Найти площадь фигуры, ограниченную линиями

.

График квадратичной функции – парабола. Корни – 0, 4, ветви вниз. График

– биссектриса первого координатного угла. Вот площадь, которую надо найти:

Рис. 10. Искомая площадь

Но для этого сначала надо найти точки пересечения и решить стандартную задачу.

1. Находим точки пересечения. Для этого решаем систему: .

Отсюда получаем квадратное уравнение относительно :

Мы нашли , то есть, пределы интегрирования. Это первое важное действие.

Теперь стандартное действие:

2. = =( )

Искомая площадь равна 4,5

Случай, когда часть площади плоской фигуры лежит под осью.

Во втором примере часть площади находится под осью , но на методику это не влияет.

Итак, требуется найти площадь фигуры, ограниченной линиями

Сначала построим графики, посмотрим, какую площадь нам нужно найти. Рис. 11.

Первая функция – парабола, ветви вниз. График второй функции – прямая линия.

Есть две точки пересечения, их придется найти, а именно взять пределы интегрирования, и тогда будем решать задачу по знакомому нам плану.

Рис. 11. Площадь фигуры, ограниченной линиями

Первое действие – найти пределы интегрирования и второе – найти площадь.

Пределы интегрирования найдем из системы .

То есть, пределы интегрирования найдены.

= ( )

Ответ: ед 2

Итак, мы показали, каким образом можно вычислять площади плоских фигур с помощью определенного интеграла.

Найти площадь фигуры, ограниченной линиями:

Занятие 119. Вычисление площади с помощью интеграла.

Вычислите площадь фигуры, ограниченной линиями

Занятие 120. Практическое занятие 45. Самостоятельная работа №19.

Вычислите площадь фигуры, ограниченной линиями

Вычислите площадь фигуры, ограниченной линиями

Вычислите площадь фигуры, ограниченной линиями

Вычислите площадь фигуры, ограниченной линиями

Вычислите площадь фигуры, ограниченной линиями

Вычислите площадь фигуры, ограниченной линиями

Занятие 121. Решение задач на применение интеграла.

Найдите все первообразные функции f ( x )= x 4 +3 x 2 +5

Найдите площадь фигуры, ограниченной графиком функции f ( x )= x 2 +5х+6, прямыми х=-1, х=2 и осью абсцисс.

Является ли функция первообразной функции

Занятие 122. Решение задач на применение интеграла.

Найдите все функции, которые имеют одну и ту же производную:

Найдите площадь фигуры, ограниченной осью абсцисс и графиком функции

Найдём точки пересечения графика функции и оси ОХ.

Найдите все первообразные для функции у (х) =

Найдите первообразную, график которой проходит через точку (1;

Для какой из функций функция является первообразной?

Занятие 123. Практическое занятие 46. Решение задач на применение интеграла.

Найдите площадь фигуры, ограниченной линиями

Для какой из функций функция является первообразной?

Найдите все функции, имеющие производную: у=

Найдите первообразную функции f ( x ) = 10 x 4 +х, значение которой при х=0 равно 6.

Найдите первообразную, график которой проходит через точку (1;

Занятие 124. Практическое занятие 47. Контрольная работа № 15.

Найдите площадь фигуры, ограниченной линиями

Найдите все первообразные для функции

Найдите площадь фигуры, ограниченной линиями

Найдите все функции, имеющие производную

Найдите первообразную функции график которой проходит через точку (2; 10).

Найдите площадь фигуры, ограниченной линиями

Найдите все функции, имеющие производную

Найдите первообразную функции график которой проходит через точку (-3; 10).

Найдите площадь фигуры, ограниченной линиями

Найдите все первообразные для функции

Найдите площадь фигуры, ограниченной осью абсцисс и графиком функции f ( x )=

Найдите первообразную функции y ( x ) = x 2 – 5, график которой проходит через точку ( 3; 4).

Найдите площадь фигуры, ограниченной линиями

Найдите все функции, имеющие производную

Найдите первообразную функции график которой проходит через точку (-2; 2).

Найдите площадь фигуры, ограниченной осью абсцисс и графиком функции

Найдите все функции, имеющие производную

Найдите первообразную функции график которой проходит через точку (2; 4).

Найдите площадь фигуры, ограниченной линиями

Найдите все первообразные для функции

Найдите площадь фигуры, ограниченной осями координат и графиком функции и прямой х= 2.

Найдите первообразную функции которая принимает отрицательное значение при х=1.

Найдите все функции, которые имеют одну и ту же производную

Занятие 125. Практическое занятие 48. Решение задач на применение интеграла.

Приложение интеграла к решению задач в геометрии

Основными формулами при решении задач с интегралами по геометрии являются:

— длина дуги

— объем тела вращения

— площадь плоской фигуры

Пример 1. Вычислить объем тела вращения, образованного вращением кривой y = x 2 вокруг оси ОХ, x ∈ [0, 2].

Решение. На первом этапе определяется используемая для решения задачи формула. В рассматриваемой задаче все сказано в условии «вычислить объем тела вращения». Следовательно, используем формулу .

Переходим ко второму этапу решения задачи. Пределы интегрирования также заданы условием задачи (x ∈ [0, 2]), следовательно, остается только подставить все необходимое в формулу.

На третьем этапе необходимо вычислить полученный интеграл, который, кстати, является табличным интегралом.

Приложение интеграла к решению задач в механике

Основными формулами при решении задач с интегралами по механике являются:

— работа переменной силы

— путь, пройденный телом

— статистический момент

— координата х центра тяжести

Пример 2. Тело движется со скоростью v(t) = t + 2 (м/с). Найти путь, который пройдет тело за 2 секунды после начала движения.

Решение. На первом этапе определяется необходимая для решения задачи формула. Из условия задачи видно, что используется формула

Пределы интегрирования также заданы условием задачи ( t ₁ = 0 — время начала движения; t ₂ = 2 — время завершения движения), следовательно, остается только подставить все необходимое в формулу и вычислить полученный интеграл.

Примечание: при вычислении интеграл был приведен к сумме табличных интегралов.

Решение. На первом этапе определяется используемая для решения задачи формула. Взаимосвязь между ускорением и скоростью аналогична взаимосвязи между скоростью и путем. Для определения зависимости пути от времени используется формула Для определения же зависимости скорости от времени формула .

В рассматриваемой задаче нет дополнительных условий, поэтому применяется неопределенный интеграл и пределы интегрирования не нужны.
Следовательно, решение задачи сводится к последовательному вычислению двух неопределенных интегралов:

1. Задача о вычислении пути

Согласно физическому смыслу первой производной, производная функции в точке есть мгновенная скорость точки, т.е. . Отсюда, . Интегрируя полученное равенство в пределах от t ₁ до t ₂ получаем

Тогда путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью (е) за отрезок времени [ ]выражается интегралом

(1)

Пример 1. Скорость прямолинейного движения тела выражается формулой = 2t+3t 2 (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Пример 2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v =(6t 2 +2t) м/с, второе – со скоростью v 2 =(4t+5) м/с. На каком расстояния друг от друга они окажутся через 5 с?

Решение. Искомая величина есть разность расстояний, пройденных телами за 5 с.

2. Задача о вычислении работы переменной силы

Пусть материальная точка под действием силы F движется по прямой. Если действующая сила постоянна, а пройденный путь равен s, то как известно из курса физики, работа А этой F вычисляется по формуле:

Работу переменной силы f(x) при перемещении по оси Оx материальной точки от x=a до x=b, находим по формуле (3):

A= (2)

Решении задач на вычисление работы силы упругости, связанных с растяжением и сжатием пружин, основывается на законе Гука. По закону Гука сила F, растягивающая или сжимающая пружину, пропорциональная этому растяжению или сжатию, т.е. F=kx, где x – величина растяжения или сжатия, k – коэффициент пропорциональности.

Пример 1. Сила упругости F пружины, растянутой на 1 1 = 0,05 м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 1 ₂ =0,1 м?

Решение. Подставив данные в формулу закона Гука, получим: 3=k*0.05, т.е. k=60, следовательно, сила упругости выражается соотношением F=60x. Найдем работу переменной силы по формуле (2), полагая, что а=0; b=0,1:

A= =0,3Дж

3. Задача о силе давления жидкости

Согласно закону Паскаля величина P давления жидкости на горизонтальную площадку вычисляется по формуле P=gphS, (4)

Где g – ускорение свободного падения в м/с 2 ;

p– плотность жидкости в кг/м 3 ;

h – глубина погружения площадки в м;

По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.

Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у ₁ = f ₁ (x) и у ₂ = f ₂ (х); система координат выбрана так, как указано на рисунке 1.

Для решения задачи разобьем пластину на n частей (малых горизонтальных полосок) прямыми, параллельными поверхности жидкости (т.е. параллельными оси OY). На глубине х выделим одну из них и обозначим через f(x) ее длину, а через ее ширину. Приняв полоску за прямоугольник, находим ее площадь .

Найдем дифференциал dp этой функции.

Тогда по закону Паскаля интегрируя полученное равенство в пределах от х = а до х = b, получим

P=g (3)

Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м 3 ), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м.

Решение. Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой (3). Стенка имеет форму прямоугольника, поэтому Так как пределы интегрирования а=0 и b=0,4, то получим:

Прирост численности популяции N(t) за промежуток времени от t ₀ до T равен .

Объем тела вращения

Решение: Построим тело вращения, образованного вращением фигуры вокруг оси 0х

Воспользуемся формулой Ньютона-Лейбница.

и формулой нахождения объемов тел вращения.

Далее подставляем значения в формулу и рассчитываем объем тела вращения.

№ 2. Сила в 1 Н растягивает пружину на 3 см. Какую работу она при этом производит?

Если F–сила, А – работа S– перемещение, то F = A’(S).

Обратимся к физике.

По закону Гука сила пропорциональна растяжению или сжатию пружины, т. е. F = kx, где k – коэффициент пропорциональности, х – величина растяжения или сжатия.

Используя данные задачи, найдите коэффициент k. Подставим данные в задаче величины в уравнение, выражающее закон Гука. Получим: .

Следовательно, сила, растягивающая нашу пружину, выразится следующим образом: .

Так как сила начинает действовать на пружину в состоянии покоя, то работа

№ 3. Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м 3 ), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м.

Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой

Р=

Стенка имеет форму прямоугольника, поэтому f(x)=0.7x, xϵ [0;0.4] Так как пределы интегрирования а=0 и b=0,4, то получим:

№ 4 Скорость прямолинейного движения тела выражается формулой . Найти путь, пройденный телом за 5 секунд от начала движения.

Физический смысл производной: если тело движется по закону S = S(t), то скорость тела в момент времени t ₀ равна значению производной функции S(t) в этой точке, т. е. v = S’(t ₀ ). Тогда обратное утверждение: если скорость движения тела задана уравнением v = v(t), то путь, пройденный телом от момента времени t = a до момента времени t = b равен . Подставим уравнение скорости в формулу и рассчитаем путь.

Занятие 126. Практическое занятие 49. Решение задач на применение интеграла.

При вычислении площадей фигур могут представиться следующие случаи:

а) Фигура расположена над осью OX и ограничена осью OX, кривой y=f (x) и двумя прямыми x=a; x=b Площадь этой фигуры находится по формуле 1 или 2.

Необходимо вычислить площадь плоской фигуры, ограниченной прямыми: x−2 y+4=0; x+ y−5=0; y=0

Очевидно, что искомая площадь равна сумме площадей AMN и NMC, а следовательно, сумме определённых интегралов:

1. ВЫЧИСЛЕНИЕ ПУТИ, ПРОЙДЕННОГО ТОЧКОЙ

Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:

2. ВЫЧИСЛЕНИЕ РАБОТЫ СИЛЫ

1. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,22 до 0,32 м?

Решение: используя равенство, имеем 50=0,01k, т. е. k = 5000 Н/м. Находим пределы интегрирования: а = 0,22 — 0,2 = 0,02 (м), b=0,32— 0,2 = 0,12(м). Теперь по формуле (2) получим

3. ВЫЧИСЛЕНИЕ РАБОТЫ, ПРОИЗВОДИМОЙ ПРИ ПОДНЯТИИ ГРУЗА

Задача. Цилиндрическая цистерна с радиусом основания 0,5 м и высотой 2 м заполнена водой. Вычислить работу, которую необходимо произвести, чтобы выкачать воду из цистерны.

Решение: выделим на глубине x горизонтальный слой высотой dx. Работа А, которую надо произвести, чтобы поднять слой воды весом Р на высоту х, равна Px.

Изменение глубины х на малую величину dх вызовет изменение объема V на величину dV =π r 2 dx; изменение веса Р на величину dP = 9807 r 2 dx; при этом совершаемая работа А изменится на величину dА=9807π r 2 xdx. Проинтегрировав это равенство при изменении x от 0 до Н, получим

4. ВЫЧИСЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ

Если площадка, испытывающая давление жидкости, не горизонтальна, то давление на нее различно на разных глубинах, следовательно, сила давления на площадку есть функция глубины ее погружения P(x )

При вычислении координаты центра масс можно любую часть фигуры заменить на материальную точку, поместив ее в центр масс этой части, и приписать ей массу, равную массе рассматриваемой части фигуры.

C уммарная масса М стержня равна

координата центра масс x равна

При решении физических задач математическими методами пользуемся следующими формулами и соотношениями :

Для вычисления механической работы:

Вычисление производной F(x)=A’ (x); N(t)=A’ (t).

Для вычисления массы тонкого стержня:

Для вычисления количества электричества:

Для вычисления перемещения и скорости:

Вычисление производной V(t)=S’ (t) Вычисление интеграла S=, где V – скорость перемещения, S – перемещение, t – время.

Источник