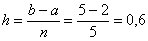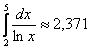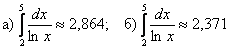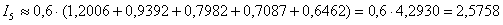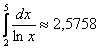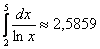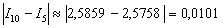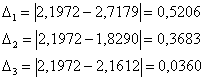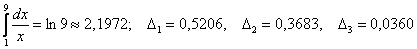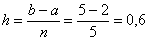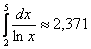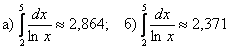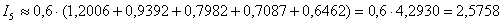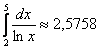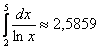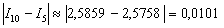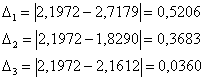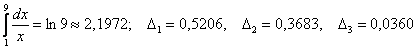интеграл по формуле правых прямоугольников
Метод прямоугольников
Метод прямоугольников – это, пожалуй, самый простой метод приближённого вычисления определённого интеграла. И парадокс состоит в том, что по этой причине (видимо) он довольно редко встречается на практике. Неудивительно, что данная статья появилась на свет через несколько лет после того, как я рассказал о более распространённых методах трапеции и Симпсона, где упомянул о прямоугольниках лишь вскользь. Однако на сегодняшний день раздел об интегралах практически завершён и поэтому настало время закрыть этот маленький пробел. Читаем, вникаем и смотрим видео! ….о чём? Об интегралах, конечно =)
Постановка задачи уже была озвучена на указанном выше уроке, и сейчас мы быстренько актуализируем материал:
Рассмотрим интеграл 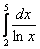
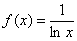
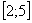
Разбиваем промежуток интегрирования на 5, 10, 20 или бОльшее количество равных (хотя это не обязательно) отрезков, чем больше – тем точнее будет приближение. На каждом отрезке строим прямоугольник, одна из сторон которого лежит на оси 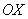

Очевидно, что прямоугольники можно построить многими способами, но стандартно рассматривают 3 модификации:
1) метод левых прямоугольников;
2) метод правых прямоугольников;
3) метод средних прямоугольников.
Оформим дальнейшие выкладки в рамках «полноценного» задания:
Вычислить определённый интеграл 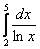
а) методом левых прямоугольников;
б) методом правых прямоугольников.
Промежуток интегрирования разделить на 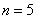
Решение: признАюсь сразу, я специально выбрал такое малое значение 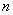
Вычислим шаг разбиения (длину каждого промежуточного отрезка):
Метод левых прямоугольников получил своё называние из-за того, 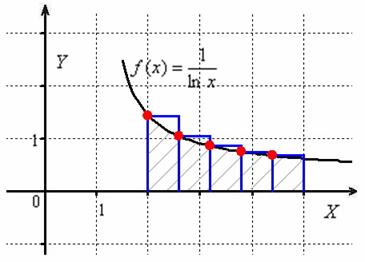
что высОты прямоугольников на промежуточных отрезках равны значениям функции в левых концах данных отрезков: 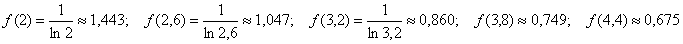
Ни в коем случае не забываем, что округление следует проводить до трёх знаков после запятой – это существенное требование условия, и «самодеятельность» здесь чревата пометкой «оформите задачу, как следует».
Вычислим площадь ступенчатой фигуры, которая равна сумме площадей прямоугольников: 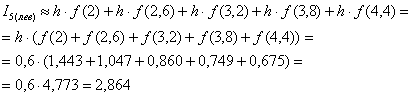
Таким образом, площадь криволинейной трапеции: 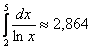
При использовании «правого» метода высОты прямоугольников равны значениям функции в правых концах промежуточных отрезков: 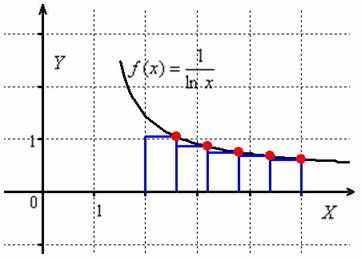
Вычислим недостающее значение 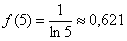
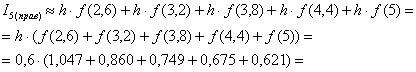
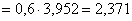
Запишем формулы в общем виде. Если функция 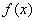
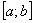
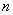
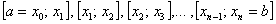
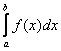
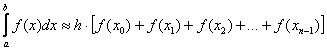
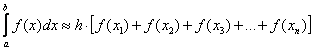
(формула в следующей задаче) – средних прямоугольников,
где 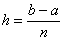
На практике рассчитываемые значения 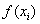

а сами вычисления проводить в Экселе. И быстро, и без ошибок:
Ответ:
Наверное, вы уже поняли, в чём состоит метод средних прямоугольников:
Вычислить приближенно определенный интеграл 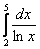
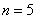
Решение: во-первых, обращаем внимание, что интеграл нужно вычислить с точностью до 0,01. Что подразумевает такая формулировка?
Если в предыдущей задаче требовалось прОсто округлить результаты до 3 знаков после запятой (а уж насколько они будут правдивы – не важно), то здесь найденное приближённое значение площади 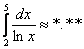

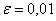
И во-вторых, в условии задачи не сказано, какую модификацию метода прямоугольников использовать для решения. И действительно, какую?
По умолчанию всегда используйте метод средних прямоугольников
Почему? А он при прочих равных условиях (том же самом разбиении) даёт гораздо более точное приближение. Это строго обосновано в теории, и это очень хорошо видно на чертеже: 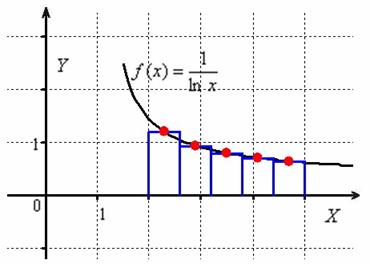
В качестве высот прямоугольников здесь принимаются значения функции, вычисленные в серединах промежуточных отрезков, и в общем виде формула приближённых вычислений запишется следующим образом: 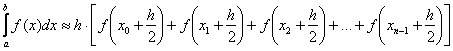
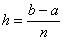
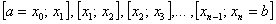
Следует отметить, что формулу средних прямоугольников можно записать несколькими способами, но чтобы не разводить путаницу, я остановлюсь на единственном варианте, который вы видите выше.
Вычисления, как и в предыдущем примере, удобно свести в таблицу. Длина промежуточных отрезков, понятно, та же самая: 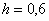
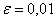
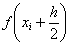
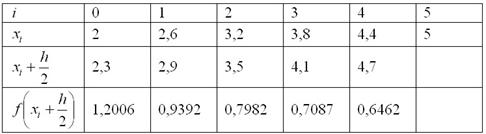
Вычислим площадь ступенчатой фигуры:
Давайте посмотрим, как автоматизировать этот процесс:
Таким образом, по формуле средних прямоугольников:
Как оценить точность приближения? Иными словами, насколько далёк результат от истины (площади 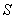
Вычислим более точное приближение 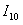
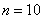
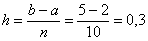
Найдём середину первого промежуточного отрезка 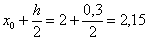
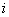
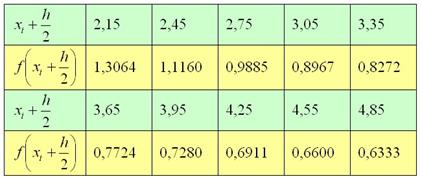
В Экселе вычисления проводятся «в один ряд» (кстати, потренируйтесь), а вот в тетради таблицу, скорее всего, придётся сделать двухэтажной (если у вас, конечно, не сверхмелкий почерк).
Вычислим суммарную площадь десяти прямоугольников: 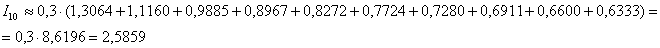
Таким образом, более точное приближение:
Теперь находим модуль разности между двумя приближениями:
Как я уже отмечал в статье Приближённое вычисление определенных интегралов, на практике довольно часто встречается упрощённый подход: поскольку разность 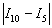
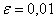
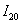
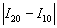
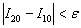
Однако существует более эффективный путь решения, основанный на применении правила Рунге, которое утверждает, что при использовании метода средних прямоугольников мы ошибаемся в оценке определённого интеграла менее чем на 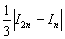
В нашем случае: 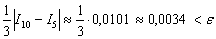
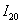
Округляем наиболее точное приближение 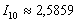
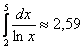
Ещё раз – что это значит? Это значит, что площадь 
В Примере 2 урока метод трапеций и метод Симпсона я вычислил приближённое значение этого же интеграла методом трапеций. Любознательные читатели могут сравнить полученные здесь и там результаты.
Вернемся ещё к одному маленькому нюансу, который выпал из поля зрения в самом начале урока: обязательно ли в рассматриваемом задании интеграл должен быть неберущимся? Конечно, нет. Приближённые методы вычисления прекрасно работают и для берущихся определённых интегралов. Заключительный школьный, а точнее, техникумовский пример для самостоятельного решения:
Вычислить интеграл 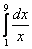
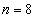
1) методом левых прямоугольников;
2) методом правых прямоугольников;
3) методом средних прямоугольников.
Вычислить более точное значение интеграла с помощью формулы Ньютона-Лейбница. Для каждого из трёх случаев найти абсолютную погрешность. Вычисления округлять до 4 знаков после запятой.
Не нужно пугаться такого развёрнутого условия – всё элементарно «перещёлкивается» в Экселе. Напоминаю, что абсолютная погрешность – это модуль разности между точным и приближённым значением. Кстати, обратите внимание на принципиальную разницу: если в предыдущих примерах речь шла лишь об оценке погрешности, то здесь нам будут известны конкретные значения этих погрешностей (т.к. интеграл берётся, и мы достоверно знаем 4 верных цифры после запятой).
Краткое решение и ответ уже, наверное, показались на вашем экране.
И, завершая эту небольшую статью, хочу отметить, что иногда метод прямоугольников ошибочно называют «плохим», «неточным» и т.п. Ничего подобного! Если уж на то пошло, его корректнее назвать «медленным» методом. Иными словами, чтобы достигнуть определённой точности – нужно рассмотреть бОльшее количество отрезков разбиения по сравнению с более эффективными методом трапеций и ещё более «быстрым» методом Симпсона.
Которые я и предлагаю вам изучить!
Пример 3: Решение: вычислим шаг разбиения: 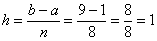
Заполним расчётную таблицу: 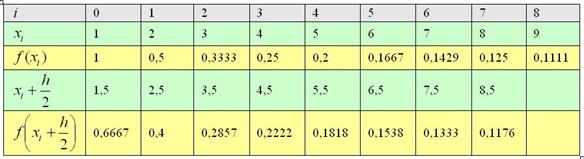
Вычислим интеграл приближённо методом:
1) левых прямоугольников: 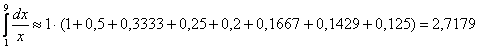
2) правых прямоугольников: 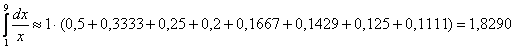
3) средних прямоугольников: 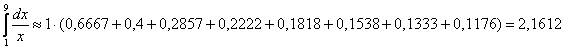
Вычислим интеграл более точно по формуле Ньютона-Лейбница: 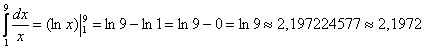
и соответствующие абсолютные погрешности вычислений:
Ответ: 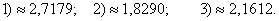
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Метод прямоугольников
Метод прямоугольников – это, пожалуй, самый простой метод приближённого вычисления определённого интеграла. И парадокс состоит в том, что по этой причине (видимо) он довольно редко встречается на практике. Неудивительно, что данная статья появилась на свет через несколько лет после того, как я рассказал о более распространённых методах трапеции и Симпсона, где упомянул о прямоугольниках лишь вскользь. Однако на сегодняшний день раздел об интегралах практически завершён и поэтому настало время закрыть этот маленький пробел. Читаем, вникаем и смотрим видео! ….о чём? Об интегралах, конечно =)
Постановка задачи уже была озвучена на указанном выше уроке, и сейчас мы быстренько актуализируем материал:
Рассмотрим интеграл 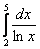
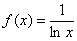
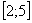
Разбиваем промежуток интегрирования на 5, 10, 20 или бОльшее количество равных (хотя это не обязательно) отрезков, чем больше – тем точнее будет приближение. На каждом отрезке строим прямоугольник, одна из сторон которого лежит на оси 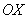

Очевидно, что прямоугольники можно построить многими способами, но стандартно рассматривают 3 модификации:
1) метод левых прямоугольников;
2) метод правых прямоугольников;
3) метод средних прямоугольников.
Оформим дальнейшие выкладки в рамках «полноценного» задания:
Вычислить определённый интеграл 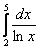
а) методом левых прямоугольников;
б) методом правых прямоугольников.
Промежуток интегрирования разделить на 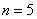
Решение: признАюсь сразу, я специально выбрал такое малое значение 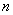
Вычислим шаг разбиения (длину каждого промежуточного отрезка):
Метод левых прямоугольников получил своё называние из-за того, 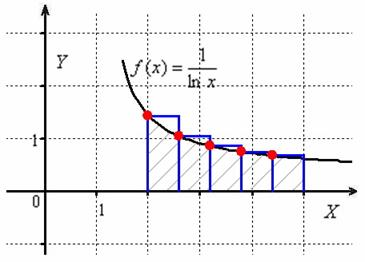
что высОты прямоугольников на промежуточных отрезках равны значениям функции в левых концах данных отрезков: 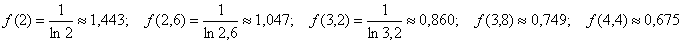
Ни в коем случае не забываем, что округление следует проводить до трёх знаков после запятой – это существенное требование условия, и «самодеятельность» здесь чревата пометкой «оформите задачу, как следует».
Вычислим площадь ступенчатой фигуры, которая равна сумме площадей прямоугольников: 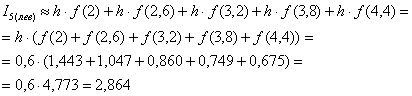
Таким образом, площадь криволинейной трапеции: 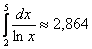
При использовании «правого» метода высОты прямоугольников равны значениям функции в правых концах промежуточных отрезков: 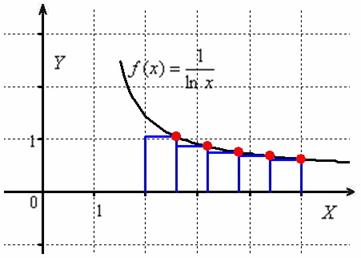
Вычислим недостающее значение 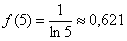
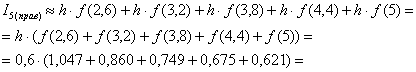
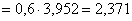
Запишем формулы в общем виде. Если функция 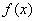
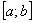
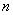
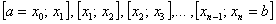
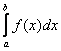
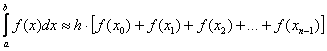
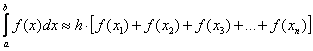
(формула в следующей задаче) – средних прямоугольников,
где 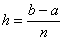
На практике рассчитываемые значения 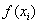

а сами вычисления проводить в Экселе. И быстро, и без ошибок:
Ответ:
Наверное, вы уже поняли, в чём состоит метод средних прямоугольников:
Вычислить приближенно определенный интеграл 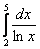
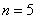
Решение: во-первых, обращаем внимание, что интеграл нужно вычислить с точностью до 0,01. Что подразумевает такая формулировка?
Если в предыдущей задаче требовалось прОсто округлить результаты до 3 знаков после запятой (а уж насколько они будут правдивы – не важно), то здесь найденное приближённое значение площади 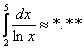

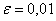
И во-вторых, в условии задачи не сказано, какую модификацию метода прямоугольников использовать для решения. И действительно, какую?
По умолчанию всегда используйте метод средних прямоугольников
Почему? А он при прочих равных условиях (том же самом разбиении) даёт гораздо более точное приближение. Это строго обосновано в теории, и это очень хорошо видно на чертеже: 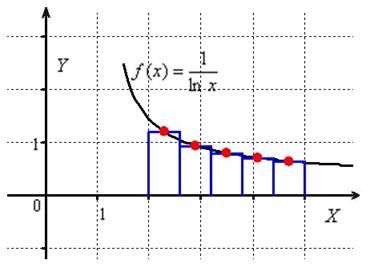
В качестве высот прямоугольников здесь принимаются значения функции, вычисленные в серединах промежуточных отрезков, и в общем виде формула приближённых вычислений запишется следующим образом: 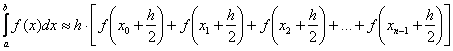
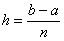
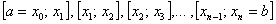
Следует отметить, что формулу средних прямоугольников можно записать несколькими способами, но чтобы не разводить путаницу, я остановлюсь на единственном варианте, который вы видите выше.
Вычисления, как и в предыдущем примере, удобно свести в таблицу. Длина промежуточных отрезков, понятно, та же самая: 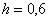
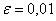
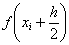
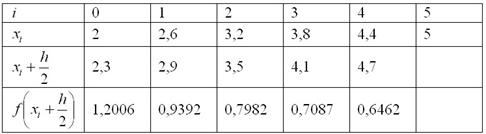
Вычислим площадь ступенчатой фигуры:
Давайте посмотрим, как автоматизировать этот процесс:
Таким образом, по формуле средних прямоугольников:
Как оценить точность приближения? Иными словами, насколько далёк результат от истины (площади 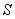
Вычислим более точное приближение 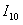
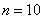
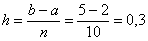
Найдём середину первого промежуточного отрезка 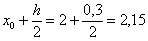
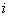
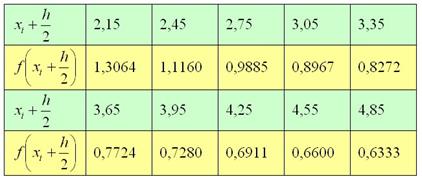
В Экселе вычисления проводятся «в один ряд» (кстати, потренируйтесь), а вот в тетради таблицу, скорее всего, придётся сделать двухэтажной (если у вас, конечно, не сверхмелкий почерк).
Вычислим суммарную площадь десяти прямоугольников: 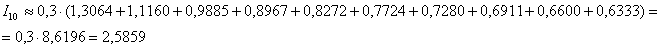
Таким образом, более точное приближение:
Теперь находим модуль разности между двумя приближениями:
Как я уже отмечал в статье Приближённое вычисление определенных интегралов, на практике довольно часто встречается упрощённый подход: поскольку разность 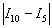
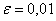
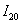
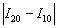
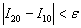
Однако существует более эффективный путь решения, основанный на применении правила Рунге, которое утверждает, что при использовании метода средних прямоугольников мы ошибаемся в оценке определённого интеграла менее чем на 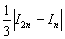
В нашем случае: 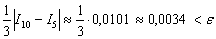
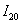
Округляем наиболее точное приближение 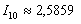
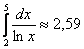
Ещё раз – что это значит? Это значит, что площадь 
В Примере 2 урока метод трапеций и метод Симпсона я вычислил приближённое значение этого же интеграла методом трапеций. Любознательные читатели могут сравнить полученные здесь и там результаты.
Вернемся ещё к одному маленькому нюансу, который выпал из поля зрения в самом начале урока: обязательно ли в рассматриваемом задании интеграл должен быть неберущимся? Конечно, нет. Приближённые методы вычисления прекрасно работают и для берущихся определённых интегралов. Заключительный школьный, а точнее, техникумовский пример для самостоятельного решения:
Вычислить интеграл 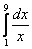
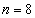
1) методом левых прямоугольников;
2) методом правых прямоугольников;
3) методом средних прямоугольников.
Вычислить более точное значение интеграла с помощью формулы Ньютона-Лейбница. Для каждого из трёх случаев найти абсолютную погрешность. Вычисления округлять до 4 знаков после запятой.
Не нужно пугаться такого развёрнутого условия – всё элементарно «перещёлкивается» в Экселе. Напоминаю, что абсолютная погрешность – это модуль разности между точным и приближённым значением. Кстати, обратите внимание на принципиальную разницу: если в предыдущих примерах речь шла лишь об оценке погрешности, то здесь нам будут известны конкретные значения этих погрешностей (т.к. интеграл берётся, и мы достоверно знаем 4 верных цифры после запятой).
Краткое решение и ответ уже, наверное, показались на вашем экране.
И, завершая эту небольшую статью, хочу отметить, что иногда метод прямоугольников ошибочно называют «плохим», «неточным» и т.п. Ничего подобного! Если уж на то пошло, его корректнее назвать «медленным» методом. Иными словами, чтобы достигнуть определённой точности – нужно рассмотреть бОльшее количество отрезков разбиения по сравнению с более эффективными методом трапеций и ещё более «быстрым» методом Симпсона.
Которые я и предлагаю вам изучить!
Пример 3: Решение: вычислим шаг разбиения: 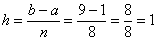
Заполним расчётную таблицу: 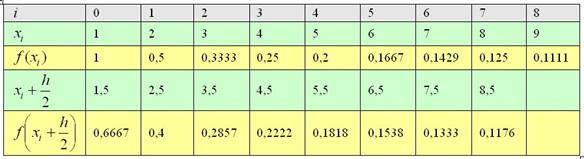
Вычислим интеграл приближённо методом:
1) левых прямоугольников: 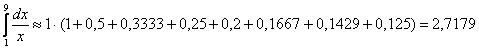
2) правых прямоугольников: 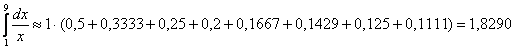
3) средних прямоугольников: 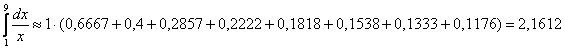
Вычислим интеграл более точно по формуле Ньютона-Лейбница: 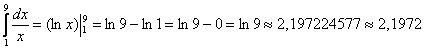
и соответствующие абсолютные погрешности вычислений:
Ответ: 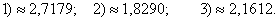
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5