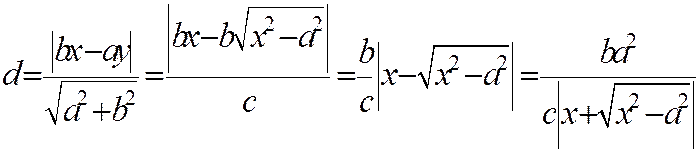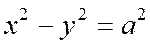исследование формы гиперболы по ее уравнению

20.03.202313.04.2023 admin 0 Комментариев

Исследование формы гиперболы по ее уравнению.

Определим форму гиперболы по ее каноническому уравнению (4).

1) Координаты точки О (0; 0) не удовлетворяют уравнению (4), поэтому гипербола, определяемая этим уравнением, не проходит через начало координат.

не имеет действительных решений. Следовательно, гипербола не пересекает ось Оу.

3) Так как в уравнение (4) переменные х и у входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат.

4) Определим область изменения переменных х и у;для этого из уравнения (4) находим

, (5)

. (6)

Из (5) следует, что |х| ≥ а, т.е. х ≥ а или х ≤ –а; из (6) следует, что у – любое действительное число. Таким образом, все точки гиперболы расположены слева oт прямой х = – а и справа от прямой х = а.

5) Из (5) следует также, что

Это означает, что гипербола состоит из двух ветвей, одна из которых расположена справа от прямой х = а (правая ветвь гиперболы), а другая – слева от прямой х = – а (левая ветвь гиперболы).

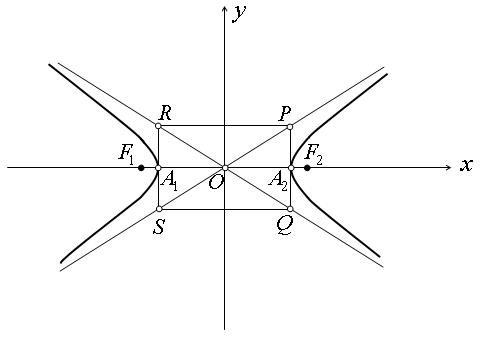
Гипербола имеет форму, изображенную на рис. 2.

Определение 4. Точки А₁ (а; 0) и А₂ (а; 0) пересечения гиперболы с осью Ох называются вершинами гиперболы. Отрезок A₁A₂ (A₁A₂=2a),соединяющий вершины гиперболы, называется действительной осью.Отрезок B₁B₂ (B₁B₂=2b), соединяющий точки B₁ (0; b) и В₂ (0; –b), называется мнимой осью.Число а называется действительной полуосью, число b – мнимой полуосью.Оси А₁А₂ и В₁В₂ являются осями симметрии гиперболы. Точка О пересечения осей симметрии называется центром гиперболы.

У гиперболы (4) фокусы F₁ и F₂ всегда находятся на действительной оси.

Можно показать (так же, как и в случае эллипса), что фокальные радиусы для точки М (х; у), расположенной на правой ветви гиперболы, вычисляются по формулам

и , (7)

а для точки М (х; у), расположенной на левой ветви, – по формулам

и . (8)

Асимптоты гиперболы.

Определение 5. Прямая y=kx+m называется наклонной асимптотойкривой y = f(x) при х → +∞,если

. (9)

Аналогично определяется асимптота при х → –∞. Докажем, что прямые

(10)

являются асимптотами гиперболы (4) при х → ±∞.

Так как прямые (10) и гипербола (4) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 3). Напишем уравнения прямых (10) и гиперболы (4), соответствующие первой четверти:

Положив и , найдем

Следовательно, прямые (10) являются асимптотами гиперболы (4).

Отметим, что асимптоты (10) являются продолжениями диагоналей прямоугольника, стороны которого параллельны осям Ох и Оу и равны соответственно 2а и 2b, а его центр находится в начале координат.

При этом ветви гиперболы расположены внутри вертикальных углов, образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис. 4).

Эксцентриситет гиперболы.

Определение 6. Эксцентриситетом гиперболыназывается отношение расстояния между фокусами к длине действительной оси и обозначается буквой ε:

(11)

5. Сопряженная гипербола. Рассмотрим уравнение вида

. (12)

При переходе к новой системе координат, полученной в результате поворота осей старой системы вокруг начала координат на угол α = 90° (или α = –90°), уравнение (12) преобразуется в уравнение гиперболы

Следовательно, кривая, определяемая уравнением (12), есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2а – на оси Ох.

Две гиперболы, которые определяются уравнениями

в одной и той же системе координат и при одних и тех же значениях а и b, называются сопряженнымидруг с другом.

Равносторонняя гипербола.

Определение 7. Гипербола называется равносторонней,если длины ее полуосей равны между собой, т.е. а=b. В этом случае уравнение гиперболы принимает вид

. (13)

Равносторонняя гипербола определяется одним параметром а и асимптотами являются биссектрисы координатных углов

У всех равносторонних гипербол один и тот же эксцентриситет

Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат Ox’y’, полученной в результате поворота осей старой системы вокруг начала координат на угол α = –45° (рис. 5). Составим уравнение равносторонней гиперболы относительно новой системы координат Ох’у’.

Учитывая равенство (13), получим x’y’ = а 2 /2. (14)

Определение 8. Уравнение (14) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.

Из уравнения (14) следует, что переменные х’ и у’ – величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратной пропорциональной зависимости.

Если центр гиперболы находится не в начале координат, а в точке О'(х₀; у₀), а оси гиперболы параллельны осям координат, то уравнение гиперболы будет иметь вид

или (15)

Это уравнения гиперболы со смещенным центром.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Исследование формы гиперболы

Так как в каноническое уравнение гиперболы координаты х и у входят во второй степени. То оси Ох и Оу являются осями симметрии гиперболы, заданной уравнением: 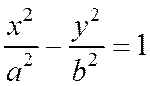. (1)

а начало координат – центром симметрии.

Из уравнения (1) следует, что

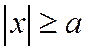
т.е. или 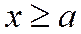, или . Геометрически это означает, что между прямыми и нет ни одной точки гиперболы (1).

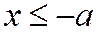
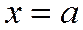
Ось симметрии Оу не пересекает гиперболу, заданную уравнением (1), и называется мнимой осью. Ось Ох – пересекает гиперболу (1) в двух точках:

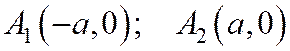
Эта ось называется действительной осью гиперболы. Точки, в которых действительная ось пересекается гиперболу, называются вершинами гиперболы.

Числа а и b в каноническом уравнении называются действительной и мнимой полуосями гиперболы.

Решая уравнение (1) относительно у, беря лишь положительное значение: 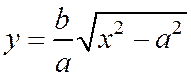(2)

и считая 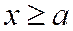, мы получим точки гиперболы (1), лежащие в первой четверти. Из уравнения (2) следует, что у в полуинтервале есть возрастающая функция; при этом

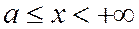
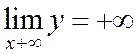
Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением первой степени, а гипербола – второй.

Рассмотрим уравнение прямой (3)

Найдем расстояние 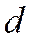от точки М(х, у), лежащей на дуге гиперболы, определяемой уравнением (2), до прямой (3); переписывая уравнение (3) в виде , находим:

Отсюда следует, то на полуинтервале расстояние от точки М(х, у) рассматриваемой части гиперболы до прямой (3) есть убывающая функция от х и (рис. 167). Прямая, определяемая уравнением называется асимптотой гиперболы.

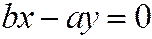
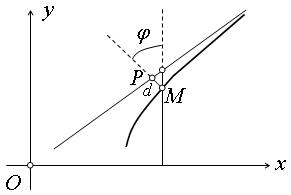
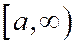
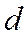
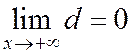
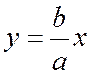
В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно начала координат, расстояние от точки М(х, у), лежащей на дуге гиперболы, заданной уравнением 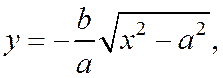до прямой стремиться к нулю при . Так как гипербола, заданная каноническим уравнением, симметрична и относительно оси Оу, то она имеет вторую асимптоту ,

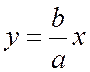
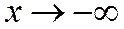
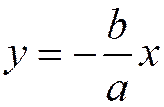
которая обладает свойством, аналогичным свойству первой асимптоты по отношению к дугам гиперболы, расположенным во второй и четвертой четвертях.

Асимптоты гиперболы являются диагоналями прямоугольника , , , .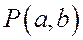

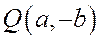
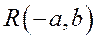
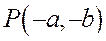
При одной и той же абсциссе х ординаты точки ветви гиперболы, лежащей в первой четверти, с ординатой точки асимптоты 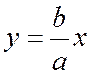связаны неравенством: .

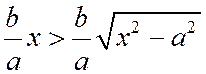
Отсюда и из того, что гипербола симметрична относительно осей координат, следует, что она имеет две ветви, заключенные в двух областях: одна из них ограничена отрезком и продолжениями отрезков и за точки и , другая симметрична этой области относительно мнимой оси гиперболы (рис 168).

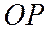
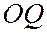
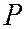
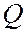
Рис.168

Гипербола, у которой полуоси равны, называются равносторонней. Каноническое уравнение равносторонней гиперболы имеет вид

Уравнение асимптот равносторонней гиперболы таковы:

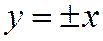
это биссектрисы углов между ее осями симметрии. Асимптоты равносторонней гиперболы взаимно перпендикулярны.

Обратно, если асимптоты гиперболы взаимно перпендикулярны, то ее полуоси равны между собой и, значит гипербола равносторонняя.

Источник

Исследование формы гиперболы по ее каноническому уравнению

Определение. Пускай на плоскости заданы две точки F1и F2, расстояние между которыми равняется 2c. Пускай, помимо этого, задано положительное число a, меньшее c. Преувеличением именуется множество точек той же плоскости, для каждой из которых модуль разности расстояний до точек F1 и F2, именуемых фокусами преувеличения, имеется число постоянное, равное 2а.

Вывод канонического уравнения

Для вывода уравнения преувеличения, которое мы потом назовём каноническим, выберем на плоскости прямоугольную декартову совокупность координат следующим образом: ось

совершим через фокусы преувеличения, а ось

– перпендикулярно ей через середину отрезка F1F2 (рис. 3.1). По определению преувеличении удовлетворяют те, и лишь те точки М плоскости, для которых

Чтобы получить уравнение преувеличения остаётся лишь записать равенство (1) в координатах. В выбранной совокупности координат фокусы преувеличения имеют следующие координаты: F1 (–c; 0); F2 (c; 0). Координаты произвольной (либо текущей) точки множества постоянно обозначаются x и y. Так, M(x; y). Так как

то уравнение (1) равносильно следующему:

которое, со своей стороны, равносильно уравнению:

Оба эти уравнения являются уравнениями преувеличения, но они имеют громоздкий вид, неудобны для применения и для запоминания, исходя из этого мы преобразуем их к более несложному виду. Совершим следующую цепочку преобразований: