к какой группе шкал измерений относятся интервальная шкала и шкала отношений
Виды шкал: наименований, порядка, интервальная, отношений
В психолого-педагогических исследованиях применяют классификацию шкал, предложенную С.Стивенсоном (см. рис. 1), согласно которой четыре основных способа измерения, связанные с различными правилами, называют измерительными шкалами (номинальная, порядковая, интервальная и шкала отношений).
1. Номинальная шкала (шкала наименований), которую правильнее было бы считать классификацией, а не измерением, делит все объекты на группы по какому-либо признаку (различию). Этим признакам присваиваются определенные числа (код), что создает удобства при дальнейшей обработке экспериментальных данных. Никакого количественного соотношения между объектами в номинальной шкале нет.
Примеры:
В процессе проверки соответствия подготовки выпускников школ требованиям ГОС появляется группа аттестованных и не аттестованных учеников.
2. Шкала порядка (порядковая, ранговая, ординальная) предназначена для измерения (обозначения) степени различия какого-либо признака или свойства у разных объектов. Самым ярким примером порядковой шкалы является пятибалльная система оценки ЗУН учащихся. Для нее разработаны критерии и различные методы измерения. 3начительно труднее применять порядковую шкалу для количественных оценок других качеств личности (в воспитательном процессе). Имеется несколько разновидностей порядкового шкалирования(измерения):
— ранжирование (в ряд),
— группировка (ранжирование по группам),
— метод полярных профилей.
Ранжирование. Изучаемые объекты располагаются в ряд (упорядочиваются) по степени выраженности какого-либо качества. Первое место в этом ряду занимает объект с наиболее высоким уровнем данного качества, и ему присваивается наивысший балл (числовое значение выбирается произвольно). Затем каждому объекту ранжированного ряда присваиваются более низкие оценки, соответствующие занимаемым местам.
Группировка всей совокупности объектов наблюдения в несколько рангов, достаточно ясно отличающихся друг от друга по степени измеряемого признака.
Пример: учащиеся класса согласно пятибалльной системе оценки ЗУН делятся на отличников, хорошистов и т. д.
Парное сравнение. Учащиеся сопоставляются друг с. другом (каждый с каждым) по какому-либо качеству. Если они одинаковы, то каждый получает по баллу. Если у одного этого качества больше, чем у другого, первый получает два балла, второй – 0 (как при спортивных играх по круговой системе). Суммируя полученные каждым баллы, получаем количественное выражение уровня развития данного качества у каждого учащегося (его ранг).
Рейтинг. В этом приеме оценка объекта производится путем усреднения оценочных суждений группой компетентных экспертов. Имея общие критерии оценки (в порядковой шкале, в баллах), эксперты независимо друг от друга (в устной или письменной форме) выносят свои суждения. Усредненный результат экспертной оценки является достаточно объективным и называется рейтингом.
Пример. Оценка степени доверия кандидату на выборную должность дается в полярной шкале:
(Доверяю полностью) 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 (Совсем не доверяю)
Примеры: температурные шкалы; шкалы стандартизированного тестирования интеллекта.
Интервальная шкала – количественная. В ней возможны все арифметические действия над числами, кроме операции деления. Таким образом, в интервальной шкале нельзя определить во сколько раз один объект больше или меньше другого. Например, если ученик ответил правильно на 10 заданий, то это не означает, что он знает вдвое больше ученика, ответившего на 5 заданий теста.
4. Шкала отношений отличается от интервальной только тем, что ее нулевая точка не произвольна, а указывает на полное отсутствие измеряемого свойства. Сюда относятся и все количественные данные, получаемые пересчетом объектов какого-либо множества (число учащихся, уроков и т. п.).
Уровни измерения и математические вычисления, используемые на данных уровнях, показаны в табл. 1. Из этой таблицы видно, что переход от одного уровня к другому сопровождается расширением класса допустимых математико-статистических операций. Как следует из таблицы, наилучшей является шкала отношений, которую на сегодняшний день удалось реализовать только в рамках физических измерений.
Типы шкал



Существует четыре основных типа шкал (по Стивенсу):
1. Номинальная шкала (шкала наименований).
2. Порядковая шкала (ординальная, ранговая).
3. Интервальная (шкала равных интервалов).
4. Шкала равных отношений (относительная).
Номинальная шкала (шкала наименований) –это шкала, классифицирующая по названию. Название не измеряется количественно, оно лишь позволяет отличить один объект от другого.
Шкала наименований позволяет подсчитать частоту, встречаемость разных наименований, а затем работать с этой частотой, с помощью математических методов. Допустимо только ограниченное количество статистических расчетов, базирующихся на подсчете частот. К ним относятся процентные соотношения, мода, хи-квадрат, биноминальный критерий, угловое преобразование Фишера.
Порядковая шкала (ординальная, ранговая) – это шкала, классифицирующая по принципу «больше – меньше». Если в номинальной шкале безразлично, в каком порядке находятся ячейки, то в порядковой шкале они образуют последовательность от ячейки «самое малое» к ячейке «самое большое» или наоборот. Здесь мы не знаем, на сколько именно значение следующей ячейки больше или меньше значения предыдущей. Знаем лишь, что они образуют последовательность. Все методы использующие ранжирование основаны на порядковых шкалах.
Единица измерения здесь – расстояние в один класс (ранг), при этом расстояние это может быть разным. Для анализа данных, измеренных на основе этой шкалы, применимы все непараметрические критерии, кроме того, имеют смысл расчеты процентилей, квартилей, медианы и ранговой корреляции.
Шкала равных отношений (относительная шкала)
Классифицирует объекты или субъекты пропорционально степени выраженности измеряемого свойства. Шкала предполагает наличие нулевой точки отсчета, наиболее информативная шкала. Она обладает всеми свойствами номинальной, порядковой и интервальной шкал. К ней применимы все параметрические и непараметрические методы обработки. С помощью таких шкал можно определять, классифицировать и ранжировать объекты, сравнивать интервалы и разницы.
Примерами таких шкал являются: килограммы, метры, градусы и т.д.
Шкалы дают возможность:
Используемые в маркетинге методы шкалирования условно подразделяются на две группы:
— сравнительные методы, предполагающие прямое сравнение объектов;
— несравнительные методы, заключающиеся в самостоятельной оценке каждого обьекта.
К сравнительным методам относятся попарное сравнение, упорядоченное шкалирование, шкалирование с постоянной суммой и Q-сортировка.
Транзитивность предпочтений – это допущение, сделанное для преобразования данных попарного сравнения в упорядоченные. Допущение предполагает, что если торговой марке А отдается предпочтение перед торговой маркой В, а торговой марке В перед торговой маркой С, то торговой марке А будет отдано предпочтение перед торговой маркой С.
Шкалирование с постоянной суммой – респондентов просят распределить постоянные суммы баллов (фишек, процентов, долей) между объектами сравнения по определенному критерию. Если свойство несущественное респондент может поставить ноль. Если какое то свойство в два раза важнее другого, оно получает в два раза больше баллов.
Пример: в результате исследования выявлено, что потребитель выбирает товар по трем признакам: цена, удобство покупки, прочность. При этом, у потребителей различных групп доходности весомость каждого из факторов различна. Для потребителей с высокими доходами на первом месте по весомости стоит удобство, для потребителей с низкими доходами – цена. Потребителю предлагается оценить всю сумму свойств в 100% и разделить эти проценты между свойствами, в соответствии с их значимостью лично для него.
Q-cортировка разработана для быстрого установления различий между большим количеством объектов. Этот метод заключается в процессе упорядочивания, при котором объекты разбиваются на группы в зависимости от схожести по определенному критерию.
Например, респонденту выдается 20 утверждений, написанных на карточках и предлагается разделить эти карточки на 5 групп в зависимости от того, насколько он с этими утверждениями согласен.
Методы несравнительного шкалирования. При их использовании респонденты не сравнивают рассматриваемый объект ни с каким другим, поэтому такие шкалы еще называют монадическими или однопредметными.
К ним относятся следующие шкалы:
1. Непрерывные рейтинговые шкалы;
2. Детализированные рейтинговые шкалы.
Непрерывные рейтинговые шкалы (графические шкалы), при использовании, которых респонденты ставят отметки в соответствующей точке отрезка соединяющей крайние значения критерия. Шкала может иметь различные формы, они легко составляются.
Например: плохой-1 балл, а наилучший- 10 баллов.
Детализированных рейтинговы хшкал существует несколько видов:
2. Семантический дифференциал;
Это шкалы содержащие числа и/или краткое описание, связанное с каждой категорией отношения к объекту исследования. Расположение категорий на шкале определенным образом упорядочено.
Шкала Лайкерта – от респондента требуется определить степень согласия или несогласия для каждого набора утверждений о рассматриваемых объектах. Обычно каждый пункт шкалы имеет 5 категорий для ответа от абсолютного несогласия, до полного согласия: каждому утверждению присваиваются определенные баллы.
Семантический дифференциал – 7- балльная шкала с противоположными оценками в крайних точках (слабая – мощная, ненадежная – надежная). Респонденты делают отметки на шкале, которые отражают их мнение, и можно затем сформировать портрет фирмы (профиль) по степени ее надежности. Если в одинаковой шкале на одном листе дать оценку по надежности и другим фирмам, их можно сравнить (профильный анализ). Отдельные пункты семантического дифференциала могут принимать значения от –3 до +3 или от 1 до 7 при обработке. С его помощью можно представить многие параметры не метрического характера, например, – образ фирмы в глазах потребителя.
Шкала Степеля – 10 бальная шкала, состоящая из одной характеристики в середине шкалы с диапазоном противоположных числовых значений.
Ее значения от –5 до +5 без нейтральной нулевой точки. Шкала изображается вертикально. Респондентов просят распределить, выбирая число на шкале, насколько верно каждый термин описывает объект. Респондент предполагает, что чем выше число, тем ближе термин к описанию объекта. Например, допустим выбор универмага: Респонденту предлагается оценить, насколько точно каждая фраза описывает каждый универмаг. Он, выбирает какое то из положительных значений, если считает, что фраза довольно точно описывает данный универмаг, либо какое то из отрицательных, если она не соответствует ситуации в магазине.
Высокое качество Плохой сервис
Данные анализируются так же как семантический дифференциал. Несравнительные детализированные рейтинговые шкалы не обязательно должны использоваться только в рамках вышеуказанных форматов. Они могут принимать много различных форм.
Но при разработке любой другой формы шкалы необходимо ответить на следующие вопросы:
1. Количество используемых категорий;
2. Сбалансирована или не сбалансирована шкала;
3. Количество категорий четное или нечетное;
4. Допустим ли неопределенный ответ;
5. Каков характер вербального описания;
6. Каков формат шкалы.
Принимают во внимание два противоположных фактора:
— чем больше категорий в шкале, тем больше степень различий между объектами, но тем меньше респондентов способных справиться с анкетой
— количество категорий должно равняться семи плюс-минус два.
Кроме того, при разработке шкал учитывают:
— способ сбора данных;
— Величина коэффициента корреляции и общепринятая мера связи зависит от числа категорий в шкале, поэтому, если данные будут анализироваться с помощью сложных статистических методик, то число категорий должно быть равно семи.
— В сбалансированной шкале количество категорий одинаково. В несбалансированной шкале их количество разное. Для получения объективных данных шкалы должны быть сбалансированы.
Однако, если велика вероятность смещения в положительную или отрицательную сторону, для исследования больше подходит шкала с наибольшим числом смещений в положительную сторону.
— При нечетном количестве категорий центральное положение в шкале отображает нейтральность характеристики или безразличие респондента. При расположении такой нейтральной категории можно сильно повлиять на ответ. Если хотя бы у одного респондента возможно нейтральное или безразличное отношение, то категорий должно быть нечетное количество.
— Должна быть предусмотрена допустимость неопределенного ответа – возможность респонденту уйти от ответа (не знаю, не помню).
-Характером и степенью вербального описания, которое используется для шкалы можно значительно повлиять на ответы. Подробное словесное описание каждой категории может не увеличить точность, а уменьшить ее, так как от обилия слов отвечающий человек теряется. Сила аргумента тоже может влиять.
Существует несколько вариантов форм шкалы: вертикальная форма;
Горизонтальная форма. Категории шкалы могут обозначаться линиями, графами, делением. Шкалы могут иметь или не иметь числовые значения. Числовые значения могут быть со знаками «+», «−» или и те и другие.
Шкалы могут быть многомерными. Их разработка требует специальной подготовки. Измеряемая характеристика чаще всего здесь формируется в несколько приемов и называется конструкцией.
Измерение. Шкалы измерений
Известное изречение гласит «все познается в сравнении».
Для идентификации объектов и их характеристик во множестве их проявлений требуется большое количество и разнообразие мер. С учетом особенностей измеряемых объектов и задач измерений меры группируют и используют для построения шкал измерений.
Шкала измерений – упорядоченное множество проявлений количественных или качественных характеристик объектов, а также самих объектов. Указанное множество может быть образовано из наименований и обозначений (в том числе в цифровой форме) объектов и их характеристик, а также из значений и числовых значений (для количественных характеристик).
Согласно РМГ 83-2007 [7] «шкала измерений – отображение множества различных проявлений количественного или качественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений)». «Измерение – сравнение конкретного проявления измеряемого свойства (величины) со шкалой измерений этого свойства (величины) в целях получения результата измерений (оценки свойства или значения величины)».
Под качественной характеристикой в определении шкалы измерений и далее понимается описание объектов, их свойств и состояний, в словесной форме, в том числе с использованием наименований и обозначений.
Количественная характеристика – характеристика, которая может быть представлена числовым значением, равным отношению количественного содержания этой характеристики к еѐ базовой реализации, называемой единицей измерения.
Шкала наименований – шкала, состоящая из множества наименований (обозначений) объектов или проявлений их характеристик, в соответствии которым поставлено описание объекта (конкретная реализация объекта, его графическое изображение, математическая формула, график и т.п.) или проявлений его характеристик.
Наименование (обозначение) в этом случае рассматривают как обобщенную характеристику объекта или его свойств и состояний. С помощью шкалы наименований устанавливают эквивалентность (равноценность) измеряемого объекта или его характеристик и описания, поставленному в соответствие тому или иному наименованию (обозначению). Это позволяет отнести объект к какой-либо группе или выделить его, путем присвоения индивидуального наименования (обозначения), после чего наименования (обозначения) применяются как идентификаторы объектов (характеристик объектов). При построении шкал наименований могут использоваться числа, но лишь как метки объектов. Примерами таких шкал являются: атласы цветов (до 1000 наименований), запахов (сырой, затхлый, кислый и т.д.), вкуса (чистый, полный, гармоничный и т.д.); множество номеров телефонов, автомашин, паспортов; разделение людей по полу, расе, национальности; классификаторы промышленной продукции, специальностей высшего образования; терминологические справочники и т.п.
Числа, знаки, обозначения, наименования, составляющие шкалу наименований, разрешается менять местами. Для результатов измерений, полученных с использованием этой шкалы, нет отношений типа «больше — меньше», не применимы понятия единица измерения, нуль, размерность. С ними могут проводиться только некоторые математические операции. Например, числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Оценки экспертов часто осуществляются с использованием шкал порядка. Типичным примером являются задачи ранжирования и классификации промышленных объектов, подлежащих экологическому страхованию.
В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше — меньше», «лучше — хуже» и т.п. Однако нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).
Шкалы наименований и порядка, для которых не определены единицы измерений, называют также условными шкалами или не метрическими шкалами.
Абсолютная шкала – шкала числовых значений количественной характеристики. Отличительные признаки абсолютных шкал: наличие естественного нуля и отсутствие необходимости в единице измерений. С использованием абсолютных шкал измеряют коэффициенты усиления, ослабления, амплитудной модуляции, нелинейных искажений, отражения, коэффициент полезного действия и т. п. Результаты измерений в абсолютных шкалах при необходимости выражают в процентах, промилле, байтах, битах, децибелах.
Разновидностью абсолютных шкал являются дискретные (счетные) шкалы, в которых результат измерения выражается числом частиц, квантов, или других объектов, эквивалентных по проявлению измеряемого свойства. Например, шкалы для электрического заряда ядер атомов, числа квантов (в фотохимии), количества информации. Иногда за единицу измерений (со специальным названием) в таких шкалах принимают какое-то определенное число частиц (квантов), например один моль – число частиц, равное числу Авогадро.
Абсолютная шкала, диапазон значений которой находится в пределах от нуля до единицы (или некоторого предельного значения по спецификации шкалы) называют абсолютной ограниченной шкалой.
Шкалы разностей (интервалов), отношений и абсолютные классифицируют как метрические или физические шкалы. Эти шкалы допускают логарифмическое преобразование, часто применяемое на практике, что приводит к изменению типа шкал. Такие шкалы называют логарифмическими. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.
Практически реализация шкал измерений достигается путем стандартизации как самих шкал и единиц измерений, так и, при необходимости, способов и условий (спецификаций) их однозначного воспроизведения.
Измерение с помощью шкал заключается в установлении соответствия объекта или его характеристики отметке на шкале измерений. После чего объекту измерений приписывают количественную или качественную определенность, соответствующую выявленной отметке шкалы.
Управленческая теория измерений.
Шкалы и накладываемые ими ограничения
Управленческая теория измерений.
Шкалы и накладываемые ими ограничения
К. э. н., доцент кафедры финансового менеджмента, управленческого учёта и международных стандартов финансовой деятельности факультета ВШФМ РАНХиГС при Президенте РФ, руководитель консультационного бюро Института экономических стратегий, преподаватель школ бизнеса РАНХиГС, НИУ ВШЭ, МГУ, РСПП, ИНЭС и др.
Шкалы и их классификации
Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.
Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).
Шкалирование — это:
Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.
Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается.
Шкалы, как правило, объединяют в три основные группы:
Иногда все шкалы измерения делят на два класса:
Далее мы последовательно разберём все типы шкал.
Как считать очки в десятиборье?
Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.
Номинальные шкалы
Допустимые преобразования
Этим понятием математики строго описывают шкалы. Тип шкалы задаётся группой её допустимых преобразований.
Допустимые преобразования — это такие преобразования, которые не меняют соотношения между объектами измерения и, соответственно, выводы, сделанные по результатам измерений. Например, при измерении длины переход от аршинов к метрам не меняет соотношений между длинами рассматриваемых объектов: если первый объект длиннее второго в пять раз, то это будет установлено при измерении как в аршинах, так и в метрах. Обратите внимание, что при этом численное значение длины в аршинах отличается от длины в метрах — не меняется лишь результат сравнения длин двух объектов.
Аналогично денежные суммы можно сопоставлять как в рублях, так и в иностранной валюте. Особенность, связанная с изменяющимися курсами валют: результат сопоставления денежных сумм в разных валютах меняется во времени. С аршинами и метрами ситуация иная: их соотношение вечно. Вот вам и проблема курсовых разниц в экономике. О ней сейчас не место говорить, но запомните её.
Порядковые шкалы
Порядковая шкала отражает более высокий уровень измерений, учитывающий, к какой категории принадлежит объект и в каком отношении он находится с другими объектами. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между ними.
Пример. Простейшим примером порядковой шкалы служат оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе тот же смысл выражается словесно — «неудовлетворительно», «удовлетворительно», «хорошо», «отлично». Этим подчёркивается «нечисловой» характер оценок знаний студентов.
Фактически измерение по порядковой шкале представляет собой операцию упорядочения. Предполагаются сравнения «больше — меньше» или «лучше — хуже». Например, мнения экспертов часто выражаются в порядковой шкале, то есть эксперт может сказать (и обосновать), что один показатель качества продукции важнее, чем другой; первый технологический объект опаснее, чем второй, и т. д. Но он не в состоянии сказать, во сколько раз или насколько он более важен, или, соответственно, более опасен.
Допустимые преобразования. Порядковая шкала допускает любое возрастающее преобразование, то есть такое, которое не меняет порядок шкалы.
Типы порядковых шкал. Используют два типа порядковых шкал, которые различны с практической точки зрения:
Обдумывание измерений некоторых показателей следует начать с выбора между ранговым и балльным типами шкал.
Ранговые порядковые шкалы
Ранговые шкалы — это шкалы, где числа служат только для присвоения мест. Экспертов часто просят ранжировать (упорядочить) объекты экспертизы, то есть расположить их в порядке возрастания (или убывания) интенсивности исследуемой характеристики. Ранг — это номер объекта экспертизы в упорядоченном ряду значений характеристики у различных объектов. Формально ранги выражаются числами 1, 2, 3. Важно помнить, что измерения 1, 2, 3 и 6, 10, 50 означают одно и то же: первая альтернатива заняла первое место, вторая — второе место и т. д. В ранговых шкалах нет информации о величине различий между оцениваемыми объектами. Такие шкалы используются тогда, когда объект трудно описать несколькими характеристиками, которые потом оцениваются качественно (баллами, например) или количественно. В практике менеджмента рейтинги часто основаны на ранговых шкалах.
Ранговые измерения (процедуры ранжирования). Различают несколько основных типов алгоритмов ранжирования:
Простейший (и неверный) перевод результатов парных сравнений в ранги и в весовые коэффициенты
Заманчива идея получить весовые коэффициенты, то есть количественную меру, из порядковых измерений. Однако, как правило, такое действие некорректно — оно многозначно и потому единственный и корректный вывод для задач менеджмента невозможен. Вместе с тем оно популярно, особенно среди людей, плохо знающих математику.
Приведём пример наиболее простой и популярной модификации метода парных сравнений. Допустим, эксперт проводит оценку четырёх методов, которые связаны с решением кадровых вопросов в корпоративном проекте:
Z1 — повышение квалификации в процессе выполнения проекта;
Z2 — привлечение кадров со стороны;
Z3 — подготовка кадров в своём корпоративном университете;
Z4 — разовое повышение квалификации.
| Zi/Zj | Z1 | Z2 | Z3 | Z4 |
| Z1 | 1 | 1 | 1 | |
| Z2 | 0 | 0 | 0 | |
| Z3 | 0 | 1 | 1 | |
| Z4 | 0 | 1 | 0 |
Составим матрицу бинарных предпочтений эксперта, где 1 означает, что один метод „предпочтительнее”, чем другой, с которым он сравнивается. Определим оценку каждого метода (складываем по строкам): C1 = 3; C2 = 0; C3 = 2; C4 = 1. Получаем порядок предпочтения методов: Z1, Z3, Z4, Z2. Пока всё это корректные действия. Затем наступает черед „творчества”.
Простейший (и неверный) перевод результатов парных сравнений в весовые коэффициенты. Если нужны „веса” указанных четырёх альтернатив, то можно нормировать числа <С>и получить „веса”
Однако анализ корректности метода даёт отрицательный результат. Дело в том, что объектам могут быть присвоены и другие веса (см. подобный пример ниже). Почему некорректно? Потому что в результате его применений вес v1 оказывается в три раза больше, чем v4, а этого эксперт, который проводил парное сравнение, не утверждал! Подделка очевидна, так как в результате обработки мы добавили весомую толику информации от себя к тому, что говорили эксперты.
Корректный перевод результатов парных сравнений в интервальную шкалу
При опросе экспертов в августе 2001 г. попарно сравнивалось качество бензина в четырех компаниях: «ТНК», «Лукойл», «Юкос» и «Татнефть». При сравнениях четырёх компаний получается 6 пар для сравнения:
| Пары | Частота выбора первого элемента пары | Частота выбора второго элемента пары |
| «ТНК» — «Лукойл» | π(1,2) = 0,508 | π(2,1) = 0,492 |
| «ТНК» — «Юкос» | π(1,3) = 0,331 | π(3,1) = 0,669 |
| «ТНК» — «Татнефть» | π(1,4) = 0,990 | π(4,1) = 0,010 |
| «Лукойл» — «Юкос» | π(2,3) = 0,338 | π(3,2) = 0,662 |
| «Лукойл» — «Татнефть» | π(2,4) = 0,990 | π(4,2) = 0,010 |
| «Юкос» — «Татнефть» | π(3,4) = 0,997 | π(4,3) = 0,003 |
Балльные порядковые шкалы
Балльные шкалы используются очень часто, примеры мы уже приводили. Однако важно понимать, что каждому баллу необходимо присвоить качественную характеристику, в противном случае может пострадать корректность. Приведу пример: в конце 1990-х гг. я был назначен ответственным преподавателем (качество, контроль, апелляции) на устном экзамене по экономике для абитуриентов НИУ ВШЭ. Только что на ректорате ввели 10-балльную шкалу. Экспромт не удался — первый блин, как обычно, вышел комом. Моя работа заключалась, в том числе, и в „обеспечении справедливости”, то есть чтобы за примерно одни и те же ответы преподаватели в разных комиссиях ставили одинаковые баллы. Разброс в оценках оказался ужасающим — от 4 до 7 за похожие ответы. Буквально на следующий день ошибка в дефиниции шкалы была исправлена, а получившаяся шкала (см. таблица 2) успешно работает до сих пор (с небольшим изменением). Многие вузы взяли её на вооружение. Обращаю внимание читателей, что в соответствии со спецификой каждого предмета преподаватель конкретизирует шкалу.
| Балл | Качественная характеристика |
| 10 | Пять с плюсом — исключительные знания (кое-что из ответа студента даже преподаватель не знал) |
| 9 | Отлично, твёрдая пятёрка |
| 8 | Пять с минусом |
| 7 | Четыре с плюсом |
| 6 | Четыре, твёрдая четвёрка |
| 5 | Четыре с минусом |
| 4 | Три с плюсом |
| 3 | Три, твёрдая оценка «удовлетворительно» |
| 2 | Три с минусом |
| 1 | Неудовлетворительно |
Важный вопрос: какова идеальная размерность балльной шкалы? Ответ: сколько качеств, столько и баллов. Баллы обозначают упорядоченные качества, и каждому качеству присваивают свой балл. Обратное неверно: если взять за основу 10-балльную шкалу и каждому баллу попытаться „присвоить” определённое качество, то можно столкнуться с ситуацией, что качеств может оказаться не 10, а всего 7. Поэтому следует отталкиваться именно от количества качеств, которые вы можете выделить.
Балльные измерения. Балльные измерения формально просты, но коварны возможностью допустить необоснованные оценки и тем самым всё испортить. Существует два подхода к выставлению балльных оценок:
Перевод результатов балльных оценок в весовые коэффициенты. Если такой перевод делается одним экспертом — это операция сомнительная, но популярная. Во врезке приведён один из популярных методов — метод последовательных сравнений.
Перевод рангов в весовые коэффициенты одним экспертом. Метод последовательных сравнений
Количественные шкалы
Количественные шкалы отражают более высокий уровень измерений, учитывающий не только то, в каком отношении измеряемый объект находится с другими объектами, но и степень их различия. Примеры использования количественных шкал мы видим повсюду.
Допустимые преобразования. Количественные шкалы определены с точностью до преобразований, которые не меняют единицы измерения (линейных или иных функциональных преобразований).
Типы количественных шкал. Различают количественные шкалы:
Расположение шкал в этом списке не случайно. Первая (шкала интервалов) — самая слабая по информативности и самая сильная в плане надёжности оценок, последняя (абсолютная шкала) — наиболее информативная (измерения могут быть очень надёжными), но при этом допускающая наименее надёжные оценки. Оценка степени соответствия некоторому идеалу максимально затруднена — помните разницу между оценкой и измерением?
Шкала интервалов (интервальная шкала) точно определяет величину интервала между точками на шкале. Для проведения измерений необходимо задать интервал (2 точки). Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования вида: F(Х) = а · Х + b, где а > 0.
Шкала степенная. Шкала степеней (степенная) допускает степенное преобразование (F(Х) = АХВ). В области техники она вполне адекватна — у неё тоже две степени свободы, как у шкалы интервалов. В экономике она, напротив, является исключением, поэтому подробно рассматривать её не будем.
Шкала отношений. Из количественных шкал в науке и практике наиболее распространены шкалы отношений. В них есть естественное начало отсчёта — ноль (то есть отсутствие величины), но нет естественной единицы измерения.
Примеры использования шкалы отношений:
Шкала отношений допускает преобразования, изменяющие только масштаб, то есть преобразования подобия: F(Х) = аХ, где а > 0 (линейные возрастающие преобразования без свободного члена).
Примеры преобразования шкалы отношений:
Базовая точка в шкале отношений одна — «единица». Эта условная «единица» может быть, например, 100 (проценты) или 1 (доли). Таким образом, измерения в долях и процентах эквивалентны, что очевидно и без всякой теории.
Однако выводы, которые делаются по результатам процентных измерений, могут быть ошибочными (см. врезку). Возникают сопутствующие вопросы:
Корректность процентных измерений. Рейтинг Путина vs стоимость свинины
Вывод: по темпам роста (в научной терминологии «прироста») свинина побеждает Путина: 44% vs 68%.
Корректны ли эти измерения? Решите сами и объясните (что гораздо сложнее). Точно сформулировать, насколько такие сравнения корректны, удается лишь 10% слушателей программ МВА. Это ещё один довод в пользу изучения шкал. Хотя бы на уровне знакомства.
Степени свободы шкал
Для проведения измерений в шкалах отношений и разностей мы должны задавать одну точку. В шкале отношений она „играет роль единицы”, то есть соответствует переводу базового эмпирического элемента в единицу действительной оси. Для шкалы разностей это „нулевая точка”, то есть нужно задать отношение таким образом, чтобы „точка отсчёта” эмпирической системы превращалась в числовой ноль.
В этой связи математики различают шкалы по степеням свободы:
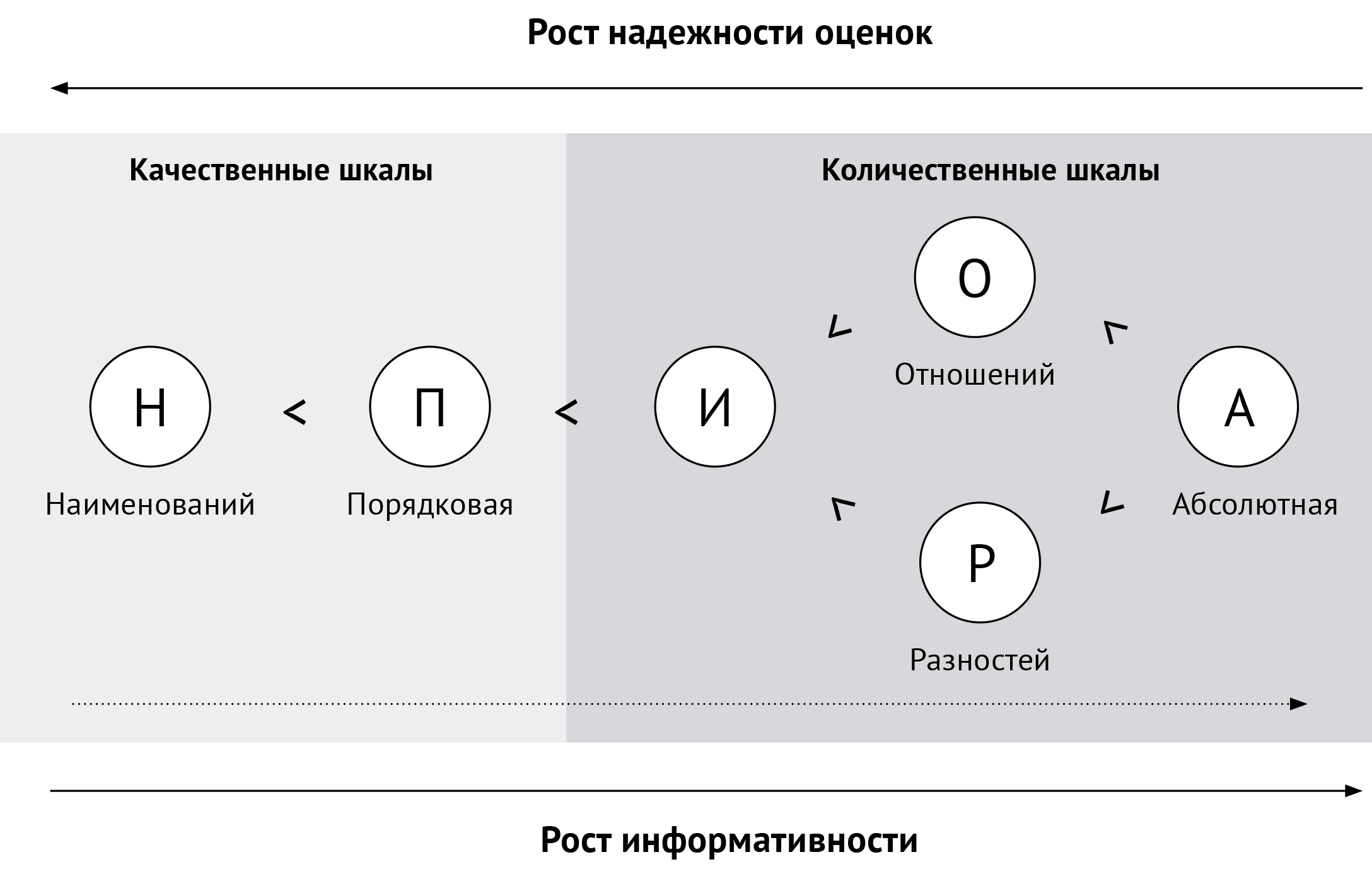
Иерархия шкал измерений
Напомним, что все шкалы делят на две большие группы: качественные и количественные. Наиболее распространённая классификация шкал — континуальная (рис. 3). В ней шкалы упорядочены по мере повышения их способности удовлетворять требованиям информативности и надёжности проведения оценок. Слева — самая слабая по информативности и самая надёжная, справа — наиболее информативная и наименее надёжная.
Рис. 3. Иерархия шкал измерений
В следующей части мы поговорим о том, как собственно выставлять оценки чему-либо. Хорошая обработка результатов измерений — это достоверная система оценок. А какими математическими свойствами она должна обладать? Есть ли научный ответ на этот вопрос?