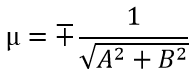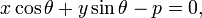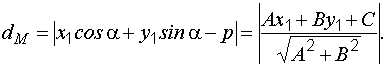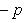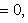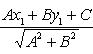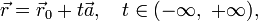к нормальному уравнению прямой имеет отношение

Нормальное уравнение прямой

В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.

Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:

где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).

Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором . (Если точки O и R совпадают, то направление n можно взять произвольным).

Выразим уравнение прямой L через два параметра: длину отрезка 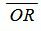и угол φ между вектором n и осью Ox.

Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:

Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора на прямую R равна r, т.е.

Скалярное произведение векторов n и имеет следующий вид:

где − обозначен скалярное произведение векторов n и , а | · |− норма (длина) вектора, α−угол между векторами n и .

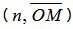
Поскольку n единичный вектор, то (4) можно записать так:

Учитывая, что n=<cosφ, sinφ>, 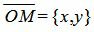, мы получим:

Тогда из уравнений (3), (5), (6) следует:

Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.

Решение. Имеем: φ=60°, r=4. Вычисляем:

,

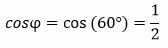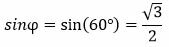Подставляя вычисленные значения в (7) получим:

Приведение общего уравнения прямой на плоскости к нормальному виду

Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что

Возвышая в квадрат первые два равенства в (9) и складывая их, получим:

Упростим выражение и найдем t:

Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).

Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.

Пример 2. Задано общее уравнение прямой

Построить нормальное уравнение прямой.

Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):

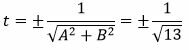Так как C>0, то знак t отрицательный:

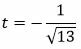Умножим уравнение (12) на t:

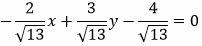Ответ. Нормальное уравнение прямой (12) имеет следующий вид:

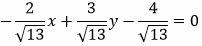Отметим, что число 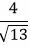является расстоянием от начала координат до прямой (12).

Источник

Нормальное уравнение прямой на плоскости, расстояние от точки до прямой

Пусть дана некоторая прямая L. Проведём через начало координат прямую n, перпендикулярно данной и назовём её нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L. На нормали введём направление от точки O к точке N.

Обозначим через угол, на которой нужно повернуть против часовой стрелки ось Ox до совмещения её положительного направления с направлением нормали, через p длину отрезка ON.

. (1)

будет нормальным уравнением прямой.

С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости до прямой. Пусть — точка, не лежащая на прямой, заданной нормальным уравнением. Требуется определить расстояние d от точки до прямой. Это расстояние определяется по формуле

. (2)

Общее уравнение прямой можно привести к нормальному виду. Пусть

— общее уравнение прямой, а

— её нормальное уравнение.

Так как оба уравнения определяют одну и ту же прямую, их коэффициенты пропорциональны.

Очевидно, для получения нормального уравнения следует все члены общего уравнения умножить на постоянный множитель , вычисляемый по формуле

. (3)

В этой формуле берётся знак, противоположный знаку C в общем уравнении прямой.

Таким образом, получаем уравнение

, (4)

которое и будет нормальным уравнением прямой на плоскости.

Пример 1. Привести общее уравнение прямой к нормальному виду.

Решение. Вычисляем нормирующий множитель:

(знак, противоположный C).

Умножаем все члены общего уравнения на нормирующий множитель и получаем:

.

Пример 2. Привести общее уравнение прямой к нормальному виду.

Решение. Вычисляем нормирующий множитель:

(знак, противоположный C).

Умножаем все члены общего уравнения на нормирующий множитель и получаем:

.

Пример 3. Найти расстояние от точки до прямой .

Решение. Приведём данное уравнение к нормальному виду. Вычисляем нормирующий множитель:

(знак, противоположный C).

Умножаем все члены общего уравнения на нормирующий множитель и получаем нормальное уравнение:

.

По формуле (2) находим искомое расстояние:

.

Источник

Нормальное уравнение прямой

Как привести уравнение прямой к нормальному виду

Для того, чтобы найти нормальное уравнение прямой, заданной уравнением Ax+By+C=0, необходимо разделить данное уравнение на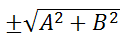

при этом знак «минус» берётся, когда C>0, а знак «плюс» берётся, когда C x cosα + y sinα − p = 0

Это и есть нормальное уравнение прямой

То же самое получим, если обе части уравнения Ах + By + С = 0 умножим на число

x cosα + y sinα − p = 0

Графически это можно представить следующем образом

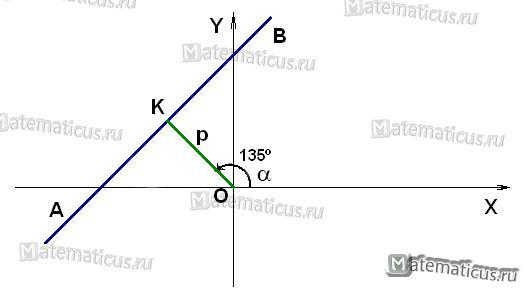
Прямая AB с полярным расстоянием p (длина перпендикуляра, опущенного на прямую из начала координат OK) и полярным углом α (угол измеренный в положительном направлении между положительным направлением оси Ox и направлением этого перпендикуляра) представляется уравнением:

x cosα + y sinα − p = 0

Если p=0, то прямая проходит через начало координат, а угол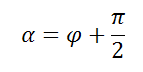

задаёт угол наклона прямой.

Пример 1
Привести уравнение 3x-4y+5=0 к нормальному виду. Здесь A=3, B=-4, C=5>0. Поэтому делим на
получаем

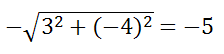
Это уравнение вида

x cosα + y sinα − p = 0

Источник

Нормальное уравнение прямой

29) Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А 2 + В 2 не равно 0. Это уравнение первого порядка называют общим уравнением прямой.

Определение. Каждый ненулевой вектор (a₁, a₂), компоненты которого удовлетворяют условию Аa₁ + Вa₂ = 0 называется направляющим вектором прямой Ах + Ву + С = 0.

30) Нормальное уравнение прямой имеет вид 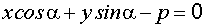,где – расстояние от прямой до начала координат; a – угол между нормалью к прямой и осью .

Расстояние от точки 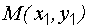до прямой определяется по формуле

34) Э́ллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F₁ и F₂ (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

причем | F₁F₂ | > 2a > 0.

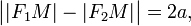
36) Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусомпараболы). Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом. Уравнение параболы: .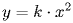

37) Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве. Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X‘X и Y‘Y. Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ.

39) Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой.

41)Нормальное уравнение прямой

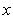
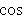
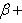
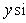
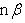
. Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

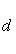
42) Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. Доказывается, что этот угол не зависит от выбора такой плоскости. Угол между двумя параллельными плоскостями принимается равным нулю.

43) Векторное параметрическое уравнение прямой в пространстве:

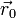
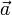
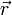
где — радиус-вектор некоторой фиксированной точки M₀, лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой, — радиус-вектор произвольной точки прямой.

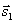
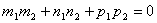
44) Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным. Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l₁ параллельна l₂ тогда и только тогда, когда параллелен . Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Источник

Общее уравнение прямой: описание, примеры, решение задач

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Общее уравнение прямой: основные сведения

указанная теорема состоит из двух пунктов, докажем каждый из них.

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Рассмотрим конкретный пример общего уравнения прямой.

Неполное уравнение общей прямой

Разберем все вариации неполного общего уравнения прямой.

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Решение

На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Общее уравнение прямой, проходящей через заданную точку плоскости

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Решение

Решение

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Решение

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Решение

Осуществим переход от общего уравнения к каноническому:

Решение

Произведем нужные действия по алгоритму:

Решение

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

Каноническое уравнение преобразуется к общему по следующей схеме:

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

Решение

Осуществим переход от параметрических уравнений к каноническому:

Перейдем от канонического к общему:

Решение:

Просто перепишем уравнение в необходимом виде:

Составление общего уравнения прямой

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Решение

Решение

Источник