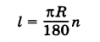Как найти длину дуги окружности
Как найти длину дуги окружности
Определение длины дуги
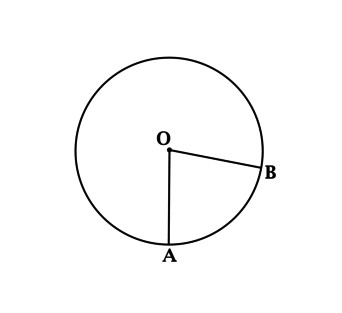
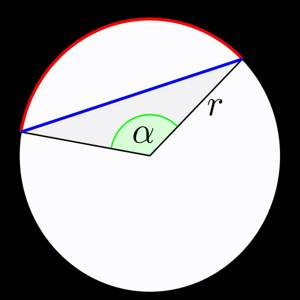
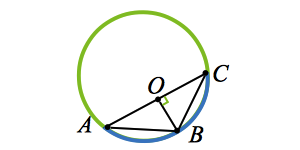
Часть фигуры, которая образует окружность, точки которой равноудалены, называется дугой. Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
Определение длины дуги
Формула расчёта длинны дуги
Расчет длины дуги производится по следующей формуле:
r – радиус окружности
Пример расчёта длинны дуги
Длина дуги окружности равна 14,82 сантиметра.
В элементарной геометрии под дугой понимается подмножество окружности, расположенной между двумя расположенными на ней точками. На практике решать задачи по определению ее длины инженерам и архитекторам приходится достаточно часто, поскольку этот геометрический элемент широко распространен в самых разнообразных конструкциях.
Пожалуй, первым, перед кем встала эта задача, были древние зодчие, которым так или иначе приходилось определять этот параметр для сооружения сводов, широко используемых для перекрытия промежутков между опорами в круглых, многоугольных или эллиптических зданиях. Если внимательно присмотреться к дошедшим до наших дней шедеврам древнегреческого, древнеримского и особенно арабского зодчества, то можно заметить, что в их конструкциях дуги и своды встречаются чрезвычайно часто. Творения современных архитекторов ими не так богаты, но эти геометрические элементы наличествуют, конечно же, и в них.
Длину различных дуг необходимо рассчитывать при сооружении автомобильных и железных дорог, а также автодромов, причем во многих случаях от правильности и точности вычислений во многом зависит безопасность движения. Дело в том, что многие повороты магистралей с точки зрения геометрии представляют собой именно дуги, и по движению по ним на транспорт воздействуют различные физические силы. Параметры их результирующей во многом определяются длиной дуги, а также ее центральным углом и радиусом.
Конструкторам машин и механизмов приходится вычислить длины различных дуг для правильной и точной компоновки составных частей различных агрегатов. В данном случае ошибки в расчетах чреваты тем, что важные и ответственные детали будут неправильно взаимодействовать друг с другом и механизм просто не сможет функционировать так, как планируют его создатели. В качестве примеров конструкций, изобилующих такими геометрическими элементами, как дуги, можно привести двигатели внутреннего сгорания, коробки переключения передач, дерево- и металлообрабатывающее оборудование, кузовные элементы легковых и грузовых автомобилей и т.д.
Дуги достаточно широко встречаются в медицине, в частности, в стоматологии. Например, они используются для исправления неправильного прикуса. Корректирующие элементы, называемые брекетами (или брекет-системами) и имеющие соответствующую форму, изготавливаются из специальных сплавов, и устанавливаются таким образом, чтобы изменить положение зубов. Само собой разумеется, что для того, чтобы лечение проходило успешно, эти дуги должны быть очень точно рассчитаны. Кроме того, дуги очень широко используются в травматологии, и, пожалуй, самым ярким примером тому является знаменитый аппарат Илизарова, изобретенный российским врачом в 1951 году и чрезвычайно успешно используемый по сей день. Неотъемлемыми его частями являются металлические дуги, снабженные отверстиями, через которые продеваются специальные спицы, и являющиеся основными опорам всей конструкции.
Окружность и круг
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Содержание
Общие определения
Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.
Отрезок, который соединяет две точки окружности, является ее хордой.
Длина окружности вычисляется по формуле: C=2\pi R
Площадь круга: S=\pi R^
Центральным углом называется такой угол, который находится между двух радиусов.
Длину дуги можно найти по формуле:
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC \cdot BC = EC \cdot DC
Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
\angle COD = \cup CD = \alpha ^
Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
\angle AOB = 2 \angle ADB
Опирающийся на диаметр, вписанный угол, прямой.
\angle CBD = \angle CED = \angle CAD = 90^
Вписанные углы, которые опираются на одну дугу, тождественны.
\angle ADB = \angle AEB = \angle AFB
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ <\circ>.
\angle ADB + \angle AKB = 180^
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac<1> <2>\left ( \cup DmC + \cup AlB \right )
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^ < \circ>.
\angle A + \angle C = \angle B + \angle D = 180^
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
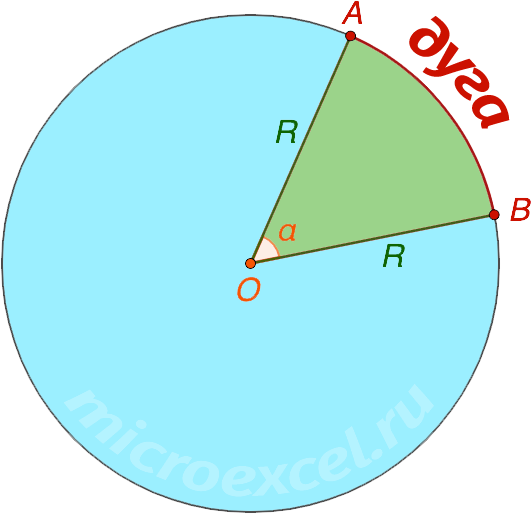
Длина дуги окружности
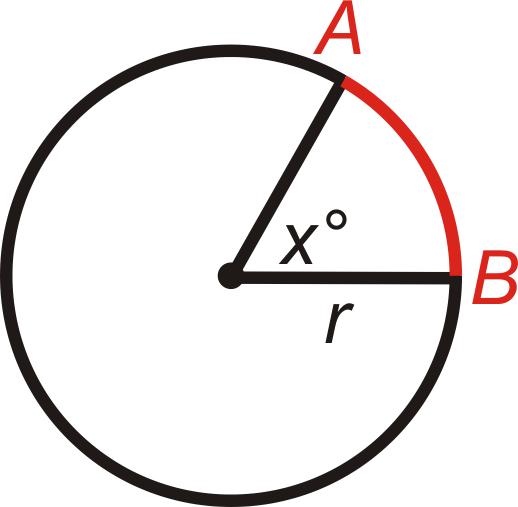
Длина дуги окружности — это число, характеризующее протяжённость дуги окружности в единицах измерения длины.
Содержание
[править] Обозначения
x1 — абсцисса первой точки дуги;
y1 — ордината первой точки дуги;
x2 — абсцисса второй точки дуги;
y2 — ордината второй точки дуги;
x 2 + y 2 = R 2 — каноническое уравнение окружности;
r = R — уравнение окружности в полярных координатах;
Lдуг.окр — длина дуги окружности.
[править] Формула
[править] Вывод формулы
[править] 1-ый способ
[править] 2-ой способ
[править] Другие формулы
Персональные инструменты
Пространства имён
Варианты
Просмотры
Действия
Поиск
Навигация
Инструменты
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи или на ее странице обсуждения).
В текстах могут упоминаться организации, признанные на территории Российской Федерации террористическими и/или в отношении которых судом принято вступившее в законную силу решение о запрете деятельности — см. полный список, а также деятельность которых запрещена по решению суда — см. полный список.
Геометрия
План урока:
Длина окружности и число пи
Окружность представляет собой линию, а значит, у нее есть длина. Действительно, представим себе нить, опоясывающую какой-нибудь круглый предмет. Если эту нить разрезать, то ее можно будет развернуть на плоскости в отрезок. Её длина и будет длиной окружности.
Однако определить точно эту длину довольно сложно, так как окружность является «кривой» линией, а до этого в курсе геометрии мы рассматривали только длины отрезков. Для приближенной оценки длины окружности можно использовать правильные многоугольники.
Возьмем произвольную окружность и впишем в нее правильный n-угольник, и одновременно ещё один n-угольник опишем около окружности. Можно считать, что периметры этих n-угольника приближенно равны длине окружности, причем периметр вписанного многоугольника – это приближение с округлением в меньшую сторону (оценка снизу), а периметр описанного многоугольника – это уже оценка сверху.
Обычно длину окружности обозначают буквой С. Обозначим периметры вписанного и описанного многоугольника как Рв и Ро. Тогда можно записать двойное неравенство:
Далее будем увеличивать число n. При этом n-угольник будет всё плотнее «прилегать» к окружности, и тем самым его периметр будет являться все более точным приближением длины окружности.
Напомним две формулы, которые мы вывели, изучая правильные многоугольники:
Здесь аn – это сторона n-угольника, R – радиус описанной окружности, r – радиус вписанной окружности. Из второй формулы можно выразить R и подставить это выражение в первую формулу:
Здесь R радиус окружности, ав и ао – стороны вписанного и описанного многоугольника соответственно. Умножим эти равенства на n, чтобы в левой части получился периметр многоугольников:
Это неравенство позволяет для любой окружности оценить отношение длины ее окружности к ее диаметру (2R – это как раз диаметр окружности).
Можно доказать, что при увеличении n величина
при росте n, наоборот, убывает, но также стремится к пределу. Более того, оказывается, что эти пределы у обоих выражений одинаковы, то есть являются одним и тем же числом. Это значит, что и само отношение длины окружности к диаметру является этим же числом, которое традиционно обозначается буквой π. Записать этот факт можно так:
Ещё раз обратите внимание, что число π (читается как «число пи») не зависит от диаметра окружности или расположения ее центра, это некоторое постоянное число. Обычно его определяют так:
Чем большее n мы сюда подставим, тем более точную оценку числа π мы получим. Ещё Архимед использовал в этом неравенстве n = 96 (это значение было удобно взять, так как соответствующие значения синуса и тангенса угла 180°/96 уже умели вычислять в Древней Греции). Если мы воспользуемся калькулятором, то при n = 96 получим:
Вы можете и сами найти более точную оценку числа пи, используя неравенство (1) и калькулятор, умеющий высчитывать синусы и тангенсы. Попробуйте, например, подставить в него n = 1 000 000.
Используя метод многоугольников, Людольфу ван Цейлену в 1596 г. удалось вычислить 20 верных десятичных знаков числа пи после запятой:
Дальнейший прогресс в этой области был связан уже с использованием более сложных методов, основанных на бесконечных рядах чисел. Также в XVIII в. было доказано, что число π – иррациональное, то есть оно является бесконечной непериодической десятичной дробью. На сегодня даже на обычном персональном компьютере можно вычислить триллионы цифр после запятой в числе π. В большинстве школьных задач число π принимается равным 3,14. Однако если в задаче не просят округлить ответ, то вместо числа π вообще не надо ничего подставлять.
Из определения числа π вытекает формула для вычисления длины окружности c радиусом R или диаметром D:
Задание. Найдите длину окружности, если ее радиус составляет 5 см.
Решение. Просто подставляем в формулу число 5:
Обратите внимание, что вместо числа π НЕ надо подставлять его приближенное значение, так как в условии не говорится, что ответ надо округлять. Только та запись, в которой число π оставлено как есть, является точным, а не приближенным ответом.
Задание. Диаметр окружности составляет 40 см. Вычислите приближенно ее длину, принимая число π примерно равным 3,14.
Решение. Так как ответ надо будет округлить, то вместо числа π подставим значение 3,14:
Задание. Длина окружности составляет 100 см. Вычислите приближенно её радиус.
Решение. Из формулы для длины окружности легко получить формулу и для вычисления радиуса:
Задание. Вычислите радиус Земли, если известно, что длина экватора составляет 40 000 км.
Решение. Задача аналогична предыдущей, только вместо длины окружности надо подставить 40 000 км:
Задание. Автомобиль проехал 1978 метров, при этом одно из его колес совершило 1000 оборотов. Вычислите приближенно диаметр этого колеса.
Решение. В таких задачах неявно предполагается, что колесо плавно катится по дороге, а не скользит по нему. Можно посчитать, какое передвижение соответствует 1 обороту колеса:
1978 м : 1000 обор. = 1,978 м/об
Это величина как раз является длиной окружности колеса. Тогда легко найти и диаметр:
Длина дуги
Иногда требуется вычислить не длину всей окружности, а только лишь длину ее части, то есть дуги.
Напомним, что дуги имеют такую характеристику, как градусную меру, которая равна величине центрального угла, на который дуга опирается. Оказывается, что длина дуги окружности и ее градусная мера связаны. Для начала попытаемся найти длину дуги величиной в 1°. Напомним, что вся окружность составляет 360°. Значит, ее можно разбить на 360 маленьких дуг по 1°. Так как все эти дуги одинаковы, то длина каждой из них будет в 360 раз меньше длины все окружности:
Теперь предположим, что нам надо найти длину дуги с градусной мерой α, причем α – это целое число. Тогда мы можем разбить эту дугу на α маленьких дуг по 1°, и ее длина будет равна сумме их длин:
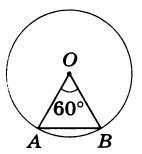
Задание. На окружности с радиусом 6 см отмечена дуга величиной в 30°. Найдите ее длину.
Решение. Просто подставляем в формулу числа:
Задание. На железнодорожном пути есть закругленный участок радиусом 5 км, а его длина составляет 400 м. Какова градусная мера этого закругления? Дайте приближенный ответ без использования числа π.
Решение. Выведем из формулы выражение для угла α:
Задание. Длина дуги окружности равна 20 см, ей соответствует центральный угол в 60°. Каков радиус окружности? Ответ не округляйте.
Решение. Теперь из формулы выражаем радиус окружности:
Задание. Точки А и В разбивают окружность на две дуги. Длина меньшей дуги равна 63, а опирается она на центральный угол в 28°. Какова длина большей дуги?
Решение. Сначала найдем радиус окружности:
Вся окружность составляет 360°. Если градусная мера меньшей дуги – это 28°, то у большей дуги градусная мера (обозначим ее как β) определяется так:
Задание. Какой должна быть градусная мера дуги, чтобы ее длина в точности совпадала с длиной радиуса?
Решение. Запишем формулу:
Площадь круга
Напомним, что кругом называется часть плоскости, ограниченная окружностью. Для нахождения площади круга можно использовать все тот же метод многоугольников, который мы применили для нахождения длины окружности и вычисления числа π.
Возьмем окружность и впишем в нее n-угольник. В свою очередь в него впишем окружность.
Выпишем изученные нами ранее две формулы:
Здесь r и R – радиусы вписанной и описанной окружности соответственно, Р – периметр многоугольника, Sмног. – площадь многоугольника. С ростом n периметр многоугольника приближается к длине описанной окружности, что можно записать в таком виде
Одновременно с этим и площадь многоугольника приближается к площади круга (имеется ввиду больший, то есть описанный круг), что позволяет вычислить ее:
Задание. Определите площадь круга, ограниченного окружностью 10 см.
Решение. В этой задаче надо просто подставить числа в формулу:
Решение. Здесь надо из формулы площади получить выражение для вычисления радиуса:
Задание. Во сколько раз увеличится площадь круга, если его радиус увеличится в 2 раза?
Решение. Пусть радиус исходного круга – это R. Тогда его площадь рассчитывается так:
Примечание. В общем случае увеличение радиуса круга в k раз приводит к увеличению его площади в k 2 раз.
Задание. Ваня и Петя решили купить пиццу. Сначала Ваня заметил пиццу диаметром 30 см, цена которой – 300 рублей. Но тут же Петя обнаружил на витрине такую же пиццу диаметром 40 см, которая стоила уже 450 рублей, и предложил ее купить. Ваня сказал, что этот невыгодная покупка, ведь радиус у второй пиццы больше только на треть, а цена больше уже наполовину. Прав ли Ваня?
Решение. Масса пиццы пропорциональна их площади. У второй пиццы радиус больше в 4/3 раза (так как 40/30 = 4/3), значит, площадь у нее больше в
Получается, что вторая пицца больше в 1,78 раза, а цена у нее выше только в 1,5 раза. То есть выгодней купить именно вторую, то есть большую пиццу.
Ответ: Ваня не прав, лучше купить пиццу диаметром 40 см.
Примечание. В этой задаче можно было посчитать площадь каждой пиццы, а потом поделить их стоимость на площадь и получить цену 1 см 2 пиццы в каждом варианте. Ответ бы при этом не изменился.
Задание. Завод изготавливает круглые столы радиусом 1,5 метра. Их поверхность надо покрывать лаком, причем на каждый 1 м 2 поверхности необходимо тратить 20 г лака. Лак закупается раз в месяц, и в течение ближайшего месяца завод должен изготовить 5000 столов. Сколько лака должен закупить завод на ближайший месяц?
Решение. Считаем площадь поверхности каждого стола:
Площадь сектора
Напомним, что сектором называется часть круга, образованная двумя его радиусами. Если же в круге проведена хорда, то она отсекает от него сегмент:
Проведем из центра окружности 360 радиусов, причем угол между соседними радиусами будет ровно 1°. В результате мы разобьем окружность на 360 одинаковых секторов, площадь каждого такого сектора будет в 360 раз меньше площади круга:
Теперь рассмотрим сектор, который образован дугой величиной в α градусов. Если α – целое число, то такой сектор можно составить из α секторов, каждый из которых составляет по 1°. Тогда площадь сектора круга будет определяться формулой:
Задание. Круговой сектор опирается на дугу в 45°, а его радиус составляет 40. Определите площадь этого сектора.
Решение. Используем выведенную формулу:
Решение. Из формулы площади сектора выразим радиус окружности:
Задание. На сторонах произвольного прямоугольника построены полукруги:
Докажите, что площадь полукруга, опирающегося на полуокружность, равна сумме площадей полукругов, опирающихся на катеты.
Решение. Полукруг представляет собой сектор с центральным углом α = 180°, поэтому его площадь может быть рассчитана так:
Заметим, что эти стороны являются диаметрами полукругов. Обозначим как D1 диаметр полукруга, опирающегося на гипотенузу, а два других диаметра как D2 и D3. Тогда можно выполнить преобразования:
Именно это равенство нам и требовалось доказать.
Теперь рассмотрим более сложную задачу, в которой необходимо определить площадь сегмента.
Задание. В окружности радиусом 20 проведена хорда длиной 12. Она разбивает окружность на два круговых сегмента. Найдите площадь каждого из них. При расчете примите π ≈3,14.
Чтобы найти площадь меньшего сегмента, можно вычесть из площади кругового сектора площадь треугольника АВО. Для нахождения обоих площадей в любом случае надо сначала определить величину угла ∠АОВ. Это можно сделать, применив теорему косинусов:
Далее надо рассчитать площадь ∆АВС. Это можно сделать с помощью разных формул, мы используем формулу с синусом угла. Для этого предварительно вычислим синус ∠АОВ, применив основное тригонометрическое тождество:
Осталось вычесть из площади сектора площадь ∆АВС, чтобы найти площадь кругового сегмента S1:
Примечание. В подобных задачах ответы и промежуточные ответы могут немного отличаться в зависимости от того, с какой точностью берется число π, вычисляется ∠АОВ и его синус, и как именно округляются промежуточные результаты и т. п. Более точные расчеты показывают, что в описанной задаче величины S1 и S2 примерно равны:
Площадь кольца и других сложных фигур
Если какая-либо фигура образована с помощью нескольких окружностей, то найти ее площадь можно, представив ее в виде суммы площадей нескольких более простых фигур. В качестве простейшего примера можно привести кольцо. По сути оно представляет собой круг, в котором есть круговое отверстие:
Если обозначить наружный радиус кольца буквой R, а радиус отверстия буквой r, то площадь кольца можно найти, вычтя из площади большего круга площадь отверстия:
Задание. Внешний радиус кольца составляет 20 см, а радиус отверстия в нем равен 15 см. Определите площадь кольца.
Решение. Подставляем числа в формулу:
Задание. Есть диск радиусом 1 метр. Необходимо вырезать в нем отверстие так, чтобы масса диска уменьшилась в два раза. Какой радиус должен быть у отверстия?
Решение. Можно считать, что масса диска пропорциональна его площади, поэтому нам надо, чтобы площадь диска уменьшилась вдвое. Начальная площадь диска определяется так:
Площадь кольца должна быть вдвое меньше, то есть она будет составлять π/2. Если радиус отверстия мы обозначим как r, то можно составить уравнение:
В прямоугольной плите с габаритами 180 и 60 см сделано 27 отверстий диаметром 10 см. Вычислите площадь этой плиты. Считайте, что π ≈ 3,1416, и округлите ответ до целых.
Решение. Надо найти площадь плиты без учета отверстий, а потом вычесть из нее площадь всех отверстий. Площадь плиты равна произведению ее сторон
Задание. Из вершин квадрата со стороной а проведены дуги радиусом а/2. В результате получили следующую фигуру:
Найдите заштрихованную площадь.
Решение. Площадь заштрихованной области может быть получена, если из площади квадрата мы вычтем площади 4 секторов. Площадь квадрата рассчитывается так:
Задание. В квадрате, сторона которого обозначается буквой а, из вершин провели дуги, чей радиус совпадает со стороной квадрата. В результате в центре квадрата получили следующую фигуру:
Определите, какую долю квадрата занимает эта центральная фигура. Ответ дайте в процентах и округлите его до десятых.
Решение. Задача решается в несколько действий, причем нам потребуется составить формулы для вычисления площадей вспомогательных фигур. Сначала найдем площадь маленького треугольника с «кривыми» сторонами, для чего используем такое построение:
Площадь, которую мы пытаемся найти, обозначена здесь как S1. Ее можно получить, просто вычтя из площади квадрата (она составляет а 2 ) площади двух секторов и площадь треугольника. Треугольник на рисунке – равносторонний, ведь и сторона квадрата, и радиусы окружностей равны величине а. Тогда каждый его угол составляет 60°, и его площадь можно найти так:
Также мы можем найти центральные углы обоих секторов. Так как углы в квадраты составляют 90°, а в равностороннем треугольнике 60°, то эти углы окажутся равными 90° – 60° = 30°. Тогда площадь сектора вычисляется по формуле:
На следующем шаге вычислим площадь другой фигуры:
Попытаемся выразить величину S2. Для этого из площади квадрата надо вычесть площадь сектора, у которого центральный угол составляет 90°. Найдем площадь этого сектора:
Здесь мы ищем площадь S3. Обратите внимание, что ее можно выразить через уже найденные нами величины S1 и S2:
Мы составили выражения для всех необходимых нам вспомогательных фигур. Теперь вернемся к исходному рисунке и отметим на нем эти вспомогательные фигуры:
Итак, мы составили выражение для вычисления площади центральной фигуры. По условию надо указать, сколько процентов она составляет от площади всего квадрата. Для ответа на этот вопрос поделим площадь фигуры на площадь квадрата и умножив это отношение на 100%:
В рамках этого урока мы узнали, как вычислять длину окружности и дуги, площади круга, сектора, сегмента, кольца и других фигур, одна или несколько сторон которых представляют собой дуги окружности. Эти навыки могут пригодиться и в реальной жизни, так как именно от площади многих предметов часто зависит потребность в краске, лаке, клее и т. п.
Как вычислить радиус дуги
На данной странице калькулятор поможет рассчитать длину дуги окружности онлайн. Для расчета задайте радиус, угол между радиусами.
Чтобы найти длину дуги, когда не известен радиус, например, на чертеже или у предмета, то используют формулу Гюйгенса. При расчете по этой формуле есть погрешность, примерно от 0,5% до 0,02%.
Дуга окружности – это часть окружности ограниченная двумя точками.
Гибочный калькулятор
Чаще всего стоит задача определения параметров дуги по её габаритным размерам. Для этого мы предлагаем гибочный калькулятор.
 |
Введите значения H и h в миллиметрах
Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм. на заготовку.
Вы можете скачать ПК версию гибочного калькулятора по этой ссылке.
140030, МО, Люберецкий район, пос. Малаховка, Касимовское шоссе, д. 3Г
Право собственности ООО «ПК РАДИУС» © 2002–2017. Все права защищены.
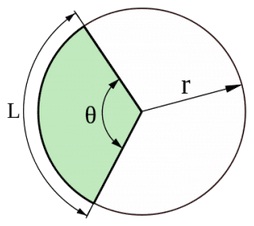
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Нахождение длины окружности и площади круга
Заметим, что закрашенная фигура состоит из двух непересекающихся частей, равных \(\frac14\) и \(\frac12\) от \(\frac14\) круга:
Таким образом, ее площадь равна \[\dfrac14S+\dfrac12\cdot \left(\dfrac14S\right)=\dfrac38S=\dfrac38\cdot 2,8=1,05.\]
Длины дуг относятся так же, как их градусные меры. Так как \(O\) – центр окружности, то \(\angle AOB\) – центральный.
Градусная мера большей дуги в \(240 : 120 = 2\) раза больше, чем градусная мера меньшей дуги.
Длина дуги \(AB\) данного сектора равна \(\dfrac<18> <\pi>\cdot \dfrac<2\pi> <9>= 4\) см.
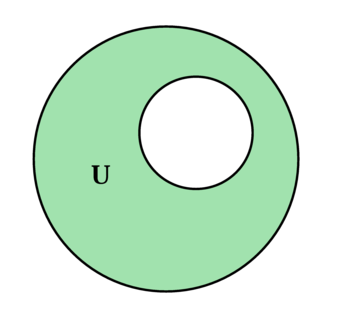
Внутри большой окружности расположена маленькая, радиус которой в 2,5 раза меньше, чем радиус большой окружности. Найдите отношение площади зеленой области \(U\) к площади круга, ограниченного большой окружностью.
Задачи на нахождение площади круга — обязательная часть ЕГЭ по математике. Как правило, этой теме отводится сразу несколько заданий в аттестационном испытании. Понимать алгоритм нахождения длины окружности и площади круга должны все старшеклассники, независимо от уровня их подготовки.
Если подобные планиметрические задачи вызывают у вас затруднения, рекомендуем обратиться к образовательному порталу «Школково». С нами вы сможете восполнить пробелы в знаниях.
В соответствующем разделе сайта представлена большая подборка задач на нахождение длины окружности и площади круга, подобных тем, которые включены в ЕГЭ. Научившись их правильно выполнять, выпускник сможет успешно справиться с экзаменом.
Основные моменты
Задачи, в которых требуется применить формулы площади, могут быть прямыми и обратными. В первом случае известны параметры элементов фигуры. При этом искомой величиной является площадь. Во втором случае, наоборот, площадь известна, а найти необходимо какой-либо элемент фигуры. Алгоритм вычисления правильного ответа в подобных заданиях различается только порядком применения базовых формул. Именно поэтому, приступая к решению таких задач, необходимо повторить теоретический материал.
На образовательном портале «Школково» представлена вся базовая информация по теме «Нахождение длины окружности или дуги и площади круга», а также по другим темам, например, «Центральный угол окружности». Ее наши специалисты подготовили и изложили в максимально доступной форме.
Вспомнив основные формулы, учащиеся могут приступить к выполнению задач на нахождение площади круга, подобных тем, которые включены в ЕГЭ, в режиме онлайн. Для каждого упражнения на сайте представлено подробное решение и дан правильный ответ. При необходимости любое задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и обсудить с преподавателем.
Формулы площади сектора круга и длины его дуги
Понятие об окружности и круге
Перед тем как приводить формулу площади сектора окружности, рассмотрим, что собой представляет указанная фигура. Согласно математическому определению, под окружностью понимают такую фигуру на плоскости, все точки которой равноудалены от некоторой одной точки (центра).
Вам будет интересно: Вячеславна или Вячеславовна? Учимся правильно писать.
Когда рассматривают окружность, то пользуются следующей терминологией:
Площадь круга и длина окружности
Отмеченные в названии пункта величины рассчитываются с использованием двух простых формул. Они приведены ниже:
Как видно из приведенных выражений, чтобы рассчитать площадь и длину достаточно знать только радиус окружности.
Площадь сектора круга и длина его дуги
Перед тем как рассматривать соответствующие формулы, напомним, что угол в геометрии принято выражать двумя основными способами:
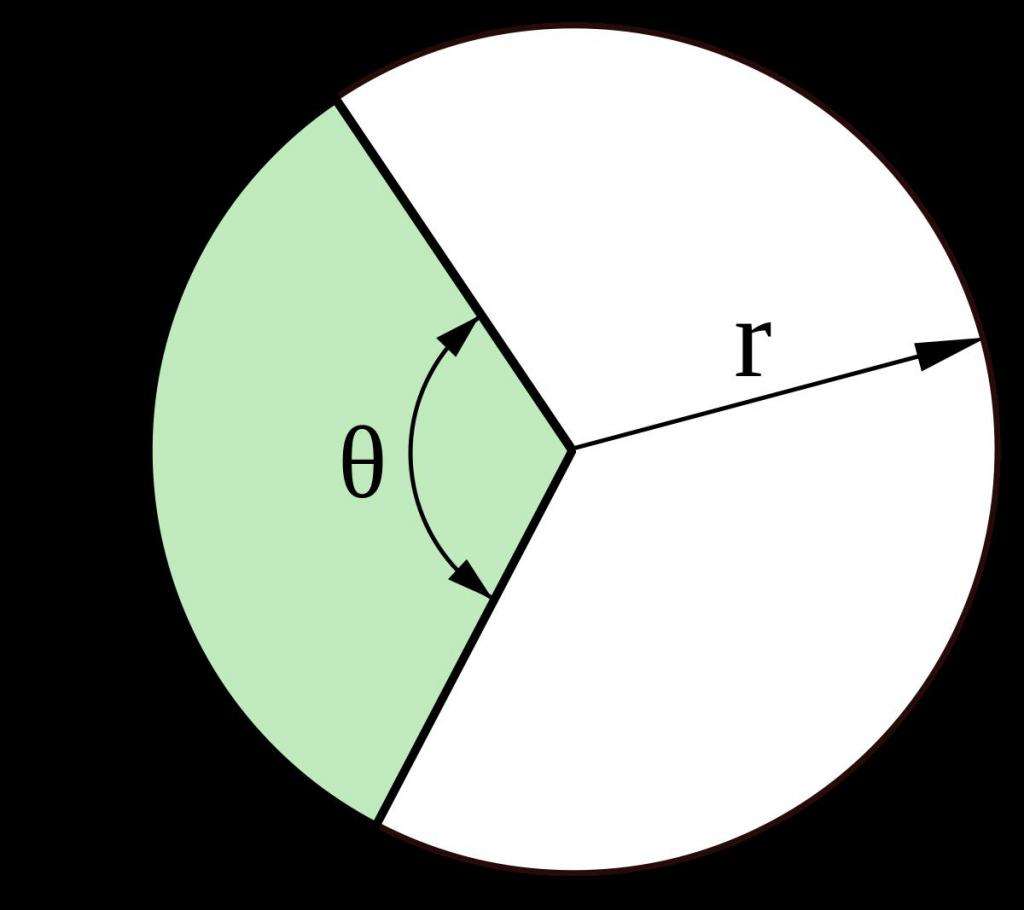
Получив представление о том, что такое сектор для круга, легко понять, как вычислить его площадь и длину соответствующей дуги. Из рисунка выше видно, что дуге сектора соответствует угол θ. Мы знаем, что полная окружность соответствует 2*pi радианам, значит, формула площади кругового сектора примет вид: S1 = S*θ/(2*pi) = pi*R2*θ/(2*pi) = θ*R2/2. Здесь угол θ выражен в радианах. Аналогичная формула площади сектора в случае, если угол θ измеряется в градусах, будет иметь вид: S1 = pi*θ*R2/360.
Длина дуги, образующей сектор, вычисляется по формуле: L1 = θ*2*pi*R/(2*pi) = θ*R. И если θ известен в градусах, тогда: L1 = pi*θ*R/180.
Пример решения задачи
Покажем на примере простой задачи, как пользоваться формулами площади сектора круга и длины его дуги.
Известно, что колесо имеет 12 спиц. Когда колесо делает один полный оборот, то оно преодолевает расстояние 1,5 метра. Чему равна площадь, заключенная между двумя соседними спицами колеса, и чему равна длина дуги между ними?
Как видно из соответствующих формул, чтобы ими пользоваться, необходимо знать две величины: радиус окружности и угол дуги. Радиус можно вычислить, исходя из знания длины окружности колеса, поскольку пройденное им расстояние за один оборот, точно ей соответствует. Имеем: 2*R*pi = 1,5, откуда: R = 1,5/(2*pi) = 0,2387 метра. Угол между ближайшими спицами можно определить, зная их число. Полагая, что все 12 спиц делят равномерно круг на равные сектора, мы получаем 12 одинаковых секторов. Соответственно, угловая мера дуги между двумя спицами равна: θ = 2*pi/12 = pi/6 = 0,5236 радиан.
Мы нашли все необходимые величины, теперь их можно подставить в формулы и посчитать требуемые условием задачи значения. Получаем: S1 = 0,5236*(0,2387)2/2 = 0,0149 м2, или 149 см2; L1 = 0,5236*0,2387 = 0,125 м, или 12,5 см.
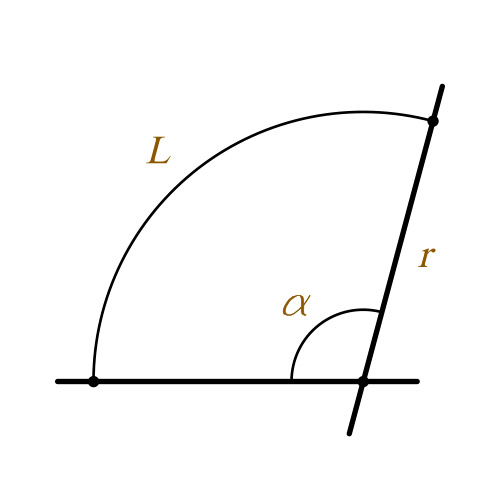
Как найти длину дуги окружности
Формула для нахождения длины дуги окружности довольно проста, и очень часто на важных экзаменах типа ЕГЭ встречаются такие задачи, которые невозможно решить без ее применения. Также необходимо ее знать для сдачи международных стандартизированных тестов, например SAT и других.
Чему равна длина дуги окружности?
Формула выглядит следующим образом:
Что собой представляет каждый из элементов формулы:
Как видно, чтобы решить задачу, в условии должны присутствовать r и α. Без этих двух величин длину дуги найти невозможно.
Каким образом выводится эта формула и почему она так выглядит?
Все предельно легко. Станет намного понятнее, если в знаменателе поставить 360°, а в числителе спереди добавить двойку. Также можно α не оставить в дроби, вывести ее и написать со знаком умножения. Это вполне можно себе позволить, так как данный элемент стоит в числителе. Тогда общий вид станет таким:
Просто для удобства сократили 2 и 360°. А теперь, если приглядеться, то можно заметить очень знакомую формулу длины всей окружности, а именно — 2πr. Весь круг состоит из 360°, потому мы делим полученную меру на 360 частей. Затем мы умножаем на число α, то есть на то количество «кусков пирога», которое нам требуется. Но всем доподлинно известно, что число (то есть длина всей окружности) не может делиться на градус. Что же делать в таком случае? Обычно, как правило, градус сокращается с градусом центрального угла, то есть с α. После же остаются только числа, а в итоге получается конечный ответ.
Этим можно объяснить то, почему длина дуги окружности находится таким образом и имеет такой вид.
Пример задачи средней сложности с применением данной формулы
Условие: Имеется окружность с радиусом 10 сантиметров. Градусная мера центрального угла составляет 90°. Найти длину дуги окружности, образованную этим углом.
Решение: l = 10π × 90° / 180° = 10π × 1 / 2=5π
Также возможно, чтоб вместо градусной меры давалась бы радианная мера угла. Ни в коем случае не стоит пугаться, ведь на сей раз задача стала намного легче. Чтобы перевести радианную меру в градусную, нужно данное число умножить на 180° / π. Значит, теперь можно подставить вместо α следующую комбинацию: m × 180° / π. Где m — это радианное значение. А дальше 180 и число π сокращаются и получается совершенно упрощенная формула, которая выглядит следующим образом:
Необходимость расчётов
Геометрическими формулами, связанными с подсчетом площади сектора, объема сегмента и периметра полукруга, следует виртуозно владеть людям, связавшим свою жизнь со строительством или благоустройством территорий. Чтобы обновить после зимы элементы архитектуры городского парка и закрасить дефекты абстрактных скульптур, не нужно вспоминать сложные уравнения, достаточно применить знание геометрических формул.
К примеру, для правильного нахождения веса декоративного камня, предназначенного для окантовки части клумбы, нужно уметь быстро посчитать размер полуокружности на поверхности ландшафта. Затем необходимо определиться с ценой и принять решение, какой камень можно покупать с учетом сметы. Аналогичная задача возникает при строительстве альпийской горки. Тяжесть камня обеспечит круговую укладку, это свойство позволит высадить декоративные растения в запланированных местах сечения, придав конструкции форму трапеции.
Что представляет собой часть клумбы? Это сектор геометрической фигуры. Внешняя его часть — окантовка клумбы — чаще всего представляет собой дугу окружности. Существует две методики вычисления этой величины:
Определение методики расчета в полевых условиях зависит от наличия инструментов и особенностей рельефа местности. Но сначала немного теории. Дугой называют часть окружности, расположенную между двумя произвольными точками, находящимися на ней.
Для удобства рассмотрим пример с двумя точками A и B, расположенными на окружности на небольшом расстоянии друг от друга. Они делят её на 2 части — большую и меньшую. Каждая из них называется дугой окружности.
Градусная мера
Длина дуги между точками окружности является функцией центрального угла, образованного радиусами круга (см. рисунок) в прямо пропорциональной зависимости. На этом основана градусная мера.
За 1° дуги принимают часть окружности.
Определим значение l для угла 120° с радиусом, равным 5 мм: l=3,14*30*5/180=2,62 мм.
Применение хорды и высоты
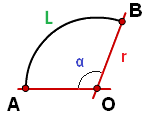
Существует методика расчета длины дуги по хорде и высоте перпендикуляра. Она получила название формулы Гюйгенса. Хорда представляет собой часть прямой, расположенной внутри окружности. Проходящая через центр хорда называется диаметром.
Формулу Гюйгенса применяют, если центральный угол меньше 60 градусов. Для проведения вычислений необходимо сначала соединить точки окружности прямой линией. Это будет хорда. Далее нужно провести перпендикуляр из ее середины, а из точки соприкосновения перпендикуляра с дугой начертить две прямые линии к концам хорды.
Замерив хорды L и l, можно получить значение дуги, обозначенной на рисунке синим цветом. Если L равна 30 мм, а l — 20 мм, то Р=2*20+3,33=43,33 мм.
Теперь, когда существует понимание методики расчета, можно воспользоваться онлайн-калькулятором. Этот инструмент хорош для проверки полученного экспериментальным путем результата, особенно при обработке большого количества данных, когда необходимо быстро получить ответ.
Онлайн-калькулятор позволяет сохранять полученные значения в буферной памяти компьютера. Оформить данные в виде произвольной таблицы или графика в системе координат не составит труда. Длина дуги окружности по онлайн-калькулятору считается с использованием любой из двух формул: либо по градусной мере, либо по хорде и высоте. Образно говоря, эти формулы являются синонимами, они взаимозаменяемы.
Практика с задачами
Нужно сказать несколько слов об изучении геометрии в средних классах общеобразовательной школы. Существует категория учащихся, для которых формулы сложны для восприятия. Таким ученикам требуется наглядный материал.
На уроке геометрии при изучении материала по вычислениям параметров окружности можно провести практическое занятие. Для этого следует предварительно подготовиться: сделать небольшой чертеж-проекцию гимнастического кольца. Цель занятия — научиться использовать формулы в процессе работы. Ход урока:
Далее следует разделить класс на 4 небольших группы. Каждой из них нужно дать задание по проведению вычислений с использованием изученных формул.
На выполнение задания отводится 12 минут. После истечения времени от каждой из четырех групп выходит ученик, поясняет формулу и записывает на доске полученный результат. Эти ответы сравниваются с уже готовыми замерами, записанными ранее на правой стороне доски.
Следующие 7 минут урока отводятся на обсуждение полученного результата и анализа возникновения погрешности.
Усложнение формулы
Группе продвинутых учеников предлагается задание «Как изменить градусную формулу?». Можно ли найти значение радиуса, используя другие геометрические выражения, например, представить его как половину диаметра круга? В этом случае формулы будет выглядеть следующим образом: r=1/2d, тогда l= πd/360*n.
Базовая цель уроков математики — развитие аналитического мышления учащихся достигается в процессе обсуждения и сравнения различных методик расчета. В качестве дополнительного задания можно предложить ученикам посчитать значение кривой линии наружного края школьной клумбы. Затем следует попросить обосновать свои расчеты.
Использование наглядности поможет учащимся подружиться с формулами, увидеть роль геометрии в повседневной практической жизни и облегчить усвоение конкретного материала.
Из этой статьи вы узнаете, как выглядит формула длины дуги окружности через угол, а также научитесь определять длину дуги сектора по формуле Гюйгенса. Также на страницу добавлены онлайн-калькуляторы для вычисления по данным формулам.
Дугой окружности (сектора) называют часть окружности, ограниченную двумя точками.
Чтобы определить длину дуги окружности, введите заданные данные в поля для ввода онлайн-калькулятора.
Длина дуги через радиус и угол
Для определения длины дуги можно воспользоваться формулой:
$R$ — радиус окружности;
$α$ — угол, которым характеризуется дуга;
Рассмотрим пример на использование этой формулы.
Задача
Решение:
$l = 3.14 cdot 9 cdot frac = 7.85$ см.
Проверим длину дуги окружности с помощью онлайн-калькулятора. Результат совпадает, значит ответ верный.
Готовые работы на аналогичную тему
Длина дуги по формуле Гюйгенса
По формуле Гюйгенса длина дуги рассчитывается следующим образом:
$l ≈ 2 cdot AB + frac13 cdot ( 2 cdot AB — AC)$, здесь
$AC$ — хорда, соединяющая концы дуги;
Также посмотрим, как использовать формулу Гюйгенса.
Задача
Решение:
$l = 2 cdot 2.19 + frac13 cdot (2 cdot 2.19 — 3.51) = 4.67$ см.
Результат совпадает, а значит, ответ — верный.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Окружность – геометрическое место точек, равноудаленных от данной точки.
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Теорема 4:
Равные хорды стягивают равные дуги.
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l α = π R 180 ∘ ⋅ α
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Модуль геометрия: задания, связанные с окружностями.
Здравствуйте!
Расскажите, пожалуйста, как найти длину дуги окружности. Что нужно знать из теории и на примере, желательно. Только основное, не нужно сильно углубляться.
Спасибо!
Как найти длину дуги окружности
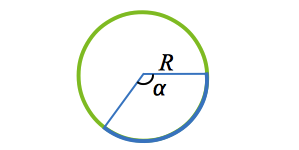
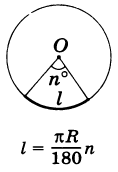
Длину дуги окружности принято измерять в градусах, так как она описывается концами радиусов и пропорциональна величине центрального угла, который образован этими же радиусами.
1 градус дуги окружности равен части этой окружности.
Обратим внимание, что величина центрального угла никоим образом не зависит от длины дуги.
Рассмотрим формулу для вычисления длины дуги окружности.
Запишем длину дуги окружности, для которой центральный угол равен n:
Поскольку длина окружности равна, то соответствовать развернутому углу будет длина дуги. В таком случае длина дуги центрального угла в 1 градус будет равна.
Таким образом, длина дуги центрального угла n градусов будет рассчитываться по формуле:
Пример.
Вычислить длину дуги окружности, радиус которой равен 3 см, а градусная мера составляет 150 градусов.
Решение.
Запишем формулу длины дуги центрального угла в n градусов:
Подставим известные значения:
(см).
Ответ. 7,85 см.
Еще используется понятие радиальной меры угла. Если понадобится такая информация — пишите.
Всего хорошего!
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
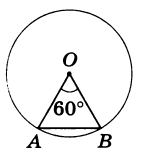
Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n° (рис.1).
Пример 1. По данной хорде к найти длину ее дуги, если она соответствует центральному углу в 60° (рис.2).
bullet 60 = frac
Единицей радианной меры углов является радиан. Угол в один радиан — это центральный угол, у которого длина дуги равна радиусу (рис.3).
Пример 2. Найти радианные меры углов параллелограмма ABCD, если ∠ A = 36°.
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить длину дуги сектора круга, а также разберем примеры решения задач для демонстрации их применения на практике.
Определение дуги сектора круга
Дуга – это участок между двумя точками на окружности.
Дуга сектора круга – это участок между двумя точками на окружности, которые получены в результате пересечения этой окружности двумя радиусами, образовавшими сектор круга.
На рисунке ниже: AB – это дуга зеленого сектора круга с радиусом R (или r).
Формулы для нахождения длины дуги сектора
Через центральный угол в градусах и радиус
Через угол сектора в радианах и радиус
Длина (L) дуги сектора равна произведению радиуса (r) и центрального угла, выраженного в радианах (aрад).
Примеры задач
Задание 1
Дан круг с радиусом 15 см. Найдите длину дуги сектора, угол которого равен 30°.
Решение
Воспользуемся формулой расчета, в которой используется центральный угол в градусах:
Задание 2
Длина дуги сектора равняется 24 см. Найдите, чему равен его угол (в радианах и градусах), если радиус круга составляет 12 см.
Решение
Для начала вычислим угол в радианах:
1 радиан ≈ 57,2958°
Следовательно, центральный угол приблизительно равняется 114,59 ° (2 рад ⋅ 57,2958°).
Длина дуги
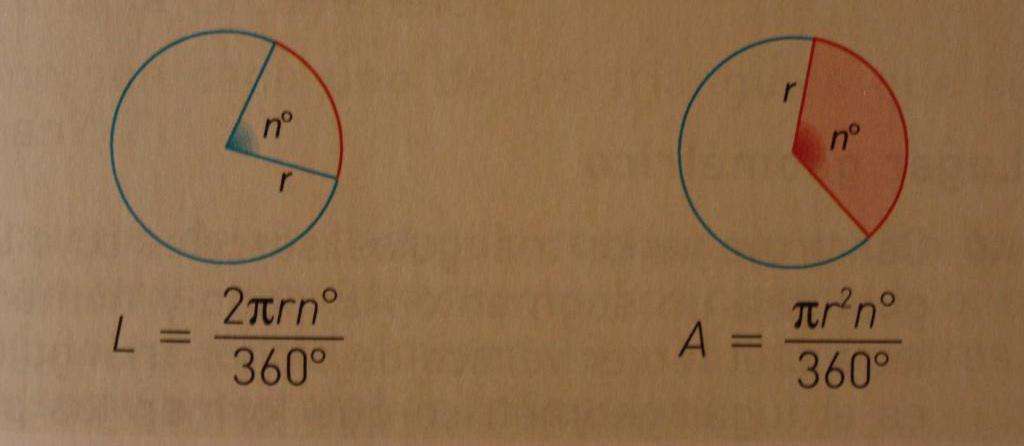
Если взять окружность и провести в ней два радиуса, то образуется центральный угол, измеряемый в градусах. Дуга, которую описывает радиус, пропорциональна соответствующему ему центральному углу. Длина дуги пропорциональна величине радиуса окружности и величине центрального угла. Дуги окружности, как и углы измеряются в градусах и его долях. За 1 градус принято считать одну трехсот шестидесятую часть окружности. Центральный угла исчисляется тем же количеством градусов, что и дуга, на которую опирается угол. Длину дуги следует определять по формуле:
r — величина радиуса дуги;
n°- величина центрального угла;
π — величина постоянная, 3,1415;
180°- половина окружности.
Определение длины дуги с помощью онлайн калькулятора намного сэкономит ваши усилия и время.
Длина окружности
Возьмем циркуль. Установим ножку циркуля с иглой в точку « O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Диаметр окружности обозначается буквой « D ». На рисунке выше — это отрезок « BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение « D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Разбор примера
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2 π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Разбор примера
Определите диаметр окружности, если её длина равна 56,52 дм. ( π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки « A » и « B ». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга « AB » и черная дуга « AB ». Точки « A » и « B » называют концами дуг.
Соединим точки « A » и « B » отрезком. Полученный отрезок называют хордой.
Точки « A » и « B » делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга « AB ».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
Как найти длину дуги кривой с помощью интеграла
Вычисление длины дуги кривой, заданной в прямоугольных координатах
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.
Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).
.
Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:
.
Этот предел интегральной суммы равен определённому интегралу
(1).
Формула выше и есть формула для вычисления дуги кривой.
Пример 1. Найти длину дуги кривой 
, если 
.
Решение. Находим производную данной функции:
Используем формулу (1), подставляя найденную производную:
Ответ: длина дуги кривой равна 74.
Пример 2. Найти длину окружности 
.
Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:
,
откуда находим производную функции:
Используем формулу (1) подставляя в неё производную, получаем:
Ответ: длина всей окружности равна 
.
Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:
. (2)
Вычисление длины дуги кривой, заданной параметрически
Найдём теперь длину дуги кривой в том случае, когда кривая задана параметрическими уравнениями:
В этом случае длину дуги кривой следует находить по формуле
(3).
Пример 3. Найти длину дуги кривой, заданной параметрическими уравнениями
если 
.
Решение. Рассчитаем интервал, в котором будет меняться значение t, если :
Вычислим производные функций x и y:
Используем формулу (3):
.
Ответ: длина дуги кривой равна 26.
Если параметрическими уравнениями
задана пространственная кривая, то длина её дуги вычисляется по формуле:
. (4)
Пример 4. Найти длину дуги винтовой линии, заданной параметрическими уравнениями
Решение. Вычислим производные функций x, y и z:
Используем формулу (4):
Вычисление длины дуги кривой, заданной в полярных координатах
Пусть кривая задана в полярных координатах:
Длина её дуги вычисляется по формуле:
(5).
Пример 5. Найти длину дуги кривой, заданной в полярных координатах 
.
Решение. Вычислим производную функции:
.
.
Урок математики по теме «Длина окружности и длина дуги окружности». 9-й класс
Разделы: Математика
Класс: 9
Цель урока:
Тип урока: урок деятельного типа.
Оборудование: распечатки для выполнения задания «Лови ошибку!» и решения задач из различных источников для подготовки к ОГЭ и дополнительного домашнего задания, интерактивная доска, учебно-методическое пособие для подготовки к ОГЭ в 2019 году. 40 вариантов под редакцией Лысенко Ф.Ф. (у каждого ученика).
Ход урока
1. Организационный момент. Мотивация учебной деятельности
Учитель. Приветствует всех. Предлагает вспомнить тему прошлого урока и тематику домашнего задания
Предполагаемые ответы учеников (длина окружности, длина дуги окружности).
Учитель. И если сегодня у нас не будет нового теоретического материала, значит что же нам предстоит делать на этом уроке?
Предполагаемые ответы учеников (решать задачи, повторять теоретический материал).
Учитель, с учётом ответов учащихся сообщает цель урока, акцентируя внимание на эпиграфе урока, особенно на заключительном предложении, подчёркивая важность формирования у себя регулятивных универсальных учебных действий.
II. Актуализация знаний учащихся
1.1 Проверка домашнего задания (три человека работают у доски)
а) Учитель, обращаясь к классу, выясняет, кто сможет решить дополнительную задачу с объяснениями у доски и сообщает, что это была задача с сайта «Решу ОГЭ» №24 по структуре ОГЭ. Решение с использованием интерактивной доски.
1 ученик. №24. Решу ОГЭ №311 650
Найти:
а) радиус окружности, описанной около треугольника;
б) длину окружности;
в) длину дуги ВС.
Решение:
Применив свойство пропорции получим: 
б) По формуле вычисления длины окружности через полученное значение радиуса находим: 
.
Ответ: 2; 4
, .
б) 2 ученик (ГВЭ) Учебник № 1101(1)
С = 6,28 · 4= 25,12
Ответ: 25,12.
в) 3 ученик. Учебник №1109(1)
Ответ: .
1.2 Учитель проверяет решение домашней работы у доски, а класс выполняет самостоятельную работу по карточкам с последующей проверкой.
(Для диагностики и формирования регулятивных учебных действий использовать такой вид занятий как «Лови ошибку»).
Ответить на вопросы: «да» или «нет», заполнив таблицу
Да
2, 6, 8, 9
Нет
1, 3, 4, 5, 7
1. Окружность – это шар, все точки которого находятся на заданном расстоянии от одной данной точки. (нет)
2. Любой равносторонний треугольник является правильным? (Да)
3. Любой равносторонний четырёхугольник является правильным? (Нет, например ромб)
4. Угол, лежащий напротив радиуса – прямой. (нет)
5. Стороны треугольника пропорциональны косинусам противолежащих углов. (нет)
6. Сторона квадрата, вписанного в окружность равна. Длина этой окружности равна 12. (да)
7. Сторона правильного шестиугольника, вписанного в окружность, равна 6. Длина этой окружности равна 6. (нет)
8. Длина окружности более чем в 3 раза превышает диаметр этой окружности. (да)
9. Длина дуги прямо пропорциональна её градусной мере. (да)
1.3 Самопроверка ответов с последующей самооценкой. (Правильные ответы заготовлены для проверки).
Критерии оценивания
Менее 3 баллов
3-4 балла
5-6 баллов
7-9 баллов
«2»
«3»
«4»
«5»
III. Решение задач
1 тип (прямоугольный треугольник в окружности …)
Учитель обращает внимание на 4 и 5 вопросы «Лови ошибку» и выясняют с классом правильный ответ, подводит итог с классом: применение каких дополнительных теоретических сведений требовалось для решения задачи и правильного ответа на вопросы.
Предлагает решить задачи (Лысенко. Варианты №5,6. Задание №16), но добавить вопрос: найти С окружности.
Решение: АВ=13, R = 6,5; С=13.
Ответ: R = 6,5; С=13.
Вариант №6. Задание №16
Решение: АВ=10, R = 5; С=10.
Ответ: R = 5; С=10.
IV. Физкульминутка
V. Решение задач нового типа по рассматриваемой теме
Учитель предлагает продолжить работу с учебно-методическим пособием по подготовке ОГЭ. Лысенко Ф.Ф. (40 вариантов).
Лысенко Вариант №13. Задание №16
Решение:
Пусть длина большей дуги СД равна х.
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Ответ: 221.
Лысенко Вариант №14. Задание №16
Решение:
Пусть длина большей дуги равна х. Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Ответ: 355.
VI. Рефлексия учебной деятельности
VII. Информация о домашнем задании
Стр. 284 вопросы 1,6,7,10 № 1108 (практич.содер.; межпред. Связь) №1104(б)
Индивидуальные задания. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите длину окружности, если AB = 15, AC = 25 (теорема о касательной и секущей, проведенных к окружности из одной точки).
Дополнительные задачи
1 часть. 50 вариантов заданий. ОГЭ 2019. Под редакцией И.В.Ященко. Задание №17.
Вариант 1.
Вариант 2
Вариант 3.
2 часть
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите длину окружности, если AB = 15, AC = 25 (теорема о касательной и секущей, проведенных к окружности из одной точки).
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
Длина дуги окружности. Радианная мера угла
Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n° (рис.1).
Пример 1. По данной хорде к найти длину ее дуги, если она соответствует центральному углу в 60° (рис.2).
Единицей радианной меры углов является радиан. Угол в один радиан — это центральный угол, у которого длина дуги равна радиусу (рис.3).
Пример 2. Найти радианные меры углов параллелограмма ABCD, если ∠ A = 36°.
Простая формула для определения радиуса дуги
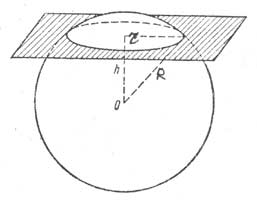
Полезно знать математический способ, позволяющий рассчитать радиус дуги. Он особенно удобен, когда требуется точно разметить плавную дугу с помощью большого импровизированного циркуля, а не гибкого лекала, после того как вам стали известны три опорные точки или два главных размера.
Как видно на рисунке справа, требуется знать лишь высоту и длину дуги. Подставьте эти размеры в простую формулу и вычислите радиус. Получив результат, настройте циркуль на этот размер и начертите идеальную дугу требуемого радиуса.
Например, если нужно построить дугу длиной 240 и высотой 30 мм, следует действовать так:
Сначала подставьте эти размеры в формулу. В нашем случае L=120, Н=30, поэтому (1202+302): (2×30) = (14400+900): 60= 153000:60 = 255.
Теперь сделайте для этого радиуса циркуль, как показано на фото внизу. Выровняйте один конец с серединой дуги на заготовке. Проведите из этой точки под прямым углом по линейке прямую линию и поставьте на нее второй конец циркуля. Теперь вы можете начертить идеальную дугу, которая соединит все три опорные точки.
Длина дуги окружности. Длина окружности
Длина дуги окружности. Длина окружности
Длина окружности обозначается буквой C и вычисляется по формуле:
C = 2πR,
где R — радиус окружности.
Вывод формулы, выражающей длину окружности
Путь C и C’ — длины окружностей радиусов R и R’. Впишем в каждую из них правильный n-угольник и обозначим через Pn и P’n их периметры, а через an и a’n их стороны. Используя формулу для вычисления стороны правильного n-угольника an = 2R sin (180°/n) получаем:
Pn = n · an = n · 2R sin (180°/n),
P’n = n · a’n = n · 2R’ sin (180°/n).
Следовательно,
Pn / P’n = 2R / 2R’. (1)
Это равенство справедливо при любом значении n. Будем теперь неограниченно увеличивать число n. Так как Pn → C, P’n → C’, n → ∞, то предел отношения Pn / P’n равен C / C’. С другой стороны, в силу равенства (1) этот предел равен 2R / 2R’. Таким образом, C / C’ = 2R / 2R’. Из этого равенства следует, что C / 2R = C’ / 2R’, т. е. отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π («пи»).
Из равенства C / 2R = π получаем формулу для вычисления длины окружности радиуса R:
С = 2πR.
Длина дуги окружности
Так как длина всей окружности равна 2πR, то длина l дуги в 1° равна 2πR / 360 = πR / 180.
Поэтому длина l дуги окружности с градусной мерой α выражается формулой
l = (πR / 180) · α.
8) Радиан как единица измерения угловых величин.
Радиа́н — основная единица измерения плоских углов в современной математике и физике. Радиан определяется как угловая величина дуги, длина которой равна её радиусу. Таким образом, величина полного угла равна 2π радиан.
Поскольку длина дуги окружности пропорциональна её угловой мере и радиусу, длина дуги окружности радиуса R и угловой величины α, измеренной в радианах, равна Rα.
Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине её радиуса, радиан — величина безразмерная. Поэтому обозначение радиана (рад) часто опускается.
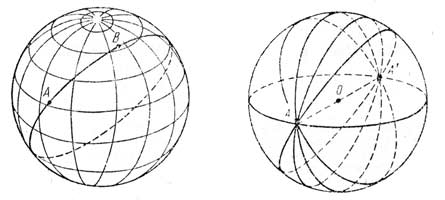
9 )Основные понятия сферической тригонометрии. Сферой. или сферической поверхностью называется геометрическое место точек в пространстве равноудаленных от некоторой точки называемой центром сферы. Радиусом сферы называется отрезок прямой соединяющий центр сферы с любой из ее точек.
Всякое сечение сферы плоскостью является окружностью, которая в сферической тригонометрии часто называется кругом. Сечение проходящее через центр сферы больше всякого другого сечения. Оно называется большим кругом. Радиус большого круга равен радиусу сферы.Точки пересечения оси круга с поверхностью сферы в диаметрально противоположенных направлениях называются полюсами круга. Сферическим радиусом большого круга называется дуга другого большого круга заключенная между любой точкой данного большого круга и его полюсом.
Дуга большого круга называемая в судовождении ортодромией является кратчайшем настоянием между двумя точками на сфере подобно тому, как прямая линия является кратчайшем расстоянием между двумя точками на плоскости.
Сферическим треугольником называется фигура на сфере ограниченная тремя пересекающимися попарно ДБК которые не пересекаются в одной точке. В задачах решаются треугольники стороны которых не превосходят 180гр. Т.е. эти треугольники помещаются на одной половине сферы. Сумма сторон сферического треугольника находится в приделах 0
По форме сферические треугольники разделяют на косоугольныепрямоугольные и четвертные или прямостороннии. Два сферических треугольника, у которого вершины одного являются полюсами сторон другого называются взаимно полярными треугольниками.
Противолежащие стороны и углы двух взаимно полярных треугольников дополняют друг друга до 180.
Эта формула показывает, что величина r принимает максимальное значение r=R при h=0, то есть является диаметральной плоскостью. В этом случае окружность на сфере и называется большой окружностью. В геометрии на сфере большие окружности играют роль прямых на плоскости. При h>0 мы имеем rмалой окружностью.
Так как через всякие три точки пространства, не лежащие на одной прямой, проходит единственная плоскость, то через всякие две точки сферы, не являющиеся диаметрально противоположными проходит единственная диаметральная плоскость. Поэтому через всякие две точки сферы, не являющиеся диаметрально противоположными, проходит единственная большая окружность (рис.2). Этот факт вполне аналогичен тому, что на плоскости через всякие две точки проходит единственная прямая. Через две диаметрально противоположные точки сферы, напротив, можно провести бесконечное множество больших окружностей (рис.3). Так как всякие две диаметральные плоскости сферы пересекаются по её диаметру, то всякие две большие окружности пересекаются в двух диаметрально противоположных точках сферы (рис.4). Здесь мы наблюдаем отличие сферической геометрии от плоской геометрии, в которой две прямые пересекаются не более чем в одной точке.
Так как плоскость делит пространство на две области, то большая окружность делит сферу на две области (рис.2); эти области называются полусферами, а сама окружность – краем этих полусфер. Далее, так как две пересекающееся плоскости делят пространство на четыре области, то две большие окружности делят сферу на четыре области (рис.4). Наконец, так как три плоскости, пересекающиеся в одной точке, делят пространство на восемь областей, то три большие окружности, не пересекающиеся в одной точке, делят сферу на восемь областей (на рис.5) изображены восемь областей ABC, ABC¢, AB¢C, A¢BC, AB¢C¢, A¢BC¢, A¢B¢C, A¢B¢C¢, на которые делят сферу большие окружности AB, AC и BC, причём точки A¢,B¢,C¢ диаметрально противоположны точкам A,B,C и, следовательно, области ABC и A¢B¢C¢, ABC¢ и A¢B¢C, AB¢C и A¢BC¢, A¢BC и AB¢C¢ попарно диаметрально противоположны).
Если первые два из этих свойств аналогичны свойствам прямых на плоскости, которая делится на две области прямой и на четыре области двумя пересекающимися прямыми, то третье из указанных свойств не вполне аналогично соответствующему свойству прямых на плоскости, так как три попарно пересекающиеся прямые, не проходящие все три через одну точку, делят плоскость не на восемь, а на семь частей (рис.6).
Рис 6.
10) решение сферических навигационных треугольников расчет расстояния между точками
12)
Гео́ид (буквально — «нечто подобное Земле») — геометрическое тело, отражающее свойства потенциала силы тяжести на Земле (вблизи земной поверхности). Геоид определяется как эквипотенциальная поверхность земного поля тяжести (уровенная поверхность), приблизительно совпадающая со средним уровнем вод Мирового океана в невозмущённом состоянии и условно продолженная под материками. Отличие реального среднего уровня моря от геоида может достигать 1 м.
По определению эквипотенциальной поверхности, поверхность геоида везде перпендикулярна отвесной линии.
Референц-эллипсоид (от лат. referens – сообщающий, вспомогательный) – земной эллипсоид, с определёнными размерами и положением в теле Земли, служащий вспомогательной математической поверхностью, к которой приводят результаты всех геодезических измерений на земной поверхности и на которую тем самым проектируются пункты опорной геодезической сети.
Референц-эллипсоид наилучшим образом согласуюется с поверхностью геоида на ограниченной части его поверхности.
Требования к референц-эллипсоиду:
1)Ось вращения должна быть параллельна оси вращения Земли
2)Плоскость экватора должна быть параллельна плоскости Земного экватора
14) Масштабы.
Числовой масштаб — дробь, числитель которой — единица, а знаменатель — число, показывающее, скольким единицам длины на местности равна единица длины на карте. Например, дробь 1/200000 означает, что одной единице длины на карте соответствует 200 000 таких же единиц длины на местности (1 см на карте равен 200 000 см на местности и т. п.).
Линейный масштаб указывает, какое число более крупных единиц расстояния на местности содержится в одной более мелкой единице на карте (например, 5 миль в 1 см).
Для перехода от числового масштаба к линейному знаменатель числового масштаба делят на длину морской мили, выраженную в тех единицах, к которым приводится линейный масштаб. Например, числовой масштаб 1/200000, тогда линейный масштаб будет 200000/185200 = 1,03 мили в 1 см.
Для перехода от линейного масштаба к числовому линейную длину изображения одной мили на карте делят на длину морской мили в тех же единицах, в которых длина мили дана на карте. Например, линейный масштаб 5 миль в 1 см, тогда числовой масштаб 1/51852100 = 1/926000.
Произвольные проекции
В произвольных проекциях имеются искажения и углов, и площадей, но в значительно меньшей степени, чем в равновеликих и равноугольных проекциях, поэтому они наиболее употребляемые.
Частным случаем произвольных проекций являются равнопромежуточные проекции, в которых сохраняются расстояния по некоторым выбранным направлениям: например, прямая азимутальная проекция, в которой правильно изображаются расстояния от полюса.
Цилиндрические проекции
В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг другу. Таким образом задается прямоугольная сетка цилиндрических проекций
Промежутки между параллелями пропорциональны разностям долгот. Промежутки между меридианами определяются принятым характером изображения или способом проектирования точек земной поверхности на боковую поверхность цилиндра. Из определения проекций следует, что их сетка меридианов и параллелей ортогональна. Цилиндрические проекции можно рассматривать как частный случай конических, когда вершина конуса в бесконечности.
По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и поперечные цилиндрические проекции в зависимости от расположения изображаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.
Существуют разные способы образования цилиндрических проекций. Наглядным представляется проектирование земной поверхности на боковую поверхность цилиндра, которая затем развертывается на плоскости. Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору, во втором — по двум стандартным параллелям, симметричным относительно экватора.
Цилиндрические проекции применяются при составлении карт мелких и крупных масштабов — от общегеографических до специальных. Так, например, аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равноугольных проекциях (на шаре).
В прямых цилиндрических проекциях одинаково изображаются одни и те же участки земной поверхности вдоль линии разреза — по восточной и западной рамкам карты (дублируемые участки карты) и обеспечивается удобство чтения по широтным поясам (например, на картах растительности, осадков) или по меридиональным зонам (например, на картах часовых поясов).
Косые цилиндрические проекции при широте полюса косой системы, близкой к полярным широтам, имеют географическую сетку, дающую представление о сферичности земного шара. С уменьшением широты полюса кривизна параллелей увеличивается, а их протяжение уменьшается, поэтому уменьшаются и искажения (эффект сферичности). В прямых проекциях полюс показывается прямой линией, по длине, равной экватору, но в некоторых из них (проекции Меркатора, Уэтча) полюс изобразить невозможно. Полюс представляется точкой в косых и поперечных проекциях. При ширине полосы до 4,5° можно использовать касательный цилиндр, при увеличении ширины полосы следует применять секущий цилиндр, то есть вводить редукционный коэффициент
Конические проекции
По характеру искажений конические проекции могут быть различными. Наибольшее распространение получили равноугольные и равнопромежуточные проекции. Образование конических проекций можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида).
В прямых конических проекциях оси земного шара и конуса совпадают. При этом конус берется или касательный, или секущий.
После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость. При проектировании по методу линейной перспективы получаются перспективные конические проекции, обладающие только промежуточными свойствами по характеру искажений.
В зависимости от размеров изображаемой территории в конических проекциях принимаются одна или две параллели, вдоль которых сохраняются длины без искажений. Одна параллель (касательная) принимается при небольшом протяжении по широте; две параллели (секущие) — при большом протяжении для уменьшения уклонений масштабов от единицы. В литературе их называют стандартными параллелями.
Азимутальные проекции
В азимутальных проекциях параллели изображаются концентрическими окружностями, а меридианы — пучком прямых, исходящих из центра
Углы между меридианами проекции равны соответствующим разностям долгот. Промежутки между параллелями определяются принятым характером изображения (равноугольным или другим) или способом проектирования точек земной поверхности на картинную плоскость. Нормальная сетка азимутальных проекций ортогональна. Их можно рассматривать как частный случай конических проекций.
Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.
В зависимости от искажений, азимутальные проекции подразделяются на равноугольные, равновеликие и с промежуточными свойствами. В проекции масштаб длин может сохраняться в точке или вдоль одной из параллелей (вдоль альмукантарата). В первом случае предполагается касательная картинная плоскость, во втором — секущая. В прямых проекциях формулы даются для поверхности эллипсоида или шара (в зависимости от масштаба карт), в косых и поперечных — только для поверхности шара.
Азимутальную равновеликую проекцию называют также стереографической. Она получается проведением лучей из некоторой фиксированной точки поверхности Земли на плоскость, касательную к поверхности Земли в противолежащей точке.
Особый вид азимутальной проекции — гномоническая. Она получается проведением лучей из центра Земли к некоторой касательной к поверхности Земли плоскости. Гномоническая проекция не сохраняет ни площадей, ни углов, но зато на ней кратчайший путь между любыми двумя точками (то есть дуга большого круга) всегда изображается прямой линией; соответственно меридианы и экватор на ней изображаются прямыми линиями.
Псевдоконические проекции
В псевдоконических проекциях параллели изображаются дугами концентрических окружностей, один из меридианов, называемый средним — прямой линией, а остальные — кривыми, симметричными относительно среднего.
Примером псевдоконической проекции может служит равновеликая псевдоконическая проекция Бонна.
Поликонические проекции
В поликонических проекциях экватор изображается прямой, а остальные параллели изображаются дугами эксцентрических окружностей. Меридианы изображаются кривыми, симметричными относительно центрального прямого меридиана, перпендикулярного экватору.
Кроме вышеперечисленных встречаются и другие проекции, не относящиеся к указанным видам.
17) локсодромия — кривая на поверхности вращения, пересекающая все меридианы под постоянным углом, называемым локсодромическим путевым углом.
Если передвигаться с фиксированным путевым углом по Земле, которую условно принять за сферу или эллипсоид, то траектория движения объекта и будет локсодромией. Локсодрома не является кратчайшим путём между двумя пунктами (исключение — меридианы и экватор). Тем не менее, в старину суда и путешественники нередко двигались по локсодромам, так как идти под постоянным углом к Полярной звезде проще и удобнее. С изобретением компаса мореплаватели перешли на движение по «магнитным локсодромам», то есть по линиям с постоянным углом к магнитному северу, что дало возможность продолжать движение и в облачную погоду. Но как только были выяснены магнитные склонения во всех местах Земли, люди вновь перешли на обычные локсодромы. Даже в XX веке локсодромия использовалась при расчёте требуемого курса при прокладке маршрута самолётов и морских судов. Со временем, когда появились приборы с достаточной вычислительной мощностью для вычисления текущего требуемого путевого угла, начали активно применять ортодромию (кратчайший путь), особенно для дальних маршрутов самолётов.
Ортодромия — кратчайшая линия между двумя точками на поверхности вращения. В картографии и навигации — название геодезической линии кратчайшего расстояния между двумя точками на поверхности земного шара, наименьший из отрезков дуги большого круга, проходящей через эти точки. В отличие от локсодромии ортодромия пересекает меридианы под разными углами. В судо- и самолётовождении, где Земля принимается за шар, ортодромия представляет собой дугу большого круга.
Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах одного диаметра Земли, можно провести только одну ортодромию.
В большинстве картографических проекций ортодромии изображаются кривыми линиями (за исключением, быть может, меридианов и экватора). Это неудобно для прокладки кратчайших маршрутов. В гномонической проекции все ортодромии изображены прямыми линиями.
Параллели (за исключением экватора) не являются ортодромиями.
локсодромия,- линия на поверхности вращения, пересекающая все меридианы под
Для сферы с первой квадратичной формой
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МЕРКАТОРСКОЙ ПРОЕКЦИИ. ПОНЯТИЕ О ПЛАНАХ
Рис2
. Удлинение параллелей будет тем значительнее, чем ближе они к полюсу.
Найдем математическую закономерность, которая определяет характер растяжения каждой параллели. Обозначим (рис. 3) радиус параллели АВ, лежащей в широте φ, через г, а радиус Земли — через R. В прямоугольном треугольнике ВОС
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.