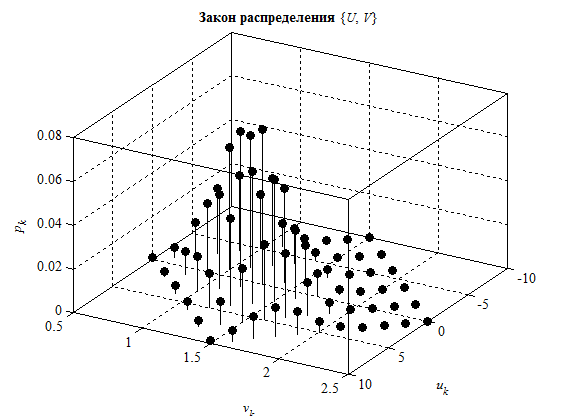
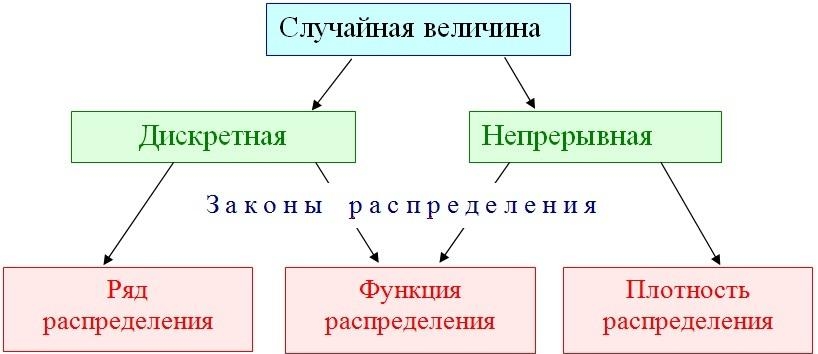
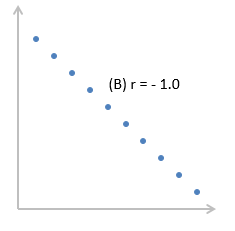
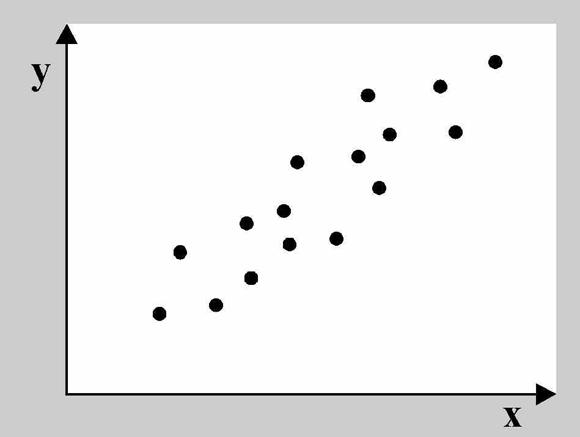
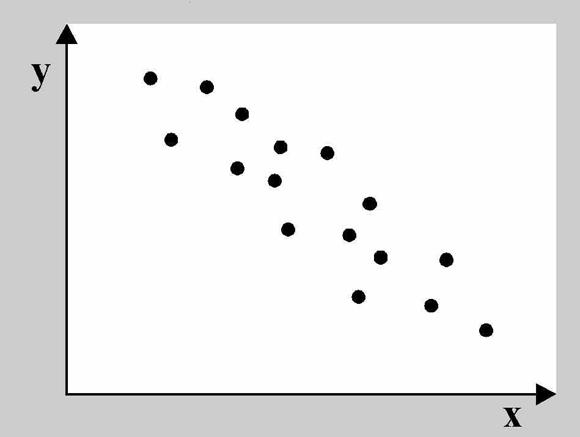
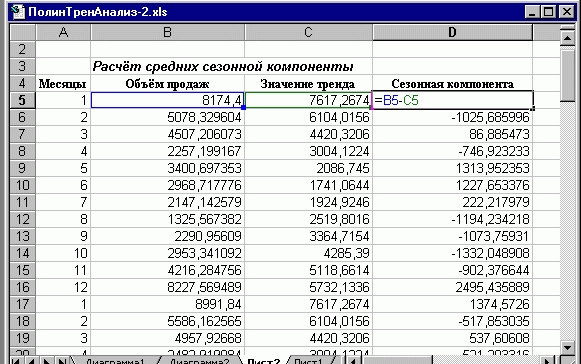
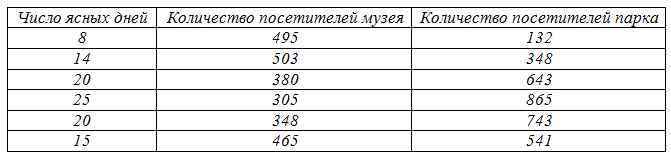
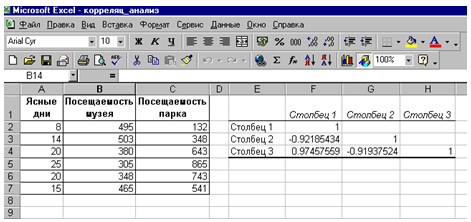
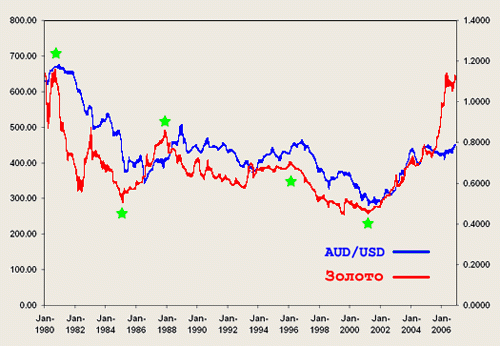
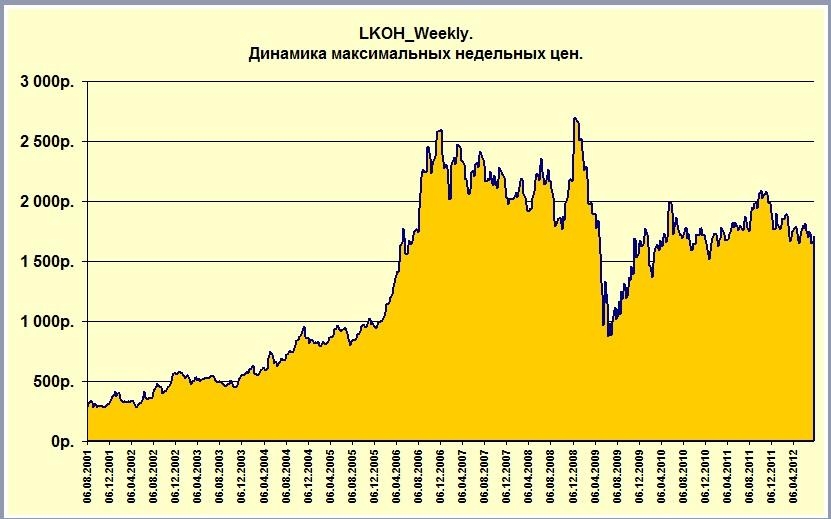
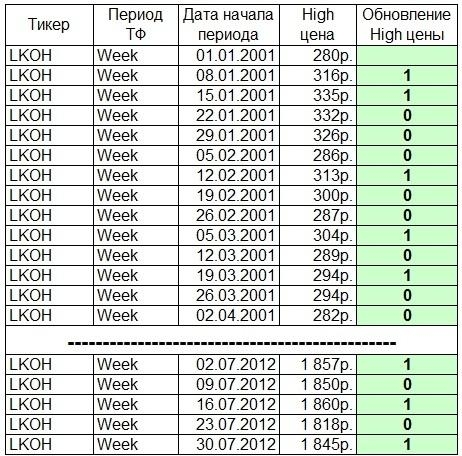
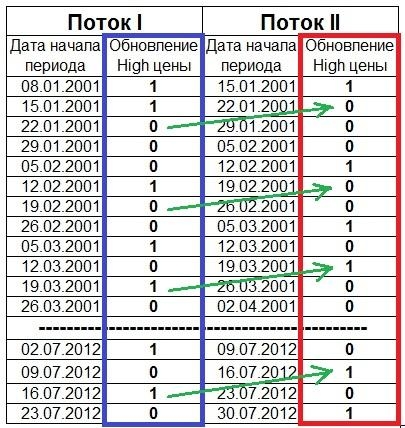
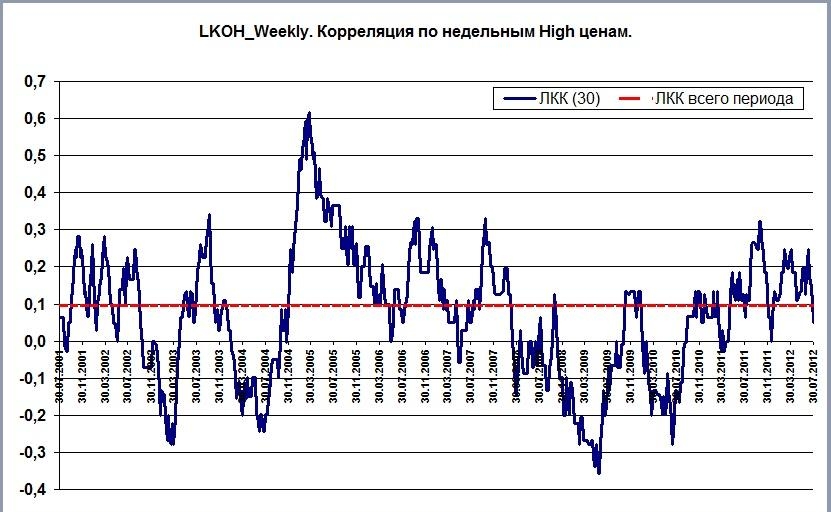
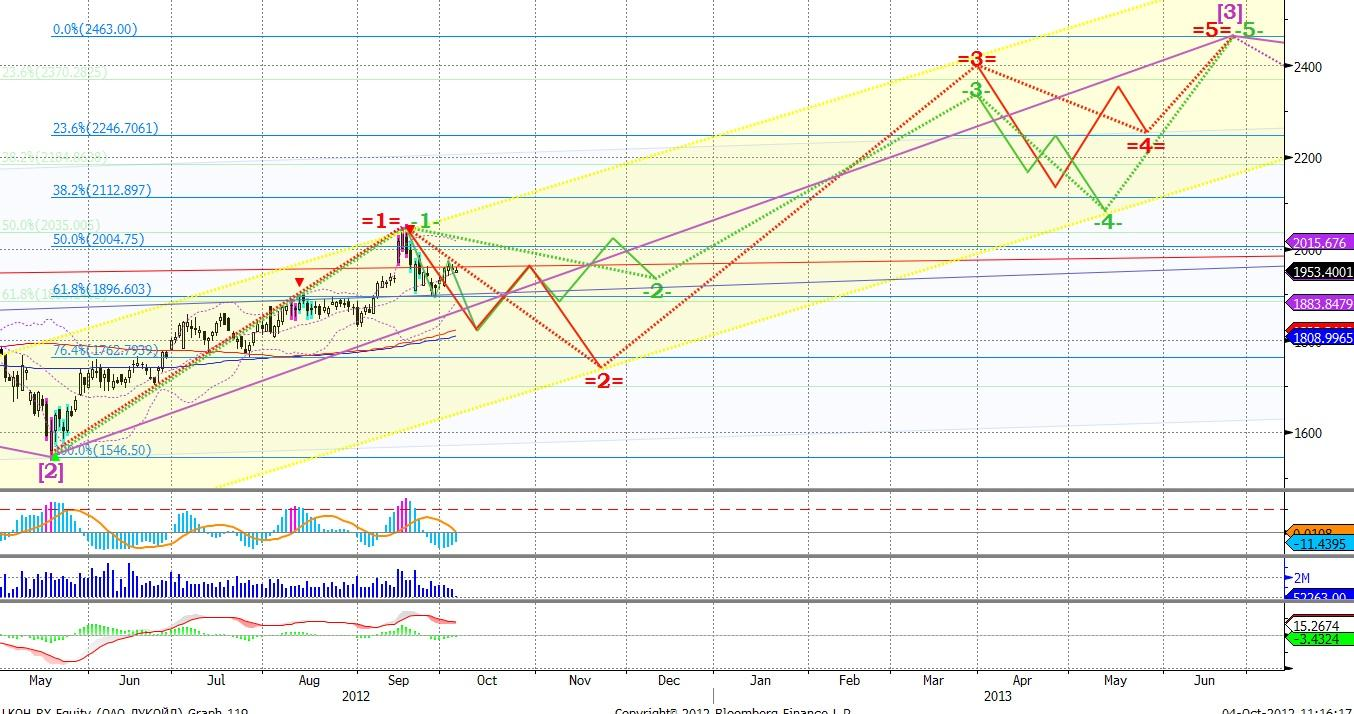
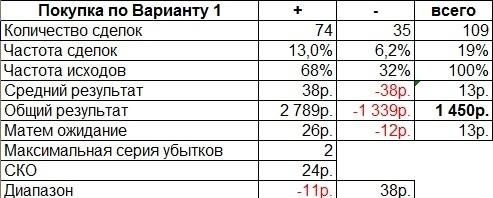
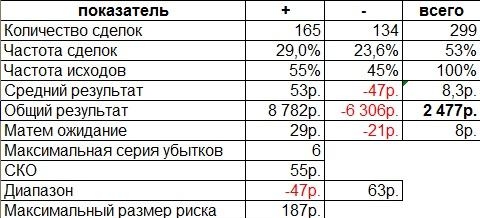
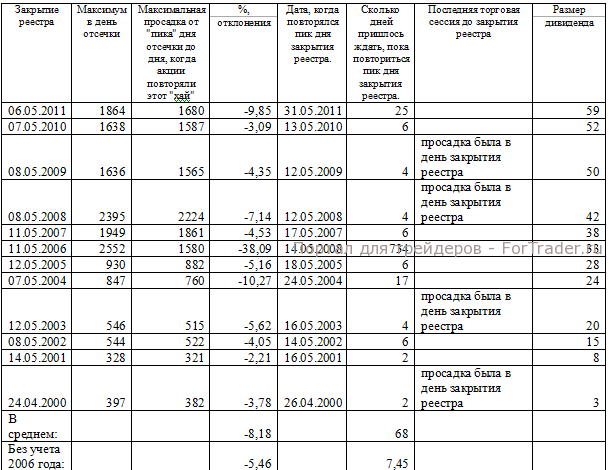
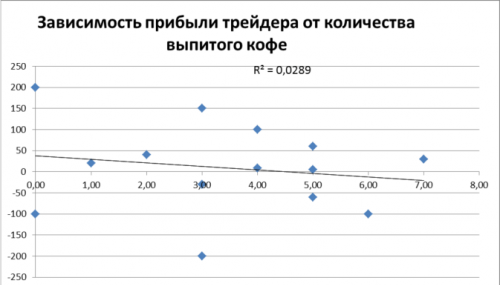
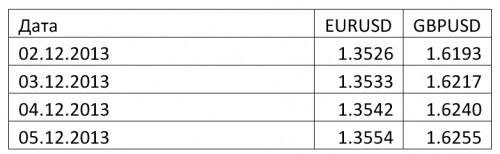
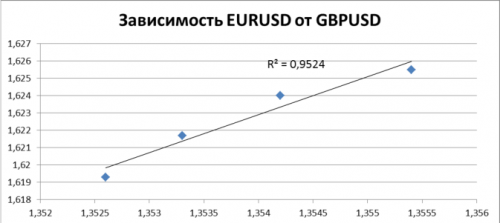
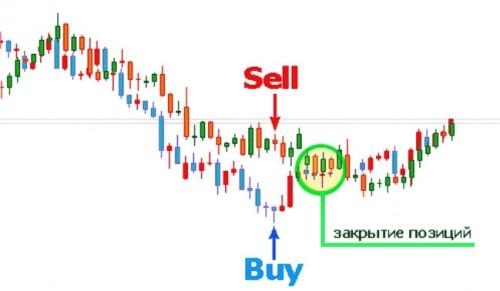
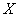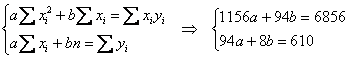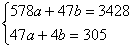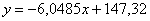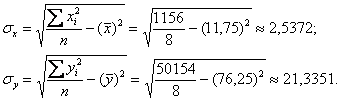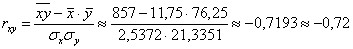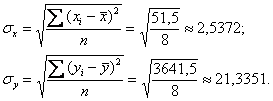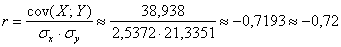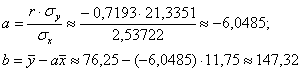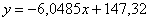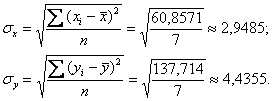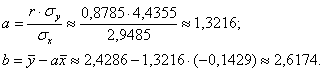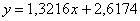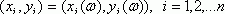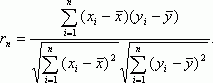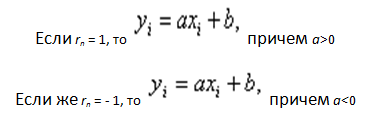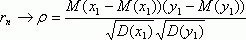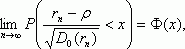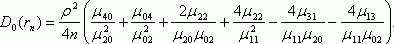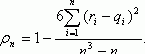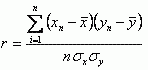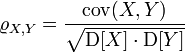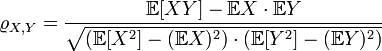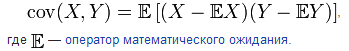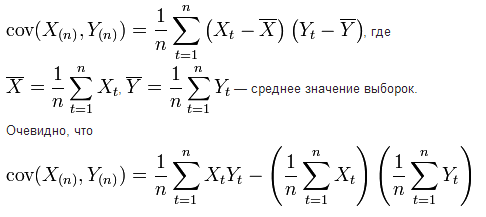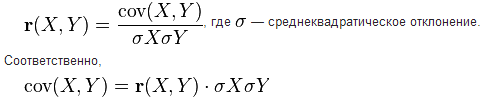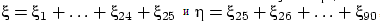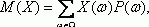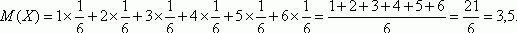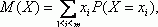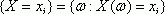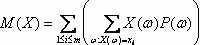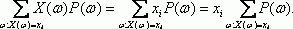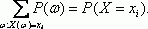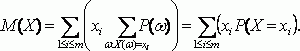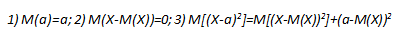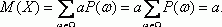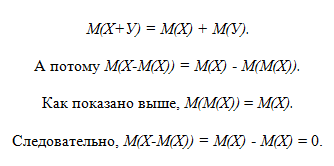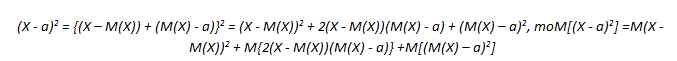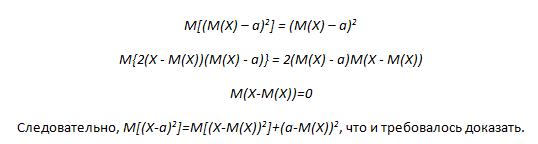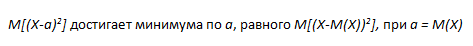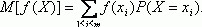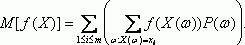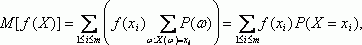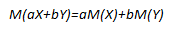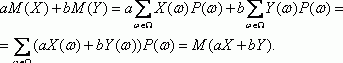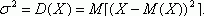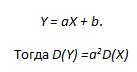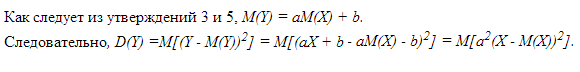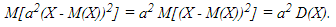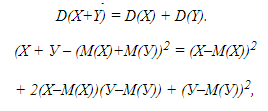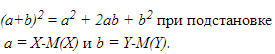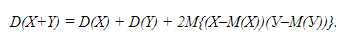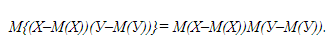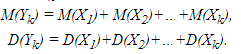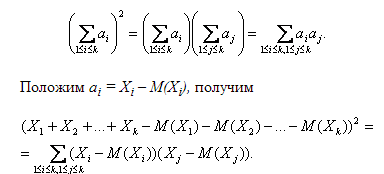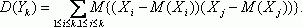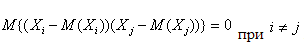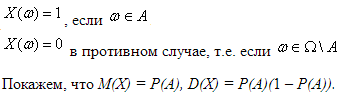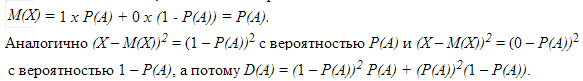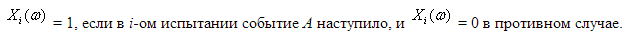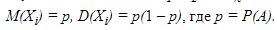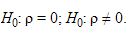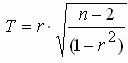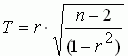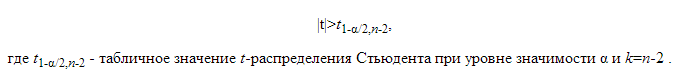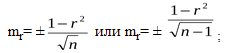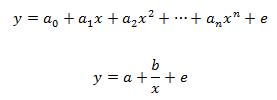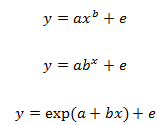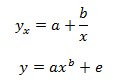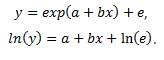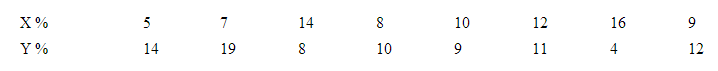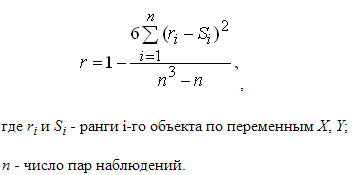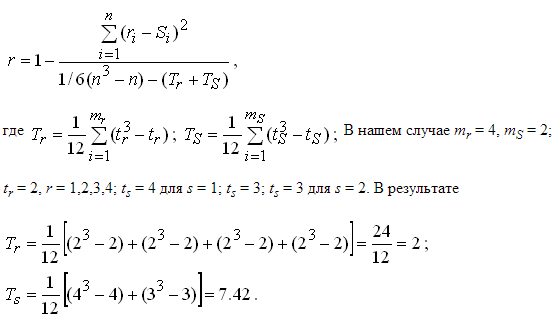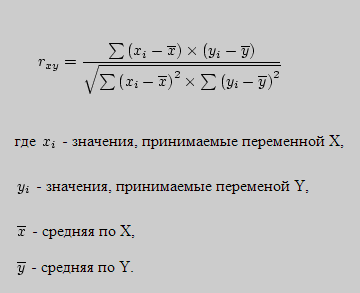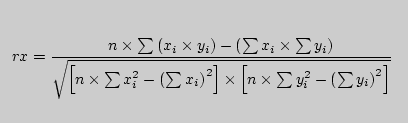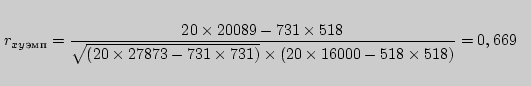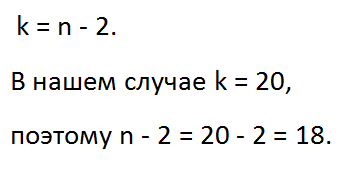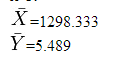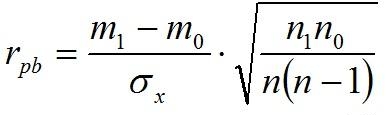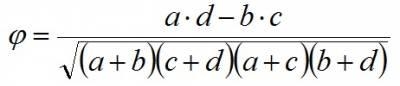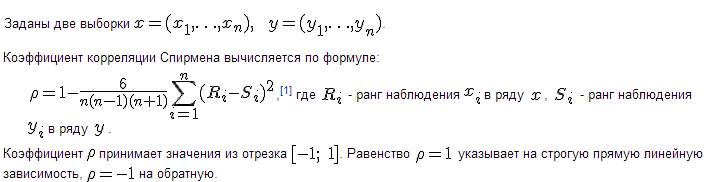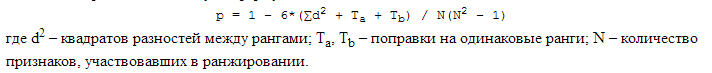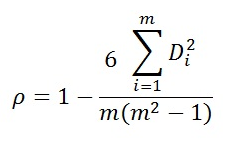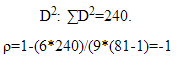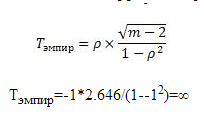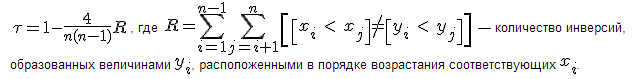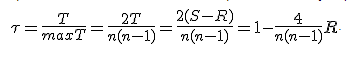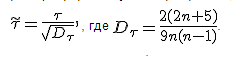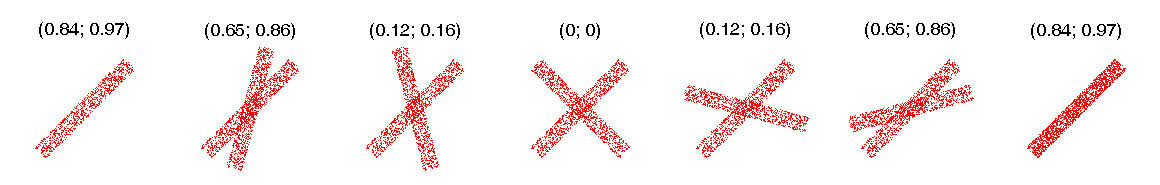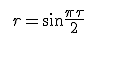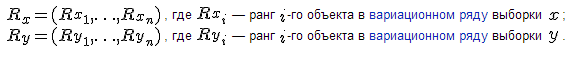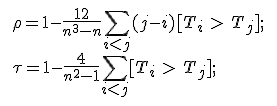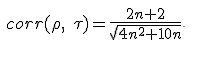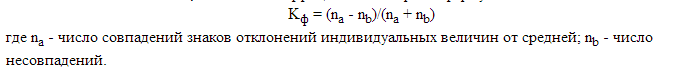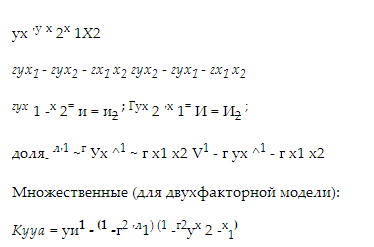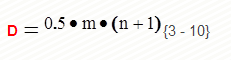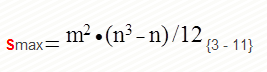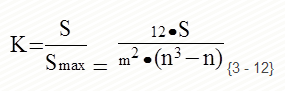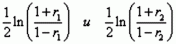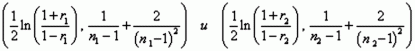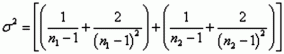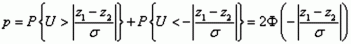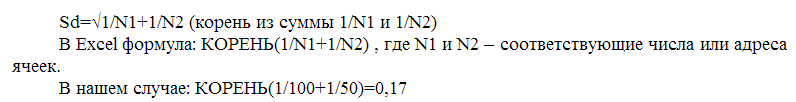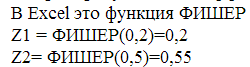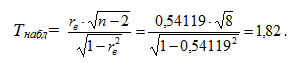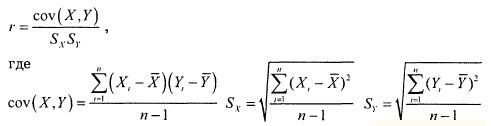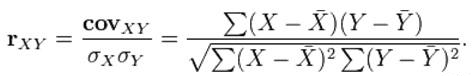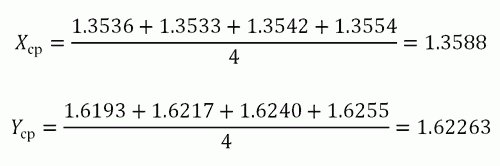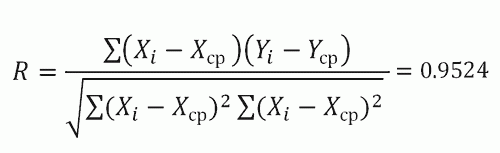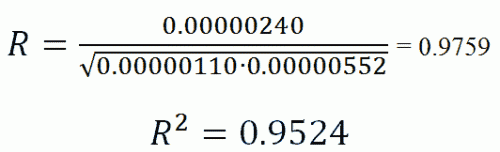Как найти коэффициент корреляции
Как найти коэффициент корреляции
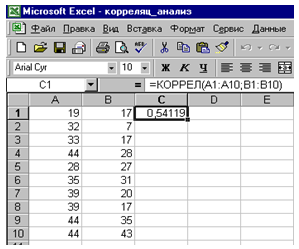
Расчет коэффициента корреляции
Методы расчета коэффициента корреляции
Размещено на www.rnz.ru
В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:
Шкала Чеддока количественной оценки степени тесноты связи
| Величина показателя тесноты связи | Характер связи |
|---|---|
| До |±0,3| | Практически отсутствует |
| |±0,3|-|±0,5| | Слабая |
| |±0,5|-|±0,7| | Умеренная |
| |±0,7|-|±1,0| | Сильная |
При интерпретации значения коэффициента линейной корреляции по направлению связи выделяют прямую и обратную. В случае наличия прямой связи с повышением или снижением величины факторного признака происходит повышение или снижение показателей результативного признака, т.е. изменение фактора и результата происходит в одном направлении. Например, повышение величины прибыли способствует росту показателей рентабельности. При наличии обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с динамикой факторного признака. Например, с повышением производительности труда уменьшается себестоимость единицы выпускаемой продукции и т.п.
Формула расчета коэффициента корреляции
В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента. Общая формула для расчета коэффициента корреляции имеет следующий вид:

Опираясь на математические свойства средней, общую формулу можно представить следующим образом, получив следующее выражение:
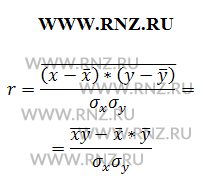
Выполняя дальнейшие преобразование, можно получить следующие формулы вычисления коэффициента корреляции Пирсона:
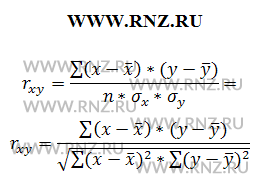
Выполняя вычисление по итоговым данным для расчета показателя корреляции, его можно рассчитать с использованием следующих формул:
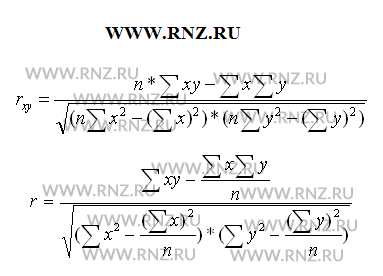
Методом расчета показателя корреляции является вычисление данного показателя с использованием его взаимосвязи с дисперсиями факторного и результативного признаков по следующей формуле:

Также показатель тесноты связи можно определить на основе его взаимосвязи с показателями уравнения регрессии, используя следующее отношение:
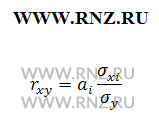
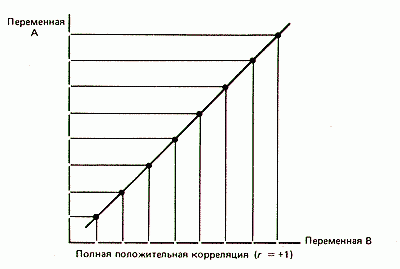
В том случае, когда rxy = 1, то это означает, что все точки (х, у) расположены на прямой и зависимость между х и у относится к функциональным. При указанном условии прямые линии регрессии совпадают. Указанное положение действует также в случае исследования трех и более показателей, если они подчинены закону нормального распределения.
Пример расчета коэффициента корреляции
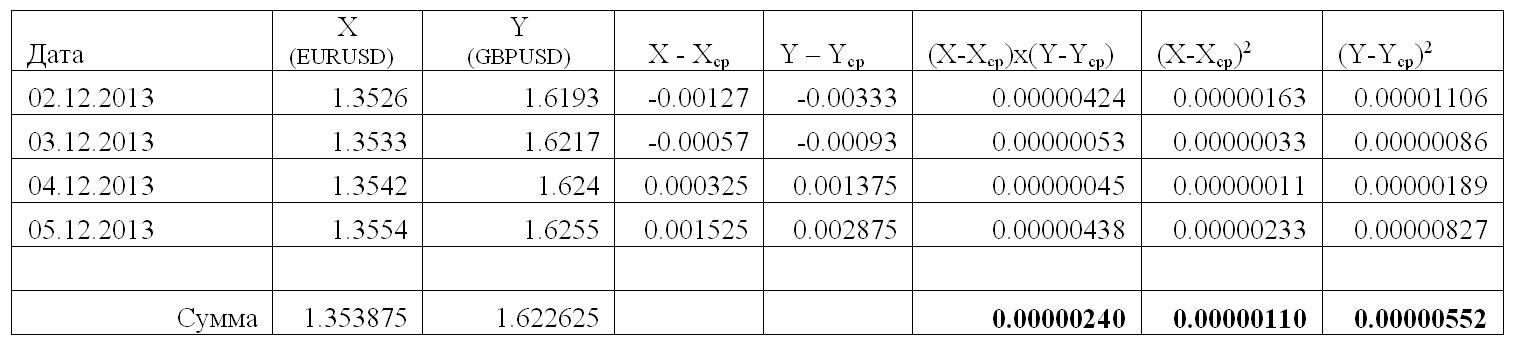
Приведем пример расчета коэффициента корреляции Пирсона для значений, приведенных в следующей таблице. Для этого используем следующие данные (пример условный):
| Значение показателя X | Значение показателя Y |
|---|---|
| 1,1 | 1,3 |
| 1,9 | 1,1 |
| 1,5 | 1,2 |
| 1,9 | 0,5 |
| 1,9 | 1,5 |
| 1,1 | 1,7 |
| 0,9 | 2 |
| 1 | 0,9 |
| 1,3 | 1,2 |
| 1,5 | 1,7 |
Количество наблюдений менее 30, поэтому в нашем примере для расчета парного коэффициента корреляции используем следующую формулу:
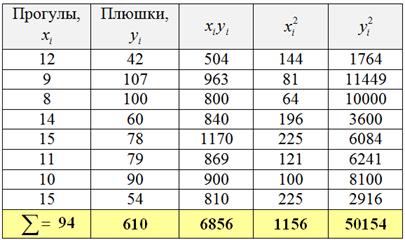
Для этого составим вспомогательную таблицу:
| № п/п | X | Y | xy | x 2 | y 2 |
|---|---|---|---|---|---|
| 1 | 1,1 | 1,3 | 1,43 | 1,21 | 1,69 |
| 2 | 1,9 | 1,1 | 2,09 | 3,61 | 1,21 |
| 3 | 1,5 | 1,2 | 1,8 | 2,25 | 1,44 |
| 4 | 1,9 | 0,5 | 0,95 | 3,61 | 0,25 |
| 5 | 1,9 | 1,5 | 2,85 | 3,61 | 2,25 |
| 6 | 1,1 | 1,7 | 1,87 | 1,21 | 2,89 |
| 7 | 0,9 | 2 | 1,8 | 0,81 | 4 |
| 8 | 1 | 0,9 | 0,9 | 1 | 0,81 |
| 9 | 1,3 | 1,2 | 1,56 | 1,69 | 1,44 |
| 10 | 1,5 | 1,7 | 2,55 | 2,25 | 2,89 |
| Итого | 14,1 | 13,1 | 17,8 | 21,25 | 18,87 |
Полученное значение коэффициента корреляции Пирсона говорит о наличии обратной связи между X и Y. Величина коэффициента корреляции Пирсона показывает, что связь между X и Y слабая.
Онлайн калькулятор расчета коэффициента корреляции
В заключении приводим небольшой онлайн калькулятор расчета коэффициента корреляции онлайн, используя который, Вы можете самостоятельно выполнить расчет значения коэффициента корреляции Пирсона и получить интерпретацию рассчитанного значения. При заполнении формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить расчет коэффициента корреляции онлайн быстро и точно. В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значения показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!
Онлайн-калькулятор расчета коэффициента корреляции:
19. Линейный коэффициент корреляции
Эта тема планировалась более 10 лет назад и вот, наконец, я здесь…. И вы здесь! И это замечательно! Даже не то слово. Это корреляционно.
О корреляции речь зашла в статьях в статьях об аналитической и комбинационной группировке, в результате чего перед нами нарисовались некоторые эмпирические показателями корреляции (прочитайте хотя бы «по диагонали»!). И сейчас на очереди линейный коэффициент корреляции, популярный настолько, что по умолчанию под коэффициентом корреляции понимают именно его. …Да, всё верно – существует довольно много разных коэффициентов корреляции. Однако всему своё время.
Материал данной темы состоит из двух уровней:
– начального, для всех – вплоть до студенток психологических и социологических факультетов, школьников, бабушек, дедушек, etc и
– продвинутого, где я разберу более редкие задачи, а некоторые даже не буду разбирать 🙂
В результате вы научитесь БЫСТРО решать типовые задачи (видео прилагается) и для самых ленивых есть калькуляторы. И пока не запамятовал, хочу порекомендовать корреляционно-регрессионный анализ для ваших научных работ и практических исследований – наряду со статистическими гипотезами, это самая настоящая находка в плане новизны и творческих изысканий.
Оглавление:
то было для «чайников», для начала достаточно…
…и в этот момент я благоговейно улыбаюсь – как здорово, что все мы здесь сегодня собрались:
Имеются выборочные данные по 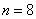
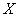
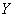
И сразу обращаю внимание, что в условии приведены несгруппированные данные. Помимо этого варианта, есть задачи, где изначально дана комбинационная таблица, и их мы тоже разберём. Сначала одно, затем другое.
1) высказать предположение о наличии и направлении корреляционной зависимости признака-результата 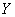
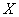
2) анализируя диаграмму рассеяния, сделать вывод о форме зависимости;
3) найти уравнение линейной регрессии 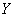
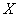
4) вычислить линейный коэффициент корреляции, сделать вывод;
5) вычислить коэффициент детерминации, сделать вывод,
и позже будет ещё 5-6 пунктов для продвинутых читателей (см. конец урока).
Решение:
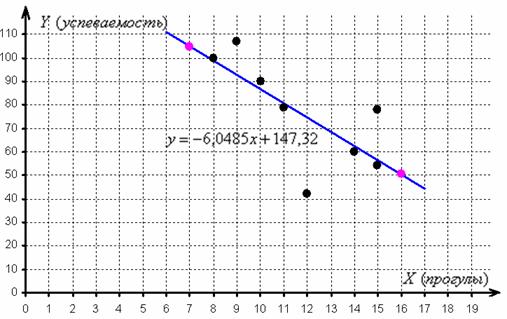
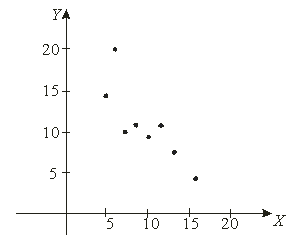
1) Прежде всего, повторим, что такое корреляционная зависимость. Очевидно, что чем больше студент прогуливает, тем более вероятно, что у него плохая успеваемость. Но всегда ли это так? Нет, не всегда. Успеваемость зависит от многих факторов. Один студент может посещать все пары, но все равно учиться посредственно, а другой – учиться неплохо даже при достаточно большом количестве прогулов. Однако общая тенденция состоит в том, что с увеличением количества прогулов средняя успеваемость студентов будет падать. Такая нежёсткая зависимость и называется корреляционной.
По своему направлению зависимость бывает прямой («чем больше, тем больше») и обратной («чем больше, тем меньше»). В данной задаче мы высказали предположение о наличии обратной корреляционной зависимости 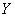
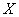
Проверить выдвинутое предположение проще всего графически, и в этом нам поможет:
диаграмма рассеяния
– это множество точек 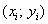
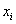
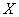
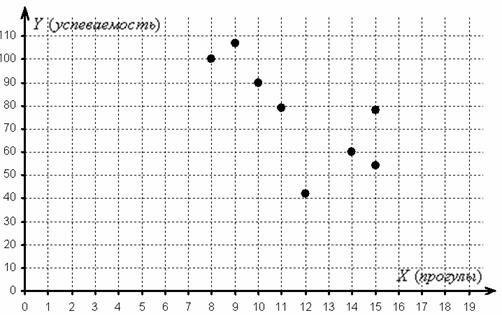
Обратите, кстати, внимание как раз на тот момент, что при одном и том же количестве прогулов (15) двое студентов имеют существенно разные результаты.
2) По диаграмме рассеяния хорошо видно, что с увеличением числа прогулов успеваемость преимущественно падает, что подтверждает наличие обратной корреляционной зависимости успеваемости от количества прогулов. Более того, почти все точки «выстроились» примерно по прямой, что даёт основание предположить, что данная зависимость близкА к линейной.
И здесь я анонсирую дальнейшие действия: сейчас нам предстоит найти уравнение прямой, ТАКОЙ, которая проходит максимально близко к эмпирическим точкам, а также оценить тесноту линейной корреляционной зависимости – насколько близко расположены эти точки к построенной прямой.
Технически существует два пути решения:
– сначала найти уравнение прямой и затем оценить тесноту зависимости;
– сначала найти тесноту и затем составить уравнение.
В практически задачах чаще встречается второй вариант, но я начну с первого, он более последователен. Построим:
3) уравнение линейной регрессии  на
на 
Это и есть та самая оптимальная прямая 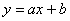
Обратите внимание, что в отличие от задач урока МНК у нас появился дополнительный столбец 
Коэффициенты функции 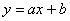
Сократим оба уравнения на 2, всё попроще будет:
Систему решим по формулам Крамера: 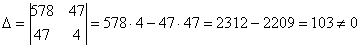
И проверка forever, подставим полученные значения 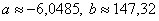
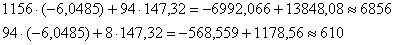
в результате получены соответствующие правые части, значит, система решена верно.
Таким образом, искомое уравнение регрессии:
Данное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а». И обратите особое внимание, что эта функция возвращает нам средние (среднеожидаемые) значения «игрек» для различных значений «икс».
Почему это регрессия именно « 
Найдём пару удобных точек для построения прямой: 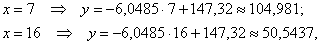
отметим их на чертеже (малиновый цвет) и проведём линию регрессии:
Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью него можно интерполировать (оценить) неизвестные промежуточные значения, так при количестве прогулов 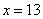
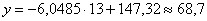
И, конечно, осуществимо прогнозирование, так при 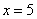
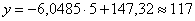
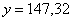
Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе эмпирические точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак 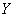
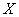
Прояснить данный вопрос нам поможет:
4) линейный коэффициент корреляции
Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной корреляции Пирсона 🙂
– «выборочный» – потому что мы рассматриваем выборочную совокупность;
– «линейный» – потому что он оценивает тесноту линейной корреляционной зависимости;
– «пАрной» – потому что у нас два признака (бывает хуже);
– и «Пирсона» – в честь английского статистика Карла Пирсона, это он автор понятия «корреляция».
И в зависимости от фантазии автора задачи вам может встретиться любая комбинация этих слов. Теперь нас не застанешь врасплох, Карл.
Линейный коэффициент корреляции вычислим по формуле: 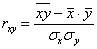
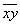
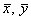
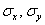
Осталось разгрести всё это добро 🙂 Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние значения:
Стандартные отклонения найдём как корни из соответствующих дисперсий, вычисленных по формуле:
Таким образом, коэффициент корреляции:
И расшифровка: коэффициент корреляции может изменяться в пределах 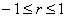
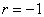
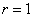
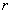
Для оценки тесноты связи будем использовать уже знакомую шкалу Чеддока: 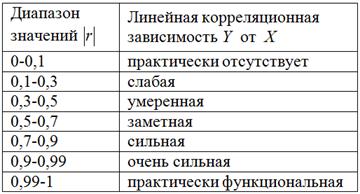
При этом если 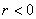
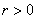
В нашем случае 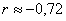
Линейный коэффициент корреляции – это частный аналог эмпирического корреляционного отношения. Но в отличие от отношения, он показывает не только тесноту, но ещё и направление зависимости, ну и, конечно, здесь определена её форма (линейная).
5) Коэффициент детерминации
– это частный аналог эмпирического коэффициента детерминации – есть квадрат коэффициента корреляции:
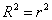
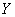
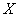
В нашей задаче:
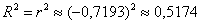
! Примечание: но это не является какой-то «абсолютной истиной», это всего лишь оценка в рамках построенной модели.
Задание выполнено
Но точку ставить рано. Теперь второй способ решения, в котором мы сначала находим коэффициент корреляции, а затем уравнение регрессии.
Линейный коэффициент корреляции вычислим по формуле: 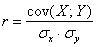
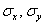
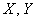
Член в числителе называют корреляционным моментом или коэффициентом ковариации (совместной вариации) признаков, он рассчитывается следующим образом: 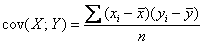
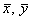
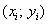
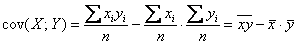
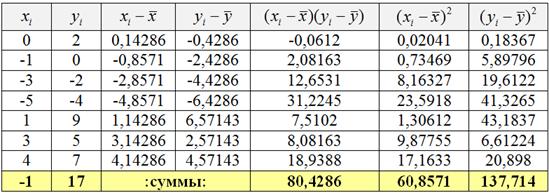
Заполним расчётную таблицу: 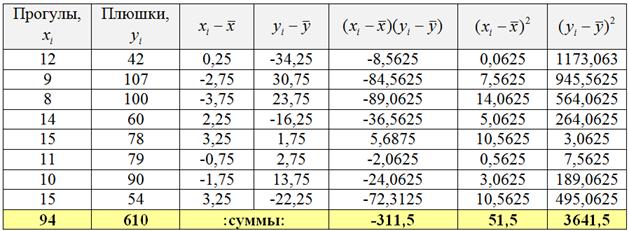
При этом сначала рассчитываем левые нижние суммы и средние значения признаков:
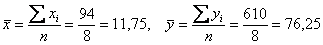
Вычислим коэффициент ковариации: 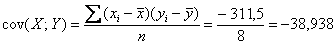
Стандартные отклонения вычислим как квадратные корни из дисперсий:
Таким образом, коэффициент корреляции:
И если нам известны значения 
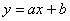
Таким образом, искомое уравнение:
Теперь смотрим ролик о том, как это всё быстро подсчитать и построить:

Если под рукой нет Экселя, ничего страшного, разобранную задачу не так трудно решить в обычной клетчатой тетради. А если Эксель есть и времени нет, то можно воспользоваться моим калькулятором. Да, вы можете найти аналоги в Сети, но, скорее всего, это будет не совсем то, что нужно 😉
Какой способ решения выбрать? Ориентируйтесь на свой учебный план и методичку. По умолчанию лучше использовать 2-й способ, он несколько короче, и, вероятно, потому и встречается чаще. Кстати, если вам нужно построить ТОЛЬКО уравнение регрессии, то уместен 1-й способ, ибо там мы находим это уравнение в первую очередь.
Следующая задача много-много лет назад была предложена курсантам местной школы милиции (тогда ещё милиции), и это чуть ли не первая задача по теме, которая встретилась в моей профессиональной карьере. И я безмерно рад предложить её вам сейчас, разумеется, с дополнительными пунктами:)
В результате 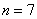

…да, числа могут быть и отрицательными.
По данным наблюдений вычислить линейный коэффициент корреляции и детерминации, сделать выводы. Найти параметры линейной регрессии 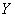
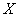
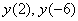
Из условия следует, что признак 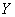
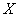
Все данные уже забиты в Эксель, и вам осталось аккуратно выполнить расчёты. В образце я решил задачу вторым, более распространённым способом. И, конечно же, выполните проверку первым путём.
Следует отметить, что в целях экономии места я специально подобрал задачи с малым объёмом выборки. На практике обычно предлагают 10 или 20 пар чисел, реже 30, и максимальная выборка, которая мне встречалась в студенческих работах – 100. …Соврал малость, 80.
И сейчас я вас приглашаю на следующий урок, назову его Уравнение линейной регрессии, где мы рассчитаем и найдём всё то же самое – только для комбинационной группировки. Плюс немного глубже копнём уравнения регрессии (их два).
Решения и ответы:
Пример 68. Решение: вычислим суммы и средние значения признаков 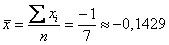
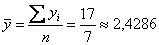
Вычислим коэффициент ковариации: 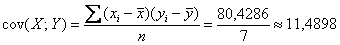
Вычислим средние квадратические отклонения:
Вычислим коэффициент корреляции: 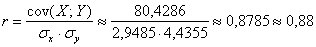
Вычислим коэффициент детерминации:
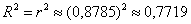
Вычислим коэффициенты линейной регрессии 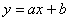
Таким образом, искомое уравнение регрессии:
Данное уравнение показывает, что с увеличением значения «икс» на одну единицу «игрек» увеличивается в среднем примерно на 1,32 единицы (смысл коэффициента «а»).
При 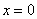
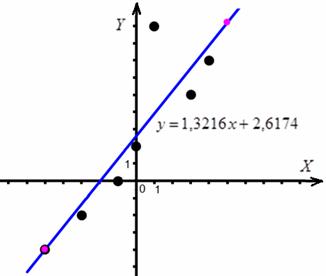
Найдём пару точек для построения прямой: 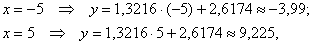
и выполним чертёж:
Вычислим:
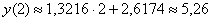
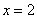
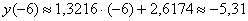
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Линейный коэффициент корреляции Пирсона
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
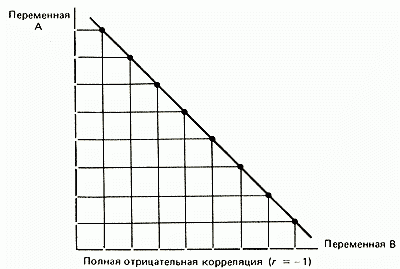
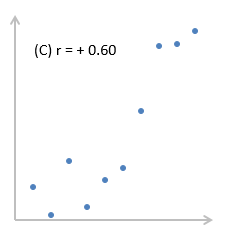
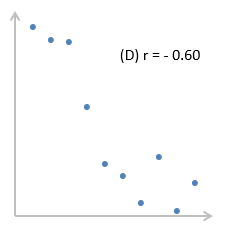
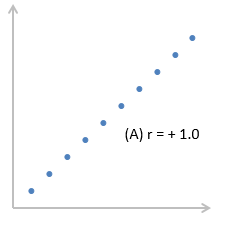
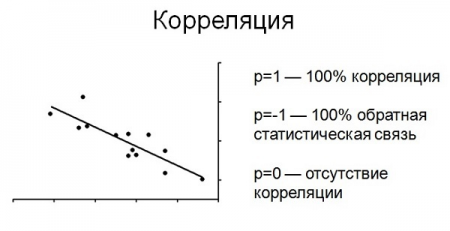
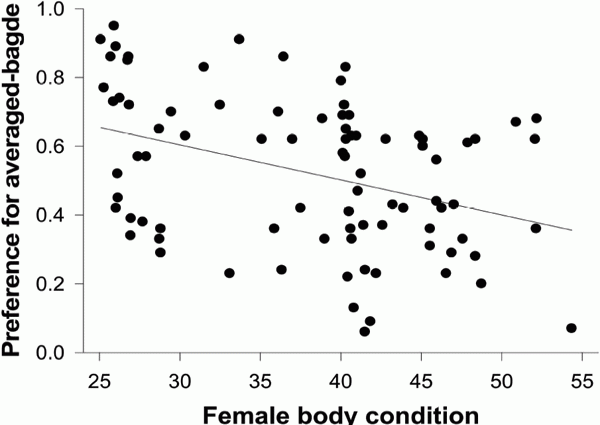
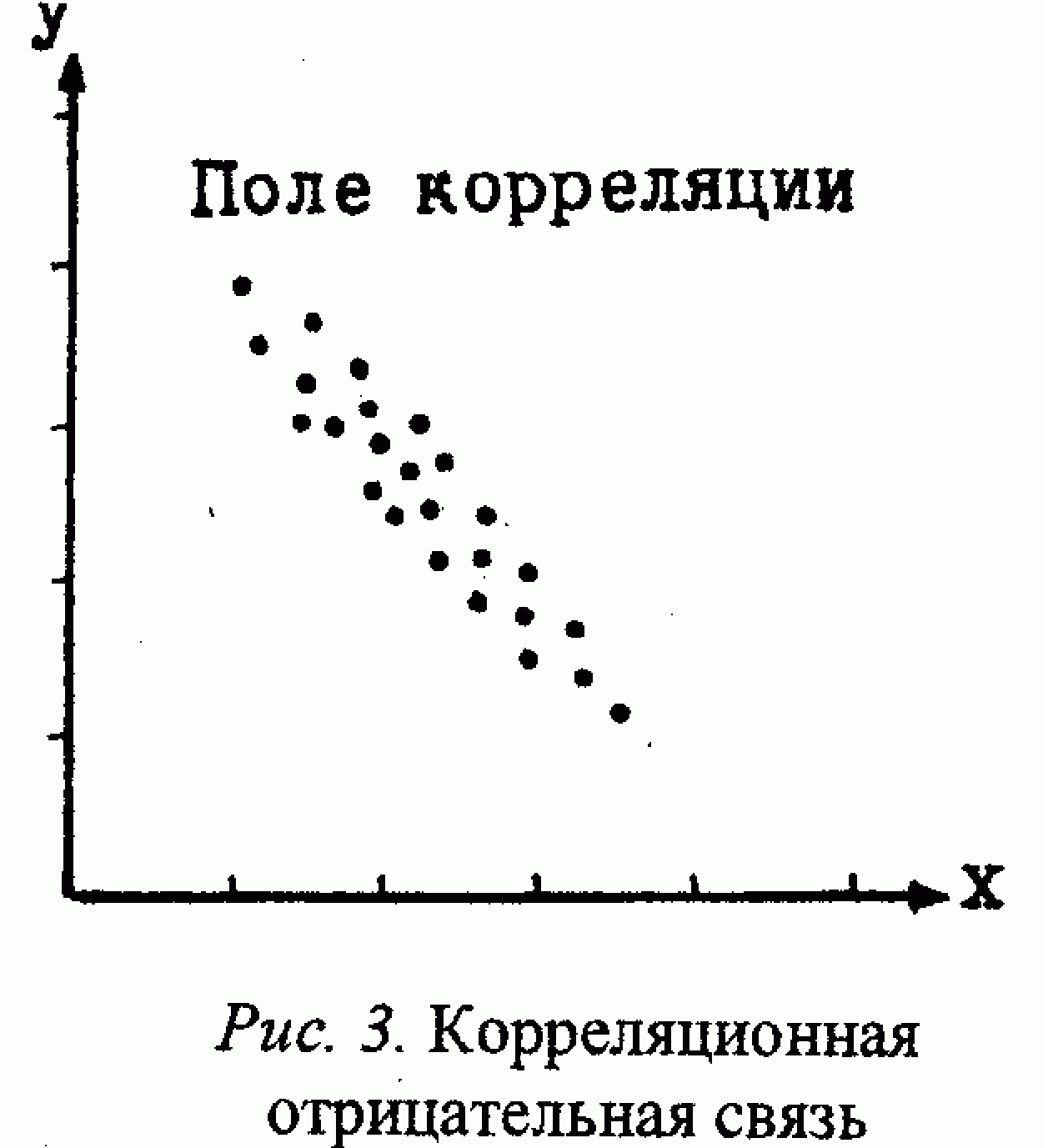
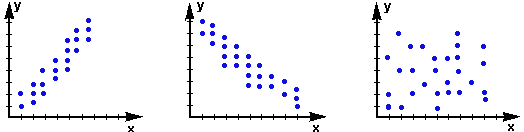
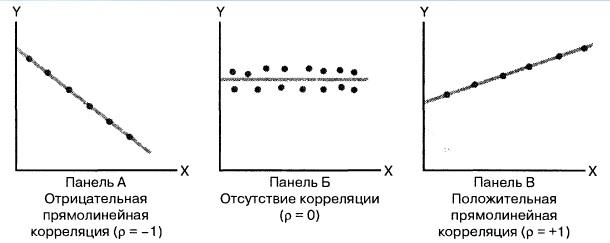
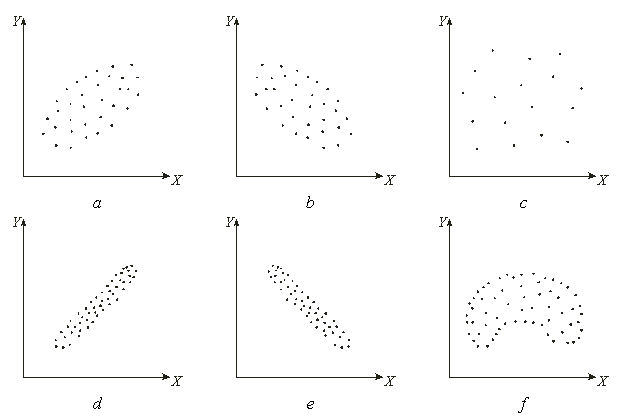
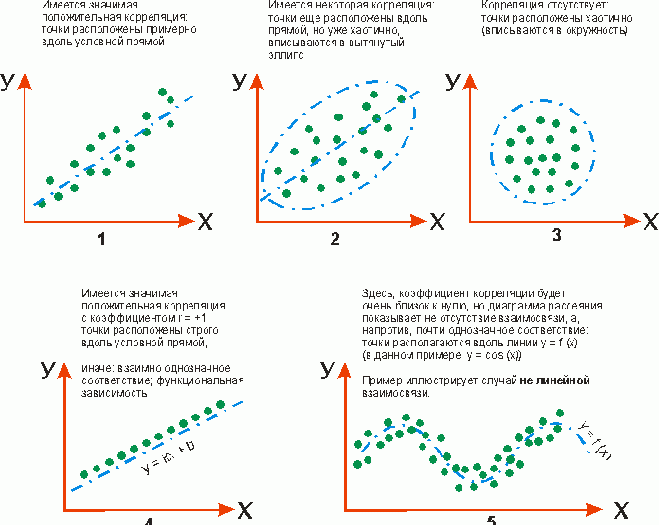
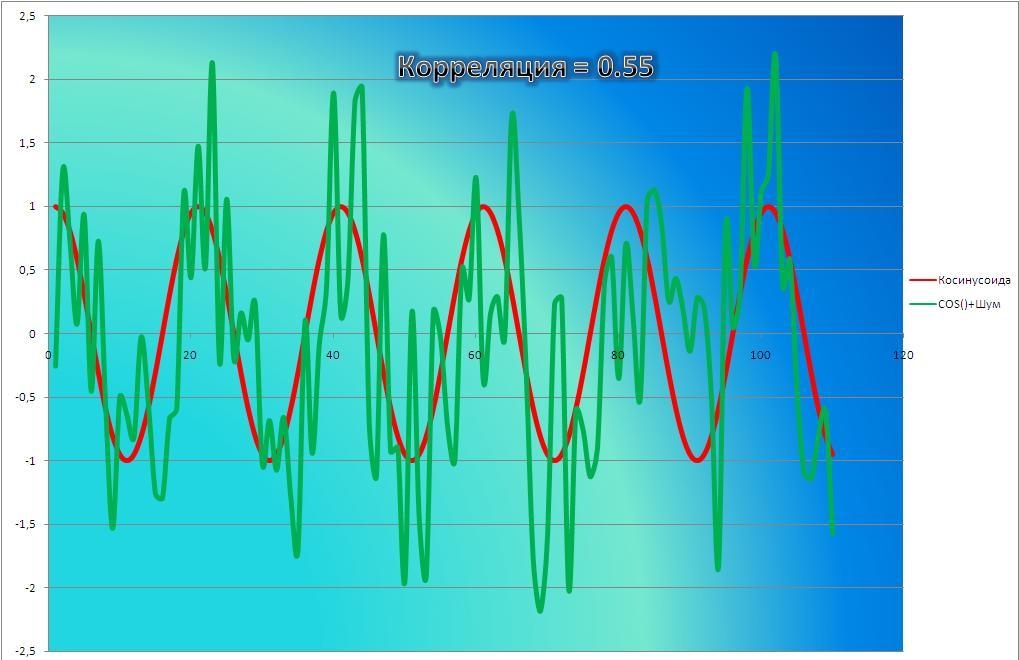
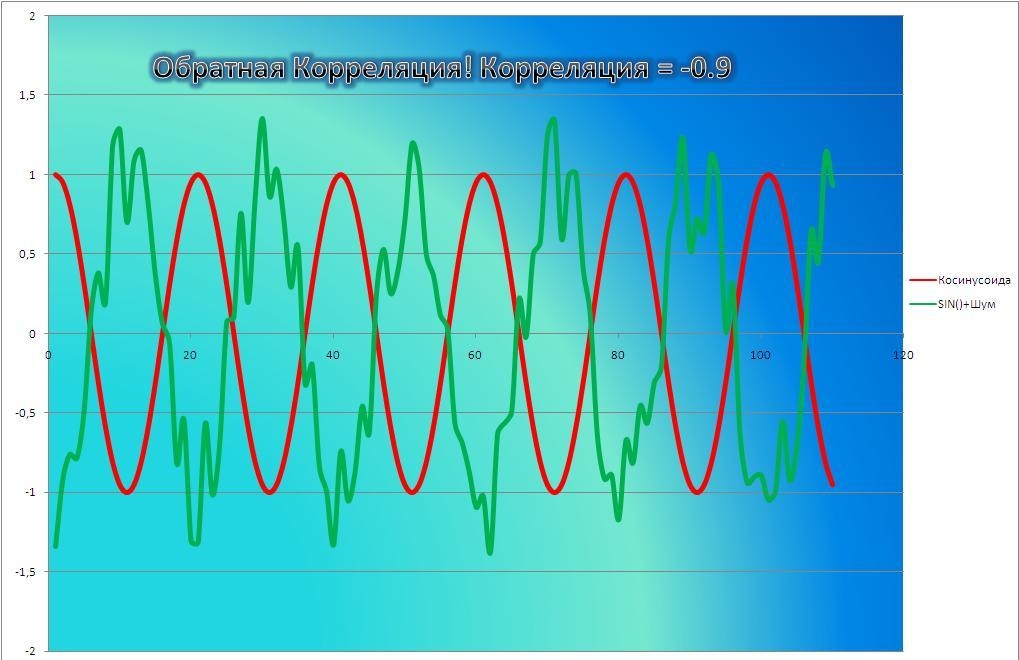
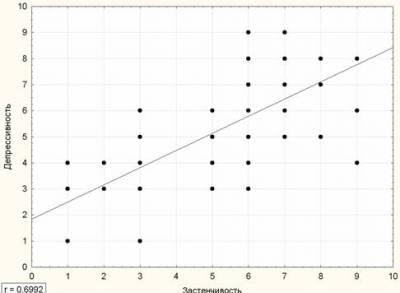
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r 2 = 0,01 или 1%, при r = 0,5 r 2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
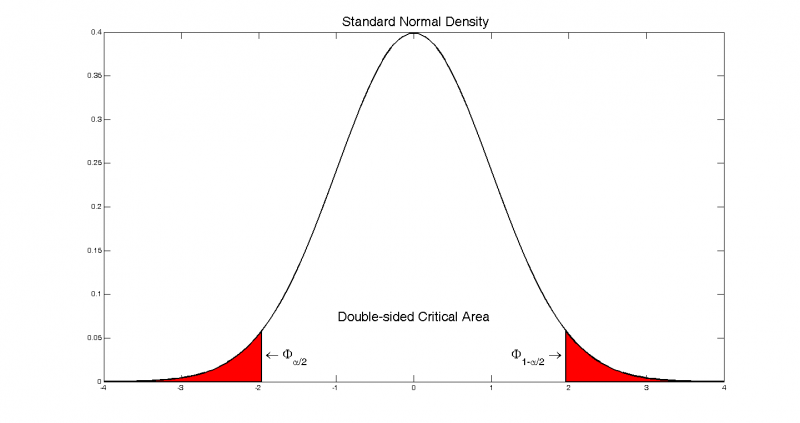
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
Распределение z для тех же r имеет следующий вид.
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
Нижняя граница z:
Верхняя граница z:
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Верхняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
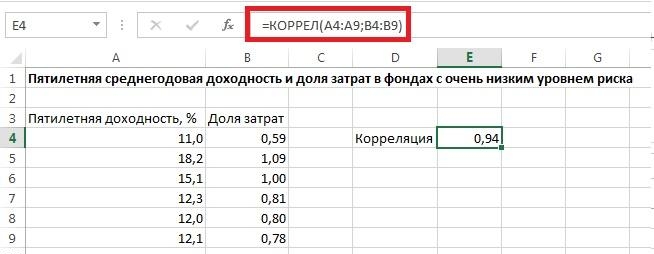
Как посчитать коэффициент корреляции в Excel
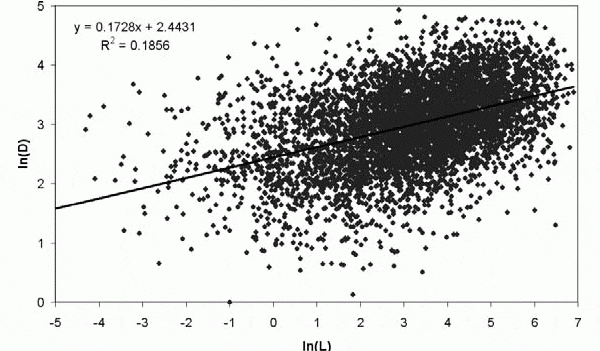
Корреляционный анализ в Excel лучше начинать с визуализации.
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
Коэффициент корреляции
Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение коэффициента корреляции
Содержание
Для чего нужен коэффициент корреляции?
Связь, которая существует между случайными величинами разной природы, например, между величиной Х и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь). В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
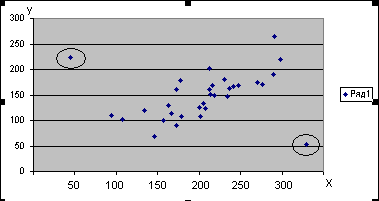
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину Хi (число страниц) и Yi (средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси Х и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (Хi, Yi) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.
Термин «корреляция» означает «связь». В эконометрике этот термин обычно используется в сочетании «коэффициенты корреляции». Рассмотрим линейный и непараметрические парные коэффициенты корреляции. Обсудим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов:
Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, как известно, называется число:
Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи. Если случайные векторанезависимы и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при безграничном возрастании объема выборки (сходимость по вероятности):
Более того, выборочный коэффициент корреляции является асимптотически нормальным. Это означает, что
Она имеет довольно сложное выражение:
где теоретические центральные моменты порядка k и m:
Коэффициенты корреляции типа rn используются во многих алгоритмах многомерного статистического анализа. В теоретических рассмотрениях часто считают, что случайные вектора имеют двумерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных. Почему же распространено представление о двумерном нормальном распределении? Дело в том, что теория в этом случае проще. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если
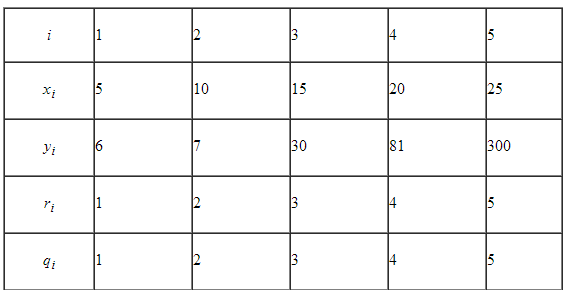
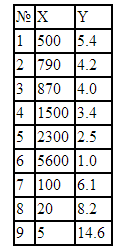
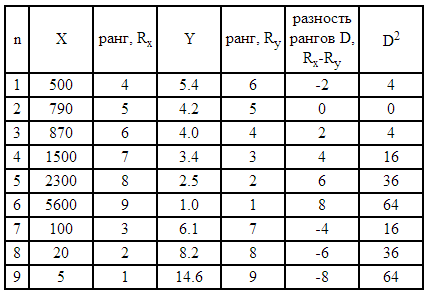
Для расчета непараметрического коэффициента ранговой корреляции Спирмена необходимо сделать следующее. Для каждого xi рассчитать его ранг ri в вариационном ряду, построенном по выборке Для каждого yi рассчитать его ранг qi в вариационном ряду, построенном по выборке Для набора из n пар (ri, qi), i=1,2. n вычислить линейный коэффициент корреляции. Он называется коэффициентом ранговой корреляции, поскольку определяется через ранги.В качестве примера рассмотрим данные из таблицы:
Для данных таблицы коэффициент линейной корреляции равен 0,83, непосредственной линейной связи нет. А вот коэффициент ранговой корреляции равен 1, поскольку увеличение одной переменной однозначно соответствует увеличению другой переменной. Во многих экономических задачах, например, при выборе инвестиционных проектов, достаточно именно монотонной зависимости одной переменной от другой.
Поскольку суммы рангов и их квадратов нетрудно подсчитать, то коэффициент ранговой корреляции Спирмена равен
Отметим, что коэффициент ранговой корреляции Спирмена остается постоянным при любом строго возрастающем преобразовании шкалы измерения результатов наблюдений. Другими словами, он является адекватным в порядковой шкале, как и другие ранговые статистики, например, статистики Вилкоксона, Смирнова, типа омега-квадрат для проверки однородности независимых выборок.
Широко используется также коэффициент ранговой корреляции Кендалла, коэффициент ранговой конкордации Кендалла и Б. Смита и др. Наиболее подробное обсуждение этой тематики содержится в монографии, необходимые для практических расчетов таблицы имеются в справочнике. Дискуссия о выборе вида коэффициентов корреляции продолжается до настоящего времени.
Формула и переменные коэффициента корреляции
Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными. Он вычисляется следующим образом:
— если коэффициент корреляции близок к 1, то между переменными наблюдается положительная корреляция. Иными словами, отмечается высокая степень связи входной и выходной переменных. В данном случае, если значения входной переменной x будут возрастать, то и выходная переменная также будет увеличиваться;
— промежуточные значения, близкие к 0, будут указывать на слабую корреляцию между переменными и, соответственно, низкую зависимость. Иными словами, поведение входной переменной x не будет совсем (или почти совсем) влиять на поведение y.
Коэффициент корреляции равен квадратному корню коэффициента детерминации, поэтому может применяться для оценки значимости регрессионных моделей. Очевидно, что если корреляция между переменными высокая, то, зная поведение входной переменной, проще предсказать поведение выходной, и полученное предвидение будет точнее (говорят, что входная переменная хорошо «объясняет» выходную). Однако, чем выше корреляция наблюдается между переменными, тем очевиднее связь между ними, например, взаимозависимость между ростом и весом людей, однако данное соотношение настолько очевидно, что не представляет интереса.
где символ Е обозначает мат ожидание.
Предполагается, что все математические ожидания Е в правой части данного выражения определены.
Случайные величины, имеющие нулевую ковариацию, называются некоррелированными. Независимые случайные величины всегда некоррелированы, но не наоборот. Обсудим достоинства и недостатки ковариации, как величины, характеризующей зависимость двух случайных величин.
1. Если ковариация отлична от нуля, то случайные величины зависимы. Чтобы судить о наличии зависимости согласно любому из определений независимости, требуется знать совместное распределение пары случайных величин. Но найти совместное распределение часто бывает сложнее, чем посчитать мат. ожидание произведения случайных величин. Если нам повезёт, и мат ожидание произведения случайных величин не будет равняться произведению их математических ожиданий, мы скажем, что случайные величины зависимы, не находя их совместного распределения! Это очень хорошо.
Нужно как-то нормировать ковариацию, получив из неё «безразмерную» величину, абсолютное значение которой: не менялось бы при умножении случайных величин на число и свидетельствовало бы о «силе зависимости» случайных величин.
Бывают гораздо более слабые зависимости. Так, если по последовательности независимых случайных величин построить величины:
то эти величины зависимы, но очень «слабо»: через единственное общее слагаемое Е25. Сильно ли зависимы число гербов в первых двадцати пяти подбрасываниях монеты и число гербов в испытаниях с двадцать пятого по девяностое? Итак, следующая величина есть всего лишь ковариация, нормированная нужным образом.
Свойства мартиц ковариации:
Определение 1. Мат ожиданием случайной величины Х называется число:
Пример. Вычислим мат ожидание числа, выпавшего на верхней грани игрального кубика. Непосредственно из определения 1 следует, что
Утверждение 2. Пусть случайная величина Х принимает значения х1, х2,…, хm. Тогда справедливо равенство:
может состоять из нескольких элементарных событий. Иногда соотношение принимают как определение мат ожидания. Однако с помощью определения, как показано далее, более легко установить свойства мат. ожидания, нужные для построения вероятностных моделей реальных явлений, чем с помощью соотношения. Для доказательства соотношения сгруппируем в члены с одинаковыми значениями случайной величины:
Поскольку постоянный множитель можно вынести за знак суммы, то
По определению вероятности события:
С помощью двух последних соотношений получаем требуемое:
Понятие мат ожидания в вероятностно-статистической теории соответствует понятию центра тяжести в механике. Поместим в точки х1, х2,…, хm на числовой оси массы P(X=x1), P(X=x2),…, P(X=xm) соответственно. Тогда равенство показывает, что центр тяжести этой системы материальных точек совпадает с мат ожиданием, что показывает естественность определения.
Для доказательства рассмотрим сначала случайную величину, являющуюся постоянной, т.е. функция отображает пространство элементарных событий в единственную точку. Поскольку постоянный множитель можно выносить за знак суммы, то
Из сказанного вытекает
поскольку второе слагаемое в равенстве 3) всегда неотрицательно и равно 0 только при указанном значении а.
Для доказательства сгруппируем в правой части равенства, определяющего мат ожидание, члены с одинаковыми значениями:
Пользуясь тем, что постоянный множитель можно выносить за знак суммы, и определением вероятности случайного события, получаем:
что и требовалось доказать.
С помощью определения мат. ожидания и свойств символа суммирования получаем цепочку равенств:
Выше показано, как зависит мат. ожидание от перехода к другому началу отсчета и к другой единице измерения, а также к функциям от случайных величин. Полученные результаты постоянно используются в технико-экономическом анализе, при оценке финансово-хозяйственной деятельности предприятия, при переходе от одной валюты к другой во внешнеэкономических расчетах, в нормативно-технической документации и др. Рассматриваемые результаты позволяют применять одни и те же расчетные формулы при различных параметрах масштаба и сдвига.
3. Дисперсия. Мат ожидание показывает, вокруг какой точки группируются значения случайной величины. Необходимо также уметь измерить изменчивость случайной величины относительно мат ожидания.
Определение 5. Дисперсией случайной величины Х называется число
Поскольку постоянный множитель можно выносить за знак суммы, то
Утверждение 8 показывает, в частности, как меняется дисперсия результата наблюдений при изменении начала отсчета и единицы измерения. Оно дает правило преобразования расчетных формул при переходе к другим значениям параметров сдвига и масштаба.
Утверждение 9. Если случайные величины Х и У независимы, то дисперсия их суммы Х+У равна сумме дисперсий. Для доказательства воспользуемся тождеством:
которое вытекает из известной формулы элементарной алгебры:
Из утверждений 3 и 5 и определения дисперсии следует, что:
Согласно утверждению 6 из независимости Х и У вытекает независимость Х-М(Х) и У-М(У). Из утверждения 7 следует, что:
Из утверждения 3 правая часть последнего равенства равна 0, откуда с учетом двух предыдущих равенств и следует заключение утверждения 9.
Соотношения, сформулированные в утверждении 10, являются основными при изучении выборочных характеристик, поскольку результаты наблюдений или измерений, включенные в выборку, обычно рассматриваются в математической статистике, теории принятия решений и эконометрике как реализации независимых случайных величин.
Для любого набора числовых случайных величин (не только независимых) мат. ожидание их суммы равно сумме их математических ожиданий. Это утверждение является обобщением утверждения 5. Строгое доказательство легко проводится методом математической индукции.
При выводе формулы для дисперсии D(Yk) воспользуемся следующим свойством символа суммирования:
Воспользуемся теперь тем, что мат ожидание суммы равно сумме математических ожиданий:
Как показано при доказательстве утверждения 9, из попарной независимости рассматриваемых случайных величин следует, что
Следовательно, в сумме (8) остаются только члены с i=j, а они равны как раз D(Xi). Полученные в утверждениях 8-10 фундаментальные свойства таких характеристик случайных величин, как мат. ожидание и дисперсия, постоянно используются практически во всех вероятностно-статистических моделях реальных явлений и процессов.
Пример 9. Рассмотрим событие А и случайную величину Х такую, что
Вынося общий множитель, получаем, что:
Пример 10. Рассмотрим k независимых испытаний, в каждом из которых некоторое событие А может наступить, а может и не наступить. Введем случайные величины X1, X2,…, Xk следующим образом:
Тогда случайные величины X1, X2,…, Xk попарно независимы. Как показано в примере 9
Свойства коэффициента корреляции
Коэффициент корреляции р для генеральной совокупности, как правило, неизвестен, поэтому он оценивается по экспериментальным данным, представляющим собой выборку объема n пар значений (Xi, Yi), полученную при совместномизмерении двух признаков Х и Y. Коэффициент корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r.
1. Коэффициенты корреляции способны характеризовать только линейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи.
3. При независимом варьировании признаков, когда связь между ними отсутствует.
4. При положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный (+) знак и находится в пределах от 0 до +1.
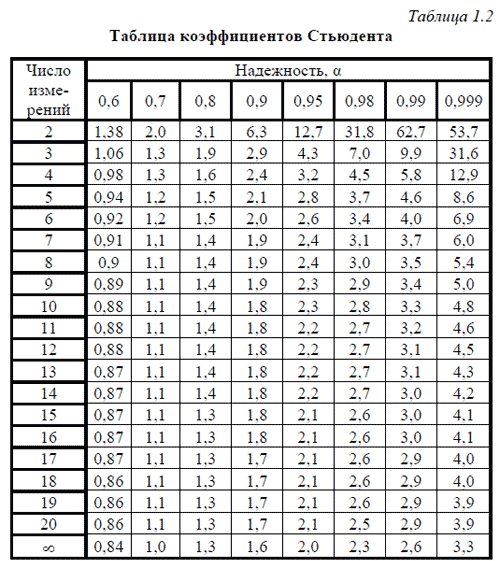
7. Только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции.
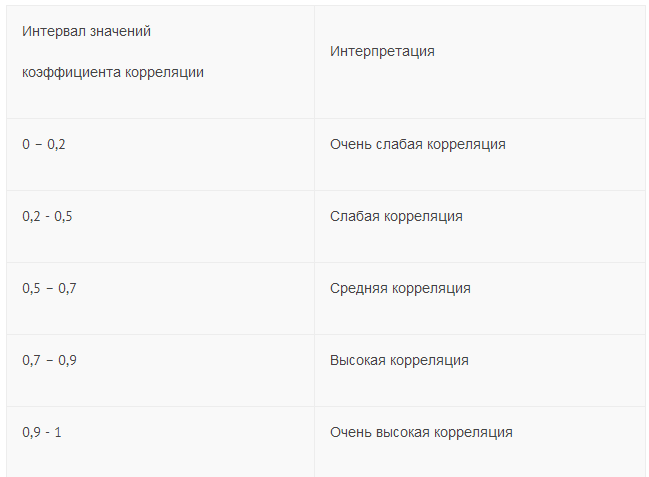
В практической деятельности, когда число коррелируемых пар признаков Х и Y невелико, то при оценке зависимости между показателями используется следующую градацию:
Оценка корреляционной связи по коэффициенту корреляции
При изучении корреляционной связи важным направлением анализа является оценка степени тесноты связи. Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой.
При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. А вопрос необходимо ли вообще изучать более подробно данную связь и практически ее использовать, решается с учетом степени тесноты связи. Зная количественную оценку тесноты корреляционной связи, таким образом, можно решить следующую группу вопросов: необходимо ли глубокое изучение данной связи между признаками и целесообразно ли ее практическое применение; сопоставляя оценки тесноты связи для различных условий, можно судить о степени различий в ее проявлении в конкретных условиях; последовательное рассмотрение и сравнение признака у с различными факторами (х1, х21, …) позволяет выявить, какие из этих факторов в данных конкретных условиях являются главными, решающими факторами, а какие второстепенными, незначительными факторами;
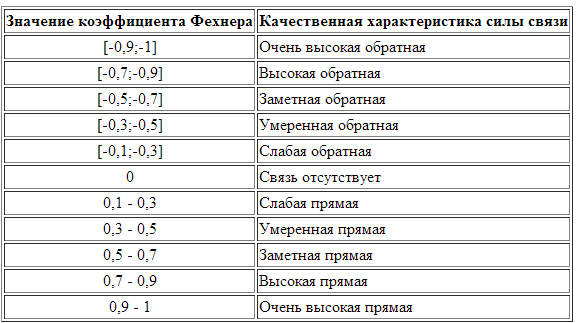
Для характеристики степени тесноты корреляционной связи могут применяться различные статистические показатели: коэффициент Фехнера (КФ), коэффициент линейной (парной) корреляции (r), коэффициент детерминации, корреляционное отношение ( ), индекс корреляции, коэффициент множественной корреляции (R), коэффициент частной корреляции (r) и др. В данном вопросе рассмотрим коэффициент линейной корреляции (r) и корреляционное отношение.
Более совершенным статистических показателем степени тесноты корреляционной связи является линейный коэффициент корреляции (r), предложенный в конце XIX в. При расчете коэффициента корреляции сопоставляются абсолютные значения отклонений индивидуальных величин факториального признака х и результативного признака у от их средних.
Однако непосредственно сопоставлять между собой эти полученные результаты нельзя, т.к. признаки, как правило, выражены в различных единицах и даже при наличии одинаковых единиц измерения будут иметь различные по величине средние и различные вариации. В этой связи сравнению подлежат отклонения, выраженные в относительных величинах, т.е. в долях среднего квадратического отклонения (их называют нормированными отклонениями).
Обычно задается вопрос, какие значения коэффициента корреляции указывают на сильную зависимость, а какие на слабую. Этот вопрос не имеет ответа. Строгая теория по этому поводу ничего не говорит. Тем не менее, во многих пособиях приводится ответ, но к огорчению новичков, в каждой книге ответ свой! Отчасти это связано с тем, что в разных дисциплинах сложились разные традиции интерпретации коэффициента.
Имейте в виду, что значения, приведенные в таблице, могут служить лишь неточными ориентирами. Заметьте, что в таблице рассматривается модуль коэффициента корреляции.
Есть случаи, когда корреляция может говорить о причинно следственной связи. Это случаи, когда одна из переменых общективна, а вторая субъективна. К объективным переменным относятся возраст, стаж, рост, которые просто не могут зависеть от субъективных переменных: настроения, особенностей личности, мотивации и т.д. Однако, такие объективные переменные, как вес, количество детей в семье, частота смены места работы, количество контактов и т.п. могут и часто зависят от субъективных психологических показателей.
К примеру, профессионализм рабочего повышается со стажем. Стаж и профессионализм коррелируют и мы можем быть уверены, что для повышения профессионализма стаж является объективной причиной. Объективные переменные, основанные на времени всегда являются причиной при наличии корреляции с субъективными характеристиками. В остальных случаях нужно очень осторожно относиться к причинно-следственным интерпретациям коэффициента корреляции.
Если причинно-следственная связь обоснована в теоретической части работы и подтверждается многими авторами, то корреляцию так же можно интерпретировать как причинно-следственную связь.
— нулевая корреляция. Предполагает отсутствие закономерной взаимосвязи между переменными;
Значения коэффициента корреляции
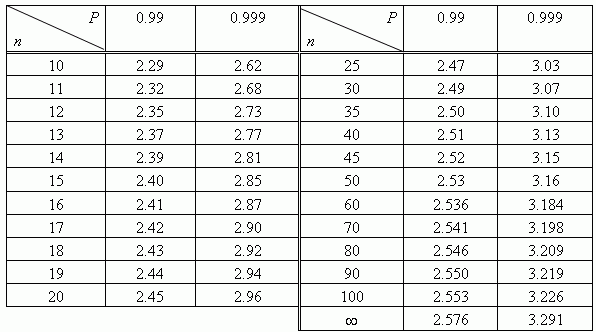
Решение этого вопроса дается с помощью распределения вероятностей для выборочного коэффициента корреляции при условии, что генеральный коэффициент корреляции = 0. Существует таблица случайных отклонений от нуля произведения
в зависимости от вероятности Р и объема выборки n.
Если выборочный коэффициент корреляции окажется больше приведенного в таблице граничного значения, то с надежностью Р можно утверждать, что генеральный коэффициент корреляции ρ(X,Y) отличен от нуля. Значимость коэффициента корреляции можно проверить, решив следующую задачу проверки гипотез. Выдвигаются гипотезы:
Задается уровень значимости. Статистика Т определяется по формуле:
Если Т, полученное по выборке, удовлетворяет условию, то отвергается и коэффициент корреляции считается значимым. При проверке значимости коэффициента корреляции рангов исходят из того, что в случае справедливости нулевой гипотезы об отсутствии корреляционной связи между переменными, при n>10, статистика:
имеет t-распределение Стьюдента с k=n-2 степенями свободы. Коэффициент корреляции значим на уровне а, если фактически наблюдаемое значение t будет больше критического по абсолютной величине:
При интерпретации коэффициента корреляции следует понимать, что:
— Корреляция между двумя случайными величинами может быть вызвана влиянием других факторов, и для объяснения полученных результатов нужно хорошо знать область приложения;
Обсуждая рисунке, мы употребляли термин тенденция, поскольку между переменными X и Y нет причинно-следственных связей. Наличие корреляции не означает наличия причинно-следственных связей между переменными X и Y, т.е. изменение значения одной из переменных не обязательно приводит к изменению значения другой. Сильная корреляция может быть случайной и объясняться третьей переменной, оставшейся за рамками анализа. В таких ситуациях необходимо проводить дополнительное исследование. Таким образом, можно утверждать, что причинно-следственные связи порождают корреляцию, но корреляция не означает наличия причинно-следственных связей.
Средняя ошибка коэффициента корреляции
Коэффициенты корреляции и регрессии, характеризующие зависимость между признаками групп животных, являются статистическими величинами, поэтому обладают свойством репрезентативности. Достоверность их величин устанавливают при помощи ошибок репрезентативности, вытекающих из самой сущности выборочного обследования, при котором целое характеризуется на основании изучения части.
Ошибки коэффициентов корреляции вычисляют по следующим формулам:
— для коэффициента корреляции r при многочисленной выборке (n>30):
— для r при малочисленной выборке (n
Показатели связи имеют реальный смысл, если они оказываются статистическими достоверными. Практическое же значение они приобретают лишь тогда, когда имеют достаточную величину. Например, коэффициент корреляции между многоплодием свиноматок и энергий роста их потомства 0,25 0,03 имеет вполне реальный смысл, так как он более чем в восемь раз превосходит свою квадратическую ошибку (tp = 8,3). Однако практическое значение этого показателя весьма невелико: он свидетельствует, что всего 6% общей вариации признака (r2=0,252=0,06=6%) зависит от изменчивости другого, связанного с ним признака; 94% составляют так называемую остаточную вариацию, не зависящую от связи признаков между собой. Поэтому строить практические расчеты на основании коэффициента корреляции, значение которого не превышает 0,5, по меньшей мере, ненадежно. Однако практическая значимость показателей связи зависит от цели исследования, т.е. от того, с какой степенью точности допустимы их вычисления и какова может быть их величина в заданных условиях.
Когда не следует рассчитывать коэффициент корреляции?
Расчет r может ввести в заблуждение, если:
1. Соотношение между двумя переменными нелинейное, например квадратичное. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др. Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: полиномы разных степеней; равносторонняя гипербола.
К нелинейным регрессиям по оцениваемым параметрам относятся функции: степенная; показательная; экспоненциальная.
Параметры нелинейной регрессии по включенным переменным оцениваются, как и в линейной регрессии, методом наименьших квадратов, поскольку эти функции линейны по параметрам.
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени. Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.
Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу. Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях широко используется степенная функция.
Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры a и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду. Соответственно оценки параметров a и b могут быть найдены с помощью МНК.
В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель, поскольку логарифмируя ее по натуральному основанию, получим линейную форму модели:
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.
2. Данные включают более одного наблюдения по каждому случаю. Количественная характеристика социально-экономических процессов в непосредственной связи с их качественной сущностью невозможна без глубокого статистического исследования. Использование различных способов и приемов статистической методологии предполагает наличие исчерпывающей и достоверной информации об изучаемом объекте, что включает этапы сбора статистической информации и ее первичной обработки, сведения и группировки результатов наблюдения в определенные совокупности, обобщения и анализа полученных материалов.
Если при сборе статистических данных допущена ошибка или материал оказался недоброкачественным, это повлияет на правильность и достоверность как теоретических, так и практических выводов. Поэтому статистическое наблюдение от начальной до завершающей стадии должно быть тщательно продуманным и четко организованным.
Однако не всякий сбор сведений является статистическим наблюдением. О статистическом наблюдении можно говорить лишь тогда, когда, во-первых, обеспечивается регистрация устанавливаемых фактов в специальных учетных документах и, во-вторых, изучаются статистические закономерности, т.е. такие, которые проявляются только в массовом процессе, в большом числе единиц какой-то совокупности. Поэтому статистическое наблюдение должно быть планомерным, массовым и систематическим.
К статистическому наблюдению предъявляются следующие требования: полноты и практической ценности статистических данных; достоверности и точности данных; их единообразия и сопоставимости. Любое статистическое исследование необходимо начинать с точной формулировки его цели и конкретных задач, а тем самым и тех сведений, которые могут быть получены в процессе наблюдения. После этого определяются объект и единица наблюдения, разрабатывается программа, выбираются вид и способ наблюдения.
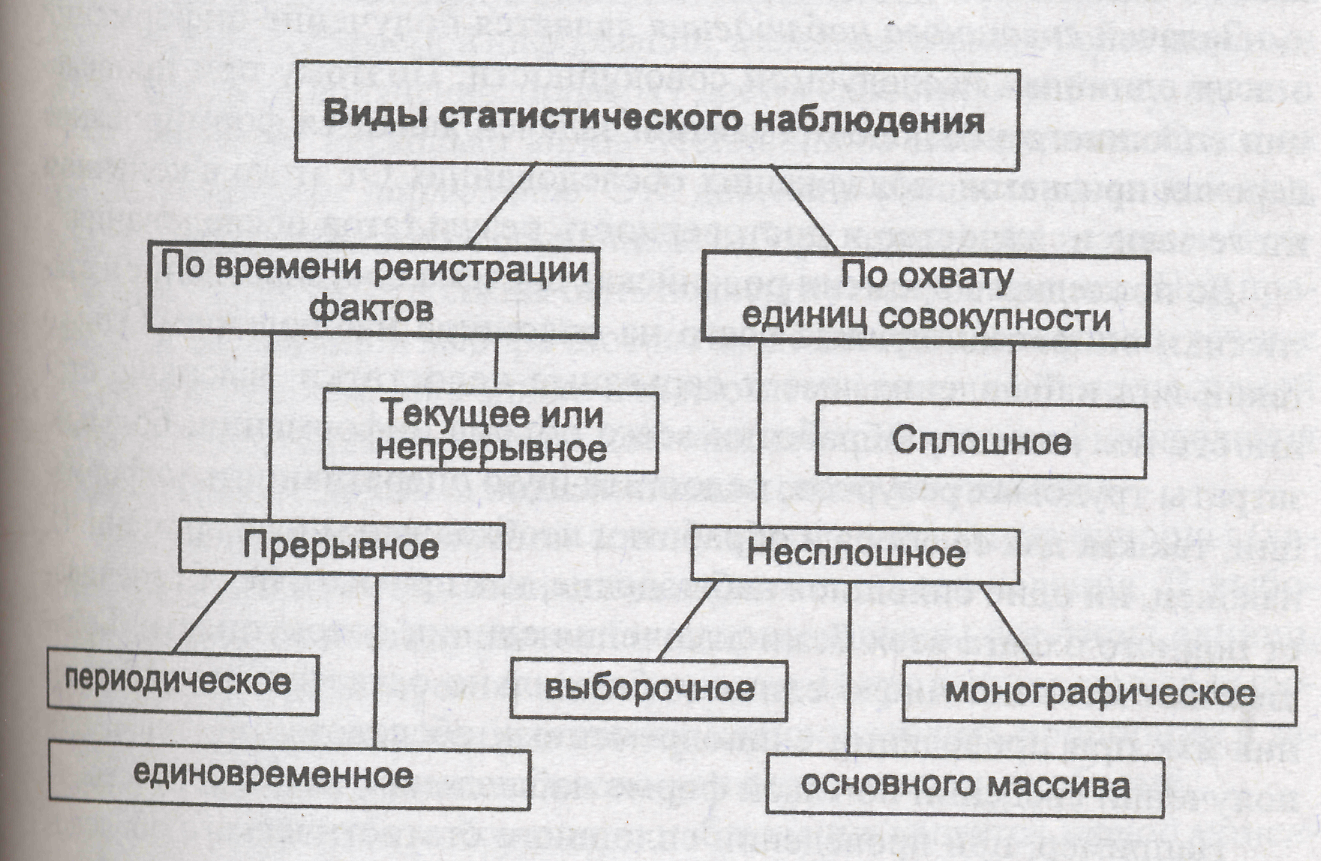
С точки зрения полноты охвата фактов статистическое наблюдение может быть сплошным и несплошным. Сплошное наблюдение представляет собой полный учет всех единиц изучаемой совокупности. Несплошное наблюдение организуют как учет части единиц совокупности, на основе которой можно получить обобщающую характеристику всей совокупности. К видам несплошного наблюдения относятся: способ основного массива, выборочные наблюдения, монографические описания.
При непосредственном учете фактов сведения получают путем личного учета единиц совокупности: пересчета, взвешивания, измерения и т.д. Документальный способ сбора статистической информации базируется на систематических записях в первичных документах, подтверждающих тот или иной факт. В ряде случаев для заполнения статистических формуляров прибегают к опросу населения, который может быть произведен экспедиционным, анкетным или корреспондентским способом.
Существуют различные способы формирования выборочной совокупности. Это, во-первых, индивидуальный отбор, включающий такие разновидности, как собственно случайный, механический, стратифицированный, и, во-вторых, серийный, или гнездовой, отбор.
3. Есть аномальные значения (выбросы).Любая изучаемая совокупность может содержать единицы наблюдения, значения признаков которых резко выделяются из основной массы значений. Такие нетипичные значения признаков (выбросы) могут быть обусловлены воздействием каких-либо сугубо случайных обстоятельств, возникать в результате ошибок наблюдения или же быть объективно присущими наблюдаемому явлению. В любом случае они являются аномальными для совокупности, так как нарушают статистическую закономерность изучаемого явления. Следовательно, статистическое изучение совокупности без предварительного выявления и анализа возможных аномальных наблюдений может не только исказить значения обобщающих показателей (средней, дисперсии, среднего квадратического отклонения и др.), но и привести к серьезным ошибкам в выводах о статистических свойствах совокупности, сделанных на основе полученных оценок показателей.
Для выявления и исключения аномальных единиц наблюдения построена диаграмма рассеяния изучаемых признаков.
4. Данные содержат ярко выраженные подгруппы наблюдений. Собранный в процессе статистического наблюдения материал нуждается в определенной обработке, сведении разрозненных данных воедино. Научно организованная обработка материалов наблюдения (по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой.
Сводка представляет собой второй этап статистического исследования. Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности.
Интервалы бывают: равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова; неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе; открытые, когда имеется только либо верхняя, либо нижняя граница; закрытые, когда имеются и нижняя, и верхняя границы.
При проведении группировки приходится решать ряд задач: выделение группировочного признака; определение числа групп и величины интервалов; при наличии нескольких группировочных признаков описание того, как они комбинируются между собой; установление показателей, которыми должны характеризоваться группы, т.е. сказуемого группировки.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная).
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей). Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками. В зависимости от числа положенных в их основание признаков различают простые и многомерные группировки. Группировка, выполненная по одному признаку, называется простой.
Многомерная группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации. Структурная группировка применяется для характеристики структуры совокупности и структуры сдвигов.
Структурный называется группировка, в которой происходит разделение выделенных с помощью технологической группировки типов явлений, однородных совокупностей на группы, характеризующие их структуру по какого либо варьирующему признаку. Например, группировка населения по размеру среднедушевого дохода. Анализ структурных группировок взятых за ряд периодов или моментов времени, показывает изменения структуры изучаемых явлений, то есть структурные сдвиги. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития.
Виды коэффициента корреляции
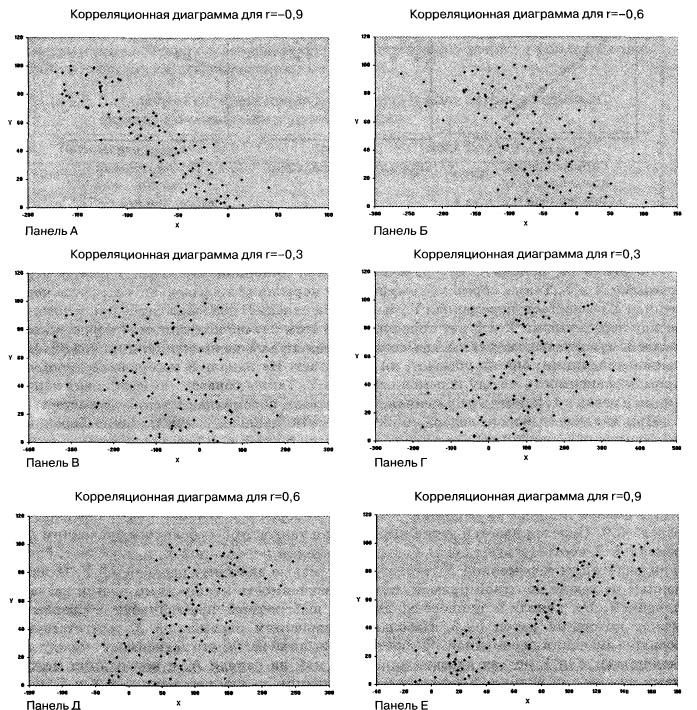
Взаимосвязь между этими случайными величинами можно проанализировать с использованием диаграммы рассеивания. С помощью этой диаграммы можно установить, есть ли связь между переменными и какого она вида. Для представленных данных диаграмма рассеивания имеет вид:
Анализ этой диаграммы показывает, что при увеличении цен продажа имеет тенденцию к снижению. Более того, можно грубо оценить, что этот спад идет по прямой. Взаимосвязь между переменными Х и Y можно представить следующими диаграммами:
То есть в данном случае проблема оценки тесноты связи решается с использованием ранжирования или упорядочивания объектов по степени выраженности измеряемых признаков. При этом каждому объекту присваивается определенный номер, называемый рангом.
Например. Если 4 объекта оказались равнозначными в отношении рассматриваемого признака и невозможно определить, какие из следующих рангов (4, 5, 6, 7) приписать этим объектам, то каждому объекту приписывается средний ранг, равный (4+5+6+7)/4 = 5.5. При наличии связанных рангов ранговый коэффициент корреляции Спирмена вычисляется по формуле:
Определить коэффициент корреляции рангов. Решение. В первой ранжировке имеем четыре группы неразличимых рангов. Во второй ранжировке имеем две таких группы:
Используя формулу, имеем r = 0.917. Примечание. Коэффициент корреляции рангов может использоваться для изучения связи между ординальными (порядковыми) переменными, которые еще называются качественными. В отличие от количественных переменных, для которых можно определить, на сколько или во сколько раз проявления одного признака у одного объекта больше (меньше), чем у другого, для качественных признаков этого определить нельзя.
Например. По некоторой дисциплине два студента имеют соответственно оценки «отлично» и «удовлетворительно». В этом случае можно утверждать, что уровень подготовки у первого студента выше, чем у другого, но нельзя сказать, на сколько или во сколько раз.
Коэффициент корреляции Пирсона
Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. В общем виде формула для подсчета коэффициента корреляции такова:
Расчет коэффициента корреляции Пирсона предполагает, что переменные X и Y распределены нормально. Даная формула предполагает, что из каждого значения xi переменной X, должно вычитаться ее среднее значение x. Это не удобно, поэтому для расчета коэффициента корреляции используют не данную формулу, а ее аналог, получаемый с помощью преобразований:
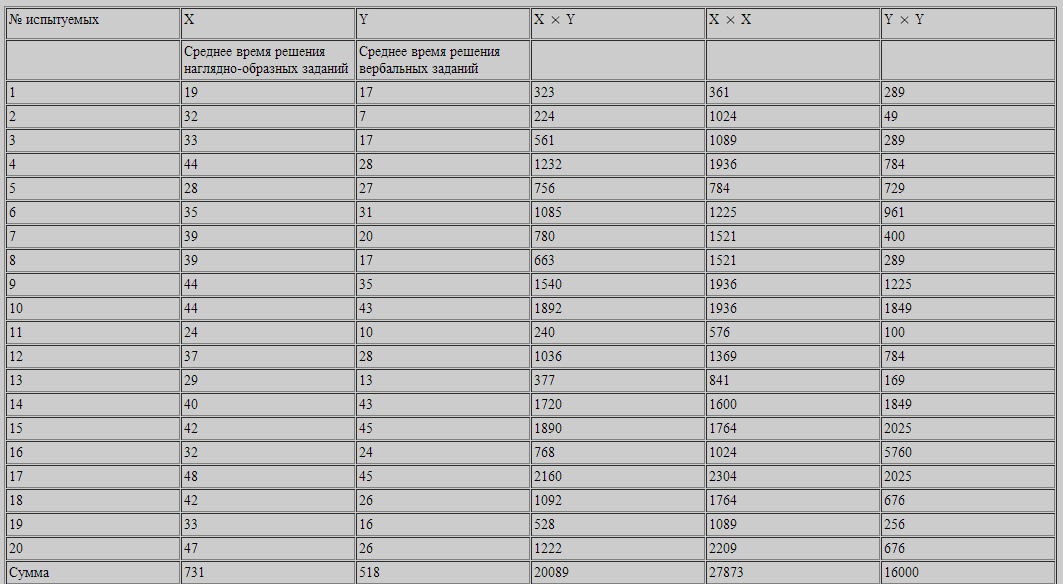
Для решения данной задачи представим исходные данные в виде таблицы, в которой введены дополнительные столбцы, необходимые для расчета по формуле В таблице 12 даны индивидуальные значения переменных X и Y, построчные произведения переменных X и Y, квадраты переменных всех индивидуальных значений переменных X и Y, а также суммы всех вышеперечисленных величин.
Рассчитываем эмпирическую величину коэффициента корреляции по формуле:
Определяем критические значения для полученного коэффициента корреляции. Величины критических значений коэффициентов линейной корреляции Пирсона даны по абсолютной величине. Следовательно, при получении как положительного, так и отрицательного коэффициента корреляции по формуле оценка уровня значимости этого коэффициента проводится по той же таблице приложения без учета знака, а знак добавляется для дальнейшей интерпретации характера связи между переменными X и Y. При нахождении критических значений для вычисленного коэффициента корреляции Пирсона число степеней свободы рассчитывается как:
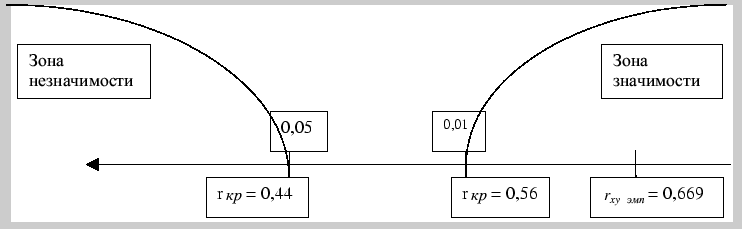
Строим соответствующую «ось значимости»:
Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия: сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений, распределения переменных X и Y должны быть близки к нормальному, число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.
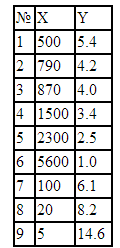
Пример решения задачи при помощи коэффициента Пирсона. На основании наблюдений за развивающимся сайтом и изменением его средневзвешенной позиции по основным запросам в поисковой системе необходимо проверить, можно ли говорить о линейной зависимости между позицией сайта и числом посетителей. Исходные данные: X (число посетителей в сутки), Y (усредненная позиция сайта в поисковой системе). В таблице представлены значения признаков X и Y:
1. На основании исходных данных, приведенных в таблице, расчитаем средние значения для X и Y:
Все необходимые для расчета коэффициента корреляции промежуточные данные и их суммы представлены в таблице:
Оценим полученное нами эмпирическое значение коэффициента Пирсона, сравнив его с соответствующим критическим значением для заданного уровня значимости из таблицы критических значений коэффициента корреляции Пирсона. Для выборки с числом элементов m = 9 и уровнем значимости p = 0,05 критическое значение коэффициента Пирсона = 0,67, с уровнем значимости p = 0,01 критическое значение коэффициента Пирсона = 0,8. Так как абсолютное значение, полученного нами коэффициента корреляции меньше критического значения, взятого из таблицы (находится вне зоны значимости), мы принимаем гипотезу Н0 об отсутcтвии корреляционной зависимости между выборками. Полученный результат свидетельствует об отсутствии линейной зависимости между числом посетителей сайта и его позицией в поисковой системе, однако это не означает, что эти параметры не связаны между собой.
Модификация коэффициента корреляции Пирсона
До сих пор мы подробно рассматривали два вида коэффициентов корреляции: коэффициент линейной корреляции Пирсона для интервальных шкал и коэффициент ранговой корреляции Спирмена. Существуют и другие типы коэффициентов для различных сочетаний шкал. Для коррелирования переменных, измеренных в дихотомической и интервальной шкале используют точечно-бисериальный коэффициент корреляции.
Чаще всего данный вид коэффициента корреляции применяется для расчета связи пунктов теста с суммарной шкалой. Это один из видов проверки валидности. Случаи, когда одна из переменных представлена в дихотомической шкале, а другая в ранговой (порядковой), требуют применения коэффициента рангово-бисериальной корреляции:
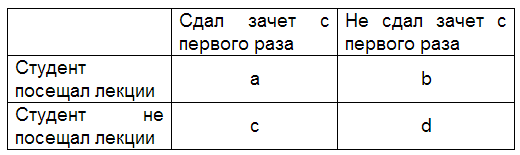
Если обе переменные представляют собой дихотомическую шкалу то следует использовать коэффициент четырехклеточной сопряженности Пирсона. Классификация объектов по дихотомической шкале приведет к построению четырехклеточной таблицы. К примеру, студент может посетить более 50% лекций, а может и не посетить, может сдать зачет с первого раза, а может и не сдать. На основе такой классификации построим таблицу:
В клетки a,b,c,d таблицы следует вписать количество объектов, обладающих соответствующими признаками. Формула расчета коэффициента четырехклеточной сопряженности Пирсона:
Коэффициент корреляции Спирмена
Преимущество: можно ранжировать по признакам, которые нельзя выразить численно: субъективные оценки, предпочтения и т.д. При экспертных оценках можно ранжировать оценки разных экспертов и найти их корреляции друг с другом, чтобы затем исключить из рассмотрения оценки эксперта, слабо коррелирующие с оценками других. Коэффициент корреляции рангов применяется для оценки устойчивости тенденции динамики.
Недостатки: недостатком коэффициента корреляции рангов является то, что одинаковым разностям рангов могут соответствовать совершенно отличные разности значений (в случае количественных признаков). Недоучет размеров отклонений признаков от их средних величин занижает меру тесноты связи. Поэтому для количественных признаков корреляция рангов обладает меньшей информативностью, чем коэффициент корреляции числовых значений этих признаков.
Свойства коэффициента ранговой корреляции Спирмена:
2. Ограниченность. Для оценки данных необходима выборка от 5 до 40 наблюдений по каждой переменной. При большом количестве одинаковых рангов по сопоставляемым переменным коэффициент дает приближенные значения. При совпадении значений вносится поправка на одинаковые ранги. В этом случае формула имеет вид:
3. Независимость. Чтобы получить адекватный результат, необязательно наличие нормального закона распределения коррелируемых рядов.
Коэффициент корреляции рангов используется для оценки качества связи между двумя совокупностями. Кроме этого, его статистическая значимость применяется при анализе данных на гетероскедастичность.
Повторяющиеся ранги для X и Y есть. В этом случае вводится поправка на связки в ранговых рядах. Поправка рассчитывается для каждого ряда отдельно. Поправка для каждого ряда рассчитывается с учетом всех связок в этом ряду: поправка для связок рангов в ряду X; поправка для связок рангов в ряду Y; номер связки в ряду X; количество одинаковых рангов в связке с номером j; номер связки в ряду Y; количество одинаковых рангов в связке с номером k.
Пример решения задачи с использованием коэффициента Спирмана: На основании наблюдений за развивающимся сайтом и изменением его средневзвешенной позиции по основны м запросам в поисковой системе необходимо проверить, можно ли говорить о линейная зависимость между позицией сайта и числом посетителей.
Исходные данные: X (число посетителей в сутки), Y (усредненная позиция сайта в поисковой системе). В таблице представлены значения признаков X и Y:
Проранжируем каждый из элементов признаков (X и Y) в порядке возрастания значений (самому маленькому элемнту присвоим ранг 1 и т. д. до самого большого элемента последовательности, который получит ранг m). Результаты ранжирования представлены в таблице:
Найдем сумму квадратов разностей рангов, сложив для этого элементы столбца. Подставим полученные значения в формулу, и найдем значение коэффициента Спирмена.
Оценка коэффициента корреляции Спирмена. Оценим полученное нами эмпирическое значение коэффициента Спирмена, сравнив его с соответствующим критическим значением для заданного уровня значимости из таблицы критических значений коэффициента ранговой корреляции Спирмена. Для выборки с числом элементов m = 9 и уровнем значимости p = 0,05 критическое значение коэффициента Спирмена = 0,68.
Так как абсолютное значение, полученного нами коэффициента корреляции больше критического значения, взятого из таблицы, мы отклоняем гипотезу H0 об отсуттвии корреляционной зависимости между выборками и принимаем альтернативную гипотезу о статистической значимости отличия коэффициента корреляции от нуля, и наличии связи.
Оценка коэффициента корреляции Спирмена на основании t-критерия. Произведем оценку значимости полученного нами коэффициента ранговой корреляции Спирмена, используя таблицу «Стьюдента».
Так как коэффициент ранговой корреляции больше t-критерия мы отклоняем гипотезу H0 об отсуттвии корреляционной зависимости между выборками и принимаем альтернативную гипотезу о статистической значимости отличия коэффициента корреляции от нуля, и наличии отрицательной связи между числом посетителей сайта и его позицией в поисковой системе.
Заметим, что для тех же исходных данных при подсчете коэффициента корреляции Пирсона в результате было получено заключение об отсутствии связи. Такой результат можно обьяснить тем, что коэффициент корреляции Пирсона подтверждает илиопровергает наличие линейной зависимости. Коэффициент рангов Спирмена подтверждает присутствие монотонно-возрастающей или убывающей зависимости (не обязательно линейной). В нашем случае зависимость нелинейная, но монотонно-убывающая.
Коэффициент корреляции Кендалла
Коэффициент корреляции Кенделла вычисляется по формуле:
Для измерения степени согласия Кенделл предложил следующий коэффициент:
Таким образом, коэффициент Кенделла можно считать мерой неупорядоченности второй последовательности относительно первой. Статистическая проверка наличия корреляции. Нулевая гипотеза Н0: Выборки x и y не коррелируют. Рассмотрим центрированную и нормированную статистику Кенделла:
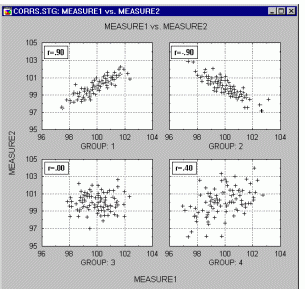
Ниже приведены примеры вычисления корреляций Кенделла и Спирмена. Значения коэффициентов указаны над каждым изображением. Заметно, что в большинстве случаев коэффициент Спирмена больше коэффициента Кенделла. Объяснение этого эффекта приводится ниже. Направление линейной зависимости.
Коэффициенты корреляции реагируют на изменение направления и зашумлённость линейной зависимости между переменными. Наклон линейного тренда.
Коэффициенты корреляции реагируют на изменение направления, но не реагируют на изменение наклона тренда. На первом, четвёртом и седьмом рисунках дисперсия одной из переменных близка к нулю, поэтому не удаётся зафиксировать факт линейной зависимости. Нелинейная зависимость.
Корреляции Кенделла и Спирмена не отражают меры нелинейной зависимости между переменными. Линейная и нелинейная зависимости. На каждой из приведённых ниже иллюстраций осуществляется переход от линейной зависимости к нелинейной. Коэффициенты корреляции Кенделла и Спирмена реагируют на это одинаковым образом.
По мере смены линейной зависимости нелинейной значения коэффициентов корреляции падают. В случае выборок из нормального распределения коэффициент корреляции Кенделла может быть использован для оценки коэффициента корреляции Пирсона по формуле:
Выборкам x и y соответствуют последовательности рангов:
Проведем операцию упорядочивания рангов.
Коэффициент корреляции Кенделла и коэффициент корреляции Спирмена выражаются через ранги следующим образом:
Заметно, что в случае с коэффициентом Спирмана инверсиям придаются дополнительные веса, таким образом коэффициент Спирмана сильнее реагирует на несогласие ранжировок, чем коэффициент Кенделла. Этот эффект проявляется в приведённых выше примерах: в большинстве из них коэффициент Спирмана больше коэффициент Кенделла.
Утверждение. Если выборки x и y не коррелируют (выполняется гипотеза Н0), то величины Кенделла и Спирмена сильно закоррелированы. Коэффициент корреляции между ними можно вычислить по формуле:
Коэффициент корреляции знаков Фехнера
Расчет коэффициента Фехнера состоит из следующих этапов:
1. Определяют средние значения для каждого признака (X и Y).
2. Определяют знаки отклонения (-,+) от среднего значения каждого из признаков.
3. Если знаки совпадают, присваивают значение А, иначе В.
4. Считают количество А и В, вычисляя коэффициент Фехнера по формуле:
Найдем индексы Фехнера для примера.
Коэффициент множественной ранговой корреляции (конкордации)
До сих пор рассматривались модели простой корреляции, т.е. корреляционной зависимости между двумя признаками Однако в практике экономического анализа часто приходится изучать явления, которые складываются под влиянием не одного, а многих различных факторов, каждый из которых в отдельности может не производить решающего влияния Совокупный же влияние факторов иногда оказывается достаточно сильным, чтобы по их изменениях можно было делать виснет овкы о величинах показателя изучаемого явления Методы измерения корреляционной связи одновременно между двумя, тремя и более корреляционными признакам создают учение о множественной корреляции.
В моделях множественной корреляции зависимая переменная рассматривается как функция нескольких (в общем случае п) независимых переменных. Множественное корреляционное уравнение устанавливает связь между исследуемыми признаками и позволяет вычислить ожидаемые значения результативного признака под влиянием включенных в анализ признаков-факторов, связанных да аниме уравнением.
Для оценки степени тесноты связи между результативным и факторными признаками вычисляют коэффициент множественной корреляции Величина его всегда положительное число, которое находится в пределах от 0 до 1. В множественных корреляционно-регрессионных моделях коэффициент простой корреляции между результативным признаком и факторными, а также между самими факторными признаками.
Методы корреляции произведения моментов Пирсона и линейного регрессионного анализа Гальтона были обобщены и расширены в 1897 г. Джорджем Эдни Юлом до модели множественной линейной регрессии, предполагающей использование многомерного нормального распределения. Методы множественной корреляции позволяют оценить связь между множеством непрерывных независимых переменных и одной зависимой непрерывной переменной. Коэффициент множественной корреляции обозначается через R0. Его вычисление требует решения совместной системы линейных уравнений. Число линейных уравнений равно числу независимых переменных.
Иногда необходимо исключить эффект третьей переменной, с тем чтобы определить «чистую» связьмежду любой парой переменных. Частный (парциальный) коэффициент корреляции выражает связь между двумя переменными при исключенном (элиминированном) влиянии еще одной или несколко других переменных. В простейшем случае частный коэффициент корреляции вычисляется как функция парных корреляций (произведений моментов) между Y, X1 и Х2.
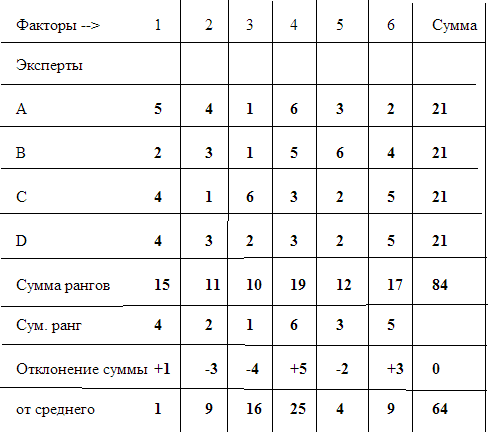
При небходимости можно воспользоваться услугами группы из m-экспертов, установить результирующиеранги целей, но тогда возникнет вопрос о согласованности мнений этих экспертов или конкордации. Пусть у нас имеются ранжировки 4 экспертов по отношению к 6 факторам, которые определяют эффективность некоторой системы.
Заметим, что полная сумма рангов составляет 84, что дает в среднем по 14 на фактор. Для общего случая n факторов и m экспертов среднее значение суммы рангов для любого фактора определится выражением.
Теперь можно оценить степень согласованности мнений экспертов по отношению к шести факторам. Для каждого из факторов наблюдается отклонение суммы рангов, указанных экспертами, от среднего значения такой суммы. Поскольку сумма этих отклонений всегда равна нулю, для их усреднения разумно использовать квадраты значений.
В нашем случае сумма таких квадратов составит S= 64, а в общем случае эта сумма будет наибольшей только при полном совпадении мнений всех экспертов по отношению ко всем факторам:
М. Кэндэллом предложен показатель согласованности или коэффициент конкордации, определяемый как:
В нашем примере значение коэффициента конкордации составляет около 0,229, что при четырех экспертах и шести факторах достаточно, чтобы с вероятностью не более 0.05 считать мнения экспертов несогласованными. Дело в том, что как раз случайность ранжировок, их некоррелированность просчитывается достаточно просто. Так для нашего примера указанная вероятность соответствует сумме квадратов отклонений S = 143,3, что намного больше 64.
Здесь обычно используются элементарные приемы нормирования. Если цель 3 имеет ранг 1, цель 8 имеет ранг 2 и т. д., а сумма рангов составляет 55, то весовой коэффициент для цели 3 будет наибольшим и сумма весов всех 10 целей составит 1. Вес цели придется определять как:
Имеющийся опыт свидетельствует о возможностях существенно повысить представительность, обоснованность и, главное, достоверность суждений экспертов. В качестве “побочного эффекта” можно составить мнение о профессиональности каждого эксперта.
Сравнение коэффициентов корреляции
Для проверки гипотезы о равенстве двух корреляций (H0) величины сравниваемых корреляций r1 и r2 подвергаются преобразованию Фишера:
Определенные таким образом z1 и z2 можно считать нормально распределенными с параметрами распределений:
Сравнение двух коэффициентов корреляции необходимо, когда нужно узнать, какой из них достоверно выше или ниже, иными словами, насколько достоверно различие между ними. Для сравнения коэффициентов корреляции применяем следующий алгоритм и сразу же разберем его на примере. Исходные данные:
— N1 (количество пар значений для первого коэффициента) = 100;
— R1 (первый коэффициент корреляции) = 0,2;
— N2 (количество пар значений для второго коэффициента) = 50;
— R2 (второй коэффициент корреляции) = 0,5.
1. Вычисляем ошибку разницы по формуле:
2. Преобразуем оба коэффициента с помощью z-преобразования Фишера:
3. Вычисляем значения t-критерия по формуле:
Получившееся значение проверяется по таблице критических значений t-критерия Стьюдента.
4. Проверяем значимость полученного значения. Вычисляем количество степеней свободы (df), далее пользуемся таблицей критических значений t-критерия Стьюдента или используем Excel:
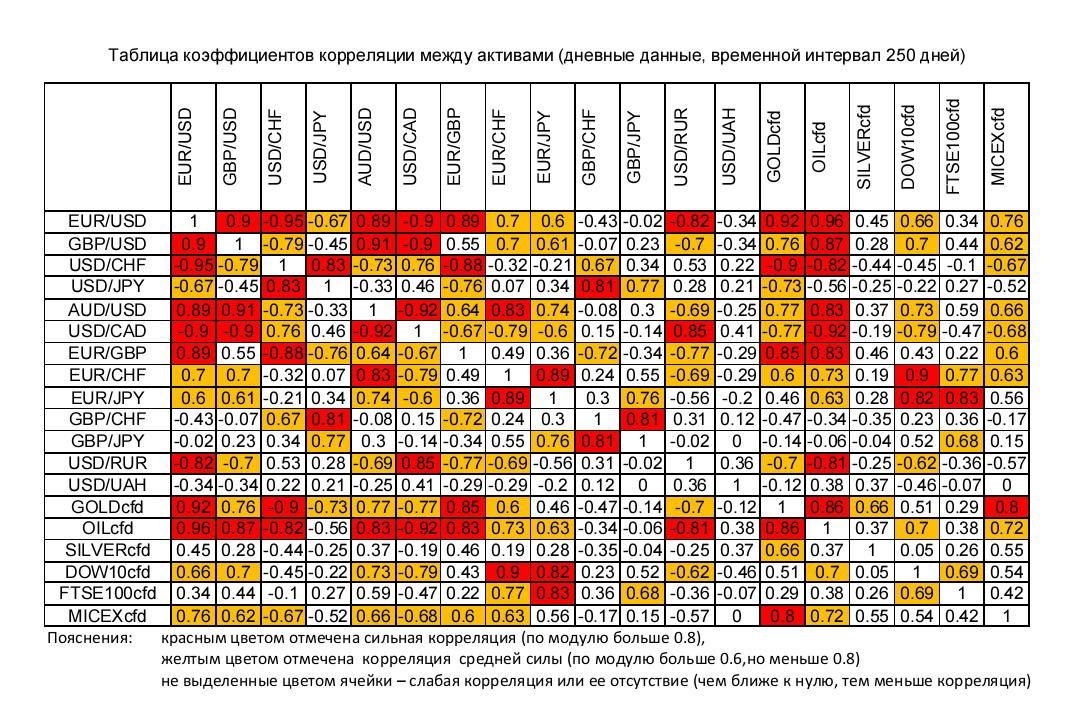
Использование Excel для вычисления коэффициента корреляции
Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами.
Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры тесноты такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (x, y) из совместной генеральной совокупности X и Y. Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции, предполагающий, что выборки X и Y распределены по нормальному закону.
Для более точного ответа на вопрос о наличии линейной корреляционной связи необходима проверка соответствующей статистической гипотезы.
Алгоритм решения. Для выявления степени взаимосвязи, прежде всего, не-обходимо ввести данные в таблицу MS Excel. Затем вычисляется значение коэффициента корреляции. Для этого курсор установите в ячейку C1. На панели инструментов нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку ОК. Указателем мыши введите диапазон данных выборки Х в поле массив1 (А1:А10). В поле массив2 введите диапазон данных выборки Y (В1:В10). Нажмите кнопку ОК.
В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами. Для реализации процедуры необходимо:
— выполнить команду Анализ данных и в появившемся списке Инструменты анализа выбрать строку Корреляция инажать кнопку ОК;
— впоявившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов;
— в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам);
— указать выходной интервал, то есть ввести ссылку на ячейку, с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.
В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки истолбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой. Рассматривается отдельно каждый коэффициент корреляции между соответствующими параметрами. Отметим, что хотя в результате будет получена треугольная матрица, корреляционная матрица симметрична. Подразумевается, что в пустых клетках в правой верхней половине таблицы находятся те же коэффициенты корреляции, что и в нижней левой (симметрично относительно диагонали).
Пример. Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков. Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.
Алгоритм решения. Для выполнения корреляционного анализа введите в диапазон A1:G3 исходные данные (рис. 3). Затем выберите пункт Анализ данных и далее укажите строку корреляция. В появившемся диалоговом окне укажите Входной интервал (А2:С7). Укажите, что данные рассматриваются по столбцам. Укажите выходной диапазон (Е1) и нажмите кнопку ОК.
Выборочный коэффициент корреляции:
В Excel для вычисления коэффициента корреляции используется функция =КОРРЕЛ():
Перепробовал все какие нашел формулы из Интернета, все выдают какую-то лажу, в частности коэффициент корреляции по ним получается то больше единицы, то всегда 0, то не получается единицей в указанном выше случае. Коэффициент корреляции получаю делением на произведение среднеквадратичных отклонений, дисперсию для стандартного отклонения считаю как взвешенную по вероятностям сумму разниц квадратов значений случайной величины и её мат. ожидания (мат ожидание рассчитываю как взвешенные по вероятности значения случайной величины).
Посмотрела Ваш файл. Вы пытаетесь найти совместное распределение как произведение распределений двух величин. Это означает, что две Ваши величины независимы, и корреляция между ними должна быть равна 0. Дополнение.Скриншот вычисления при правильно подобранных совместных вероятностях.
Принципы интерпретации коэффициента корреляции
Основные принципы интерпретации различных коэффициентов корреляции одинаковы. В случае дихотомической шкалы мы говорим о вероятности совпадения (прямого или обратного) ответов типа да/нет, в случае рангов о вероятности совпадения порядка, в случае коэффициента линейной корреляции мы говорим о степени совместного изменения переменных или о их взаимосвязи.
Полученный коэффициент нужно проверить на значимость, которая зависит от вероятности ошибки и количества человек. Коэффициент корреляции может быть формально небольшим, к примеру r=0,17, но если исследование проведено на 500 человек и вероятность ошибки (р) менее 0,05, то мы признаём значимым даже такой небольшой коэффициент. С другой стороны, при выборке в 5 человек очень большой коэффициент мы признаем незначимым, т.к. из-за малого количества человек мы можем совершить ошибочный вывод об этой корреляции.
Таким образом, для нас главное узнать какой должна быть вероятность ошибки и количество человек, чтобы признать полученный коэффициент действительно значимым.
Таблицы критических значений предназначены чтобы можно было найти критическое значение коэффициента корреляции, т.е. такое, после которого взаимосвязь можно считать значимой и неслучайной. При этом значение вероятности ошибки задаётся исследователем. В таблицах обычно есть критические значения коэффициентов корреляции для р
В примерах, приведённых выше для количества человек n=89 и p
Применение коэффициента корреляции на практике
Одним из способов использования корреляции пар в торговле является устранение расхождения инструментов. Например, трейдер выбрал для своей работы две валютные пары, которые коррелируют с К = 0.8. В этом случае, при наблюдении за движением подопытных, человек заметит, что К время от времени меняется, то несколько увеличиваясь, то несколько уменьшаясь. Тем не менее, средние значения коэффициента все равно находятся в диапазоне 0.7
В первоначальном виде арбитраж возник на заре развития вторичных (региональных) бирж, когда один итот же актив торговался на разных площадках по разным ценам и с 44 каждым годом разрыв этой цены стремительно сокращался, а вместе с ним скорость арбитражных стратегий и их объем.
Сегодня существует в качестве межбиржевого варианта, когда актив торгуется на биржах разных стран, например на токийской и нью-йоркской, лондонской и франкфуртской. А также на NYSE и NASDAQ в качестве арбитража разных активов, например двух-трех акций из одного сектора.
Основные поводыри для Американского фондового рынка следующие (в порядке убывания силы глобального влияния):
Теперь вопрос: почему акции так одинаково ходят и кто за всем этим стоит? Да все, особенно скальперы, роботы-скальперы, люди-скальперы. Роботы-арбитражеры в первую очередь, а также алгоритмы, котирующие акцию (читай маркетмейеры). Ведь иначе невозможно было бы такую массу акций заставить двигаться более менее одинаково, речь, понятно, внутри дня. Потому что, если мы взглянем на большие таймфреймы, то выясниться, что многие сектора живут своей отдельной жизнью. Вот например, график месячный, с 2000 года:
Действующие лица те же. В общем есть некое понимание, что графики похожи, но одни сильнее рынка в целом, а другие слабее, в абсолютном выражении, при расчете на начало года. Это все глобально, на год, а вот на месяц:
Стиль торговли таким образом называется «арбитраж», торгуется, как правило, минимум два инструмента, причем часто в разные стороны, но можно торговать один, рассматривая другие инструменты, как поводырей. Стиль сегодня очень роботизирован, но и для «мануальных скальперов» еще есть место.
Теперь, как определить «главного» в секторе/индустрии. Те, кто первый в столбце, те и рулят, как правило. НО. В случае, если нет глобальных новостей по сектору или если нет отчетов у разных акций из этого сектора. Т.е. их главенство имеет место быть в самый скучный понедельник, а не в день статистики, запасов газа, безработицы да еще с отчетом старших акций.
Вычисление коэффициента корреляции портфеля
Ожидаемая доходность нашего портфеля равна средневзвешенной ожидаемых значений доходностей отдельных акций:
Для того, чтобы найти дисперсию и стандартное отклонение доходности портфеля, мы должны знать значения ковариации акций А и В. Ковариация служит для измерения степени совместной изменчивости двух акций. Общая формула вычисления ковариации:
Эта матрица очень похожа на матрицу ковариаций. Заполнив матрицу, надо просто сложить полученные в ней величины и найдем дисперсию портфеля:
Вычислим дисперсию портфеля:
Стандартное отклонение равно квадратному корню из дисперсии, то есть:
Легко подсчитать, что только в том случае, если коэффициент корреляции двух акций равен +1, то стандартное отклонение портфеля равно средневзвешенному стандартных отклонений доходности отдельных акций:
и можно было бы добиться, изменяя пропорции X1 и X2 акций в портфеле, чтобы стандартное отклонение портфеля было равно нулю. К сожалению, в реальности, отрицательная корреляция акций практически не встречается.
Применение линейного коэффициента корреляции в трейдинге
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.
Линейный коэффициент корреляции (далее ЛКК) (коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле:
Коэффициент корреляции изменяется в пределах [-1…+1]. Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Примеры применения ЛКК в трейдинге. Области применения ЛКК в трейдинге достаточно широки. Например, долго считалось, что при падении фондовых рынков в целом растет спрос на золото. То есть между динамикой фондовых рынков и динамикой цен на золото существует обратная корреляционная зависимость. Другой пример. Рост котировок нефти и рост рынков, вес «нефтянки» в которых высок и является значимым. К таким рынкам относится и фондовый рынок России. Но в последние несколько лет, а именно в основном начиная с 2007 года, такие зависимости явно изменились. И либо сильно ослабли, либо исчезли совсем.
У приведенных выше примеров есть одна общая особенность: они построены строго на двух потоках данных, как того и требует формула расчета ЛКК. Тем не менее, в одной из книг, посвященных теории управления капиталом (а именно, Р.Винс «Математика управления капиталом») я нашел интересный подход к построению ЛКК на массиве, состоящем только из одного потока данных. Это может быть, например, непрерывный поток исходов в системных сделках или поток цен какой-то одной акции. О таком методе построения ЛКК ниже.
Торговая стратегия, построенная на коэффициенте корреляции
На рисунке показана динамика максимальных недельных цен в акциях LKOH. Расчет ЛКК должен дать ответы на вопросы: Есть ли зависимость между максимальными ценами двух любых соседних недель. Если зависимость есть, то какова ее направленность? Коллеги, если упростить, то вопрос можно сформулировать так: Если на истекшей неделе Лукойл обновил свой недельный максимум по сравнению с предыдущей неделей, то можем ли мы ожидать продолжения роста и на будущей неделе? Для расчета ЛКК поток данных требует некоторой трансформации. Составим таблицу:
В таблице на рисунке в последнем столбце, построенном на основе данных столбца «High цена», логика расчета следующая: если максимум текущей недели выше, чем максимум предыдущей недели, то в ячейке стоит значение 1. В противном случае значение равно 0. Таким образом, поток цен преобразован в поток единиц и нулей. Далее произведем расчет ЛКК на основе данных столбца «Обновление High цены». Поскольку для расчета ЛКК необходимо два потока данных, то сделаем следующее:
Начиная с 30й недели выборки (август 2001 года) для каждой недели рассчитаем значение ЛКК по последним 30 неделям. То есть для каждой недели рассчитаем т.н. «скользящее» значение ЛКК с периодом n=30 (по аналогии со скользящей средней), поскольку при n>30 в общем случае значение ЛКК считается значимым. Результаты расчетов отражены на рисунке:
Выводы по рисунка: На протяжении всего периода выборки у акций Лукойла наблюдается неярко выраженная положительная корреляция между максимальными ценами соседних недель (красная линия графика с ЛКК = +0,1). То есть факт обновления максимальной цены на текущей неделе по сравнению с предыдущей позволяет сделать предположение о том, что на следующей неделе в сравнении с текущей вероятность обновления максимума выше вероятности НЕобновления максимума.
В точках, где синяя линия находится выше красной, корреляция между недельными максимумами выше средней за период и имеет прямую направленность. В таких точках при обновлении недельных максимумов на текущей неделе наиболее вероятно обновление максимумов в течение следующей недели. В точках, где синяя линия находится ниже красной, корреляция между недельными максимумами ниже средней за период и имеет в основном обратную направленность. В таких точках, в отличие от ситуации п.5, наиболее вероятно обновление максимумов в течение следующей недели при НЕобновлении недельных максимумов текущей недели.
Коллеги, на основании последних двух выводов у меня сформировалась идея тестирования стратегии, построенной на принципах такого парного корреляционного эффекта.
Торговля ациями по коэффициенту корреляции
Само решение принимается в промежутке между закрытием торговой недели и открытием следующей торговой недели. В случае формирования торгового сигнала трейдеру необходимо находиться в рынке утром первого дня торговой недели для открытия позиции и вечером последнего дня торговой недели для выхода из бумаг. Для тестирования такой стратегии вполне хватило возможностей Excel. У недельного Лукойла критическим значением ЛКК оказалось значение 0,15. Приведу пару примеров для иллюстрации:
Сигнал от 25.06.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1855 (>0,15) и обновлен максимум предыдущей недели (1805 руб. > 1765 руб.). На основании этого на Open свечи 02.07.12 совершена покупка по 1804 руб. Позиция закрыта на Close свечи 02.07.12, то есть 06.07.12, по цене 1825 руб. Рентабельность сделки составила +1,2% при периоде удержания позиции 5 сессий.
Сигнал от 07.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1098 (
Сигнал от 21.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1336 ( 0,15 + новый максимум)
Из 600 недель тестового периода сигналы по Варианту 1 возникли в 109 случаях (19% потока или каждая пятая неделя). Из 109 сигналов 74 отработали в плюс (68%, или два из трех сигналов). Средний результат положительного исхода равен по модулю среднему результату отрицательного исхода (38 руб./акция) Общий положительный результат потока сигналов сформирован за счет превышения в 2 раза количества положительных исходов над отрицательными исходами.
Покупка по Варианту 2 (ЛККкр
В целом стратегия показала неплохой тренд-следящий результат, а так же оказалась достаточно устойчива в условиях падения 2008 года. Особенно, если учесть усилия трейдера по следованию сигналам. Коллеги, за сим пока все по описанию линейной корреляции и ее применении в трейдинге.
Коэффициент корреляции валютных пар
Рассмотрим такое явление, как межвалютная корреляция на Форексе. Данная методика может существенно повысить понимание рыночных процессов, а также улучшить качество ваших краткосрочных и среднесрочных прогнозов. Существует две разновидности межвалютной корреляции, которые могут помочь в работе трейдера. Рассмотрим подробнее.
Как анализировать корреляцию?
Для того чтобы легче было понять взаимосвязи и соотношение с числом коэффициента корреляции я подготовил рисунки, которые наглядно показывают коэффициент и визуальное сходство двух рядов. В качестве примера взяты рад косинуса и зашумлённый ряд косинусоиды, от амплитуды зашумления зависит коэффициент корреляции:
Изменение коэффициента корреляции ценовых графиков
В качестве примера корреляции двух пар с положительным К, можно вспомнить о EUR/USD и EUR / JPY. В обоих случаях мы покупаем EUR и продаем вторую валюту. Некоторые пары движутся относительно друг друга, но со временем К может меняться. Например, чтобы определить для своей работы две коррелирующие между собой валютные пары, достаточно найти такую из всего ассортимента, предоставляемого ДЦ, которая бы имела очень низкую волатильность. В 2012 году в качестве такого инструмента вполне могла бы выступать EUR/CHF. Не каждый день ширина ее движения на рынке превышала бы 30 пунктов, что можно считать малой величиной, относительно аналогичных показателей других пар.
Данную валютную пару можно без труда разложить на две пары, используя для этого ту валюту, которая “разбавит” выбранный нами инструмент. Для этого мы берем USD, который позволит представить нам EUR/CHF, как EUR/USD*USD/CHF. Действительно, если перемножить две новых долларовых пары, то в результате мы вновь получаем исследуемую нами EUR/CHF. Данное преобразование говорит о том, что обе пары будут коррелировать между собой, так как их произведение будет демонстрировать значения пары EUR/CHF, а они относительно малы, о чем говорили в самом начале примера.
Для уверенной торговли необходимо иметь четкое представление не только об особенностях отдельных инструментов торговли, но и об их взаимодействии друг с другом. Существуют целые торговые стратегии, построенные с использованием К. Могут применяться даже наложения одного ценового графика на другой, для выявления аналогий в движениях цены. Коэффициент может периодически рассчитываться заново, учитывая последние изменения в поведении ценовых графиков.
Коэффициент корреляции в анализе инвестиционного портфеля
Согласно Марковицу, любой инвестор должен основывать свой выбор исключительно на ожидаемой доходности и стандартном отклонении при выборе портфеля. Таким образом, осуществив оценку различных комбинаций портфелей, ондолжен выбрать «лучший», исходя из соотношения ожидаемой доходности и стандартного отклонения этих портфелей. При этом соотношение доходность-риск портфеля остается обычным: чем выше доходность, тем выше риск.
На рисунке выше жирной линией отображена «эффективная граница», а большими точками отмечены возможные комбинации портфелей.
Для построения минимально-дисперсионной границы и определения «эффективной границы» нам будут необходимы значения ожидаемых доходностей, рисков (стандартных отклонений) и ковариации активов. Имея эти данные можно приступить к нахождению «эффективных портфелей».
Начнем с расчета ожидаемой доходности портфеля по формуле:
И как следствие найдем стандартное отклонение портфеля, которое является квадратным корнем из дисперсии. Для наглядности приведем пример построения эффективной границы при помощи Microsoft Excel, а точнее при помощи встроенного в него компонента Поиск решения.
Рассчитаем ожидаемую доходность, дисперсию и стандартное отклонение средневзвешенного портфеля:
Как видно из таблицы, для определения дисперсии портфеля нужно просто просуммировать данные в ячейках B19-D19, а квадратный корень из значения ячейки C21 даст нам стандартное отклонение портфеля в ячейке C22. Произведение долей бумаг на их ожидаемую доходность даст нам ожидаемую доходность нашего портфеля, которая отражена в ячейке C23. Окончательный результат средневзвешенного портфеля представлен ниже.
Средняя (ожидаемая) месячная доходность средневзвешенного портфеля 0,28% при риске 6,94%. Теперь можноприменить тот самый второй принцип, о котором было написано выше, т.е. обеспечить минимальный риск при заданном уровне доходности. Для этого воспользуемся функцией «Поиск Решений» из меню «Сервис». Если нет, значит надо открыть «Сервис» выбрать «Надстройки» и установить «Поиск решений». Запускаем «Поиск решений», в пункте «Установить указанную ячейку» указываем ячейку С22, которую будем минимизировать за счет изменения долей бумаг в портфеле, т.е. варьированием значений в ячейках A16-A18. Далее надо добавить два условия, а именно:
— сумма долей должна равняться 1, т.е. ячейка A19 = 1;
— задать доходность, которая нас интересует, к примеру, доходность 0.28% (ячейка С23), которая получилась при расчете средневзвешенного портфеля.
Так как мы запрещаем наличие «коротких» позиций по бумагам в меню «Параметры» надо установить галочку «Неотрицательные значения». Вот так должно выглядеть:
В результате мы получаем:
Итак, задав «Поиск решений» найти минимальное стандартное отклонение при заданной ожидаемой доходности в 0,33% мы получили оптимальный портфель, состоящий на 83% из РАО ЕЭС, на 17% из Лукойла и на 0% из Ростелекома. Несмотря на то, что уровень доходности тот же, что и при средневзвешенном портфеле, риск снизился.
Парный трейдинг и коэффициент корреляции
Понятие корреляция лежит в основе многих прибыльных торговых стратегий валютного рынка. В качестве примера можно привести парный трейдинг, основанный на корреляции валютных пар, позволяющий получить стабильную высокую прибыль на разных коррелирующих инструментах (об этом мы писали в предыдущих статьях) и торгового робота Octopus Arbitrage, его реализующего. В этой статье мы попытаемся просто и доступно объяснить суть корреляции и показать, как это можно применить на практике для парного трейдинга.
Почему было решено посвятить этой теме отдельную статью? Дело вот в чем. Несмотря на то, что корреляция нашла широкое практическое применение, доступное объяснение найти весьма трудно.
Рассмотрим пример. Насколько связаны между собой количество прибыли, которую заработал трейдер за торговую сессию от количества выпитых им чашек кофе за тот же период? Т.е. имеем две величины: количество кружек кофе и прибыль.
Ну что ж, похоже количество выпитого кофе на получение прибыли трейдером не влияет никак. Коэфициент корреляции R2 всего лишь 0,0289, линия тренда почти горизонтальна. Почему так? Возможно, помимо выпитого кофе существует множество факторов, оказывающих куда более существенное влияния на получение прибыли: факторы рынка, работа ДЦ, особенности выбранной торговой стратегии, личные качества трейдера и т.д.
Теперь разберем другой пример. Рассмотрим связь между валютными парами EUR/USD и GBP / USD. Были взяты скользящие средние дневных цен с 2 по 5 декабря 2013 года. Было взято четыре точки для простоты дальнейшего объяснения расчетов. Как правило, для подобных расчетов, точек нужно брать больше.
Теперь, аналогично, предыдущему примеру на основании этих данных построим график в Excel.
Так, здесь видно, что зависимость гораздо сильнее, так как R2 близко к единице, а линия тренда расположена почти под 45о. Можно сказать, что величины здесь коррелируют. Теперь рассмотрим, как рассчитывается коэффициент R. Здесь, к сожалению, без формул не обойтись. Однако, на самом деле, все заумные формулы можно свести к уровню седьмого класса средней школы. Для начала определимся, что у нас есть две «случайные» величины. Обозначим EURUSD как X, а GBPUSD как Y.
Далее хочу отметить, что большинство понятий, математической статистики базируются на среднем значении выборки. Проще говоря, на среднем арифметическом, т.е. сумма всех элементов, поделенная на их число. Вычислим среднее для величин X и Y.
Далее, приведем формулу расчета R2. В ней нет ничего сложного, как может показаться на первый взгляд. Здесь просто используются вычисленные нами средние арифметические:
Подставив выделенное в формулу получаем:
Таким образом, мы получили, посчитав «вручную», то, что автоматически делает Excel. Коэффициент R2 называется еще «коэффициентом Пирсона». Корреляция по EURUSD и GBPUSD, на самом деле, достаточно сильная, на это конечно есть фундаментальные причины, рассмотрение которых находится за рамками этой статьи.
При расхождении инструментов открываются встречные позиции, при возвращении корреляции в исходное положение, встречные ордера закрываются, прибыль фиксируется на одной или обеих позициях
Безусловно, в нашей статье, описаны только основные принципы корреляции и парного трейдинга, поняв которые можно четко уяснить суть. Однако, для того, чтобы получать прибыль на FOREX, одних этих знаний недостаточно. Необходимо использовать специальные индикаторы, понимать расхождение каждой из пар и многое другое. Сколько трейдеров уже набили себе шишек на этом пути!
Кроме того, необходимо постоянно быть «в рынке», двадцать четыре часа в сутки, семь дней в неделю, чтобы «не проспать», когда разойдется или же наоборот сойдется корреляция. При этом для устойчивого получения прибыли необходимо использовать не две валютные пары, а больше. Трейдер просто физически не сможет этого сделать. Как же здесь быть?
Коэффициент корреляции в психологических исследованиях
Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны. Построим аналогичный график для Застенчивости и Общительности.
Коэффициент корреляции отражает степень приближенности точек на графике к прямой. Приведём примеры графиков, отражающих различную степень взаимосвязи (корреляции) переменных исследования. Сильная положительная корреляция:
Слабая положительная корреляция:
Источники и ссылки
Полезное
Смотреть что такое «Коэффициент корреляции» в других словарях:
Коэффициент корреляции — Математическое представление о степени связи между двумя сериями измерений. Коэффициент +1 обозначает четкую позитивную корреляцию: высокие показатели по одному параметру (например, рост) точно соотносятся с высокими показателями по другому… … Большая психологическая энциклопедия
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ — англ. coefficient, correlation; нем. Korrelationskoeffizient. Мера тесноты связи двух или более переменных. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
коэффициент корреляции — — [http://www.dunwoodypress.com/148/PDF/Biotech Eng Rus.pdf] Тематики биотехнологии EN correlation coefficient … Справочник технического переводчика
Коэффициент корреляции — Корреляция статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к… … Википедия
коэффициент корреляции — 1.33. коэффициент корреляции Отношение ковариации двух случайных величин к произведению их стандартных отклонений: Примечания 1. Эта величина всегда будет принимать значения от минус 1 до плюс 1, включая крайние значения. 2. Если две случайные… … Словарь-справочник терминов нормативно-технической документации
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ — (correlation coefficient) мера ассоциации одной переменной с другой. См. Корреляция; Коэффициент корреляции производного значения Пирсона; Коэффициент ранговой корреляции спирмена … Большой толковый социологический словарь
Коэффициент корреляции — CORRELATION COEFFICIENT Показатель степени линейной зависимости между двумя переменными величинами: Коэффициент корреляции может изменяться в пределах от 1 до 1. Если большим значениям одной величины соответствуют большие значения другой (и… … Словарь-справочник по экономике
коэффициент корреляции — koreliacijos koeficientas statusas T sritis automatika atitikmenys: angl. correlation coefficient vok. Korrelationskoeffizient, m rus. коэффициент корреляции, m pranc. coefficient de corrélation, m … Automatikos terminų žodynas
коэффициент корреляции — koreliacijos koeficientas statusas T sritis fizika atitikmenys: angl. correlation coefficient vok. Korrelationskoeffizient, m rus. коэффициент корреляции, m pranc. coefficient de corrélation, m … Fizikos terminų žodynas

 на
на