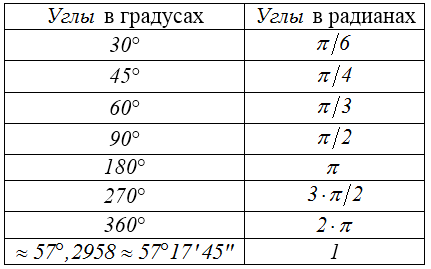
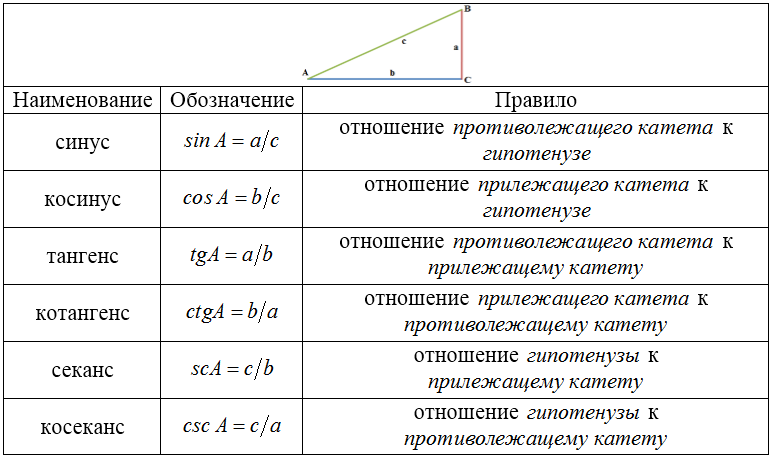
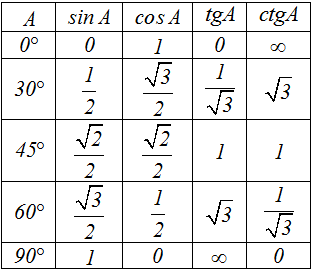
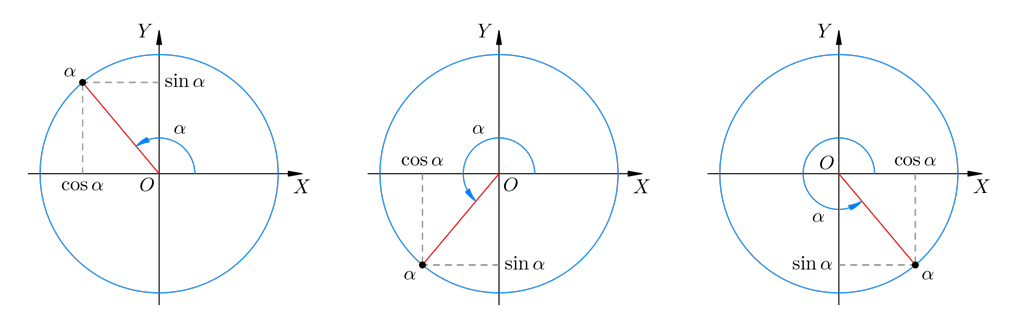
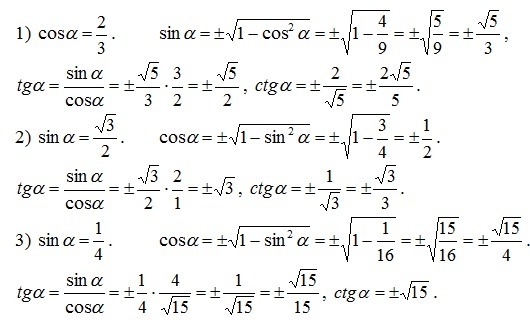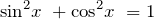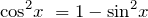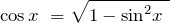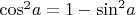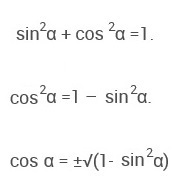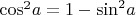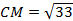Как найти косинус через синус
Как найти косинус через синус
Формулы связи тригонометрических функций. Примеры из ЕГЭ
\(sin^2 776^° +cos^2 776^° =1\)
\(tg\, 3x\cdot ctg\, 3x=1\)
\(sin^2x+cos^23x≠1\)
\(tg\, x\cdot ctg\, y≠1\)
Примеры применения формул связи
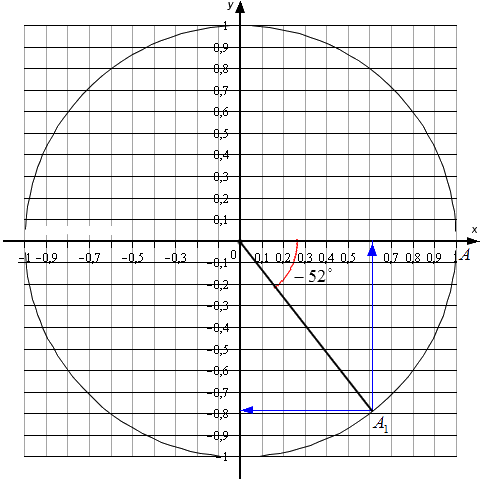
Пример. Найдите \(5sin\,α\), если \(cos\,α=\frac<2\sqrt<6>><5>\) и \(α∈(\frac<3π><2>;2π)\).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:
Подставим вместо косинуса его значение:
Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида \(x^2=a\) (при \(a>0\)) два корня \(x_1=\sqrt\) и \(x_2=-\sqrt\). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»
Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).
Значит, в нашем случае \(sin\,α=-\frac<1><5>\) т.е. \(5sin\,α=5\cdot(-\frac<1><5>)=-1\).
Пример.Найдите \(tg\,α\), если \(cos\,α=\) \(\frac<\sqrt<10>><10>\) и \(α∈(\frac<3π><2>;2π)\).
Решение. Есть 2 пути решения этой задачи:
— напрямую вычислить тангенс через формулу \(tg^2α+1=\) \(\frac<1>
— сначала с помощью тождества \(sin^2α+cos^2α=1\) найти \(sin\,α\), а потом через формулу \(tg\,α=\) \(\frac
В учебниках обычно идут первым путем, поэтому мы пойдем вторым.
Теперь вычислим косинус по упомянутой выше формуле:
Опять перед нами стоит выбор плюс или минус. Отметим отрезок \((\frac<π><2>;π)\) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.
Осталось найти синус:
Опять используем круг, чтобы определить знак.
Пример (ЕГЭ). Найдите \(tg^2 α\), если \(5 sin^2α+13 cos^2α=6\).
Решение. Давайте пойдем от того, что известно. В равенстве \(5 sin^2α+13 cos^2α=6\) синус заменим на косинус:
Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения \(tg^2α\) хорошо подходит формула \(tg^2α+1=\) \(\frac<1>
Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.
Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.
Приводим дроби к общему знаменателю.
\(1-cos^2α\) можно заменить на \(sin^2 α\).
Как выразить косинус через синус?
Для того, чтобы выразить косинус через синус, вспомним основное тригонометрическое тождество:
Таким образом, если известен синус, то косинус найти можно так:
Возможны 2 варианта:
Пример
1) Синус угла α = 0,3 и 90 автор вопроса выбрал этот ответ лучшим
Чтобы выразить косинус через синус надо знать формулу: sin²α + cos²α = 1.
А еще существует вот такая инструкция, по которой можно выразить косинус через синус:
Тригонометрические тождества ( или равенства ) очень часто используются в решении задач по геометрии.
Для того чтобы выразить косинус через синус необходимо знать одно из основных тригонометрических тождеств, которое, кстати несложно запомнить sin²α + cos²α = 1 ( сумма квадратов синуса и косинуса угла равна единице ).
Из этого тождества без особых проблем можно выразить как косинус угла, так и синус. Но поскольку в вопросе спрашивается все же именно про косинус угла, выразим его из вышеуказанного тригонометрического тождества:
Все, остается просто поставить в данную формулу значение sin²α и провести вычисления.
Как найти косинус угла, если известен синус?
Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).
Из основного тригонометрического тождества:
выразим косинус в квадрате угла а:
Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.
Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0
Примеры.
Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).
-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:
Рассмотрим пример для случая, когда угол находится в 4 четверти:
Решение такое же (см. пример 1).
Перед выбором ответа рассуждаем так:
Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.
Как найти косинус угла, если известен синус?
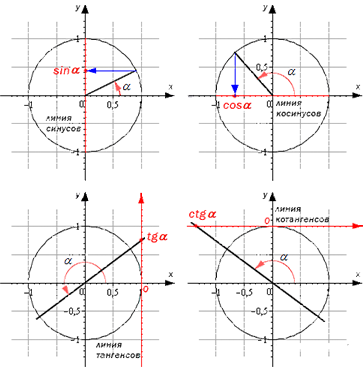
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества: sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Всё ещё сложно? Наши эксперты помогут разобраться Все услуги
Как найти cos
Здравствуйте!
Помогите разобраться как найти cos, tg и ctg, если известен только sin.
Спасибо!
Разберемся, как найти cos, tg и ctg, если известен только sin.
Начнем с косинуса.
Синус и косинус связывает много тригонометрических тождеств, но наиболее часто используется и является зачастую самым удобным основное тригонометрическое тождество. С его помощью можно найти квадрат косинуса или сам косинус. Приведем вариант тождества для вычисления косинуса через синус:
Так можно найти квадрат косинуса:
Так можно найти косинус:
Рассмотрим тангенс.
Поскольку тангенс можно найти через отношение синуса на косинус, а косинус можно выразить через синус, то получим следующую формулу:
с котангенсом ситуация похожа на тангенс, только котангенс равен отношению косинуса к синусу, поскольку котангенс является обратной функцией к тангенсу. Получим соответственно обратную формулу и для его нахождения по сравнению с тангенсом:
Есть, конечно же, и другие формулы для вычисления значений заданных функций через синус, но представленные выше являются основными, тем более их можно не заучивать наизусть, а при необходимости вывести самостоятельно. Как видите, для этого достаточно знать только одну формулу и основное свойство функций тангенс и котангенс.
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
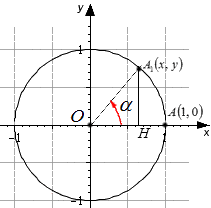
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Как найти синус угла, если известен косинус?
Для решения задачи следует воспользоваться основным тригонометрическим тождеством: сумма квадратов синуса и косинуса одного и того же угла равна 1.
Отсюда синус угла равен плюс минус корню квадратному из разности 1 и квадрата косинуса угла.
Какой знак перед корнем квадратным брать зависит от того, где находится угол, косинус которого известен.
Если в условии задачи значение косинуса больше нуля (равенство нулю рассмотрено, как частный случай, ниже, хотя применимы рассуждения и для нуля), то угол находится либо в 1-й, либо в 4-й четверти.
Для определенности в условии задачи обычно дается ограничение для угла.
Если указано, что 0
Решение. Находим разность 1 и квадрата значения cos a, т.е. квадрата (-0,8).
-0,8 возводим в квадрат, получим (-0,8)*(-0,8) = 0, 64. Подставим его в искомую разность:
Ответ: sina=-0,6.
Рассмотрим для краткости изложения этот же пример для случая, когда угол находится во второй четверти:
Решение будет точно таким же, как для примера 1.
Изменится лишь выбор ответа. Рассуждения будут следующими:
Так как по условию угол находится во 2 четверти, то искомое значение синуса будет положительным. Значит выбираем 0,6.
Как найти косинус угла, если известен синус?
Ответ мой будет аналогичным ответу на похожий вопрос (см. здесь).
Из основного тригонометрического тождества:
выразим косинус в квадрате угла а:
Знак перед корнем зависит от ограничения, которое накладывается для определенности в условии задачи.
Если дано положительное значение синуса,то угол находится в 1-й или во 2-й четверти. В первой четверти (0
Примеры.
Решение. Находим разность 1 и квадрата значения sina, т.е. квадрата (-0,6).
-0,6 в квадрате находится так: (-0,6)*(-0,6) = 0,36. Подставим его в искомую разность:
Рассмотрим пример для случая, когда угол находится в 4 четверти:
Решение такое же (см. пример 1).
Перед выбором ответа рассуждаем так:
Т. к. по условию угол расположен в 4 четверти, то значение косинуса будет больше нуля. Значит выбираем 0,8.
Что-то из них по тригонометрии равен отношению того к отношению этого, т.е надо перевернуть доску другой стороной кверху если синус угла наклона внизу и вернуть в исходное положение для того чтобы найти косинус угла наклона!
Всё предельно просто и основные вычисления строятся на базе одного всем известного уравнения, при котором сумма квадратов cos и sin одного и того же угла дают в итоге единицу.
Основным моментом, который может вызвать затруднения станет постановка положительного или отрицательного знак перед корнем.
Для таких случаев нужно помнить всегда главное тригонометрическое тождество
косинус квадрат альфа+ синус квадрат альфа=1
и вот отсюда уже выводим
Будем считать, что основное тригонометрическое тождество помнят все.
Формулу вспомнили, а дальше все легко.
В левой части уравнения оставляем косинус угла в квадрате, а в правую часть (где уже присутствует единица) перекидываем квадрат синуса угла. Получается следующее:
Нам нужен не квадрат косинуса, а косинус, поэтому уравнение выше преобразовываем и получаем:
Косинус угла равен квадратному корню единицы минус квадрат синуса (cos=sqrt(1-sin^2)).
Найти косинус угла можно из этого выражения:
Как называется формула не помню:
С уроков в школе примерно 10-11 класс, я помню формулу основного тригонометрического тождества, которую мы учили наизусть:
Получаем искомую функцию:
Таким несложным способом можно найти косинус, если известен синус. И использовать его при решении задач.
Сначала воспользуемся теоремой Пифагора
теперь подставляем полученные данные
Не стоит забывать, что при нахождении косинуса, следует убрать его квадрат и вычислить его квадратный корень. То есть те же значения после цифры равно поставить в квадратный корень при вычислении.
Между синусом и косинусом для одного и того же угла можно найти взаимосвязь, которая позволит найти косинус, зная синус. Вот так выглядит эта взаимосвязь:
Получается чтобы найти косинус в данном случае нам просто напросто будет нужно произвести извлечение корня из выражения (1-sin в квадрате конкретного угла).
По правде сказать, я практически ничего не помню про синусы, косинусы и тангенсы с котангенсами. Какие-то формулы смутно маячат на задворках моей памяти, но вспомнить их для меня уже затруднительно. А все потому, что после окончания школы я ими не занималась, поскольку дальнейшее мое образование было гуманитарного толка, и математику я уже больше не изучала.
Тем не менее я считаю, что изучение всех этих функций в школе пользу приносит. В частности, мозги развивает. Так что, может быть, эти синусы и косинусы мне и пригодились в некоторым смысле. Как знать, вдруг мое мышление было бы другим без их изучения.
Перепишем ваше неравенство следующим образом
Здесь sgrt2=2^(1/2) – квадратный корень из 2. Сокращение sgrt происходит от английских слов square root – квадратный корень. Так часто пишут в интернете. Удобно произвести такую замену
Тогда неравенство (1) запишется так cos(2A)-sgrt2*sinA>1. Вспомним хорошо известную в тригонометрии формулу для косинуса двойного угла cos(2A)=1-2sin^2(A), где sin^2(A) – синус А в квадрате. Тогда наше неравенство сводится к виду 1-2sin^2(A)-sgrt2*sinA>1.
Перепишем его так (единицы сокращаются)
Основные тригонометрические тождества: их формулировки и вывод
Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.
Связь между sin и cos одного угла
Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.
sin 2 α + cos 2 α = 1
В тригонометрии выражение sin 2 α + cos 2 α = 1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.
Тангенс и котангенс через синус и косинус
Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.
t g α = sin α cos α c t g α = cos α sin α
Отсюда следует, что полученные тождества t g α = sin α cos α и c t g α = cos α sin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.
Связь между тангенсом и котангенсом
Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.
Тангенс и косинус, котангенс и синус
Тригонометрические формулы
Тригонометрические формулы — элементарные функции, которые выражают зависимость всех сторон прямоугольного треугольника от острых углов при гипотенузе (или зависимость хорд и высот от его центрального угла в круге).
К прямым функциям тригонометрии относят: sin x (синус), cos x (косинус). К производным: tg x (тангенс), ctg x (котангенс). А также другие тригонометрические функции: sec x (секанс) и cosec x (косеканс).
Косинус и синус в тригонометрии являются Вещественнозначными функциями, которые неограниченно дифференцируются и являются периодически непрерывными. Остальные же наоборот дифференцируются в области определении, однако, как и прямые тригонометрические функции есть непрерывными.
Значения функция для некоторых углов представлены в следующей таблице. Обозначение «∞» говорит о том, что функция в данной точке не определена и стремится к бесконечности.
Основные тригонометрические тождества:
Переход от произведения к сумме:
Переход от суммы к произведению:

Возникновение тригонометрии и тригонометрических формул связанно с астрономией, строительным делом и землемерием. Не смотря на то, что некоторые факты и понятия были
известны еще две тысячи лет назад, сам термин тригонометрия появился относительно недавно. Впервые способ решать зависимости между сторонами треугольника нашли Гиппарх и Клавдий Птолемеи (ІІ н.е.). Только намного позже эти зависимости стали называть тригонометрическими формулами.
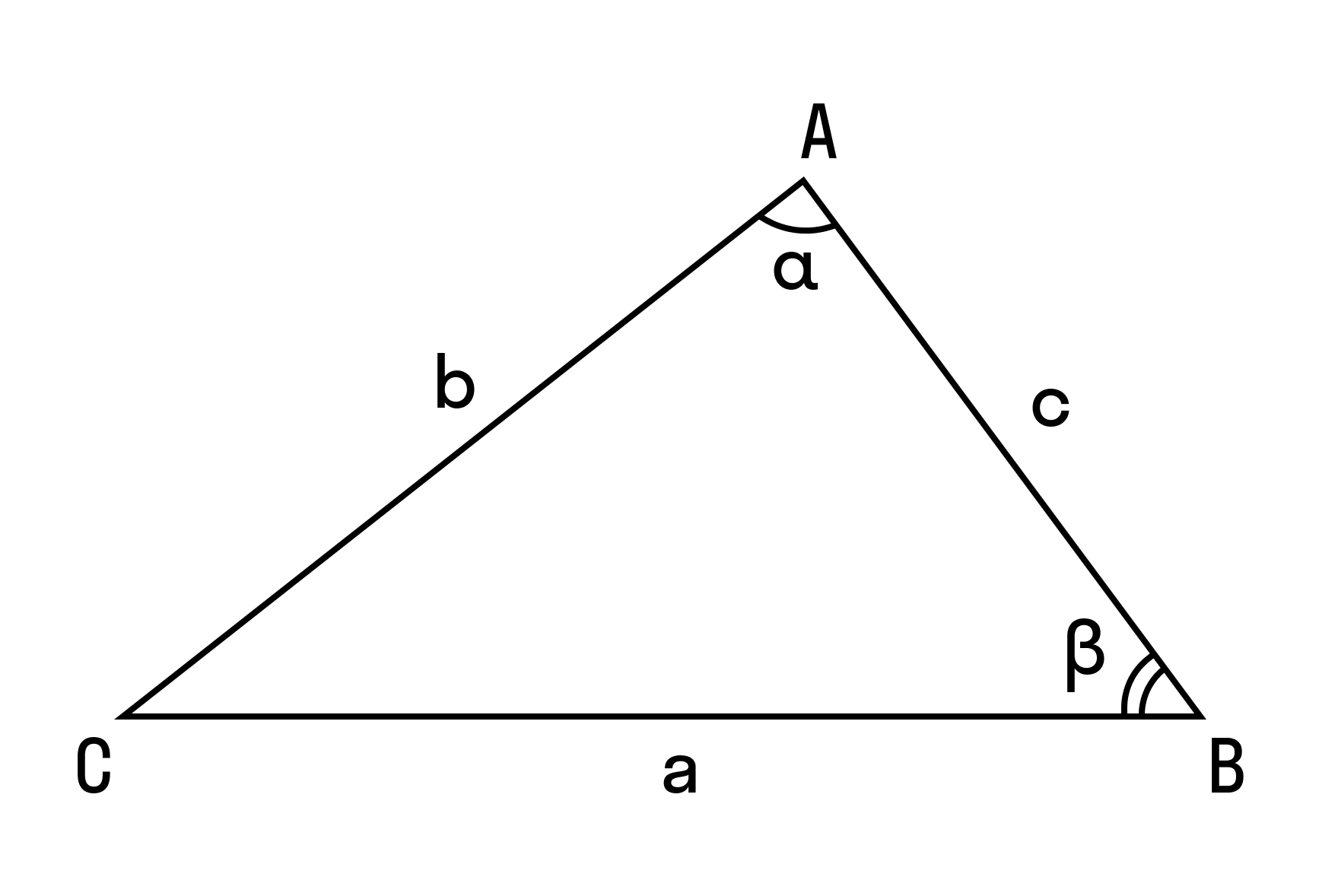
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
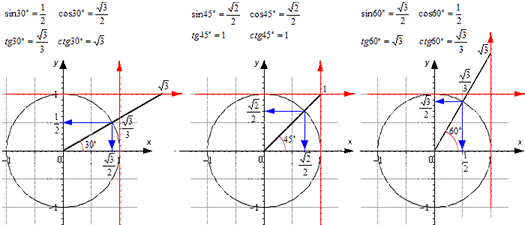
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Сведение к углу
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Формулы перехода от синуса к косинусу
Определения синуса, косинуса, тангенса и котангенса.
Знаки тригонометрических функций:
Значения тригонометрических функций
Формулы синуса, косинуса, тангенса и котангенса угла (–α):
sin (–α) = – sin α
cos (–α) = cos α
tg (–α) = – tg α
ctg (–α) = – ctg α
Все формулы приведения можно получить, пользуясь следующими правилами:
1. В правой части формулы ставится тот знак, который имеет левая часть при условии
2. Если в левой части формулы угол равен 







Формулы двойного угла.
Формулы перехода от суммы к произведению.
Формулы перехода от произведения к сумме.
Формулы понижения степени.
Преобразование выражения a·cos 


где вспомогательный аргумент определяется из условий
Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β – sin α · sin β cos α – β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = – 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 – cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 – cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 – cos α
Формулы понижения степени
sin 2 α = 1 – cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α – sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 – 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 ( – 1 ) n 2 – k · C k n · cos ( ( n – 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 C k n · cos ( ( n – 2 k ) α )
sin n α = 1 2 n – 1 ∑ k = 0 n – 1 2 ( – 1 ) n – 1 2 – k · C k n · sin ( ( n – 2 k ) α ) cos n α = 1 2 n – 1 ∑ k = 0 n – 1 2 C k n · cos ( ( n – 2 k ) α )
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α – β ) – cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α – β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α – β ) + sin ( α + β ) )
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции – синус, косинус, тангенс и котангенс, – могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 – t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 – t g 2 α 2 c t g α = 1 – t g 2 α 2 2 t g α 2
Тригонометрические формулы
Тригонометрические формулы основаны на тригонометрических функциях (ТФ) углов.
Распространены две системы измерения углов: градусная и радианная.
Попробуй обратиться за помощью к преподавателям
Полезно помнить следующую таблицу градусной и радианной меры некоторых часто встречающихся углов:
Определение синуса, косинуса и тангенса, знаки синуса, косинуса и тангенса
ТФ острого угла можно определить из прямоугольного треугольника:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Полезно помнить значения основных ТФ для часто встречающихся значений углов:
Обратные тригонометрические функции (ОТФ)
ОТФ многозначны. Поэтому из всего множества значений каждой из них выделяют главные, а наименования указывают со строчной буквы:
Как найти угол имея цифровое значение синуса, косинуса, тангенса?
Как найти угол имея цифровое значение синуса, косинуса, тангенса,котангенса? например есть значение sin a=0,3452 какой угол этому соответствует?
Функции: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), называются тригонометрическими. Они выражают зависимости длин сторон от углов треугольника при гипотенузе. Определяются отношением какой-либо из сторон треугольника к другой. То есть, показывают, насколько одна сторона больше другой. Это отношение может быть характерно только для строго определенного угла. Выражаются тригонометрические функции в безразмерных единицах.
Итак, ответ получен:
Синусу угла альфа со значением 0,3452 соответствует угол 20,194 градуса.
Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Геометрическое определение синуса и косинуса
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Как из косинуса получить синус – (sin cos)
Как найти угол, если известен синус 🚩 найти угол по синусу онлайн 🚩 Математика
Синус и косинус — пара основных тригонометрических функций, которые косвенно выражают величину угла в градусах. Всего таких функций существует больше десятка и среди них есть те, что позволяют по значению, например, синуса восстановить величину угла в градусах. Для практической работы с ними можно использовать программный калькулятор или сетевые сервисы.
Используйте функцию арксинус для вычисления величины угла в градусах, если известно значение синуса этого угла. Если угол обозначить буквой α, в общем виде такое решение можно записать так: α = arcsin(sin(α)). Если у вас есть возможность пользоваться компьютером, для практических расчетов проще всего использовать встроенный калькулятор операционной системы. В последних двух версиях ОС Windows его можно запустить так: нажмите клавишу Win, наберите буквы «ка» и надавите Enter. В более ранних выпусках этой ОС ссылку «Калькулятор» ищите в подразделе «Стандартные» раздела «Все программы» главного меню системы.
После запуска приложения переключите его в режим, позволяющий работать с тригонометрическими функциями. Сделать это можно выбором строки «Инженерный» в разделе «Вид» меню калькулятора или нажатием клавиш Alt + 2.
Введите значение синуса. По умолчанию в интерфейсе калькулятора нет кнопки для вычисления арксинуса. Чтобы получить возможность использовать эту функцию, вам нужно инвертировать значения кнопок по умолчанию — кликните по клавише Inv в окне программы. В более ранних версиях эту кнопку заменяет чекбокс с таким же обозначением — поставьте в нем отметку.
Кликните по кнопке вычисления синуса — после инвертирования функций ее обозначение сменится на sin⁻¹. Калькулятор рассчитает угол и отобразит его величину.
Можно использовать в расчетах и различные онлайн-сервисы, которых более чем достаточно в интернете. Например, перейдите на страницу http://planetcalc.com/326/, прокрутите ее немного вниз и в поле Input введите значение синуса. Для запуска процедуры вычисления здесь предназначена оранжевая кнопка с надписью Calculate — кликните по ней. Результат вычислений вы найдете в первой строке таблицы под этой кнопкой. Кроме арксинуса в ней отображаются и величины арккосинуса, арктангенса и арккотангенса введенного значения.
Такие понятия как синус, косинус, тангенс вряд ли кому-то часто встречаются в повседневной жизни. Однако, если вы сели решать математические задачки с сыном-старшеклассником, неплохо было бы вспомнить, что же это за понятия, и как найти, например, косинус.
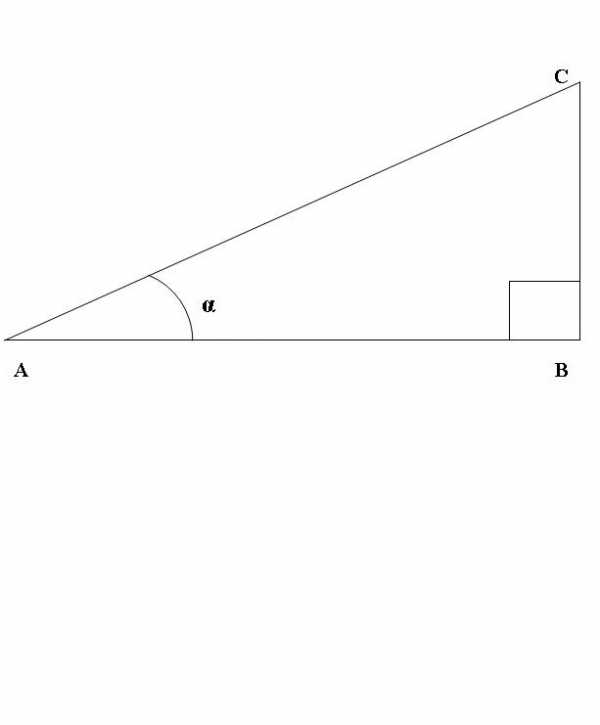
Для того чтобы получить формулу, связывающую синус и косинус угла, необходимо дать или вспомнить некоторые определения. Так, синус угла — это отношение (частное от деления) противолежащего катета прямоугольного треугольника к гипотенузе. Косинус угла — это отношение прилежащего катета к гипотенузе.
Нарисуем прямоугольный треугольник АВС, где угол АВС — прямой (рис.1). Рассмотрим соотношение синуса и косинуса угла САВ. По данному выше определению
sin CAB=BC/AC, cos CAB=AB/AC. Вспоминаем теорему Пифагора — АВ^2 + BC^2 = AC^2, где ^2 — операция возведения в квадрат.
Разделим левую и правую части уравнения на квадрат гипотенузы AC. Тогда предыдущее равенство будет выглядеть так:
АВ^2/AC^2 + BC^2/AC^2 = 1.
Для удобства перепишем равенство, полученное на шаге 2, следующим образом:
(AB/AC)^2 + (BC/AC)^2 = 1.
Согласно определениям, данным на шаге 1, получаем:
cos^2(CAB) + sin^2(CAB) = 1, т.е.
cos(CAB)=SQRT(1-sin^2(CAB)), где SQRT — операция взятия квадратного корня.
Величина синуса и косинуса любого угла не может быть больше 1.
Косинус, как и синус, относят к «прямым» тригонометрическим функциям. Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного угла по известному значению косинуса от этой же величины.
Есть и еще более экзотический вариант с использованием определения косинуса и тангенса через острые углы прямоугольного треугольника. Косинусу в таком определении соответствует отношение длины прилежащего к рассматриваемому углу катета к длине гипотенузы. Зная значение косинуса можно подобрать соответствующие ему длины этих двух сторон. Например, если cos(α)=0,5, то прилежащий катет можно принять равным 10см, а гипотенузу — 20см. Конкретные числа здесь значения не имеют — одинаковое и правильное решение вы получите с любыми значениями, имеющими такое же соотношение. Затем по теореме Пифагора определите длину недостающей стороны — противолежащего катета. Она будет равна квадратному корню из разницы между длинами возведенных в квадрат гипотенузы и известного катета: √(20²-10²)=√300. Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.
При наличии доступа в интернет используйте онлайн-сервисы, которые размещают на своих страницах калькуляторы тригонометрических функций. Например, перейдите на страницу http://planetcalc.ru/307/ и в поле «Угол» введите величину угла, тангенс которого требуется определить. Если это значение дано не в градусах, а в радианах, градах, угловых минутах или секундах, поставьте отметку в соответствующем поле. Затем нажмите оранжевую кнопку «Рассчитать», и скрипты сервиса произведут необходимые вычисления. Ответ прочтите в поле «Значение» строки «Тангенс» из таблицы, размещенной ниже оранжевой кнопки отправки данных. Кроме тангенса в этой таблице можно увидеть значения еще десяти тригонометрических функций, соответствующих введенному углу. Если доступа в интернет нет, можно использовать программу-калькулятор, входящую в состав операционной системы Windows. Для ее запуска нажмите клавишу Win, введите пару букв названия программы — «ка» — и нажмите Enter. Внутренняя поисковая система найдет и запустит нужное приложение. В версиях, выпущенных раньше, чем такой механизм поиска был встроен в главное меню ОС (например, Windows XP), используйте для запуска пункт «Выполнить» в том же меню — введите в окошко диалога calc и кликните по кнопке OK.
Переключите интерфейс из режима «Обычный» в «Инженерный» — нажмите «горячие клавиши» Alt + 2 или выберите пункт с названием этого режима в разделе «Вид» меню калькулятора.
Наберите величину угла, тангенс которого требуется определить. По умолчанию калькулятор считает введенное значение градусной мерой, но если вам оно дано в радианах или градах, поставьте соответствующую отметку под основным окошком калькулятора. Затем нажмите кнопку, помеченную надписью tan, и программа рассчитает и отобразит результат с точностью до 32 знаков после запятой. Его можно скопировать простым нажатием клавиш Ctrl + C, чтобы затем использовать по своему усмотрению.
Одной из фундаментальных основ точных наук является понятие о тригонометрических функциях. Они определяют простые отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Найти его, зная угол, можно большим количеством способов, включающих экспериментальные, вычислительные методы, а также использование справочной информации.
Используйте калькулятор с функцией вычисления синуса для получения нужных значений на основании знания угла. Подобный функционал сегодня имеют даже самые простые устройства. При этом вычисления производятся с очень высокой степенью точности (как правило, до восьми и более знаков после запятой).
Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами подобных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в любую ячейку формулу, состоящую из вызова функции вычисления синуса с нужным аргументом. Нажмите Enter. В ячейке отобразится искомая величина. Преимуществом электронных таблиц является возможность быстрого расчета значений функций для большого набора аргументов.
Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками после запятой.
Найдите приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого необходимо найти. Начертите еще один отрезок, пересекающий первый в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два уже существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Разделите второе значение на первое. Это и будет искомая величина.
Рассчитайте синус угла, используя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х — (х^3)/3! + (х^5)/5! — (х^7)/7! + (х^9)/9! — … Для повышения скорости расчетов записывайте текущее значение числителя и знаменателя последнего члена ряда, производя вычисление следующего значения на основе предыдущего. Увеличивайте длину ряда для получения более точной величины.
Как из косинуса получить тангенс
1) Определить четверть угла (примерно), а из неё знак синуса 2) sin^2 a + cos^2 a = 1, отсюда найти синус (интегралы-то зачем? квадратного корня хватит) 3) tg a = sin a / cos a
вот ты не умничай, а купи у меня таблицы Брадиса и логарифмическую линейку.. и не говори мне, что не знаешь, что это такое…
тангенс от арккосинуса
как найти синус и косинус если знаем тангенс и катангенс? плиз помогите
Синус и косинус можно будет узнать с точностью до знака из соотношений: 1+tg²x = 1/cos²x 1+ctg²x = 1/sin²x Отсюда cos(x) = ±1/√(1+tg²x) sin(x) = ±1/√(1+ctg²x) При этом знаки у синуса и косинуса должны быть согласованы: если тангенс или котангенс положительны, то синус и косинус имеют одинаковый знак; а если тангенс или котангенс отрицательны, то знаки синуса и косинуса противоположны.
В таблице тригонометрических величин за среднюю школу
tg(x) = sin(x)/cos(x) sin^2(x) = 1-cos^2(x) tg^2(x) = (1 — cos^2(x))/cos^2(x) = 1/cos^2(x) — 1 tg^2(x)*cos^2(x) = 1 — cos^2(x) cos^2(x)*(tg^2(x) + 1) = 1 cos^2(x) = 1/(tg^2(x) + 1) cos(x) = sqrt(1/(tg^2(x) + 1) с синусом все абсолютно аналогично, только проще через котангенс считать.
Тригонометрические формулы. Их вывод
Наиболее часто встречающиеся тригонометрические формулы:
\(\blacktriangleright\) Основные тождества: \[\begin
\(\blacktriangleright\) Формулы сложения углов: \[\begin
\(\blacktriangleright\) Формулы понижения степени: \[\begin
\(\blacktriangleright\) Формулы произведения функций: \[\begin
\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin
\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
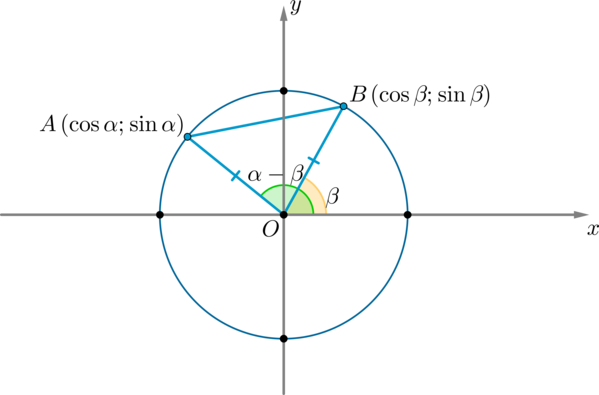
\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства \((1)\) и \((2)\) :
Отсюда и получается наша формула.
\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :
\(\blacktriangleright\) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)
разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm
5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)
6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)
\(\blacktriangleright\) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)
2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)
\(\blacktriangleright\) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
\(a\sin x+b\cos x=\sqrt
\(\sqrt
Значит, формула выглядит следующим образом: \[<\large
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)
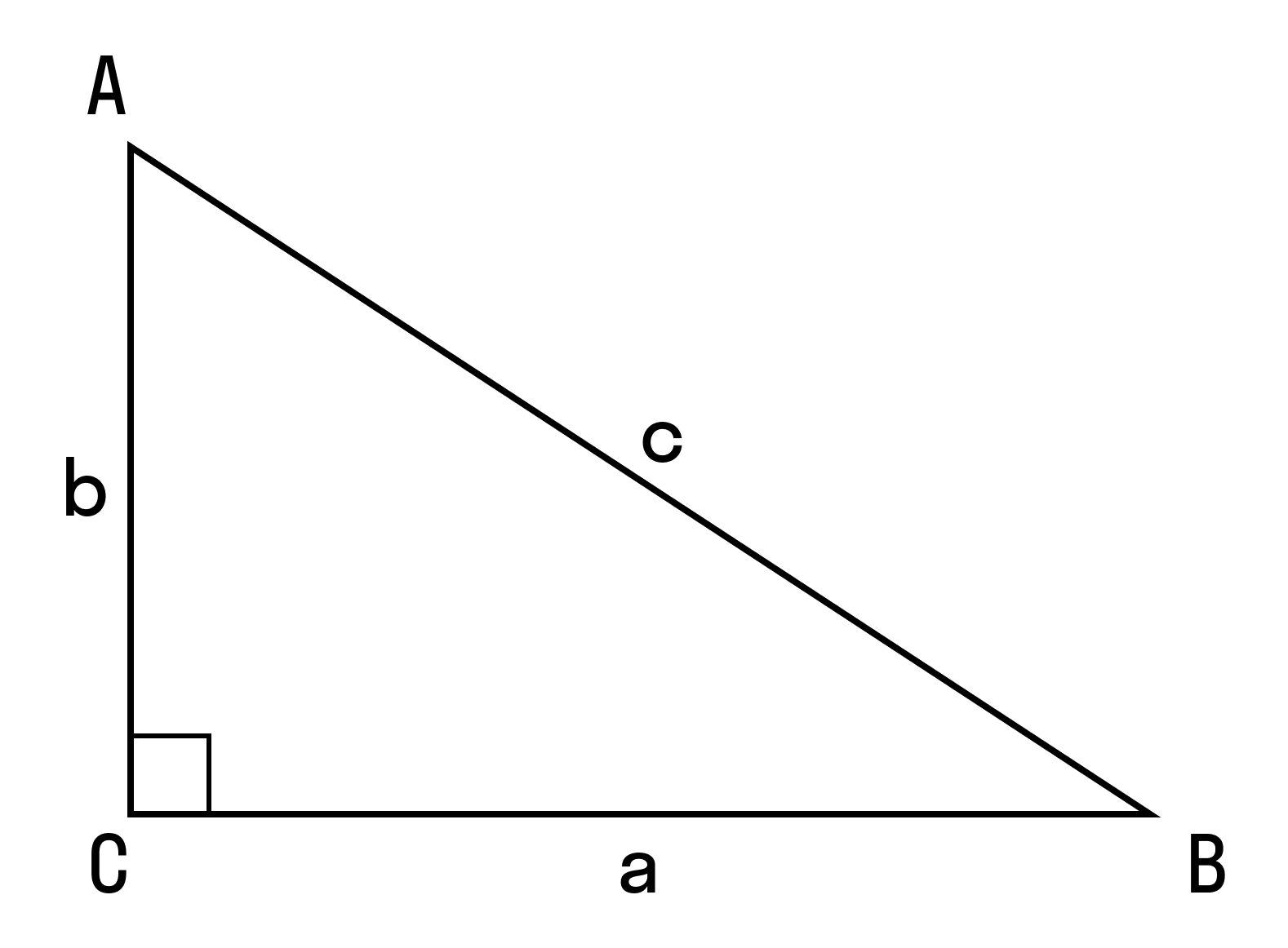
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
В статье мы расскажем, как находить значения:
Как вычисляются синусы и косинусы углов?
Предположим, стоит задача найти косинус и синус угла \(30^°\). Отложим на круге угол в \(30^°\) и найдем какая точка соответствует этому углу.
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают \(0,1\); \(0,2\); \(0,3\) и т.д., а сразу наносят стандартные значения для синуса и косинуса: \(±\frac<1><2>=±0,5\); \(±\frac<\sqrt<2>> <2>≈±0,707\); \(±\frac<\sqrt<3>> <2>≈±0,866\).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
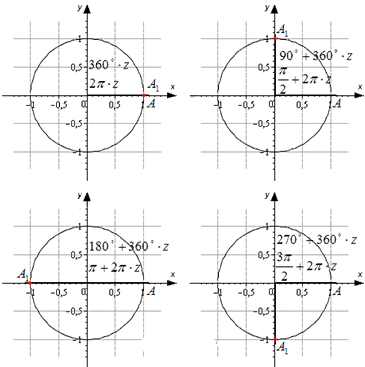
Как отметить любой угол на тригонометрическом круге?
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна \(360^°\), полуокружности \(180^°\), а четверти \(90^°\);
Углы в \(0^°\), \(30^°\), \(45^°\) и \(60^°\) выглядят так:
Задание 1 . Отметьте на окружности точки соответствующие углам: \(720^°\), \(225^°\), \(300^°\), \(870^°\), \(900^°\), \(-330^°\), \(-630^°\), \(-210^°\).
Как находить синус и косинус любого угла?
\(-540^°\) на тригонометрическом круге совпадает с \(-1\) на оси косинусов. То есть, координаты этой точки: \((-1;0)\). Значит, \(\cos(-540^°)=-1\), а \(\sin(-540^° )=0\).
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).
Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения \(54\sqrt<3>\cos(510^°)\).
Решение. \(510^°=360^°+150^°=360^°+180^°-30^°.\)
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Формулы суммы и разности синусов и косинусов
Формулы сложения.
sin (α + β) = sin α · cos β + sin β · cos α
sin (α – β) = sin α · cos β – sin β · cos α
cos (α + β) = cos α · cos β – sin α · sin β
cos (α – β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 – tg α · tg β)
tg (α – β) = (tg α – tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β – ctg α)
ctg (α – β) = (ctg α · ctg β – 1) ÷ (ctg β + ctg α)
Геометрическое определение синуса и косинуса
|BD| – длина дуги окружности с центром в точке A.
α – угол, выраженный в радианах.
Синус ( sin α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|. Косинус ( cos α ) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Тригонометрические функции суммы и разности углов
Список формул
Запишем формулы суммы и разности синусов и косинусов. Как Вы понимаете, их четыре штуки: две для синусов и две для косинусов.
Теперь дадим их формулировки. При формулировании формул суммы и разности синусов и косинусов угол 



Стоит отметить, что формулы суммы и разности синусов и косинусов справедливы для любых углов 

Формулы двойного угла.
tg 2α = (2tg α) ÷ (1 – tg² α)
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Примеры использования
Разберем несколько примеров использования формул суммы синусов и косинусов, а также разности синусов и косинусов.
В некоторых случаях использование формул суммы и разности синусов и косинусов позволяет вычислять значения тригонометрических выражений, когда углы отличны от основных углов (
Вычислите точное значение разности синусов 165 и 75 градусов.
Таким образом, имеем

Несомненно, главная ценность формул суммы и разности синусов и косинусов заключается в том, что они позволяют перейти от суммы и разности к произведению тригонометрических функций (по этой причине эти формулы часто называют формулами перехода от суммы к произведению тригонометрических функций). А это в свою очередь может быть полезно, например, при преобразовании тригонометрических выражений или при решении тригонометрический уравнений. Но эти темы требуют отдельного разговора.
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
 | Выражение квадрата синуса через косинус двойного угла |
 | Выражение квадрата косинуса через косинус двойного угла |
 | Выражение квадрата тангенса через косинус двойного угла |
| Выражение квадрата синуса через косинус двойного угла |
 |
| Выражение квадрата косинуса через косинус двойного угла |
 |
| Выражение квадрата тангенса через косинус двойного угла |
 |
Основные тригонометрические тождества
Вывод формул
Также нам потребуется представление углов 







Теперь подробно разберем вывод формулы суммы синусов двух углов вида 
Сначала в сумме 







После приведения подобных слагаемых получаем 

Для вывода остальных формул нужно лишь проделать аналогичные действия. Приведем вывод формул разности синусов, а также суммы и разности косинусов:
Итак, мы разобрали доказательство всех формул суммы и разности синусов и косинусов.
Соотношение между косинусом и тангенсом:
1/cos 2 α−tan 2 α=1 или sec 2 α−tan 2 α=1.
Данная формула является следствием основного тригонометрического тождества и получается из него делением левой и правой части на cos2α. Предполагается, что α≠π/2+πn,n∈Z.
Соотношение между синусом и котангенсом:
1/sin 2 α−cot 2 α=1 или csc 2 α−cot 2 α=1.
Эта формула также следует из основного тригонометрического тождества (получается из него делением левой и правой части на sin2α. Здесь предполагается, что α≠πn,n∈Z.
Формулы приведения
Тригонометрические функции
Онлайн калькулятор тригонометрических функций вычисляет синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec) для угла заданного в градусах, радианах, градах, минутах или секундах.
Тригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
haversin — гаверсинус (половина от синус-верзус)
exsec — экссеканс
excsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.
Найти угол, зная косинус угла: примеры решения
Вы будете перенаправлены на Автор24
Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.
Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.
Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:
Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ
Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.
Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ
Решение:
Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ
Решение:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 07.05.2022
Таблица синусов и косинусов углов от 0 до 360 градусов
Таблица синусов и косинусов может пригодится учащимся, студентам и инженерам для произведения тригонометрических расчетов. Она позволяет найти синус и косинус любого целого угла от 0 до 360 градусов.
Пользоваться таблицей очень просто — найдите нужный угол и в той же строке увидите синус и косинус этого угла. Для примера возьмем угол, равный 30 градусам. Найдя его в таблице мы увидим, что Cos(30) = 0,866025404, а Sin(30) = 0,5.
| Угол (градусы) | Косинус (Cos) | Синус (Sin) |
|---|---|---|
| 0° | 1 | 0 |
| 1° | 0,999847695 | 0,017452406 |
| 2° | 0,999390827 | 0,034899497 |
| 3° | 0,998629535 | 0,052335956 |
| 4° | 0,99756405 | 0,069756474 |
| 5° | 0,996194698 | 0,087155743 |
| 6° | 0,994521895 | 0,104528463 |
| 7° | 0,992546152 | 0,121869343 |
| 8° | 0,990268069 | 0,139173101 |
| 9° | 0,987688341 | 0,156434465 |
| 10° | 0,984807753 | 0,173648178 |
| 11° | 0,981627183 | 0,190808995 |
| 12° | 0,978147601 | 0,207911691 |
| 13° | 0,974370065 | 0,224951054 |
| 14° | 0,970295726 | 0,241921896 |
| 15° | 0,965925826 | 0,258819045 |
| 16° | 0,961261696 | 0,275637356 |
| 17° | 0,956304756 | 0,292371705 |
| 18° | 0,951056516 | 0,309016994 |
| 19° | 0,945518576 | 0,325568154 |
| 20° | 0,939692621 | 0,342020143 |
| 21° | 0,933580426 | 0,35836795 |
| 22° | 0,927183855 | 0,374606593 |
| 23° | 0,920504853 | 0,390731128 |
| 24° | 0,913545458 | 0,406736643 |
| 25° | 0,906307787 | 0,422618262 |
| 26° | 0,898794046 | 0,438371147 |
| 27° | 0,891006524 | 0,4539905 |
| 28° | 0,882947593 | 0,469471563 |
| 29° | 0,874619707 | 0,48480962 |
| 30° | 0,866025404 | 0,5 |
| 31° | 0,857167301 | 0,515038075 |
| 32° | 0,848048096 | 0,529919264 |
| 33° | 0,838670568 | 0,544639035 |
| 34° | 0,829037573 | 0,559192903 |
| 35° | 0,819152044 | 0,573576436 |
| 36° | 0,809016994 | 0,587785252 |
| 37° | 0,79863551 | 0,601815023 |
| 38° | 0,788010754 | 0,615661475 |
| 39° | 0,777145961 | 0,629320391 |
| 40° | 0,766044443 | 0,64278761 |
| 41° | 0,75470958 | 0,656059029 |
| 42° | 0,743144825 | 0,669130606 |
| 43° | 0,731353702 | 0,68199836 |
| 44° | 0,7193398 | 0,69465837 |
| 45° | 0,707106781 | 0,707106781 |
| 46° | 0,69465837 | 0,7193398 |
| 47° | 0,68199836 | 0,731353702 |
| 48° | 0,669130606 | 0,743144825 |
| 49° | 0,656059029 | 0,75470958 |
| 50° | 0,64278761 | 0,766044443 |
| 51° | 0,629320391 | 0,777145961 |
| 52° | 0,615661475 | 0,788010754 |
| 53° | 0,601815023 | 0,79863551 |
| 54° | 0,587785252 | 0,809016994 |
| 55° | 0,573576436 | 0,819152044 |
| 56° | 0,559192903 | 0,829037573 |
| 57° | 0,544639035 | 0,838670568 |
| 58° | 0,529919264 | 0,848048096 |
| 59° | 0,515038075 | 0,857167301 |
| 60° | 0,5 | 0,866025404 |
| 61° | 0,48480962 | 0,874619707 |
| 62° | 0,469471563 | 0,882947593 |
| 63° | 0,4539905 | 0,891006524 |
| 64° | 0,438371147 | 0,898794046 |
| 65° | 0,422618262 | 0,906307787 |
| 66° | 0,406736643 | 0,913545458 |
| 67° | 0,390731128 | 0,920504853 |
| 68° | 0,374606593 | 0,927183855 |
| 69° | 0,35836795 | 0,933580426 |
| 70° | 0,342020143 | 0,939692621 |
| 71° | 0,325568154 | 0,945518576 |
| 72° | 0,309016994 | 0,951056516 |
| 73° | 0,292371705 | 0,956304756 |
| 74° | 0,275637356 | 0,961261696 |
| 75° | 0,258819045 | 0,965925826 |
| 76° | 0,241921896 | 0,970295726 |
| 77° | 0,224951054 | 0,974370065 |
| 78° | 0,207911691 | 0,978147601 |
| 79° | 0,190808995 | 0,981627183 |
| 80° | 0,173648178 | 0,984807753 |
| 81° | 0,156434465 | 0,987688341 |
| 82° | 0,139173101 | 0,990268069 |
| 83° | 0,121869343 | 0,992546152 |
| 84° | 0,104528463 | 0,994521895 |
| 85° | 0,087155743 | 0,996194698 |
| 86° | 0,069756474 | 0,99756405 |
| 87° | 0,052335956 | 0,998629535 |
| 88° | 0,034899497 | 0,999390827 |
| 89° | 0,017452406 | 0,999847695 |
| 90° | 0 | 1 |
| 91° | -0,017452406 | 0,999847695 |
| 92° | -0,034899497 | 0,999390827 |
| 93° | -0,052335956 | 0,998629535 |
| 94° | -0,069756474 | 0,99756405 |
| 95° | -0,087155743 | 0,996194698 |
| 96° | -0,104528463 | 0,994521895 |
| 97° | -0,121869343 | 0,992546152 |
| 98° | -0,139173101 | 0,990268069 |
| 99° | -0,156434465 | 0,987688341 |
| 100° | -0,173648178 | 0,984807753 |
| 101° | -0,190808995 | 0,981627183 |
| 102° | -0,207911691 | 0,978147601 |
| 103° | -0,224951054 | 0,974370065 |
| 104° | -0,241921896 | 0,970295726 |
| 105° | -0,258819045 | 0,965925826 |
| 106° | -0,275637356 | 0,961261696 |
| 107° | -0,292371705 | 0,956304756 |
| 108° | -0,309016994 | 0,951056516 |
| 109° | -0,325568154 | 0,945518576 |
| 110° | -0,342020143 | 0,939692621 |
| 111° | -0,35836795 | 0,933580426 |
| 112° | -0,374606593 | 0,927183855 |
| 113° | -0,390731128 | 0,920504853 |
| 114° | -0,406736643 | 0,913545458 |
| 115° | -0,422618262 | 0,906307787 |
| 116° | -0,438371147 | 0,898794046 |
| 117° | -0,4539905 | 0,891006524 |
| 118° | -0,469471563 | 0,882947593 |
| 119° | -0,48480962 | 0,874619707 |
| 120° | -0,5 | 0,866025404 |
| 121° | -0,515038075 | 0,857167301 |
| 122° | -0,529919264 | 0,848048096 |
| 123° | -0,544639035 | 0,838670568 |
| 124° | -0,559192903 | 0,829037573 |
| 125° | -0,573576436 | 0,819152044 |
| 126° | -0,587785252 | 0,809016994 |
| 127° | -0,601815023 | 0,79863551 |
| 128° | -0,615661475 | 0,788010754 |
| 129° | -0,629320391 | 0,777145961 |
| 130° | -0,64278761 | 0,766044443 |
| 131° | -0,656059029 | 0,75470958 |
| 132° | -0,669130606 | 0,743144825 |
| 133° | -0,68199836 | 0,731353702 |
| 134° | -0,69465837 | 0,7193398 |
| 135° | -0,707106781 | 0,707106781 |
| 136° | -0,7193398 | 0,69465837 |
| 137° | -0,731353702 | 0,68199836 |
| 138° | -0,743144825 | 0,669130606 |
| 139° | -0,75470958 | 0,656059029 |
| 140° | -0,766044443 | 0,64278761 |
| 141° | -0,777145961 | 0,629320391 |
| 142° | -0,788010754 | 0,615661475 |
| 143° | -0,79863551 | 0,601815023 |
| 144° | -0,809016994 | 0,587785252 |
| 145° | -0,819152044 | 0,573576436 |
| 146° | -0,829037573 | 0,559192903 |
| 147° | -0,838670568 | 0,544639035 |
| 148° | -0,848048096 | 0,529919264 |
| 149° | -0,857167301 | 0,515038075 |
| 150° | -0,866025404 | 0,5 |
| 151° | -0,874619707 | 0,48480962 |
| 152° | -0,882947593 | 0,469471563 |
| 153° | -0,891006524 | 0,4539905 |
| 154° | -0,898794046 | 0,438371147 |
| 155° | -0,906307787 | 0,422618262 |
| 156° | -0,913545458 | 0,406736643 |
| 157° | -0,920504853 | 0,390731128 |
| 158° | -0,927183855 | 0,374606593 |
| 159° | -0,933580426 | 0,35836795 |
| 160° | -0,939692621 | 0,342020143 |
| 161° | -0,945518576 | 0,325568154 |
| 162° | -0,951056516 | 0,309016994 |
| 163° | -0,956304756 | 0,292371705 |
| 164° | -0,961261696 | 0,275637356 |
| 165° | -0,965925826 | 0,258819045 |
| 166° | -0,970295726 | 0,241921896 |
| 167° | -0,974370065 | 0,224951054 |
| 168° | -0,978147601 | 0,207911691 |
| 169° | -0,981627183 | 0,190808995 |
| 170° | -0,984807753 | 0,173648178 |
| 171° | -0,987688341 | 0,156434465 |
| 172° | -0,990268069 | 0,139173101 |
| 173° | -0,992546152 | 0,121869343 |
| 174° | -0,994521895 | 0,104528463 |
| 175° | -0,996194698 | 0,087155743 |
| 176° | -0,99756405 | 0,069756474 |
| 177° | -0,998629535 | 0,052335956 |
| 178° | -0,999390827 | 0,034899497 |
| 179° | -0,999847695 | 0,017452406 |
| 180° | -1 | 1,22515E-16 |
| 181° | -0,999847695 | -0,017452406 |
| 182° | -0,999390827 | -0,034899497 |
| 183° | -0,998629535 | -0,052335956 |
| 184° | -0,99756405 | -0,069756474 |
| 185° | -0,996194698 | -0,087155743 |
| 186° | -0,994521895 | -0,104528463 |
| 187° | -0,992546152 | -0,121869343 |
| 188° | -0,990268069 | -0,139173101 |
| 189° | -0,987688341 | -0,156434465 |
| 190° | -0,984807753 | -0,173648178 |
| 191° | -0,981627183 | -0,190808995 |
| 192° | -0,978147601 | -0,207911691 |
| 193° | -0,974370065 | -0,224951054 |
| 194° | -0,970295726 | -0,241921896 |
| 195° | -0,965925826 | -0,258819045 |
| 196° | -0,961261696 | -0,275637356 |
| 197° | -0,956304756 | -0,292371705 |
| 198° | -0,951056516 | -0,309016994 |
| 199° | -0,945518576 | -0,325568154 |
| 200° | -0,939692621 | -0,342020143 |
| 201° | -0,933580426 | -0,35836795 |
| 202° | -0,927183855 | -0,374606593 |
| 203° | -0,920504853 | -0,390731128 |
| 204° | -0,913545458 | -0,406736643 |
| 205° | -0,906307787 | -0,422618262 |
| 206° | -0,898794046 | -0,438371147 |
| 207° | -0,891006524 | -0,4539905 |
| 208° | -0,882947593 | -0,469471563 |
| 209° | -0,874619707 | -0,48480962 |
| 210° | -0,866025404 | -0,5 |
| 211° | -0,857167301 | -0,515038075 |
| 212° | -0,848048096 | -0,529919264 |
| 213° | -0,838670568 | -0,544639035 |
| 214° | -0,829037573 | -0,559192903 |
| 215° | -0,819152044 | -0,573576436 |
| 216° | -0,809016994 | -0,587785252 |
| 217° | -0,79863551 | -0,601815023 |
| 218° | -0,788010754 | -0,615661475 |
| 219° | -0,777145961 | -0,629320391 |
| 220° | -0,766044443 | -0,64278761 |
| 221° | -0,75470958 | -0,656059029 |
| 222° | -0,743144825 | -0,669130606 |
| 223° | -0,731353702 | -0,68199836 |
| 224° | -0,7193398 | -0,69465837 |
| 225° | -0,707106781 | -0,707106781 |
| 226° | -0,69465837 | -0,7193398 |
| 227° | -0,68199836 | -0,731353702 |
| 228° | -0,669130606 | -0,743144825 |
| 229° | -0,656059029 | -0,75470958 |
| 230° | -0,64278761 | -0,766044443 |
| 231° | -0,629320391 | -0,777145961 |
| 232° | -0,615661475 | -0,788010754 |
| 233° | -0,601815023 | -0,79863551 |
| 234° | -0,587785252 | -0,809016994 |
| 235° | -0,573576436 | -0,819152044 |
| 236° | -0,559192903 | -0,829037573 |
| 237° | -0,544639035 | -0,838670568 |
| 238° | -0,529919264 | -0,848048096 |
| 239° | -0,515038075 | -0,857167301 |
| 240° | -0,5 | -0,866025404 |
| 241° | -0,48480962 | -0,874619707 |
| 242° | -0,469471563 | -0,882947593 |
| 243° | -0,4539905 | -0,891006524 |
| 244° | -0,438371147 | -0,898794046 |
| 245° | -0,422618262 | -0,906307787 |
| 246° | -0,406736643 | -0,913545458 |
| 247° | -0,390731128 | -0,920504853 |
| 248° | -0,374606593 | -0,927183855 |
| 249° | -0,35836795 | -0,933580426 |
| 250° | -0,342020143 | -0,939692621 |
| 251° | -0,325568154 | -0,945518576 |
| 252° | -0,309016994 | -0,951056516 |
| 253° | -0,292371705 | -0,956304756 |
| 254° | -0,275637356 | -0,961261696 |
| 255° | -0,258819045 | -0,965925826 |
| 256° | -0,241921896 | -0,970295726 |
| 257° | -0,224951054 | -0,974370065 |
| 258° | -0,207911691 | -0,978147601 |
| 259° | -0,190808995 | -0,981627183 |
| 260° | -0,173648178 | -0,984807753 |
| 261° | -0,156434465 | -0,987688341 |
| 262° | -0,139173101 | -0,990268069 |
| 263° | -0,121869343 | -0,992546152 |
| 264° | -0,104528463 | -0,994521895 |
| 265° | -0,087155743 | -0,996194698 |
| 266° | -0,069756474 | -0,99756405 |
| 267° | -0,052335956 | -0,998629535 |
| 268° | -0,034899497 | -0,999390827 |
| 269° | -0,017452406 | -0,999847695 |
| 270° | -1,83772E-16 | -1 |
| 271° | 0,017452406 | -0,999847695 |
| 272° | 0,034899497 | -0,999390827 |
| 273° | 0,052335956 | -0,998629535 |
| 274° | 0,069756474 | -0,99756405 |
| 275° | 0,087155743 | -0,996194698 |
| 276° | 0,104528463 | -0,994521895 |
| 277° | 0,121869343 | -0,992546152 |
| 278° | 0,139173101 | -0,990268069 |
| 279° | 0,156434465 | -0,987688341 |
| 280° | 0,173648178 | -0,984807753 |
| 281° | 0,190808995 | -0,981627183 |
| 282° | 0,207911691 | -0,978147601 |
| 283° | 0,224951054 | -0,974370065 |
| 284° | 0,241921896 | -0,970295726 |
| 285° | 0,258819045 | -0,965925826 |
| 286° | 0,275637356 | -0,961261696 |
| 287° | 0,292371705 | -0,956304756 |
| 288° | 0,309016994 | -0,951056516 |
| 289° | 0,325568154 | -0,945518576 |
| 290° | 0,342020143 | -0,939692621 |
| 291° | 0,35836795 | -0,933580426 |
| 292° | 0,374606593 | -0,927183855 |
| 293° | 0,390731128 | -0,920504853 |
| 294° | 0,406736643 | -0,913545458 |
| 295° | 0,422618262 | -0,906307787 |
| 296° | 0,438371147 | -0,898794046 |
| 297° | 0,4539905 | -0,891006524 |
| 298° | 0,469471563 | -0,882947593 |
| 299° | 0,48480962 | -0,874619707 |
| 300° | 0,5 | -0,866025404 |
| 301° | 0,515038075 | -0,857167301 |
| 302° | 0,529919264 | -0,848048096 |
| 303° | 0,544639035 | -0,838670568 |
| 304° | 0,559192903 | -0,829037573 |
| 305° | 0,573576436 | -0,819152044 |
| 306° | 0,587785252 | -0,809016994 |
| 307° | 0,601815023 | -0,79863551 |
| 308° | 0,615661475 | -0,788010754 |
| 309° | 0,629320391 | -0,777145961 |
| 310° | 0,64278761 | -0,766044443 |
| 311° | 0,656059029 | -0,75470958 |
| 312° | 0,669130606 | -0,743144825 |
| 313° | 0,68199836 | -0,731353702 |
| 314° | 0,69465837 | -0,7193398 |
| 315° | 0,707106781 | -0,707106781 |
| 316° | 0,7193398 | -0,69465837 |
| 317° | 0,731353702 | -0,68199836 |
| 318° | 0,743144825 | -0,669130606 |
| 319° | 0,75470958 | -0,656059029 |
| 320° | 0,766044443 | -0,64278761 |
| 321° | 0,777145961 | -0,629320391 |
| 322° | 0,788010754 | -0,615661475 |
| 323° | 0,79863551 | -0,601815023 |
| 324° | 0,809016994 | -0,587785252 |
| 325° | 0,819152044 | -0,573576436 |
| 326° | 0,829037573 | -0,559192903 |
| 327° | 0,838670568 | -0,544639035 |
| 328° | 0,848048096 | -0,529919264 |
| 329° | 0,857167301 | -0,515038075 |
| 330° | 0,866025404 | -0,5 |
| 331° | 0,874619707 | -0,48480962 |
| 332° | 0,882947593 | -0,469471563 |
| 333° | 0,891006524 | -0,4539905 |
| 334° | 0,898794046 | -0,438371147 |
| 335° | 0,906307787 | -0,422618262 |
| 336° | 0,913545458 | -0,406736643 |
| 337° | 0,920504853 | -0,390731128 |
| 338° | 0,927183855 | -0,374606593 |
| 339° | 0,933580426 | -0,35836795 |
| 340° | 0,939692621 | -0,342020143 |
| 341° | 0,945518576 | -0,325568154 |
| 342° | 0,951056516 | -0,309016994 |
| 343° | 0,956304756 | -0,292371705 |
| 344° | 0,961261696 | -0,275637356 |
| 345° | 0,965925826 | -0,258819045 |
| 346° | 0,970295726 | -0,241921896 |
| 347° | 0,974370065 | -0,224951054 |
| 348° | 0,978147601 | -0,207911691 |
| 349° | 0,981627183 | -0,190808995 |
| 350° | 0,984807753 | -0,173648178 |
| 351° | 0,987688341 | -0,156434465 |
| 352° | 0,990268069 | -0,139173101 |
| 353° | 0,992546152 | -0,121869343 |
| 354° | 0,994521895 | -0,104528463 |
| 355° | 0,996194698 | -0,087155743 |
| 356° | 0,99756405 | -0,069756474 |
| 357° | 0,998629535 | -0,052335956 |
| 358° | 0,999390827 | -0,034899497 |
| 359° | 0,999847695 | -0,017452406 |
| 360° | 1 | 0 |
Часто используемые значения косинуса
Косинус 0 градусов = 1
Косинус 30 градусов = 0,866025404 = <\frac <\sqrt<3>><2>>
Косинус 45 градусов = 0,707106781 = <\frac <\sqrt<2>><2>>
Косинус 60 градусов = 0,5 = <\frac <1><2>>
Косинус 90 градусов = 0