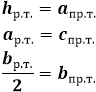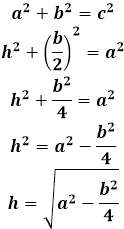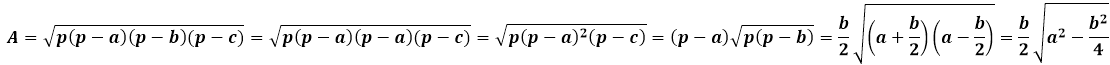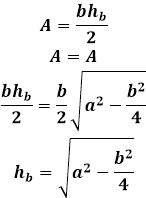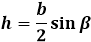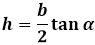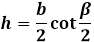Как найти основание равнобедренного треугольника
Как найти основание равнобедренного треугольника
Как найти основание равнобедренного треугольника?
Вариант 1
Если известно, чему равна боковая сторона, а также высота, опущенная на основание.
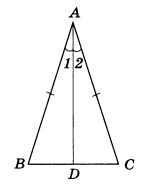
Как известно, высота перпендикулярна основанию, а в случае с равнобедренным треугольником она разбивает его на 2 равных прямоугольных треугольника.
Можно по теореме Пифагора найти половину основания, а затем это значение умножить на 2.
Вариант 2
Если известно, чему равна боковая сторона и один из углов.
Нужно воспользоваться теоремой синусов:
a/sinα = b/sinβ = c/sinγ.
c = (a*sinγ)/sinα.
Так как в равнобедренном треугольнике углы при основании равны, то легко можно найти 2 оставшихся угла, исходя из того, что сумма 3 углов равна 180 градусов.
1.) Допустим, мы знаем, чему равна боковая сторона и угол треугольника (любой из трех). Тогда мы сначала легко вычисляем два других угла треугольника, помня, что их сумма всегда равна 180 градусам, а затем применяем теорему синусов:
следовательно с (основание) будет равно:
2.) Допустим, мы знаем чему равна боковая сторона и высота нашего треугольника. Тогда мы сначала находим половину его основания (она является катетом треугольника, полученного делением исходного равнобедренного треугольника его высотой на два прямоугольных треугольника), применив теорему Пифагора.
Чтобы найти основание равнобедренного треугольника, необходимо вспомнить геометрию.
Так как у нас нет никаких данных задачи, значит следует указать только формулы, по которым можно найти основание.
Основание можно найти применив теорему Пифагора по формуле:
Чтобы понять, как правильно решать, вот примерная задача:
А вот решение для задачи:
Для того, чтобы найти основание равнобедренного треугольника? нам необходимо знать или один из углов, или же высоту треугольника, которая проводится к его основанию. Основание можно вычислить по следующей, вполне легкой формуле:
Для начала вспомним, какой треугольник называется равнобедренным и из этих его свойств будем уже находить величину основания.
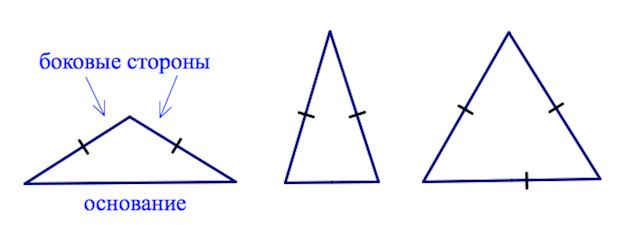
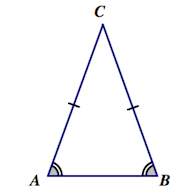
Как видим из рисунка, равнобедренный треугольник- это треугольник, у которого две стороны равны и они называются боковыми. Третья же сторона является основанием этого треугольника. Равные стороны называются боковыми.
Какие же свойства имеет равнобедренный треугольник, которые помогут нам найти его основание?
Углы при основании у равнобедренного треугольника равны между собой.
Высота, которую мы опускаем с верхнего угла на основание одновременно является и биссектрисой и медианой.
Чтобы найти площадь равнобедренного треугольника нужно разделить на 2 произведение основания на высоту, проведенную к этому основанию.
К сожалению, нам не даны условия задачи, поэтому можно использовать несколько формул. Все будет зависеть от данных задачи.
Используя эти свойства, мы для нахождения основания можем использовать следующие формулы:
Так же нам может помочь в решении теорема синусов.
Равнобедренный треугольник: свойства, признаки и формулы
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
| Равнобедренным называется треугольник, у которого две стороны равны. |
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
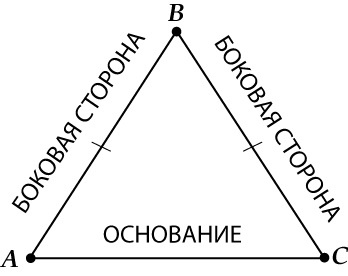
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
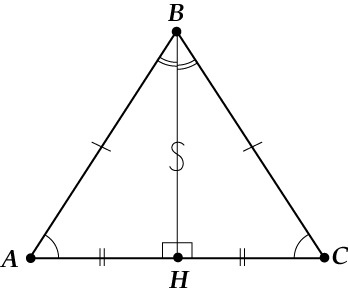
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
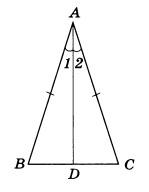
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
как найти основание равнобедренного треугольника
Здравствуйте!
Как найти радиус описанной окружности треугольника? Какие есть способы?
Спасибо!
Основанием равнобедренного треугольника является та из его сторон, длина которой отличается от двух других, равных между собой, сторон.
Рассмотрим варианты того, как найти основание равнобедренного треугольника.
1-й способ. Использование теоремы синусов.
Согласно теореме синусов стороны треугольника являются прямо пропорциональными величинами к значению синусов противоположных углов:
Из этого равенства можно выразить любую искомую сторону через другую сторону и синусы двух углов.
Рассмотрим пример того, как найти основание равнобедренного треугольника, используя теорему синусов.
Пример 1.
У равнобедренного треугольника боковые стороны равны 17 см, а угол при основании равен 30 градусов. Найдем основание данного треугольника.
Решение.
Используем теорему о сумме углов треугольника:
Подставим в теорему синусов известные значения и получим:
Воспользуемся формулой приведения для синуса 120 градусов, согласно которой получим:
Подставим полученное значение в формулу для вычисления длины основания:

2-й способ. Использование теоремы косинусов.
Согласно теореме косинусов квадрат одной стороны треугольника равен сумме квадратов остальных двух сторон и минус произведение этих сторон на косинус угла между ними умноженное на 2:
Равнобедренный треугольник: свойства, признаки и формулы
Содержание:
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
Доказательство теоремы:
Вывод:
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
Доказательство теоремы:
Доказательство от противного.
Признаки равнобедренного треугольника
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
Формулы длины стороны (основания — b):
Формулы длины равных сторон — (а):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Площадь равнобедренного треугольника
Формула площади треугольника через высоту h и основание b, (S):
Основание треугольника

Средняя оценка: 4.7
Всего получено оценок: 115.
Средняя оценка: 4.7
Всего получено оценок: 115.
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
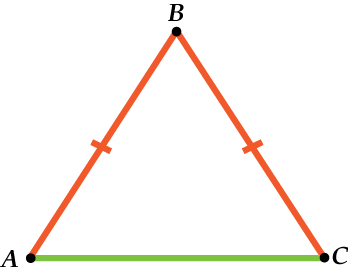
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
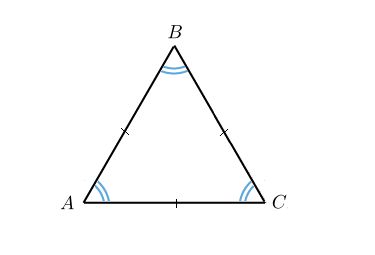
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Равнобедренный треугольник
Среди всех треугольников есть два особенных вида: прямоугольные и равнобедренные.
Чем же эти виды треугольников такие уж особенные?
Ну, во-первых, такие треугольники чрезвычайно часто оказываются главными «действующими лицами» задач ЕГЭ первой части.
А во-вторых, задачи про прямоугольные и равнобедренные треугольники решаются гораздо легче, чем другие задачи по геометрии.
Нужно всего лишь знать несколько правил и свойств. Все самое интересное о прямоугольных треугольниках обсуждается в соответствующей теме, а сейчас рассмотрим равнобедренные треугольники.
Равнобедренный треугольник — коротко о главном
Определение равнобедренного треугольника
Равнобедренный треугольник – треугольник, у которого есть две равные стороны.
Свойства равнобедренного треугольника
Углы при основании равнобедренного треугольника равны: \( \displaystyle \angle A\ =\angle C\);
Высота, проведённая к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой: \( \displaystyle BH\) — высота, медиана и биссектриса.
Признаки равнобедренного треугольника
Если в некотором треугольнике два угла равны, то он – равнобедренный;
Если в некотором треугольнике совпадают высота и биссектриса или высота и медиана или медиана и биссектриса, проведённые к одной стороне, то такой треугольник – равнобедренный.
Определение равнобедренного треугольника
Треугольник называется равнобедренным, если у него есть две равные стороны.
Посмотри как это выглядит:
Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон.
Две равные стороны называются боковыми сторонами, а третья сторона – основанием.
И снова внимание на картинку:
Может быть, конечно, и так:
Так что будь внимательным: боковая сторона – одна из двух равных сторон в равнобедренном треугольнике, а основание – третья сторона.
Чем же так уж хорош равнобедренный треугольник?
Чтобы это понять, давай проведём высоту к основанию. Ты помнишь, что такое высота?
Высота равнобедренного треугольника
Высота — это просто линия, проведённая из вершины треугольника перпендикулярно противоположной стороне.
Итак, провели высоту. Что же получилось?
Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.
Тоже два прямоугольных….
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
Видишь, два прямоугольных треугольника (Δ. и Δ. ) – одинаковые!
Или, как математики любят говорить? Равные!
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Доказательство равенства треугольников
Посмотри внимательно, у нас есть:
И, значит, \( \displaystyle AH\text< >=\text< >CH\)!
Да мы просто найдём и \( \displaystyle AH\), и \( \displaystyle CH\) из теоремы Пифагора (помня ещё при этом, что \( \displaystyle AB=BC\))
Удостоверились? Ну вот, теперь у нас
А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.
Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.
Отметим на картинке все одинаковые элементы (углы и стороны).
Видишь, как интересно? Получилось, что:
Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – делит угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник.
Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?
То есть, как говорят математики, каковы признаки равнобедренного треугольника?
Признаки равнобедренного треугольника
И оказывается, что нужно просто «перевернуть» все высказывания наоборот. Так, конечно, не всегда бывает, но равнобедренный треугольник всё-таки отличная штука! Что же получится после «переворачивания»?
Если в каком-то треугольнике есть два равных угла, то такой треугольник –равнобедренный (ну и естественно, углы эти окажутся при основании).
Если в каком-то треугольнике высота и медиана, или высота и биссектриса, или биссектриса и медиана, проведённые к какой-то стороне, совпадут, то такой треугольник – равнобедренный, а сторона эта – основание.
Ну вот смотри:
Если совпадают высота и медиана, то:
Если совпадают высота и биссектриса, то:
Если совпадают биссектриса и медиана, то:
Ну вот, не забывай и пользуйся:
Как пользоваться признаками равнобедренного треугольника при решении задач
Давай посмотрим, как это выглядит в задачах.
2 задачи на равнобедренный треугольник
Задача 1 (самая простая)
В треугольнике \( \displaystyle ABC\) стороны \( \displaystyle AB\) и \( \displaystyle AC\) равны, а \( \displaystyle \angle BAC=70<>^\circ \).
Найти \( \displaystyle \angle ABC\).
Решение
Что здесь основание? Конечно, \( \displaystyle BC\).
Вспоминаем, что если \( \displaystyle AB=AC\), то и \( \displaystyle \angle B=\angle C\).
Равнобедренный треугольник, свойства, признаки и формулы
Равнобедренный треугольник, свойства, признаки и формулы
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.
Рис. 1. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Различают следующие виды равнобедренных треугольников:
– остроугольный – все углы острые;
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.
Рис. 2. Равнобедренный треугольник
2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.
Рис. 3. Равнобедренный треугольник
АН1 = СН2 – высота, АМ1 = СМ2 – медиана, АL1 = СL2 – биссектриса, проведённые из углов при основании
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Рис. 4. Равнобедренный треугольник
ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок
4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.
Рис. 5. Равнобедренный треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
Признаки равнобедренного треугольника:
– если в треугольнике два угла равны, то он равнобедренный;
– если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
– если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
– если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Формулы равнобедренного треугольника:
Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).
Рис. 6. Равнобедренный треугольник
Формулы длины основания (b):



Формулы длины равных сторон (а):

Формулы углов:
Рис. 7. Равнобедренный треугольник



Формулы периметра (Р) равнобедренного треугольника:
Рис. 8. Равнобедренный треугольник


Формулы площади (S) равнобедренного треугольника:



Равнобедренный треугольник в природе, технике и культуре:
Рис. 1. Структура молекулы сероводорода
Длина боковой стороны – связи HS = 133,6 пм, а вершинный угол ∠HSH = 92,1°.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Как найти основание равнобедренного треугольника?
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Рис. 1. Углы произвольного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Видео
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.

По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Математика Объем прямоугольника – формула расчета
Математика Переместительное свойство сложения – примеры (5 класс, математика)
Как найти основание равнобедренного треугольника если известен периметр и боковая сторона?
Боковая сторона известна. Вторая боковая сторона имеет то же самое числовое значение, раз треугольник равнобедренный, периметр известен. Что же мешает Вам найти основание? Думаю только то, что Вы не знаете, что периметр треугольника – это сумма всех его трёх сторон:
Р = а + в + с, где Р – периметр, а, в, с – стороны.
Так как в равнобедренном треугольнике две стороны равны, то формула его периметра такова:
Р = 2а + с.
Найти сумму боковых сторон равнобедренного треугольника не составляет труда. Для того чтобы найти основание, следует помнить то, что изучается в начальных классах: чтобы найти одно из слагаемых, надо из суммы вычесть второе слагаемое.
Перевожу: сумма – периметр – Вам известна. Первое слагаемое Вы нашли – это 2а, где а – сторона равнобедренного треугольника. Чтобы найти основание (с), надо из периметра вычесть значение двух сторон равнобедренного треугольника, то есть:
с = Р – 2а.
Допустим, Р = 30 см, а = 12 см, тогда с = 30 – 24, то есть с = 6 (см).
Равнобедренные треугольники
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Как найти основание равнобедренного треугольника по двум сторонам
Треугольник – это геометрическая фигура, которая имеет минимально допустимое для многоугольников число сторон и вершин и следственно является примитивной фигурой, в которой присутствуют углы. Дозволено сказать, что это самый «снисканный» многоугольник в истории математики – он применялся для выведения большого числа тригонометрических функций и теорем. И среди этих элементарных фигур есть больше примитивные и менее. К первым относится равнобедренный треугольник, состоящий из идентичных боковых сторон и основания.
Инструкция
2. Если же вестима только длина всей из боковых сторон (a), то для вычисления длины основания (b) необходима добавочная информация – скажем, величина угла между ними (?). В этом случае дозволено воспользоваться теоремой косинусов, из которой вытекает, что длина стороны треугольника (не неукоснительно равнобедренного) равна квадратному корню из суммы квадратов длин 2-х других сторон, из которой вычтено удвоенное произведение их длин на косинус угла между ними. Потому что в равнобедренном треугольнике длины задействованных a формуле сторон идентичны, то ее дозволено упростить: b = a*?(2*(1-cos(?))).
4. Если помимо длин боковых сторон (a) дана величина угла (?), прилегающего к основанию, то дозволено применить теорему о проекциях: длина стороны равна сумме произведений 2-х других сторон на косинус угла, тот, что всякая из них образует с этой стороной. Потому что в равнобедренном треугольнике эти стороны, как и задействованные углы, имеют идентичную величину, то записать формулу дозволено так: b = 2*a*cos(?).
Совет 2: Как обнаружить длину стороны треугольника по координатам
Геометрические задачи всякого яруса высокого яруса трудности полагают наличия у человека знания решать элементарные задачи. В отвратном случае вероятность приобретения требуемого итога гораздо снижается. Помимо процесса фактически интуитивного нащупывания верного метода, ведущего к надобному вам выводу, вы с необходимостью обязаны уметь рассчитывать площади, знать крупное число вспомогательных теорем, вольно проводить вычисления в координатной плоскости.
Инструкция
3. Обращайте внимание на некоторые характерные элементы данные, которые содержат в себе подсказку. К примеру, в тексте может быть упомянуто, что вершина треугольника лежит на одной из осей (что теснее дает вам информацию об одной из координат), проходит через предисловие координат. Все это значимо выписать, дабы владеть полной информацией.
4. Не забывайте о формулах, дозволяющих выразить стороны треугольника через другие его элементы, а также о существующих пропорциональных отношениях. К числу минимальных вспомогательных уравнений, которые вам сгодятся, относятся формулы для нахождения высоты, медианы и биссектрисы треугольников. Помимо того, запомните, что две стороны треугольника находятся в таком же отношении друг к другу, как и отрезки, на которые разбивает биссектриса, проведенная к третьей его стороне.
5. Будьте готовы к тому, что если вы используете в решении те либо иные формулы либо теоремы, вас могут попросить подтвердить их либо описать процедуру итога.
Как найти основание равнобедренного треугольника?
Как найти основание равнобедренного треугольника?
В категории Естественные науки Спросил Fearlessfire
2 Ответов 28078 Просмотров 1 месяц назад
Для добавления вопроса на сайт, блог или форум просто скопируйте и вставьте в html код:
Основание равнобедренного треугольника можно найти по следующей формуле

Ответил Anna Shakhmina 1 месяц назад
Ответил Anna Shakhmina 1 месяц назад
Смотря, что дано в данном треугольнике. Если в равнобедренном треугольнике дана сторона и угол, который находится напротив основания, то можете провести из этого угла высоту треугольника. В результате, по свойству равностороннего треугольника вы получите два равных прямоугольника.
В этом прямоугольнике один из катетов будет половиной основания, а угол, напортив него, половиной заданного угла. Гипотенузой прямоугольного треугольника, будет известная нам сторона равностороннего треугольника.
Есть правило в тригонометрии: катет прямоугольного треугольника равен гипотенузе, умноженной на синус угла, противолежащего этому катету.
Найдите половину основания, умножив величину гипотенузы (сторона равностороннего треугольника) на синус половины угла, противолежащего основанию. Увеличив полученную величину в два раза, вы получите искомое основание. Удачи!
Как найти основание равнобедренного треугольника?
1.) Допустим, мы знаем, чему равна боковая сторона и угол треугольника (любой из трех). Тогда мы сначала легко вычисляем два других угла треугольника, помня, что их сумма всегда равна 180 градусам, а затем применяем теорему синусов:
следовательно с (основание) будет равно:
2.) Допустим, мы знаем чему равна боковая сторона и высота нашего треугольника. Тогда мы сначала находим половину его основания (она является катетом треугольника, полученного делением исходного равнобедренного треугольника его высотой на два прямоугольных треугольника), применив теорему Пифагора.
Чтобы найти основание равнобедренного треугольника, необходимо вспомнить геометрию.
Так как у нас нет никаких данных задачи, значит следует указать только формулы, по которым можно найти основание.
Основание можно найти применив теорему Пифагора по формуле:
Чтобы понять, как правильно решать, вот примерная задача:
А вот решение для задачи:
Для того, чтобы найти основание равнобедренного треугольника? нам необходимо знать или один из углов, или же высоту треугольника, которая проводится к его основанию. Основание можно вычислить по следующей, вполне легкой формуле:
Вариант 1
Если известно, чему равна боковая сторона, а также высота, опущенная на основание.
Как известно, высота перпендикулярна основанию, а в случае с равнобедренным треугольником она разбивает его на 2 равных прямоугольных треугольника.
Можно по теореме Пифагора найти половину основания, а затем это значение умножить на 2.
Вариант 2
Если известно, чему равна боковая сторона и один из углов.
Нужно воспользоваться теоремой синусов:
a/sinα = b/sinβ = c/sinγ.
c = (a*sinγ)/sinα.
Так как в равнобедренном треугольнике углы при основании равны, то легко можно найти 2 оставшихся угла, исходя из того, что сумма 3 углов равна 180 градусов.
При решении задач с равнобедренным треугольником нужно использовать свойства как равнобедренного треугольника, так и прямоугольного, поскольку высота равнобедренного треугольника делит его на 2 одинаковых прямоугольных.
Основание равнобедренного треугольника ищется, когда есть какие-то исходные данные. Например известны сторона и угол. Тогда поступаем следующим образом:
Находим третий угол ( 180 градусов минус сумму двух углов) и используем теорему косинусов:
Для начала вспомним, какой треугольник называется равнобедренным и из этих его свойств будем уже находить величину основания.
Как видим из рисунка, равнобедренный треугольник- это треугольник, у которого две стороны равны и они называются боковыми. Третья же сторона является основанием этого треугольника. Равные стороны называются боковыми.
Какие же свойства имеет равнобедренный треугольник, которые помогут нам найти его основание?
Углы при основании у равнобедренного треугольника равны между собой.
Высота, которую мы опускаем с верхнего угла на основание одновременно является и биссектрисой и медианой.
Чтобы найти площадь равнобедренного треугольника нужно разделить на 2 произведение основания на высоту, проведенную к этому основанию.
К сожалению, нам не даны условия задачи, поэтому можно использовать несколько формул. Все будет зависеть от данных задачи.
Используя эти свойства, мы для нахождения основания можем использовать следующие формулы:
Так же нам может помочь в решении теорема синусов.
Для начала нужно понять, что такое равнобедренный треугольник, таким треугольником называют треугольник у которого две стороны равны. Ниже рисунок такого треугольника:
К сожалению нет данных в вопросе. Например, если задана площадь и высота ВH. Тогда основание (на рисунке выше сторона АС) будет равна площадь разделить на высоту BH и умножить на 0,5.
Если же нам известна одна сторона и высота треугольника, можно воспользоваться теоремой Пифагора. Ниже представлена формула, по которой можно вычислить основание:
Возможно и другие варианты, например, если известна сторона и угол, тогда можно воспользоваться теоремой косинусов или синусов.
Можно найти для начала значение половины основания, а затем умножить это значение на два. Смысл в том, что мы опускаем на основание из противоположного угла высоту (она в равнобедренном треугольнике совпадает с биссектрисой и медианой), получается два прямоугольных треугольника. Вспоминаем теорему Пифагора, вычисляем разницу между гипотенузой и высотой, извлекаем корень. Конечно, в этом случае по условиям задачи нам должно быть известно значение высоты.
Если же известно значение боковой стороны и противоположного основанию угла, то легче всего пойти через формулу синусов:
Также можно воспользоваться формулой косинусов:
В задачах такого типа всегда даётся вариант, где у вас известен один угол, если вы знаете одну сторону угла равнобедренного треугольника. То вы умножаете значения на два угла и высоту равнобедренного треугольника. Таким образом вы получите чему равно основание этого треугольника.
Бисектриса тоже может вам помоч.
Чему равняется основание возможно узнать, если у нас есть данные чему равна одна боковая сторона (а вторая боковая будет равняться также) и высота. В этом случае воспользуемся такой формулой:
Но также можно решить эту задачку и другим способом, для этого должны знать чему равняется боковая сторона и один из углов.
Медиаторы бывают разные по толщине, форме. Есть даже металлические. Есть фирменные и именные. На концертных выступлениях разных групп, в микрофонной стойке они встроены в рядок, чтобы играющий мог брать, если потеряет, или уронит, или вдруг медиатор лопнет. Что бывает нередко.
В домашних условиях легко изготовить медиатор из старой кредитной карты. А раньше, в дикой молодости, мы вырезали их из крышек для банок. Дешево и сердито))
В продаже на али, я видел специальный компостер, или степлер, или корректнее, такой дырокол, позволяющий сразу пробивать медиатор из карты. Очень удобно, я считаю.
Кто-то даже коллекционирует медиаторы, покупая их в разных музыкальных магазинах мира.
Если ваша лучшая подружка пристает к вашему избраннику, то вы уверены, что она вам подружка, тем более лучшая? А делать ничего наверное не стоит,ну желательно конечно отдалить «подружку» от вашего дома и от вас, просто потому что это дружбой ну никак нельзя назвать. Если ваш избранник никак на это не реагирует, то замечательно, если реагирует, задам тот же вопрос, а вы уверенны, что он ваш избранник?
Основание равнобедренного треугольника, с примерами
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Среди всех треугольников есть два особенных вида: прямоугольные треугольники и равнобедренные треугольники. Чем же эти виды треугольников такие уж особенные? Ну, во-первых, такие треугольники чрезвычайно часто оказываются главными действующими «лицами» задач ЕГЭ первой части.
А во-вторых, задачи про прямоугольные и равнобедренные треугольники решаются гораздо легче, чем другие задачи по геометрии. Нужно всего лишь знать несколько правил и свойств. Все самое интересное о прямоугольных треугольниках обсуждается в соответствующей теме, а сейчас рассмотрим равнобедренные треугольники.
И прежде всего, что же такое – равнобедренный треугольник. Или, как говорят математики, каково определение равнобедренного треугольника?
| Треугольник называется равнобедренным, если у него есть две равные стороны. |
Посмотри, как это выглядит:
Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон. Две равные стороны называются боковыми сторонами, а третья сторона – основанием.
И снова внимание на картинку:
Может быть, конечно, и так:
Так что будь внимательным: боковая сторона – одна из двух равных сторон в равнобедренном треугольнике, а основание – третья сторона.
Чем же так уж хорош равнобедренный треугольник? Чтобы это понять, давай проведём высоту к основанию. Ты помнишь, что такое высота?
 | Это просто линия, проведённая из вершины треугольника перпендикулярно противоположной стороне. Итак, провели высоту. |
Что же получилось? Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, самом «кособедренном» треугольнике.
 | Тоже два прямоугольных…. |
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
 | Видишь, два прямоугольных треугольника ( и ) – одинаковые! Или, как математически любят говорить? равные! |
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём? Посмотри внимательно, у нас есть:
 | (ещё говорят, — общая) |
Видишь, как интересно? Получилось, что:
Как же об этом принято говорить у математиков? Давай по порядку:
(Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник. Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать равнобедренный треугольник? То есть, как говорят математики, каковы признаки равнобедренного треугольника?
И оказывается, что нужно просто «перевернуть» все высказывания наоборот. Так, конечно, не всегда бывает, но равнобедренный треугольник всё-таки отличная штука! Что же получится после «переворачивания»?
| I. Если в каком-то треугольнике есть два равных угла, то такой треугольник – равнобедренный (ну и естественно, углы эти окажутся при основании). |
























































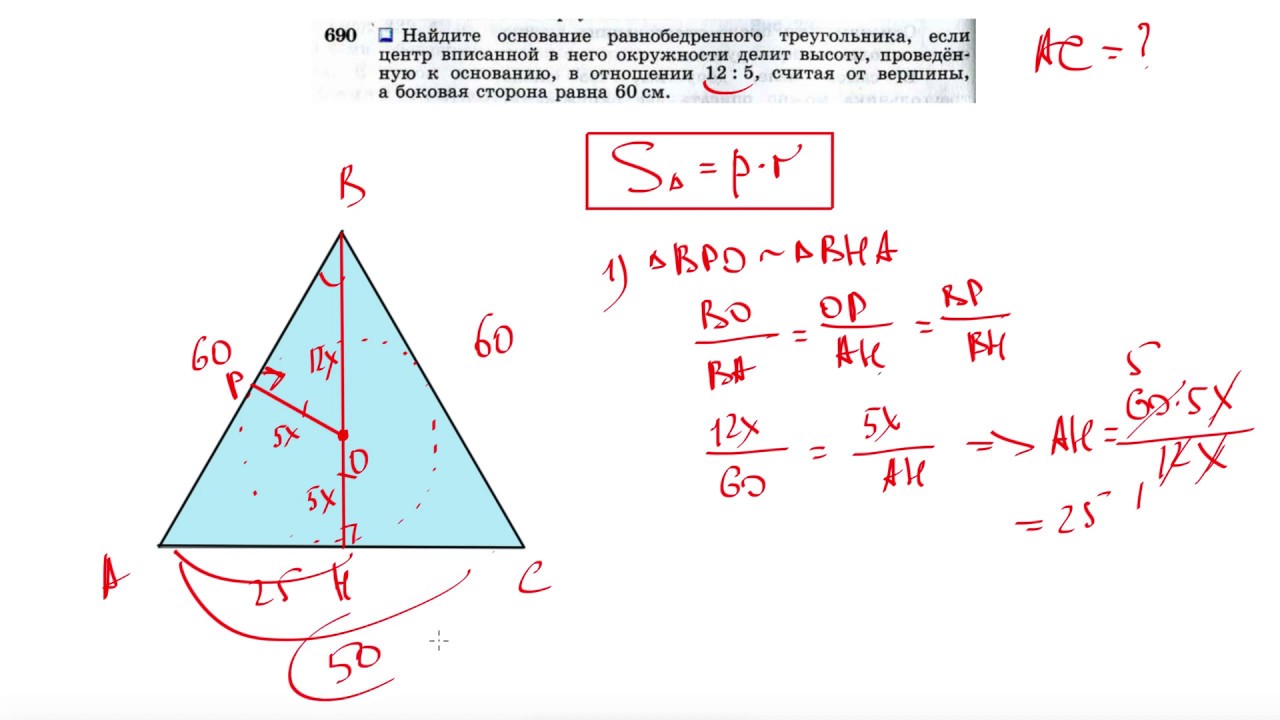










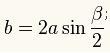
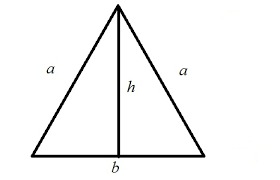
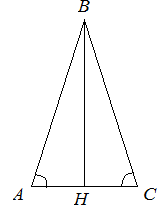
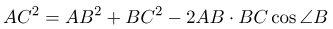
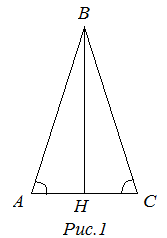


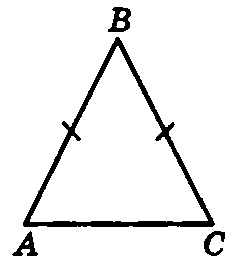
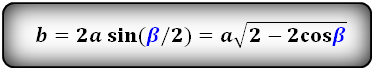
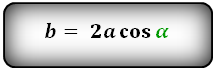
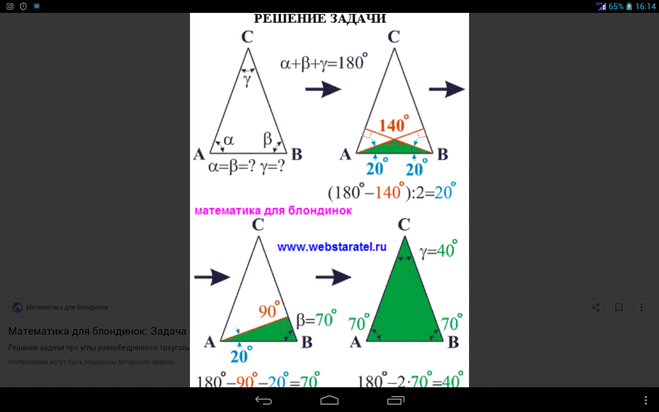





















 Рис. 1. Равнобедренный треугольник
Рис. 1. Равнобедренный треугольник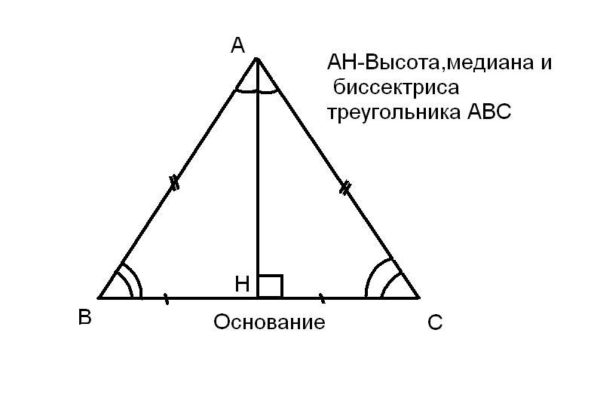 Рис. 2. Свойство равнобедренного треугольника
Рис. 2. Свойство равнобедренного треугольника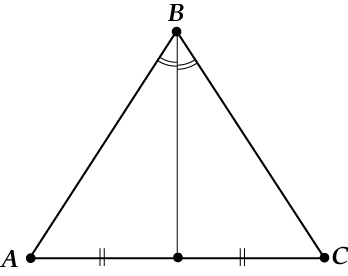 Рис. 3. Высота, опущенная на основание равнобедренного треугольника
Рис. 3. Высота, опущенная на основание равнобедренного треугольника