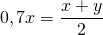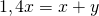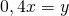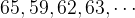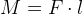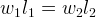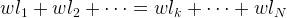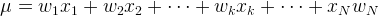Как найти среднее арифметическое число
Как найти среднее арифметическое число
Среднее арифметическое
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.
Обозначим среднее арифметическое буквой « m ». По определению выше найдем сумму всех чисел.
Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.
В итоге мы получаем формулу среднего арифметического:
Для чего нужно среднее арифметическое?
Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.
Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой цене вам продавать мячи.
Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены в магазинах и составим таблицу.
| Магазин | Цена футбольного мяча |
|---|---|
| «Спорт-товары» | 290 руб. |
| «Adidas» | 360 руб. |
| «Все для футбола» | 310 руб. |
Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?
Если выбрать самую низкую ( 290 руб.), то мы будем продавать товар себе в убыток. Если выбрать самую высокую ( 360 руб.), то покупатели не будут приобретать футбольные мячи у нас.
Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.
Вычислим среднее арифметическое цен на футбольные мячи:
Средняя цена =
| 290 + 360 + 310 |
| 3 |
=
| 960 |
| 3 |
= 320 руб.
Таким образом, мы получили среднюю цену ( 320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не слишком дорого.
Средняя скорость движения
Со средним арифметическим тесно связано понятие средней скорости движения.
Наблюдая за движением транспорта в городе, можно заметить, что машины, то разгоняются и едут с большой скоростью, то замедляются и едут с маленькой скоростью.
Таких участков на пути следования автотранспорта бывает много. Поэтому для удобства расчётов, используют понятие средней скорости движения.
Средняя скорость движения — это весь пройденный путь разделить на всё время движения.
Рассмотрим задачу на среднюю скорость.
Разбор примера
Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец 0,3 ч по просёлочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всём пути.
Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем, и всё время, которое автомобиль двигался.
S1 = 90 · 3,2 = 288 (км) — шоссе.
S2 = 45 · 1,5 = 67,5 (км) — грунтовая дорога.
S3 = 30 · 0,3 = 9 (км) — просёлочная дорога.
S = 288 + 67,5 + 9 = 364,5 (км) — весь путь, пройденный автомобилем.
t = 3,2 + 1,5 + 0,3 = 5 (ч) — всё время.
Vср = 364,5 : 5 = 72,9 (км/ч) — средняя скорость движения автомобиля.
Ответ: Vср = 72,9 (км/ч) — средняя скорость движения автомобиля.
Математика
План урока:
Понятие среднего арифметического
К сестрам Марине, Наталье, Елене в гости приехала бабушка. Она привезла своим внучкам гостинцы: восемнадцать конфет, шесть шоколадок, шесть киндер-сюрпризов. Сказала угощение разделить поровну. Определите, сколько сладостей достанется каждой девочке?
Ответ на вопрос, можно получить двумя способами. Рассмотрим их.
Чтобы выяснить, сколько сладостей достанется одной девочке, нужно каждый вид угощения разделить поровну – на 3.
Разделим конфеты между детьми:
Теперь известно, что каждому ребенку досталось 6 конфет.
Каждой внучке досталось две шоколадки.
Разделим шоколадные яйца:
Выяснили, бабушка привезла по два киндер-сюрприза.
Стало известно, сколько гостинцев получил один ребенок. Теперь, вычислим, сколько сладостей досталось каждой девочке. Сложим количество конфет(6), шоколадок(2), киндер-сюрпризов(2), имеющихся у одной девочки:
Получается, бабушка привезла по 10 сладостей.
Запишем решение задачи.
Как видите, способ, довольно простой, ноимеет длинную запись, занимает много времени. Рассмотрим второй способ решения задач такого вида.
Известно, сколько гостинцев привезла бабушка: конфет–восемнадцать, шоколадок – шесть, киндер-сюрпризов – шесть. Чтобы узнать количество гостинцев, доставшееся каждой сестре, сложим гостинцы и разделим поровну. То есть, суммируем привезенные подарки, делим на 3. Такой способ решения, имеет название в математике – «Нахождение среднего арифметического». Сформулируем, определение, среднего арифметического:
Используя, рассмотренное определение, найдем общее количество угощения, для этого сложим количество сладостей каждого вида конфеты + шоколадки + киндеры:
Получается, что всего было 30 угощений. Теперь, эту сумму(30) делим на количество слагаемых(3), использованных в сумме:
Каждой внучке досталось по 10 сладостей.
Запишем решение этой задачи с использованием второго способа.
Как видите, второй способ, более краткий и удобный. Главное – запомнить изученное определение. Ведь, решение задач такого вида часто встречается на протяжении всего учебного процесса!
Алгоритм нахождения среднего арифметического
Рассмотрим следующую задачу.
Два брата-садовода продавали собранные фрукты. Первый брат продал яблок на 25000 рублей, а второй брат продал груш на сумму 15000 рублей. Все заработанные деньги братья разделили поровну. Сколько денег заработал каждый садовод?
Чтобы ответить на вопрос, необходимо использовать изученное правило.
Чтобы найти среднее арифметическое нескольких чисел, нужно сумму этих чисел разделить на их количество. Для этого:
1. Определяем количество слагаемых;
2. Находим сумму всех слагаемых;
3. Делим полученную сумму на количество слагаемых
В начале давайте определим количество слагаемых. Так как фрукты продавали два садовода, то и делить выручку будем между ними. То есть количество слагаемых в сумме – два.
Теперь можем найти общую сумму, заработанную братьями. Для этого, складываем выручку первого и второго брата:
Всего они заработали 40000 рублей.
Зная, что общая сумма равна 40000 рублей, мы можем найти сумму заработка каждого садовода. Для этого полученную сумму (40000) делим на количество слагаемых (2):
40000 : 2 = 20000.
Получается, заработок садовода составил 20000 рублей.
В ходе решения данной задачи мы составили алгоритм нахождения среднего арифметического.
Алгоритм вычисления среднего арифметического:
1. Находим слагаемые и считаем их количество;
2. Суммируем все слагаемые;
3. Полученную сумму делим на количество слагаемых
Держи табличку всегда под рукой, тогда сможешь найти среднее арифметическое любых чисел!
Найди среднее арифметическое чисел 10,20,30,40.
Чтобы выполнить необходимые вычисления, вспоминаем,
Мы уже знаем, что для вычисления заданий, такого вида, существует специальный алгоритм. Используя данный алгоритм,выполним все необходимые действия.
Следуя определенному алгоритму, мы без труда выполнили задание.
Запомни формулу среднего арифметического!
В заключение нашего урока рассмотрим еще одну задачу.
В школе четыре пятых класса 5А,5Б,5В,5Г. 5А – 22 ученика, 5Б –30 учеников, 5В – 28 детей, 5Г – 20. Найдите, сколько детей училось бы в каждом классе, если во всех классах учеников будет поровну.
Исходя из условия, в этой задаче нужно найти среднее количество учеников в одном классе. Чтобы ответить на главный вопрос, необходимо воспользоваться алгоритмом вычисления среднего арифметического.
Значит, если бы во всех пятых классах школы, училось равное количество учеников, в каждом классе было по 25 детей.
Сегодня вы узнали, как найти среднее арифметическое число. Внимательно рассмотрите урок, и запомните основные определения и алгоритмы! Тогда, любая контрольная будет по плечу!
Интересные факты
Когда трескается стекло, трещина распространяется со скоростью 5000 км/ч.
Как найти среднее арифметическое
Как найти среднее арифметическое чисел? Повторим правило и рассмотрим его применение на конкретных примерах.
Чтобы найти среднее арифметическое чисел, надо:
1) сложить эти числа;
2) результат разделить на количество слагаемых:
Найти среднее арифметическое чисел:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат поделить на 2:
2) 12,6, 14,7 и 16,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3:
(12,6 + 14,7 + 16,5):3=14,6.
3) 40,52, 44,63, 52,34 и 58,29.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4:
(40,52 + 44,63 + 52,34 + 58,29):4=48,945.
4) 17,4. 21,6, 25,2, 28,7 и 30,1.
Чтобы найти среднее арифметическое пяти чисел, надо сложить эти числа и результат разделить на 5:
(17,4 + 21,6 + 25,2 + 28,7 + 30,1):5=24,6.
81 Comments
КЛАСС Я ВСЁ ПОНЯЛ!
Все ясно,просто моментально вспомнила
Я понял но это не точно
Я ВООБЩЕ ВСЕ ПОНЯЛА. Д/З НА 10 СДЕЛАЛА. ( ПРИМЕРЫ ЛИШНЕЕ )
Если каждую новую тему постараться разобрать сразу же, не откладывая на «когда-нибудь потом», то оказывается, что математика — не такой уж сложный предмет.
Поля, желаю Вам дальнейших успехов в учебе!
Среднее арифметическое 4 чисел равно 7.6, а среднее арифметическое 10 других чисел равно 3.6. Найдите значение среднего арифметического этих 14 чисел. Помогите решить, пожалуйста.
Как найти среднее арифметическое число 5,24
Данил, Вы имеете в виду среднее арифметическое чисел 5 и 24? Чтобы найти среднее арифметическое 5 и 24, надо сумму этих чисел разделить на количество слагаемых: (5+24):2=29:2=14,5.
Количество чисел — три. Чтобы найти среднее арифметическое этих чисел, надо их сложить и сумму разделить на 3: (-3+0+9):3=2.
как найти среднее арифметическое чисел с дробями?
Валерия, так же, как и с другими числами: найти их сумму и разделить на количество слагаемых.
Спасибо за статью!Статья очень помогла!
Непомогло у меня числа
5, 7, 10, 12, 16
Как решить-среднее арифметическое семи чисел равно 10,2,а среднее арифметическое трёх других чисел-6,8.Найдите среднее арифметическое этих десяти чисел.
Валентина, специально в ответ на аналогичный вопрос Вероники написала пост (ссылка вверху, за 27.08.2014)
Спасибо я всё понял
Все довольно понятно, но вся соль в том, что у меня 3 числа — неизвестны. :\
Лол, перепутал. Не правильно прочитал Д/З, спасибо за статью!
Отличная новость, Илья! Поздравляю!
Как и любое другое среднее арифметическое чисел: сложить и поделить на их количество. Если у Вас три числа- (60+75+270)6:3. Если два — (6075+270):2.
среднее арифметическое чисел равно 47.первые три числа равны 37 6 81 найдите четвертое число
Супер!! Оказывается все ОЧЕНЬ легко!! Так мало написанно, но понятно!! 🙂
Среднее арифметическое чисел:
x; 3; 2,1; 2,1
равно 2,55
Найти x
А откуда нужно брать знаменатель?
Делим на количество слагаемых. То есть сколько чисел, среднее арифметическое которых надо найти, дано, на то и делим.
Ребят помогите вот что нам сказали сделать: среднее арефметическое 2 чисел=18.1число=350% второго числа.
Пусть x — I число, тогда II — 3,5x (так как составляет 350% от I-го). Так как их среднее арифметическое равно 18, сосавим и решим уравнение: (x+3,5x):2=18; 4,5x=18∙2; x=36:4,5; x=8. Следовательно, I число равно 8, II — 3,5∙8=28.
Дедушке Вите 90 лет. Средний возраст внуков 20. Среднее арифметическое дедушки и его внуков 22 года. Найдите кол-во внуков. Помогите решить
Пусть n — количество внуков у дедушки. Чтобы найти средний возраст внуков, надо сумму лет всех внуков и разделить на количество внуков, то есть на n. Таким образом, (сумма лет всех внуков):n=20, следовательно,
сумма лет всех внуков=20n.
Чтобы найти средний возраст дедушки и внуков, надо сложить сумму лет всех внуков и дедушки и разделить на (n+1): (сумма лет всех внуков + 90):(n+1)=22.
Значит, (20n + 90):(n+1)=22. Остаётся решить уравнение.
20n + 90=22(n+1)
20n-22n=22-90
n=34.
Ответ: 34 внука.
Повезло деду :D) 34 внука иметь)
Среднее арифметическое восьми чисел равно 4,3. После того как
из этого набора убрали некоторое число, среднее арифметическое
нового набора стало 3,7. Найдите это число. ПОМОГИТЕ РЕШИТ))
1) Среднее арифметическое восьми чисел равно частному от деления суммы этих восьми чисел на 8. По условию, среднее арифметическое этих восьми чисел равно 4,3. Значит, сумма восьми чисел равна 4,3∙8=34,4.
2) Среднее арифметическое семи чисел равно частному от деления суммы семи чисел на 7. По условию, среднее арифметическое семи чисел равно 3,7. Значит, сумма семи чисел равна 3,7∙7=25,9.
3) Разность между суммой восьми чисел и суммой семи чисел и есть то число, которое убрали:
34,4-25,9=8,5.
Спасибо большое все легко и понятно)
Очень благодарна вам и вашему сайту)
Удачи вам в дальнейшем)
Спасибо, Полина! И Вам удачи и успехов в учёбе!
средняя арифметическая 9и чисел равно 16и. если один из этих чисел равен 0 тогда сколько будет ср.арифметическая остальных?
Среднее арифметическое 9 чисел (а1+а2+…+а8+0):9=16.Отсюда а1+а2+…+а8+0=16∙9=144.
Значит, среднее арифметическое оставшихся восьми чисел (а1+а2+…+а8):8=144:8=18.
Среднее арифметическое трёх чисел 15. Найти эти числа, если второе число число в 1,4 раза,а третье в 1.2 раза больше первого.
Пусть первое из чисел равно х, тогда второе — 1,4х, а третье — 1,2х. Так как их среднее арифметическое равно 15, составим и решим уравнение:(х+1,4х+1,2х):3=15.
Светлана Ивановна, если я правильно вас поняла то в моём случае:записать формулу среднего арифметического трёх чисел одно из ко орых в 3 раза больше другого и в 2 раза меньше третьего, это записываем так(х+3х+3х×2):3,заранее спасибо за ответ
Елена, всё верно.
Среднее арифметическое двух чисел равно 14 одно из чисел 12,4 как найти другое число
(х+12,4):2=14. Отсюда х=28-12,4=15,6.
Среднее арифметическое двух положительных чисел на 30% меньше большего из этих чисел. На сколько процентов оно больше меньшего из этих чисел? (Ответ запишите числом). Помогите, пожалуйста решить!
Примем большее из данных двух положительных чисел за x, а меньшее — за y. Тогда среднее арифметическое этих чисел равно 0,7x.Имеем:
Отсюда x=y:0,4; x=2,5y. Соответственно, среднее арифметическое 0,7x=0,7∙2,5y=1,75y составляет 175% от меньшего числа y. А значит, среднее арифметическое на 75% больше меньшего из чисел.
Плиз,помогите не могу сообразить.Я считаю показатель с 9 утра до 9 вечера,и с 9 вечера до 9 утра,то есть днём допустим у меня показатель 121руб,а вечером 221,среднее получается 171,но если я беру общий показатель за день,то он 141руб.А как мне из дневного и вечернего показателя высчитать общий?А показатель считается так:Я беру выручку и делю на количество.
Олеся, извините, но я не понимаю, о каком показателе Вы говорите.
Светлана Михайловна доброго времени! Подскажите пожалуйста как определить среднее арифметическое нескольких углов. результат нужен в градусах. Спасибо. Сергей
Наверное, просто найти среднее арифметическое градусных мер и результат округлить до градусов (в 1 градусе 60 минут. Соответственно, до 30 минут округляем с недостатком, от 30 и более — с избытком).
Большое спасибо за ответ.
Здравствуйте, как найти среднее арефметическое в таком примере,с двух сторон не известные числа
Пример: …14,18,25,44,30…
Нужно найти какие цифры нужно вставить по краям
Артём, условие неполное, данных недостаточно.
Здравствуйте помогите найти средеарифметическое двух чисел 1,536 и 1,540
Здравствуйте, не могли бы вы помочь… совсем забыла математику. задача:среднее для серии из 70 значений 30. Какова сумма этих значений?
Среднее арифметическое нескольких чисел равно сумме этих чисел, делённой на количество слагаемых. Следовательно, чтобы найти сумму, надо известное среднее арифметическое умножить на количество слагаемых: 30∙70=2100.
А если в ряду есть отрицательные и положительные числа, как тогда?
среднее арифметическое двух чисел 7,2,чему равна сумма
(a1+a2):2=7,2. Отсюда a1+a2=7,2∙2=14,4.
Я чётка всё поняла это так легко
Не решить у меня числа 1,8;5;7.
Дроби никто не отменял: (1+8+5+7):4=5,25 или 5 1/4.
Здравствуйте как найти среднее арифметическое число 24,35 и 17,69
Сложить и разделить на 2:
(24,35+17,69):2=21,02.
Как найти среднее арифметическое чисел 73;74;83 и а равное 11,4
мне не помогло, у меня с иксом
Денис, значит, у Вас среднее арифметическое известно, и нужно найти одно из чисел. Для этого составьте и решите уравнение.
Помогите решить: 85,37; 49; 63,2; 76,43 найти среднее арефметическое
Среднее арифметическое чисел равно сумме этих чисел, делённой на количество слагаемых: (85,37+49+63,2+76,43):4. Осталось вычислить.
если среднее геометрическое число двух чисел равно 16,а среднее арифметическое равно 20, найдите их?
Пусть эти числа x и y. Среднее арифметическое (x+y):2=20, x+y=40.
Среднее геометрическое √(xy)=16, xy=256. Искомые числа — 32 и 8.
Как найти среднее арифметическое число
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.
Среднее арифметическое, размах, мода и медиана
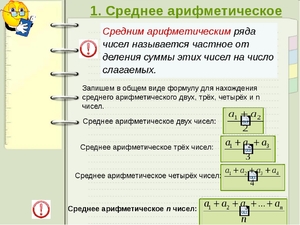
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Для ряда a1,a1. an среднее арифметическое вычисляется по формуле:
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.
Среднее арифметическое
Предлагаемая здесь программа расчета среднего арифметического умеет не только считать статистические параметры исследуемого множества чисел, но и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.
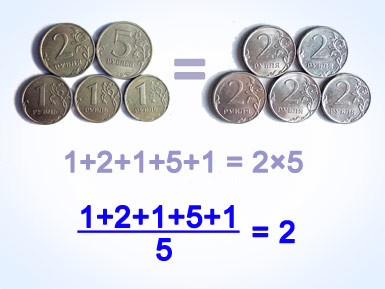
Среднее арифметическое [1] значение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:
Расчет среднего арифметического
Введите исходные данные
Что-то пошло не так. Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°
Дисперсия [2] , σ 2
Среднеквадратическое отклонение [3] , σ
Коэффициент вариации [4] , V
Размах вариации [5] , R
Среднее линейное отклонение [6] , δ
Design by Sergey Ov for abc2home.ru
ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:
Сохранить расчет среднего арифметического в истории браузера
Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов
После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднего арифметического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.
Страницы по теме «Расчет средних значений»
Свойства среднего арифметического
1. Среднее арифметическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.
2. Кроме того среднее арифметическое подчиняется неравенству о средних для множества положительных вещественных чисел
то есть для любого множества действительных чисел среднее арифметическое никогда не бывает больше среднего квадратического [1] :
Прикладное значение среднего арифметического
Среднее арифметическое значений исследуемых данных находит широкое прикладное применение в метрологии и статистике. При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение будет являться оценкой ошибки измерений, поэтому дисперсия и среднеквадратическое отклонение так же включены в результаты расчетов.
Задания ЕГЭ, на тему «Среднее арифметическое»
Среднее арифметическое 7 натуральных чисел равно 12. К ним добавили восьмое число такое, что среднее арифметическое этих восьми чисел равно 14. Найдите восьмое число.
Согласно оределению среднего арифметического для 7 чисел имеем:
А для 8 чисел получется, что
по определению среднего арифметического сумма множества чисел равна призведению среднего арафметического и их количества и по условию задачи имеем:
(включаем логику [обычную])
а). Очевидно, что левая часть полученного равенства 2.2 делится на 5, поэтому n тоже должно делиться на 5. По условию 40 n n = 45.
Таким образом, написано 45 целых чисел.
б). Подставим в равенство 2.2 полученное для n значение, тогда
в). Для определения наибольшего возможного количества целых положительных чисел удовлетворяющих условиям задачи, возпользуемся выражениями 2.1 и 2.3 с подставленным значением n. С учетом того, что p ≥ 0 получаем:
k + m ≤ 45;
m = 36 + k
или подставляя в первое значение m:
Таким образом положительных чисел может быть не более 4.
Ответ: а) 45; б) отрицательных; в) 4.
P.S. На этой странице используется Бета версия программы расчета среднего арифметического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Другие кому-то, возможно, более привычные определения:
Среднее арифметическое нескольких чисел равно сумме этих чисел, делённой на количество слагаемых в этой сумме (Математика, 5 класс).
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых (Алгебра, Макарычев, 7 класс).
2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:
3. Среднеквадратическое отклонение σ вычисляется как корень квадратный от дисперсий и возвращает нас в область сопоставимых со средним арифметическим величин:
4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:
5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:
6. Среднее линейное отклонение определяется как средняя арифметическая величина абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:
Среднее арифметическое
Содержание
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому: тому, что это такое, как найти среднее арифметическое натуральных чисел и дробей, и где это может пригодиться.
Знакомство со средним арифметическим
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического натуральных чисел
Теперь разделим эту сумму расстояний на количество часов.
Рассмотрим другую задачу.
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Как найти среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
$$1.4 \cdot x + x = 15$$
Вычислим, сколько съел каждый из кроликов.
Сначала найдём значение выражения.
$$1.4 \cdot x + x = 2.4 \cdot x = 15$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
$$6.25 \cdot 1.4 = 8.75$$
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
Значит, наше решение было верным.
Как найти среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Умножаем обе части дроби на один и тот же дополнительный множитель.
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
Теперь подбираем дополнительные множители и складываем наши дроби.
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.
Как находить и вычислять для двух среднее арифметическое значение
Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.
Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.
В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.
Подсчёт среднего арифметического пары
Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:
Формула
Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:
В этой формуле применяется следующее обозначение:
А и В – это заранее выбранные числа, для которых необходимо находить значение.
Нахождение значения для трёх
Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:
Формула
Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:
В данной формуле принято следующее обозначение:
А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.
Вычисление среднего арифметического четырёх
Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:
Формула
Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:
В данной формуле переменные имеют следующее значение:
А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.
Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.
Подсчёт среднего арифметического пяти
Выполнение данной операции потребует проведения определённого алгоритма действий.
Формула
Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:
В данной формуле переменные имеют такое обозначение:
А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.
Универсальная формула вычисления
Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического, можно обратить внимание на то, что у них есть общая закономерность.
Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.
Главным при определении формулы является принцип расчёта среднего арифметического.
Данный принцип как было видно из приведённых примеров, выглядит таким образом:
Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:
(А+В+…+N)/N
Данная формула содержит следующие переменные:
А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.
N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.
Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.
Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.
Видео
Из видео вы узнаете, как находить среднее арифметическое.
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Среднее арифметическое
Среднее арифметическое – это частное от деления суммы чисел на их количество.
Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых, то есть на 2:
Значит среднее арифметическое двух чисел (4 и 6) равно 5.
Пример 2. Найти среднее арифметическое чисел 15, 8, 20 и 13.
Решение: Сначала найдём сумму данных чисел:
15 + 8 + 20 + 13 = 56.
Затем разделим полученный результат на количество слагаемых:
Из данных примеров можно сделать вывод, что для нахождения среднего арифметического, нужно сложить все числа и поделить их сумму на их количество.
Рассмотрим задачи, в которых требуется найти средне арифметическое нескольких чисел, относящихся к одной величине.
Задача 1. Утром температура была 15 градусов, днём она поднялась до 27 градусов, а вечером опустилась до 19, ночью температура достигла отметки в 11 градусов. Найти среднюю температуру за сутки.
Решение: Сначала найдём общую сумму температур за сутки:
15 + 27 + 19 + 11 = 72,
затем разделим полученную сумму на 4:
Ответ: средняя температура за сутки равна 18 градусам.
Задача 2. В магазине продали 6 килограммов яблок по цене 55 рублей за килограмм и 4 килограмма груш по цене 75 рублей за килограмм. Какая средняя цена 1 килограмма фруктов?
Решение: Сначала посчитаем сколько всего денег получил магазин за фрукты:
55 · 6 = 330 (р) — выручка за яблоки;
75 · 4 = 300 (р) — выручка за груши;
330 + 300 = 630 (р) — общая выручка за фрукты.
Затем найдём общий вес фруктов:
теперь разделим общую выручку на общий вес проданных фруктов и получим среднюю цену за 1 кг:
Ответ: средняя цена 1 килограмма проданных фруктов — 63 рубля.
Что такое среднее арифметическое чисел: двух, трех, четырех и тд
В данной публикации мы рассмотрим, что такое среднее арифметическое чисел (двух, трех, четырех и т.д.), приведем формулу, с помощью которой его можно найти, а также разберем примеры задач для лучшего понимания теоретического материала.
Определение и формула
Среднее арифметическое двух и более чисел – это отношение их общей суммы к их количеству. Вычисляется следующим образом:
Частные случаи формулы:
» data-order=» » style=»min-width:66.4828%; width:66.4828%;»> » style=»min-width:66.4828%; width:66.4828%;»>  |
» data-order=» «> «>  |
» data-order=» «> «>  |
Примечание: Для обозначения среднего арифметического обычно используется греческая буква μ (читается как “мю”).
Примеры задач
Задание 1
У Пети было 4 яблока, у Даши – 6, а у Лены – 5. Они решили сложить все фрукты вместе и разделить поровну на каждого. Вычислите, сколько яблок достанется каждому.
Решение
В данном случае у нас три числа, и требуется найти их среднее арифметическое. Для этого воспользуемся представленной выше формулой:
Ответ: каждому полагается 5 яблок.
Задание 2
На преодоление дистанции из точки A в точку B спортсмен потратил 5 часов, при этом его скорость была следующей: первые два часа – 6 км/ч, затем два часа – 9 км/ч, и последние 60 минут – 7 км/ч. Найдите среднюю скорость.
Решение
Итак, нам нужно вычислить среднее арифметическое пяти чисел, которые соответствуют скоростям за каждый час бега:
Ответ: средняя скорость спортсмена – 7,4 км/ч.
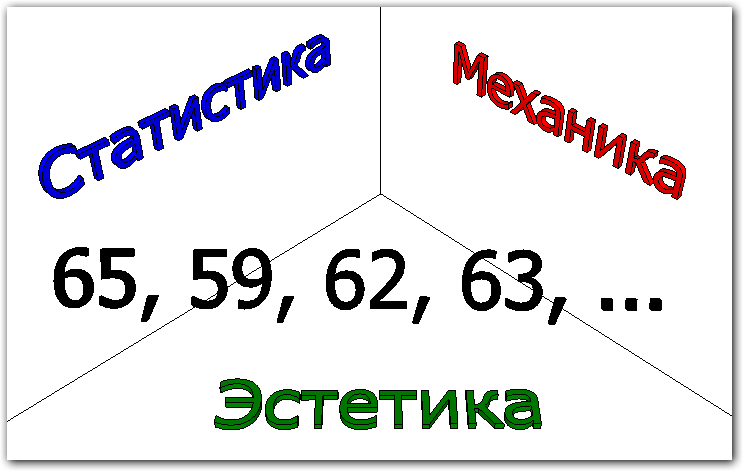
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
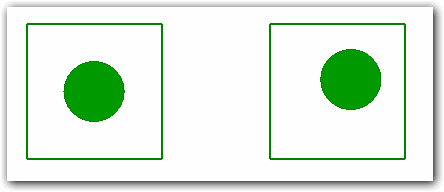
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
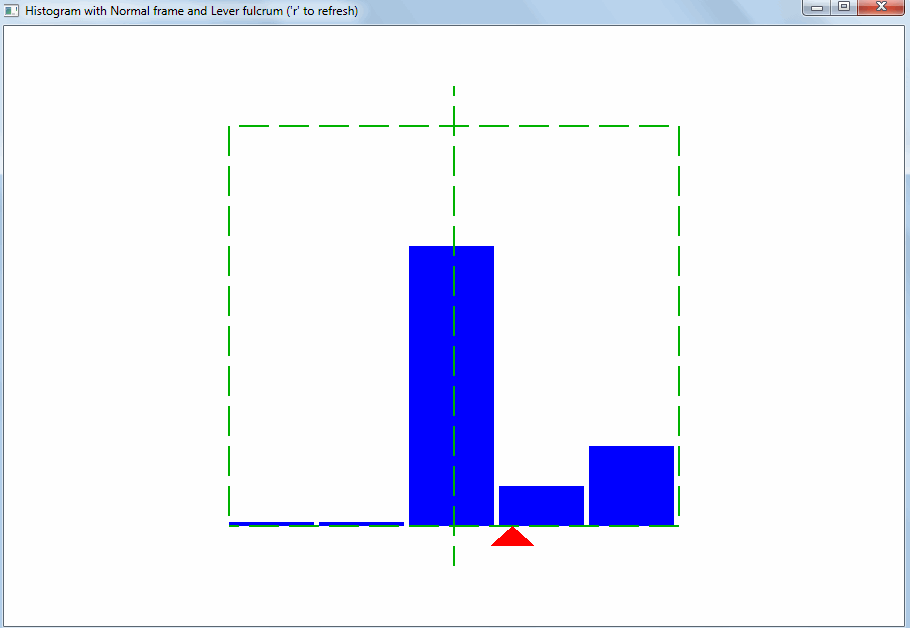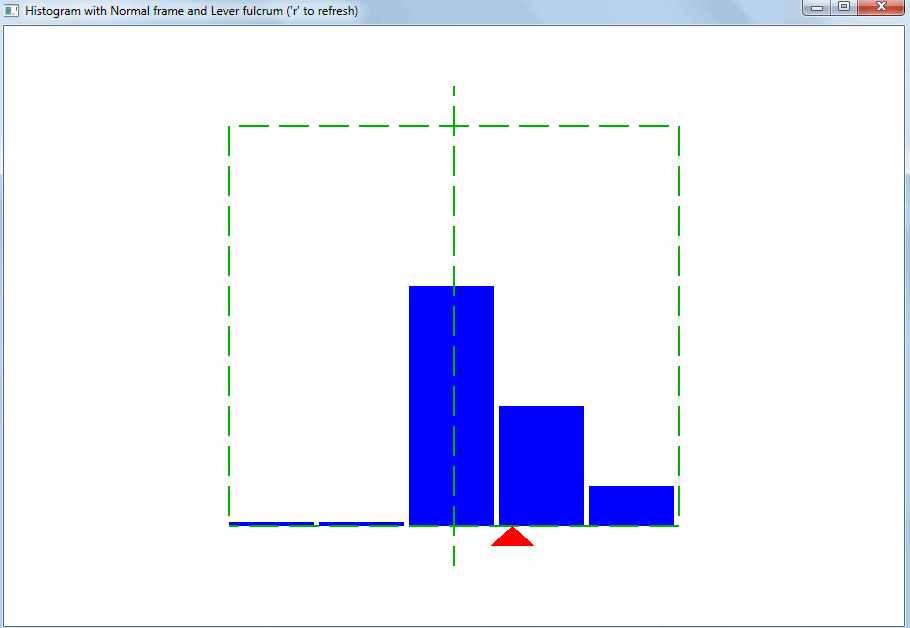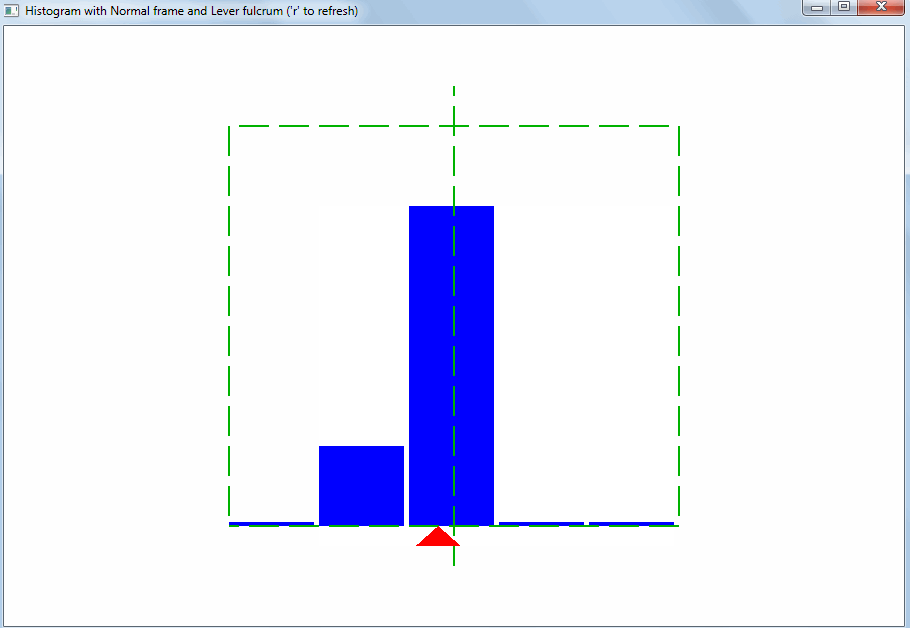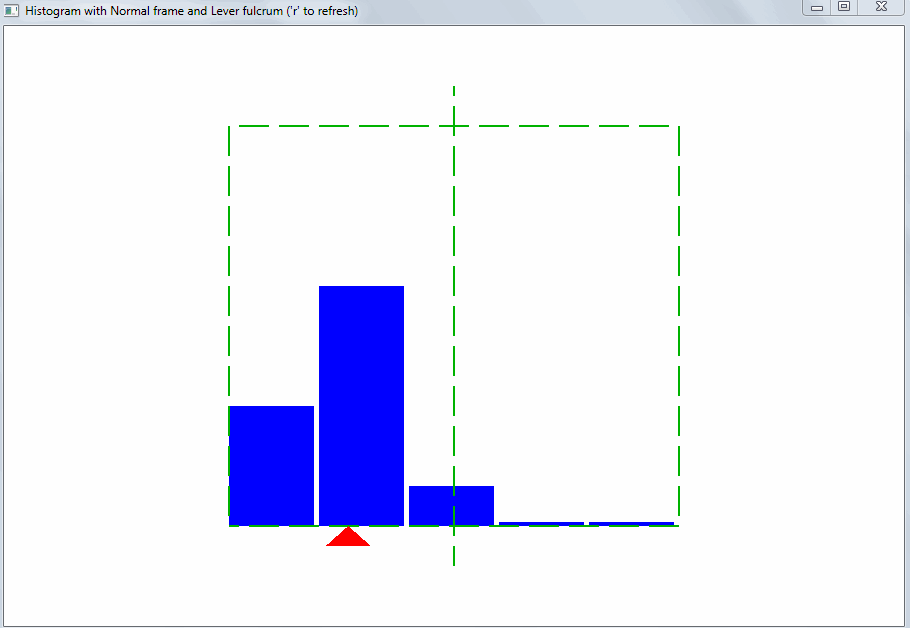
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
Среднее арифметическое
Вы будете перенаправлены на Автор24
Среднее арифметическое — очень важное понятие из мира математики, используемое во многих других дисциплинах. Например, среднее арифметическое используют для того чтобы найти какое-то усреднённое значение. В частности, в экономических дисциплинах можно воспользоваться этим понятием для расчёта среднего дохода в месяц и других показателей.
Часто понятием среднего арифметического пользуются и учёные: химики с помощью него могут посчитать, сколько в среднем получается необходимого вещества при повторных проведениях опыта, а специалисты агропромышленности — среднюю урожайность яблок или другой сельскохозяйственной культуры.
Что такое среднеарифметическое значение
Средним арифметическим называют сумму всех чисел (например, полученных при повторном проведении одного и того же опыта), поделённых на количество этих чисел.
Важно! Нельзя складывать и искать среднее арифметическое между величинами с разными единицами измерения и разной размерностью.
Примерами величин, которые нельзя складывать так как они имеют разную размерность, являются масса и расстояние. Масса измеряется в килограммах или граммах, а расстояние измеряется в сантиметрах, метрах и других единицах измерения.
Если значения какой-либо величины заданы с помощью разных единиц измерения, то в таком виде их также нельзя складывать и, соответственно, искать среднее арифметическое между ними.
Если же привести их к одинаковой единице измерения, то можно сложить их между собой.
Готовые работы на аналогичную тему
Как посчитать среднее арифметическое
Решение:
$l_3=1,7 м = 1,7 \cdot 100 см= 170$ см.
Теперь мы можем найти среднюю длину его прыжка:
Ответ: В среднем Эдуард прыгает на длину в 171 см.
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 06.04.2022
Среднее арифметическое
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1] и является одной из наиболее распространенных мер центральной тенденции.
Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).
Содержание
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E<xi> есть математическое ожидание этой выборки.
На практике разница между μ и 

Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры
Непрерывная случайная величина
Для непрерывно распределённой величины 

Некоторые проблемы применения среднего
Отсутствие робастности
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.
В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост 
Направления
Особую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:
В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).
Среднее арифметическое чисел + калькулятор #
В учебниках дано такое понятие среднего арифметического:
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.
Говоря о значениях каких − то величин, часто имеют в виду их средние значения. Например, когда говорят, что с 1 га поля собрали 38 ц пшеницы, то это не означает, что с каждого гектара поля было собрано именно такое количество центнеров пшеницы. Эту величину получили, разделив массу всего урожая, выраженную в центнерах, на площадь всего поля, выраженную в гектарах. Величина 38 ц является средней урожайностью с 1 га данного поля.
Еще один пример. Если автомобиль проехал 120 км за 1,5 ч, то, разделив длину пути на время, получим среднюю скорость движения автомобиля. Она равна 80 км/ч. При этом автомобиль мог останавливаться, ехать со скоростью большей либо меньшей, чем 80 км/ч.
Объясним более просто. К примеру, у нас есть три числа: 2, 4 и 6. Нужно найти их среднее арифметическое.
Чтобы найти среднее арифметическое, сложите все величины и разделите результат на их количество.
Сумма чисел всегда равна сумме такого же количества средних арифметических.
Среднее арифметическое никогда не будет больше самого большого из заданных чисел и меньше, чем самое маленькое. К примеру, если даны числа 5,8,99, то среднее арифметическое никогда не будет меньше 5 и больше 99. Представьте 3 стакана с водой: одном налито 5 мл, в другом 8, а в третьем 99 мл. Разольем эту воду по этим стаканам так, чтобы в каждом стало одинаково, ничего не выплескивая и не добавляя. Нам придется из большего добавить в среднее и меньшее, значит большее при нахождении среднего арифметического уменьшится, а меньшее увеличится до одного и того же числа. Эта информация пригодится для самопроверки при решении задач.
Задачи на среднее арифметическое условно можно разделить на 2 типа.
Задачи на нахождение среднего арифметического
Задача 1
В течении недели в 8 ч утра Саша измерял температуру воздуха. Он получил такие результаты: 20°С; 18°С; 16°С; 15°С; 14°С; 17°С; 19°С. Найдите среднее значение проведенных измерений.
(20 + 18 + 16 + 15 + 14 + 17 + 19) : 7 = 119 : 7 = 17
Ответ: 17°С.
Задача 2
Поезд ехал со скоростью 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч. Найдите среднюю скорость поезда на протяжении всего пути.
Задача 3
Автомобиль ехал 3 ч со скоростью 56,4 км/ч и 4 ч со скоростью 62,7 км/ч. Найдите среднюю скорость автомобиля на всем пути.
Задание 4
Задание 5
Задание 6
Среднее арифметическое четырех чисел равно 2,1, а среднее арифметическое трех других чисел − 2,8. Найдите среднее арифметическое этих семи чисел.
Схема для лучшего понимания задачи.
Если упростить условие, то нам даны такие числа и нужно найти среднее арифметическое:
2,1 2,1 2,1 2,1 2,8 2,8 2,8
Это просто, неправда ли?
Задание 7
Среднее арифметическое семи чисел равно 10,2, а среднее арифметическое трех других чисел − 6,8. Найдите среднее арифметическое этих десяти чисел.
Задачи на нахождение величины по известному среднему арифметическому
Задача 1
Среднее арифметическое чисел 7,8 и x равно 7,2. Найдите число x.
Чтобы найти среднее арифметическое, нужно сложить величины и разделить на их количество, в данном случае на 2. Составим уравнение.
(7,8 + x) : 2 = 7,2
7,8 + x = 7,2 * 2
x = 14,4 − 7,8
x = 6,6
Ответ: 6,6
Задача 2
Среднее арифметическое чисел 6,4 и y равно 8,5. Найдите число y.
Задача 3
Среднее арифметическое двух чисел, одно из которых в 4 раза меньше второго, равно 10. Найдите эти числа.
Решение задачи через х
Пусть x − одно число, тогда:
4x − второе число.
Составим уравнение:
(x + 4x) : 2 = 10
5x = 10 * 2
x = 20 : 5
x = 4 − одно число;
4x = 4 * 4 = 16 − второе число.
Ответ: 4 и 16.
Задача 4
Среднее арифметическое двух чисел, одно из которых на 4,6 больше второго, равно 8,2. Найдите эти числа.
Пусть x − второе число, тогда:
x + 4,6 − первое число.
Составим уравнение:
(x + x + 4,6) : 2 = 8,2
2x + 4,6 = 8,2 * 2
2x = 16,4 − 4,6
x = 11,8 : 2
x = 5,9 − второе число;
x + 4,6 = 5,9 + 4,6 = 10,5 − первое число.
Ответ: 5,9 и 10,5.
Задача 5
Принимая участие в математической олимпиаде, Дима решил 10 задач. За каждую задачу он мог получить не более 12 баллов. За первые восемь задач мальчик получил среднюю оценку 7 баллов. Сколько баллов получил Дима за каждую из оставшихся двух задач, если среднее количество баллов за одну задачу составляло 8 баллов?
За первые 8 задач мальчик получил среднюю оценку 7 баллов. Это можно представить как
7 7 7 7 7 7 7 7
Но когда он решил все 10 задач, средняя оценка стала равна 8. То есть стало так:
8 8 8 8 8 8 8 8 8 8
Задача 6
Автомобиль ехал 3,4 ч по шоссе со скоростью 90 км/ч и 1,6 ч по грунтовой дороге. С какой скоростью ехал автомобиль по грунтовой дороге, если средняя скорость на протяжении всего пути составляла 75,6 км/ч?
Задача 7
Купили 2 кг конфет одного вида по 255 р. за килограмм, 4 кг конфет второго вида по 285 р. за килограмм и еще 3 кг конфет третьего вида. Средняя цена купленных конфет составляла 260 р. за килограмм. Сколько стоил килограмм конфет третьего вида?
Задача 8
Средний возраст одиннадцати футболистов команды равен 22 годам. Во время игры одного из футболистов удалили с поля, после чего средний возраст оставшихся игроков составил 21 год. Сколько лет было футболисту, который покинул поле?
Условно будет выглядеть так:
22 22 22 22 22 22 22 22 22 22 22
21 21 21 21 21 21 21 21 21 21
Калькулятор для нахождения среднего арифметического
Ну вот, вроде разобрали основные примеры очень подробно. Если остались вопросы, задавайте в комментариях.
Как найти число зная среднее арифметическое
Среднее арифметическое — это число, равное сумме всех чисел множества, делённой на их количество.
Среднее арифметическое двух чисел вычисляется по формуле:
Xср — среднее арифметическое 2-х чисел;
X1 — первое число;
X2 — второе число.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета среднего арифметического двух чисел (среднее между двумя числами). С помощью этого калькулятора вы в один клик сможете рассчитать среднее арифметическое 2-х чисел, если известны исходные числа.
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Что такое среднее арифметическое
Средним арифметическим нескольких величин является отношение суммы этих величин к их количеству.
Среднее арифметическое определенного ряда чисел называется сумма всех этих чисел, поделенная на количество слагаемых. Таким образом, среднее арифметическое является средним значением числового ряда.
Чему равно среднее арифметическое нескольких чисел? А равно они сумме этих чисел, которая поделена на количество слагаемых в этой сумме.
Как найти среднее арифметическое число
В вычислении или нахождении среднего арифметического нескольких чисел, нет ничего сложного, достаточно сложить все представленные числа, а полученную сумму разделить на количество слагаемых. Полученный результат и будет средним арифметическим этих чисел.
Рассмотрим этот процесс более подробно. Что же нам нужно сделать для вычисления среднего арифметического и получения конечного результата этого числа.
Во-первых, для его вычисления нужно определить набор чисел или их количество. В этот набор могут входить большие и маленькие числа, и их количество может быть каким угодно.
Во-вторых, все эти числа нужно сложить и получить их сумму. Естественно, если числа несложные и их небольшое количество, то вычисления можно произвести, записав от руки. А если же набор чисел впечатляющий, то лучше воспользоваться калькулятором или электронной таблицей.
И, в-четвертых, полученную от сложения сумму необходимо разделить на количество чисел. В итоге мы получим результат, который и будет средним арифметическим числом этого ряда.
Для чего нужно среднее арифметическое
Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.
Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.
Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.
Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.
Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,
15 + 20 + 25 + 25 + 30 = 115
Теперь разделим эту сумму на количество дней
Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.
Домашнее задание
1.Путем нехитрых вычислений найдите среднее арифметическое число посещаемости учеников вашего класса за неделю.
2. Найдите среднее арифметическое:
3. Решите задачу:
Тема среднего арифметического и среднего геометрического входит в программу математики 6-7 классов. Так как параграф довольно прост для понимания, его быстро проходят, и к завершению учебного года школьники его забывают. Но знания в базовой статистике нужны для сдачи ЕГЭ, а также для международных экзаменов SAT. Да и для повседневной жизни развитое аналитическое мышление никогда не помешает.
Как вычислить среднее арифметическое и среднее геометрическое чисел
Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?
Решение: (11 + 4 + 3) / 3 = 6
В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.
Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.
Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:
Решение: ∛(4 × 2 × 8) = 4
В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое — ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.
Может ли так произойти, что среднее арифметическое станет равным среднему геометрическому?
Конечно, может. Но только в двух случаях. Если имеется ряд чисел, состоящий только либо из единиц, либо из нулей. Примечательно также то, что ответ не зависит от их количества.
Доказательство с единицами: (1 + 1 + 1) / 3 = 3 / 3 = 1 (среднее арифметическое).
∛(1 × 1 × 1) = ∛1 = 1(среднее геометрическое).
Доказательство с нулями: (0 + 0) / 2=0 (среднее арифметическое).
√(0 × 0) = 0 (среднее геометрическое).
Другого варианта нет и быть не может.
Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.
Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.
В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.
Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:
Формула
Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:
В этой формуле применяется следующее обозначение:
А и В – это заранее выбранные числа, для которых необходимо находить значение.
Нахождение значения для трёх
Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:
Формула
Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:
В данной формуле принято следующее обозначение:
А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.
Вычисление среднего арифметического четырёх
Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:
Формула
Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:
В данной формуле переменные имеют следующее значение:
А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.
Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.
Подсчёт среднего арифметического пяти
Выполнение данной операции потребует проведения определённого алгоритма действий.
Формула
Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:
В данной формуле переменные имеют такое обозначение:
А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.
Универсальная формула вычисления
Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.
Главным при определении формулы является принцип расчёта среднего арифметическог о.
Данный принцип как было видно из приведённых примеров, выглядит таким образом:
Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:
Данная формула содержит следующие переменные:
А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.
N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.
Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.
Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.
В математике среднее арифметическое значение чисел (или просто среднее) — это сумма всех чисел в данном наборе, разделенная на их количество. Это наиболее обобщенное и распространенное понятие средней величины. Как вы уже поняли, чтобы найти нужно суммировать все данные вам числа, а полученный результат разделить на количество слагаемых.
Что такое среднее арифметическое?
Давайте рассмотрим пример.
Для начала найдем сумму всех данных чисел.
Теперь разделим получившуюся сумму на количество слагаемых. Так как у нас слагаемых три, соответственно, мы будем делить на три.
Следовательно, среднее значение чисел 6, 7 и 11 — это 8. Почему именно 8? Да потому, что сумма 6, 7 и 11 будет такая же, как трех восьмерок. Это отлично видно на иллюстрации.
Среднее значение чем-то напоминает «выравнивание» ряда чисел. Как видите, кучки карандашей стали одного уровня.
Рассмотрим еще один пример, чтобы закрепить полученные знания.
Пример 2. Даны числа: 3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29. Нужно найти их среднее арифметическое значение.
3 + 7 + 5 + 13 + 20 + 23 + 39 + 23 + 40 + 23 + 14 + 12 + 56 + 23 + 29 = 330
Делим на количество слагаемых (в этом случае — 15).
Следовательно, среднее значение данного ряда чисел равно 22.
Зная это, рассмотрим еще один пример.
Находим сумму чисел.
3 + (-7) + 5 + 13 + (-2) = 12
Так как слагаемых 5, разделим получившуюся сумму на 5.
В наше время технологического прогресса гораздо удобнее использовать для нахождения среднего значения компьютерные программы. Microsoft Office Excel — одна из них. Искать среднее значение в Excel быстро и просто. Тем более, эта программа входит в пакет программ от Microsoft Office. Рассмотрим краткую инструкцию, значение с помощью этой программы.
Чтобы было более понятно, опробуем полученные знания.
Очень удобно использовать эту функцию для ведения учета, накладных или когда вам просто нужно найти среднее значение из очень длинного ряда чисел. Поэтому ее часто используют в офисах и крупных компаниях. Это позволяет сохранять порядок в записях и дает возможность быстро посчитать что-либо (например, средний доход за месяц). Также с помощью Excel можно найти среднее значение функции.
Ответ: каждому досталось по 4 груши.
Пример 2. На курсы английского языка в понедельник пришло 15 человек, во вторник — 10, в среду — 12, в четверг — 11, в пятницу — 7, в субботу — 14, в воскресенье — 8. Найти среднюю посещаемость курсов за неделю.
Решение: Найдем среднее арифметическое:
| 15 + 10 + 12 + 11 + 7 + 14 + 8 | 77 | 7 | 7 |
Ответ: в среднем на курсы английского языка приходило 11 человек в день.
Пример 3. Гонщик ехала два часа со скоростью 120 км/ч и час со скоростью 90 км/ч. Найдите среднюю скорость автомобиля во время гонки.
Решение: Найдем среднее арифметическое скоростей автомобиля за каждый час пути:
| 120 + 120 + 90 | 330 | 3 | 3 |
Ответ: средняя скорость автомобиля во время гонки была 110 км/ч.
Пример 4. Среднее арифметическое 3 чисел равно 6, а среднее арифметическое 7 других чисел равно 3. Чему равно среднее арифметическое этих десяти чисел?
Решение: Так как среднее арифметическое 3-х чисел равно 6 то их сумма равна 6 · 3 = 18, аналогично сумма оставшихся 7-ми чисел равна 7 · 3 = 21.
Значит сумма всех 10-ти чисел будет 18 + 21 = 39, а среднее арифметическое равно
Как найти среднее арифметическое число в Excel
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
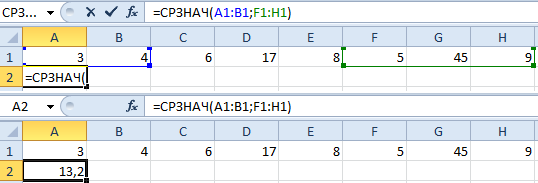
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
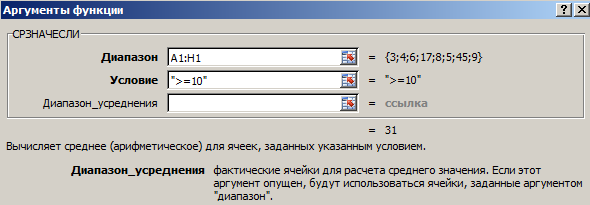
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
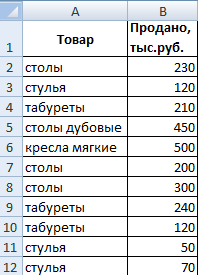
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
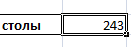
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
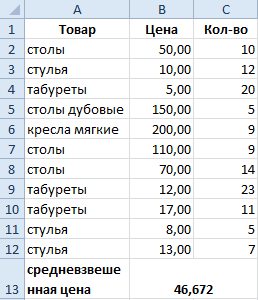
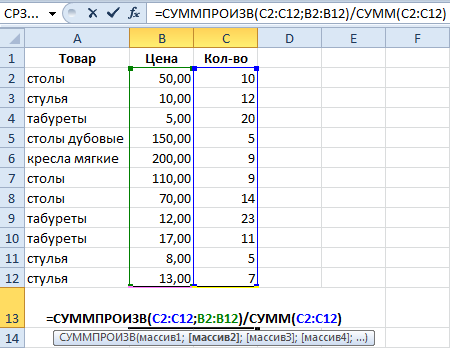
Как посчитать средневзвешенную цену в Excel?
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Как найти среднее арифметическое чисел
Среднее арифметическое чисел – это средняя величина определенного ряда чисел, полученная путем несложного расчета. Данное значение широко используется специалистами в области статистики, экономики и других смежных наук. Посчитать его может каждый, часто без помощи вычислительной техники. Рассмотрим несколько примеров.
Рассчитайте среднее арифметическое двух чисел таким образом:
Используйте формулу: “(a+b) / 2”,
где a, b – заданные числа для нахождения среднего арифметического.
Расчет среднего арифметического трех чисел:
Используйте формулу “(a+b+c) / 3”,
где a, b, с – заданные числа для нахождения среднего арифметического.
Аналогичным образом рассчитывается среднее арифметическое четырех чисел:
Воспользуйтесь формулой: “(a+b+c+d) / 4”,
где a, b, с, d – заданные числа для нахождения среднего арифметического.
Выполните такой же алгоритм нахождения, как и в предыдущих расчетах:
Воспользуйтесь формулой: “(a+b+c+d+e) / 5”,
де a, b, с, d, e – заданные числа для нахождения среднего арифметического.
Количество чисел, из которого нужно извлечь среднюю арифметическую величину, может быть достаточно большим. Поэтому рассчитывайте результат по единому логическому принципу:
Теперь вы знаете, что среднее арифметическое чисел находится очень просто. Но будьте внимательны и не ленитесь проверить результат, поскольку даже в самых простых расчетах легко допустить грубую ошибку.
Поделиться советом: “Как найти среднее арифметическое чисел”
Алгебра
План урока:
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:
Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.
В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.
Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.
Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
в то время как размах выборки второго спортсмена равен
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:
Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:
Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.