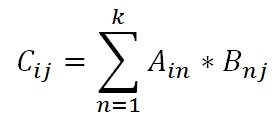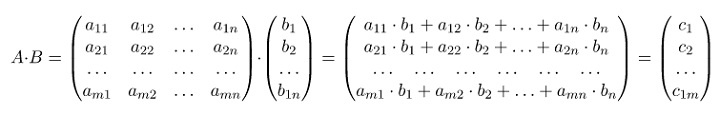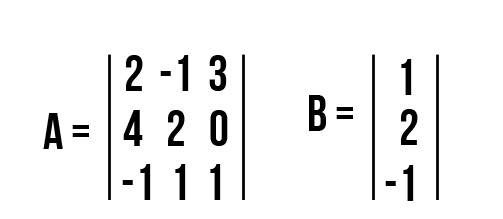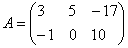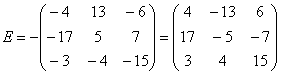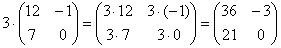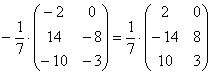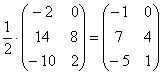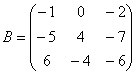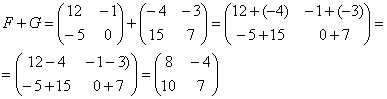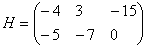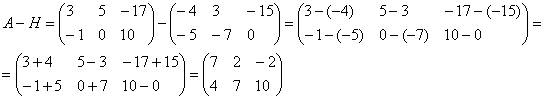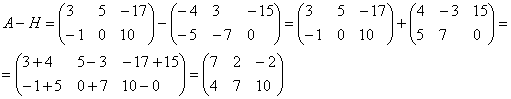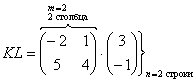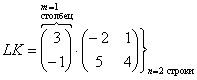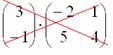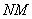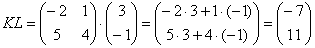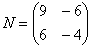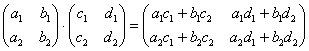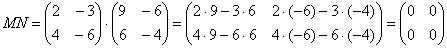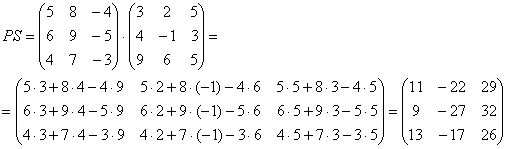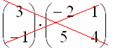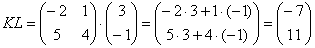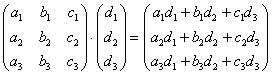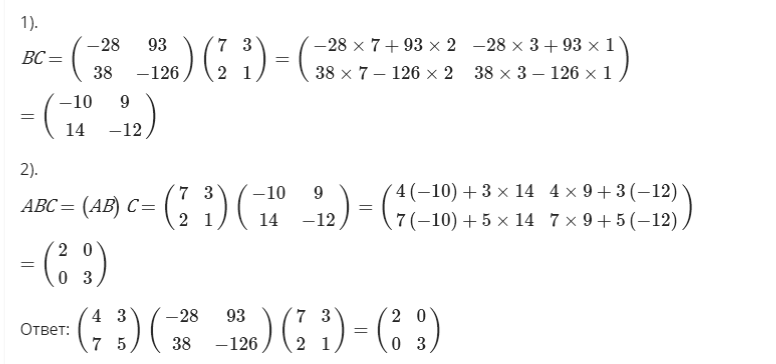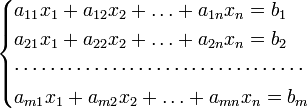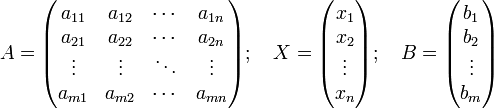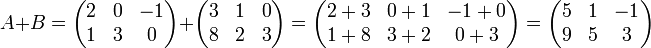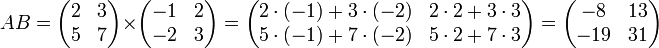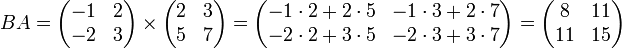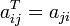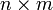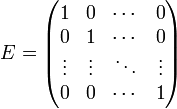Как перемножать матрицы
Как перемножать матрицы
Умножение матриц
Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Алгоритм умножения матриц
Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.
Пример 7
$A= \begin
$B=\begin
Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.
$B \cdot A = \begin
Пример 8
$A= \begin
Пример 9
$A= \begin
Пример 11
$A=\begin
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
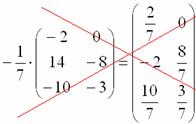
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Знакомство с матрицами
Понятие и базовые операции.
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.


Простые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.


Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

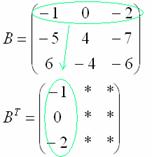
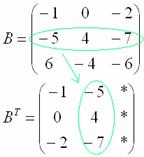
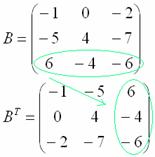
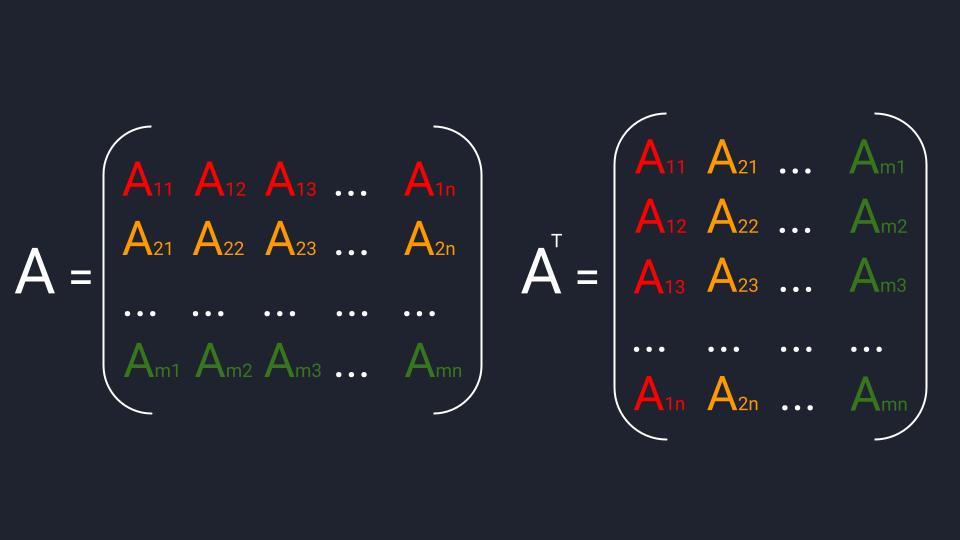
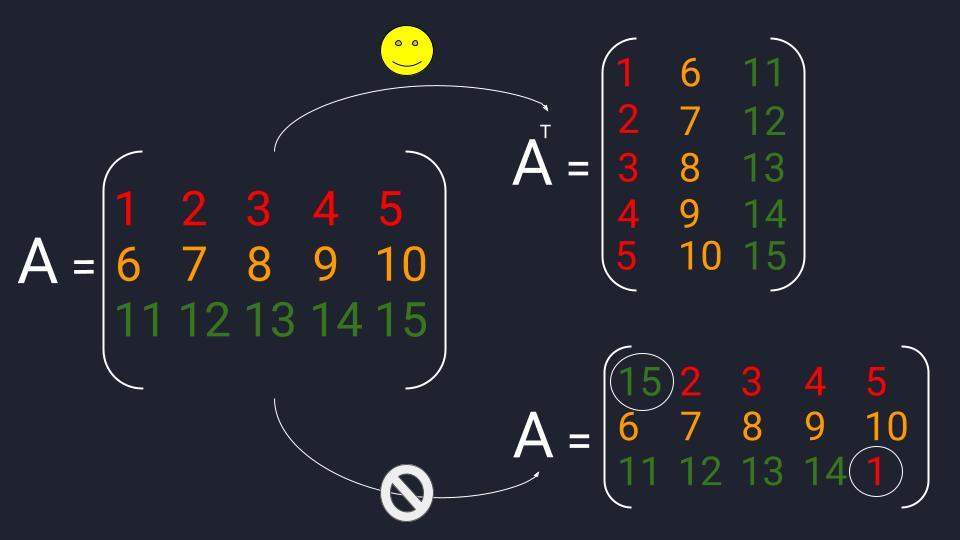
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.


Умножение матриц
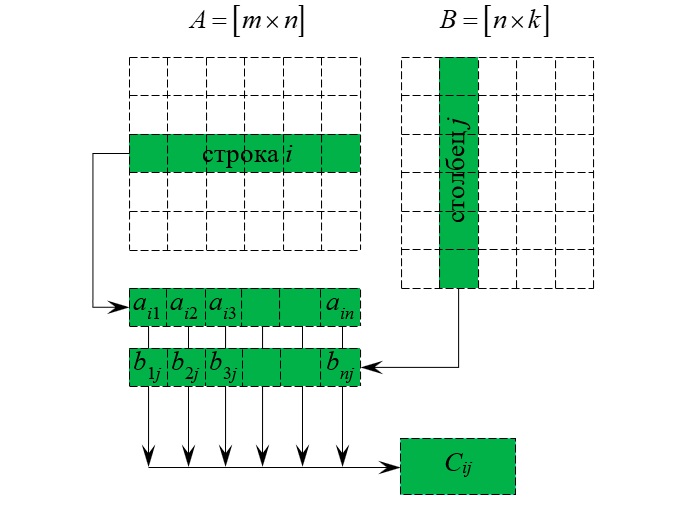
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
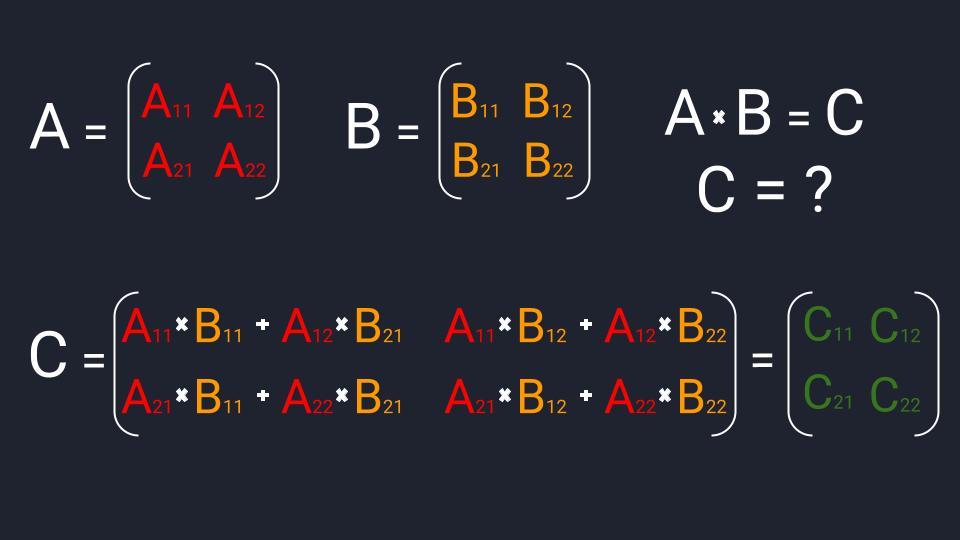

Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽
Умножение матриц
Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
Согласованные матрицы
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
Ну и что с того?
Определение умножения
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
Данный процесс легко понять по картинке:
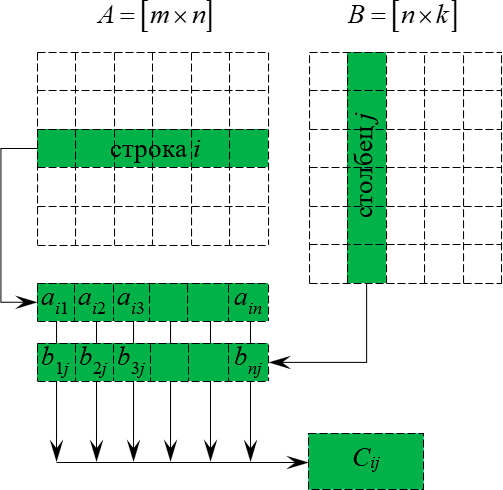
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
Тогда их скалярным произведением будет именно сумма попарных произведений:
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Умножение квадратных матриц
Задача 2. Выполните умножение:
Решение. Опять согласованные матрицы, поэтому выполняем действия:\[\]
Как видим, получилась матрица, заполненная нулями
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Основные свойства матричного произведения
В двух словах. Умножение матриц:
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
Но если поменять матрицы местами, то получим совсем другой результат:
Тем не менее, умножение матриц ассоциативно:
\[\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)\]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
\[A\cdot E=E\cdot A=A\]
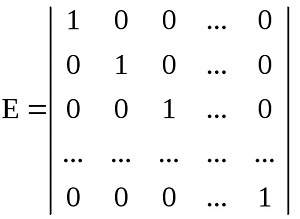
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Задача 4. Найдите все возможные попарные произведения матриц:
Решение. Для начала запишем размеры матриц:
\[A=\left[ 2\times 4 \right];\ B=\left[ 4\times 2 \right];\ C=\left[ 2\times 2 \right]\]
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
\[A \cdot B=\left[ 2\times 4 \right]\cdot \left[ 4\times 2 \right]=\left[ 2\times 2 \right]\]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
\[B \cdot A=\left[ 4\times 2 \right]\cdot \left[ 2\times 4 \right]=\left[ 4\times 4 \right]\]
\[B\cdot C=\left[ \begin
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Задача 6. Выполните умножение:
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
\[A\cdot A=\left[ n\times n \right]\cdot \left[ n\times n \right]=\left[ n\times n \right]\]
И обозначаются точно так же, как и обычные степени:
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
\[\begin
\[\begin
Задача 8. Возведите матрицу в указанную степень:
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
\[\begin
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
Задача 9. Возведите матрицу в указанную степень:
Решение. Не будем искать закономерности. Работаем «напролом»:
\[ <<\left[ \begin
Для начала возведём эту матрицу в квадрат:
\[\begin
Теперь возведём в куб:
\[\begin
Вот и всё. Задача решена.
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
Правило умножения матриц: примеры с решением
Обновлено: 18 Мая 2022
Мы помним, что матрицы – это таблицы взаимосвязанных элементов, которые позволяют упростить математические вычисления и систематизировать определённую информацию. Их можно складывать, вычитать, умножать между собой. В этой статье подробнее остановимся на последнем алгоритме – матричном произведении.
Умножение матриц — определение
Матричное умножение – это одна из основных операций, которая проводится исключительно с согласованными матрицами.
При произведении матриц A и B получается новая матрица C. В математическом виде формула будет выглядеть так:
Но для начала разберёмся, что такое согласованные матрицы.
Согласованные матрицы
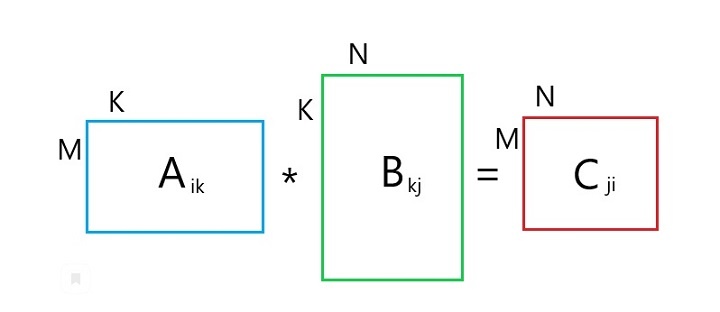
Согласованными матрицами называют матрицы вида A = [m ☓ n] и B = [n ☓ k], где количество столбцов А равно количеству строк В.
Индексы показывают координаты равных элементов.
Для того, чтобы умножить А и В, нужно взять строку в первой матрице и столбец во второй, перемножить одинаковые элементы и сложить полученные произведения.
Основные свойства матричного произведения
Размеры, то есть количество строк (m) и столбцов (n), влияют на особенности матричного произведения. Следовательно, для двух главных видов – квадратных и прямоугольных – действуют разные свойства произведения. Однако умножение любого вида всегда некоммуникативное. Это означает, что матрицы нельзя менять местами (АВ ≠ ВА).
Умножение квадратных матриц
Для квадратных матриц существует единичная матрица Е. В ней элементы по главной диагонали равны единице, а оставшиеся – нулю. Произведение любой квадратной матрицы на неё не влияет на результат.
В математическом виде это выглядит так: ЕА = АЕ = А
Также существует обратная матрица А (-1), при умножении на которую исходная A = [m ☓ n] даёт в результате единичную матрицу E.
Следовательно, формула такова: АА(-1) = Е
Умножение прямоугольных матриц
Существуют четыре основных свойства умножения:
Напомним, что у нулевой матрицы все элементы равны нулю.
Произведение трех матриц
Произведение АВС можно получить двумя альтернативными способами:
Данное свойство называется ассоциативностью матричного умножения и действует на все виды согласованных матриц. Сами они не переставляются, меняется только порядок их умножения.
Умножение матрицы на число
Для умножения на число необходимо умножить каждый матричный элемент на это число:
Дроби вносить не нужно, поскольку они могут затруднить дальнейшие операции.
Умножение матрицы на вектор
Здесь работает правило «строка на столбец».
При умножении на вектор-столбец важно, чтобы количество столбцов в матрице совпадало с количеством строк в векторе-столбце. Результатом произведения будет вектор-столбец.
При умножении на вектор-строку матрица должна быть только вектором-столбцом. Важно, чтобы количество строк в векторе-столбце совпадало с количеством столбцов в векторе-строке. Результатом произведения будет квадратная матрица.
Примеры задач на умножение матриц
Задача №1: выполнить умножение и найти С, если A = [m ☓ n] и B = [n ☓ k] равны.
Задача №2: вычислить С, если А = [m ☓ n] и вектор-столбец В равны.
c21 = a11·b12 + a12·b22 = 4⋅1 + 2⋅2 + 0⋅2 = 8
c31 = a21·b11 + a22·b21 = −1⋅1 + 1⋅2 + 1⋅(−1) = 0
Изучение матричных операций очень увлекательное, но сложное занятие. Если у вас нет времени на учёбу, ФениксХэлп может помочь в решении контрольных и самостоятельных работ, написании статей и диссертаций.
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов: 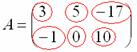
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: 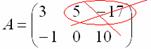
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки: 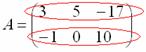
и три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 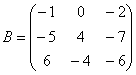
Если в матрице один столбец 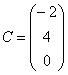
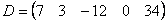
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: 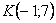
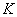
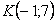
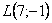
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице 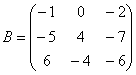
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: 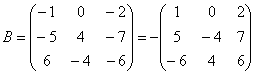
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: 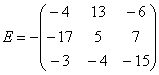
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
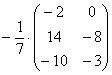
Сначала рассмотрим то, чего делать НЕ НАДО: 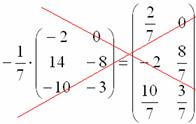
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 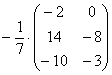
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
В этом случае можно и НУЖНО умножить все элементы матрицы на 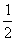
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Транспонировать матрицу
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
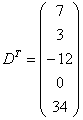
Транспонированная матрица обычно обозначается надстрочным индексом 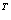
Транспонировать матрицу
Сначала переписываем первую строку в первый столбец:
Потом переписываем вторую строку во второй столбец:
И, наконец, переписываем третью строку в третий столбец:
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Сложить матрицы 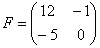
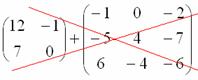
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Найти разность матриц 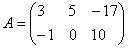
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу 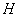
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу 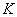
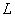
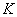
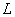
Пример:
Можно ли умножить матрицу 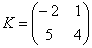
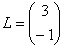
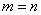
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
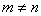
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, 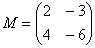
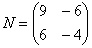
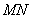
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Умножить матрицу 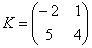
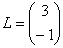
Я буду сразу приводить формулу для каждого случая:
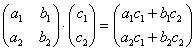
Умножить матрицу 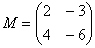
Формула:
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение 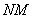
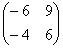
Обратите внимание, что 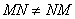
Таким образом, при умножении переставлять матрицы нельзя!
Если в задании предложено умножить матрицу 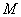
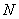
Переходим к матрицам третьего порядка:
Умножить матрицу 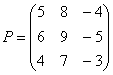
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу 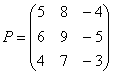
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.
А пока спектакль закончен.
После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Основные операции над матрицами (сложение, умножение, транспонирование) и их свойства.
В этой теме будут рассмотрены такие операции, как сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы. Все обозначения, которые используются на данной странице, взяты из предыдущей темы «Матрицы. Виды матриц. Основные термины».
Сложение и вычитание матриц.
Аналогичное определение вводят и для разности матриц:
Стоит обратить внимание, что операции сложения и вычитания определены только для матриц одинакового размера. Вообще, сложение и вычитание матриц – операции, ясные интуитивно, ибо означают они, по сути, всего лишь суммирование или вычитание соответствующих элементов.
Заданы три матрицы:
Умножение матрицы на число.
Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.
Произведение двух матриц.
Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.
Аналогично предыдущему, имеем:
Кстати сказать, зачастую нет резона расписывать подробно нахождение каждого элемента матрицы-результата. Для матриц, размер которых невелик, можно поступать и так:
Транспонированная матрица.
Некоторые свойства операций над матрицами.
В следующей части будет рассмотрена операция возведения матрицы в целую неотрицательную степень, а также решены примеры, в которых потребуется выполнение нескольких операций над матрицами.
Умножение матриц.
Умножение матриц – это одна из самых распространенных операций с матрицами. Матрица, которая получается после умножения, называется произведением матриц.
Произведением матрицы Am×n на матрицу Bn×k будет матрица Cm×k такая, что элемент матрицы C, находящийся в i-ой строке и j-ом столбце, то есть элемент cij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B.
Процесс умножения матриц возможен только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы.
Пример:
Можно ли умножить матрицу 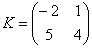

m = n, значит, умножать данные матрицы можно.
Если же матрицы поменять местами, то, при таких матрицах, умножение уже не будет возможно.
m ≠ n, таким образом, выполнять умножение нельзя:
Довольно часто можно встретить задания с подвохом, когда ученику предлагается умножить матрицы, умножение которых заведомо невозможно.
Обратите внимание, что иногда можно умножать матрицы и так, и так. К примеру, для матриц, 
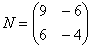
Операция умножения матриц.
Операция умножения матриц – это не очень сложное действие. Умножение матриц лучше понимать на конкретных примерах, т.к. только определение может сильно запутать.
Начнем с самого простого примера:
Необходимо умножить 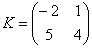

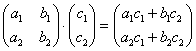
Далее более сложный пример:
Умножить 

Формула для этого случая: 
Умножение матриц и результат:
В результате получена т.н. нулевая матрица.
Очень важно помнить, что здесь не работает «правило перестановки мест слагаемых» так как почти всегда MN ≠ NM. Поэтому, производя операцию умножения матриц их ни в коем случае нельзя менять местами.
Теперь рассмотрим примеры умножения матриц третьего порядка:
Умножить 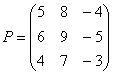
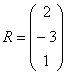
Формула очень похожа на прошлые:
Решение матрицы: 
Умножение матрицы на число.
Умножение матрицы на число – это тоже самое умножение матриц, только вместо второй матрицы берется простое число. Как можно догадаться, такое умножение выполнять гораздо проще.
Пример умножения матрицы на число:
Тут все понятно – для того, чтобы умножить матрицу на число, необходимо каждый элемент матрицы последовательно умножить на указанное число. В данном случае – на 3.
Еще один полезный пример:
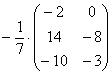
Первым делом покажем то, чего делать не надо:
При умножении матрицы на дробное число не нужно вносить дробь в матрицу, так как это в первую очередь только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем.

Что стоит сделать в данном случае – это внести минус в матрицу:

Если бы у вас был пример, когда все элементы матрицы делились бы на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
В данном примере можно и нужно умножить все элементы матрицы на ½, т.к. каждый элемент матрицы делится на 2 без остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
Умножение матриц: эффективная реализация шаг за шагом
Введение
Умножение матриц — это один из базовых алгоритмов, который широко применяется в различных численных методах, и в частности в алгоритмах машинного обучения. Многие реализации прямого и обратного распространения сигнала в сверточных слоях неронной сети базируются на этой операции. Так порой до 90-95% всего времени, затрачиваемого на машинное обучение, приходится именно на эту операцию. Почему так происходит? Ответ кроется в очень эффективной реализации этого алгоритма для процессоров, графических ускорителей (а в последнее время и специальных ускорителей матричного умножения). Матричное умножение — один из немногих алгоритмов, которые позволяет эффективно задействовать все вычислительные ресурсы современных процессоров и графических ускорителей. Поэтому не удивительно, что многие алгоритмы стараются свести к матричному умножению — дополнительная расходы, связанные с подготовкой данных, как правило с лихвой окупаются общим ускорением алгоритмов.
Так как реализован алгоритм матричного умножения? Хотя сейчас существуют множество реализаций данного алгоритма, в том числе и в открытых исходных кодах. Но к сожалению, код данных реализаций (большей частью на ассемблере) весьма сложен. Существует хорошая англоязычная статья, подробно описывающая эти алгоритмы. К моему удивлению, я не обнаружил аналогов на Хабре. Как по мне, этого повода вполне достаточно, чтобы написать собственную статью. С целью ограничить объем изложения, я ограничился описанием однопоточного алгоритма для обычных процессоров. Тема многопоточности и алгоритмов для графических ускорителей явно заслуживает отдельной статьи.
Процесс изложения будет вестись ввиде шагов с примерами по последовательному ускорению алгоритма. Я старался писать максимально упрощая задачу, но не более того. Надеюсь у меня получилось…
Постановка задачи (0-й шаг)
В общем случае функция матричного умножения описывается как:
Где матрица A имеет размер M х K, матрица B — K х N, и матрица C — M х N.
Мы без ущерба для изложения, можем считать, что a = 0 и b = 1:
Ее реализация на С++ «в лоб» по формуле будет выглядеть следующим образом:
120 GFLOPS (float-32) если ограничится использованием AVX2/FMA и
200 GFLOPS при использовании AVX-512). Так, что нужно предпринять, чтобы приблизится к теоретическому пределу? Далее мы в ходе ряда последовательных оптимизаций придем к решению, которое во многом воспроизводит то, что используется во многих стандартных библиотеках. В процессе оптимизации, я буду задействовать только AVX2/FMA, AVX-512 я касаться не буду, так как их распостраненность пока невелика.
Устраняем очевидные недостатки (1-й шаг)
Сначала устраним самые очевидные недостатки алгоритма:
Результат тестовых замеров показывает время выполнения в 250 мс, или 11.4 GFLOPS. Т.е. такими небольшими правками мы получили ускорение в 8 раз!
Векторизуем внутренний цикл (2-й шаг)
Запускаем тесты, получаем время 217 мс или 13.1 GFLOPS. Упс! Ускорение всего на 15%. Какже так? Тут нужно учитывать, два фактора:
Дальнейшие наши шаги по оптимизации алгоритма будут направлены на минимизацию доступа в память.
Пишем микроядро (3-й шаг)
В предыдущей версии на 1 FMA операцию приходится 2 загрузки и 1 выгрузка.
Больше всего загрузок и выгрузок происходит с результирующей матрицей С: данные из нее нужно загрузить, прибавить к ним произведение C[i][j] += A[i][k]*B[k][j], а потом сохранить. И так много раз. Наиболее быстрая память, с которой может работать процессор — это его собственные регистры. Если мы будем хранить результирующее значение матрицы С в регистре процессора, то в процессе расчета нужно будет подгружать только значение матриц A и B. Теперь у нас на 1 FMA операцию приходится только 2 загрузки.
Если мы будем хранить в регистрах значения двух соседних столбцов матрицы C[i][j] и C[i][j+1], то сможем повторно использовать загруженное значение матрицы A[i][k]. И на 1 FMA операцию потребуется только 1.5 загрузки. Кроме того, сохраняя результат в 2 независимых регистра, мы позволим процессору выполнять 2 FMA операции за такт. Аналогично можно хранить в регистрах значения двух соседних строк — тогда будет осуществляться экономия на загрузке значений матрицы B.
Всего настольные процессоры Интел начиная с 2-го поколения имеют 16 256-bit векторных регистров (справедливо для 64-bit режима процессора). 12 из них можно использовать для хранения кусочка результирующей матрицы С размером 6×16. В итоге мы сможем выполнить 12*8 = 96 FMA операций загрузив из памяти только 16 + 6 = 22 значений. И того нам удалось сократить доступ к памяти с 2.0 до 0.23 загрузки на 1 FMA операцию — почти в 10 раз!
Функция которая осуществляет вычисление такого маленького кусочка матрицы С, обычно называется микроядром, ниже приведен пример такой функции:
Введем небольшую вспомогательную функцию для инициализации начального значения матрицы С:
Здесь lda, ldb, ldc — длина строчки (Leading Dimension в общем случае) соответсвующей матрицы.
Тогда функция умножения примет следующий вид:
Запускаем ее и получаем время исполнения 78.5 мс или 36.2 GFLOPS. Т.е. использование микроядра позволило ускорить матричное умножение почти в 3 раза. Но полученное быстродействие все еще далеко от максимального. Где теперь узкое место?
Переупорядочиваем матрицу B (4-й шаг)
Микроядро за каждую итерацию загружает два 256-bit вектора из матрицы B.
Причем каждый раз из новой строчки. Это делает невозможным для процессора эффективное кеширование этих данных. Для исправления этой ситуации сделаем два изменения:
Здесь стоит отметить, что загрузка и выгрузка AVX векторов оптимально работает при выровненных данных, потому используются специальные функции для выделения памяти.
Функция переупорядочивания матрицы B:
Ну и собственно 4-я версия функции gemm:
Результаты тестирования (29.5 мс или 96.5 GFLOPS) показывают, что мы на правильном пути. Фактически достигнуто около 80% от теоретически возможного максимума.
Победа? К сожалению нет. Просто размер матриц, который мы использовали для тестирования (M=N=K=1152) оказался удобным для данной версии алгоритма. Если увеличить К в 100 раз (M=1152, N=1152, K=115200), то эффективность алгоритма упадет до 39.5 GFLOPS — почти в 2.5 раза.
Локализуем данные в кэше L1 (5-й шаг)
Так почему же с ростом параметра K, падает эффективность алгоритма? Ответ кроется в величине буфера, который мы использовали для хранения переупорядоченных значений B. При больших значениях K он просто не влазит в кэш процессора. Решением проблемы будет ограничение его величины до размера кэша данных L1. Для процессоров Интел размер кэша данных L1 составляет 32 kb. C ограничением размера буфера, микроядро будет пробегать не по всем значениям K, а только по диапазону, который влазит в L1 кэш. Результаты промежуточных расчетов матрицы С будут храниться в основной памяти.
Введем макроядро — вспомогательную функцию, которая производит расчеты над областью данных, которые влазят в кэш:
В главной функции у нас добавится цикл по K, в котором мы будем вызывать макроядро:
Результаты замеров показывают, что мы движемся в правильном направлении: для (M=1152, N=1152, K=115200) производительность алгоритма составила 78.1 GFLOPS. Это значительно лучше, чем в прошлой версии, но все еще хуже, чем для матрицы средних размеров.
Переупорядочиваем матрицу A и локализуем в кэше L2 (6-й шаг)
Ограничив размер K, который обрабатывается за один проход микроядра, мы сумели локализовать данные матрицы B в кэше L1. Данных, которые подгружаются из матрицы A почти в три раза меньше. Но давайте попробуем локализовать и их, заодно переупорядочив данные, чтобы они лежали последовательно. Напишем для этого специальную функцию:
Так как, данные матрицы A теперь идут последовательно, то параметр lda в макроядре нам больше не нужен. Также поменялись параметры вызова микроядра:
Размер буфера для переупорядоченной матрицы A ограничиваем размером L2 кэша процессора (он обычно составляет от 256 до 1024 kb для разных типов процессоров). В главной функции добавляется дополнительный цикл по переменной M:
Результаты тестовых замеров для (M=1152, N=1152, K=115200) — 88.9 GFLOPS — приблизились еще на один шаг к результату для матриц среднего размера.
Задействуем кэш L3 (7-й шаг)
В процессорах помимо кэша L1 и L2 еще часто бывает кэш L3 (обычно его размер составляет 1-2 MB на ядро). Попробуем задействовать и его, например, для хранения переупорядоченных значений матриц B, чтобы избежать лишних вызовов функции reorder_b_16. В функции макроядра появится дополнительные параметр reorderB, который будет сообщать о том, что данныe матрицы B уже упорядочены:
В основной функции добавится цикл по N:
Результаты замеров для (M=1152, N=1152, K=115200) дают результат в 97.3 GFLOPS. Т.е. мы даже немного превысили результат для матриц среднего размера. Фактически мы получили универсальный алгоритм (на самом деле нет, про ограничения в следующем разделе), который практически одинаково эффективно (порядка 80% от теоретически достижимого макимума) работает для любого размера матриц. На этом предлагаю остановиться и описать, что у нас в итоге получилось.
Общая схема алгоритма
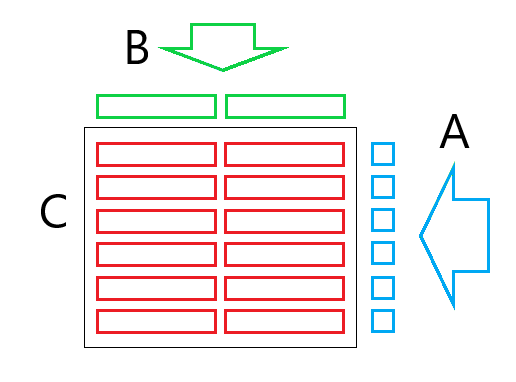
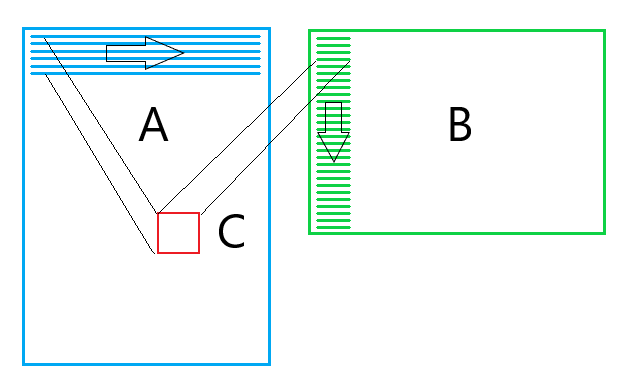
На рисунке ниже приведена схема получившегося алгоритма:
Микро ядро
Макро ядро
Основная функция
Что осталось за кадром?
В процессе изложения основных принципов, которые используются в алгоритме матричного умножения, я сознательно упростил задачу, иначе она бы не влезла ни в одну статью. Ниже я опишу некоторые вопросы, которые неважны для понимания основной сути алгоритма, но очень важны для практической их реализации:
Заключение
Приведенный алгоритм матричного умножения позволяет эффективно задействовать ресурсы современных процессоров. Но он наглядно показывает, что максимальная утилизация ресурсов современных процессоров — это далеко нетривиальная задача. Подход с использованием микроядер и максимальной локализации данных в кэше процессора можно с успехом использовать и для других алгоритмов.
Код проекта с алгоритмами из статьи можно найти на Github.
Умножение матриц и алгоритм решения задач
Время чтения: 14 минут
Алгоритм умножения матриц в различных случаях
Умножаем данные в строке для первой матрицы на соответствующие данные в столбцах из второй матрицы.
Правило умножения произведения двух и более матриц
Умножение двух матриц. Произведение матриц (С= А x В) — является действием только для матриц А и В которые согласованы между собой. Для данных значений, число столбцов у матрицы А должно равняться количеству строк матрицы В:
\[m \cdot n\] \[m \cdot p\] \[p \cdot n\]
Пример №1:
Необходимо выполнить умножение двух матриц:
\[A=a_\] у которой размеры \[m \times n\]
\[B=b_\] у которой размеры \[p \times n\]
Необходимо вычислить матрицу C.
Для вычисления применим формулу:
Умножение трёх матриц
Чтобы вычислить произведение трех матриц применяют два способа.
Пример №2:
Выполним умножение матриц двумя способами.

Умножение матрицы на число
Произведение значение матрицы, равное числу A на некое значение К, будет выглядеть следующим образом.
Размер будет таким же, как и в исходной матрице, который получен путем перемножения на заданное число все матричных элементов.
Матричное умножение. Медленное достижение мифической цели
В недавней работе был установлен новый рекорд скорости по умножению двух матриц. Она также знаменует и конец эпохи для метода, который ученые применяли для исследований на протяжении десятилетий.

Математики стремятся к достижению мифической цели — второй степени (exponent two), то есть к умножению пары матриц n х n всего за n 2 шагов. Исследователи подбираются все ближе к своей цели, но получится ли у них когда-нибудь достичь ее?
Для специалистов в области Computer Science и математиков сама идея о «второй степени» связана с представлениями о совершенном мире.
«Трудно разграничить научное мышление и беспочвенные мечтания», — признается Крис Уманс из Калифорнийского технологического института. «Я хочу, чтобы степень была равна двум, потому что это красиво».
С точки зрения необходимого количества шагов «вторая степень» — это идеальная скорость выполнения одной из самых фундаментальных математических операций — матричного умножения. Если вторая степень достижима, то матричное умножение получится выполнять максимально быстро, насколько это физически возможно. Если это не так, то мы застряли в мире, который не соответствует нашим мечтам.
Матрицы представляют собой массивы чисел. Когда две матрицы согласованы (число столбцов в первом сомножителе равно числу строк во втором), их можно перемножить, чтобы получить третью. Например, если вы начнете с пары матриц 2 х 2, их произведение также будет матрицей 2 х 2, содержащей четыре элемента. В более общем смысле, произведение пары матриц размером n х n представляет собой другую матрицу размером n х n с n 2 элементами.
И хотя никто точно не знает, можно ли этого достичь, исследователи продолжают продвигаться в этом направлении.
Статья, опубликованная в октябре, подбирается к цели еще ближе и описывает самый быстрый на данный момент метод умножения двух матриц. Результат, который получили Джош Алман, докторант Гарвардского университета, и Вирджиния Василевска Уильямс из Массачусетского технологического института, уменьшает степень предыдущего лучшего показателя примерно на одну стотысячную. Это действительно большое достижение в данной области, добытое кропотливым трудом.
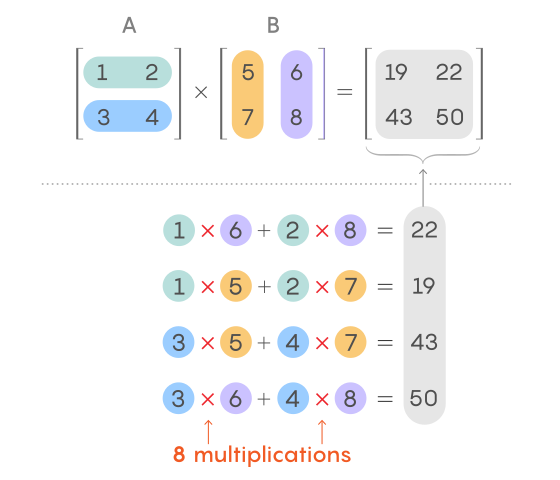
Чтобы получше разобраться в этом процессе и понять, как его можно усовершенствовать, давайте начнем с пары матриц 2 х 2, A и B. При вычислении каждого элемента их произведения вы используете соответствующую строку из A и соответствующий столбец из B. Чтобы получить верхний правый элемент, умножьте первое число в первой строке A на первое число во втором столбце B, затем умножьте второе число в первой строке A на второе число во втором столбце B и сложите эти два произведения.

Самуэль Веласко / Quanta Magazine
Эта операция известна как получение «скалярного произведения» строки со столбцом (иногда называется «внутренним произведением»). Чтобы вычислить другие элементы в произведении матриц, повторите процедуру с соответствующими строками и столбцами.
В целом, классический метод умножения матриц 2 х 2 состоит из восьми умножений и нескольких сложений. Как правило, этот способ умножения двух матриц размера n х n требует n 3 умножений.
С увеличением размера матриц количество умножений, необходимых для нахождения их произведения, растет намного быстрее, чем количество сложений. Чтобы найти произведение матриц 2 х 2 требуется всего восемь промежуточных умножений, а чтобы найти произведение матриц 4 х 4 их требуется уже 64. Однако количество сложений, необходимых для получения суммы этих матриц, не так значительно отличается. Обычно количество сложений равно количеству элементов в матрице, то есть четыре для матриц 2 х 2 и 16 для матриц 4 х 4. Эта разница между сложением и умножением позволяет понять, почему исследователи измеряют скорость умножения матриц исключительно с точки зрения количества требуемых умножений.
«Умножения — это наше всё, — утверждает Уманс, — Показатель степени в итоге полностью зависит только от количества умножений. Сложения в некотором смысле исчезают».
На протяжении веков люди считали, что n 3 — это самый быстрый способ умножения матриц. По имеющимся сведениям, в 1969 году Фолькер Штрассен намеревался доказать, что невозможно умножить матрицы 2 х 2, используя менее восьми умножений. Видимо, он все-таки не смог найти доказательства, а через некоторое время и понял почему: на самом деле, существует способ сделать это с помощью семи умножений!
Штрассен придумал сложный набор соотношений, которые позволили заменить одно из этих восьми умножений 14 дополнительными сложениями. Может показаться, что разница совершенно незначительна, но она оправдывает себя, так как умножение вносит больший вклад, чем сложение. Найдя способ избавиться от одного умножения для маленьких матриц 2 х 2, Штрассен открыл возможность, которую он мог использовать при умножении бOльших матриц.
«Это крошечное изменение приводит к огромным улучшениям в работе с большими матрицами», — говорит Уильямс.

Вирджиния Василевска Уильямс из Массачусетского технологического института и Джош Алман из Гарвардского университета открыли самый быстрый способ перемножения двух матриц за n 2.3728596 шагов. Джаред Чарни; Ричард Т.К. Хоук
Предположим, вы хотите перемножить пару матриц 8 х 8. Один из способов сделать это — разбить каждую большую матрицу на четыре матрицы размером 4 х 4 так, чтобы каждая имела по четыре элемента. Поскольку элементы матрицы также могут являться матрицами, вы можете считать исходные матрицы парой матриц 2 х 2, каждый из четырех элементов которых сам по себе является матрицей 4 х 4. Посредством некоторых манипуляций каждая из этих матриц размером 4 х 4 может быть разбита на четыре матрицы размером 2 х 2.
Смысл этого многократного разбиения больших матриц на более мелкие заключается в том, что можно снова и снова применять алгоритм Штрассена к меньшим матрицам и с помощью его метода сокращать количество шагов на каждом этапе. В целом алгоритм Штрассена увеличил скорость умножения матриц с n 3 до n 2.81 мультипликативных шагов.
Следующий важный шаг в развитии идеи произошел в конце 1970-х, когда появился принципиально новый подход к решению этой задачи. Он подразумевает перевод матричного умножения в другую вычислительную задачу линейной алгебры с использованием объектов, называемых тензорами. Тензоры, используемые в этой задаче, представляют собой трехмерные массивы чисел, состоящие из множества различных частей, каждая из которых выглядит как небольшая задача на умножение матриц.
Умножение матриц и эта задача, связанная с тензорами, в определенном смысле эквивалентны друг другу, но для решения последней исследователи уже имели более быстрые процедуры. Таким образом, перед ними встала задача определить «обменный курс» между ними: Матрицы какого размера можно перемножить при тех же вычислительных затратах, которые требуются для решения тензорной задачи?
«Это очень распространенная в теоретической информатике концепция: преобразовывать задачи и проводить аналогию между ними, чтобы показать, что они одинаково простые или сложные», — сказал Алман.
В 1981 году Арнольд Шёнхаге использовал этот подход, чтобы доказать, что умножение матриц возможно выполнить за n 2.522 шагов. Позднее Штрассен назвал этот подход «лазерным методом» (laser method).
За последние несколько десятилетий каждое улучшение в процессе умножения матриц происходило за счет усовершенствования лазерного метода, поскольку исследователи находили все более эффективные способы трансформации задачи. В своем новом доказательстве Алман и Уильямс стирают различие между 2 задачами и показывают, что уменьшить число умножений возможно. «В целом Джош и Вирджиния нашли способ применить машинные вычисления в рамках лазерного метода и получили лучшие на настоящий момент результаты», — сказал Генри Кон из Microsoft Research.
Но, несмотря на все эти гонки и победы, становится ясно, что в случае с этим подходом действует закон убывающей доходности, или убывающей отдачи. Скорее всего, усовершенствование Алмана и Уильямс почти полностью исчерпало возможности лазерного метода, но так и не позволило достичь конечной теоретической цели.
«Маловероятно, что получится приблизиться ко второй степени, используя это семейство методов», — отметил Уманс.
Для этого потребуется открытие новых методов и стойкая вера в то, что это вообще возможно.
Уильямс вспоминает один из разговоров со Штрассеном об этом: «Я спросила его, считает ли он, что возможно получить вторую степень для матричного умножения, и он ответил: «Нет, нет, нет, никогда!».
Перемножение матриц
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.
Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.
Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).
Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.
У каждого элемента матрицы есть 2 нижних индекса ( aij ) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности 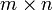
Содержание
История
Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.
Матрица как запись коэффициентов системы линейных уравнений
Систему из m уравнений с n неизвестными
можно представить в матричном виде
и тогда всю систему можно записать так:
где A имеет смысл таблицы коэффициентов aij системы уравнений.
A − 1 A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений
Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.
Операции над матрицами
cij = aij + bij
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть
Все элементы нулевой матрицы равны нулю.
| cij = | ∑ | aikbkj |
| k |
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность 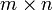
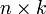
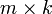
Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.
Транспонирование матрицы (обозначение: A T ) — операция, при которой матрица отражается относительно главной диагонали, то есть
Если A — матрица размера 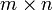
Квадратная матрица и смежные определения
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю
Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности 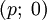
Свойства матриц
Элементарные преобразования матриц
Элементарными преобразованиями строк матрицы называются следующие преобразования:
Элементарные преобразование столбцов матрицы определяются аналогично.
Типы матриц
Матрица линейного оператора
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис 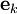
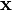
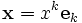
где x k — координаты вектора 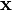
Пусть 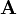
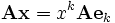
Вектора 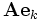
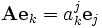
Подставим разложение в предыдущую формулу, получим
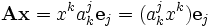
Выражение 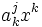


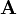
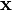
См. также
Литература
Ссылки
Полезное
Смотреть что такое «Перемножение матриц» в других словарях:
перемножение матриц — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN matrix multiplication … Справочник технического переводчика
Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия
Матрица достижимости — простого ориентированого графа бинарная матрица замыкания по транзитивности отношения (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.… … Википедия
матрица — ы, ж., МАТРИС matrice f., нем. Matrize <лат. matris. 1. Форма, в которой отливают буквы, знаки при книгопечатании. Сл. 18. А велено на печатном дворе против тех образцов вырезать пунсоны стальные и ими пробить матрицы на меди, и, отлив те… … Исторический словарь галлицизмов русского языка
матрис — МАТРИЦА ы, ж., МАТРИС matrice f., нем. Matrize <лат. matris. 1. Форма, в которой отливают буквы, знаки при книгопечатании. Сл. 18. А велено на печатном дворе против тех образцов вырезать пунсоны стальные и ими пробить матрицы на меди, и, отлив … Исторический словарь галлицизмов русского языка
Compressive sensing — Эта статья или раздел грубый перевод статьи на другом языке (см. Проверка переводов). Он мог быть сгенерирован программой переводчиком или сделан человеком со слабыми познаниями в языке оригинала. Вы можете помочь … Википедия
пакет Linpack — Тестовая программа для оценки быстродействия профессиональных ПЭВМ при вычислениях с плавающей точкой (перемножение матриц размером 100×100 или 300 х 300 точек). [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ.… … Справочник технического переводчика
Гипотеза Штрассена — В теории сложности вычислений и линейной алгебре гипотеза Штрассена утверждает, что для любой заданной скорости (до определённого предела) существует алгоритм, позволяющий перемножать достаточно большие матрицы с такой скоростью. Были найдены… … Википедия
Факторизация — Эта статья о математической концепции. Другие значения термина в заглавии статьи см. на Фактор. Иллюстрация полинома x2 + … Википедия
SAFER — Создатель: Джеймс Мэсси Создан: 1993 г. Опубликован … Википедия
Перемножение матриц
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.
Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.
Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).
Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.
У каждого элемента матрицы есть 2 нижних индекса ( aij ) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности 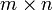
Содержание
История
Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.
Матрица как запись коэффициентов системы линейных уравнений
Систему из m уравнений с n неизвестными
можно представить в матричном виде
и тогда всю систему можно записать так:
где A имеет смысл таблицы коэффициентов aij системы уравнений.
A − 1 A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений
Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.
Операции над матрицами
cij = aij + bij
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть
Все элементы нулевой матрицы равны нулю.
| cij = | ∑ | aikbkj |
| k |
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность 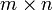
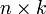
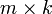
Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.
Транспонирование матрицы (обозначение: A T ) — операция, при которой матрица отражается относительно главной диагонали, то есть
Если A — матрица размера 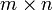
Квадратная матрица и смежные определения
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю
Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности 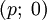
Свойства матриц
Элементарные преобразования матриц
Элементарными преобразованиями строк матрицы называются следующие преобразования:
Элементарные преобразование столбцов матрицы определяются аналогично.
Типы матриц
Матрица линейного оператора
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис 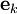
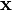
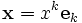
где x k — координаты вектора 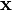
Пусть 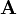
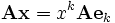
Вектора 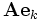
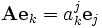
Подставим разложение в предыдущую формулу, получим
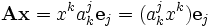
Выражение 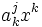


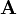
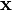
См. также
Литература
Ссылки
Полезное
Смотреть что такое «Перемножение матриц» в других словарях:
перемножение матриц — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN matrix multiplication … Справочник технического переводчика
Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия
Матрица достижимости — простого ориентированого графа бинарная матрица замыкания по транзитивности отношения (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.… … Википедия
матрица — ы, ж., МАТРИС matrice f., нем. Matrize <лат. matris. 1. Форма, в которой отливают буквы, знаки при книгопечатании. Сл. 18. А велено на печатном дворе против тех образцов вырезать пунсоны стальные и ими пробить матрицы на меди, и, отлив те… … Исторический словарь галлицизмов русского языка
матрис — МАТРИЦА ы, ж., МАТРИС matrice f., нем. Matrize <лат. matris. 1. Форма, в которой отливают буквы, знаки при книгопечатании. Сл. 18. А велено на печатном дворе против тех образцов вырезать пунсоны стальные и ими пробить матрицы на меди, и, отлив … Исторический словарь галлицизмов русского языка
Compressive sensing — Эта статья или раздел грубый перевод статьи на другом языке (см. Проверка переводов). Он мог быть сгенерирован программой переводчиком или сделан человеком со слабыми познаниями в языке оригинала. Вы можете помочь … Википедия
пакет Linpack — Тестовая программа для оценки быстродействия профессиональных ПЭВМ при вычислениях с плавающей точкой (перемножение матриц размером 100×100 или 300 х 300 точек). [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ.… … Справочник технического переводчика
Гипотеза Штрассена — В теории сложности вычислений и линейной алгебре гипотеза Штрассена утверждает, что для любой заданной скорости (до определённого предела) существует алгоритм, позволяющий перемножать достаточно большие матрицы с такой скоростью. Были найдены… … Википедия
Факторизация — Эта статья о математической концепции. Другие значения термина в заглавии статьи см. на Фактор. Иллюстрация полинома x2 + … Википедия
SAFER — Создатель: Джеймс Мэсси Создан: 1993 г. Опубликован … Википедия