Как пользоваться логарифмической линейкой

29.08.202229.08.2022 admin 0 Комментариев

Как пользоваться логарифмической линейкой

Круговая логарифмическая линейка КЛ-1

В отличие от обычных логарифмических линеек, она не позволяет считать логарифмы и кубы, точность ниже на один разряд, ну и как обычной линейкой ей не воспользуешься (и спину не почешешь), зато она очень компактная, её можно носить в кармане.

Быстрые вычисления

Прилагаемая (ниже) инструкция предлагает умножать и делить в три движения: вращением подвижной шкалы на указатель, вращением стрелки до нужного значения, и вращением циферблата до другого значения. Однако гораздо интереснее использовать оба циферблата, подвижный и неподвижный с обратной стороны линейки, и делать вычисления в два движения. При этом возможно получать сразу весь спектр значений, просто вращая циферблат, и тут же считывая значения.

Для этого на неподвижном циферблате нужно стрелкой выставить либо множитель (в случае умножения), либо делимое (в случае деления), и, перевернув линейку, вращением подвижного циферблата выставить второй множитель на стрелку, либо делитель на указатель, и сразу прочитать результат. Продолжая вращать циферблат, тут же считываем другие значения функции. Обычный калькулятор такое не умеет делать.

Дюймы в сантиметры

Градусы Фарингейта в градусы Цельсия

На неподвижном циферблате выставляем значение 1.8, из градусов по Фаренгейту вычитаем в уме 32 и устанавливаем полученное значение напротив неподвижного указателя, считываем на стрелке градусы по Цельсию. Для обратного вычисления устанавливаем значение на стрелке, и к значению на указателе прибавляем в уме 32.

20*1.8+32 = 36+32 = 68

(100-32)/1.8 = 68 ⁄₁.8 = 37.8 (37.7778)

Мили в километры

Выставляем на неподвижной шкале значение 1.6, вращением подвижной шкалы получаем мили в километрах или километры в милях.

Посчитаем скорость разгона машины времени в фильме “Назад в будущее”: 88*1.6=141км/ч (140.8)

Время и расстояние от скорости

Чтобы узнать за сколько времени проедем 400 километров при скорости 60 км/ч, выставляем на неподвижном циферблате значение 6, и крутим подвижный циферблат до значения 4, получаем 6.66 часов (6 часов 40 минут).

Инструкция к линейке

У имеющейся у меня линейки инструкция очень потрёпана, ведь она аж 1966 года выпуска. Поэтому я решил оцифровать её для сохранности в электронном виде.

Полная инструкция к логарифмической линейке “КЛ-1”:

Круговая логарифмическая линейка “КЛ-1”

ВНИМАНИЕ! Вытаскивание головок из корпуса не допускается.

Круговая логарифмическая линейка “КЛ-1” предназначена для выполнения наиболее часто встречающихся в практике математических операций: умножения, деления, комбинированных действий, возведения в кладрат, извлечения квадратного корня, нахождения тригонометрических функций синуса и тангенса, а также соответствующих обратных тригонометрических функций, вычисления площади круга.

Логарифмическая линейка состоит из корпуса с двумя головками, 2-х циферблатов, один из которых вращается при помощи головки с черной точкой и 2-х стрелок, которые вращаются при помощи головки с красной точкой. Против головки с черной точкой над подвижным циферблатом имеется неподвижный указатель.

Выполнение математических операций на линейке “КЛ-1” производится следующим образом:

I. Умножение

II. Деление

III. Комбинированные действия

IV. Возведение в квадрат

V. Извлечение квадратного корня

VI. Нахождение тригонометрических функций угла

VII. Нахождение обратных тригонометрических функций

VIII. Вычисление площади круга

Техническо-сбытовая организация “Рассвет” г. Москва, А-57, ул. Острякова, дом №8.
СТУ 36-16-64-64
Артикул В-46
Штамп ОТК
Цена 3 руб. 10 коп.

Штамп с датой выпуска: 20 июня 1966

Сейчас логарифмические линейки выпускаются только в наручных часах. Человечество что-то потеряло, полностью перейдя от аналоговых вычислителей на чисто цифровые.

П.С.: фотографии не мои, взяты в интернете. На последнем снимке на циферблате маркировка завода МЛТЗКП, если кто знает что означает эта аббревиатура, прошу сообщить мне. Я смог расшифровать лишь её часть: “Московский Л? Т? Завод Контрольных Приборов”, выпускал эту линейку “Московский опытный завод контрольных приборов “Контрольприбор”“.

Источник

Линейка логарифмическая – забытое счетное устройство из прошлого?

Логарифмическая линейка (фото см. ниже) была придумана как прибор для экономии умственных затрат и времени, связанных с математическими расчетами. Особое распространение она получила в практике инженеров в институтах, ориентированных на научно-исследовательскую деятельность, и в статистических бюро до момента внедрения электронной вычислительной техники.

Линейка логарифмическая: история

Прообразом счетного устройства была шкала для вычислений английского математика Э. Гантера. Он придумал ее в 1623 г., вскоре после открытия логарифмов, для упрощения работы с ними. Шкала использовалась в сочетании с циркулем. Им отмеривались необходимые градуированные отрезки, которые потом складывались или вычитались. Операции с числами заменялись действиями с логарифмами. Используя их основные свойства, умножить, делить, возводить в степень или вычислять корень числа оказалось намного проще.

В 1623 году линейка логарифмическая была усовершенствована У. Отредом. Он добавил вторую подвижную шкалу. Она перемещалась вдоль основной линейки. Отмерять отрезки и считывать результаты исчислений стало легче. Для повышения точности устройства в 1650 году была реализована попытка увеличения длины шкалы за счет ее расположения по спирали на вращающемся цилиндре.

Добавление в конструкцию бегунка (1850 г.) сделало процесс исчисления еще более удобными. Дальнейшее усовершенствование механизма и способа нанесения логарифмических шкал на стандартную линейку не добавили точности прибору.

Устройство

Линейка логарифмическая (стандартная) изготавливалась из плотной древесины, стойкой к истиранию. Для этого в промышленных масштабах использовалось грушевое дерево. Из него изготавливался корпус и движок – планка меньшего размера, монтируемая во внутреннем пазе. Ее можно перемещать параллельно основанию. Бегунок изготавливался из алюминия или стали со смотровым окошком из стекла или пластика. На него нанесена тонкая вертикальная линия (визир). Бегунок двигается по боковым направляющим и подпружинивается стальной пластинкой. Корпус и движок облицованы светлым целлулоидом, на котором тиснением нанесены шкалы. Их деления заполнены типографской краской.

Разновидности

Стандартная линейка логарифмическая имеет длину измерительной шкалы 25 см. Выпускался еще карманный вариант длиной 12,5 см и устройство повышенной точности 50 см. Существовало деление линеек на первый и второй сорта в зависимости от качества исполнения. Внимание уделялось четкости наносимых штрихов, обозначений и вспомогательных линий. Движок и корпус должны были быть ровными и идеально подогнаны друг к другу. Изделия второго сорта могли иметь незначительные царапины и точки на целлулоиде, но они не искажали обозначений. Также мог присутствовать незначительный люфт в пазах и прогиб.

Существовали и другие карманные (похожие на часы диаметром 5 см) варианты устройства – логарифмическая дисковая (типа «Спутник») и круговая (КЛ-1) линейки. Они отличались и конструкцией, и меньшей точностью измерений. В первом случае для установки чисел на замкнутых круговых логарифмических шкалах использовалась прозрачная крышка с линией-визиром. Во втором – механизм управления (две вращающиеся ручки) был смонтирован на корпусе: одной управлялся дисковый движок, другая управляла стрелкой-визиром.

Возможности

Логарифмической линейкой общего назначения можно было осуществлять деление и умножение чисел, возведить их в квадрат и куб, извлекать корень, решать уравнения. Кроме этого, по шкалам производились тригонометрические вычисления (синус и тангенс) по заданным углам, определялись мантиссы логарифмов и обратные действия – находились числа по их значениям.

Правильность вычислений во многом зависела от качества линейки (длинны ее шкал). В идеале можно было надеяться на точность до третьего знака после запятой. Такие показатели были вполне достаточными для технических расчетов в XIX веке.

Возникает вопрос: как пользоваться логарифмической линейкой? Одного знания назначения шкал и способов нахождения на них чисел еще не достаточно для произведения расчетов. Чтобы использовать все возможности линейки, нужно понимать, что такое логарифм, знать его характеристики и свойства, а также принципы построения и зависимости шкал.

Как считать на логарифмической линейке

Для уверенной работы с устройством требовались определенные навыки. Сравнительно простые вычисления с одним бегунком. Для удобства движок (чтобы не отвлекал) можно удалять. Установив черту на значения любого числа на основной (D) шкале можно сразу же по визиру получить результат возведения его в квадрат на шкале выше (A) и в куб – на самой верхней (K). Внизу (L) будет значение его логарифма.

Деление и умножение чисел производится с помощью движка. Применяются свойства логарифмов. Согласно им, итог умножения двух чисел равен результату сложения их логарифмов (аналогично: деление и разница). Зная это, можно достаточно быстро производить расчеты, используя графические шкалы.

Чем сложна логарифмическая линейка? Инструкция по ее правильному использованию шла в комплекте с каждым экземпляром. Кроме знания свойств и характеристик логарифмов, нужно было уметь правильно находить исходные числа на шкалах и уметь в нужном месте считывать результаты, в том числе самостоятельно определять точное место расположения запятой.

Актуальность

Как пользоваться логарифмической линейкой, в наше время знают и помнят немногие, и с уверенностью можно утверждать, что число таких людей будет снижаться.

Логарифмическая линейка из разряда карманных счетных приспособлений давно стала раритетом. Для уверенной работы с ней нужна постоянная практика. Методика расчетов с примерами и разъяснениями тянет на брошюру в 50 листов.

Для среднестатистического человека, далекого от высшей математики, логарифмическая линейка может представлять какую-то ценность разве что справочными материалами, размещенными на обратной стороне корпуса (плотность некоторых веществ, температура плавления и пр.). Преподаватели даже не утруждаются вводить запрет на ее наличие при сдаче экзаменов и зачетов, понимая, что разобраться с тонкостями ее использования современному студенту очень сложно.

Источник

Что такое логарифмическая линейка и как ей правильно пользоваться

Уильям Отред — изобретатель логарифмической линейки

Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов. — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.

История изобретения

В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.

Форстер был восхищен и позднее писал: «Это превосходило любой из инструментов, которые были мне известны. Я удивлялся, почему он скрывал это полезнейшее изобретение многие годы. » Сам Отред говорил, что он «просто изогнул и свернул шкалу Гюнтера в кольцо», и к тому же был уверен, что «настоящее искусство [математики] не нуждается в инструментах. », их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.

Споры об авторстве

Логарифмическая линейка значительно облегчила сложные вычисления для инженеров и ученых. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.

Как пользоваться логарифмической линейкой

Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.

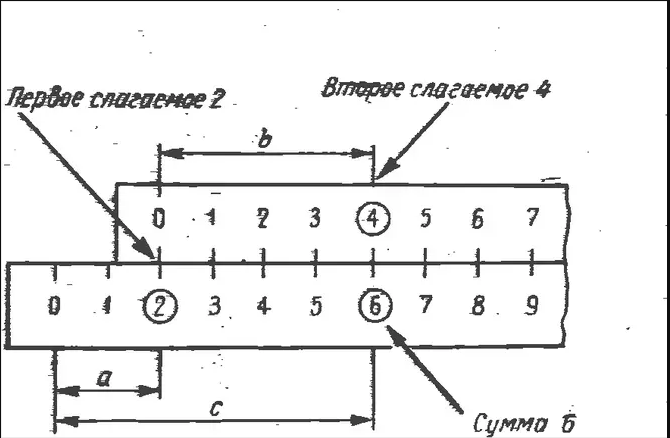
Сложение

Представим, что нам нужно найти сумму двух и четырех. На одной линейке (нижней) откладываем два деления (на рисунке отрезок а), вторую линейку (верхнюю) сдвигаем вправо на эти же два деления, после чего откладываем на ней еще четыре деления (отрезок b на рисунке). Смотрим на нижней линейке, над каким числом находится точка, в которую мы пришли — это шесть.

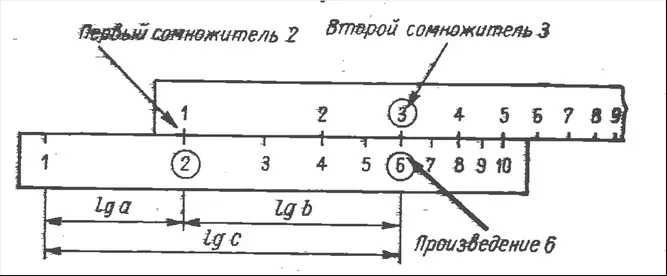
Умножение

На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса).

Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).

Источник

Логарифмическая линейка

Логарифмическая линейка – устройство, предназначенное для упрощения и ускорения работы с логарифмическими таблицами. Использование логарифмической линейки значительно упрощало операции умножения, деления, возведение в степень, извлечения корня и расчет тригонометрических и логарифмических функций. Различного вида логарифмические линейки широко использовались вплоть до начала восьмидесятых годов, пока небыли вытеснены электронными калькуляторами.

Содержание

1. История создания логарифмической шкалы.

Первую попытку упростить и ускорить работу с логарифмическими таблицами предпринял Эдмунд Гюнтер, профессор астрономии Грэшемского колледжа. Он разработал шкалу, состоящую из нескольких отрезков, располагающихся параллельно на деревянной или медной пластине. На каждый отрезок наносились деления, соответствующие логарифмам чисел или тригонометрических величин.

Рассмотрим пример построения логарифмической шкалы. Возьмем за основу отрезок АВ (рисунок ниже) и примем его за единицу. Следовательно, его можно принять за lg 10, так как lg 10 = 1; Теперь рассчитаем длины отрезков, соответствующих десятичным логарифмам чисел 1,2,…9, c точностью до тысячных долей:

Нанесем эти отрезки на шкалу, учитывая, что отрезок АВ = 1:

Для вычисления с помощью этой шкалы необходимо определить сумму или разность длин от начала шкалы до логарифмов исходных чисел. Далее находим логарифм, соответствующий полученной длине, и по его значению определяем произведение или частное. Например, для умножения 2 на 4 надо сложить длину отрезка для числа 2 (0.301) с длинной отрезка для числа 4 (0.602). Далее находим значение, соответствующее длине отрезка 0.903. Это будет число 8. Таким образом, 2*4 = 8. Обычно такая шкала использовалась вместе с двумя циркулями, позволяющими быстро и точно определять длину результирующего отрезка.

Описание логарифмической шкалы Эдмунд Гюнтер опубликовал в 1620 году, так же в этой книге были опубликованы таблицы логарифмов синусов и котангенсов. Изобретение Гюнтера пользовалось большой популярностью и описывалось во многих книгах. Так, например, описание логарифмической шкалы встречается в книге французского механика Н. Биона «Конструкция и применение математических инструментов», опубликованной в 1723 году. Шкала, описанная в этой книге, имела длину 600 мм и ширину 37. Она состояла из шести частей, предназначавшихся для операций с числами, синусами, тангенсами, синусами-верзусами (sin ver a = 1 – cos a), синусами и тангенсами малых углов, синусами и тангенсами румбов. Так же на шкале предусматривались участки для работы с равномерными величинами – «линия меридиана» и «линия равных частей».

2. История создания логарифмической линейки.

Логарифмическая шкала Гюнтера являлась прародителем логарифмической линейки и подвергалась многократным доработкам. Так в 1624 году Эдмунд Уингейт издал книгу, в которой описал модификацию шкалы Гюнтера, позволяющую легко возводить числа в квадрат и в куб, а также извлекать квадратные и кубические корни. Для этого Уингейт поместил две шкалы, построенные в масштабе 1:2, на одной прямой и три шкалы в масштабе 1:3 – на другой. Перенося с помощью измерительного циркуля отрезки с обычной шкалы на шкалу с масштабом 1:2 или 1:3 и наоборот, можно возводить числа в квадрат или в куб и извлекать квадратные или кубические корни.

Дальнейшие усовершенствования привели к созданию логарифмической линейки, однако, авторство этого изобретения оспаривают два ученых Уильям Отред и Ричард Деламейн.

Впервые о своем изобретении Отред рассказал в 1630 году своему ученику и другу Уильяму Фостеру, учителю математики из Лондона. На тот момент Отред изготовил два типа логарифмических линеек – прямоугольную и круглую. Эти изобретения настолько поразили Фостера, что он уговорил передать ему описание изобретения для последующей публикации.

Осенью этого же года Отред рассказал об изобретении круговой логарифмической линейки своему бывшему ассистенту и учителю математики Ричарду Деламейну, который в ответ на рассказ заявил: «Подобное изобретение сделал и я!» и в этом же 1930ом году опубликовал книгу «Граммелогия, или Математическое кольцо», в которой описал круговую логарифмическую линейку и правила ее использования.

Линейка Деламейна содержала до 13 шкал и состояла из вращающегося внутри кольца круга. Так же на линейке располагался указатель, который передвигался вдоль радиуса, облегчая использование инструмента. В книге так же описывалась методика гравировки таких линеек и способы проверки их точности.

Книга Фостера и Отреда, посвященная описанию круглой логарифмической линейки, была издана в Лондоне только в 1632 году и называлась «Круги пропорций». Линейка, описанная в этой книге, содержала восемь шкал (одна шкала была равномерная, а семь остальных – шкалы логарифмов чисел, синусов и тангенсов), выгравированных на медной пластинке. Для облегчения счета на пластинке закреплялись два указателя (см. рисунок справа).

В следующей книге Фореста «Дополнение к использованию инструмента, называемого Кругами Пропорций», изданной в 1633 году, описывалась прямоугольная логарифмическая линейка Отреда. Она состояла из двух частей, на каждой из которой была нанесена логарифмическая шкала. При вычислении эти части линейки зажимались левой рукой, и правой рукой одна из частей сдвигалась относительно другой.

Авторы логарифмических линеек оспаривали первенство изобретения. Так Деламейн обвинял Отреда в воровстве, утверждая, что он не изобрел круговую линейку, а все сведения о ней почерпнул из его (Деламейна) книги. В ответ на подобные заявления Отред подробно описал историю своего изобретения и заметил, что оно было сделано около 12 лет назад. Кто из них прав так и не удалось выяснить. Видимо придется признать, что изобретение логарифмической линейки было сделано независимо друг от друга Уильямом Отредом и Ричардом Деламейном.

Примерно в те же годы Томасом Брауном была разработана плоская спиральная логарифмическая линейка, позволяющая, благодаря увеличению длины шкалы, повысить точность вычислений. Однако, это изобретение не получило широкой известности и вскоре было забыто. Вновь этот тип логарифмических линеек был изобретен в 1748 году Джорджем Адаме. Линейка Адаме размещалась на медной пластинке диаметром 305 мм и имела 10 витков шкалы.

Примерно 1650 году Милбурн предложил способ увеличения длины шкалы логарифмической линейки путем нанесении спиралевидной шкалы на боковую поверхность цилиндра.

В 1654 году англичанин Роберт Биссакер разработал прямоугольную логарифмическую линейку, состоящую из трех частей длинной 60 см, закрепленных параллельно друг другу. Две внешние части были неподвижно закреплены с помощью медных оправ, а третья (движок) свободно передвигалась между ними. Каждой шкале на неподвижных частях соответствовала аналогичная шкала на движке. Причем шкалы были на обоих сторонах логарифмической линейки.

Независимо от Роберта Биссакера аналогичную структуру линейки разработал в 1657 году Сет Патридж, учитель математике из Лондона.

Следующее усовершенствование линейки произвел Томас Эверард. Во-первых, он применил на практике идеи Уингента, расположив на линейке двойные и тройные шкалы для возведения чисел в квадрат и куб, извлечения квадратного и кубического корней.

Во-вторых, он отметил на шкалах особые точки – числа, наиболее часто встречающиеся при расчетах:

— сторона квадрата, вписанного в круг диаметра 1 (0,707);

— сторона квадрата, равновеликого кругу диаметра 1 (0,886);

— длина окружности с диаметром 1 (3.14);

— объем стандартного галлона вина в кубических дюймах (231);

— объем стандартного бушеля солода (2150,42);

— объем стандартного галлона эля (282).

Основное предназначение линейки Эверарда было определение объема сосудов. Универсальная линейка была разработана в 1779 году Джейсом Уаттом, шотландским изобретателем-механиком.

Джеймс Уатт в то время занимался разработкой паровых машин и для их расчета пользовался логарифмическими шкалами, нанесенными на линейки. Подобные линейки были широко известны, однако, их точность оставляла желать лучшего. Мистер Уатт и мистер Соутерн разработали удобное расположение логарифмических шкал для универсального использования и пригласили опытнейших специалистов своего времени для градуировки первого образца. Копии этого образца были переданы мастерам, работающим над паровой машиной.

В 1850 году девятнадцатилетний французский офицер Амедей Маннхейм создал прямоугольную логарифмическую линейку, ставшую прообразом современных линеек и обеспечивающую точность до трех десятичных знаков. Этот инструмент он описал в книге «Модифицированная вычислительная линейка», изданной в 1851 году. В течение 20-30 лет эта модель выпускалась только во Франции, а затем ее стали изготавливать в Англии, Германии и США. Вскоре линейка Маннхейма завоевала популярность во всем мире.

Логарифмическая линейка долгие годы оставалась самым массовым и доступным прибором индивидуального вычисления, несмотря на бурное развитие вычислительных машин. Естественно, она обладала небольшой точностью и скоростью решения по сравнению с вычислительными машинами, однако, на практике большинство исходных данных были не точные, а приближенные величины, определенные с той или иной степенью точности. А, как известно, результаты вычислений с приближенными числами будут всегда приближенные. Этот факт и высокая стоимость вычислительной техники позволили Логарифмической линейке просуществовать практически до конца 20 столетия.

3. Устройство логарифмической линейки.

Рассмотрим логарифмические линейки, используемые во второй половине 20 века в России. Стандартная логарифмическая линейка состояла из трех, покрытых белым целлулоидом, частей: корпуса (M,N), движка (Q) и бегунка (Б). На корпусе линейки наносилось шесть шкал длиной по 25 см каждая. Длина шкалы в 25 см позволяла получить результаты с точностью до четырех значащих цифр с ошибкой, не превосходящей единицы последнего знака.

На движке так же было нанесено шесть неравномерных шкал длиной 25 см, по три с лицевой и обратной сторон.

Бегунок представлял собой прямоугольную рамку со стеклом, на середине которого нанесена тонкая черта – указатель. Бегунок удерживался на линейке зацепляясь краями рамки. Между бегунком и линейкой устанавливалась пружинка, помогающая свободно перемещаться бегунку и удерживаться ему на линейке.

На обратной стороне линейки приводились справочные данные: математические и физические константы, коэффициенты линейного расширения, модули упругости, удельные веса тел и другие данные.

Рассмотрим назначение шкал линейки.

Шкала А служит для вычисления квадратов чисел, откладываемых на шкале D. Так же можно с помощью шкал А и В вычислять квадратные корни чисел.

Шкала В точно такая же, как шкала А. На этих шкалах нанесены отрезки, пропорциональные (m/2)*lg X. Цена наименьшего деления на участках от 1 до 2, от 2 до 5, от 5 до 10, от 10 до 20, от 20 до 50, от 50 до 100 равна соответственно 0.02, 0.05, 0.1, 0.2, 0.5 и 1.

Шкала L – равномерная. На ней отложены мантиссы (дробная часть десятичного логарифма) логарифмов шкалы D. Наименьшее деление этой шкалы соответствует 0.002, а метки, обозначенные цифрами 1,2,3,4. читаются как 0.1, 0.2, 0.3, 04…

Шкалы D и С называются основными. На них нанесены отрезки, пропорциональные m*lg X, при Х изменяемом от 1 до 10. Значение наименьших делений этих шкал на участке от 1 до 2 означает 0.01, на участке от 2 до 4 они означают 0.02, на участке от 4 до 10 – 0.05.

Шкала R – это шкала обратных значений. Она представляет собой шкалу С (D), но в перевернутом виде. Таким образом, метка 10 этой шкалы будет на левом конце, а 1 – на правом. На этой шкале любой отрезок P от начала шкалы равняется 250-250* lg p = 250* lg (1/p).

Шкалы Sin, S&T и Tg используются при вычислениях с тригонометрическими функциями. Отрезки на этих шкалах пропорциональны следующим функциям:

Для шкалы синусов (Sin): y = k ( lg sin Vs + 1 ),

Для шкалы синусов и тангенсов (S&T): y = k [ lg 1/2( sin V + tg V ) +2],

Для шкалы тангенсов (Tg): y = k ( lg tg Vt + 1 ),

Следует помнить, что каждая метка (риска) на шкалах линейке имеет не одно определенное значение, а всякое другое, которое может быть получено умножением этого значения на 10 в любой степени. То есть, числа … 1525, 152.5, 15.25, 1.525, 0.1525 … будут расположены в одном месте логарифмической линейки.

4. Работа с логарифмической линейкой.

С помощью логарифмической линейки можно производить умножение, деление, возведение в степень и извлечение корней, определять натуральные значения тригонометрических функций заданных углов и по заданным натуральным значениям тригонометрических функций находить соответствующие им углы, определять логарифмы и антилогарифмы чисел, находить логарифмы тригонометрических функций и производить различные вычисления.

Рассмотрим подробно правила выполнения перечисленных выше операций с помощью логарифмической линейки и начнем с умножения и деления.

4.1. Умножение и деление.

Умножение и деление с помощью линейки основывается на свойстве логарифмов:

lg X*Y = lg X + lg Y lg X/Y = lg X – lg Y

Следовательно, операция умножения сводится к сложению соответствующих отрезков на логарифмических шкалах C и D, а операция деления – к вычитанию этих отрезков. Рассмотрим пример, в котором требуется вычислить X = 41.4 x 12 = 496,8:

1. Ставим указатель бегунка на деление 41.4 на шкале D.

2. Передвигаем движок вправо так, чтобы крайняя левая цифра шкалы C (1) была под указателем бегунка.

3. Ставим указатель бегунка на деление 12 на шкале C.

4. По указателю бегунка считываем число на шкале D (497).

5. Приблизительный результат умножения 497.

Рассмотрим деление на примере y = 5.15/1.31 = 3.931…:

1. Устанавливаем указатель бегунка на деление 5.15 шкалы D.

2. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с делением 1.31 шкалы С.

3. Устанавливаем указатель бегунка на левую крайнюю цифру шкалы С (1).

4. По указателю бегунка считываем число на шкале D (393).

5. Приблизительный результат деления будет 3.93.

4.2. Возведение в степень и извлечение корня.

Для возведения в квадрат или в куб числа М устанавливают указатель бегунка на деление шкалы D, соответствующее числу М. По указателю бегунка на шкале А считывают квадрат числа М, а на шкале К – куб числа М. При этом необходимо вручную учитывать порядок результата.

Рассмотрим пример возведения числа 42 в куб и квадрат с помощью логарифмической линейки:

1. Устанавливаем бегунок на деление 4.2 шкалы D.

2. По указанию бегунка считываем число на шкале А (17.64).

4. Приблизительный результат возведения числа 42 в квадрат будет 17.64*10 2 = 1764.

5. По указанию бегунка считываем число на шкале К (74).

6. Определяем порядок результата возведения в куб. В этом случае n = 1, m = 3, следовательно, порядок результата будет 1*3 = 3.

7. Приблизительный результат возведения числа 42 в куб будет 74*10 3 = 74000.

Извлечение корня – действие, обратное возведению в степень, поэтому для того, чтобы извлечь квадратный корень из числа устанавливают указатель бегунка на деление, соответствующее этому числу на шкале А, а результат извлечения смотрят по указателю бегунка на шкале D. Для извлечения кубического корня указатель устанавливают по шкале К, а результат опять же будет на шкале D. Так же, как и при возведении в степень, порядок результата необходимо рассчитывать вручную.

4.3. Работа с логарифмами.

Для нахождении десятичного логарифма числа необходимо указатель бегунка установить на деление шкалы D, соответствующее этому числу. И по указателю бегунка на шкале L определить мантиссу (дробная часть) логарифма. Затем спереди приписать к ней характеристику (целая часть) логарифма. Рассмотрим пример нахождения десятичного логарифма числа 473 (lg 473 = 2.67486…):

1. Устанавливаем указатель бегунка на деление шкалы D, соответствующее числу 473. В нашем случае это будет деление 4.73.

2. Определяем значение мантиссы на шкале L по указателю бегунка (675).

4. Приблизительный результат вычисления десятичного логарифма числа 473 будет 2.675.

Для нахождения числа по заданному десятичному логарифму (потенцирование) устанавливают указатель бегунка на деление шкалы L, соответствующее мантиссе логарифма. По указателю бегунка определяют число, соответствующее мантиссе. Далее вручную определяют порядок результата, исходя из характеристики логарифма.

Рассмотрим пример определения числа, заданного десятичным логарифмом 2.675:

1. Устанавливаем указатель бегунка на деление шкалы L, соответствующее мантиссе заданного десятичного логарифма (675).

2. Определяем по указателю бегунка значение на шкале D (4.73).

4. Приблизительный результат потенцирования: 4.73*10 2 = 473.

4.4. Тригонометрические расчеты.

Логарифмические шкалы Sin, S&T и Tg позволяют производить разнообразные действия над формулами, содержащими тригонометрические функции. Однако, эти шкалы предназначались только для работы с синусами и тангенсами, поэтому при работе с косинусами и котангенсами было необходимо предварительно выразить их через синусы и тангенсы по формулам:

ctg a = 1/tg a, для а от 0 0 до 45 0 ;

Рассмотрим на примерах методы работы на логарифмической линейке при вычислении тригонометрических функций. Для начала вычислим значение 43*tg6 0 35` = 4.9625…:

1. Устанавливаем указатель бегунка на деление 4.3 шкалы D.

2. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с началом шкалы Tg.

3. Устанавливаем указатель бегунка на деление 6 0 35` шкалы Tg.

4. По указателю бегунка считываем ответ со шкалы D. В нашем примере это будет примерно 4.96.

Аналогичные действия необходимо предпринять и при работе с синусами и косинусами. Рассмотрим пример 345*cos 82 0 50` = 43.0408…:

1. Преобразуем косинус в синус: 345*cos 82 0 50` = 345*sin 7 0 10`.

2. Устанавливаем указатель бегунка на деление 3.45 шкалы D.

3. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с началом шкалы Sin.

4. Устанавливаем указатель бегунка на деление 7 0 10` шкалы Sin.

5. По указателю бегунка считываем ответ со шкалы D. В нашем случае это будет примерно 43.

Если же под верхний штрих правого выреза установить, например, 31 0 шкалы Sin, то на шкале С (напротив правого крайнего штриха (цифра 10) шкалы D) будет значение sin 31 0 (примерно 0.515).

Так же с помощью логарифмической линейки можно находить углы по значениям синуса или тангенса. Рассмотрим пример нахождения угла, которому соответствует tg a = 0.22:

1. Находим на шкале С значение заданного тангенса (0.22).

2. Совмещаем найденное деление шкалы С с началом шкалы D.

Для нахождения угла по заданному синусу (например, sin a = 0.56) совмещаем деление шкалы С, соответствующее синусу (0.56), с концом шкалы D. Переворачиваем линейку и на шкале Sin в правом вырезе напротив верхнего штриха считываем значение искомого угла (примерно 34 0 ).

Стоит помнить, что при определении угла по значению тригонометрической функции, необходимо вручную учитывать в какой четверти находится искомый угол.

Часто при расчетах требуется переводить углы из градусов в радианы. Для этих целей на линейке предусмотрена специальная отметка 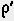. Рассмотрим использование отметки на примере перевода 36 0 12` в радианы:

1. Выражаем заданный угол в минутах (36 0 *60+12` = 2172`).

2. Устанавливаем бегунок на деление 2.172 шкалы D.

3. Подводим под указатель бегунка штрих шкалы С, отмеченный знаком .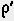

4. Считываем ответ на шкале D напротив конца шкалы C (примерно 0.632 рад).

Рассмотрим перевод угла из радиан в градусы на примере 0.35 рад:

1. Устанавливаем бегунок на деление 3.5 шкалы D.

2. Подводим под указатель бегунка конец шкалы С.

3. Устанавливаем бегунок на деление шкалы С, отмеченное символом .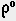

4. По указателю бегунка со шкалы D считываем ответ (примерно 1.2).

5. Ответ считан в минутах без учета порядка. Переведем ответ в градусы и учтем порядок: 1.2/60 = 0.02. С учетом порядка ответ будет примерно 20 градусов.

5. Виды логарифмических линеек.

Часто на логарифмические линейки наносили дополнительные шкалы со значениями функций часто употребляемых на практике, например, в электротехнических, геодезических и других расчетах. Большое распространение имели и дисковые логарифмические линейки. Ниже приведены различные виды логарифмических линеек.

На логарифмических линейках закончим обзор домеханического этапа и перейдем к следующему этапу истории развития ЭВМ – Механическому этапу.

Источник

Логарифмическая линейка: история первого «компьютера» VXII века

Логарифмическая линейка — это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.

Уильям Отред — изобретатель логарифмической линейки

История изобретения

Споры об авторстве

Как пользоваться логарифмической линейкой

Источник

Как пользоваться логарифмической линейкой?

В двух словах не объяснить. Логарифмическая линейка позволяла делать МНОЖЕСТВО самых разных вычислений.

Чтобы пользоваться логарифмической линейкой, нужно понимать, что она состоит из трех подвижных относительно друг друга частей: корпуса, движка и стеклянного бегунка.

На корпусе логарифмической линейки нанесено 6 различных шкал (4 на лицевой стороне и 2 на гранях), на движке нанесено еще три шкалы, на обратной стороне движка еще три шкалы. На стекло бегунка также нанесена риска, которая помогает при вычислениях. Установив на шкале какое либо число, и двигая движок вдоль корпуса, можно вычислять сразу множество параметров: умножение, деление, возведение в степень, извлечение корня, определять тригонометрические функции углов, и наоборот, находить углы по функциям, определять логарифмы числе и логарифмы тригонометрических функций.

По этой ссылке можно скачать пособие по пользованию логарифмической линейкой.

Источник

Логарифмическая линейка

Логарифмическая линейка — это калькулятор из XVII века. В далёком 1623 году Э. Гантер (математик из Англии) придумал вычислительную шкалу – прообраз современной логарифмической линейки. Впоследствии он пережил ряд изменений. К 1850 году, с внедрением бегунка, линейка приобрела более привычный вид.

Конструкция логарифмической линейки

Логарифмическая линейка состоит из двух основных частей:

Основа выполнена в виде обычной линейки, но по центру имеется продольно расположенный паз, по которому передвигается бегунок. Две части совмещаются в определенных местах, для облегчения вычислений.

Линейка изготавливалась из прочного дерева, которое устойчиво к трению. Для таких целей часто использовали древесину груши. Шкалы и градуировка произведена с помощью тиснения и заполнена краской, так надписи не стираются с поверхности линейки. На бегунке присутствовало небольшое окошка из пластика или железа и стекла. Свобода перемещений только в продольной оси.

Как работает логарифмическая линейка?

На линейке в общей сложности есть 7 шкал. 4 из них нанесены на основе, а 3 на бегунке. Вдоль боковых граней имеется обычная сантиметровая разметка.
Чтобы ориентироваться по шкалам – они подписаны стандартными символами:

Названия и количество могут несколько варьироваться. Подвижная часть вынимается, на оборотной стороне нанесены еще шкалы.

Как считать логарифмической линейкой

Чтобы правильно производить вычисления, нужно совместить в окошке, если оно имеется, или на разметочной линии нужные для счёта числа. Допустим, необходимо умножить число 180 на 0,4, значит нужно произвести действия по алгоритму:

С помощью логарифмической линейки можно быстро производить умножение и другие математические операции. Кстати, преподаватели не запрещают ей пользоваться на уроках. Хотя многие молодые преподаватели не знают, что такое логарифмическая линейка.

Формулы для решения геометрических задач на прямоугольный треугольник.

Источник

Счётная логарифмическая линейка

Предисловие 3
I. Принципы устройства логарифмической линейки 5
II. Описание логарифмической линейки 8
III. Цена делений основной шкалы 10
IV. Установка и чтение чисел на основной шкале 11
V. Порядок чисел 12
VI. Умножение 14
VII. Деление 18
VIII. Умножение и деление на шкале квадратов и с помощью обратной шкалы 20
IX. Комбинированные действия умножения и деления 23
X. Возведение в квадрат 25
XI. Извлечение квадратного корня 28
XII. Возведение в куб 32
XIII. Извлечение кубического корня 33
XIV. Логарифмы чисел 36
XV. Тригонометрические функции 40
XVI. Применение логарифмической линейки в некоторых практических расчетах 47
Литература 54

Леонид Сергеевич Хренов
Юлий Васильевич Визиров

Логарифмическая линейка

Предисловие 3
Введение 5

Нормальная счетная логарифмическая линейка
§ 1. Описание линейки 11
§ 2. Шкалы линейки 15
§ 3. Установка и чтение чисел по шкалам линейки 17
§ 4. Порядок чисел 20
§ 5. Алгебраические и тригонометрические действия на линейке 21
§ 6. Особые значки на шкалах линейки 31
§ 7. Применение линейки при расчетах 32
§ 8. Различные логарифмические линейки 37

Дисковая счетная логарифмическая линейка «Спутник»
§ 9. Описание линейки «Спутник» 43
§ 10. Установка и чтение чисел по шкалам линейки «Спутник» 46
§ 11. Применение линейки «Спутник» 52

Круговая счетная логарифмическая линейка КЛ-1
§ 12. Описание линейки КЛ-1 62
§ 13. Установка и чтение чисел по шкалам линейки КЛ*1 „64
§ 14. Применение линейки КЛ-1 67

Заключение 75
Приложения 76
1. Основные правила приближенных вычислений 76
2. Памятка вычислителя 77
Литература 78

Василий Семёнович Кущенко

Логарифмическая линейка

От автора 4
Введение 5

Глава I. Устройство и чтение шкал логарифмической линейки 7
§ 1. Описание логарифмической линейки —
§ 2. Понятие о равномерных шкалах —
§ 3. Основные шкалы 12
§ 4. Обратная шкала 17
§ 5. Шкалы квадратов 18
§ 6. Шкала кубов 19
§ 7. Шкала логарифмов —
§ 8. Шкалы тригонометрических величин —
§ 9. Дополнительные штрихи на шкалах логарифмической линейки 20
§ 10. Понятие о порядке чисел —

Глава II. Основные действия на логарифмической линейке 22
§ 1. Предварительные замечания —
§ 2. Умножение 23
§ 3. Деление 25
§ 4. Возведение чисел в квадрат 27
§ 5. Извлечение квадратного корня из чисел 28
§ 6. Возведение чисел в куб 29
§ 7. Извлечение кубического корня из чисел 30
§ 8. Логарифмирование и потенцирование 31
§ 9. Вычисления с помощью обратной шкалы 32
§ 10. Вычисление тригонометрических функций 34
§ 11. Перевод градусов в радианы и обратно 39
§ 12. Точность вычислений на логарифмической линейке 40
§ 13. Хронометраж линейки 41

Глава III. Решение задач и уравнений с помощью логарифмической линейки 42
§ 1. Пропорции —
§ 2. Решение прямоугольных треугольников 44
§ 3. Решение геометрических задач 46
§ 4. Решение алгебраических и трансцендентных уравнений методом итерации 48
§ 5. Решение систем линейных алгебраических уравнений методом релаксации 51

Глава IV. Упражнения на логарифмической линейке 55
§ 1. Примеры и задачи —
§ 2. Типичные варианты зачетной работы по логарифмической линейке 59
§ 3. Некоторые часто встречающиеся величины 60
Ответы 61
Литература 62

Дмитрий Степанович Миков

Счётная логарифмическая линейка

Предисловие
Введение 3
§ 1. Описание счетной логарифмической линейки 4
§ 2. Основные свойства логарифмов 7
§ 3. Соотношения шкал логарифмической линейки 7

Действия с числами
§ 4. Установка и чтение чисел на шкалах линейки 19
§ 5. Порядок чисел 20
§ 6. Умножение чисел 20
§ 7. Деление чисел 22
§ 8. Совместное умножение и деление 22
§ 9. Возведение в квадраг 24
§ 10. Извлечение квадратного корня 25
§ 11. Возведение в куб 26
§ 12. Извлечение кубичного корня 26
§ 13. Возведение в степень 2/3 27
§ 14. Возведение в степень 3/2 28
§ 15. Извлечение корней с показателями 2/3 и 3/2 29
§ 16. Нахождение обратных значений чисел30
§ 17. Вычисление процентного отношения чисел 31
§ 18. Вычисление чисел по процентам 32
§ 19. Решение пропорций 33
§ 20. Линейка как таблица прямой и обратной пропорциональности 33
§ 21. Умножение и деление одного числа на ряд других чисел 34
§ 22. Перемножение ряда сомножителей 35
§ 23. Сложение и вычитание чисел 35
§ 24. Вычисление квадратного корня из суммы или разности квадратов чисел 36
§ 25. Вычисление кубичного корня из суммы или разности кубов чисел 37

Логарифмы
§ 26. Отыскание логарифмов чисел 39
§ 27. Отыскание чисел по логарифмам 39
§ 28. Перевод десятичных логарифмов в натуральные и обратно 40
§ 29. Возведение в любую степень 40
§ 30. Извлечение корня любой степени 40

Источник

Инструкция: Как пользоваться логарифмической линейкой в часах

Логарифмическая линейка или счётная линейка — вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб) и вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и другие операции. Также, если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени.

Не пугайтесь! Вам не нужно ежедневно вычислять основания и логарифмы, косинусы и арктангенсы. В большинстве случаев логарифмические линейки, встроенные в часы, не оснащены шкалами для вычисления значений тригонометрических функций.

Ряд наручных часов оснащены вычислительными линейками, функции которых приближены к повседневной жизни.

Итак, часы Citizen Promaster Sky – уже по обозначениям на отградуированной шкале понятно, что они прекрасно приспособлены для расчета расхода топлива при автомобильных поездках или путешествиях на моторном катере.

Начнем с самого простого. Круговая логарифмическая линейка состоит из линейки на безеле и линейки на циферблате. Поворачивайте безель до совмещения значения на линейке безеля с нужной отметкой на циферблате.

Для того, чтобы поделить 150 на 3, следует число 15 (=150) на внешней шкале установить против числа 30 (3) на внутренней шкале. Результат отсчитывается на внутренней шкале напротив «10» и равен 50.

В интернете можно найти пример Тройного правила, или расчета скорости снижения с помощью круговой вычислительной линейки на часах.

Летчик в планере, находящийся на высоте 3300 метров, определяет, что он теряет высоту со скоростью одного метра в секунду, т.е. 60 м в минуту. Сколько у него остается времени до конца полета? Для того, чтобы знать ответ, следует установить число 33 (=3300) на внешней шкале против числа 60 на внутренней шкале. Результат находится против знака «10» на внутренней шкале и составляет 55 минут.

Но оставим в покое авиационные задачи и применим это правило для расчета в более близкой сфере. На какое расстояние вам хватит 40 литров бензина при расходе топлива 8 литров на 100 километров? Устанавливаем число 40 напротив числа 8. Получаем 50, с учетом масштаба 1 к 10 – на 500 км.

На различных часах есть множество обозначений, облегчающих пересчет мер длины.

Источник

Как пользоваться логарифмической линейкой

На уроках информатики, изучая тему «История вычислительной техники», упоминается устройство логарифмическая линейка. Что это такое? Как она выглядит? Как ей пользоваться? Рассмотрим историю создания данного устройства и принцип работы.

Логарифмическая линейка — это счетный прибор, применявшийся до появления калькуляторов и персональных компьютеров. Это было достаточно универсальное устройство, на котором можно было умножать, делить, возводить в квадрат и куб, вычислять квадратные и кубические корни, синусы, тангенсы и другие значения. Выполнялись эти математические операции с достаточно большой точностью — до 3–4 знаков после запятой.

История логарифмической линейки

В 1622 году Уильям Отред (William Oughtred 5 марта 1575—30 июня 1660) создает, пожалуй, один из самых успешных аналоговых вычислительных механизмов — логарифмическую линейку. Отред является одним из создателей современной математической символики — автор нескольких стандартных в современной математике обозначений и знаков операций:

«Все его мысли были сосредоточены на математике, и он все время размышлял или чертил линии и фигуры на земле… Его дом был полон юных джентльменов, которые приезжали отовсюду, чтобы поучиться у него».

Неизвестный современник Отреда

Отред внёс решающий вклад в изобретение удобной для пользования логарифмической линейки тем, что предложил использовать две одинаковые шкалы, скользящие одна вдоль другой. Саму идею логарифмической шкалы ранее опубликовал валлиец Эдмунд Гюнтер, но для выполнения вычислений эту шкалу нужно было тщательно измерять двумя циркулями.

Гюнтер ввел также общепринятое теперь обозначение log и термины косинус и котангенс. В 1620 году вышла книга Гюнтера, где дано описание его логарифмической шкалы, а также помещены таблицы логарифмов, синусов и котангенсов. Что же касается самого логарифма, то его изобрел, как известно, шотландец Джон Непер. Видя недоумение Форстера, высоко ценившего данное изобретение, Отред показал своему ученику два изготовленных им вычислительных инструмента — две логарифмические линейки.

Первая линейка Отреда имела две логарифмические шкалы, одна из которых могла смещаться относительно другой, неподвижной. Второй инструмент представлял собой кольцо, внутри которого вращался на оси круг. На круге (снаружи) и внутри кольца были изображены “свернутые в окружность” логарифмические шкалы. Обе линейки позволяли обходиться без циркулей.

Логарифическая линейка Отреда

В 1632 году в Лондоне вышла книга Отреда и Форстера “Круги пропорций” с описанием круговой логарифмической линейки (уже иной конструкции), а описание прямоугольной логарифмической линейки Отреда дано в книге Форстера “Дополнение к использованию инструмента, называемого “Кругами пропорций”, вышедшей в следующем году.

Линейка Ричарда Деламейна (который был в свое время ассистентом Отреда), описанная им в брошюре “Граммелогия, или Математическое кольцо”, появившейся в 1630 году, тоже представляла собой кольцо, внутри которого вращался круг. Потом эта брошюра с изменениями и дополнениями издавалась еще несколько раз. Деламейн описал несколько вариантов таких линеек (содержащих до 13 шкал). В специальном углублении Деламейн поместил плоский указатель, способный двигаться вдоль радиуса, что облегчало использование линейки. Предлагались и другие конструкции. Деламейн не только представил описания линеек, но и дал методику градуировки, предложил способы проверки точности и привел примеры использования своих устройств.

А в 1654 году англичанин Роберт Биссакер предложил конструкцию прямоугольной логарифмической линейки, общий вид которой сохранился до нашего времени…

Источник

masterok

Мастерок.жж.рф

Хочу все знать

Признаюсь честно мне уже не довелось плотно разобраться и поработать с этим инструментом. А ведь это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.

Кто же изобрел логарифмическую линейку?

Споры об авторстве

Как пользоваться логарифмической линейкой

Для начала введем переменные: a ∙ b = с при a = 2, b = 3. Затем возведем в логарифм обе части равенства и получим Lg (a) + lg (b)= lg (с). Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3. На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса). Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).

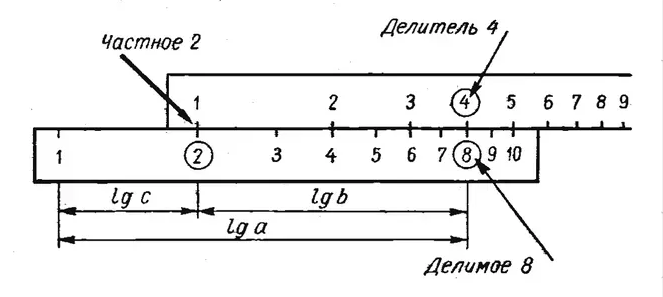
Пусть a/b = с при a = 8, b = 4. Возведем в логарифм обе части равенства и тогда получим: Lg (a) — lg (b) = lg (с). Разность логарифмов делимого и делителя дает логарифм частного, в нашем случае — 2. На основной шкале корпуса линейки выбирается делимое, на которое устанавливается волосок бегунка. Под волосок подводится делитель, найденный на основной шкале движка. Результат определяется на основной шкале корпуса напротив начала или конца движка.

Источник

Кто изобрел логарифмическую линейку?

Вчера, 16:21 | Политика / Размышления о политике | разместил: Око Политика | комментариев: (1) | просмотров: (1 115)

Кто же изобрел логарифмическую линейку?

В? 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.

Споры об авторстве

Как пользоваться логарифмической линейкой

Источник

Логарифмическая линейка: история первого «компьютера» VXII века

Уильям Отред — изобретатель логарифмической линейки
Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов. — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.

История изобретения
В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.

Как пользоваться логарифмической линейкой
Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.

1. Сложение

2. Умножение

3. Деление

Источник

Логарифмическая линейка

Бурный рост народного· хозяйства нашей страны требует высокой механизации труда инженеров и техников, рабочих и служащих, колхозников, всех тружеников советского общества. Немаловажное значение nриобретают механизация и техника вычислительных работ, где наряду с электронно-счетными машинами исnользуются всевозможные таблицы и счетная логарифмическая линейка. Логарифмическая линейка является достуnным и портативным счетным прибором, nозволяющим значительно сократить время и труд на всевозможные вычисления.

В настоящее время происходит быстрое развитие и внедрение в практику счетных приборов и вычислительных машин. Однако счетная логарифмическая линейка продолжает оставаться самым массовым вычислительным прибором для расчетов, не требующих большой точности и скорости. Научиться быстро и точно работать на логарифмической линейке значительно легче, чем это многим кажется.

До появления карманных калькуляторов этот инструмент служил незаменимым расчётным орудием инженера. Точность расчётов — около 3 значащих цифр.

Линейки, выпускавшиеся в СССР, в отличие от линейки на фото, почти всегда имели дополнительную сантиметровую шкалу у скошенного края, как и у обычной линейки. Стандартная линейка имела длину 30 см, что было удобно для геометрических работ с форматом А 4. При этом логарифмические шкалы имели длину 25 см, на концах обычно наносились их обозначения. Реже встречались линейки малого размера со шкалами длиной 12,5 см и большого размера — со шкалами длиной 50 см.

Внимание вычислителей заслуживает выпускаемый московским заводом «Калибр» логарифмический диск «Спутник», предназначенный, как и нормальная счетная логарифмическая линейка, для различных вычислений (логарифмические круги), преимущество которых заключалось в их компактности. В начале XX века для вычислений с повышенной (в 10—100 раз) точностью пользовались

настольными счётными вальцами — механическим устройством, в котором логарифмические шкалы нанесены на образующие цилиндров, один из которых может соосно перемещаться вдоль другого и вращаться вокруг него.

Историческая справка

Логарифмическая шкала — прямолинейный отрезок, па котором отложены логарифмы чисел и тригонометрических функций — основа устройства счетной линейки,— была предложена лондонским профессором Эдмунтом Гунтером (1581—1626), т. е. спустя примерно шесть лет после опубликования (1614) Д. Непером (1550—1617) его работы о логарифмах. В 1620 г. Э. Гунтер сделал доклад об Этом в Парижской Академии наук с демонстрацией своей линейки, на которой основными являлись шкалы — чисел, квадратов, кубов, синусов и тангенсов. Прототипом современной счетной линейки явилась конструкция прямоугольной логарифмической линейки, разработанной англичанином Р. Биссакером в 1654 г. И только в 1851 г. Мангейм (Франция) предложил к линейке бегунок; с этого времени она приняла современный вид. В России логарифмическая линейка впервые была описана А. Д. Фарварсоном в его работе «Книжица о сочинении и описании сектора шкал плоской и гунтерской со употреблением оных инструментов в решении различных математических проблем», опубликованной в 1739 г. В конце XIX в. счетные логарифмические линейки стали изготовляться на фабриках и с этого времени начали появляться не только универсальные счетные линейки со шкалами разной длины и с различными приспособлениями (микрометренными винтами, лупами и другими деталями) для уточнения и облегчения вычислений, но и специальные счетные линейки (электротехнические, для экономистов, а позднее — геодезические, для радиотехнических расчетов и др.), отличающиеся от универсальных наличием специальных шкал. К этому же времени относится и появление счетных линеек с двойными логарифмическими шкалами.

Одновременно (1622 год) свой вариант линейки, мало чем отличающийся от современного, опубликовал в трактате «Круги пропорций» Уильям Отред, который и считается автором первой логарифмической линейки. Сначала линейка Отреда была круговой, но в 1633 году было опубликовано, со ссылкой на Отреда, и описание прямоугольной линейки. Приоритет Отреда долгое время оспаривал Ричард Деламейн, который, вероятно, независимо реализовал ту же идею. Дальнейшие усовершенствования сводились к появлению второй подвижной линейки-«движка» (Роберт Биссакер, 1654 и Сет Патридж, 1657), разметке обеих сторон линейки (тоже Биссакер), добавление двух «шкал Уингейта», отметке на шкалах часто используемых чисел (Томас Эверард, 1683). Бегунок появился в середине XIX века (А. Мангейм).

Устройство и принципы использования

Принцип действия логарифмической линейки основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.

Простейшая логарифмическая линейка состоит из двух шкал в логарифмическом масштабе, способных передвигаться относительно друг друга, являя собой образец транспарантной номограммы. Более сложные линейки содержат дополнительные шкалы на корпусе и движке и прозрачный бегунок (иногда он называется также ползунко́м или визи́ром) — прозрачную рамку (из стекла, плексигласа и т.п.), на которой нанесены несколько рисок (визи́рных линий), позволяющих фиксировать на шкалах числа; бегунок может свободно двигаться вдоль корпуса, визирные линии нанесены перпендикулярно шкалам. На обратной стороне корпуса линейки могут находиться какие-либо справочные таблицы. Движок обычно размечается шкалами с обеих сторон, результаты с его обратной стороны (где часто размещаются шка́лы тригонометрических функций) могут считываться в специальных вырезах на обратной стороне корпуса линейки, пользователь может также извлечь движок из корпуса и вставить его обратной стороной вперёд.

Пример умножения 2×3 или деления 6/3. Для умножения на нижней (неподвижной) шкале находим число 2, совмещаем с ним 1 на верхней шкале (движке), находим на движке число 3 и напротив него считываем на нижней шкале результат умножения, 6. Для деления находим 6 на неподвижной шкале, выставляем напротив число 3 на движке, напротив единицы на движке считываем на нижней шкале результат деления, число 2

Для того чтобы вычислить произведение двух чисел, начало или конец подвижной шкалы совмещают с первым множителем на неподвижной шкале, а на подвижной шкале находят второй множитель. Напротив него на неподвижной шкале находится результат умножения этих чисел:

Чтобы разделить числа, на подвижной шкале находят делитель и совмещают его с делимым на неподвижной шкале. Начало (или конец) подвижной шкалы указывает на результат.

С помощью логарифмической линейки находят лишь мантиссу числа, его порядок вычисляют в уме. Точность вычисления зависит от длины шкалы и для нормальных линеек (25 см) составляет 3—4 значащих цифры. Для выполнения других операций используют бегунок и дополнительные шкалы.

Следует отметить, что, несмотря на простоту, на логарифмической линейке можно выполнять достаточно сложные расчёты. Раньше выпускались довольно объёмные пособия по их использованию.

Логарифмическая линейка в XXI веке

Логарифмические линейки широко использовались для выполнения инженерных расчётов примерно до начала 1980-х годов, когда они были вытеснены калькуляторами.

Однако в начале XXI века логарифмические линейки получили второе рождение в наручных часах:

следуя моде, производители некоторых марок (среди которых Breitling, Citizen, Orient) выпустили модели со встроенной логарифмической линейкой, выполненной в виде вращающихся колец со шкалами вокруг циферблата. Производители обычно называют такие устройства «навигационная линейка». Их достоинство — можно сразу, в отличие от микрокалькулятора, получить информацию, соответствующую табличной форме представления (например, таблицу расхода топлива на пройденное расстояние, перевода миль в километры, подсчёт пульса, определение скорости поезда и тому подобное). Однако в большинстве случаев логарифмические линейки, встроенные в часы, не оснащены шкалами для вычисления значений тригонометрических функций.

Виды линеек

Литература

Заключение

При выборе счетной логарифмической линейки той или иной конструкции следует учитывать эксплуатационные особенности каждой из них.

Источник

Логарифмическая линейка

Из Википедии — свободной энциклопедии

Логарифми́ческая лине́йка, счётная линейка — аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб), вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени.

Линейки, выпускавшиеся в СССР, в отличие от линейки на фото, почти всегда имели дополнительную сантиметровую шкалу у скошенного края, как и у обычной линейки. Стандартная линейка имела длину 30 см, что было удобно для геометрических работ с форматом А4. При этом логарифмические шкалы имели длину 25 см, на концах обычно наносились их обозначения. Реже встречались линейки малого размера со шкалами длиной 12,5 см и большого размера — со шкалами длиной 50 см.

Выпускались также круговые логарифмические линейки (логарифмические круги), преимущество которых заключалось в их компактности. В начале XX века для вычислений с повышенной (в 10—100 раз ) точностью пользовались настольными счётными вальцами — механическим устройством, в котором логарифмические шкалы нанесены на образующие цилиндров, один из которых может соосно перемещаться вдоль другого и вращаться вокруг него.

Источник

Логарифмическая линейка – аналог персональных компьютеров

Большинство видело логарифмическую линейку (или счётную линейку) только на картинке или в фильмах, таких как «Титаник» (1997 год), «Этот остров Земля» (1955 год) и «Аполлон-13» (1995 год). Если Вы являетесь поклонником «Звёздного пути», то должны знать, что Мистер Спок в нескольких эпизодах пользуется логарифмическими линейками «Jeppesen CSG-1» и «B-1». Однако было время, когда инженеры ходили не с калькуляторами или мобильными телефонами, а логарифмическими линейками на поясе. Логарифмическая линейка «Pickett» полетела на Луну вместе с космонавтами, а линейка от «K&E» сделала возможным создание атомной бомбы.

Логарифмические линейки являются частью математики и истории. Они не подвержены влиянию электромагнитных импульсов, а, значит, способны пережить Апокалипсис, который нам все пророчат. В случае с логарифмическими линейками, как и многими другими вещами в этой жизни, действует правило: чем больше, тем лучше.

История логарифмической линейки

Логарифмическая линейка была разработана английским математиком Уильямом Отредом в XVII веке. Она сохраняла свою популярность среди людей, которые всерьёз занимались математикой, вплоть до начала 1970-х годов. На самом деле идея выполнения различных вычислений при помощи линейки в то врем не была новой. Ранее Эдмунд Гюнтер разработал сектор с таким же делением, как и у логарифмической линейки, но чтобы с помощью него решить какую-либо проблему, Вам необходим был отдельный набор делительных циркулей. Прибор Отреда представлял собой круговую логарифмическую линейку. Один из его учеников, Ричард Деламейн, утверждал, что также изобрёл логарифмическую линейку. Оба мужчины обвиняли друг друга в воровстве идей.

Современные учёные считают, что они одновременно создали круговую логарифмическую линейку. Деламейн первым публично сообщил о своём изобретении, однако Отред, по всей видимости, завершил разработку логарифмической линейки раньше, чем его ученик.

Обычная логарифмическая линейка была создана Отредом примерно в 1650 году.

Теория логарифмической линейки

Логарифмические линейки связаны с открытием логарифмов Непером. Логарифмы играли важную роль в мире докомпьютерной математики. Давайте рассмотрим в качестве примера десятичный логарифм. Если 10 возвести в квадрат, получится 100. Следовательно, логарифм 100 равен 2. Если Вы возведёте 10 в пятую степень, то получите 100000. Отсюда, логарифм 100000 равен 5. Полученные цифры не обязательно должны быть целыми числами. Так, к примеру, логарифм 200 равен 2,3.

Если бы Вы тратили много времени на вычисления, то непременно создали бы таблицу чисел и их логарифмов. Вопрос: зачем? Ответ простой. Предположим, Вы захотели умножить два числа – 200 и 100. Это достаточно просто сделать, не прибегая ко всяким хитростям. Вы записываете на листке бумаги «200х100» и умножаете каждую цифру. При помощи логарифмов сделать это намного легче. Логарифм 200 равен 2,301, а логарифм 100 – 2. Сумма логарифмов 200 и 100 составляет 4,301 (2,301+2). Если Вы возведёте 10 в степень 4,3, то получите не совсем точный ответ (19998,6), поскольку мы округлили логарифм 200. Очевидно, чем больше цифр в Вашей таблице, тем лучше.

Это не совсем удачный пример. Но если Вам нужно умножить 7329 на 8115, то зная логарифмы этих чисел (3,8650 и 3,9093 соответственно), выполнить данное вычисление Вам будет очень легко. Возведите 10 в степень 7,7743, и Вы узнаете правильный ответ – 59470282 (на самом деле 59474835, но, опять же, очень близко).

Каким образом это связано с логарифмической линейкой? Логарифмическая линейка представляет собой эффективную таблицу логарифмов, выполненную из дерева, пластика или металла. Отметки наносятся на поверхность на основании логарифма числа, однако обозначаются реальными цифрами, то есть расстояние между 0 и 1, к примеру, намного больше, чем расстояние между 8 и 9.

Давайте рассмотрим принцип пользования логарифмической линейкой на простом примере: 2х3. Сдвиньте шкалу С таким образом, чтобы единица оказалась над цифрой 2 на фиксированной шкале D. Затем установите движок на отметке 3 на шкале С. А теперь Вам нужно всего лишь взглянуть на цифру на фиксированной шкале D, чтобы получить ответ (6). Принцип пользования логарифмической линейкой очень легко понять, если Вы держите её в руках. Также Вы можете воспользоваться веб-симулятором, доступным по ссылке. Скриншот расчёта Вы можете увидеть ниже.

Если Вы имеете дело с большими числами, сначала уменьшите их в n-ное количество десятков раз, а после мысленно увеличьте во столько же полученный результат. К примеру, чтобы вычислить произведение чисел 20 и 30, Вам необходимо сначала уменьшить их в 10 раз, а после в 100 раз увеличить полученный результат.

Деление и прочие операции

Деление работает почти так же, однако основано на вычитании. Если Вы сдвинете шкалу С таким образом, чтобы цифра 3 оказалась над 6 на фиксированной шкале D, то сможете под 1 на шкале С увидеть ответ 2 (шкала D). Не запутаться в числах Вам поможет прозрачный пластиковый движок с тонкой линией посередине. В некоторых линейках даже есть небольшое увеличительное стекло, позволяющее лучше рассмотреть отметки на шкале.

Получение правильного ответа

В отличие от калькулятора, логарифмическая линейка, как правило, требует, чтобы Вы имели некоторое представление об ответе, чтобы интерпретировать результаты. Также Вы должны быть в состоянии увидеть разницу между, скажем, 7,3, 7,35 и 7,351. Вот почему чем больше, тем лучше.

Обычная логарифмическая линейка имеет длину около 25 сантиметров. Карманные линейки были короткими, но непрактичными. Также существовали огромные логарифмические линейки, предназначенные для использования в классе (длина некоторых из них достигала 2 метров 15 сантиметров). Для более точных вычислений инженеры пользовались линейками, по форме напоминающими цилиндр. Они были эквивалентом логарифмических линеек длиной до 10 метров.

Выше изображена логарифмическая линейка Отиса Кинга, которая соответствовала линейке длиной 170 сантиметров, однако легко умещалась в кармане. С виду она очень похожа на телескоп. На самом же деле это логарифмическая линейка со шкалой, нанесённой по спирали вокруг инструмента. На линейке Отиса Кинга было больше цифр, чем на обычной логарифмической линейке, однако вычисления, производимые с её помощью, зачастую оказывались не совсем точными.

Как начать коллекционировать логарифмические линейки и где их взять?

Многие думают, что логарифмические линейки трудно коллекционировать, однако на самом деле это довольно легко и недорого. В своё время они были широко распространены, однако после изобретения калькулятора и компьютера вмиг стали никому не нужны. Если постараться, то можно найти людей, у которых сохранились бывшие в употреблении или абсолютно новые логарифмические линейки.

Сайт eBay – место, где Вы, как показывают результаты поиска, сможете найти более 3000 логарифмических линеек. Также их можно приобрести по дешёвке в местных магазинах. Часто люди не понимают, для чего нужны логарифмические линейки, поэтому только рады избавиться от них. Кроме того, если люди узнают, что Вы коллекционер, они могут просто так подарить Вам логарифмические линейки, которые некогда принадлежали их дальним родственникам. Им будет приятно знать, что Вы их сохраните.

Если Вы решили купить логарифмическую линейку, убедитесь, что у неё работает шкала С и не запотевает прозрачный движок. Их ремонт или замена – весьма кропотливый труд. Также избегайте линеек со следами коррозии или выцветшими отметками. Их можно восстановить, но это требует немало сил и времени. В Интернете можно найти советы, как правильно чистить различные линейки.

Если Вы приобрели логарифмическую линейку, то должны помнить, что она, как и любая другая вещь, требует особого ухода. Чтобы её подвижные части хорошо работали, протирайте их полиролью для мебели (если линейка деревянная). Раньше люди смазывали железные логарифмические линейки вазелином. Важно также постоянно поддерживать логарифмическую линейку в чистоте и следить за тем, чтобы грязь не попадала под движок.

Также не следует оставлять линейку под прямыми солнечными лучами. Кроме того, старайтесь избегать использования мыла, воды и других веществ, которые могут повредить Вашу линейку.

Логарифмические линейки когда-то были своего рода компьютерами и, возможно, заменят нам современные ПК, когда придёт Апокалипсис.

Источник

Логическая линейка используется в основном для умножение и разделение, а также для таких функций, как экспоненты, корни, логарифмы, и тригонометрия, но обычно не для сложения или вычитания. Хотя линейка похожа по названию и внешнему виду на стандартную линейку, она не предназначена для измерения длины или рисования прямых линий.

Правила слайдов существуют в различных стилях и обычно имеют линейную или круговую форму со стандартизированным набором закончил отметки (шкалы), необходимые для выполнения математических вычислений. Скользящие правила, разработанные для специализированных областей, таких как авиация или финансы, обычно имеют дополнительные шкалы, которые помогают в расчетах, характерных для этих областей.

В простейшем случае каждое умножаемое число представлено длиной на скользящей линейке. Поскольку каждая линейка имеет логарифмическую шкалу, их можно выровнять, чтобы считать сумму логарифмов и, следовательно, вычислить произведение двух чисел.

Преподобный Уильям Отред и другие разработали логарифмическую линейку в 17 веке на основе новых работ по логарифмы к Джон Напье. До появления электронный калькулятор, это был наиболее часто используемый расчетный инструмент в науке и инженерное дело. [8] Использование логарифмических линейок продолжало расти в течение 1950-х и 1960-х годов, даже когда постепенно вводились компьютеры; но примерно в 1974 году портативный электронный научный калькулятор сделал их в значительной степени устаревшими. [9] [10] [11] [12] и большинство поставщиков ушли из бизнеса.

Содержание

Базовые концепты

В своей основной форме логарифмическая линейка использует два логарифмические шкалы для быстрого умножения и деления чисел. Эти стандартные операции могут занять много времени и привести к ошибкам, если они выполняются на бумаге. Более сложные правила слайдов позволяют выполнять другие вычисления, например квадратные корни, экспоненты, логарифмы, и тригонометрические функции.

Шкалы могут быть сгруппированы по декадам, которые представляют собой числа от 1 до 10 (т. Е. 10 п до 10 п + 1 ). Таким образом, шкалы с одной декадой C и D находятся в диапазоне от 1 до 10 по всей ширине логарифмической линейки, в то время как двойные декады A и B находятся в диапазоне от 1 до 100 по ширине логической линейки.

Как правило, математические вычисления выполняются путем совмещения метки на скользящей центральной полосе с меткой на одной из закрепленных полос и последующего наблюдения за относительным положением других отметок на полосах. Числа, совмещенные с метками, дают приблизительное значение товар, частное, или другой расчетный результат.

Пользователь определяет положение десятичной точки в результате на основе мысленной оценки. Научная нотация используется для отслеживания десятичной точки в более формальных вычислениях. Шаги сложения и вычитания в вычислениях обычно выполняются мысленно или на бумаге, а не на логической линейке.

Большинство правил слайдов состоит из трех частей:

Операция

Умножение

Операции могут «зашкаливать»; например, диаграмма выше показывает, что линейка не поместила цифру 7 на верхней шкале над любым числом на нижней шкале, поэтому она не дает никакого ответа для 2 × 7. В таких случаях пользователь может сдвинуть верхнюю шкалу влево до тех пор, пока ее правый индекс не выровняется с 2, эффективно разделив на 10 (вычитая полную длину шкалы С), а затем умножив на 7, как на иллюстрации ниже. :

Метод 1 прост для понимания, но влечет за собой потерю точности. Преимущество метода 3 состоит в том, что он включает только две шкалы.

Разделение

На рисунке ниже показано вычисление 5,5 / 2. 2 на верхней шкале помещается над 5,5 на нижней шкале. 1 на верхней шкале находится над частным 2,75. Существует более одного метода для выполнения деления, но метод, представленный здесь, имеет то преимущество, что конечный результат не может быть зашкаливающим, потому что у каждого есть выбор использовать 1 на любом конце.

Прочие операции

В дополнение к логарифмической шкале некоторые линейки имеют другие математические функции закодировано на других вспомогательных шкалах. Самыми популярными являются тригонометрический, обычно синус и касательная, десятичный логарифм (бревно 10 ) (для записи значения по шкале множителя), натуральный логарифм (ln) и экспоненциальный (е Икс ) напольные весы. Некоторые правила включают Пифагорейский («P») шкала для обозначения сторон треугольников и шкала для обозначения кругов. В других есть шкалы для расчета гиперболические функции. В линейных правилах шкалы и их маркировка в высшей степени стандартизированы, причем вариации обычно возникают только в отношении того, какие шкалы включены и в каком порядке:

А, Б	двухдесятичные логарифмические шкалы, две секции, каждая из которых составляет половину длины шкал C и D, используемые для нахождения квадратных корней и квадратов чисел
CD	десятичные логарифмические шкалы, отдельные секции одинаковой длины, используемые вместе для умножения и деления, и обычно одна из них сочетается с другой шкалой для других вычислений
K	трехдесятичная логарифмическая шкала, три секции, каждая из которых составляет одну треть длины шкал C и D, используемая для нахождения кубических корней и кубов чисел
CF, DF	«сложенные» версии гамм C и D, начинающиеся с π а не из единства; это удобно в двух случаях. Сначала, когда пользователь догадывается, что продукт будет близок к 10, но не уверен, будет ли оно немного меньше или немного больше 10, сложенные весы исключают возможность отклонения от шкалы. Во-вторых, если использовать начало π, а не квадратный корень из 10, умножение или деление на π (как это принято в научных и инженерных формулах) упрощается.
CI, DI, CIF, DIF	«перевернутые» шкалы, идущие справа налево, используются для упрощения 1 /Икс шаги
S	используется для поиска синусов и косинусов по шкале C (или D)
Т, Т1, Т2	используется для поиска тангенсов и котангенсов на шкалах C и CI (или D и DI)
СТ, СТО	используется для синусов и тангенсов малых углов и преобразования градус в радиан
L	линейная шкала, используемая вместе со шкалами C и D для нахождения логарифмов по основанию 10 и степеней 10
LLn	набор логарифмических шкал, используемых для нахождения логарифмов и экспонент чисел
Ln	линейная шкала, используемая вместе со шкалами C и D для нахождения натуральных (основание e) логарифмов и е Икс >

Как пользоваться логарифмической линейкой

Чешуя на передней и задней части Койфель и Эссер (K&E) 4081-3 логарифмическая линейка

Бинарное правило скольжения, созданное Гильсоном в 1931 году, выполняло функцию сложения и вычитания, ограниченную дробями. [13]

Корни и силы

Существуют шкалы с одной декадой (C и D), двойной декадой (A и B) и тройной декадой (K). Вычислить Икс 2 > , например, найдите x на шкале D и прочитайте его квадрат на шкале A. Обращение этого процесса позволяет находить квадратные корни, аналогично для степеней 3, 1/3, 2/3 и 3/2. Следует проявлять осторожность, когда основание x находится более чем в одном месте на своей шкале. Например, на шкале A две девятки; чтобы найти квадратный корень из девяти, используйте первый; второй дает квадратный корень из 90.

Чтобы извлечь кубический корень с помощью логарифмической линейки только со шкалами C / D и A / B, выровняйте 1 на курсоре B с базовым числом на шкале A (как всегда, стараясь различать нижнюю и верхнюю половины шкалы A шкала). Сдвиньте ползунок до тех пор, пока число на шкале D, которое находится напротив 1 на курсоре C, не станет таким же, как число на курсоре B, которое совпадает с числом основания на шкале A. (Примеры: A 8, B 2, C 1, D 2; A 27, B 3, C 1, D 3.)

Корни квадратных уравнений

Тригонометрия

Шкалы S, T и ST используются для триггерных функций и кратных триггерных функций для углов в градусах.

Многие слайд-линейки имеют шкалы S, T и ST, отмеченные градусами и минутами (например, некоторые модели Койффеля и Эссера (например, дуплексные 5-дюймовые модели Doric), правила типа Мангейма поздней модели Teledyne-Post). Так называемые децитриг вместо этого в моделях используются десятичные дроби градусов.

Логарифмы и экспоненты

Логарифмы и экспоненты по основанию 10 находятся с использованием линейной шкалы L. Некоторые правила слайдов имеют шкалу Ln, которая соответствует основанию e. Логарифмы к любому другому основанию можно вычислить, изменив порядок вычисления степеней числа. Например, значения log2 могут быть определены путем совмещения крайнего левого или крайнего правого 1 на шкале C с 2 на шкале LL2, нахождения числа, логарифм которого должен быть вычислен на соответствующей шкале LL, и считывания значения log2 на шкале C. шкала.

Сложение и вычитание

Правила слайдов обычно не используются для сложения и вычитания, но, тем не менее, это можно сделать, используя два разных метода. [14]

Первый метод сложения и вычитания C и D (или любых сопоставимых шкал) требует преобразования задачи в задачу деления. Кроме того, частное двух переменных плюс один, умноженное на делитель, равно их сумме:

Для вычитания частное двух переменных минус один, умноженное на делитель, равно их разности:

Этот метод похож на метод сложения / вычитания, используемый для высокоскоростных электронных схем с логарифмическая система счисления в специализированных компьютерных приложениях, таких как Гравитационная труба (ВИНОГРАД) суперкомпьютер и скрытые марковские модели.

Второй метод использует скользящую линейную шкалу L, доступную на некоторых моделях. Сложение и вычитание выполняются перемещением курсора влево (для вычитания) или вправо (для сложения) с последующим возвратом слайда на 0 для чтения результата.

Обобщения

Физический дизайн

Стандартные линейные правила

Ширина линейки указана исходя из номинальной ширины шкалы. Весы на наиболее распространенных «10-дюймовых» моделях на самом деле составляют 25 см, поскольку они были сделаны по метрическим стандартам, хотя некоторые правила предлагают слегка увеличенные масштабы, чтобы упростить манипуляции, когда результат выходит за пределы. Карманные правила обычно 5 дюймов. Модели шириной в пару метров предназначались для развешивания в учебных классах. [17]

Обычно деления обозначают шкалу с точностью до двух. значимые фигуры, а пользователь оценивает третью цифру. Некоторые линейки высокого класса имеют курсоры-лупы, которые упрощают просмотр маркировки. Такие курсоры могут эффективно удвоить точность показаний, позволяя использовать 10-дюймовую линейку так же, как 20-дюймовую модель.

Были разработаны различные другие удобства. Тригонометрические шкалы иногда имеют двойную маркировку: черный и красный, с дополнительными углами, так называемый «дармштадский» стиль. Дуплексные скользящие линейки часто дублируют некоторые шкалы на обратной стороне. Для большей точности весы часто «разделяют». [ требуется дальнейшее объяснение ]

Круговые линейки скольжения

Круглые скользящие линейки бывают двух основных типов: один с двумя курсорами, а другой со свободным блюдом и одним курсором. Версии с двумя курсорами выполняют умножение и деление, удерживая быстрый угол между курсорами, когда они вращаются вокруг шкалы. Версия с однократным курсором работает больше как стандартная логарифмическая линейка за счет соответствующего выравнивания шкал.

Круглые скользящие линейки механически более прочные и более плавные, но их точность выравнивания шкалы чувствительна к центрированию центральной оси; смещение на 0,1 мм от центра оси может привести к ошибке центровки 0,2 мм в худшем случае. Однако шарнир предотвращает появление царапин на лице и курсорах. Шкалы максимальной точности размещены на наружных кольцах. Вместо «разделенных» шкал, в высококлассных круговых правилах используются спиральные шкалы для более сложных операций, таких как шкалы журнала регистрации. У одного восьмидюймового кругового линейки премиум-класса была 50-дюймовая спиральная шкала бревна. Примерно в 1970 году недорогая модель от B.C.Boykin (модель 510) имела 20 шкал, в том числе 50-дюймовые шкалы C-D (умножение) и логарифмические шкалы. RotaRule имеет фрикционный тормоз для курсора.

Основными недостатками круговых логарифмических линейок являются сложность размещения фигур вдоль тарелки и ограниченное количество шкал. Еще один недостаток круговых скользящих линейок состоит в том, что менее важные шкалы расположены ближе к центру и имеют меньшую точность. Большинство студентов научились пользоваться линейкой на линейных линейках и не нашли причин для перехода.

В 1952 году швейцарская часовая компания Breitling представила наручные часы для пилотов со встроенной круговой линейкой, специально предназначенные для расчетов полета: Breitling Navitimer. Круговая линейка Navitimer, которую Breitling называет «навигационным компьютером», показала скорость полета, ставка / время набора высоты / спуска, время полета, расстояние и функции расхода топлива, а также километр—морская миля и функции преобразования количества топлива из галлонов в литры.

Российская круговая логарифмическая линейка, похожая на карманные часы, которая работает как логарифмическая линейка с одним курсором, поскольку две иглы соединены вместе

Линейка с двумя шкалами, встроенная в кольцо

Круглая логарифмическая линейка Пикетта с двумя курсорами. (Ширина 10,9 см / 4,25 дюйма) Реверс имеет дополнительную шкалу и один курсор.

Breitling Навитимер наручные часы с круговой линейкой

Лицевая сторона бойкина RotaRule Model 510

Задняя сторона модели Boykin RotaRule 510

Цилиндрические скользящие линейки

Есть два основных типа цилиндрических скользящих линейок: линейки со спиральной шкалой, такие как Фуллера и линейки. Отис Кинг и Линейка Bygrave, и те, у которых есть решетки, такие как Thacher и некоторые модели Loga. В любом случае преимуществом является гораздо более длинная шкала и, следовательно, потенциально более высокая точность, чем у прямой или круговой линейки.

Отис Кинг Модель К

Логарифмическая линейка Thacher, около 1890 г.

Материалы

Традиционно правила слайдов изготавливались из твердых пород дерева, таких как красное дерево или самшит, с курсорами из стекла и металла. По крайней мере, один высокоточный инструмент был сделан из стали.

В 1895 году японская фирма Hemmi начала изготавливать логарифмические линейки из бамбука, которые обладали стабильностью размеров, прочностью и естественной самосмазкой. Эти бамбуковые правила скольжения были представлены в Швеции в сентябре 1933 года. [19] и, наверное, чуть раньше в Германии. Весы были сделаны из целлулоид, пластик или окрашенный алюминий. Позже курсоры были акрил или же поликарбонаты скольжение по Тефлон подшипники.

На всех правилах слайдов премиум-класса были выгравированы числа и шкалы, которые затем были заполнены краской или другим предметом. смола. Окрашенные или отпечатанные линейки слайдов считались плохими, потому что маркировка могла стираться. Тем не менее Пикетт, вероятно, самый успешный в Америке [ нужна цитата ] Компания по производству слайд-линейки изготовила все напечатанные весы. Премиальные правила слайдов включали в себя умные фиксаторы, чтобы правило не развалилось случайно, и бамперы для защиты весов и курсора от трения о поверхность стола.

История

Логарифмическая линейка была изобретена примерно в 1620–1630 годах, вскоре после Джон Напье публикация концепции логарифм. В 1620 г. Эдмунд Гюнтер из Оксфорда разработали вычислительное устройство с единой логарифмической шкалой; с дополнительными измерительными инструментами его можно было использовать для умножения и деления. [20] В c. 1622, г. Уильям Отред Кембриджа объединил два портативных Правила Гюнтера сделать устройство, которое узнаваемо является современной логарифмической линейкой. [21] Отред был вовлечен в яростную полемику по поводу приоритет, со своим однокурсником Ричард Деламен и предыдущие претензии Wingate. Идеи Отреда были обнародованы только в публикациях его ученика Уильяма Форстера в 1632 и 1653 годах.

В 1677 году Генри Коггесхолл создал двухфутовую складную линейку для измерения древесины, названную Логарифмическая линейка Coggeshall, расширяя возможности использования логарифмической линейки за пределы математических исследований.

В 1722 году Уорнер ввел двух- и трехдесятилетнюю шкалу, а в 1755 году Эверард ввел перевернутую шкалу; логарифмическая линейка, содержащая все эти шкалы, обычно известна как «многофазное» правило.

В 1815 г. Питер Марк Роже изобрел логарифм логарифма, который включал шкалу, отображающую логарифм логарифма. Это позволяло пользователю напрямую выполнять вычисления с использованием корней и показателей степени. Это было особенно полезно для дробных степеней.

В 1821 г. Натаниэль Боудич, описанный в Американский практический навигатор «скользящее правило», которое содержало тригонометрические функции шкалы на фиксированной части и строку лог-синусов и лог-значений на ползунке, используемом для решения задач навигации.

В 1845 году Пол Кэмерон из Глазго представил морскую логарифмическую линейку, способную отвечать на вопросы навигации, в том числе прямое восхождение и склонение солнца и главных звезд. [22]

Современная форма

Более современная форма логарифмической линейки была создана в 1859 году французским лейтенантом артиллерии. Амеде Мангейм, «которому повезло, что его правление установила фирма с национальной репутацией и приняла его французская артиллерия». Примерно в это же время инженерия стала признанной профессией, что привело к широкому распространению логарифмической линейки в Европе, но не в Соединенных Штатах. Там цилиндрическая линейка Эдвина Тэчера утвердилась после 1881 года. Дуплексная линейка была изобретена Уильямом Коксом в 1891 году и была произведена Койфель и Эссер Ко. Нью-Йорка. [23] [24]

В 1920-е годы писатель и инженер Невил Шут Норвегия (он назвал свою автобиографию Логарифмическая линейка ) был Главный калькулятор по дизайну британцев R100 дирижабль для Vickers Ltd. с 1924 года. Для расчета напряжений для каждой поперечной рамы потребовались расчеты с помощью пары калькуляторы (люди), использующие цилиндрические скользящие линейки Фуллера в течение двух или трех месяцев. Одновременное уравнение содержало до семи неизвестных величин, на решение уходило около недели, и его приходилось повторять с другим выбором провисания проволоки, если предположение о том, какой из восьми радиальных проволок провисает, было неверным и один из проводов предполагал слабина не была слабиной. После нескольких месяцев работы, заполнившей около пятидесяти листов с расчетами истина открылась »(и) вызвала удовлетворение, почти равное религиозному опыту. [25]

Немецкий ученый-ракетчик Вернер фон Браун купил два Нестлер правила слайдов в 1930-е годы. Десять лет спустя он привез их с собой, когда после Второй мировой войны переехал в США, чтобы работать над американскими космическими проектами. За всю свою жизнь он никогда не использовал другую логарифмическую линейку. Он использовал своих двух птенцов, возглавляя НАСА программа, высадившая человека на Луну в июле 1969 года. [26]

Некоторые студенты-инженеры и инженеры носили десятидюймовые логарифмические линейки в поясных кобурах, что было обычным явлением в университетских городках даже в середине 1970-х годов. До появления карманного цифрового калькулятора студенты также могли придерживаться правила десяти или двадцати дюймов для точной работы дома или в офисе. [29] нося с собой пятидюймовую карманную логарифмическую линейку.

В 2004 году исследователи образования Дэвид Б. Шер и Дин С. Натаро разработали новый тип логарифмической линейки, основанный на протокаферез, алгоритм для быстрого вычисления продуктов, предшествующий логарифму. Однако практический интерес к созданию одного из них помимо первоначального прототипа был невелик. [30]

Специализированные калькуляторы

Правила слайдов часто были в разной степени специализированы для своей области использования, например, акцизных сборов, расчета пробных отпечатков, проектирования, навигации и т. Д., Но некоторые правила слайдов чрезвычайно специализированы для очень узких приложений. Например, в каталоге John Rabone & Sons 1892 г. перечислены «Измерительная лента и датчик для крупного рогатого скота», устройство для оценки веса коровы по ее измерениям.

Для фотографических приложений было много специализированных слайдов; например, актинограф из Хертер и Дриффилд представлял собой прибор из самшита, латуни и картона с двумя слайдами для оценки контакт от времени суток, времени года и широты.

Были изобретены специальные скользящие линейки для различных форм инженерии, бизнеса и банковского дела. У них часто были общие вычисления, прямо выраженные в виде специальных шкал, например, расчеты ссуды, оптимальные объемы закупок или конкретные инженерные уравнения. Например, Fisher Controls Компания распространила индивидуальные логарифмические линейки, адаптированные для решения уравнений, используемых для выбора промышленных клапанов регулирования расхода надлежащего размера. [31]

Правила скольжения пилотного шара использовались метеорологами в метеорологических службах для определения верхних скоростей ветра от восходящего пилотного шара, заполненного водородом или гелием. [32]

Во время Второй мировой войны бомбардиры и штурманы, которым требовались быстрые вычисления, часто использовали специальные правила скольжения. Одно из ведомств ВМС США разработало универсальную логарифмическую линейку «шасси» с алюминиевым корпусом и пластиковым курсором, в которую можно было поместить целлулоидные карты (напечатанные с обеих сторон) для специальных расчетов. Этот процесс был изобретен для расчета дальности полета, расхода топлива и высоты для самолетов, а затем адаптирован для многих других целей.

В E6-B круговая логарифмическая линейка, используемая пилотами и штурманами.

Круговые слайд-правила для оценки дат овуляции и фертильности известны как калькуляторы колес. [33]

Источник

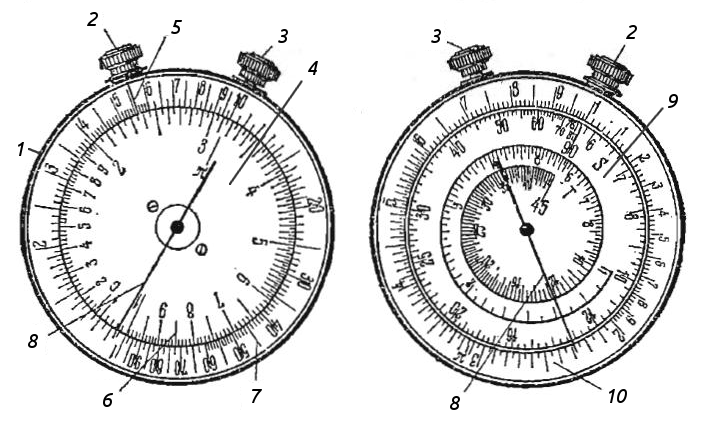
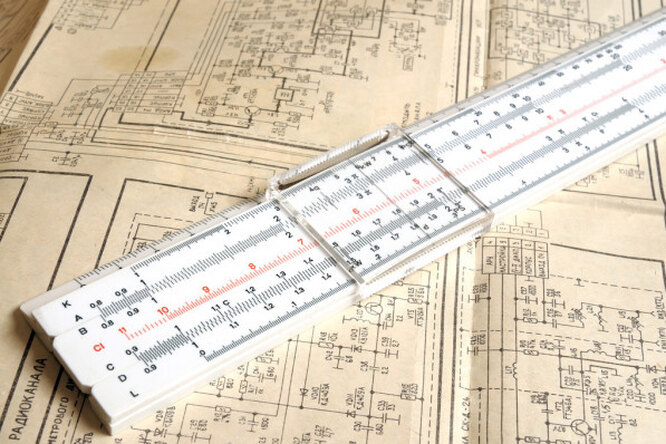
Как пользоваться логарифмической линейкой

Круговая логарифмическая линейка КЛ-1

Быстрые вычисления

Дюймы в сантиметры

Градусы Фарингейта в градусы Цельсия

Мили в километры

Время и расстояние от скорости

Инструкция к линейке

Круговая логарифмическая линейка “КЛ-1”

I. Умножение

II. Деление

III. Комбинированные действия

IV. Возведение в квадрат

V. Извлечение квадратного корня

VI. Нахождение тригонометрических функций угла

VII. Нахождение обратных тригонометрических функций

VIII. Вычисление площади круга

Линейка логарифмическая – забытое счетное устройство из прошлого?

Линейка логарифмическая: история

Устройство

Разновидности

Возможности

Как считать на логарифмической линейке

Актуальность

Что такое логарифмическая линейка и как ей правильно пользоваться

Уильям Отред — изобретатель логарифмической линейки

История изобретения

Споры об авторстве

Как пользоваться логарифмической линейкой

Сложение

Умножение

Логарифмическая линейка

Содержание

1. История создания логарифмической шкалы.

2. История создания логарифмической линейки.

3. Устройство логарифмической линейки.

4. Работа с логарифмической линейкой.

4.1. Умножение и деление.

4.2. Возведение в степень и извлечение корня.

4.3. Работа с логарифмами.

4.4. Тригонометрические расчеты.

5. Виды логарифмических линеек.

Логарифмическая линейка: история первого «компьютера» VXII века

Уильям Отред — изобретатель логарифмической линейки

История изобретения

Споры об авторстве

Как пользоваться логарифмической линейкой

Как пользоваться логарифмической линейкой?

Логарифмическая линейка

Конструкция логарифмической линейки

Как работает логарифмическая линейка?

Как считать логарифмической линейкой

Счётная логарифмическая линейка

Леонид Сергеевич Хренов Юлий Васильевич Визиров

Логарифмическая линейка

Василий Семёнович Кущенко

Логарифмическая линейка

Дмитрий Степанович Миков

Счётная логарифмическая линейка

Инструкция: Как пользоваться логарифмической линейкой в часах

Как пользоваться логарифмической линейкой

История логарифмической линейки

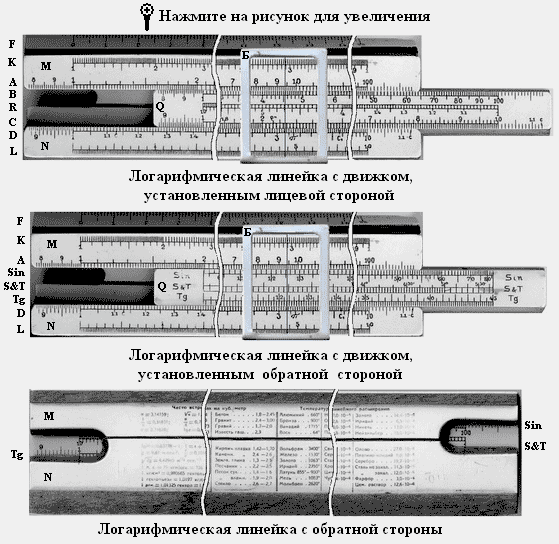
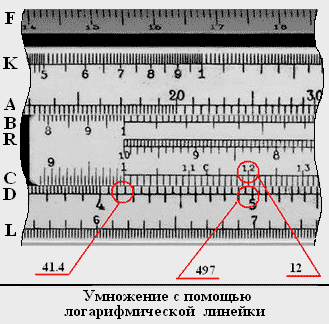
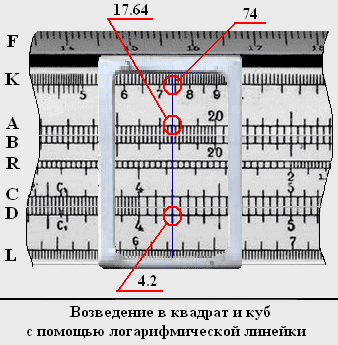
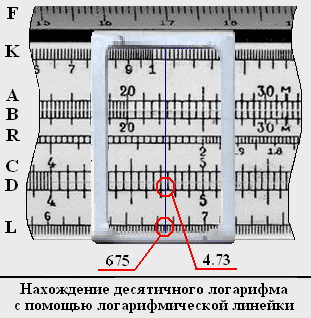
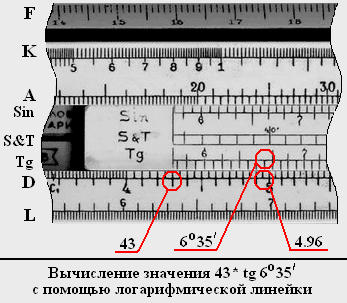
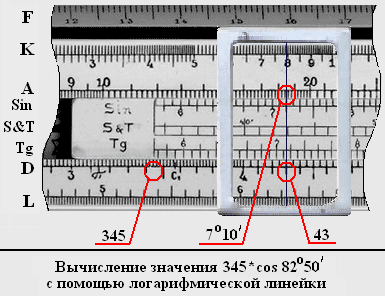
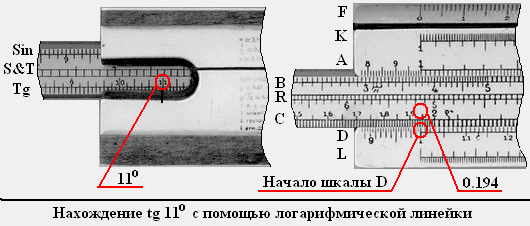
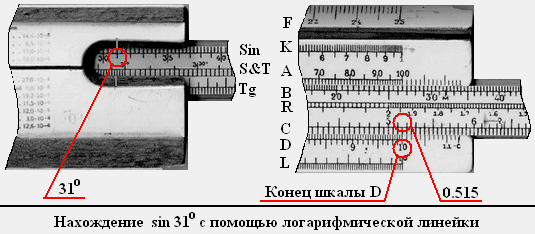
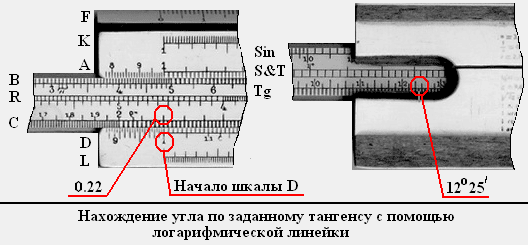
<img decoding="async" src="//l-stat.livejournal.net/img/userinfo_v8.svg" alt="Как пользоваться логарифмической линейкой" title="userinfo v8">masterok

Мастерок.жж.рф

Хочу все знать

Кто изобрел логарифмическую линейку?

Логарифмическая линейка: история первого «компьютера» VXII века

Логарифмическая линейка

Историческая справка

Устройство и принципы использования

Логарифмическая линейка в XXI веке

Виды линеек

Литература

Заключение

Логарифмическая линейка

Из Википедии — свободной энциклопедии

Логарифмическая линейка – аналог персональных компьютеров

Содержание

Базовые концепты

Операция

Леонид Сергеевич Хренов
Юлий Васильевич Визиров

masterok