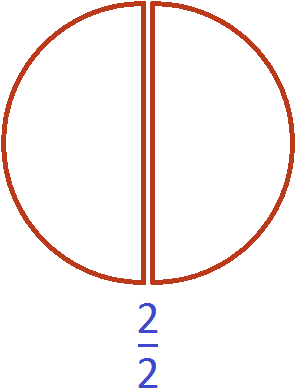
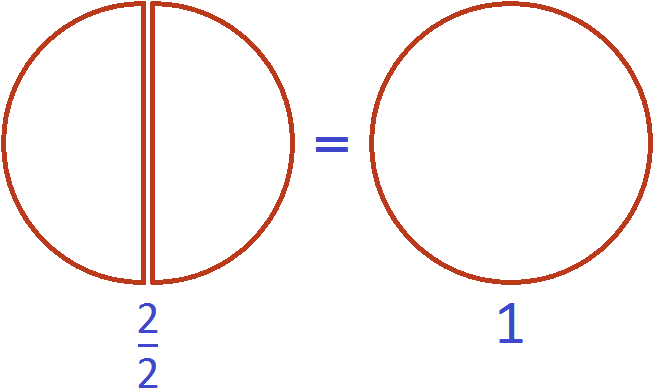
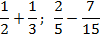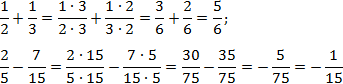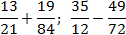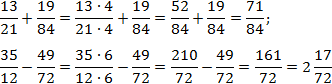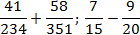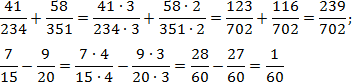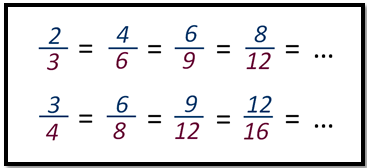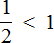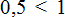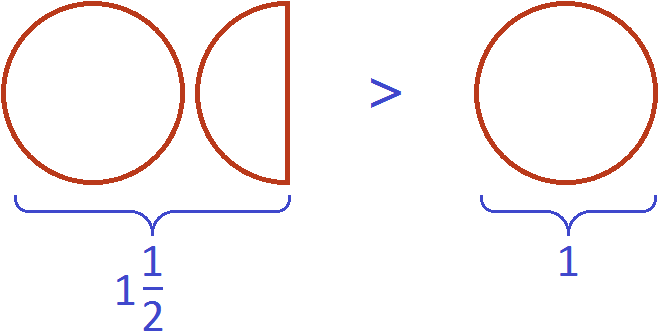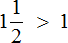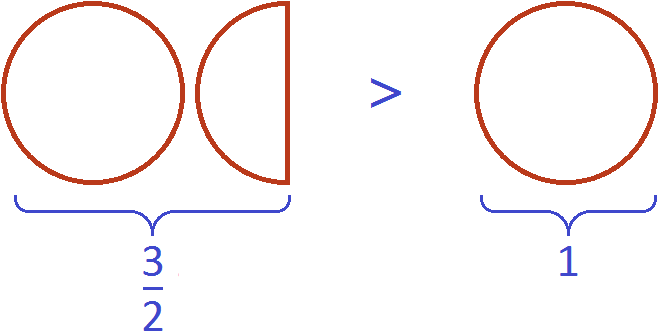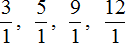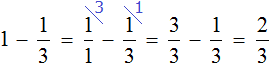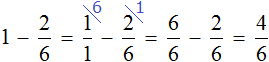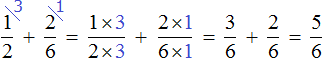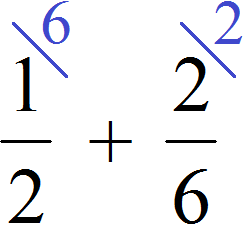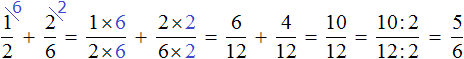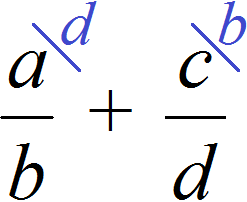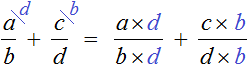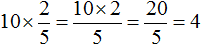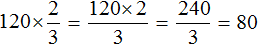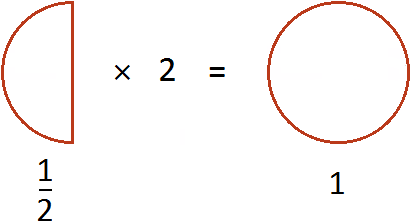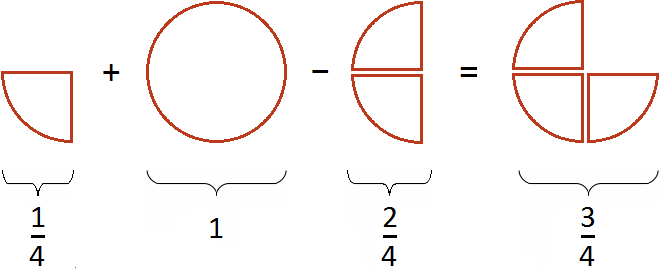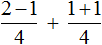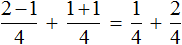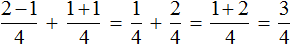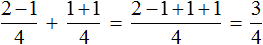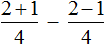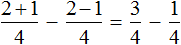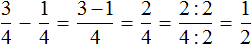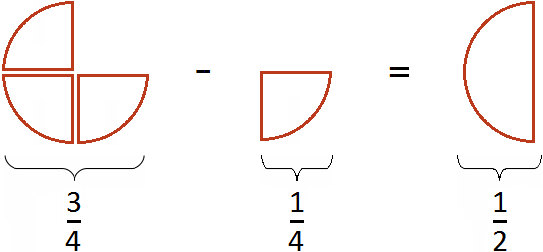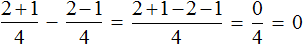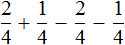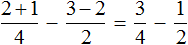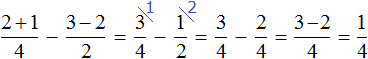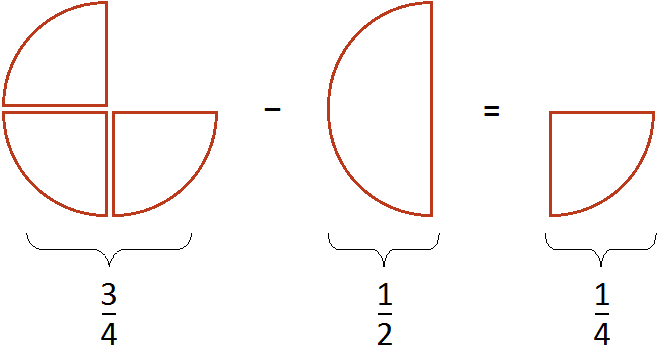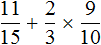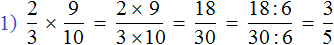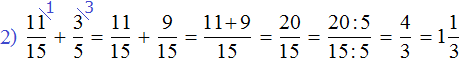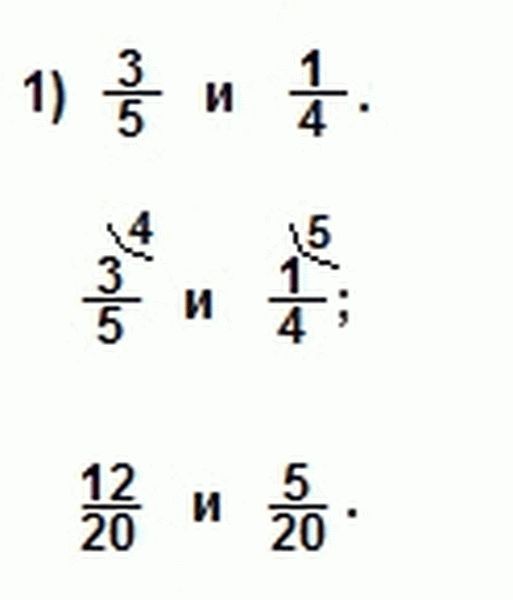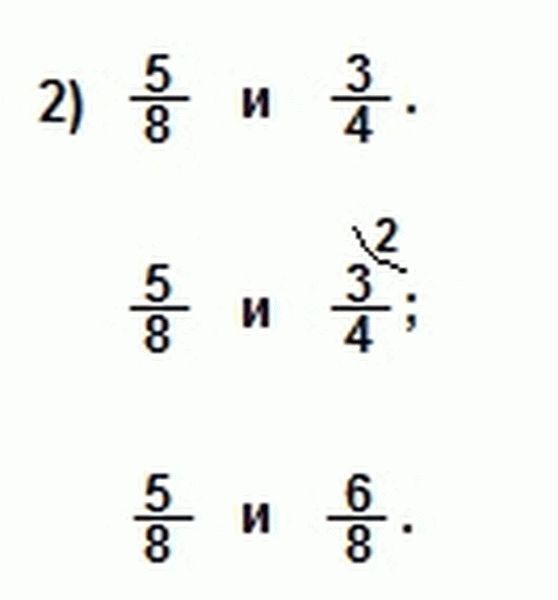Как привести дроби к общему знаменателю
Как привести дроби к общему знаменателю
Приведение дробей к общему знаменателю.
Для приведения дробей к общему знаменателю надо:
Примеры приведения дробей к общему знаменателю
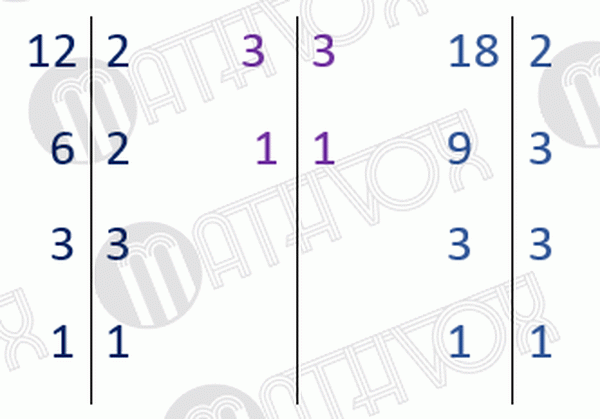
18/6 = 3 — дополнительный множитель первой дроби,
18/9 = 2 — дополнительный множитель второй дроби.
| 5 | = | 5·3 | = | 15 |
| 6 | 6·3 | 18 |
| 4 | = | 4·2 | = | 8 |
| 9 | 9·2 | 18 |
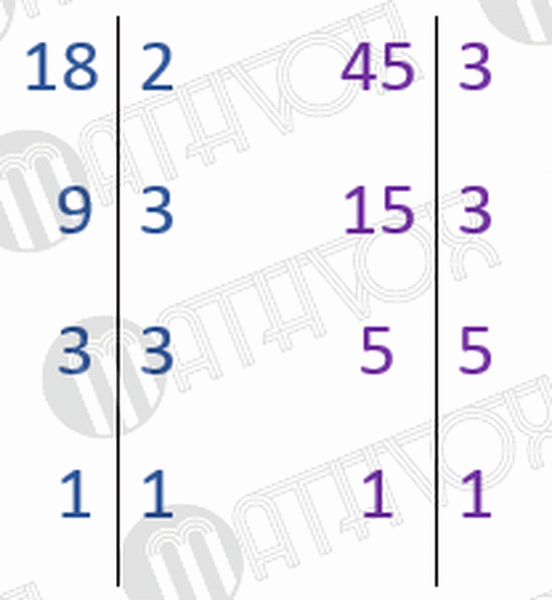
108/27 = 4 — дополнительный множитель первой дроби,
108/36 = 3 — дополнительный множитель второй дроби.
| 2 | = | 2·4 | = | 8 |
| 27 | 27·4 | 108 |
| 3 | = | 3·3 | = | 9 |
| 36 | 36·3 | 108 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
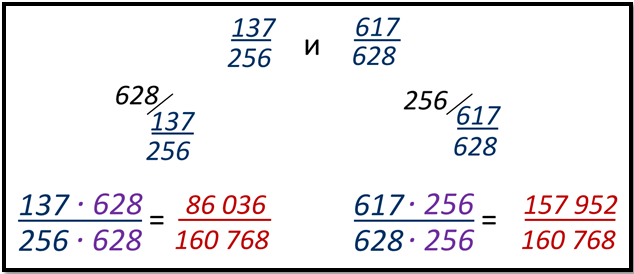
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
Задача. Найдите значения выражений:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Приведение дробей к общему знаменателю
Общий знаменатель обыкновенных дробей
Любые дроби с разными знаменателями в математике можно привести к одному и тому же общему знаменателю — заменить на равные им дроби с одинаковым знаменателем.
Есть два вида знаменателей:
Общий знаменатель — это число или выражение, которое является знаменателем для двух и более обыкновенных дробей.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Наименьший общий знаменатель — наименьшее общее кратное знаменателей данных дробей.
Производить данную операцию необходимо в ряде случаев.
Как привести дроби к общему знаменателю, алгоритм
Чтобы осуществить операцию приведения, необходимо применить основное свойство дробей: если числитель и знаменатель дроби умножить на одно и то же число, отличное от нуля, дробь не изменится. То есть если подобрать правильные множители, то можно привести знаменатели к одному и тому же числу. Искомые множители называют дополнительными.
Это объяснение лежит в основе общего правила приведения дробей.
Существует несколько способов привести дроби к общему или наименьшему общему знаменателю.
Умножение «крест-накрест»
Самый простой способ — умножение «крест-накрест». Применяется следующий пошаговый алгоритм:
Недостаток этого метода — в размерах вычислений. При умножении могут получиться большие числа, которыми тяжело оперировать.
Метод общих делителей
Иногда один из знаменателей дроби уже делится на другой без остатка. В таком случае нет нужды перемножать их, количество действий сокращается.
Этот метод хорош тем, что является более кратким вариантом умножения «крест-накрест». При этом его невозможно использовать при решении примеров, в которых числа в знаменателях не делятся друг на друга.
Метод наименьшего общего кратного
Суть приведения заключается в том, чтобы найти такое число, которое делится на каждый из знаменателей. К этому числу и необходимо привести знаменатели обеих дробей.
Наименьшее общее кратное (НОК) — это наименьшее число, на которое делится каждый из знаменателей. Обозначается он как НОК (a; b).
НОК (3; 4) = 12; НОК (8; 12) = 24.
Иногда найти НОК можно «на глаз», не выполняя дополнительных расчетов. К примеру, НОК (6; 9) = 18. Однако иногда на это может понадобиться больше времени. Описание примера таких вычислений приведено в примерах решения задач ниже.
Таким образом, основное преимущество это метода заключается в краткости вычислений. При этом его недостатком является сложность нахождения НОК в некоторых случаях.
Примеры задач с подробным решением
Задача
Решение
Для начала применим метод «крест-накрест». Тогда:
Получившуюся дробь можно сократить на 5:
Однако решение можно сократить, применив метод общих делителей. 15 делится на 5 без остатка. При таком делении дополнительным множителем для первой дроби будет число 3:
Задача
Решение
Решить эту задачу методом общих делителей невозможно, ведь 20 не делится без остатка на 15. При этом оба числа являются большими:
Вычисление методом «крест-накрест» будет слишком большим.
Оптимальным вариантом решения является метод наименьшего общего кратного.
\(НОК (15; 20) = 5\cdot3\cdot4=60\)
При делении 60 на знаменатели обеих дробей получаются дополнительные множители 4 и 3. Используем их для вычислений:
Общий знаменатель, понятие и определение.
Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.
Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.
Формула основного свойства рациональных чисел.
Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.
Наименьший общий знаменатель.
Что такое наименьший общий знаменатель?
Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:
Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.
У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2
Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2
Ответ: наименьший общий знаменатель будет равен 140.
Как привести дробь к общему знаменателю?
Нужно первую дробь \(\frac<1><20>\) домножить на 7, чтобы получить знаменатель 140.
Правила или алгоритм приведения дробей к общему знаменателю.
Алгоритм приведения дробей к наименьшему общему знаменателю:
Общий знаменатель для нескольких дробей.
Как найти общий знаменатель для нескольких дробей?
Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей \(\frac<2><11>, \frac<1><15>, \frac<3><22>\)
Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.
Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2
Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби \(\frac<2><11>, \frac<1><15>, \frac<3><22>\) к общему знаменатели равному 330.
Вопросы по теме:
Какой общий знаменатель у дробей \(\bf \frac<2><25>\) и \(\bf \frac<1><14>\)?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.
Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.
Это мы нашли наименьший общий знаменатель:
Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей \(\frac<2><25>\) и \(\frac<1><14>\) знаменателем может быть число 700, 1400 и т.д.
Приведение дробей к общему знаменателю.
Общий знаменатель и дополнительный множитель.
У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:
Пример разных знаменателей у дробей:
Как привести к общему знаменателю дроби?
У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.
Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.
Вторую дробь умножаем на дополнительный множитель 3.
Мы привели к общему знаменателю дроби:
Наименьший общий знаменатель.
Рассмотрим еще пример:
Приведем дроби \(\frac<5><8>\) и \(\frac<7><12>\) к общему знаменателю.
Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.
Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.
Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.
Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.
Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ сократить.
Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.
Например:
Приведите дроби \(\frac<1><4>\) и \(\frac<9><16>\) к наименьшему общему знаменателю.
Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:
Вопросы по теме:
Любые ли две дроби можно привести к одному общему знаменателю?
Ответ: да.
К какому знаменателю принято приводить дроби?
Ответ: к наименьшему общему знаменателю.
Пример №1:
Для дроби \(\frac<1><2>\) запишите равную дробь со знаменателем: а) 12 б) 18 в) 50?
Решение:
а) Число 2 нужно умножить на 6, чтобы получить 12. Следовательно, мы всю дробь умножаем на дополнительный множитель 6.
б) Число 2 нужно умножить на 9, чтобы получить 18. Следовательно, мы всю дробь умножаем на дополнительный множитель 9.
в) Число 2 нужно умножить на 25, чтобы получить 50. Следовательно мы всю дробь умножаем на дополнительный множитель 25.
Дроби. Приведение дробей к общему знаменателю.
Любые 2 дроби возможно привести к одинаковому знаменателю, либо, говоря другими словами, к общему знаменателю. Приведение дробей к общему знаменателю значит выразить дроби в одинаковых частях единицы с сохранением величины дроби.
Общим знаменателем дробей может стать каждое общее кратное знаменателей этих дробей (пример: произведение знаменателей). Он равен наименьшему общему кратному (НОК) знаменателей этих дробей. Дробь не изменится, если ее числитель и знаменатель умножать на одинаковое число, не равное нулю.
Зачем приводят дроби к общему знаменателю? Ниже приведены некоторые причины:
Чтобы привести дроби к общему знаменателю, необходимо:
Привести дроби 

1. Определим наименьшее общее кратное (НОК) знаменателей заданных дробей – это будет искомым наименьшим общим знаменателем:
НОЗ (наименьший общий знаменатель) = 12;
2. Разделим наименьший общий знаменатель на знаменатели заданных дробей, то есть найдем для каждой дроби дополнительный множитель:
дополнительный множитель для дроби 
дополнительный множитель для дроби 
3. Умножим числитель и знаменатель каждой дроби на дополнительный множитель:

Дроби приведены к общему знаменателю.
Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Приведение дробей к общему знаменателю
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Пример 1. Общий знаменатель
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
По правилу, сначала найдем НОК знаменателей дробей.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
Далее вычислим дополнительные множители для каждой дроби.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72
Основное свойство алгебраической дроби (продолжение)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На уроке продолжается тема предыдущего урока и более подробно рассматриваются методы приведения дробей к общему знаменателю с использованием основного свойства дроби. Умение приводить дроби к общему знаменателю является важнейшим для сложения и вычитания дробей, что будет рассмотрено на дальнейших уроках. Основной упор сделан на сложные случаи, в которых для приведения дробей к общему знаменателю требуется умение разложения многочленов на множители и нахождения наименьшего общего знаменателя для двух многочленов. В ходе изложения материала приводится большое количество примеров, что позволяет развить и наработать навыки обращения со сложными дробными выражениями. В конце урока делается анонс дальнейших тем и демонстрируется пример вычитания дробей с одинаковыми знаменателями.
Приведение дробей к общему знаменателю
Общий знаменатель обыкновенных дробей
Если обыкновенные дроби имеют одинаковые знаменатели, то про эти дроби говорят, что они имеют общий знаменатель. Например, дроби

имеют общий знаменатель 7.
Общий знаменатель — это число, которое является знаменателем для двух и более обыкновенных дробей.
Дроби, имеющие разные знаменатели, можно привести к общему знаменателю.
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это замена данных дробей, имеющих разные знаменатели, на равные им дроби, у которых одинаковые знаменатели.
Дроби можно привести либо просто к общему знаменателю, либо к наименьшему общему знаменателю.
Наименьший общий знаменатель — это наименьшее общее кратное знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю нужно:
Пример. Привести к общему знаменателю дроби 

24 : 8 = 3 (для 
24 : 12 = 2 (для 
Приведение к общему знаменателю можно записывать в более краткой форме, указывая дополнительный множитель рядом с числителем каждой дроби (сверху справа или сверху слева) и не записывая промежуточные вычисления:
К общему знаменателю можно привести и более простым способом, умножив члены первой дроби на знаменатель второй дроби, а члены второй дроби — на знаменатель первой.
Пример. Привести к общему знаменателю дроби 

В качестве общего знаменателя дробей можно взять произведение их знаменателей.
Приведение дробей к общему знаменателю используется при сложении, вычитании и сравнении дробей, у которых разные знаменатели.
Калькулятор приведения к общему знаменателю
Общий знаменатель дробей онлайн
Калькулятор приводит несколько дробей к общему знаменателю. Просто введите дроби и получите подробное решение и ответ. Можно вводить две, три дроби и более. Числители и знаменатели дробей должны быть натуральными числами.
Как привести дроби к общему знаменателю?
Чтобы выполнить с дробями такие операции, как сравнение, сложение и вычитание, дроби нужно привести к общему знаменателю.
Пример. Привести к общему знаменателю дроби и
Решение. Находим наименьшее общее кратное знаменателей дробей. НОК(12, 8) = 24. Это число и будет новым знаменателем.
Чтобы знаменатели обеих дробей стали равны 24, числитель и знаменатель первой дроби нужно домножить на 2 = 24:12, а числитель и знаменатель второй дроби — на 3 = 24:8.
Приводим к общему знаменателю первую дробь:
Приводим к общему знаменателю вторую дробь:
Общий знаменатель трёх дробей
Если к общему знаменателю требуется привести три дроби и более, то алгоритм действий в таком случае аналогичен алгоритму для двух дробей.
Чтобы разобраться лучше, рассмотрим пример.
Пример. Привести к общему знаменателю три дроби
и
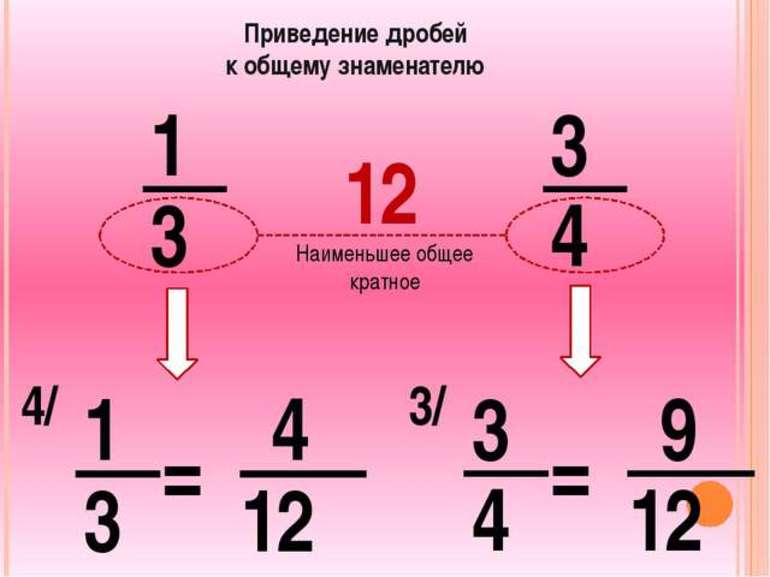
Решение. Сначала найдём наименьшее общее кратное знаменателей дробей. Число 12 делится на знаменатели всех дробей, и это наименьшее такое число. Поэтому НОК(3, 4, 6) = 12. Число 12 будет новым знаменателем.
Чтобы знаменатели дробей стали равны 12, числитель и знаменатель первой дроби нужно домножить на 4 = 12:3, числитель и знаменатель второй дроби — на 3 = 12:4, а числитель и знаменатель третьей дроби — на 2 = 12:6.
Приводим дроби к общему знаменателю и получаем:
Всё — дроби приведены! Пожалуй, самая большая сложность — правильно найти (или угадать) число, которое будет новым знаменателем.
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю – это замена дробей с разными знаменателями на равные им по величине дроби, но имеющие одинаковые знаменатели.
В данной публикации мы рассмотрим, каким образом выполняется данная операция. Также разберем практические примеры для лучшего понимания изложенного материала.
Алгоритм приведения дробей к общему знаменателю
Для того, чтобы привести дроби к наименьшему общему знаменателю, выполняем следующие шаги:
Примеры
Пример 1
к наименьшему общему знаменателю.
Решение
Сократить данные дроби не получится, поэтому сразу переходим к шагу 2 описанного выше алгоритма.
Наименьшее общее кратное (НОК) знаменателей обеих дробей – это число 48.
Дополнительный множитель: для первой дроби со знаменателем 12 равняется 4 (48:12), для второй дроби со знаменателем 16 равен 3 (48:16).
Теперь числитель и знаменатель каждой дроби умножаем на найденный для них дополнительный множитель.
Приведение дробей к общему знаменателю
Цель урока: закрепить основное свойство дроби, научить учащихся применять это свойство на практике приведения к общему знаменателю дробей, показать связь между приведением дробей к общему знаменателю и НОКом знаменателей дробей.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний
Учитель фронтально опрашивает учащихся о основном свойстве дроби. Вспоминают понятие НОКа и способы нахождения НОКа двух чисел:
Поможет нам разобраться с этой темой основное свойство дроби, которое, напомню, звучит следующим образом:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Так, например, по основному свойству дробь 2/3 можно привести к знаменателю 6, умножив и числитель, и знаменатель на 2. Эту дробь можно привести и к знаменателю 9, и 12, и к любому другому числу, кратному 3.
Напомним, что дроби можно приводить только к тем знаменателям, которые кратны исходным.
Ученики по очереди называют числа, к которым можно привести знаменатель дроби ¾.
Дробь ¾ можно привести к знаменателю 4, 8, 12 и к любому другому числу, кратному 4.
Учитель обращает внимание учеников, что можно обе дроби привести к знаменателю 12.
III. Изучение нового материала
Говорят, можно 2/3 и ¾ можно привести к общему знаменателю.
То есть если у нас есть две дроби с разными знаменателями, мы можем сделать так, чтобы знаменатели стали одинаковыми.
Приведение к общему знаменателю понадобится для сложения и вычитания обыкновенных дробей. Кроме того, сравнивать дроби с одинаковыми знаменателями очень просто.
Приведем к общему знаменателю дроби 11/12 и 17/18.
Сначала нам нужно найти такое число, которое делится на каждый из знаменателей.
Учащиеся называют свои варианты чисел.
Таких чисел очень много: 36, 72, 108 и так далее.
Затем приводим к этому числу знаменатели обеих дробей.
То есть дроби можно привести к одинаковому знаменателю 36, 72, 108, 144 и так далее. Удобнее всего выбирать наименьший из возможных общих знаменателей, так как объем вычислений в этом случае будет минимальным.
11/12=33/36. Чтобы привести 11/12 к знаменателю 36, умножим числитель и знаменатель на 3.
Кстати, число, на которое мы умножаем числитель и знаменатель, называется «дополнительным множителем».
11/12=132/144. Чтобы привести 11/12 к знаменателю 144, умножим числитель и знаменатель на 12. А это немного сложнее, чем умножать на 3.
17/18=34/36. Чтобы привести 17/18 к знаменателю 36, умножим числитель и знаменатель на 2.
17/18=136/144. Чтобы привести 17/18 к знаменателю 144, умножим числитель и знаменатель на 8. Задумались? Поэтому не усложняйте сами себе задачу. Выбирайте наименьший общий знаменатель.
Ученики делают вывод о рациональности приведения дробей к наименьшему общему знаменателю.
Для чисел 12 и 18 число 36 будет наименьшим общим кратным.
IV.Закрепление и практическое применение знаний
В математике существует много способов нахождения общего кратного чисел, а значит общего знаменателя для дробей.
Поэтому, если перед вами стоит задача приведения дробей к общему знаменателю, не торопитесь. Правильно выбранный способ может сократить ваше решение.
Приведем 7/12 и 5/48 к общему знаменателю. Вначале внимательно посмотрите на знаменатели дробей. Возможно, один из них делится на другой.
Ученики делают вывод, то знаменатель 48 делится на 12.
В этом случае дробь с большим знаменателем вообще не надо ни на что умножать. 48 и будет общим знаменателем обеих дробей. А число, полученное в результате деления 48 на 12, будет дополнительным множителем для дроби с меньшим знаменателем.
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он только в случае, когда один знаменатель делится на другой.
Существует способ, который работает для любых дробей. Суть способа заключается в нахождении наименьшего общего кратного знаменателей. Этот способ используется чаще всего.
Приведем к общему знаменателю дроби 7/410 и 5/861.
Для начала найдём НОК чисел 410 и 861.
Разложим эти числа на простые множители. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь быстро раскладывать на простые множители. Главное — помнить признаки делимости и иметь под рукой таблицу простых чисел.
Теперь записываем все множители одного из чисел, например числа 861. Потом добавляем к ним недостающие множители из разложения другого числа. В этом примере в разложении числа 410 три множителя: 2, 5 и 41. Множитель 41 уже есть в записи, а множителей 2 и 5 нет. Эти недостающие множители мы и добавим к выписанным множителям числа 861.
Наименьшее общее кратное чисел 410 и 861 равно 8610.
Теперь найдем дополнительный множитель для дроби со знаменателем 410. Для этого 8610 делим на 410. Получим 21.
Теперь найдем дополнительный множитель для дроби со знаменателем 861. Для этого 8610 делим на 861. Получим 10.
Последний этап — умножение дробей на дополнительные множители.
Если вам сложно раскладывать числа на множители, находить наименьший общий знаменатель, то следующий способ для вас.
Приведём к общему знаменателю 3/10 и 5/6.
Для этого умножаем первую дробь на знаменатель второй дроби.
А вторую — на знаменатель первой.
В результате знаменатели обеих дробей стали равными произведению исходных знаменателей.
Этот способ простой для понимания. Но приготовьтесь много считать, если используете этот способ для дробей с большими числами в числителе и знаменателе.
Учитель вместе с учениками проговаривают все возможные способы приведения, все достоинства и недостатки.
№ 275, 278, 283.
V. Подведение итогов урока. Рефлексия
Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.
Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
VI. Домашнее задание
§2, п. 10, № 299, 300.
Общий знаменатель
Самый простой способ, как привести дробь к общему знаменателю, — верхнюю и нижнюю части первой дроби умножить на значение в знаменателе второй, а верхнюю и нижнюю часть второго дробного числа — на значение в знаменателе первой. Проверочное правило, действующее в этом случае: дробь не меняется, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Даны две дроби: 3/13 и 3/7. После выполнения необходимых действий получится: 3/13*7 = 21/91, 3/7*13 =39/91.
Общий знаменатель (ОЗ) — это любое натуральное число, которое является всеобщим кратным всех данных дробей. Иными словами, это значит, что ОЗ может быть любое число из натуральных, которое обязательно будет делиться на знаменатель каждого дробного числа. Допустим, есть две обычных дробных соотношения 4/8 и 5/10. ОЗ в этом случае может быть любым значением, кратным 8 и 10. А конкретно, это значения: 80, 160, 240, 320, 400 и так далее.
Дано 3 дробных значения: 1/5, 3/10 и 9/15. Вопрос: может ли ОЗ быть числом 330? Ответ: да, потому что оно делится на знаменатель каждого соотношения без остатка: 330/5 = 66, 330/10 = 33, 330/15 = 22.
НОЗ и НОК
При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.
Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.
Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:
НОК (16, 6) =8*2*3= 48.
Число 48 и есть искомый НОЗ.
Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:
Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:
Примеры с несколькими дробями
Правило поиска ОЗ и НОЗ действует также и в отношении нескольких дробных чисел в ряде. Есть три значения: 3/9, 8/11 и 10/12. Для того чтобы переводить их, нужно совершать те же действия, которые представлены в правиле:
НОК (9; 11) = 99; НОК (99; 12) = 39; НОК (9; 11; 12) = 396;
396/9 = 44; 396/11 = 36; 396/12 = 33;
3*44/9*44 = 132/396; 8*36/11*36 =288/396; 10*33/12*33 =330/396;
Приводить дробные соотношения к ОЗ требуется во многих случаях. Вычисление этой величины необходимо, чтобы получить разность дробей, провести их сложение, умножение или деление, а также при решении задач на доли и проценты, так как процентные соотношения — это обыкновенные выражения, которые содержат дробные соотношения.
Приведение дробей к общему знаменателю
Вы будете перенаправлены на Автор24
Как приводить дроби к общему знаменателю
Если у обыкновенных дробей одинаковые знаменатели, то говорят, что эти дроби приведены к общему знаменателю.
Если у дробей знаменатели не одинаковые, то их можно свести к общему знаменателю. Для этого необходимо умножить их числители и знаменатели на определенные дополнительные множители.
Решение.
Таким образом, приведением дробей к общему знаменателю называют умножение числителя и знаменателя данных дробей на дополнительные множители, которые в результате позволяют получить дроби с одинаковыми знаменателями.
Общий знаменатель
Любое положительное общее кратное всех знаменателей некоторого набора дробей называют общим знаменателем.
Другими словами, общий знаменатель заданных обыкновенных дробей – любое натуральное число, которое можно разделить на все знаменатели заданных дробей.
Из определения вытекает бесконечное множество общих знаменателей данного набора дробей.
Решение.
Готовые работы на аналогичную тему
Решение.
Наименьший общий знаменатель
Среди всех общих знаменателей заданных дробей можно выделить наименьшее натуральное число, которое называют наименьшим общим знаменателем.
Т.к. НОК – наименьший положительный общий делитель данного набора чисел, то НОК знаменателей заданных дробей является наименьшим общим знаменателем данных дробей.
Следовательно, чтобы найти наименьший общий знаменатель дробей, нужно найти НОК знаменателей этих дробей.
Решение.
$НОК(15, 18)=2\cdot 3\cdot 3\cdot 5=90$.
Правило приведения дробей к наименьшему общему знаменателю
Чаще всего при решении задач алгебры, геометрии, физики и т.п. принято обыкновенные дроби приводить к наименьшему общему знаменателю, а не к любому общему знаменателю.
Алгоритм:
Решение.
Воспользуемся алгоритмом приведения дробей к наименьшему общему знаменателю.
$НОК(16, 22)=2\cdot 2\cdot 2\cdot 2\cdot 11=176$.
Вычислим дополнительные множители для каждой дроби:
Иногда для того, чтобы находить наименьший общий знаменатель, нужно провести ряд трудоемких вычислений, что может не оправдывать цель решения задачи. В таком случае можно воспользоваться наиболее простым способ – свести дроби к общему знаменателю, который представляет собой произведение знаменателей данных дробей.
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 08.06.2022
Урок 10 Бесплатно Приведение дробей к общему знаменателю
В этом уроке мы с вами научимся приводить дроби к одинаковому знаменателю. Это очень полезные приёмы, которые пригодятся в дальнейшем даже на экзамене в 9 классе. Поэтому будьте внимательны и изучайте материал, ничего не пропуская!
Приведение дробей к общему знаменателю
Умножим числитель и знаменатель дроби \(\mathbf<\frac<3><4>>\) на одно и то же число 2. Получим равную ей дробь \(\mathbf<\frac<6><8>>\), т.е. \(\mathbf<\frac<3> <4>= \frac<6><8>>\).
Говорят, что мы привели дробь \(\mathbf<\frac<3><4>>\) к новому знаменателю 8.
Дробь можно привести к любому знаменателю, кратному знаменателю этой дроби.
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.
При приведении дроби к новому знаменателю ее числитель и знаменатель умножают на дополнительный множитель.
Пример 1
Приведем дробь \(\mathbf<\frac<4><5>>\) к знаменателю 20
Решение:
Число 20 кратно 5, так как 20 : 5 = 4
Дополнительным множителем является число 4.
Умножив числитель и знаменатель дроби на 4, получим \(\mathbf<\frac<4> <5>= \frac<4\cdot4> <5\cdot4>= \frac<16><20>>\)
Любые две дроби можно привести к одному и тому же знаменателю, или иначе, к общему знаменателю.
Пример 2
А) \(\mathbf<\frac<7><15>>\) к знаменателю 60
Б) \(\mathbf<\frac<4><9>>\) к знаменателю 27
В) \(\mathbf<\frac<5><7>>\) к знаменателю 42
Г) \(\mathbf<\frac<6><11>>\) к знаменателю 44
Решение:
Пример 3
Решение:
У меня есть дополнительная информация к этой части урока!
Понятие общего знаменателя очень часто используется при решении математических задач.
Так как дроби отражают части чего-то целого, то приведение их к общему знаменателю позволяет сравнить эти части.
Таким образом мы узнаем, какая из них меньше или больше, а дальше сможем сделать решение задачи или сразу дать ответ на поставленный вопрос.
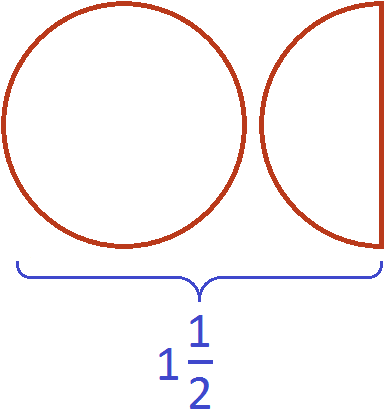
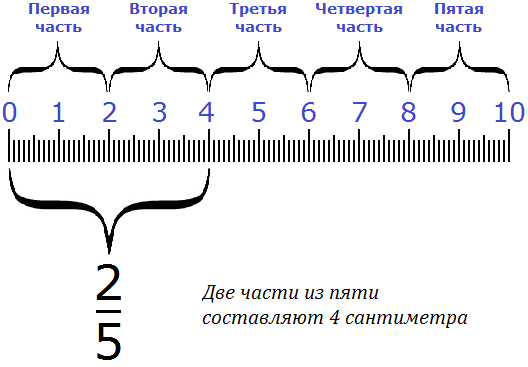
Например, если мы захотим сравнить половину яблока и две трети яблока, в ход пойдёт сравнение двух дробей: \(\mathbf<\frac<1><2>>\) и \(\mathbf<\frac<2><3>>\)
После того как мы приведём их к общему знаменателю, получим:
Отсюда уже видно, что две трети яблока будут больше, чем его половина. Общий знаменатель очень полезен в данном случае.
Пройти тест и получить оценку можно после входа или регистрации
Приведение дробей к наименьшему общему знаменателю
Общим знаменателем дробей может быть любое общее кратное их знаменателей (например, произведение знаменателей).
Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример 1
Приведем к наименьшему общему знаменателю дроби \(\mathbf<\frac<3><4>>\) и \(\mathbf<\frac<5><6>>\)
Решение:
Наименьшим общим кратным чисел 4 и 6 является 12
Чтобы привести дробь \(\mathbf<\frac<3><4>>\) к знаменателю 12, надо умножить числитель и знаменатель этой дроби на дополнительный множитель 3 (12 : 4 = 3)
Чтобы привести дробь \(\mathbf<\frac<5><6>>\) к знаменателю 12, надо числитель и знаменатель этой дроби умножить на дополнительный множитель 2 (12 : 6 = 2)
Чтобы привести дроби к наименьшему общему знаменателю, надо:
В сложных случаях наименьший общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Пример 2
Приведем дроби \(\mathbf<\frac<11><60>>\) и \(\mathbf<\frac<31><168>>\) к наименьшему общему знаменателю.
Решение:
Разложим знаменатели данных дробей на простые множители:
Дополнительными множителями для дроби \(\mathbf<\frac<11><60>>\) является произведение \(\mathbf<2\cdot7>\), т.е. тех множителей, которые надо добавить к разложению числа 60, чтобы получить разложение общего знаменателя 840.
Для дроби \(\mathbf<\frac<31><168>>\) таким же способом находим дополнительный множитель 5.
Пример 3
Приведите к наименьшему общему знаменателю дроби:
Приведение дроби к наименьшему общему знаменателю
Время чтения: 12 минут
Основное определение понятия общего знаменателя
Общий знаменатель значения — это любое из положительных данных числа, которое является кратным для всех значений дробей.
Иными словами, можно сказать, что общим знаменателем дроби, будет характеризоваться натуральное простое числовое значение. Оно должно делиться без остатка на все значения знаменателей данных дробей.
Натуральные числа имеют свойство бесконечности и поэтому ряд обыкновенных дробных значений имеет характерное множество общих значений знаменателя. Чтобы определить общий знаменатель для дроби, нужно применить его основное определение.
Рассмотрим два значения дробных выражений: 1 /6 и 3 /5
Общим дробным знаменателем будет являться любое число с положительным значением. Оно должно быть кратным значениям 6 и 5.
Перечислим подходящие значения: 30,35,65,95,125,155,185,215 и так далее.
Пример решения задачи данного типа: Зададим для решения три дробных значения: 1 /3 21 /6 5 /12.
Их необходимо проанализировать и привести к общему знаменателю, который равняется 150.
Для этого нужно выяснить, делится ли 150 на все числовые знаменатели дроби и является для них кратным числом.
Это значит, что 150 должно без остаточного значения делиться на 3,6,12.
Составляем выражения и проводим вычисления: 150/3=50; 150/6=25; 150/12=12,5.
При делении на 12 получается остаточное значение.
Из этого следует, что число 150 не будет являтся общим кратным знаменателем, для заданных дробей.
Наименьший общий знаменатель дробей
Данное определение звучит следующим образом: минимальное значение числа, на которое можно разделить знаменатель дроби, обязательно без остаточного значения.
Аббревиатура данного значения, выглядит как НОК.
В определенном перечне числовых значений, которые являются общими знаменателями данных дробей, будет иметь место наименьшее простое значение. Оно будет характеризоваться, как наименьший общий знаменатель. Сформулируем определение наименьшего общего знаменателя данных дробей.
Как правильно определить наименьший общий знаменатель числа дроби?
Так как НОК, будет иметь значение наименьшего положительного общего делителя данного набора чисел. Тогда НОК знаменателей любых дробей, представлен, как минимальный общий знаменатель дроби.
Из этого следует, что определение наименьшего знаменателя дроби, будет сводиться к определению НОК знаменателя дроби.
Рассмотрим данное правило на примере решения.
Задано два значения дроби: 3 /10 и 277 /28
Знаменатели дробей равняются 10 и 28 соответственно.
Наименьший знаменатель будет определяться как НОК чисел 10 и 28.
Разложим числа на простые множители: 10=2*5, 28=2*2*7, следовательно, НОК (15 и 28)=2*2*5*7=140.
Ответ задачи: 140.
Нет времени решать самому?
Наши эксперты помогут!
Приведение дробей к наименьшему общему знаменателю
Когда простые обыкновенные дроби, имеют одинаковые по значению знаменатели, то это характеризуется как дроби приведены к общему знаменателю.
Например: значения 45 /76 и 143 /76 приведены к общему знаменателю, числу 76. Рассмотрим еще несколько дробей. Рассмотрим еще несколько дробей 1 /3, 3 /3, 17 /3 и 1000 /3.
Все эти значения приведены к общему знаменателю 3.
В случае, если знаменатели дробных чисел, являются разными по значениям и не равны друг другу. Можно их привести к общему числовому знаменателю. Для этого значение числителя и знаменателя данных значений перемножим с дополнительным множителем.
Например: 2 /5 и 7 /4 — эти дроби имеют разные знаменатели, поэтому воспользуемся приведение к общему знаменателю, при помощи дополнительных множителей, а именно 4 и 5.
Теперь можно сформулировать определение, приведение дробей к общему знаменателю.
Приведение дробей к знаменателю одинаковых значений – это вычислительный процесс, который включает в себя: умножение числителей и знаменателей любых значений дробей на определенные значения дополнительных множителей, чтобы результаты проведенных вычислений получились дроби с одинаковыми знаменателями.
В математике существует правило, которое помогает привести дроби к общему наименьшему знаменателю.
Данное правило включает в себя три основных пункта.
Принцип приведения дробного значения к наименьшему общему знаменателю:
Примеры решения задач, используя приведение к наименьшему знаменателю.
Пример №1:
Нужно привести к наименьшему знаменателю следующие дроби: 5 /14 и 7 /18
Для решения применим алгоритм решения, рассмотренный в вышеприведенном пункте.
Для начала определим наименьшее значение общего знаменателя, который равен минимальному и кратному числу 14 и 18.
Разложим значения знаменателей на множители: 14=2*7, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=126. Следующим шагом, будет вычисление дополнительных множителей. С их помощью приведем дробные значения 5 /14 и 7 /18 будут приведены к числу 126. Дробному значению 5 /14 дополнительный множитель будет равняться 126/14=9. Для значения второй дроби равной 7 /18 аналогичный множитель будет равняться 129/18=7.
Числители и знаменатели дробей перемножаем на дополнительный множитель 9 и 7 соответственно.
Записываем следующие выражения:
Итоги проведенных вычислений: заданные дроби 5 /14 и 7 /18 приведены к общему знаменателю. Итоговое значение выражения: 45 /26 и 49 /126.
Пример №2:
Нужно привести к наименьшему знаменателю следующие дроби: 3 /12 и 5 /18. В этом примере, также применим алгоритм решения, состоящий из трех главным действий.
Используя алгоритм решения, определим наименьшее значение общего знаменателя, который равен самому минимальному значению и кратному числам 12 и 18.
Данные значений дробей, нужно перемножить на дополнительный числовой множитель равный числам 9 и 7 соответственно. Подставим эти данные и вычислим составленные выражения.
Записываем следующие выражения:
Итоги проведенных вычислений: заданные дроби 5 /14 и 7 /18 не приведены к общему знаменателю. Окончательное значение выражения 27 /108 и 35 /126 и из этого следует, что знаменатели разные.
Ответ: значение 216 не будет являться наименьшим общим знаменателем.
Аналогичным способом, используя алгоритм решения можно определить значение наименьшего знаменателя трех и более дробных значений.
Дополнительные сведения о дробях
В этом уроке мы коснёмся тех моментов, о которых не упоминали при изучении дробей, посчитав что на первых порах они создают трудности для обучения.
Правильные и неправильные дроби
В самом начале своего пути при изучении дробей мы узнали, что правильная дробь — это та дробь, у которой числитель меньше знаменателя.
В школьной литературе можно встретить другое определение правильной дроби. Выглядит оно следующим образом:
Правильная дробь всегда меньше единицы.
Как понять данное определение? Дробь сама по себе указывает на то, что какой-либо объект разделен на несколько частей. И это всегда один единственный объект. Под единицей именно это и подразумевается.
Например, пусть у нас имеется одна пицца:
В данном случае она и является единицей.
Если мы отрежем от этой пиццы половину, то есть 
В этом и заключается суть фразы «правильная дробь всегда меньше единицы».
Наша половинка пиццы является дробью 
Это выражение можно доказать. Если мы вычислим дробь 
На координатной прямой можно увидеть, как располагаются эти числа:
Видно, что рациональное число 0,5 располагается левее, чем 1. А мы помним, что чем левее число располагается на координатной прямой, тем оно меньше.
С неправильными дробями всё было наоборот. Неправильной дробью мы назвали ту дробь, у которой числитель больше знаменателя.
Но в школьной литературе можно встретить другое определение неправильной дроби. Выглядит оно следующим образом:
Неправильная дробь всегда больше единицы или равна ей.
Вместе одна целая пицца и ещё половина пиццы больше, чем просто одна целая пицца
В этом и заключается суть фразы «неправильная дробь всегда больше единицы».
Одна целая пицца и ещё половина пиццы описывается смешанной дробью и эта смешанная дробь больше единицы:
Переведём смешанную дробь обратно в неправильную дробь, чтобы не противоречить правилу. Ведь речь в данном случае идёт о неправильных дробях:
что схематически будет выглядеть так:
Выражение 

На координатной прямой можно увидеть, как располагаются эти числа:
Видно, что рациональное число 1,5 располагается правее, чем 1. А мы помним, что чем правее число располагается на координатной прямой, тем оно больше.
Неправильной также называется дробь равная единице. Речь в данном случае идет о тех дробях, у которых числитель и знаменатель равны.
Рассмотрим дробь 
Фактически речь идёт не о дроби, а об одной целой пицце:
В этом и заключается суть фразы «неправильная дробь может равняться единице».
Любое целое число отличное от нуля (не равное нулю) можно представить в виде неправильной дроби со знаменателем 1. Например, числа 3, 5, 9, 12 можно представить в виде неправильных дробей со знаменателем 1
Представление объекта в виде единицы позволяет проще решать задачи. Рассмотрим примеры.
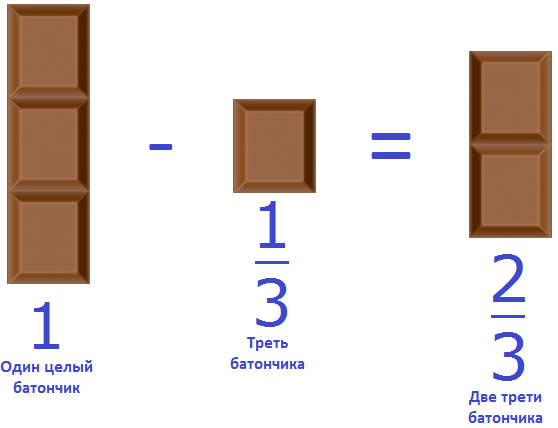
Пример 1. Куплен один шоколадный батончик. От него отрезали треть. Сколько батончика осталось?
Осталось две трети батончика. Сам батончик можно описать цифрой 1, далее из этой единицы вычесть треть:
Не приводя на бумаге никаких вычислений, можно ответить на вопрос подобной задачи. Сказано «отрезали треть» — значит сразу нужно обратить внимание на то, что знаменатель равен 3.
Если отрезали одну часть из трёх, то сколько частей должно остаться? Верно, две части. Поэтому и ответ «две части из трёх» или «две трети».
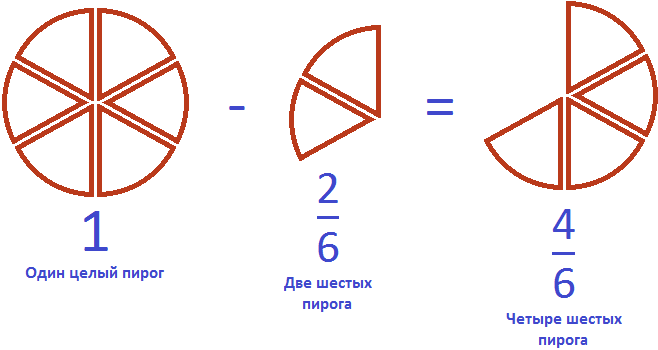
Пример 2. Куплен один пирог. От него отрезали две шестых. Сколько пирога осталось?
Осталось четыре шестых пирога. Сам пирог можно описать цифрой 1, далее из этой единицы вычесть две шестых:
Приведение дробей к общему знаменателю
Чтобы привести дроби к общему знаменателю, мы находили НОК (наименьшее общее кратное) знаменателей этих дробей. Затем делили найденный НОК на знаменатель первой дроби и получали дополнительный множитель для первой дроби.
То же самое мы делали и для второй дроби — делили НОК на знаменатель второй дроби и получали дополнительный множитель для второй дроби.
Затем дроби умножались на свои дополнительные множители. В результате они обращались в дроби, у которых одинаковые знаменатели. К примеру, выражение 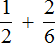
Но есть и другой способ приведения дробей к общему знаменателю. Этим способом часто пользуются школьники и ленивые студенты. Суть этого способа заключается в том, что роль дополнительных множителей берут на себя знаменатели обеих дробей, причем происходит это «крест-накрест» — знаменатель первой дроби становится дополнительным множителем второй дроби, а знаменатель второй дроби становится дополнительным множителем первой дроби.
Вычислим предыдущее выражение 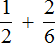
Далее числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель и вычисляем:
Преимущество данного способа в том, что не нужно находить НОК знаменателей обеих дробей. В процессе вычисления всё выравнивается само. Единственный недостаток заключается в том, что выражение становится более длинным и корявым.
Сравните выражения, которые мы вычислили сначала первым способом, а затем вторым:
Выражение, вычисленное первым способом, намного аккуратнее и короче, нежели второе.
Вторым способом мы будем пользоваться при изучении алгебры. В алгебре работать с буквенными выражениями приходиться чаще, чем с числовыми.
К примеру, если перед нами будет стоять задача привести буквенное выражение 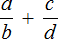
Нахождение дроби от числа
Чтобы найти дробь от числа, мы делим это число на знаменатель искомой дроби и полученный результат умножаем на числитель искомой дроби.
Например, чтобы найти 
Получили ответ 4. Значит 
Но есть и второй вариант решения. Для нахождения 

Поэтому можно взять на заметку следующее правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число умножить на искомую дробь.
Пример 2. Найти от двух часов.
Два часа это 120 минут. Чтобы найти от 120 минут, нужно 120 умножить на дробь
Значит от двух часов составляют 80 минут.
Нахождение числа по дроби
Чтобы найти всё число по его дроби, мы делили это число на числитель имеющейся дроби и полученный результат умножали на знаменатель имеющейся дроби.
Например, зная что рулетки составляет 12 см, мы можем найти длину всей рулетки. Для этого 12 нужно разделить на 2, и полученный результат умножить на 3
Получили 18. Значит длина всей рулетки равна 18 см.
Поэтому можно взять на заметку следующее правило нахождения числа по дроби:
Чтобы найти число по дроби, нужно это число разделить на данную дробь.
Пример 2. 
Чтобы найти длину всего пути, достаточно 6 разделить на дробь
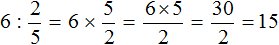
Получили ответ 15. Значит длина всего пути составляет 15 километров.
Десятичная точка в дробях
Запятую в десятичной дроби, которая отделяет целую часть от дробной, по-другому называют десятичной точкой.
Дело в том, что в некоторых источниках целая часть от дробной отделяется именно точкой, а не запятой. Например:
2.5 (две целых пять десятых)
15.65 (пятнадцать целых шестьдесят пять сотых)
Точка часто используется для записи десятичных дробей на компьютере — в программировании и при работе в математических пакетах. В остальных случаях: на письме и при подготовке документов, в десятичных дробях чаще используется запятая, а не точка.
Мы используем в десятичных дробях запятую, а не точку, поэтому разумнее называть эту запятую десятичной запятой.
Но десятичную запятую большинство людей тоже называют десятичной точкой. Что в принципе не является ошибкой, потому как речь всё равно идёт о разделителе, котором отделяет целую часть от дробной.
Давайте и мы будем называть свою запятую в десятичных дробях десятичной точкой. Это словосочетание проговаривается легче и приятнее на слух.
Десятичная точка используется для увеличения или уменьшения дроби в 10, 100, 1000 и более раз. При увеличении десятичной дроби, десятичная точка передвигается вправо, а при уменьшении — влево. Чтобы быстро запомнить это, можно воспользоваться фразами «чем правее, тем больше» и «чем левее, тем меньше».
Пример 1. Увеличить десятичную дробь 6,3 в десять раз.
Чтобы увеличить десятичную дробь 6,3 в десять раз, достаточно передвинуть десятичную точку вправо на одну цифру, получим 63.
Пример 2. Уменьшить десятичную дробь 6,3 в десять раз.
Для уменьшения дроби 6,3 в десять раз достаточно передвинуть десятичную точку влево на одну цифру, получим 0,63
Если дробь нужно увеличить (или уменьшить) в сто раз, то десятичная точка сдвигается на две цифры.
Если дробь нужно увеличить (или уменьшить) в тысячу раз, то десятичная точка сдвигается на три цифры. В общем, всё зависит от количества нулей во множителе.
Например, увеличить дробь в десять раз означает умножить её на 10. Мы помним, что для того чтобы умножить десятичную дробь на 10, нужно в этой дроби передвинуть запятую вправо на одну цифру (поскольку в числе 10 один ноль). Теперь можно не заучивать подобные правила. Такое умножение можно легко выполнить, передвинув десятичную точку.
Пример 3. Увеличить десятичную дробь 6,3 в тысячу раз.
Чтобы увеличить десятичную дробь 6,3 в тысячу раз, достаточно передвинуть десятичную точку вправо на три цифры, получим 6300. Если после запятой не хватает цифр, то вместо недостающих цифр записывают нули, что мы и сделали.
Пример 4. Уменьшить десятичную дробь 12,5 в сто раз.
Для уменьшения дроби 12,5 в сто раз, достаточно передвинуть десятичную точку влево на две цифры, получим 0,125
Десятичную точку можно использовать не только в десятичных дробях. Её можно использовать для увеличения (уменьшения) и других чисел в 10, 100 или в 1000 раз.
Возьмём к примеру целое число 325 и поставим в конце точку, получим 325 с точкой. Воспользуемся в этот раз точкой, так как её легче изобразить на рисунке:
Попробуем уменьшить это число в десять раз. Для этого достаточно будет передвинуть точку влево на одну цифру, получим 32.5
Попробуем увеличить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры вправо, получим 123000.
Попробуем уменьшить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,123
Попробуем уменьшить число 65 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,065
Попробуем увеличить число 65 в сто раз. Для этого достаточно передвинуть десятичную точку на две цифры вправо, получим 6500.
Составные выражения
Встречаются задачи, в которых требуется вычислить выражение составленное из нескольких дробей. Например,
Такое выражение вычисляется согласно порядку действий. В данном случае вычисление будет выполнено последовательно слева направо:
Если из 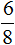
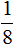
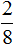
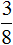

Если вам тяжело понять данный пример, попробуйте самостоятельно решить его на бумаге, делая соответствующие рисунки к каждой дроби.
Пример 2. Найти значение выражения
В данном примере сначала необходимо выполнить умножение затем сложение и вычитание
Если 
Затем если к 

Пример 3. Найти значение выражения
Сначала желательно вычислить выражения, находящиеся в числителях обеих дробей, а именно выражения 2−1 и 1+1,
Дальнейшее вычисление не составляет особого труда 

Конечно, можно было записать в одном числителе выражения, находящиеся в числителях обеих дробях. От этого ответ не изменился бы:
Но в некоторых случаях возможны подвохи, особенно если из одной дроби вычитается другая. Следующий пример демонстрирует это.
Пример 4. Найти значение выражения
Вычислим выражения, находящиеся в числителях обеих дробей, а именно выражения 2+1 и 2 −1
Ну и нетрудно догадаться, что 



Все логично. Если из пиццы вычесть 

Теперь попробуем решить данный пример, записав в одном числителе оба выражения, находящиеся в числителях обеих дробей:
Получается совсем другой ответ. Этот ответ не является правильным. Давайте посмотрим, что представляет собой выражение 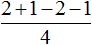
Для начала запишем его следующим образом:
Теперь попробуем проследить весь процесс вычисления этого выражения. Предположим, что имелось 
К ней добавили еще 
Затем из получившейся пиццы вычитается
Затем из получавшейся 

Получился 0, то есть пицца исчезла. Но мы знаем, что должно было остаться 
Если хочется сэкономить время и записать в числителе оба выражения, находящиеся в числителях обеих дробей, то второй числитель нужно взять в скобки. Это спасёт от ошибки:
Пример 5. Найти выражения
Вычислим выражения, находящиеся в числителях обеих дробей:
Приведем полученные дроби к общему знаменателю и как обычно вычислим полученное выражение:
Если из вычесть 

Пример 6. Найти значение выражения
В первую очередь необходимо выполнить умножение:
Далее выполняется сложение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
19 thoughts on “Дополнительные сведения о дробях”
Здравствуйте! Админ, отличный сайт, я хотел бы узнать, будет ли продолжение?
Доброго времени суток.. Занимаюсь вашими уроками уже второй день, дошел уже до 25-го.. С математикой у меня не было проблем в школе, но закончил я ее три года назад, и многое подзабыл, а надо ЕГЭ в этом году сдавать.. Поначалу первые 10 уроков казались смешными, потому что до того легкие и так подробно разъяснены что даже первоклашке не составит трудности все выучить, но все же начал читать, и увидел не мало полезных и интересных способов решения про которые не говорили учителя в школе.. Спасибо Вам большое, объясняете понятно и доходчиво, и очень этим помогаете)) хотелось бы узнать будут ли в ближайшее время темы про функции, логарифм и интегралов, нахождения точек экстремума??
Доброго времени суток. Админ, хотелось бы еще знать, на данный момент 39 уроков, это тянет на какой класс если отталкиваться от школьной программы?
Здравствуйте.
На сайте смешанная программа, не привязанная к классам. В одном уроке могут затрагиваться темы как из младших так и из старших классов. Мы посчитали, что если изучать математику в такой последовательности, то можно выйти на более менее сносный уровень владения математикой, чтобы можно было увереннее себя чувствовать в школе или другом учебном заведении
А могли бы вы порекомендовать курс или книги которые помогли стать «настоящим» математиком(что бы это не значило), с полным обоснованием всех методов без эвристик, возможно даже с методами доказательств элементарных понятий
Спасибо огромное за этот сайт разработчикам. В школе с математикой было плохо. Но всегда мечтала хорошо разбираться, долго искала что-то подобное! И вот благодаря вам мечта воплощается в реальность!
Мда, из 10 примеров решил правильно только половину. Придётся повторять сложение и вычитание рациональных чисел
10. Приведение дробей к общему знаменателю
Умножим числитель и знаменатель дроби 


Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем. При приведении дроби к новому знаменателю её числитель и знаменатель умножают на дополнительный множитель.
Пример 1. Приведём дробь 
Решение. Число 35 кратно 7, так как 35 : 7 = 5. Дополнительным множителем является число 5. Умножим числитель и знаменатель данной дроби на 5, получим
Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.
Например,
Общим знаменателем дробей может быть любое общее кратное их знаменателей (например, произведение знаменателей).
Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример 2. Приведём к наименьшему общему знаменателю дроби
Решение. Наименьшим общим кратным чисел 4 и 6 является 12.
Чтобы привести дробь 
Чтобы привести дробь 
Итак
В сложных случаях наименьший общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Пример 3. Приведём дроби 
Решение. Разложим знаменатели данных дробей на простые множители: 60 = 2 • 2 • 3 • 5; 168 = 2 • 2 • 2 • 3 • 7. Найдём наименьший общий знаменатель: 2 • 2 • 2 • 3 • 5 • 7 = 840.
Дополнительным множителем для дроби 
Для дроби 
Итак,
Вопросы для самопроверки
Выполните упражнения
275. Приведите дробь:
276. Выразите в минутах, а потом в шестидесятых долях часа:
277. Сколько содержится:
278. Сократите дроби 
279. Можно ли привести к знаменателю 36 дроби:
280. Можно ли представить в виде десятичной дроби:
В каком случае обыкновенную дробь можно представить в виде десятичной?
281. Запишите в виде десятичной дроби, приведя:
282. Запишите в виде десятичной дроби:
283. Приведите к наименьшему общему знаменателю дроби:
284. Вычислите устно:
285. Найдите пропущенные числа, если х = 0,8; 0,16; 0,06; 1:
286. На какое число надо умножить 24;8;16;6;12, чтобы получить 48?
287. С помощью транспортира разделите одну окружность на 6, а другую — на 3 равные дуги. Постройте многоугольники, изображённые на рисунке 14.
У каждого из этих многоугольников равны стороны и равны углы. Такие многоугольники называют правильными. Подумайте, является ли правильным многоугольником прямоугольник; квадрат.
288. Сократите:
289. Найдите наибольший общий делитель числителя и знаменателя и сократите дробь:
290. При каком значении х верно равенство:
291. Жук ползёт вверх по стволу дерева (рис. 15) со скоростью 6 см/с. По тому же дереву ползёт вниз гусеница.
Сейчас она находится на 60 см ниже жука. С какой скоростью ползёт гусеница, если через 5 с расстояние между ней и жуком будет 100 см?
292. Космический корабль «Вега-1» двигался к комете Галлея со скоростью 34 км/с, а сама комета двигалась ему навстречу со скоростью 46 км/с. Какое расстояние было между ними за 15 мин до встречи?
293. Сколько чётных пятизначных чисел можно составить из цифр 0, 3, 5, 6, 8? Есть ли среди них числа, кратные трём? кратные девяти?
294. Сократите:
295. Найдите значение выражения:
297. Приведите дробь:
298. Представьте в виде десятичной дроби:
299. Сократите дроби 
300. Приведите дроби к наименьшему общему знаменателю:
301. Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.
302. Из двух пунктов, расстояние между которыми 210 км, вышли одновременно навстречу друг другу два электропоезда. Скорость одного из них на 5 км/ч больше скорости другого. Найдите скорость каждого электропоезда, если они встретились через 2 ч после своего выхода.
Общий знаменатель и дополнительные множители
Содержание
На этом уроке мы познакомимся с понятием «общий знаменатель» и изучим, как привести дроби к общему знаменателю при помощи дополнительных множителей.
Опыт по приведению к общему знаменателю
Несложно сравнивать между собой, а также складывать и вычитать дроби с одинаковыми знаменателями. Но что делать, если знаменатели разные?
Можно перелить всю воду в один сосуд, то есть выполнить сложение:
То, что мы сделали, называется приведение к общему знаменателю.
Замена дробей равными им дробями с одинаковыми знаменателями называется приведение к общему знаменателю.
Дополнительные множители
Числа, на которые мы умножаем числитель и знаменатель, называются дополнительными множителями.
Дополнительный множитель – это натуральное число, на которое нужно умножить числитель и знаменатель дроби, чтобы привести ее к другому знаменателю.
Часто они пишутся над дробями, вот так:
Эта тема может показаться сложной. На самом деле часто общий знаменатель и дополнительные множители подбираются как будто сам собой, интуитивно. Это получается потому, что мы знаем таблицу умножения, и, глядя на некоторые числа, легко видим, на что можно их умножить, чтобы превратить одно в другое.
Тренировка в нахождении дополнительных множителей
Попробуем. Посмотрите на эту последовательность чисел и скажите, на что нужно умножить предыдущее число, чтобы получить последующее.
Приведение дробей к общему знаменателю
Что такое общий знаменатель?
Рассмотрим на примере:
Для этого необходимо найти наименьшее общее кратное для всех трех знаменателей. НОК (2, 3, 5) = 30. Это и есть общий знаменатель.
Найдем во сколько раз каждый знаменатель меньшего общего и умножим
каждую дробь на это число.
Чтобы теперь, например сравнить эти дроби, достаточно сравнить их числители.
Для некоторых дробей a b и c d он равен НОК ( b, d ).
Правило приведения несократимых дробей к наименьшему общему знаменателю
Правило 1. Разложить знаменатели дробей на простые множители;
2. Найти дополнительные множители знаменателей;
3. Умножить числитель и знаменатель каждой дроби на дополнительный множитель ее знаменателя.
Пример
Как привести дроби к наименьшему общему знаменателю
Чтобы привести несколько дробей к наименьшему общему знаменателю, надо:
1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Пример: приведем к наименьшему общему знаменателю дроби 3/4 и 5/6.
1) Находим наименьшее общее кратное (НОК) чисел 4 и 6. Это 12. То есть 12 – минимальное число, на которое делятся без остатка и 4, и 6.
2) Делим 12 на знаменатель каждой из двух дробей, чтобы найти их дополнительные множители:
12 : 4 = 3, 12 : 6 = 2.
Таким образом, дополнительным множителем дроби 3/4 является 3, дроби 5/6 – 2.
3) Чтобы в знаменателе обеих дробей было число 12, надо умножить их числители и знаменатели на их дополнительные множители.
Нашли общий знаменатель двух дробей – число 12.
В дроби 3/4 делим 12 на знаменатель 4 и полученный результат умножаем на числитель 3:
Мы получили числитель. Итак, в числителе у нас 9, в знаменателе 12:
В дроби 5/6 делим 12 на 6 и полученный результат умножаем на 5:
Как привести дроби к наименьшему общему знаменателю
Наименьшим общим знаменателем (НОЗ) данных несократимых дробей является наименьшее общее кратное (НОК) знаменателей этих дробей. (см. тему «Нахождение наименьшего общего кратного»: 5.3.5. Нахождение наименьшего общего кратного (НОК) данных чисел ).
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20:5=4). Для 2-й дроби дополнительный множитель равен 5 (20:4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8:4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей ). Находим НОК(16; 20)=2 4 ·5=16·5=80. Дополнительный множитель для 1-й дроби равен 5 (80:16=5). Дополнительный множитель для 2-й дроби равен 4 (80:20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30:5=6), дополнительный множитель ко 2-й дроби равен 5 (30:6=5), дополнительный множитель к 3-ей дроби равен 2 (30:15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30).
Приведение дробей к наименьшему общему знаменателю
Дроби могут иметь множество общих знаменателей.
Могут иметь общие знаменатели: 4, 8, 12, 16 и т.д.:
В множестве чисел, являющихся общим знаменателем данных дробей существует наименьшее натуральное число, которое называют наименьшим общим знаменателем.
Таким образом, из всех общих знаменателей 4, 8, 12, 16 дробей:
наименьшим общим знаменателем будет знаменатель 4, так как число 4 – наименьшее натуральное число из чисел 4, 8, 12, 16.
Определение наименьшего общего знаменателя
Наименьший общий знаменатель – это наименьшее число из всех общих знаменателей данных дробей.
Наименьший общий знаменатель будет равен 36.
Чтобы найти наименьший общий знаменатель дробей, нужно найти наименьшее общее кратное (НОК) этих знаменателей.
Как привести дроби к наименьшему общему знаменателю
Шаг 1
Найти наименьший общий знаменатель.
Шаг 2
Найти дополнительный множитель.
Шаг 3
Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Шаг 4
Записать полученные дроби с новым знаменателем.
Пример 1
Привести дроби к общему знаменателю и наименьшему общему знаменателю::
Действие 1
Найдем общий знаменатель для рассматриваемых дробей.
Чтобы найти общий знаменатель, перемножим знаменатели:
Дополнительный множитель к первой дроби:
Дробь примет вид:
Дополнительный множитель ко второй дроби:
Дробь примет вид:
Дополнительный множитель к третьей дроби:
Дробь примет вид:
Итак, были дроби:
Запишем полученные дроби с общим знаменателем:
Действие 2
Приведем дроби к наименьшему общему знаменателю:
Чтобы привести дроби к наименьшему общему знаменателю нужно:
Шаг 1
Чтобы найти наименьшее общее кратное (НОК) нужно знаменатели дробей разложить на множители.
Разложим их знаменатели на множители:
Запишем знаменатели как произведение множителей:
Из одинаковых простых множителей выберем тот множитель, который стоит в наибольшей степени, т. е.:
Наименьший общий знаменатель у этих дробей: 36.
Шаг 2
Находим дополнительные множители для этих дробей. Для этого 36 делим на 12, 3, 18 (знаменатели этих дробей):
Шаг 3
Умножим числители и знаменатели этих дробей на дополнительные множители:
Таким образом эти дроби привели к наименьшему общему знаменателю.
Ответ
приведенные к общему знаменателю:
приведенные к наименьшему общему знаменателю:
Пример 2
Привести к наименьшему общему знаменателю дроби:
Решение
Шаг 1
Найдем наименьший общий знаменатель. Для этого определим НОК. Чтобы найти НОК, разложим знаменатели на простые множители.
Представим знаменатели в виде произведения множителей:
Из одинаковых простых множителей выберем тот множитель, который стоит в наибольшей степени, т. е.:
Наименьший общий знаменатель 90.
Шаг 2
Найдем дополнительные множители для этих дробей. Для этого 90 делим на 18, 45 (знаменатели этих дробей):
Шаг 3
Умножим числители и знаменатели этих дробей на дополнительные множители:
Таким образом эти дроби привели к наименьшему общему знаменателю.
Ответ
приведенные к наименьшему общему знаменателю имеют вид:
Как привести дробь к НОЗ
Чтобы можно было выполнять операции сложения, вычитания и сравнения между простыми дробями, у них должны быть одинаковые знаменатели.
Если знаменатели дробей различны (именно так чаще и бывает), дроби следует привести к общему знаменателю.
Общим знаменателем называют число, кратное каждому из первоначальных знаменателей исходных дробей.
Наименьшим общим знаменателем (НОЗ) называют наименьший из всех возможных знаменателей или наименьшее общее кратное знаменателей исходных дробей.
Правило приведения двух дробей к НОЗ:
ПРИМЕР: Найти НОЗ дробей 18/81 и 13/45.
Дополнительный множитель для дроби 18/81 будет равен 5; для дроби 13/45 равен 9.
Умножаем числитель и знаменатель первой дроби на 5, а второй — на 9, после чего получаем две дроби с одинаковыми знаменателями: 90/405 и 117/405.
Задача 1: Что больше 14/19 или 27/33.