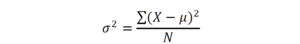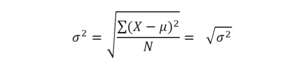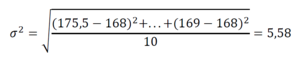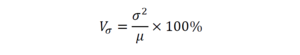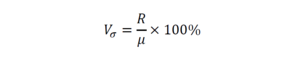Как рассчитать коэффициент вариации
Как рассчитать коэффициент вариации
Расчет коэффициента вариации
Понятие коэффициента вариации
В статистике под вариацией величин того или иного показателя в совокупности понимается различие его уровней у тех или иных единиц анализируемого состава в один и тот же период либо момент исследования. В том случае, когда выполняется анализ отличий величин показателя у одного и того же предмета, у одной и той же единицы совокупности в различные периоды или моменты времени, то это будет уже именоваться не вариацией, а колебаниями или изменениями в течении определенного периода.
Размещено на www.rnz.ru
Формула расчета коэффициента вариации
Являясь отношением среднего квадратического отклонения к средней величине, в общем случае анализируемый показатель вычисляется по следующей формуле:
Формула расчета коэффициента вариации
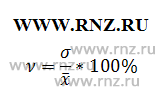
Вычисление рассматриваемого показателя посредством расчета отклонений от средней величины отражает его объективное содержание, но его получение достаточно трудоемко, и для повышения точности выводов требуются расчеты среднего показателя и отклонений без округлений или со значительным количеством цифр после запятой. Поэтому в практических вычислениях делимое может быть вычислено с использованием другой, полученной из общей, формуле вычисления среднего квадратического отклонения в форме разности среднего квадрата элемента и квадрата среднего значения. Таким образом, формула расчета исследуемого показателя, дающая более точный результат, выглядит следующим образом:
Формула расчета точного значения коэффициента вариации
Пример расчета коэффициента вариации
Приведем пример расчета коэффициента вариации цены. Исходные данные для вычисления коэффициента вариации и необходимые промежуточные расчеты приведены в таблице:
Для вычисления используем следующую формулу:
Определим средне значение: хсреднее = (17,74 + 13,69 + 16 + 11,87 + 11,21 + 15,09 + 19,49 + 19,97 + 17,03) / 9 = 15,79 руб.
Среднее квадратическое отклонение: σ = √(77,79 / 9) = 2,94.
Коэффициент вариации: ν = 2,94 / 15,79 * 100 = 18,62%.
Интерпретация. Полученное значение исследуемого показателя показывает, что колеблемость цены относительно небольшая и составляет 18,62% среднего уровня. Полученное значение также указывает на однородность исследуемой совокупности, т.к. полученное значение коэффициента вариации менее 33%.
Внимание! Расчет коэффициента вариации по 44 ФЗ имеет свои особенности, поэтому приводим отдельный пример расчета коэффициента вариации по 44 ФЗ
Онлайн калькулятор расчета коэффициента вариации
В заключении приводим небольшой онлайн калькулятор расчета коэффициента вариации онлайн, используя который, Вы можете самостоятельно выполнить расчет указанного показателя онлайн. При заполнении формы калькулятора расчета коэффициента вариации онлайн внимательно соблюдайте размерность полей, что позволит выполнить вычисления онлайн быстро и точно. Дробные величины должны вводиться с точкой, а не с запятой! В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает онлайн калькулятор расчета коэффициента вариации. Для расчета данного показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет». Обратите внимание, что расчет коэффициента вариации онлайн калькулятором осуществляется только по несгруппированным данным.
Онлайн-калькулятор расчета коэффициента вариации:
Расчет коэффициента вариации в Microsoft Excel
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
Шаг 2: расчет среднего арифметического
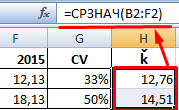
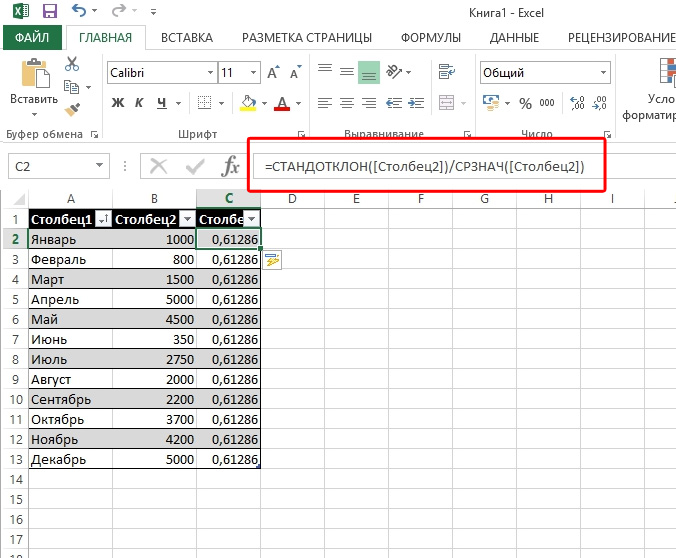
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Коэффициент вариации (CV)
Коэффициент вариации (coefficient of variation, CV) — это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.
Понимание коэффициента вариации
Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.
Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.
Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.
Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.
Обычно данный коэффициент используют в таких целях как:
КЛЮЧЕВЫЕ МОМЕНТЫ
Формула CV
Ниже приведена формула для расчета коэффициента вариации:
Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.
Коэффициент вариации в Excel и Open Office
Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.
В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.
Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:
Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:
Аналогичным образом рассчитаем среднее значение для каждого ряда данных:
Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:
Кликните по картинке для увеличения
Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.
Пример использования коэффициента вариации для выбора объекта инвестиций
Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.
Для принятия решения инвестором используется следующая 15-летняя историческая информация:
Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.
Коэффициент вариации: формула и расчет в Excel и интерпретация результатов
Коэффициент вариации в статистике применяется для сравнения разброса двух случайных величин с разными единицами измерения относительно ожидаемого значения. В итоге можно получить сопоставимые результаты. Показатель наглядно иллюстрирует однородность временного ряда.
Коэффициент вариации используется также инвесторами при портфельном анализе в качестве количественного показателя риска, связанного с вложением средств в определенные активы. Особенно эффективен в ситуации, когда у активов разная доходность и различный уровень риска. К примеру, у одного актива высокая ожидаемая доходность, а у другого – низкий уровень риска.
Как рассчитать коэффициент вариации в Excel
Коэффициент вариации представляет собой отношение среднеквадратического отклонения к среднему арифметическому. Для расчета в статистике используется следующая формула:
Коэффициент вариации позволяет сравнить риск инвестирования и доходность двух и более портфелей активов. Причем последние могут существенно отличаться. То есть показатель увязывает риск и доходность. Позволяет оценить отношение между среднеквадратическим отклонением и ожидаемой доходностью в относительном выражении. Соответственно, сопоставить полученные результаты.
При принятии инвестиционного решения необходимо учитывать следующий момент: когда ожидаемая доходность актива близка к 0, коэффициент вариации может получиться большим. Причем показатель значительно меняется при незначительном изменении доходности.
В Excel не существует встроенной функции для расчета коэффициента вариации. Но можно найти частное от стандартного отклонения и среднего арифметического значения. Рассмотрим на примере.
Доходность двух ценных бумаг за предыдущие пять лет:
Наглядно это можно продемонстрировать на графике:
Обычно показатель выражается в процентах. Поэтому для ячеек с результатами установлен процентный формат.
Значение коэффициента для компании А – 33%, что свидетельствует об относительной однородности ряда. Формула расчета коэффициента вариации в Excel:
Сравните: для компании В коэффициент вариации составил 50%: ряд не является однородным, данные значительно разбросаны относительно среднего значения.
Интерпретация результатов
Прежде чем включить в инвестиционный портфель дополнительный актив, финансовый аналитик должен обосновать свое решение. Один из способов – расчет коэффициента вариации.
Ожидаемая доходность ценных бумаг составит:
Среднеквадратическое отклонение доходности для активов компании А и В составляет:
Ценные бумаги компании В имеют более высокую ожидаемую доходность. Они превышают ожидаемую доходность компании А в 1,14 раза. Но и инвестировать в активы предприятия В рискованнее. Риск выше в 1,7 раза. Как сопоставить акции с разной ожидаемой доходностью и различным уровнем риска?
Для сопоставления активов двух компаний рассчитан коэффициент вариации доходности. Показатель для предприятия В – 50%, для предприятия А – 33%. Риск инвестирования в ценные бумаги фирмы В выше в 1,54 раза (50% / 33%). Это означает, что акции компании А имеют лучшее соотношение риск / доходность. Следовательно, предпочтительнее вложить средства именно в них.
Таким образом, коэффициент вариации показывает уровень риска, что может оказаться полезным при включении нового актива в портфель. Показатель позволяет сопоставить ожидаемую доходность и риск. То есть величины с разными единицами измерения.
Коэффициент вариации по 44-ФЗ. Пример расчёта, формула
Одной из ключевых стадий подготовки закупочной документации становится расчет начальной максимальной цены контракта (НМЦК). Законодательно предусмотрено несколько способов, с помощью которых можно производить расчеты. Чаще всего используется метод сопоставимых рыночных цен. При этом итоговая НМЦК должна определяться с учетом коэффициента вариации. Поэтому всем заказчикам необходимо понять, что включает в себя этот показатель и как его правильно определить.
Что такое коэффициент вариации
Размер НМЦК определяется еще на этапе планирования. Эта сумма должна быть отражена в плане и план-графике. Непосредственно перед подготовкой извещения она корректируется с учетом сложившейся на тот момент экономической обстановки. Вопросы, связанные с НМЦК рассматриваются в статье 22 44-ФЗ. Методики ее расчета описаны в Приказе Министерства экономики и развития № 567 от 02 октября 2013 года. В этом же документе приводятся правила определения коэффициента вариации.
Разработано несколько методик выявления НМЦК: нормативная, тарифная, проектно-сметная, затратная. Самым приоритетным считается метод сопоставимых рыночных цен. Именно его рекомендуется использовать при определении стартовой цены. Он предполагает сравнение коммерческих предложений, предоставляемых потенциальными поставщиками по запросу заказчика. Для проведения такого анализа и применяется коэффициент вариации. Он выражается в процентах.
Под коэффициентом вариации понимается мера относительного разброса предлагаемых цен. Он показывает, какую долю занимает средний разброс цен от среднего значения цены. Этот показатель может принимать следующие значения:
Для определения коэффициента разработана специальная формула. По ней легко подсчитать параметр, подставив соответствующие данные. Упростить себе задачу можно, используя калькуляторы, которые сегодня широко представлены в интернете.
Что делать, если коэффициент завышен
Если при расчете коэффициента вариации получилось значение меньше 33%, то выборка признается однородной. Следовательно, полученное значение можно использовать для определения НМЦК.
Если возникла такая ситуация, что значение коэффициента оказывается выше 33 процентов, тогда потребуется внесение корректировок в используемые данные. Для этого проводится дополнительное исследование рынка. Необходимо собрать коммерческие предложения от большего количества поставщиков и повторить расчет на основе новых данных. Если собрать дополнительные предложения не получается, можно воспользоваться сведениями из ранее заключенных договоров, которые хранятся в реестре контрактов.
В крайней ситуации, когда никак не получается добиться нужного коэффициента вариации можно исключить из выборки неподходящие предложения. Вы также можете попросить поставщика указать в своем предложении нужную вам сумму.
Правила расчета
Методика расчета коэффициента вариации прописана в приказе Минэкономразвития № 567. Согласно действующим нормам заказчик должен направить не менее пяти запросов коммерческих предложений потенциальным поставщикам. Для расчета используются не менее трех предложений, полностью соответствующих требованиям заказчика.
Стоит отметить, что приказ № 567 не является нормативным актом, следовательно, его исполнение не обязательно. За его нарушение никаких штрафных санкций не предусматривается. Однако во избежание спорных ситуаций заказчика рекомендуется пользоваться именно этими правилами расчета.
Для определения коэффициента вариации применяется следующая формула:
Среднеквадратичное отклонение позволяет определить разброс данных. Для его определения выбирают среднюю цену и меру разброса. Вычислить среднеквадратичное отклонение удается по следующей формуле:
В ситуациях, когда закупка включает в себя одновременно несколько позиций, расчет ведется по каждой из них. Это позволяет выявить товары с наибольшим разбросом цен.
Пример расчета
Предположим, что государственное учреждение проводит закупку принтеров для собственных нужд. Потенциальным поставщикам были отправлены соответствующие запросы. Было получено четыре коммерческих предложения цен: 2500 рублей, 2800 рублей, 2450 рублей и 2600 рублей.
В первую очередь необходимо рассчитать среднеарифметическое значение цены
Следующим шагом становится расчет среднеквадратичного отклонения
Осталось только рассчитать коэффициент вариации
Полученное значение коэффициента меньше 33%, следовательно, все собранные данные подходят для расчета стартовой цены контракта. Расчет НМЦК и коэффициента вариации оформляются в форме отчета, который становится обязательной частью закупочной документации.
Коэффициент вариации – важный инструмент, позволяющий оценить правильность ценовых предложений, полученных от поставщиков. Поэтому при составлении документации заказчикам необходимо учитывать правила расчета этого показателя и особенности его применения.
Прогнозируем с Excel: как посчитать коэффициент вариации
Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации. Именно расчёту последнего стоит уделить особое внимание. Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.
В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных
Что такое коэффициент вариации и для чего он нужен?
Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации. Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Коэффициент вариации станет незаменимым помощником в том случае, когда вам необходимо будет сделать прогноз по данным из заданной выборки. Этот индикатор выделит главные ряды значений, которые будут наиболее полезными для последующего прогнозирования, а также очистит выборку от малозначительных факторов. Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим. В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
Как найти среднее квадратичное отклонение?
Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.
Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.
Рассчитываем коэффициент в Экселе
К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
Вставьте формулу и укажите диапазон данных
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
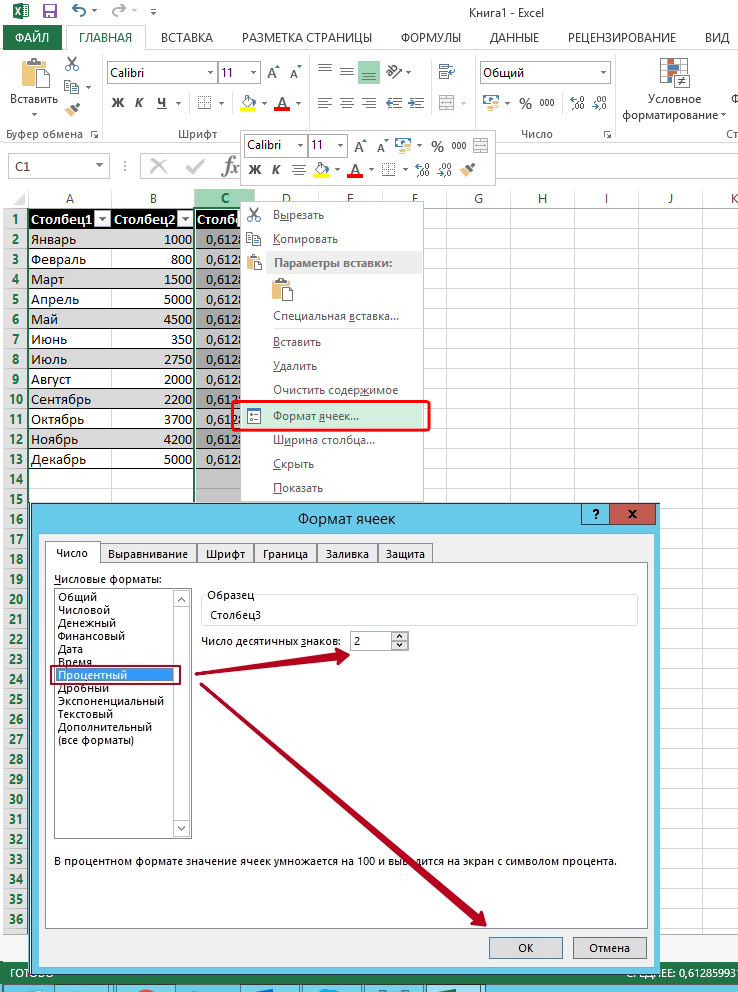
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:
Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
Выберите «Процентный», а при необходимости укажите число десятичных знаков
Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.
Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | | |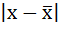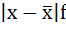
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | | | |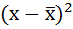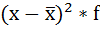
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Показатели вариации
Классификация показателей вариации
Числовые характеристики вариационного ряда
Относительные показатели вариации
Рассмотрим показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Различают следующие относительные показатели вариации (V):
Коэффициент осцилляции (VR):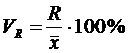 
.
Линейный коэффициент вариации (V): 
.
Коэффициент вариации (Vσ):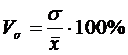 
.
Решение. В разделе «Вид статистического ряда» выбираем Интервальный ряд (рис. 1).
3. На странице ввода данных заполняем исходные данные (рис. 2). При этом открытые интервалы корректируем на закрытые: из открытого интервала «до 3» формируем закрытый 3, из интервала «15 и более» создаем интервал 17.
По умолчанию в отчет включается расчет следующих показателей вариации:
средняя взвешенная, мода, медиана, абсолютные показатели вариации (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение), относительные показатели вариации (коэффициент вариации, линейный коэффициент вариации).
Примечание: несмещенная оценка дисперсии и оценка среднеквадратического отклонения используются при проверке гипотезы о виде распределения, определении относительной ошибки выборки, и в случаях, когда это непосредственно требуется в задании. Во всех остальных случаях данные показатели можно исключить из отчета.
Расчет показателей вариации
Типы вариации
Меры вариации
Вариация существует и в пространстве и во времени.
Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.
Под вариацией во времени подразумевают изменение значений признака в различные моменты времени. Так, со временем изменяются средняя продолжительность жизни, мнения людей и т.д.
Показатели вариации делятся на две группы: абсолютные и относительные.
К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднеквадратическое отклонение. Вторая группа показателей вычисляется, как отношение абсолютных показателей к средней арифметической (медиане).
Прежде, чем определить величину размаха вариации необходимо очистить совокупность от аномальных наблюдений.
Например, нельзя вычислять размах вариации работников какого-либо частного предприятия, если наряду с заработками его работников включен заработок его владельца.
Размах вариации – важный показатель колеблемости признака, но не исчерпывающий его характеристику.
Рассмотрим среднее линейное отклонение. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант xi от по формуле:
(простая средняя),
(взвешенная средняя).
Автор: Алексей Батурин.
Из данной статьи вы узнаете:
Как рассчитать коэффициент вариации в Excel
Коэффициент вариации — это показатель, отражающий разброс значений относительно среднего (отношение стандартного отклонения к среднему значению). Коэффициент вариации измеряется в процентах и отражает однородность временного ряда.
Коэффициент вариации — это отличный показатель, который поможет вам в подготовке данных для прогноза. Коэффициент вариации — индикатор, который поможет вам выделить ряды, на которые стоит обратить внимание перед расчетом прогноза и очистить данные от случайных факторов.
Если коэффициент равен 0%, то ряд абсолютно однородный, т.е. все значения между собой равны.
Если коэффициент вариации больше 33%, то по классической теории ряд считается неоднородным, т.е. большой разброс данных относительно среднего значения.
Как рассчитать коэффициент вариации в Excel
Коэффициент вариации = отношение стандартного отклонения к среднему
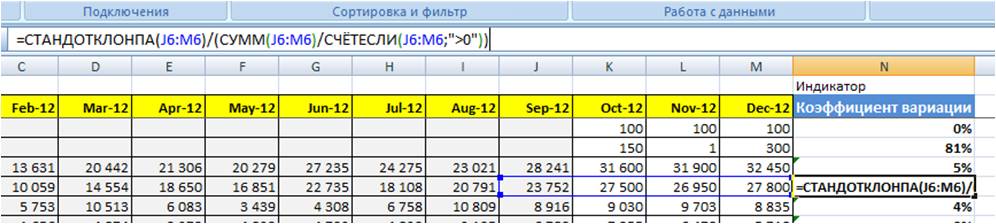
В Excel коэффициент вариации можно рассчитать с помощью следующей формулы:
=СТАНДОТКЛОНПА(ссылка на ряд)/(СУММ(ссылка на ряд)/СЧЁТЕСЛИ(ссылка на ряд;»>0″))
Вводим формулу в ячейку, получаем расчет коэффициента вариации
Протягиваем формулу на весь массив данных.
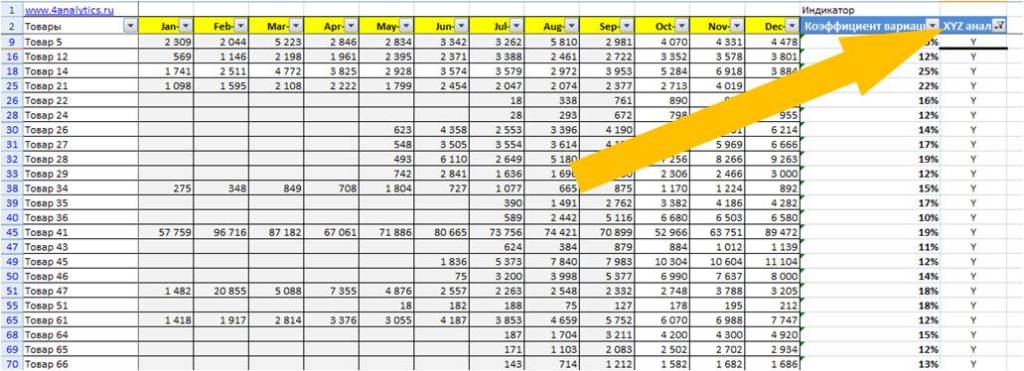
Как сделать XYZ анализ?
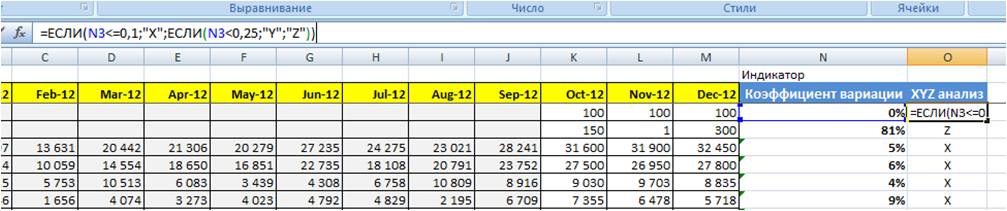
Теперь сегментируем наши коэффициенты вариации и присваиваем каждому одну из 3-х букв X Y и Z
Вводим в ячейку Excel формулу
N3 — ссылка на коэффициент вариации
Применение XYZ анализа при подготовке данных к прогнозу
Работая с большим массивом данных при подготовке данных к прогнозу, необходим индикатор, который будет подсказывать, на какие временные ряды в первую очередь стоит обратить внимание. В качестве индикатора вы можете использовать «коэффициент вариации» или XYZ анализ.
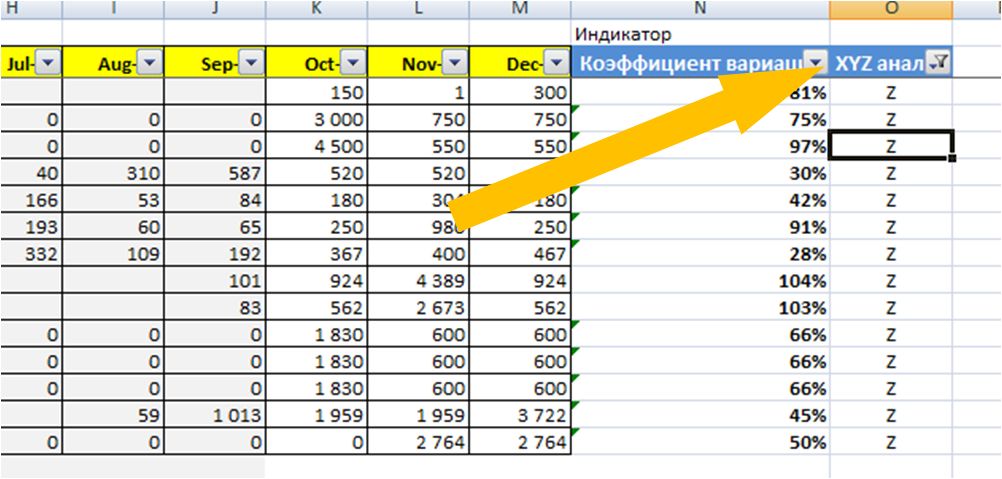
Добавляем фильтр на столбец XYZ анализ и анализируем ряды.
Сначала отфильтруем ряды с коэффициентом вариации больше 25% или Z
Изучаем ряды с большими отклонениями фактических данных за последние 4-5 месяцев. Определяем причины провалов или резких подъёмов продаж. Готовим данные для прогноза. Очищаем данные от влияния случайных факторов или корректируем дефицит.
Также, если в ряду большая неоднородность, то имеет смысл группировать временной ряд. Например,
Сделать прогноз по однородной группе более высокого уровня, а затем распределить пропорционально логики внутри группы.
О том, как сгруппировать временной ряд, читайте статью «Как сделать сводную и сгруппировать временные ряды?»
Затем выделяем ряды с коэффициентом вариации Y
Аналогично просматриваем каждый ряд, и в случае, если замечаете нестандартное поведение ряда, выявляете причины и в случае необходимости очищаете данные.
Рекомендуем создать список факторов (например, акции по стимулированию сбыта, отсутствие товара на складе, спец клиенты. ), и для каждого из факторов определить показатель, который вычитаем или прибавляем к данным для прогноза.
После того, как данные очищены от факторов, которые в будущем не повторятся и подготовлены для прогноза, мы рассчитываем прогноз продаж.
Теперь при расчете прогноза на большом количестве временных рядов, вы можете придерживаться следующей схемы:
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
Тестируйте возможности платных решений:
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Тема 9 Показатели вариации
Показатели вариации в анализе взаимосвязей
Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации.
Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.
Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Особое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.
Основными показателями, характеризующими вариацию, являются:
1) Размах вариации
2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:
где –
абсолютные значения отклонений отдельных вариантов xi от средней арифметической ; fi – частота.
3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:
4. Среднее квадратическое отклонение – корень квадратный из дисперсии:
5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:
Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:
Таблица 9.1 ‑ Данные о продаже основных марок холодильников:
Рассчитаем размах вариации.
R= 1200-460=740$
Пример вычисления размаха вариации
Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.
Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.
Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.
Между индивидуальными отклонениями от средней и колеблемостью признака существует прямая зависимость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.
Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной
По приведенным выше данным определим средневзвешенную цену холодильника:
Далее рассчитаем дисперсию:
. Следует отметить, что дисперсия еще не дает представления об однородности совокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рассчитан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, насколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. .
Рассчитаем среднее квадратическое отклонение
Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости какого-либо одного признака или для определения однородности совокупности рассчитывают относительные показатели.
Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.
Определим значение показателя вариации по вышеприведенным данным таблицы
Совокупность считается однородной, если V не превышает 33%.
Если V 25% – вариация сильная.
Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).
!! Следует отметить, что коэффициент вариации может быть более 100%, что, в частности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.
Изучая вариацию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.
При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подверженным влиянию).
Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индивидуальных значений признака, используют правило сложения дисперсий.
Общая дисперсия представляет собой сумму средней из виутригрупповой и межгрупповой и дисперсий:
Общая дисперсия характеризует вариацию признака по всей совокупности как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности.
Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рассчитывается отдельно по каждой j-ой группе.
Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:
Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:
Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении общей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчленения общей совокупности.
Теснота связи между факторным и результативным признаками оценивается на основе эмпирического корреляционного отношения:
Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.
Пример. На следующем условном примере исследуем зависимость объема выполненных работ от формы собственности проектно-изыскательских организаций.
Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности
| Форма собственности | Количество предприятий | Итого | |
| Государственная | 4 | 10,30,20,40 | 100 |
| Негосударственная | 6 | 20, 40, 60, 20, 50, 50 | 240 |
| Итого | 10 | 340 |
1) Определим средний объем работ для предприятий двух форм собственности.
2) Определим средний объем работ для каждой формы собственности.
3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.
4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.
Таблица 9.3. – Вспомогательная таблица
Пример. Средняя из внутригрупповых дисперсий
Пример. Межгрупповая дисперсия
На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:
Проверка закона сложения дисперсий: 54,0+189,8=243,8
Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фактора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.
Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:
Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика
Контрольные задания
Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.
2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.
Расчет начальной максимальной цены контракта (НМЦК) методом сопоставимых рыночных цен
Калькулятор для расчета начальной максимальной цены контракта методом сопоставимых рыночных цен по формулам, приведенным в приказе Минэкономразвития России от 02.10.2013 N 567 «Об утверждении Методических рекомендаций по применению методов определения начальной (максимальной) цены контракта, цены контракта, заключаемого с единственным поставщиком (подрядчиком, исполнителем)»
Описание работы калькулятора вы можете найти под калькулятором.
Калькулятор для расчета начальной максимальной цены контракта методом сопоставимых рыночных цен
Коммерческие предложения
Коммерческие предложения
Импортировать данные Ошибка импорта
Для определения начальной (максимальной) цены контракта (НМЦК) калькулятор выше использует формулу, приведенную в Приказе Министерства экономического развития РФ от 2 октября 2013 г. N 567 «Об утверждении Методических рекомендаций по применению методов определения начальной (максимальной) цены контракта, цены контракта, заключаемого с единственным поставщиком (подрядчиком, исполнителем)» 1
— НМЦК, определяемая методом сопоставимых рыночных цен (анализа рынка)
— количество (объем) закупаемого товара (работы, услуги)
— количество значений, используемых в расчете
— номер источника ценовой информации
— цена единицы товара, работы, услуги, представленная в источнике с номером i, скорректированная с учетом коэффициентов (индексов)
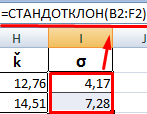
При этом калькулятор ожидает не менее трех значений в таблице коммерческих предложений, так как в целях определения НМЦК методом сопоставимых рыночных цен (анализа рынка) рекомендуется использовать не менее трех цен товара, работы, услуги, предлагаемых различными поставщиками (подрядчиками, исполнителями) 2
Также калькулятор определяет коэффициент вариации по формуле:
, выраженный в процентах, где
— коэффициент вариации
— средняя арифметическая величина цены единицы товара, работы, услуги
— среднее квадратичное отклонение, рассчитываемое по формуле
, где
— номер источника ценовой информации
— цена единицы товара, работы, услуги, представленная в источнике с номером i, скорректированная с учетом коэффициентов (индексов)
— количество значений, используемых в расчете
При этом, совокупность значений, используемых в расчете, при определении НМЦК считается неоднородной, если коэффициент вариации цены превышает 33%. Если коэффициент вариации превышает 33%, целесообразно провести дополнительные исследования в целях увеличения количества ценовой информации, используемой в расчетах 3
Показатели вариации
Расчет показателей вариации — размаха вариации, дисперсии, среднего квадратического отклонения и т. п.
Пользователь Мария попросила написать такой калькулятор: Показатели вариации и анализ частотных распределений.
Расчеты не очень сложные, поэтому вот и он. Теория, по уже сложившейся традиции, под калькулятором.
Показатели вариации
Исследуемая совокупность
Исследуемая совокупность
Импортировать данные Ошибка импорта
Вариация — это различие индивидуальных значений какого-либо признака внутри изучаемой совокупности.
Ну, например, есть класс учеников — изучаемая совокупность, у них есть, скажем, годовая оценка по русскому языку. У кого-то она «5», у кого-то «4» ну и так далее. Набор этих оценок по всему классу, вместе с их частотой (т. е. встречаемостью, скажем, у 10 человек – «5», у 7 человек – «4», у 5 человек – «3») и есть вариация, по которой можно рассчитать массу показателей.
Этим мы сейчас и займемся.
Абсолютные показатели
Размах вариации — разность между максимальным и минимальным значениями признака
Если индивидуальных значений слишком много, для упрощения расчетов данные могут группировать, т. е. объединять в интервалы. Тогда имеет смысл середины i-го интервала, или среднего значения признака на i-том интервале
Дисперсию также можно рассчитать и таким способом:
, где
Относительные показатели
Абсолютные показатели измеряются в тех же величинах, что и сам признак, и показывают абсолютный размер отклонений, поэтому их неудобно применять для сравнения изменчивости разных признаков совокупности. Поэтому дополнительно рассчитывают относительные показатели вариации, которые обычно выражают в в процентах.
Коэффициент осцилляции — характеризует колеблемость крайних значений признака вокруг средней арифметической.
Относительное линейное отклонение или линейный коэффициент вариации — характеризует долю усредненного значения абсолютных отклонений от средней арифметической.
Совокупность считается однородной при значениях меньше 40%. При значениях больше 40% говорят о большой колеблемости признаков и совокупность считается неоднородной.
Коэффициент вариации: для чего нужен, расчет, примеры, упражнения
Видео: Коэффициент вариации: для чего нужен, расчет, примеры, упражнения
Содержание:
В коэффициент вариации (CV) выражает стандартное отклонение относительно среднего. То есть он пытается объяснить, насколько велико значение стандартного отклонения по отношению к среднему.
Например, переменный рост четвероклассников имеет коэффициент вариации 12%, что означает, что стандартное отклонение составляет 12% от среднего значения.
Обозначается CV, коэффициент вариации является безразмерным и получается делением стандартного отклонения на среднее значение и умножением на сто.
Чем меньше коэффициент вариации, тем меньше отклонение данных от среднего. Например, в переменной со средним значением 10 и другой со средним значением 25, обе со стандартным отклонением 5, их коэффициенты вариации составляют 50% и 20% соответственно. Конечно, первая переменная более изменчива (дисперсия), чем вторая.
Рекомендуется работать с коэффициентом вариации для переменных, измеряемых в шкале пропорций, то есть шкалах с абсолютным нулем независимо от единицы измерения. Примером может служить переменная расстояния, которая не имеет значения, измеряется она в ярдах или метрах, ноль ярдов или ноль метров означает одно и то же: нулевое расстояние или смещение.
Для чего нужен коэффициент вариации?
Коэффициент вариации служит для:
— Коэффициент вариации часто используется как показатель надежности в научных экспериментах. Говорят, что если коэффициент вариации составляет 30% или больше, результаты эксперимента следует отбросить из-за их низкой надежности.
— Это позволяет предсказать, насколько сгруппированы вокруг среднего значения изучаемой переменной, даже не зная ее распределения. Это очень помогает при оценке ошибок и вычислении размеров выборки.
Предположим, что переменные вес и рост людей измеряются в совокупности. Вес с CV 5% и рост с CV 14%. Если вы хотите взять выборку из этой совокупности, размер выборки должен быть больше для оценок роста, чем для веса, поскольку существует большая вариативность в измерении роста, чем в измерении веса.
Важное наблюдение за полезностью коэффициента вариации заключается в том, что он теряет смысл, когда значение среднего близко к нулю. Среднее значение является делителем вычисления CV, и, следовательно, очень маленькие его значения приводят к тому, что значения CV будут очень большими и, возможно, не поддающимися вычислению.
Как рассчитывается?
Расчет коэффициента вариации относительно прост, достаточно знать среднее арифметическое и стандартное отклонение набора данных, чтобы рассчитать его по формуле:
Если они неизвестны, но данные доступны, можно предварительно рассчитать среднее арифметическое и стандартное отклонение, используя следующие формулы:
Примеры
Пример 1
Были измерены веса в кг группы из 6 человек: 45, 62, 38, 55, 48, 52. Мы хотим знать коэффициент вариации переменной веса.
Он начинается с вычисления среднего арифметического и стандартного отклонения:
Ответ: коэффициент вариации переменного веса 6 человек в выборке составляет 16,64%, при среднем весе 50 кг и стандартном отклонении 8,32 кг.
Пример 2
В отделении неотложной помощи больницы измеряют температуру тела в градусах Цельсия у 5 детей, находящихся на лечении. Результаты 39-е, 38-е, 40-е, 38-е и 40-е. Какой коэффициент вариации переменной температуры?
Он начинается с вычисления среднего арифметического и стандартного отклонения:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации температурной переменной для 5 детей в выборке составляет 2,56%, при средней температуре 39 ° C и стандартном отклонении 1 ° C.
Что касается температуры, то следует проявлять осторожность при обращении с весами, поскольку, будучи переменной, измеряемой в интервальной шкале, она не имеет абсолютного нуля. В рассматриваемом случае, что бы произошло, если бы температуры были преобразованы из градусов Цельсия в градусы Фаренгейта:
Рассчитываются среднее арифметическое и стандартное отклонение:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации температурной переменной у 5 детей в выборке составляет 1,76%, при средней температуре 102,2 ° F и стандартном отклонении 1,80 ° F.
Решенные упражнения
Упражнение 1
Вес в кг 10 сотрудников почтового отделения был измерен: 85, 62, 88, 55, 98, 52, 75, 70, 76, 77. Мы хотим знать коэффициент вариации переменной веса.
Рассчитываются среднее арифметическое и стандартное отклонение:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации переменного веса 10 человек в почтовом отделении составляет 19,74%, при среднем весе 73,80 кг и стандартном отклонении 14,57 кг.
Упражнение 2.
В одном городе измеряется рост 9 465 детей во всех школах первого класса, средний рост составляет 109,90 см со стандартным отклонением 13,59 см. Рассчитайте коэффициент вариации.
Ответ: коэффициент вариации переменного роста первоклассников города составляет 12,37%.
Упражнение 3.
Смотритель парка подозревает, что популяции черных и белых кроликов в его парке не имеют одинаковой изменчивости в размерах. Чтобы продемонстрировать это, он взял образцы по 25 кроликов из каждой популяции и получил следующие результаты:
— Белые кролики: средний вес 7,65 кг и стандартное отклонение 2,55 кг.
-Черные кролики: средний вес 6,00 кг и стандартное отклонение 2,43 кг.
Смотритель парка прав? Ответ на гипотезу смотрителя парка можно получить с помощью коэффициента вариации:
Ответ: коэффициент вариации веса черных кроликов почти на 7% больше, чем у белых кроликов, поэтому можно сказать, что смотритель парка прав в своем подозрении, что вариабельность веса двух популяций кроликов не равны.
Показатели вариации и способы их расчета
Показатели вариации делятся на две группы: абсолютные и относительные.
К абсолютным показателям относятся:
─ среднее линейное отклонение,
─ среднее квадратическое отклонение.
К относительным показателям вариации относятся:
─ относительное линейное отклонение и др.
Размах вариации (R) вычисляется как разность между наибольшим и наименьшим значениями варьирующего признака
.
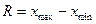
Он показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое (хmin) и самое большое значение признака (хmax).
Например, различие между максимальной и минимальной пенсией отдельных групп населения, уровнем дохода различных категорий работающих или нормами выработки у рабочих определенной специальности или квалификации.
Размах является важной характеристикой вариации, он дает первое общее представление о различии единиц внутри совокупности. Размах вариации выражается в тех именованных числах, в каких выражены значения признака.
Особенность показателя размаха вариации заключается в том, что он зависит лишь от двух крайних значений признака. По этой причине его целесообразно применять в тех случаях, когда особое значение имеет либо минимальный, либо максимальный вариант, т. е. когда размах вариации имеет важное смысловое значение.
Например, им определяются пределы, в которых могут колебаться размеры тех или иных параметров деталей; его используют при испытании стальных тросов на разрыв и т. п.
Другая сторона этой особенности заключается в том, что на величину размаха вариации большое влияние оказывает случайность. Так как из статистического ряда берутся только два значения признака, причем крайние в ряду, на размах этих значений могут оказывать влияние причины случайного характера, то и размах вариации может быть зависимым от случайных причин.
С отмеченной особенностью связано и то обстоятельство, что показатель размаха вариации не учитывает частот в вариационном ряду распределения.
Среднее линейное отклонение. Показатель размаха вариации дает обобщающую характеристику только границам (амплитуде) значений признака, но не дает характеристики вариации распределению отклонений. Распределение отклонений можно уловить, вычислив отклонения всех вариант от средней. А для того, чтобы дать им обобщающую характеристику, необходимо далее вычислить среднюю из этих отклонений, т. е. разности между значением признака и средней арифметической в данной совокупности единиц.
Из свойства средней арифметической (свойство 2) нам известно, что сумма отклонений значений признака от нее всегда равна нулю, так как сумма положительных отклонений всегда равна сумме отрицательных отклонений. Следовательно, чтобы вычислить среднюю арифметическую из отклонений, нужно условно допустить, что все отклонения, положительные и отрицательные, имеют одинаковый знак. Тогда, если взять сумму всех отклонений, условно принятых с одинаковым знаком, и разделить на их число, то полученный показатель вариации будет называться средним линейным отклонением (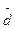 
), т. е. это средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней арифметической.
Если каждый вариант в ряду распределения повторяется один раз, то среднее линейное отклонение равно
где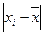 
— абсолютные значения отклонений отдельных вариантов от их средней величины;
n — объем совокупности.
Для вариационного ряда с неравными частотами формула имеет следующий вид:
, (6.1)
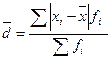
где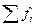 
— сумма частот вариационного ряда.
На основе данных дискретного ряда распределения табл. 6.1. рассчитаем размах вариации и среднее линейное отклонение:
| Группы сотрудников по стажу работы, лет (х) | Число сотрудников, в % к итогу (f) |  |  |  |  |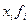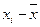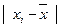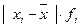
| А | |||||
| -2 | |||||
| -1 | |||||
| Итого: | X |
1) Размах вариации стажа работы равен
2) Определим среднее линейное отклонение по формуле 6.1.
Результаты вспомогательных расчетов даны в табл. 6.1 графы 3-5.
Средний стаж работы сотрудников определяем по формуле средней арифметической взвешенной (графа 2)
.
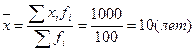
Отклонения индивидуальных значений стажа от средней с учетом и без учета знака содержатся в графах 3 и 4, а произведения отклонений по модулю на соответствующие частоты даны в графе 5.
Среднее линейное отклонение стажа работы сотрудников коммерческого банка составит
,
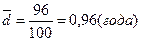
т. е. конкретные значения стажа работы сотрудников в среднем отклоняются от среднего значения признака на 0,96 года.
Среднее линейное отклонение обладает большим преимуществом перед размахом вариации в отношении полноты характеристики колеблемости признака. Однако при этом в некотором смысле нарушается элементарное правило математики, так как отклонение от среднего значения признака складывается без учета знаков.
Это обстоятельство вынуждает искать такой показатель вариации, который был бы лишен и этого недостатка. Хотя в некоторых случаях суммирование показателей без учета знаков имеет экономический смысл.
Например, в практической статистике оборот внешней торговли страны определяется как сумма экспорта и импорта, общий оборот рабочей силы — как сумма принятых и уволенных и т. д.
Отмеченный выше недостаток среднего линейного отклонения может быть устранен путем возведения в квадрат отклонений вариантов от средней величины.
Дисперсия представляет собой средний квадрат отклонения значений признака от их средней величины. Порядок ее вычисления можно выразить следующими формулами.
Если каждый вариант повторяется один раз, то дисперсия равна
.
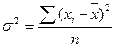
Для вариационного ряда с неравными частотами формула примет
(6.2)
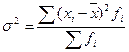
Квадратный корень из дисперсии носит название среднего квадра-гического отклонения от средней. Формулы его расчета следующие:
,
. (6.3)
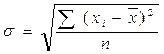
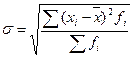
Элементарное алгебраическое преобразование формулы среднего квадратического отклонения приводит ее к следующему виду:
.
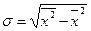
Эта формула часто оказывается более удобной в практике расчетов.
Среднее квадратическое отклонение так же, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется такое соотношение
.
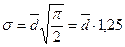
Зная это соотношение, можно по известному показателю определить неизвестный, например, по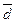 
определить σ и наоборот. Среднее квадратическое отклонение измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, процентах и т. д.). Оно является абсолютной мерой вариации.
Покажем расчет среднего квадратического отклонения по данным дискретного ряда рао пределения студентов одного из факультетов по возрасту (табл. 6.2).
| Группы студентов по возрасту лет (х) | Число студентов (f) | | ( ) |  |  |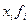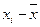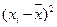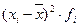
| А | |||||
| -3.9 | 15.21 | 304.2 | |||
| -2.9 | 8.41 | 672.8 | |||
| -1,9 | 3,61 | 342,9 | |||
| -0,9 | 0,81 | 89,1 | |||
| 0,1 | 0,01 | 1,3 | |||
| 1,1 | 1,21 | 205,7 | |||
| 2,1 | 4,41 | 396,9 | |||
| 3,1 | 9,61 | 576,6 | |||
| Итого | X | X | 2571,5 |
Результаты вспомогательных расчетов даны в табл. 6.2, графы 2-5.
1) Средний возраст студента определим по формуле средней арифметической взвешенной (графа 2)
Дисперсию и среднее квадратическое отклонение возраста студентов определим по формулам 6.2 и 6.3
т. е. конкретные значения возраста студентов в среднем отклоняются от их среднего значения на 1,85 года.
Коэффициент вариации. По своему абсолютному значению среднее квадратическое отклонение зависит не только от степени вариации признака, но и от абсолютных уровней вариант и средней. Поэтому сравнивать средние квадратические отклонения вариационных рядов с различными средними уровнями непосредственно нельзя. Чтобы иметь возможность для такого сравнения, нужно найти удельный вес среднего отклонения (линейного или квадратического) в среднем арифметическом показателе, выраженный в процентах, т. е. рассчитать относительные показатели вариации. Формулы коэффициента вариации таковы:
.
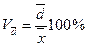
Данный показатель в статистике называется линейным коэффициентом вариации.
(6.4)
Данный показатель называется коэффициентом вариации.
Коэффициент осцилляции (VR):
.
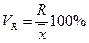
В коэффициентах вариации устраняются не только несопоставимость, связанная с различными единицами измерения изучаемого признака, но и несопоставимость, возникающая вследствие различий в величине средних арифметических. Кроме того, показатели вариации дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
По данным табл. 6.2 и выполненным выше расчетам определим коэффициент вариации но формуле 6.4
Полученная величина свидетельствует о том, что совокупность студентов по возрасту однородна по своему составу.
Важная функция обобщающих показателей вариации — это оценка надежности средних. Чем меньше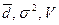 
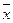
, тем однороднее полученная совокупность явлений и надежнее полученная средняя. Согласно «правилу трех сигм» в нормально распределенных или близких к ним рядах отклонения от средней арифметической, не превосходящие ±3σ, встречаются в 997 случаях из 1000. В других рядах распределения эти отклонения встречаются в 89 случаях из 100. Таким образом, зная 
и σ, можно получить общее первоначальное представление о вариационном ряде. Если, например, средняя заработная плата рабочего по фирме составила 3600 руб., а равняется 30 руб., то с вероятностью, близкой к достоверности, можно утверждать, что заработная плата рабочих фирмы колеблется в пределах (3600±30), т. е. от 3570 до 3630 руб.
Как рассчитывается коэффициент вариации и как его проанализировать
Коэффициент вариации, VAR или CV, – ключевой показатель в оценке риска проектов и доходности ценных бумаг. Он позволяет заранее проанализировать сразу два показателя, которые обладают меняющимися во времени значениями. Если показатель оказывается менее 0,1, направление инвестирования характеризуется низким уровнем риска. При показателе свыше 0,3 уровень риска необоснованно высок. Для расчета удобнее всего использовать функции СТАНДОТКЛОН и СРЗНАЧ табличного редактора Excel.
Для того чтобы сформировать качественный инвестиционный портфель, инвесторам порой приходится прибегать к оценке входящих в него активов, которые обладают разным уровнем риска и доходности. Для этой цели используется широко известный в инвестиционном анализе и эконометрике показатель.
Коэффициент вариации (Coefficient of variation – CV, VAR) – относительный финансовый показатель, который демонстрирует сравнение рассеивания значений двух случайных показателей, которые имеют разные единицы измерения относительно ожидаемого значения.
Справка! Поскольку коэффициент вариации позволяет получить сопоставимые результаты, то его применение оптимально в рамках портфельного анализа. В ней он позволяет эффективно объединить значения риска и доходности и вывести результирующее значение.
Coefficient of variation – показатель из числа относительных методов статистики, который, как NPV и IRR, применяется в рамках инвестиционного анализа. Он измеряется в процентах и может применяться для сравнения вариаций двух несвязанных между собой критериев. Его чаще всего используют финансовые и инвестиционные аналитики.
Справка! На базе коэффициента вариации оценивается так называемый «унифицированный риск» (unitized risk), поскольку он оценивает относительный разброс двух показателей по отношению к прогнозному значению.
Для чего используют показатель VAR:
Справка! XYZ-анализ – аналитический инструмент, в рамках которого продукция компании оценивается по двум параметрам: стабильность потребления и продаж.
Формула расчета коэффициента вариации
Суть расчета коэффициента вариации состоит в том, что по множеству значений рассчитывается сначала среднее квадратичное отклонение, а затем – среднее арифметическое, а после – найти их соотношение.
В общем виде формула расчета показателя VAR выглядит следующим образом:
CV = σ / t ср, где:
CV – коэффициент вариации;
σ – среднее квадратическое отклонение;
t – среднее арифметическое значение для случайной величины.
Формула расчета показателя VAR может принимать самые разнообразные интерпретации в зависимости от объекта оценки.
Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.
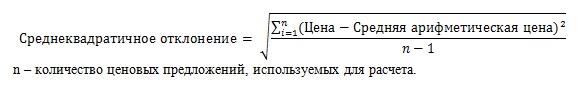
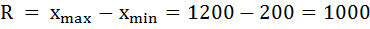
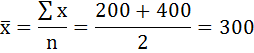
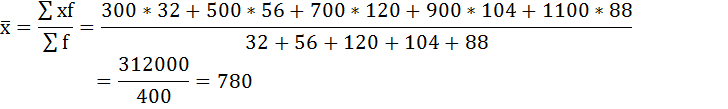
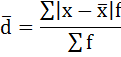
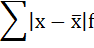
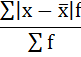
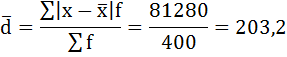
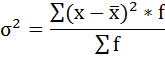
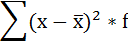
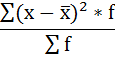
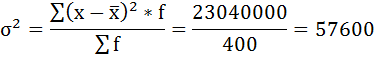
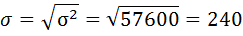
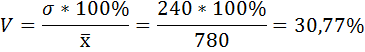
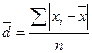
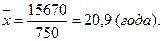
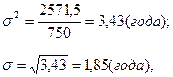
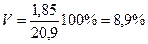
Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.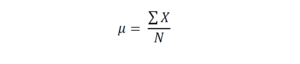
Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.
