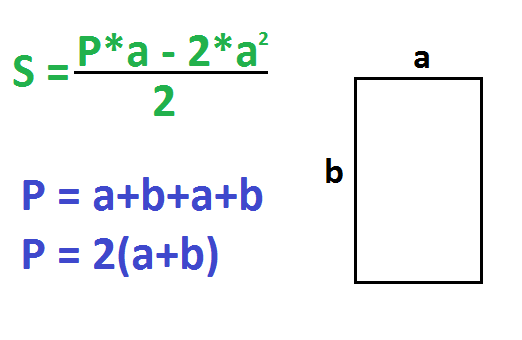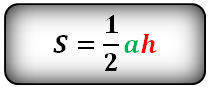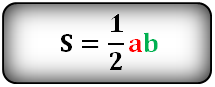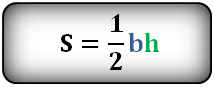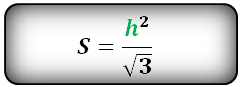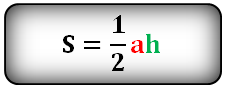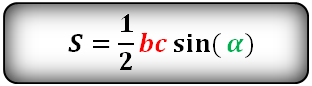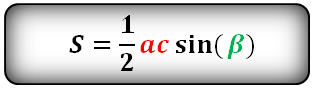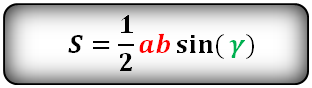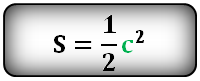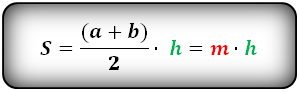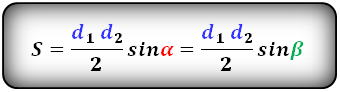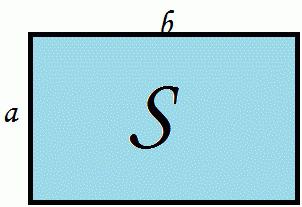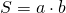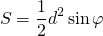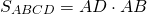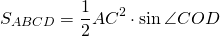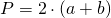Как рассчитать площадь прямоугольника

29.08.202229.08.2022 admin 0 Комментариев

Как рассчитать площадь прямоугольника

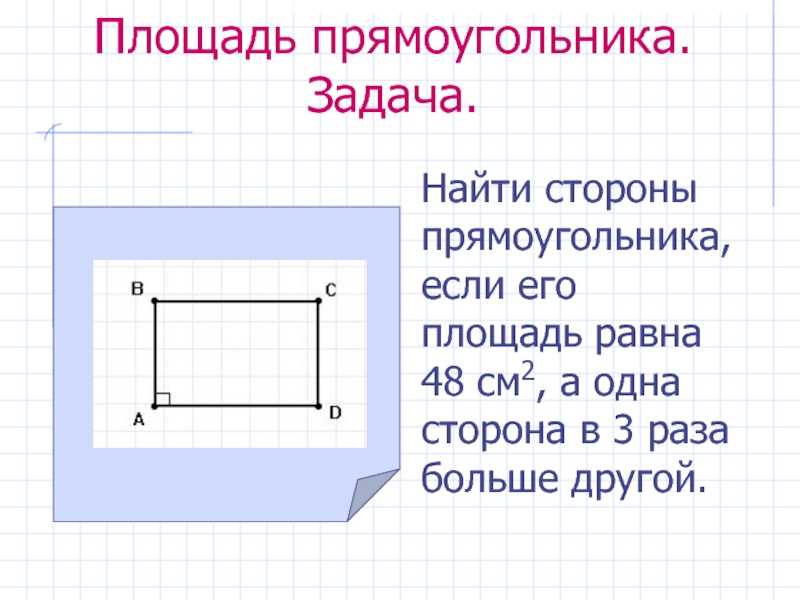
Как найти площадь прямоугольника – 9 способов с формулами и примерами

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

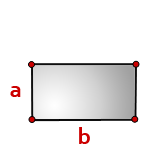
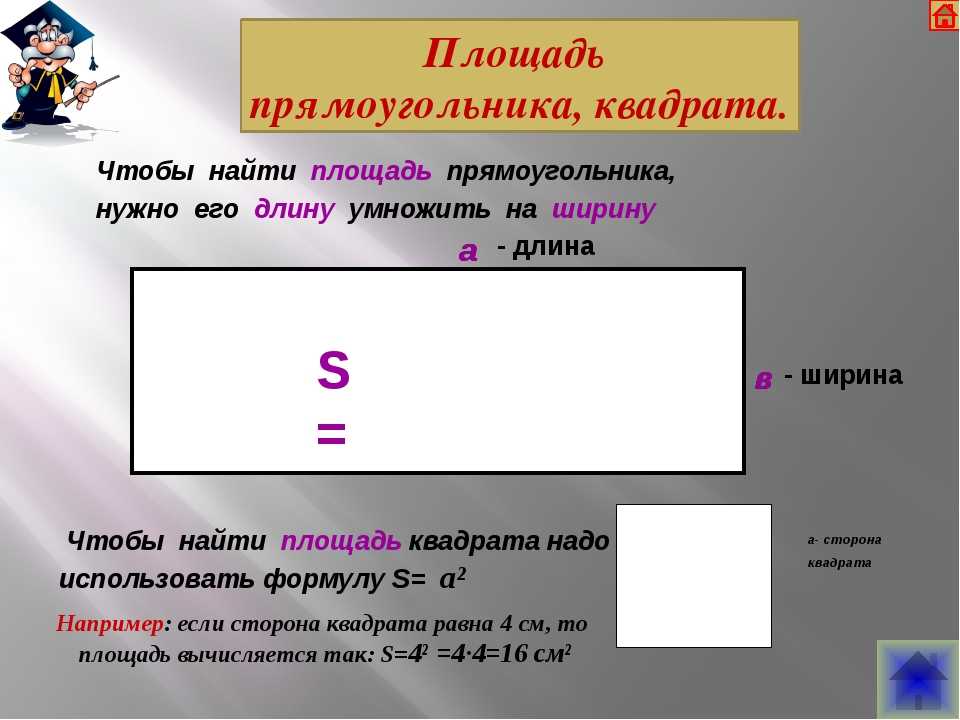
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

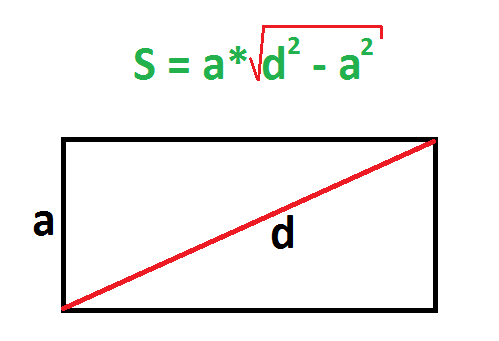
По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

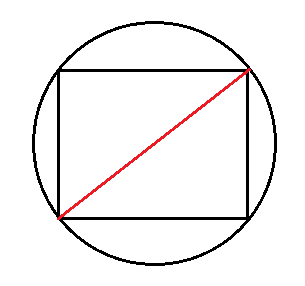
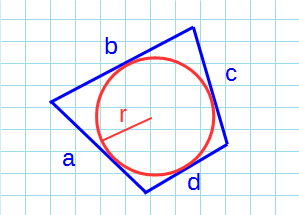
По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

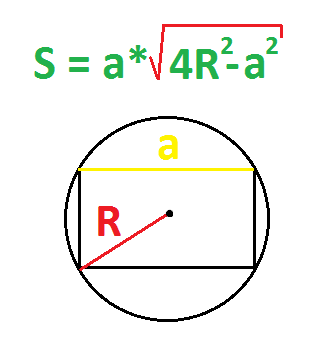
По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

По стороне и периметру – 2 способ

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

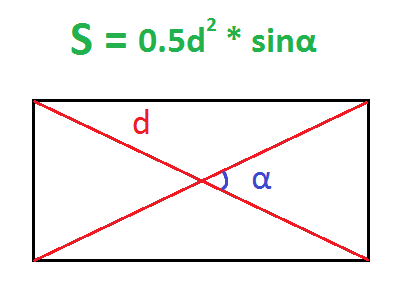
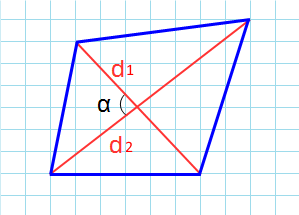
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

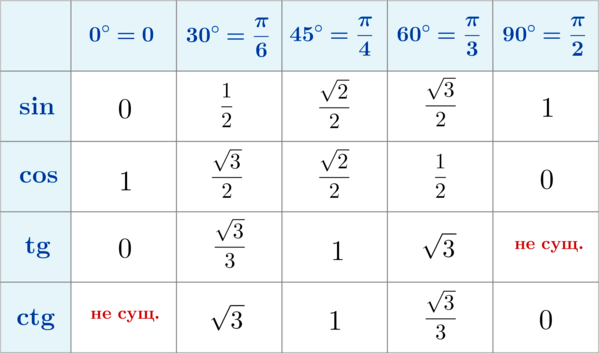
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

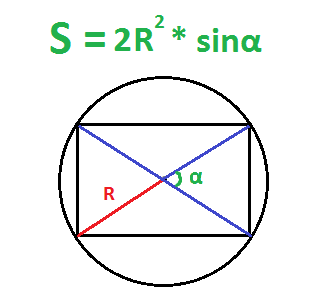
По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

По радиусу описанной окружности и углу между диагоналями – второй способ

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

Источник

Калькулятор для расчета площади прямоугольника

Площадь прямоугольника можно найти, если известны:

Предлагаем удобный и простой онлайн-сервис, который поможет вам рассчитать площадь любого прямоугольника по имеющимся линейным размерам. Его можно использовать для вычисления необходимого количества кровельного покрытия или стеновых материалов, определения площади помещений или земельных участков, при расчете давления, создаваемого разными предметами, и для решения многих других практических задач.

Функционально калькулятор состоит из трех блоков, в каждом из которых реализован алгоритм расчета площади прямоугольника по имеющимся исходным данным. Для удобства каждый блок вынесен в отдельную вкладку. Выберите ту из них, которая подходит в вашем случае, и введите исходные данные в соответствующие поля. Результат появится автоматически сразу после окончания ввода всех необходимых значений. Чтобы изменить какие-либо данные, просто введите их заново, значение площади прямоугольника пересчитается автоматически. Для удобства и наглядности применяемая формула расчета выводится рядом с итоговым результатом.

Как рассчитать площадь прямоугольника

Далее описаны все способы расчета, реализованные в нашем онлайн-калькуляторе.

Площадь прямоугольника по двум его сторонам

Это самая известная формула, которую проходят в третьем классе начальной школы: площадь прямоугольника равна произведению длин его соседних сторон. Однако расчет по ней часто вызывает затруднения, особенно если длины сторон — большие нецелые числа. Наш калькулятор выполнит любые вычисления и выдаст результат практически мгновенно.

Формула площади прямоугольника по длине его диагоналей и углу между ними

Известно, что диагонали прямоугольника равны. Это свойство часто используется для проверки формы земельных участков или каких-либо конструкций, когда необходимо сделать их прямоугольными. Поэтому достаточно измерить любую из диагоналей и любой угол (острый или тупой) в месте их пересечения. Площадь прямоугольника равна половине произведения квадрата диагонали на синус центрального угла. Поскольку синусы смежных углов равны, в исходные данные можно подставлять любой из них.

Расчет площади прямоугольника по любой стороне и диагонали

В данном случае применяется классическая формула произведения сторон, при этом одна сторона известна по условию, а вторая вычисляется по теореме Пифагора. Треугольник, по которому производится расчет, изображен на соответствующей вкладке нашего калькулятора. Там же приведена итоговая формула расчета площади прямоугольника.

Пользоваться онлайн-калькулятором расчета площади прямоугольника можно бесплатно и без каких-либо ограничений. Напишите в комментариях, насколько наш сервис оказался полезным для вас, и не забудьте добавить эту страницу в закладки, чтобы вы могли быстро найти ее при необходимости.

Источник

Площадь и сторона «А» прямоугольника

Свойства

Зная в прямоугольнике площадь и сторону можно найти вторую сторону, и затем все остальные параметры по порядку. Вторая сторона прямоугольника будет равна отношению площади к известной стороне. b=S/a

Для того чтобы найти периметр прямоугольника через площадь и сторону, необходимо подставить в формулу вместо второй стороны полученное отношение P=2(a+b)=2(a+S/a)

Диагональ прямоугольника можно найти через теорему Пифагора в прямоугольном треугольнике, который она образует. Обе диагонали прямоугольника принимают одно и то же значение. Выразив b через площадь и известную сторону, получим следующее выражение. (рис. 56.1) d_1=d_2=√(a^2+b^2 )=√(a^2+(S/a)^2 )=√(a^2+S^2/a^2 )

Используя тригонометрические отношения в полученном треугольнике можно найти углы при пересечении диагоналей со сторонами. Для этого проще всего будет использовать тангенс, как отношение катетов друг к другу. Точно также, как и в предыдущих формулах, заменяем неизвестную сторону на равное ей выражение. α=arc tan⁡〖b/a〗=arc tan⁡〖S/a^2 〗 β=arc tan⁡〖a/b=arc tan⁡〖a^2/S〗〗

Угол, образованный при пересечении диагоналей, и дополнительный ему до 180° зависят только от углов при диагонали и стороне, и равны удвоенному их значению. (рис. 56.2) γ=2α δ=2β

Радиус описанной вокруг прямоугольника окружности равен половине диагонали, так как лежит на ней и исходит из точки пересечения диагоналей. (рис. 56.3) R=d/2=√(a^2+S^2/a^2 )/2

Источник

Калькулятор расчета площади четырехугольника

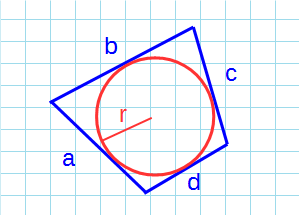
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

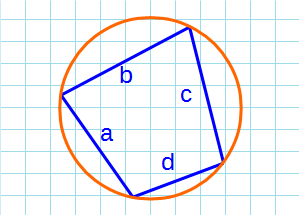
2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

Источник

Калькулятор площади прямоугольника

Прямоугольник — четыре точки, четыре попарно параллельных прямых, четыре прямых угла. Прямоугольник встречается в человеческой повседневности на каждом шагу, поэтому вопрос определения площади геометрической фигуры никогда не теряет своей актуальности.

Геометрия прямоугольника

В евклидовой геометрии прямоугольник — любой плоский четырехугольник, каждый угол которого равен 90 градусов. В геометриях Римана и Лобачевского невозможно получить четырехугольник, сумма углов которого будет равна 360 градусов — это значение всегда будет больше или меньше, следовательно, прямоугольник существует только на плоскости. Плоский параллелограмм считается прямоугольником, если выполняется хотя бы одно из перечисленных условий:

Золотой прямоугольник

Золотым называется прямоугольник, ширина и длина которого соотносятся как 1:fi, где fi приблизительно равно 1,618. Главная особенность золотого полигона состоит в том, что после удаления любого квадрата из фигуры, соотношение сторон прямоугольника останется таким же. Золотой прямоугольник широко используется в архитектуре. Соотношение 1:fi очаровало архитекторов времен Ренессанса, однако еще античные зодчие интуитивно пользовались данным правилом. К примеру, древнегреческий Пантеон в Афинах построен с учетом золотого соотношения сторон как 1 к 1,618.

Прямоугольник в реальности

Прямоугольник — наиболее распространенная плоская фигура в реальности. Прямоугольную форму имеют грани огромного количества предметов: столов, мониторов, системных блоков, полов, стен, книг, футбольных полей, деталей машин — перечислять можно бесконечно. С расчетом площадей прямоугольников постоянно имеют дело инженеры, проектировщики, землемеры, архитекторы, столяры или слесари, ведь прямоугольные детали встречаются практически на каждом шагу.

Площадь прямоугольника

Площадь геометрической фигуры — это числовая характеристика, иллюстрирующая ее размер. Площадь прямоугольника находится по простой формуле:

где a — длина прямоугольника, b — ширина.

Программный код калькулятора использует зависимости, при помощи которых можно найти площадь прямоугольника, зная только одну сторону и дополнительный параметр на выбор. В школьных задачах вместо длины или ширины могут указываться углы пересечения диагоналей альфа и бета или длина диагонали. Для корректного расчета площади важно ввести значения в соответствующие ячейки. Так, угол альфа — это угол пересечения диагоналей, которому противолежит длина прямоугольника, а углу бета противолежит ширина фигуры. На практике же проще всего будет измерить одну из сторон. Рассмотрим пару примеров на определение площади прямоугольника.

Примеры из реальной жизни

Покраска пола

Определение расхода краски — наиболее типичная бытовая задача, с которой сталкиваются многие люди. Допустим, нам необходимо покрасить пол в комнате размером 3 на 5 метров. Известно, что на обработку одного квадратного метра деревянной поверхности требуется 160 грамм краски. Следовательно, для определения расхода лакокрасочных материалов потребуется узнать площадь комнаты и разделить ее на стандартный расход. Площадь прямоугольника в бытовом случае находится очень просто: достаточно перемножить ширину и длину комнаты. Мы получим:

Таким образом, для обработки пола нам понадобится 15 × 0,16 = 2,4 кг краски или одна стандартная банка.

Школьная задача

Допустим, в задаче по геометрии требуется найти площадь прямоугольника, зная, что длина диагонали составляет 29 см, а ширина фигуры равна 20 см. Решая эту задачу вручную, нам бы потребовалось применить теорему Пифагора для нахождения второй стороны, а затем перемножить ширину и длину прямоугольника. Мы можем упростить себе задачу и просто ввести эти переменные в калькулятор. Мы получим ответ:

Кроме площади калькулятор также определил длину прямоугольника, равную 21 см. Числа 20, 21 и 29 составляют пифагорову тройку — целые числа, которые удовлетворяют условию теоремы Пифагора.

Заключение

Прямоугольник — широко распространенная фигура, и расчет ее площади никогда не теряет актуальности. И хотя формула для расчета площади проста как валенок, наш калькулятор может быть полезен как школьникам и студентам, так и представителям самых разных профессий.

Источник

Площадь неправильного четырехугольника

Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.

С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».

Как найти площадь неправильного четырехугольника?

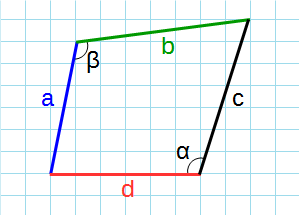
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.

Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

Источник

Стороны прямоугольника

Свойства

Зная стороны прямоугольника, можно вычислить все остальные его параметры, используя следующий ход действий. Периметр прямоугольника представляет собой удвоенную сумму его сторон, поэтому его можно сразу вычислить. P=2(a+b)

Площадь прямоугольника равна произведению его сторон, поэтому ее также можно найти сразу. S=ab

Диагонали в прямоугольнике являются конгруэнтными, каждая из них образует прямоугольный треугольник со сторонами прямоугольника. Из теоремы Пифагора каждая диагональ будет равна квадратному корню из суммы квадратов сторон прямоугольника. (рис. 56.1) d_1=d_2=√(a^2+b^2 )

Из этого же прямоугольного треугольника можно найти углы α и β при диагоналях, зная только стороны прямоугольника. Отношения катетов друг к другу дают тангенс или котангенс углов треугольника, поэтому α и β будут равны арктангенсу отношений сторон, а дальше значение в градусах можно найти, используя таблицы тангенсов. α=arc tan⁡〖b/a〗 β=arc tan⁡〖a/b〗

Углы γ и δ, образованные пересечением диагоналей, как видно из чертежа, через прямоугольный треугольник с полуосью, равны удвоенным значениям α и β соответственно. (рис.56.2) γ=2α δ=2β

Так как углы у прямоугольника все равны друг другу, вокруг него можно описать окружность. Центр окружности будет находиться в точке пересечения диагоналей, и следовательно, радиус описанной окружности будет равен половине диагонали. (рис.56.3) R=d/2=√(a^2+b^2 )/2

Источник

Калькулятор расчета площади прямоугольника

Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам. Подобный расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если нужно посчитать площадь комнаты при ремонте квартиры, для расчета необходимого количества материалов.

Удобная навигация по статье:

Калькулятор расчета площади прямоугольника

Как рассчитать площадь прямоугольника

Прямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны. Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:

Таким образом, произвести расчёт площади прямоугольника можно различными способами. Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.

Как вычислить площадь прямоугольника, имея линейные параметры его сторон?

Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.

Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».

Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?

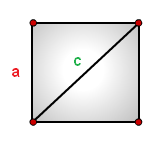
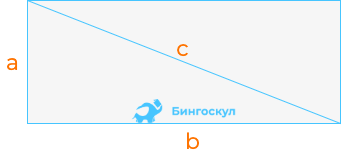
Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:

В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.

Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.

При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.

Площадь прямоугольника. Видео-урок.

Источник

Найти площадь прямоугольника через стороны

Главная » Учёба и наука » Математика » Найти площадь прямоугольника через стороны

Что такое прямоугольник

Прямоугольник — это плоская геометрическая фигура, параллелограмм, все углы которого равны 90°. Характеризуется наличием длины и ширины, состоит из четырёх сторон, 4-х вершин и прямых углов.

Противоположные стороны фигуры попарно параллельны и равны друг другу. Если длина и ширина прямоугольника равны, он является квадратом.

Частой задачей, например, в школе, является необходимость расчёта площади прямоугольника с целочисленными значениями длин его сторон: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и так далее (в мм, см, дм или м) …

Как рассчитать площадь прямоугольника онлайн

Под площадью прямоугольника подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.

Кстати, площадь прямоугольника невозможно найти, зная лишь только его периметр (в отличие от квадрата).

Всё зависит от того, какие данные у вас имеются. Данная формула и калькулятор позволит найти площадь прямоугольника через две стороны. Суть заключается в перемножении значений длин любых его двух смежных сторон.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Источник

Формулы площадей всех основных фигур

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

Формула площади круга, (S):

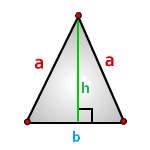
2. Формула расчета площади треугольника

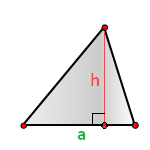
h — высота треугольника

a — основание

Площадь треугольника (S):

3. Площадь треугольника, формула Герона

p— полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

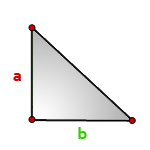
4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

Формула площади прямоугольного треугольника, (S):

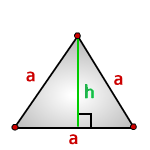
a — равные стороны

6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

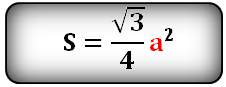
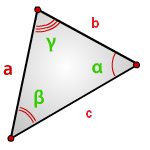
7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

8. Площадь треугольника по стороне и двум углам, формула.

Площадь треугольника через сторону и два угла (S):

9. Формула расчета площади прямоугольника

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

Формула площади трапеции, (S):

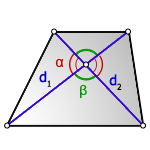
2. Формула площади трапеции через диагонали и угол между ними

Формула площади трапеции, (S):

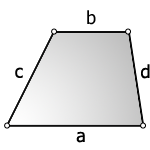
3. Формула площади трапеции через четыре стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

Формула площади равнобедренной трапеции через основания и высоту, (S):

Источник

Площадь прямоугольника

Определение площади прямоугольника

Формула расчёта площади прямоугольника

a – ширина прямоугольника

b – длина прямоугольника

S – площадь прямоугольника

К примеру, форму прямоугольников имеют полы очень многих жилых, производственных и складских помещений. Это совершенно не случайно, поскольку именно такая форма оказывается наиболее удобной и практичной при проектировании, строительстве и эксплуатации самых различных зданий. Соответственно, производить расчет площади прямоугольника очень часто приходится архитекторам, причем эти операции, ввиду простоты самой формулы, требуют затрат минимального количества времени.

Такая задача, как расчет площади прямоугольника, чрезвычайно часто стоит и перед разработчиками всевозможных машин и механизмов. В них постоянно встречаются элементы именно такой формы, и для того, чтобы сконструировать какой-либо узел, требуется, чтобы они безупречно сопрягались друг с другом, поскольку в противном случае неизбежно возникновение ситуации, когда узел или агрегат будет просто невозможно собрать. На производственных предприятиях, где осуществляется изготовления машин и механизмом, в качестве сырья часто листовой металлопрокат, также имеющий прямоугольную форму. На заготовительных и слесарных участках производится раскрой заготовок, многие из которых, прежде чем будут полностью обработаны и станут готовыми деталями, также являются прямоугольниками.

Очень многие детали корпусной мебели, которая повсеместно используется в жилых и офисных помещениях, также имеют прямоугольную форму. Особенно хорошо это заметно мастерам, которые занимаются ее сборкой. Само собой разумеется, что конструкторам мебельного производства при разработке столов, шкафов, тумбочек, антресолей и т.п. также приходится постоянно сталкиваться с расчетом прямоугольников, а тем специалистам, которые занимаются непосредственно производством – изготавливать прямоугольные элементы из древесины, ДВП, ДСП, МДФ, пластика, стекла и металлов в соответствии с чертежами.

Источник

Прямоугольник. онлайн калькулятор

Площадь прямоугольника через синус острого угла между диагоналями и длину диагонали

Диагонали в прямоугольнике равны, поэтому, чтобы вычислить площадь на основании длины диагонали и синуса острого угла между ними, следует воспользоваться следующей формулой: Площадь = Диагональ^2 × sin(острого угла между диагоналями)/2.

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.

Как найти площадь прямоугольника

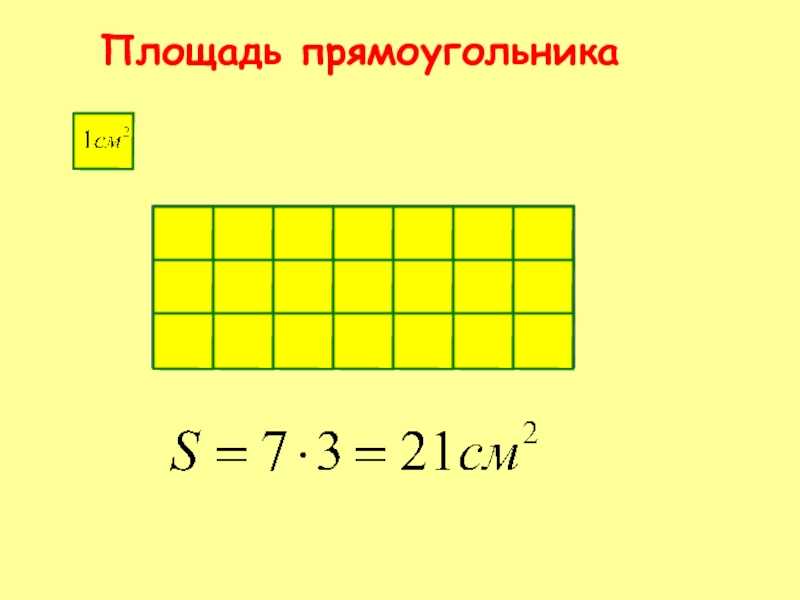
Самый простой способ нахождения площади прямоугольника – взять прозрачную бумагу, например кальку, или клеенку и расчертить ее на равные квадратики по 1 см, а потом приложить к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в сантиметрах квадратных. Например, на рисунке видно, что прямоугольник попадает в 12 квадратов, значит, его площадь равна – 12 кв. см.

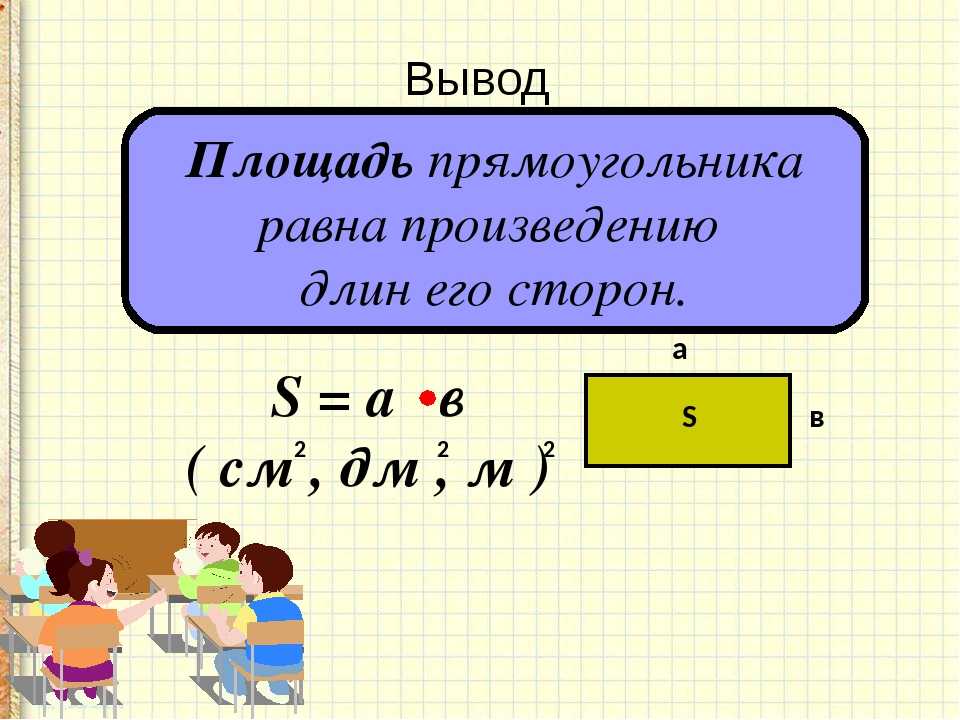
Но для нахождения площади больших объектов, например квартиры, необходим более универсальный способ, поэтому была доказана формула, чтобы найди площадь прямоугольника необходимо умножить его длину на ширину.

А теперь давайте попробуем записать правило нахождения площади прямоугольника в виде формулы. Обозначим площадь нашей фигуры буквой S, буква а – будет обозначать его длину, а буква b – ширину.

В итоге получаем вот такую формулу:

Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.см, т.к. а = 4 см, b = 3 см, а S = 4 * 3 = 12 кв.см.

Если взять две идентичные фигуры, и наложить их одну на другую, то они совпадут, а будут называться равными. У таких равных фигур будут также равны их площади и периметры.

Как вычислить площадь прямоугольника с разными сторонами

Согласно данной документации, на каждые 8 «квадратов» поверхности пола приходиться должно не менее одного «квадрата» источника естественного светового потока. На мансардных этажах эта пропорция не может быть менее 1:10.

Чтобы обеспечить качественное проведение ремонта нужно заранее выяснить, как вычислить площадь пола и другие необходимые размеры помещения. Подготовительный этап также предусматривает приобретение стройматериалов и тогда в процессе ремонта затраты будут сведены к минимуму, поскольку не получится больших остатков и стоимость доставки обойдется недорого.

Ручной способ вычислений как узнать площадь пола займет больше времени, чем при проведении расчетов на уже имеющемся строительном калькуляторе, но он позволяет узнать более точные результаты.

Задачи и упражнения

А теперь давайте рассмотрим несколько примеров.

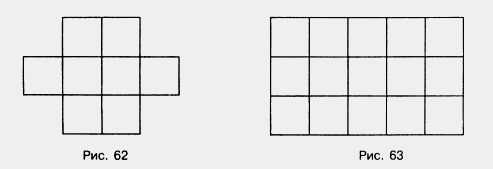
На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.

Если записать, то это будет выглядеть так:

1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.

Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:

Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.

Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:

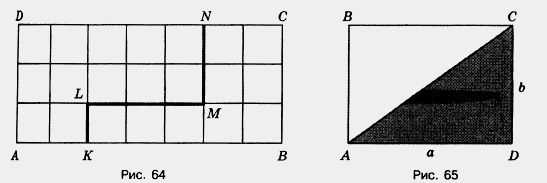
Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части. Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2.
Теперь давайте найдем площадь всего прямоугольника:

Итак, берем три и умножаем на семь и получаем 21 кв.см:

3 • 7 = 21 кв.см. При этом 21 = 12 + 9.

И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.

Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC

А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.

Представим, что сторона квадрата равна а, то:

Делаем вывод, что формула площади квадрата будет иметь такой вид:

А запись a2 называется квадратом числа а.

И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:

4 • 4, то есть 4 * 2 = 16 кв.см.

Зачем уметь находить площадь

• Во-первых, если вы знаете, как найти площадь какой-либо фигуры, то с помощью ее формулы вы без проблем сможете решать любые задачи по геометрии и тригонометрии.
• Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачки, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписаны в прямоугольник или около него.
• В-третьих, зная такую простую формулу, как S = а * b, вы получаете возможность без проблем решать любые простые бытовые задачи (например, находить S квартиры или дома), а со временем и сможете применить их к решению сложных архитектурных проектов.

То есть, если совсем упростить формулу нахождения площади, то она будет выглядеть так:

Что обозначает П – это искомая площадь, Д – это ее длина, Ш – обозначает ее ширину, а х – является знаком умножения.

А известно ли вам, что площадь любого многоугольника можно условно разбить на определенное количество квадратных блоков, которые находятся внутри этого многоугольника?
Какая разница между площадью и периметром

Давайте на примере попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут

Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны

Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

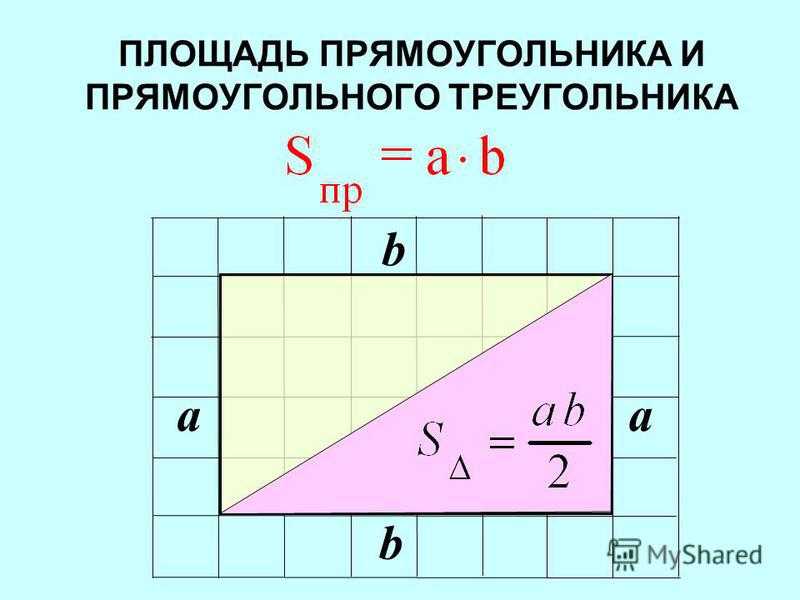
Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

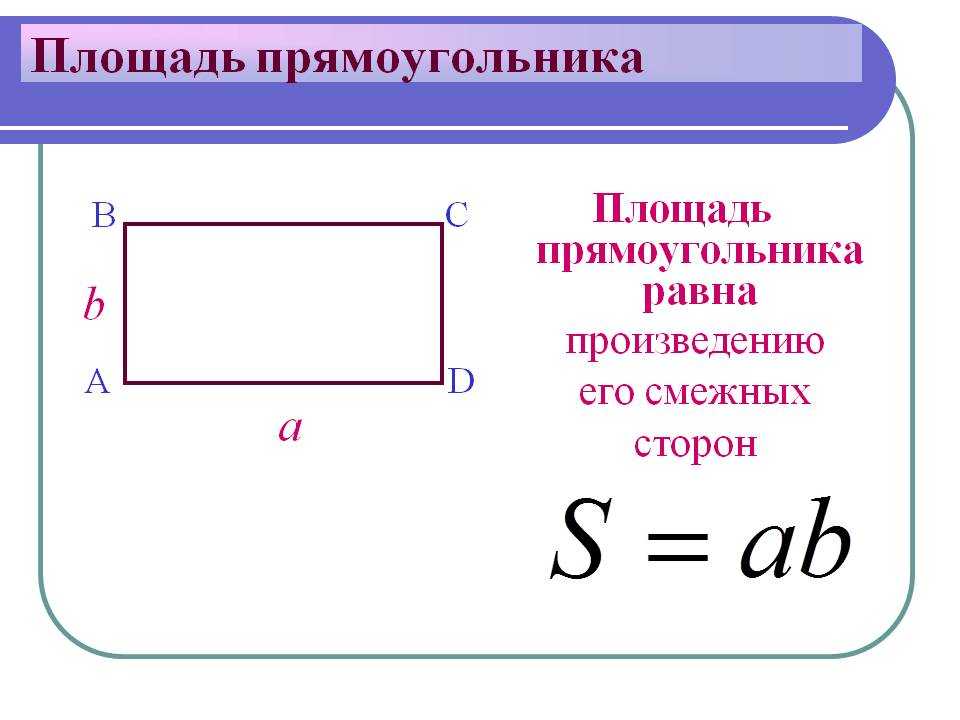
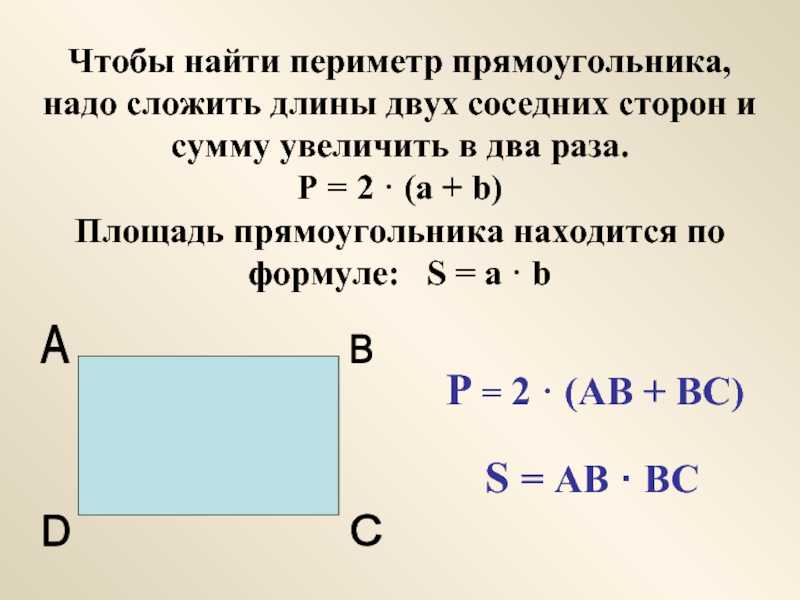
Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Формулы площади

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

S — площадь треугольника

a, b — длины 2-х сторон треугольника

С — угол между сторонами a и b

S — площадь треугольника

a — длина стороны треугольника

h — длина высоты, опущенной на сторону a

S — площадь треугольника

p — полупериметр треугольника

S — площадь треугольника

p — полупериметр треугольника

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

R — радиус описанной окружности

См. также: Программа для расчета площади треугольника.

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S — площадь квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Программа для расчета площади квадрата.

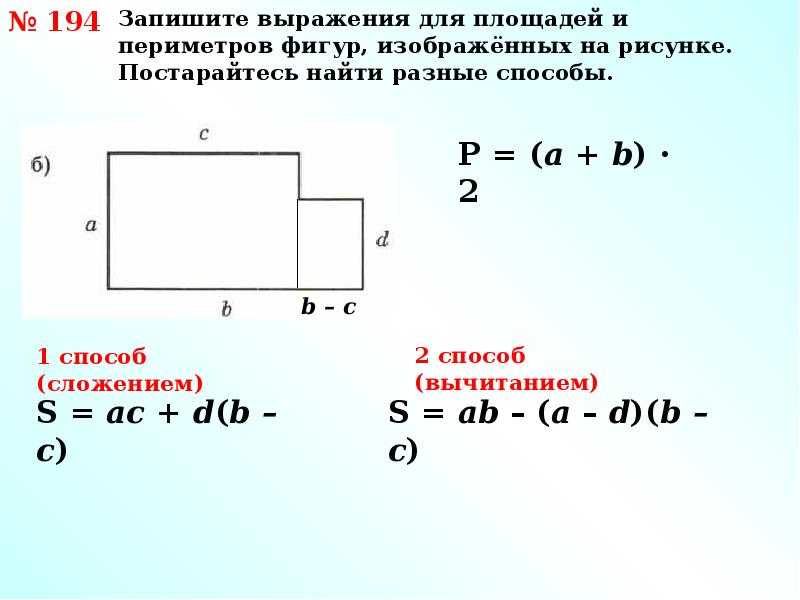
Формула площади прямоугольника:

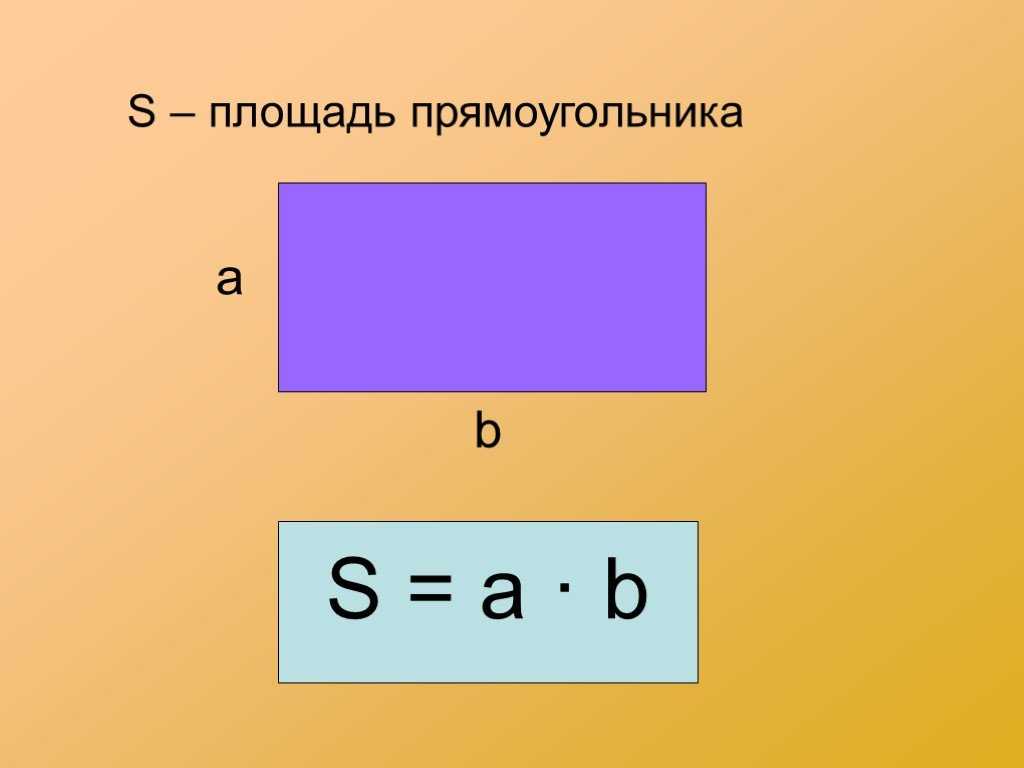
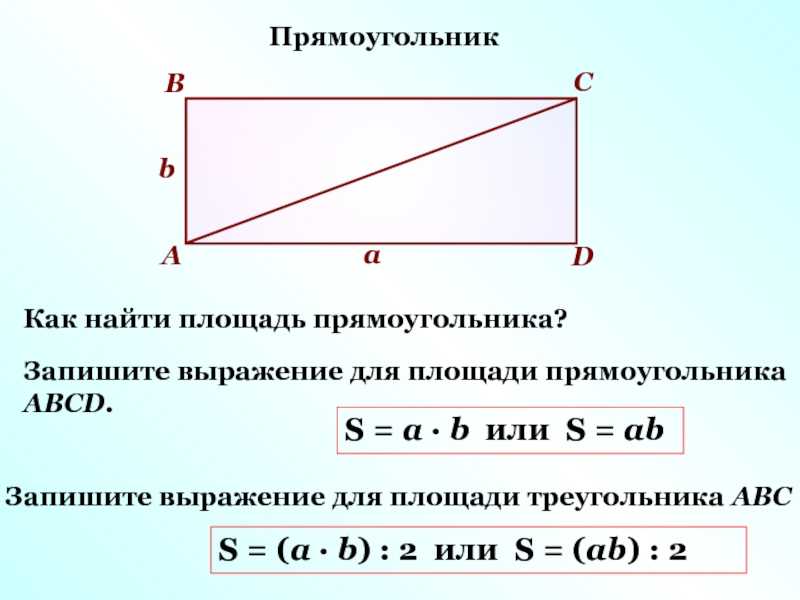
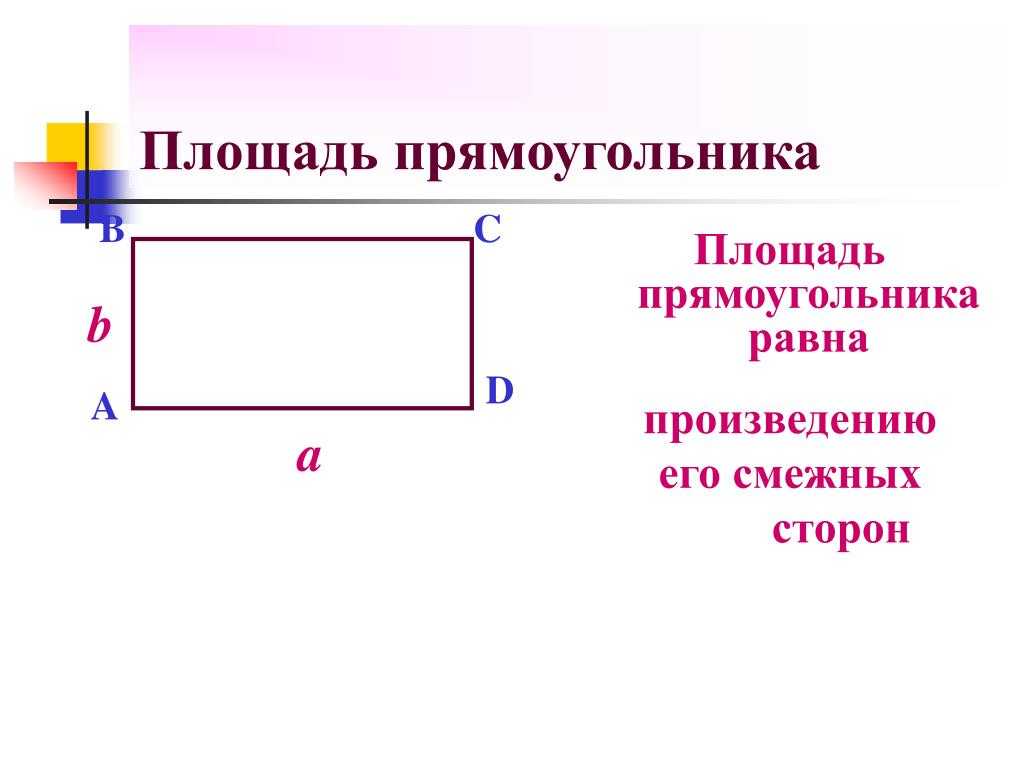
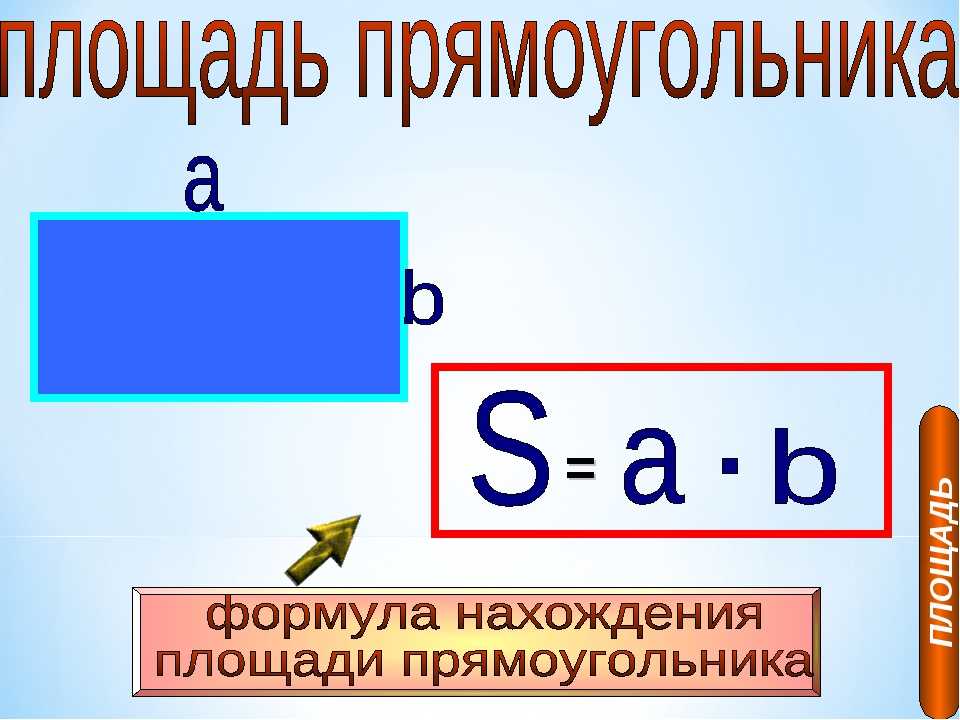
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S — площадь прямоугольника

a — длина 1-ой стороны прямоугольника

b — длина 2-ой стороны прямоугольника

См. также: Программа для расчета площади прямоугольника.

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

S — площадь параллелограмма

a — длина основания

h — длина высоты

См. также: Программа для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S — площадь трапеции

a — длина 1-ого основания

b — длина 2-ого основания

h — длина высоты трапеции

Как называется с прямыми углами четырехугольник?

Слово «четырехугольник» говорит о том, что рассматриваемая фигура состоит из четырех углов. На плоскости она будет замкнута только в том случае, если имеет четыре прямые стороны. Если противоположные стороны попарно друг другу параллельны, то такая фигура называется параллелограммом. Его четыре угла попарно равны, однако они могут принимать произвольные значения от 0o до 180o. Если все его углы будут равны 90o, то они называются прямыми. Четырехугольник с углами прямыми — это прямоугольник, и одновременно он является параллелограммом.

Прямоугольник характеризуется всего двумя параметрами: длинами его соседних сторон. Далее в статье будем обозначать их a и b. Если эти длины равны друг другу, то прямоугольник вырождается в квадрат.

Принцип расчета площади прямоугольника

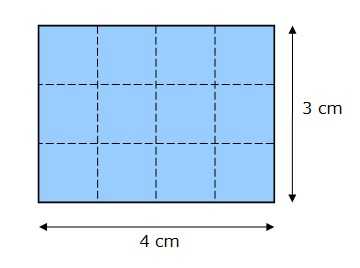
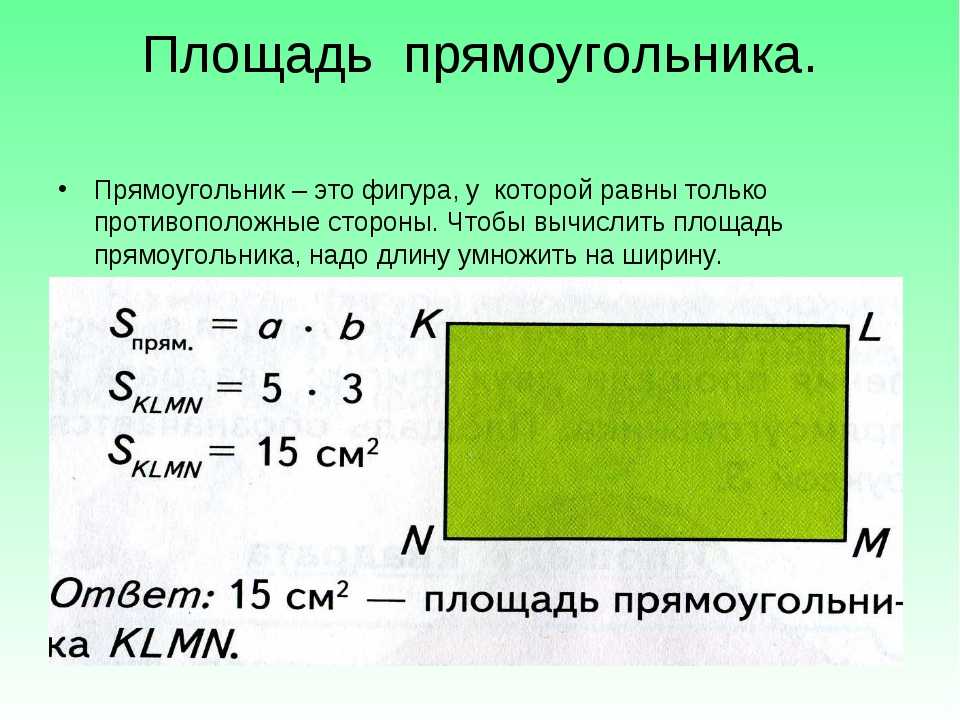
Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

Как найти площадь прямоугольника? Площадь прямоугольника можно вычислить, если известны длины его сторон либо длина диагонали и угол между диагоналями.

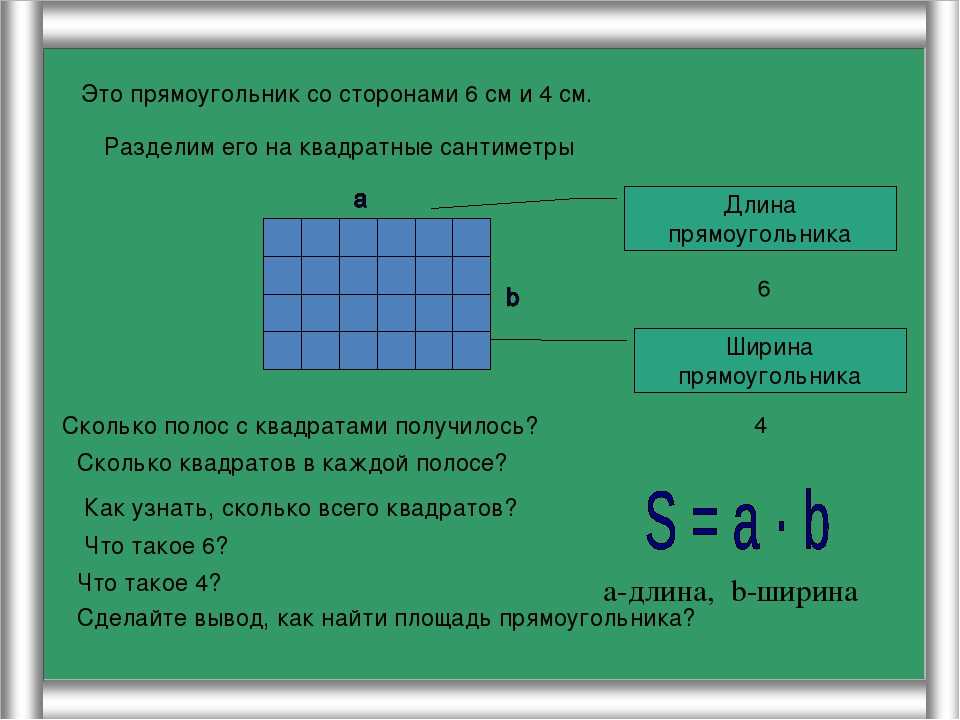
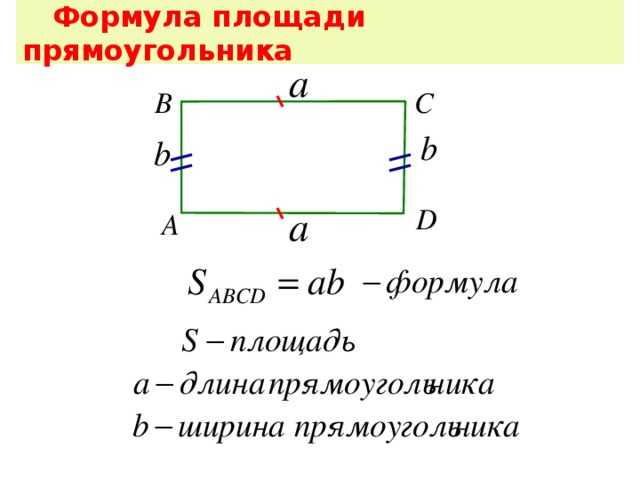
I. Площадь прямоугольника равна произведению его длины на ширину.

Формула площади прямоугольника по сторонам

II. Площадь прямоугольника равна половине произведения квадрата его диагонали на синус угла между диагоналями.

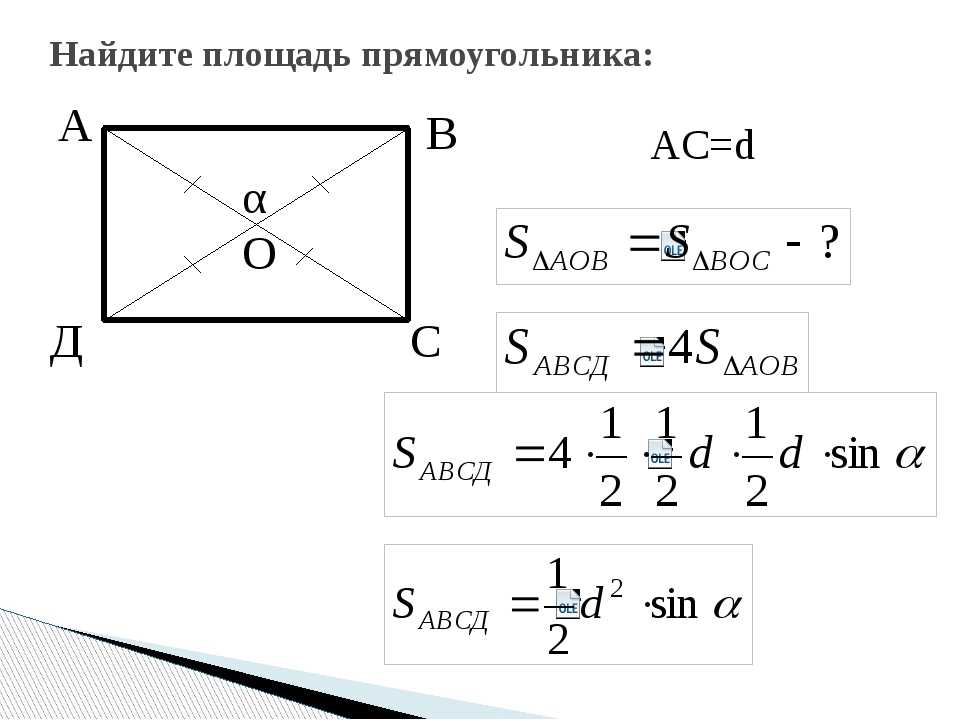
Формула площади прямоугольника по диагонали и углу между диагоналями

В качестве угла между диагоналями может быть взят любой угол — как острый, так и тупой (поскольку синус тупого угла равен синусу смежного с ним острого угла).

Например, площадь прямоугольника

ABCD можно найти как

Таким образом, если требуется найти площадь прямоугольника, задача, как правило, сводится к нахождению либо длин его сторон, либо диагонали и угла между диагоналями.

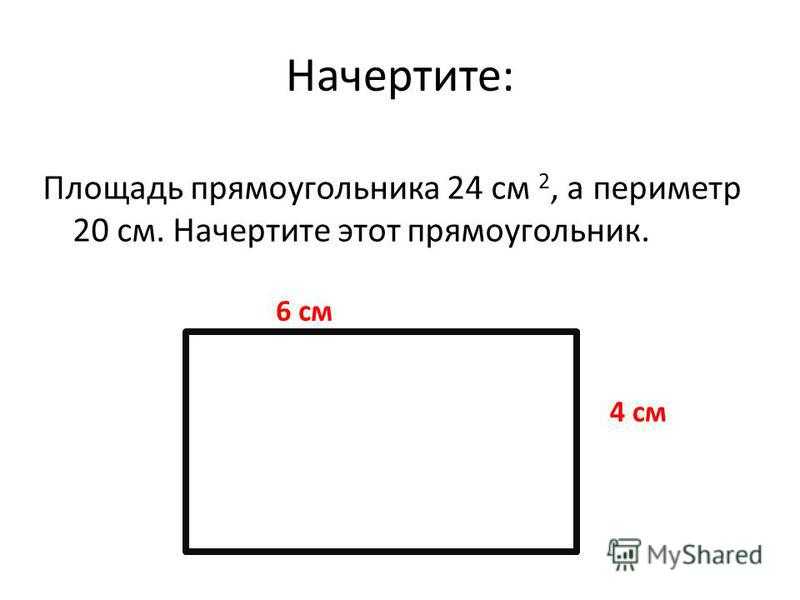
Найти площадь прямоугольника, одна сторона которого на 5 см больше другой, а периметр равен 38 см.

Формула для нахождения периметра прямоугольника —

Пусть a=x см, тогда b=(x+5) см.

По условию, периметр равен 38 см. Составим уравнение:

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

Из формулы (7) найдем \( \small b \) и подставим в (6):

Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):

Вычислим дискриминант квадратного уравнения (10):

Сторона прямоугольника вычисляется из следующих формул:

После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:

Как рассчитать площадь стен комнаты

Порядок вычисления площади стенок и пола отличается. Дело в том, что до того, как рассчитать квадратуру пола, следует узнать длину и ширину помещения, а для расчета стен потребуется измерить его высоту. Поэтому сначала узнают периметр комнаты и умножают на высоту потолков.

Например, параметры пола 3 и 4 метра, а высота помещения равна 3 метрам. В этом случае периметр стен будет равен (3 + 4) х2 = 14 м., а их площадь S = 14х3 = 42 м². При этом не следует забывать про квадратуру проемов окон и дверей. Их площадь вычитают после завершения расчетов стен

Но с другой стороны их можно не принимать во внимание и тем самым обеспечить некоторый запас материалов

Признаки и свойства прямоугольника

Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:

Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.

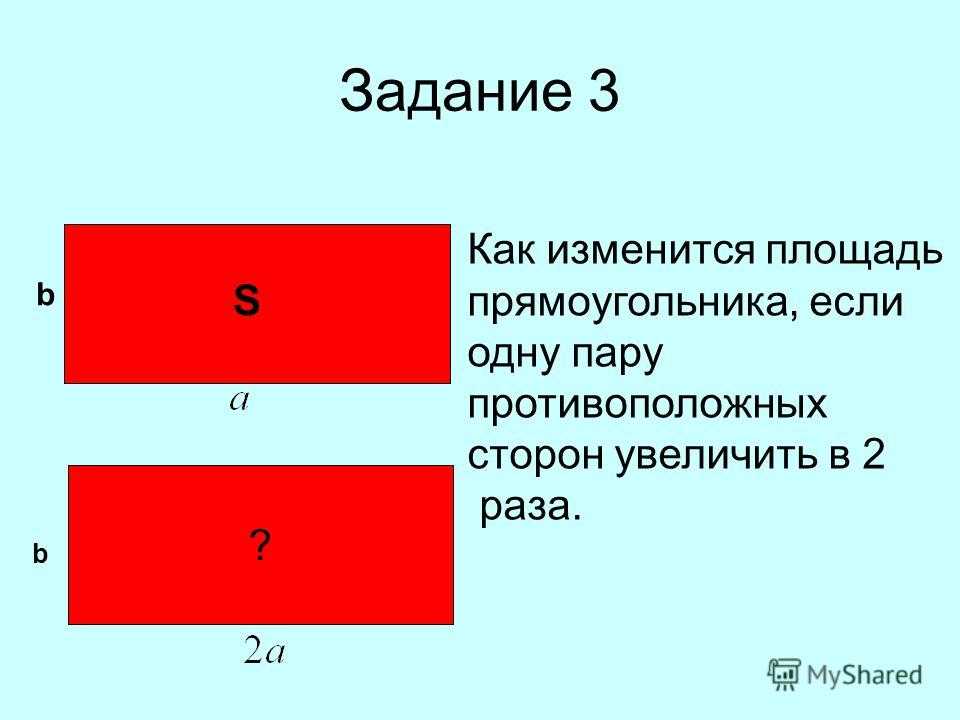
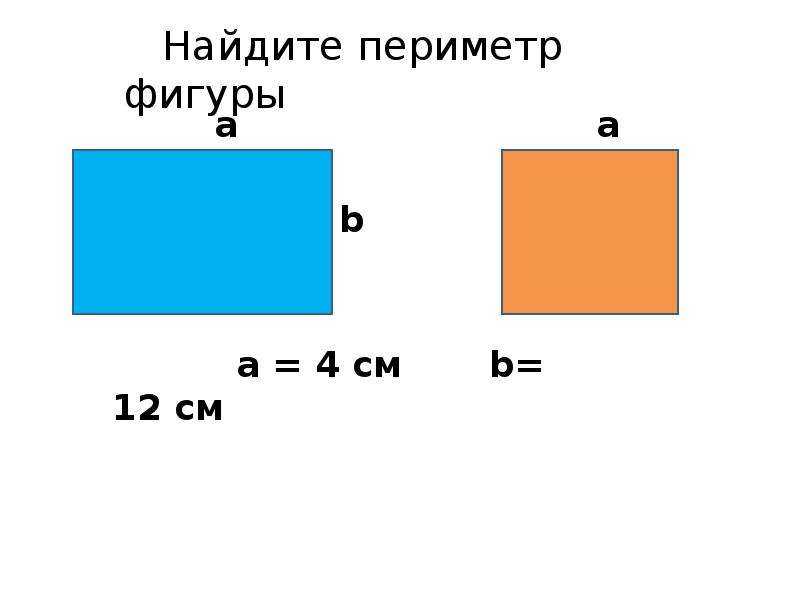
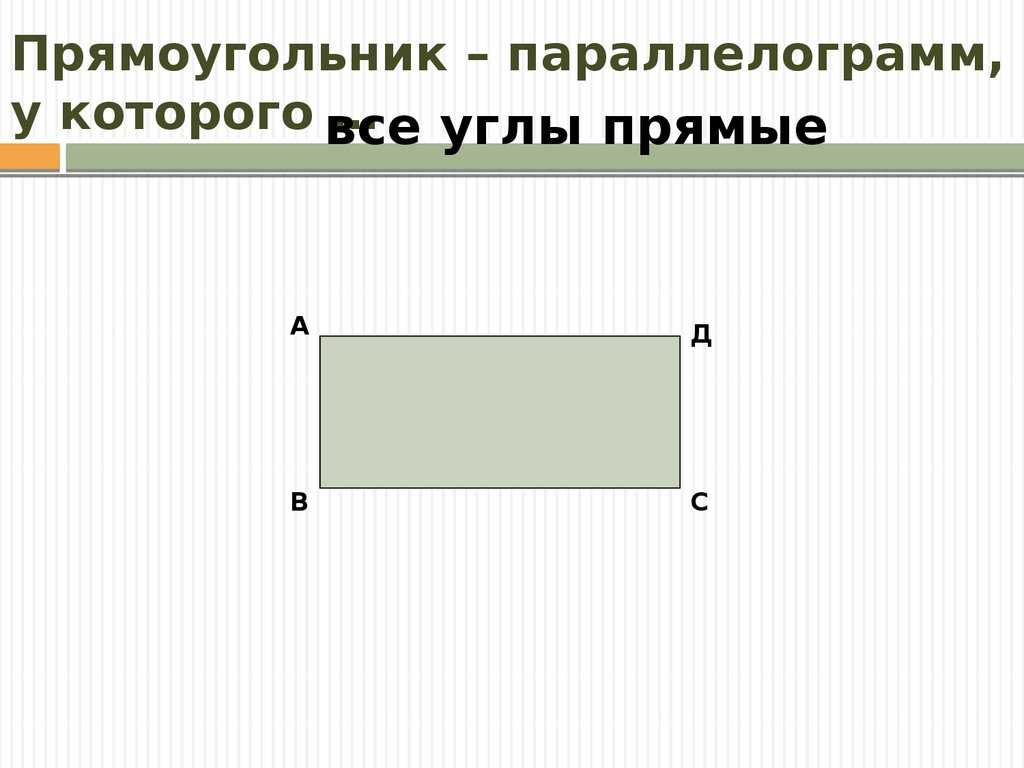
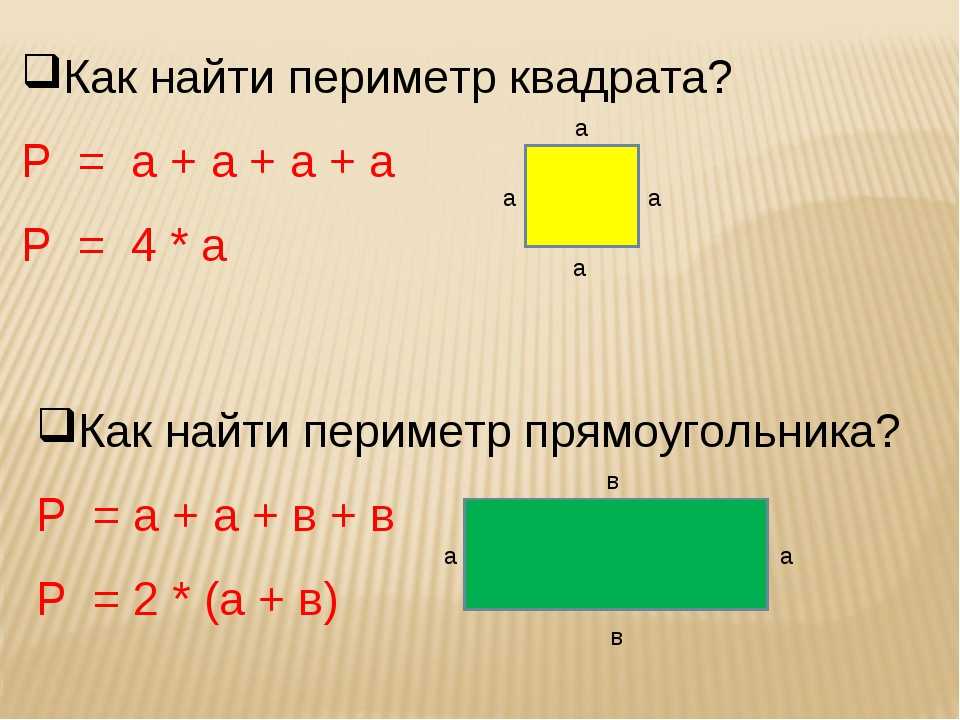
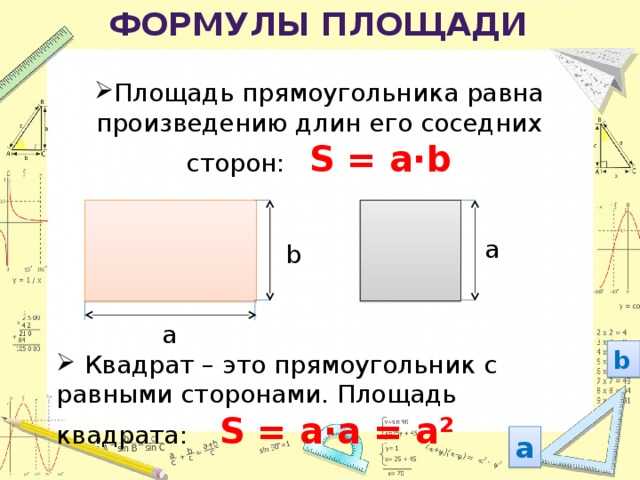
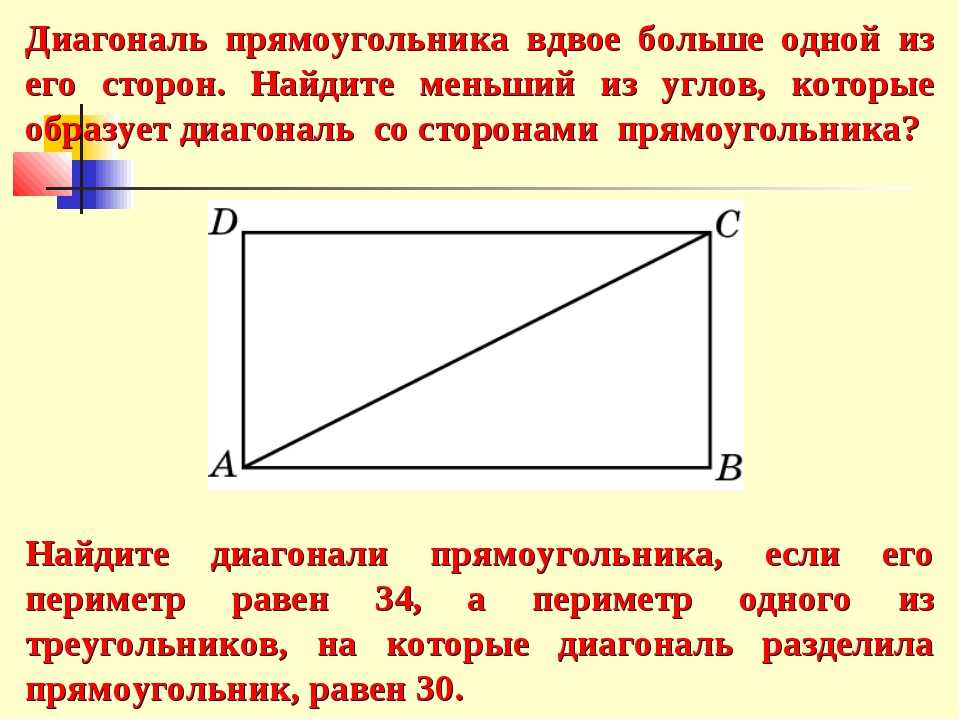
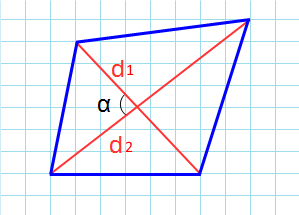
Формулы для вычисления длины сторон

В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).

Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α угол между диагональю и длиной, β острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:

Периметр и площадь

Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:

Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:

Диагонали прямоугольника

В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:

Применяются следующие формулы для расчёта длины диагонали:

Принцип расчета площади прямоугольника

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Площадь участка сложной формы

Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).

Длина стороны A

Длина стороны B

Длина стороны C

Длина стороны D

Площадь неправильного четырехугольника, зная только длины сторон, вычислить нельзя. Надеюсь, эта демонстрация поможет понять это всем, кто просил создать для этого калькулятор.

Зачем нужно знать площадь полаОпределение площади прямоугольного помещенияРасчет площади комнаты неправильной планировкиУзнаём площадь треугольного помещения

Как рассчитать площадь стен комнатыПропорции между площадью пола и окон

Невозможно проводить ремонт напольной поверхности, не зная точную площадь пола в частном домовладении или квартире. Дело в том, что сегодня стоимость строительных материалов достаточно высокая, и каждый владелец недвижимости старается максимально сэкономить на их покупке. Поэтому информация, как рассчитать площадь пола, не будет лишней для того, кто предпочитает делать ремонт собственноручно.

Источник

Как рассчитать площадь прямоугольника

Для того чтобы затеять ремонт потолка необходимо сделать приблизительный план расходов. Предварительно распланировав бюджет можно исключить множество недоразумений. Стоит посчитать, сколько брать материалов и сколько нужно отдать мастерам для ремонта, если вы решили нанять специалистов. Многие мастера в своих прайс-листах указывают цену услуг за квадратный метр, поэтому в первую очередь, нужно выяснить какая площадь у нашего потолка. Больших навыков для того чтобы определить площадь не требуется, применяется лишь простая формула из курса геометрии начального уровня.

Первым шагом для вычисления площади является определение формы потолка. Существуют простые и сложные геометрические фигуры, что относится и к потолкам. Простые фигуры – это фигуры в форме прямоугольника. А сложные – это разные «Г», «П», «Т»-образные формы потолков.

Инструменты для подсчета площади

Как для и любой процедуры необходимы инструменты для работы, так и для того чтобы измерить площадь нужен свой набор. Первое что нам нужно – это рулетка, с помощью которой определяются длины сторон. Затем стоит приготовить стремянку, чтобы дотягиваться до потолка, если пол и потолок не одинаковые. Только так можно наиболее точно производить замеры. Запасаемся листком бумаги, ручкой и калькулятором для записи и расчета данных.

Последовательность действий

Для расчета площади нам в первую очередь нужно выяснить длину сторон, поэтому это и будет нашим первым шагом. Берем стремянку и ставим в угол комнаты – это наша точка отсчета. Прикладываем рулетку к самому углу и начинаем растягивать ко второму углу, так мы узнаем длину первой стороны.

Полученный результат фиксируем на листке как данную «А». Затем таким же способом нужно измерить длину второй стороны прямоугольника – это у нас данная «В». Диагональ нам измерять не нужно, хотя если знать диагональ и одну сторону тоже можно рассчитать площадь.

Формула расчета

У нас есть длина сторон А и В, дальнейшим действием будет определить саму площадь. На помощь приходит формула:

S=A∙B, S – площадь, а А и В – это длины сторон. Так если стороны прямоугольника 3 и 4, то рассчитать помогает наша формула. 3 умножаем на 4 и получаем 12 – это и есть наша площадь.

Как видно если потолок в форме простой фигуры, то считать проще простого, но что делать, если форма потолка сложная? А для этого применяется эта же формула, только фигуру нужно разбить на простые прямоугольники. Производится расчет всех площадей и складывается между собой.

Касательно расчета площади зная диагональ и длину одной из сторон, то тут следующая формула:

Диагональ в квадрате минус длина стороны в квадрате и получаем длину второй стороны в квадрате. Итак, мы узнаем длину обеих сторон, и остальное считаем по старой формуле. Подомный расчет более громоздкий, но если известна диагональ прямоугольника, с расчетом не возникает проблем.

Если вы обращаетесь к специалистам, то весь процесс расчета и ремонта они берут на себя. Однако для самостоятельной планировки после выяснения площади необходимо рассчитать бюджет на материалы. Следует планировать объем расходных материалов больше, чем требуется примерно на 15 %. Это делается на случай неожиданной поломки или порчи во время монтирования. Правильно сделанный расчет площади прямоугольника позволит иметь приблизительную картину всех расходов. Так можно рационально распределить свой бюджет и в будущем сэкономить время и деньги, ведь лучше все сразу закупить и привезти, чем делать второй рейс за недостающим материалом.

Источник

Как найти площадь прямоугольника

Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко

Геометрическая фигура

Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.

Площадь=длина*ширина

Резюме

Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.

Источник

Узнаем как найти площадь прямоугольника

С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем жизненном пути встает очень часто и является важным не только для школьников.

Для тех, кто не знает, прямоугольник – это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.

Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.

Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.

А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.

В математике, особенно в старших классах, приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?

В виде формулы это будет выглядеть так:

Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:

S=d2,где d – диаметр.

S=b* (P – 2*b), где b – длина стороны, P – периметр.

Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.

Источник

Площадь прямоугольника

I. Площадь прямоугольника равна произведению его длины на ширину.

Формула площади прямоугольника по сторонам

Формула площади прямоугольника по диагонали и углу между диагоналями

Например, площадь прямоугольника

ABCD можно найти как

Найти площадь прямоугольника, одна сторона которого на 5 см больше другой, а периметр равен 38 см.

Формула для нахождения периметра прямоугольника —

Пусть a=x см, тогда b=(x+5) см.

По условию, периметр равен 38 см. Составим уравнение:

Источник

Как найти площадь неравностороннего прямоугольника

На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.

Через диагонали и угол между ними

Формула для нахождения площади четырехугольников через диагонали и угол между ними:

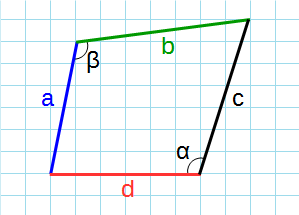
Через стороны и противолежащие углы

Формула для нахождения площади четырехугольников через стороны и противолежащие углы:

Площадь вписанного четырехугольника в окружность

Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:

Площадь описанного четырехугольника около окружности через радиус

Формула для нахождения площади описанного четырехугольника около окружности через радиус:

Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн.

Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

Площадь четырехугольника по диагоналям и углу между ними

Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

Вычисляет площадь неправильного четырехугольника с известными длинами сторон

С завидным упорством некоторые пользователи Planetcalc оставляют запросы на создание калькулятора для расчета площади неправильного четырехугольника, для которого известны только длины сторон. Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).

Источник

Как рассчитать площадь четырехугольника

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.

Через диагонали и угол между ними

Формула для нахождения площади четырехугольников через диагонали и угол между ними:

Через стороны и противолежащие углы

Формула для нахождения площади четырехугольников через стороны и противолежащие углы:

Площадь вписанного четырехугольника в окружность

Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:

Площадь описанного четырехугольника около окружности через радиус

Формула для нахождения площади описанного четырехугольника около окружности через радиус:

Источник

Площадь прямоугольника и квадрата

Площадь прямоугольника или квадрата – это часть плоскости, занимаемая данной фигурой.

Чтобы узнать сколько места они занимают, надо вычислить их площадь. Так как размеры прямоугольников даны в сантиметрах, то и за единицу измерения площади можно взять квадратный сантиметр.

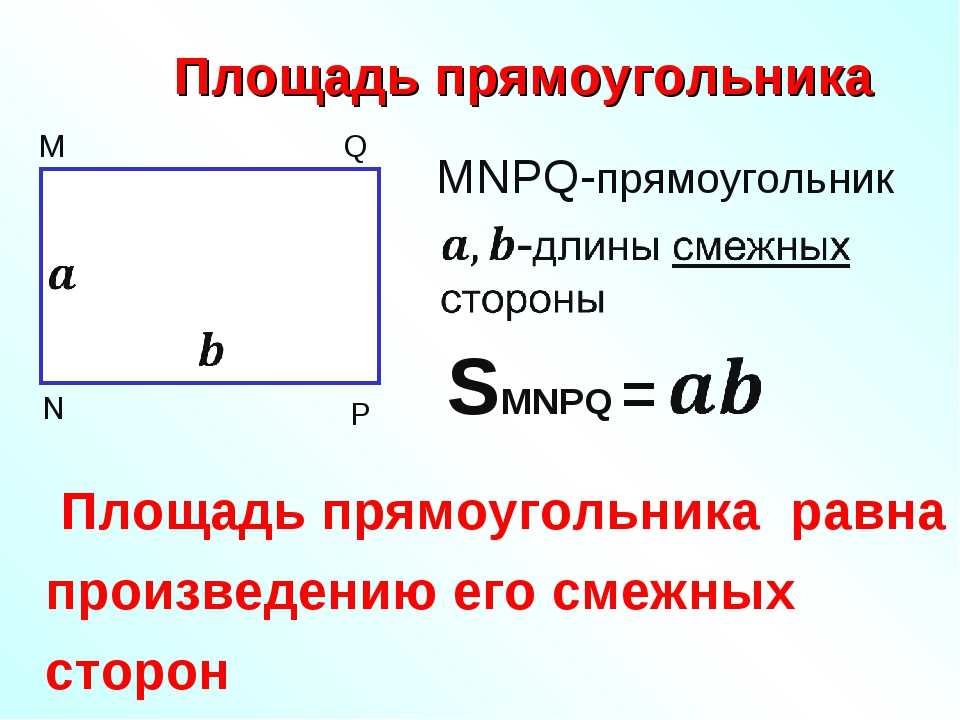
Из данного примера можно сделать вывод, что площадь прямоугольника равна произведению длин его смежных сторон. Общая формула:

где S — площадь прямоугольника, а a и b — его смежные стороны.

Рассмотрим квадрат ABCD:

Из примера можно сделать вывод, что площадь квадрата равна длине любой его стороны во второй степени. Общая формула:

где S — площадь квадрата, а a — его сторона.

Чтобы узнать площадь прямоугольника, надо взять его длину и ширину (в одинаковых единицах измерения) и найти их произведение (площадь должна быть выражена в соответствующих единицах измерения).

Задача. Длина прямоугольного дома равна 12 метром, а ширина — на 5 метров меньше. Чему равна площадь дома?

Решение: Задача будет решаться в два действия:

Источник

Площадь. Площадь прямоугольника

Фигуры на рисунке 146, а и б равны, так как они совпадают при наложении.

Очевидно, что фигуры на рисунке 146, а и в не равны. Однако каждая из них состоит из семи квадратов со стороной 1 см.

Про такие фигуры говорят, что их площади равны.

С такой величиной, как площадь, вы час

то встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т.п.

Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, прихожей и т.д.). Эти примеры иллюстрируют свойства площади фигуры.

1 ) Равные фигуры имеют равные площади.

2 ) Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Как можно измерить площадь фигуры?

Напомним, что для измерения отрезков мы вводили единичный отрезок, а для измерения углов − единичный угол.

Вообще, когда нужно измерить какую−либо величину, вводят единицу измерения.

За единицу измерения площади выбираю квадрат, сторона которого равна единичному отрезку. Такой квадрат называют единичным.

Площадь квадрата со стороной 1 м называют квадратным метром.

Площадь квадрата со стороной 1 см называют квадратным сантиметром.

Площадь квадрата со стороной 1 мм называют квадратным миллиметром.

Измерить площадь фигуры − значит подсчитать, сколько единичных квадратов в ней помещается.

Если одна сторона прямоугольника равна 6 см, а другая сторона 4 см, то этот прямоугольник можно разделить на 4 * 6 единичных квадратов (рис. 147 ). Поэтому его площадь равна 4 * 6 = 24 (см 2 ).

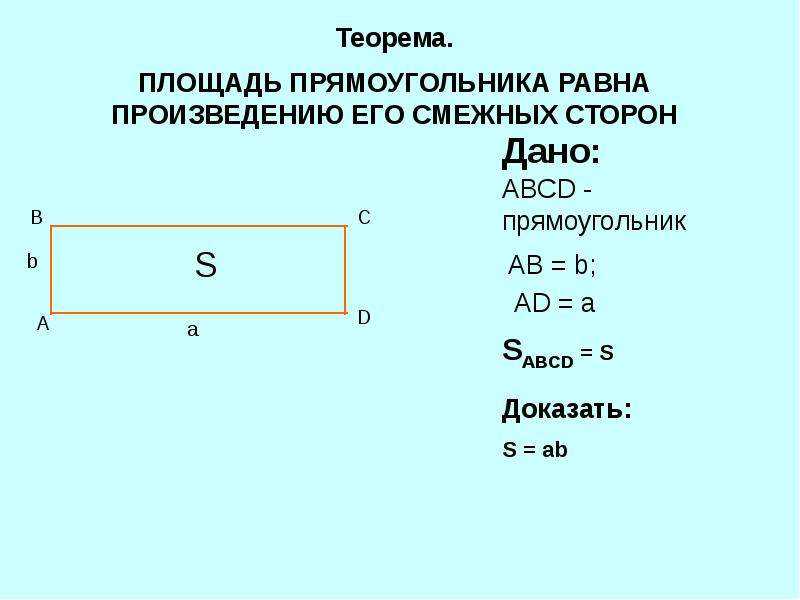
Площадь прямоугольника равна произведению длин его соседних сторон:

S = ab

Поскольку у квадрата все стороны равны, то его площадь вычисляют по формуле:

S = a 2

где a − длина стороны квадрата. Именно поэтому втору степень числа называют квадратом числа.

Вы знаете, что равные фигуры имеют равные площади. Однако если площади фигур равны, то не обязательно будут равными сами фигуры (см. рис. 146 ).

Для измерения площади земельных участков используют различные единицы измерения. Например: ар, гектар.

В быту 1 ар называют соткой.

Источник

Как рассчитать площадь по периметру. Калькулятор вычисления периметра и площади геометрических фигур

Время на чтение: 8 минут

В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.

Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.

Задача 1. Найти стороны прямоугольника из площади

Задача 2. Найти стороны прямоугольника из периметра

Задача 3. Найти площадь прямоугольника из пропорции его сторон

Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.

Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2

Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.25
S 2 = 1,25ab / 1.25

Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25

Ответ : ширину нужно уменьшить на 20%.

Как вычислить площадь фигуры зная ее периметр? и получил лучший ответ

Ответ от Ѐамис Ш [новичек]
..

Ответ от Kiss(RUSS фор всех) ки (я) [гуру]
1.выбрать центр
2.измерить расстояние от центра до углов
3.измерить стороны вашего многоугольника
4.вычислить периметры получившихся N треугольников
5.вычислить площади всех треугольников, используя формулу Герона-через полупериметр.
6.суммировать все площади
7.выбрать мой ответ лучшим.
8.все

Ответ от Semrid [гуру]
попробуй разделить периметр на 4 и потом перемножить полученное друг на друга

Ответ от ScrAll [гуру]
Вырезаешь из бумаги и взвешиваешь.
Или разбиваешь на треугольники.
Половина основания на высоту.

Ответ от Мария Кемпель [активный]
нереально

Ответ от Nemo [гуру]
Нереально. По периметру вычисляется площадь только ПРАВИЛЬНЫХ фигур. Советую кусочным способом

Ответ от Djon [гуру]
лучше всего разбить сложную фигуру на несколько простых, и посчитать площадь отдельно, затем сложить

Ответ от 3 ответа [гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Как вычислить площадь фигуры зная ее периметр?

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Частные случаи

Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.

Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.

Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.

Многоугольник

где n – количество сторон многоугольника, a – длина стороны.

Для определения площади используется выражение:

S = n/4 × a 2 × ctg(pi/n).

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Примеры из реальной жизни

Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.

Покраска забора

Отделка бахромой

Таким образом, нам понадобится 4 м бахромы для отделки платка.

Заключение

Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.

Геометрия постигает свойства и колляции двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по знаменитым формулам либо выражается одно через другое.

Инструкция

1. Прямоугольник.Задача: вычислите площадь прямоугольника, если вестимо, что его периметр равен 40, а длина b в 1,5 раза огромнее ширины a.

2. Решение.Используйте знаменитую формулу периметра, он равен сумме всех сторон фигуры. В данном случае P = 2 a + 2 b. Из исходных данных задачи вы знаете, что b = 1,5 a, следственно, P = 2 a + 2 1,5 a = 5 a, откуда a = 8. Обнаружьте длину b = 1,5 8 = 12.

3. Запишите формулу для площади прямоугольника:S = a b,Подставьте вестимые величины:S = 8 *12 = 96.

4. Квадрат.Задача: обнаружьте площадь квадрата, если периметр равен 36.

5. Решение.Квадрат – частный случай прямоугольника, где все стороны равны, следственно, его периметр равен 4 a, откуда a = 8. Площадь квадрата определите по формуле S = a? = 64.

6. Треугольник.Задача: пускай дан произвольный треугольник ABC, периметр которого равен 29. Узнайте величину его площади, если знаменито, что высота BH, опущенная на сторону AC, делит ее на отрезки с длинами 3 и 4 см.

7. Решение.Для начала припомните формулу площади для треугольника:S = 1/2 c h, где c – основание и h – высота фигуры. В нашем случае основанием будет сторона AC, которая знаменита по условию задачи: AC = 3+4 = 7, осталось обнаружить высоту BH.

11. Обнаружьте площадь треугольника ABC:S = 1/2 7 10,42 = 36,47.

Источник

Площадь прямоугольника

Площадь прямоугольника.

Площадь прямоугольника – это численная характеристика прямоугольника, показывающая размер прямоугольника.

Площадь прямоугольника:

Площадь прямоугольника – это численная характеристика прямоугольника, показывающая размер прямоугольника.

– либо диагональ прямоугольника и угол между диагоналями,

– либо периметр прямоугольника, а также или длину, или ширину прямоугольника,

– либо диагональ прямоугольника, а также или длину, или ширину прямоугольника,

– либо радиус описанной окружности, а также или длину, или ширину прямоугольника,

можно найти площадь прямоугольника.

Формулы площади прямоугольника:

1. Площадь прямоугольника через две стороны.

Площадь прямоугольника равна произведению длин двух его смежных сторон.

Рис. 1. Площадь прямоугольника

Формула площади прямоугольника через две его стороны.

2. Площадь прямоугольника через диагонали прямоугольника и угол между ними.

Рис. 2. Площадь прямоугольника

Формула площади прямоугольника через диагонали прямоугольника и угол между ними.

3. Площадь прямоугольника через периметр и одну из его сторон (длину или ширину).

Рис. 3. Площадь прямоугольника

Формула площади прямоугольника через периметр и одну из его сторон.

4. Площадь прямоугольника через диагональ и одну из его сторон (длину или ширину).

Рис. 4. Площадь прямоугольника

Формула площади прямоугольника через диагональ и одну из его сторон.

5. Площадь прямоугольника через радиус описанной окружности и одну из его сторон (длину или ширину).

Рис. 5. Площадь прямоугольника

Формула площади прямоугольника через радиус описанной окружности и одну из его сторон.

Мировая экономика

Справочники

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник

Как рассчитать площадь прямоугольника

Здравствуйте!
Как рассчитать площадь прямоугольника? Покажите, пожалуйста, на примерах. Мне так понятнее будет.
Спасибо!

Как рассчитать площадь прямоугольника
Чтобы рассчитать площадь прямоугольника его длину нужно умножить на его ширину:

Рассмотрим примеры расчета площади прямоугольника.

Пример 1.
Найдем площадь прямоугольника, у которого одна сторона равна 13 см, а смежная с ней — 15 см.

Решение.
Воспользуемся формулой, рассмотренной выше:
(кв. см).

Ответ. 195 кв. см.

Пример 2.
Найдем площадь прямоугольника, сторона которого равна 13 м, а диагональ — 17 м.

Решение.
Нарисуем произвольный прямоугольник FGHK (не забываем, что у него все углы прямые, а противоположные стороны равны).
Проведем в нем диагональ FH. Помним, что обе диагонали у прямоугольника равны, поэтому в данной задаче неважно, какую из них мы нарисуем.
Рассмотрим прямоугольный треугольник FGH (его угол FGH — прямой). Теперь можно воспользоваться теоремой Пифагора, чтобы с ее помощью найти катет GH:
(м).
Подставим нужные значения в формулу площади:
(кв. см).

Ответ. (кв. см).

На самом деле формул для расчета площади прямоугольника гораздо больше. Можно площадь найти через диагонали прямоугольника, через радиус вписанной или описанной окружности и т.д.

Источник

Формулы площадей всех фигур в геометрии — примеры вычислений

Поверхность тела и ее площадь

Это мера того, сколько пространства находится внутри плоской формы. В общем случае площадь поверхности представляет собой сумму всех областей геометрических фигур, покрывающих поверхность объекта. Рассчитать площадь поверхности тела часто требуется в повседневной жизни, например, чтобы узнать сколько краски нужно купить, чтобы покрыть стену, или шифера для ремонта крыши дома.

Люди издавна научились определять площадь плоских геометрических фигур, используя метод сетки. Он заключается в том, что на измеряемую фигуру накладывают масштабированную сетку из простейших квадратов, например, 1х1 см. После чего можно легко рассчитать квадратную площадь, посчитав количество квадратов сетки внутри формы. В этом случае каждый квадрат сетки имеет ширину 1 см и высоту 1 см, и площадь этого квадрата сетки составляет один квадратный сантиметр.

Использование сетки для подсчета квадратов в форме — это очень простой способ определения площади, но он не может быть применен для определения площади сложных фигур. Площадь таких сложных объектов может быть рассчитана с использованием простых математических формул. Самые простые и наиболее часто используемые в жизни вычисления — это площади квадратов и прямоугольников, и надо знать, как рассчитать площадь в метрах.

Часто в реальности расчеты могут быть более сложными. Например, типичный план этажа комнаты может не состоять из простого прямоугольника или квадрата. В этом случае перед тем, как рассчитать общую площадь, нужно разделить измеряемую сложную поверхность на несколько простейших геометрических фигур.

Треугольник

Формулы для нахождения площади любого треугольника представлены несколькими вариантами:

1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:

2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.

На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:

По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.

Рекомендуем: Тригонометрические формулы приведения. Подробный разбор

3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:

Простой расчет прямоугольника

Если внимательно посмотреть вокруг, можно увидеть множество примеров прямоугольников. По определению, прямоугольник представляет собой четырехсторонний многоугольник, углы которой находятся под прямым углом, равным 90 градусам. Рассчитать площадь поверхности тела прямоугольника — простая математическая операция, которая наиболее часто применяется человеком в повседневной жизни. Почему важно знать формулу площади? Многие предметы и обстановка, окружающие человека, имеют прямоугольную форму: дом, стены, пол, крыша. И очень часто надо знать их площадь для строительства или ремонта.

Если прямоугольник имеет длину b и ширину h, мы можем найти площадь S, умножив ширину на его длину. Следовательно: S=bxh.

Пример. Как рассчитать площадь прямоугольника, если известны сторона и ширина, например, длина 4 см и ширина 3 см, тогда: S=4х3=12.

Квадрат — разновидность прямоугольника с равными углами и сторонами.

Пример. Если квадрат имеет стороны 3 см, мы можем найти S, возведя в квадрат значение стороны. Следовательно, имеем: S=3х3=9.

Алгоритм проведения расчётов

Если все подготовлено, то можно переходить к самим расчётам. Если нужно вычислить площадь поверхности правильной формы, то здесь нет ничего сложного – эти формулы уж точно никто не позабудет.

Без рулетки никак Источник sv.decorexpro.com

Смотрите также: Каталог проектов прямоугольных домов

Другое дело, когда стена, пол, потолок имеют сложные очертания. Здесь уже придётся сочетать различные приёмы. То есть поделить комнату на несколько блоков, после чего рассчитать площадь каждого из них. А далее от общей площади вычесть или прибавить их.

Вовсе не обязательно мерить длину стен строго вдоль плинтусов – замер можно проводить в любом удобном месте, если, скажем, мешает мебель. То есть выше, ниже, в середине, главное соблюсти при этом строгую параллель полу и потолку. Никаких диагоналей или наклонов! В противном случае расчёты будут неверными.

При возникновении трудностей можно всегда заручиться поддержкой кого-то из домашних.

Правильная геометрия

Каких-либо сложностей касательно того, как вычислить площадь, здесь нет. В случае простого прямоугольника достаточно замерить всего две стороны и высоту, ведь у такой фигуры противоположные стороны равны. Чтобы убедиться, что комната имеет правильные очертания, достаточно приложить к углам строительный угольник, правда не всегда удаётся получить чёткую картину.

Формула для расчёта прямоугольника известна каждому:

Кажется, что формулу площади прямоугольника забыть невозможно, хотя у некоторых получается и это Источник wezanu.ritobypus.ru.net
Такая формула актуальна для стен, потолка, пола, дверей, окон и прочих прямоугольных поверхностей. В случае запланированного ремонта важно получить чистые значения. Для этого следует от площади стены вычесть площадь дверей, окон. Общую площадь всей комнаты можно рассчитать по такой формуле – h(a⋅2+b⋅2). Где h – высота помещения.

С квадратом все ещё проще – достаточно замерить одну сторону и возвести её значение в квадрат.

Помещения с неправильными очертаниями

Но как посчитать площадь комнаты, если она имеет неправильную форму поверхностей? Здесь есть некоторые нюансы:

Но ничего страшного здесь нет и не нужно углубляться в тригонометрию. Достаточно любую сложную поверхность стен или потолка визуально разделить на несколько простых плоскостей. После этого остаётся рассчитать площадь каждой фигуры и сложить их вместе.

Случай чуть-чуть посложнее – но не намного Источник wezanu.ritobypus.ru.net

Формулы параллелограмма

Параллелограмм является четырехсторонним многоугольником с двумя парами параллельных сторон одинаковой длины. По определению, прямоугольник также представляет собой тип параллелограмма, но с равными углами. Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных сторон, а расстояние между сторонами.

Из рисунка видно, что высота — это расстояние между двумя параллельными сторонами параллелограмма, расположенная под прямым углом между ними. S=ADxh. S=bxh, где AD=b — основание, h — высота.

Пример. Если параллелограмм имеет основание 3 см, а высоту 2 см, то площадь S равна произведению основания на высоту. Следовательно, имеем: S=3х2=6.

Основание трапеции

Рассмотрим, как правильно рассчитать площадь трапеции. Трапеция представляет собой четырехсторонний многоугольник с одной парой параллельных сторон. Если две непараллельные стороны имеют одинаковую длину, форма называется равнобедренной или обычной трапецией. Если непараллельные стороны имеют разную длину, она называется неравнобедренной. Однако, несмотря на эту дополнительную сложность в определении, площадь неправильной трапеции может быть рассчитана с помощью простой формулы.

Измерения для расчета площади трапеции:

Нужно обратить внимание, что высота трапеции всегда перпендикулярна основанию, точно так же, как высота параллелограмма. Пример: a=3 см, b=5 см, h=4 см. S=4х(3+5)/2=16.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2. Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Виды треугольников

Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:

Площадь любого треугольника определяется по формулам.

1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:

Площадь равностороннего треугольника:

Площадь равнобедренного треугольника:

2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:

Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.

Решение: b=14 см, h=10 см, A=1⁄2х14х10=70

Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.

Решение: Площадь треугольника =1⁄2xaxbxsin 45.

Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)

Ответ: 12,3725 см2.

Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.

Решение: Площадь равнобедренного треугольника определяется:

Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).

Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.

Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50

Все формулы по геометрии. Площади фигур

Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

Ты нашел то, что искал? Поделись с друзьями!

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Измерение площади ромба

Ромб — особый вид параллелограмма, имеющий равные стороны и равные противоположные углы. Площадь ромба можно определить, используя три способа.

1. Метод высоты основания. Сначала выберите одну любую сторону в качестве базы, так как они имеют одинаковую длину. Затем определите высоту — перпендикулярное расстояние от выбранного основания до противоположной стороны.

2. Метод диагоналей. Другая простая формула для площади ромба, когда известны длины диагоналей. Площадь составляет половину произведения диагоналей.

3. Использование тригонометрии. В тригонометрии, есть удобная формула, когда известны длина стороны и любой угол:

Поверхность круга

Круг представляет собой форму, состоящую из замкнутой изогнутой линии. Каждая часть линии находится на одном и том же расстоянии от центра области, называемом радиусом. Еще с древних времен известно, как рассчитать площадь круга, если задан радиус. Площадь круга вычисляется по формуле S=πxr2, где: S — площадь круга,

π — число пи (3.1415), r — радиус круга.

Чтобы найти площадь круга, выполняем следующие действия. Запишите заданный радиус или диаметр величины как r или d соответственно. Как рассчитать площадь круга, если задан диаметр? Это совсем несложно, нужно вычислить радиус, разделив диаметр на 2, и перемножить данные с помощью калькулятора или вручную. Полученный ответ будет в квадратных единицах.

Задача: Найти площадь круга радиусом 10 см.

Решение: Мы имеем радиус окружности =10 см. Площадь круга =3,1416×10×10=314,16.

Ответ: 314,16 см2.

Найдите площадь круга диаметром 15 см.

Решение: У нас диаметр круга =15 см. Радиус =15/2=7,5 см. Площадь круга =3,14х7,5х7,5=176,625=176,63 (округлить до 2 знаков после запятой).

Ответ: 176,63 см2.

Простые геометрические фигуры крыш

Прежде чем выполнять кровельные работы, нужно знать, как рассчитать площадь крыши, чтобы определить, сколько материала потребуется. Его количество всегда нужно брать с запасом и добавлять не менее 10 процентов от общей площади кровли для учета отходов строительства.

Предварительно перед расчетом схему кровли разбивают на простые геометрические фигуры, в нашем примере это две трапеции и два треугольника. Как рассчитать площадь крыши для трапециевидных элементов? Площадь вычисляется по следующей формуле: S=(a+b)xh/2, где: а – ширина нижнего свеса — 10 м, b – ширина по коньку — 7 м, h – высота — 5 м.

Для треугольных элементов применяется формула: S=axh/2, где: а – ширина ската по нижнему свесу — 7 м, h – высота ската — 3 м.

Трапеция

Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:

Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.

Инструментальные обмеры дома

Для измерения площади дома потребуются инструменты, чтобы очень точно выполнить расчеты, которые могут стать основой для проведения ремонтных работ, купли-продажи или страхования дома. Перед тем как рассчитать площадь, нужно взять рулетку, карандаш и блокнот, на котором нарисовать простейшую схему плана дома. Ее можно взять из паспорта застройщика или других проектных документов. С последним источником нужно быть внимательным, указанные цифры могут быть не всегда точными, например, какие-то ремонтные работы могут быть в них не учтены. Поэтому правильнее будет выполнить измерение площади самостоятельно.

Как рассчитать площадь дома вручную? Если нужно измерять площадь пола вручную, лучше всего измерить внешние стены, не забывая различных строительных углублений, подсобных помещений, верхних этажей, отдельных зданий или гаражей. Когда сделаны простые основные измерения, площадь рассчитывается путем умножения длины дома на ширину.

В зависимости от формы плана строительства может понадобится разбить его на простейшие геометрические фигуры. В этом примере дом имеет 9 метров на 12 метров, давая нам 108 квадратных метров. Гараж составляет 6 метров на 3 метра, что составляет 18 квадратных метров, общая площадь — 126 квадратных метров.

Предремонтные замеры пола

Как рассчитать площадь пола перед проведением ремонтных работ, например, замены линолеума или покраски? Для квадратного или прямоугольного помещения сначала нужно будет измерить длину и ширину комнаты. Затем умножить длину и ширину, получим длина x ширина = площадь. Таким образом, если комната имеет размеры 3 метра в ширину и 5 метров в длину, общая площадь составит 15 квадратных метров.

Это измерение можно использовать при расчете необходимого количества плиточного раствора, герметика, линолеума, которые владелец планирует использовать для своего проекта. Чтобы рассчитать площадь для подбора материалов, как правило, нужно добавить 10% коэффициент запаса: просто умножьте площадь на 1,1, а затем округлите до целого значения.

В примере, когда общая площадь составляет 15 м2, нужно будет заказать дополнительное количество плитки и раствора для 16,5 квадратных метра. Если комната не прямоугольная, нужно разделить ее на две или более элементарных геометрических фигур, чтобы рассчитать общую площадь.

Источник