Как разобрать кубик рубика 3х3
Как разобрать кубик рубика 3х3
Как разобрать и собрать кубик рубика по запчастям?
Как разобрать и собрать кубик рубика по запчастям?
Сразу же хочу отметить крестовины кубика-рубика могут быть разборными, могут быть не разборными (оставшиеся 6-ь кубиков припаяны к крестовине, они не демонтируются).![][1 ]
Но цветные квадратики полностью демонтировать с крестовины можно без проблем, они не крепятся механически, а просто защёлкиваются на своё место.
Поверните верхнюю панель кубика с таким учётом что бы его край свисал (выступал над нижней плоскостью).
Далее можно просто руками, или ножом с жёстким лезвием, или отвёрткой подделать
центральные элементы и вынуть их с небольшим усилием, то есть «отщёлкнуть».
Всё, средние элементы демонтированы, далее вынимаем угловые и остальные кубики в этой же плоскости.
Затем демонтируются кубики с остальных плоскостей, чем меньше кубиков тем проще это сделать, последние вообще будут выпадать.
Если у Вас крестовина разборная,
Всё, кубик разобран полностью.
Далее сборка в обратной последовательности, начинаем с последних элементов (только не угловых) в одной плоскости по рядам.
Кубик соберётся по цветам, то есть цвет элементов может быть ориентиром при обратной сборке, зелёный элемент рядом с зелёным и так по рядам в одной плоскости (это для примера).
Классический кубик-рубик исполнен следующим образом, из центральной части, в основном это пластмасса, отходит шесть «отростков» с отверстиями под резьбу в их центре.
Центральная часть может быть разной формы, сейчас это чаще всего шар, в старых кубиках, которые производили ещё в ХХ веке, лично я встречал отлитую из металла фигуру в виде сомкнутых друг с другом шести отростков.
Вариантов на самом деле много, но сама конструкция в целом похожа.
К этим отверстиям в главной детали крепятся центральные квадраты сторон, каждой из шести сторон, при помощи саморезов или винтиков.
Средние части, соединяющие две стороны, просто вставляются под квадраты центральной части при помощи фигурных отростков.
Углы также вставляются при помощи похожих отростков с внутренней части в отверстие, образующееся при соединении шести элементов (три центра и три угловые стороны).
В таком случае можно разобрать кубик двумя способами, основанной на личном опыте.
1 способ
В центре любой стороны снимите цветную часть, она может быть как наклейка, так и пластиковая вставка. Под ней найдете саморез, который отворачивает отвёрткой. Осталось поддеть центр чем-нибудь острым и вытащить его, далее детали снимаются при помощи сдвига в пустое пространство.
2 способ
С трёх сторон в щель углового элемента надо засунуть тонкие отвёртки и раздвигать их в разные стороны, чтобы освободить выступ с внутренней стороны угла. Вытащить его, а остальные элементы сниматься путём сдвига.
Математики в шоке: Оказывается, разобрать Кубик Рубика – гораздо сложнее, чем его собрать!
Москва, 21.08.2022, 15:14:57, редакция FTimes.ru, автор Сергей Кузнецов.
Кубик Рубика уже 40 лет является одной из самых любимых головоломок в мире. Несколько разных методов были разработаны для его сборки, описанные в бесчисленных книгах. Опытные «спидкуберы» могут решить задачу за считанные секунды.
В дополнение к таким способностям поразительной ловкости есть много захватывающих математических вопросов, связанных с Кубиком Рубика. Движение куба состоит из поворота одной из шести граней на 90, 180 или 270 градусов. Ошеломляющие 43 252 003 274 489 856 000 возможных состояний могут быть получены путем применения последовательностей ходов к возврату к тому же самому состоянию.
Несмотря на эту сложность, в 2010 году было показано, что Кубик Рубика всегда можно собрать за 20 ходов или меньше, независимо от исходного состояния. Это число называется «числом Бога», поскольку все известные методы решения, используемые людьми, обычно используют значительно больше ходов, чем это оптимальное значение.
Но как быть с противоположным вопросом: сколько ходов требуется, чтобы разобрать собранный куб? На первый взгляд, это звучит гораздо проще, чем вычисление числа Бога. В конце концов, в отличие от сборки куба, разборка не требует никаких навыков.
Подобные вопросы были заданы для перетасовки карт. Известным примером является исследование «риффовой случайности» в 1990 году математиками Дейвом Байером и Перчи Диаконисом. Колода карт определяется как «смешанная», если ее порядок является случайным, причем каждый возможный порядок имеет одинаковую вероятность появления. Байер и Дьяконис показали, что семь риффл-тасовок необходимы и достаточны, чтобы идеально смешать стандартную колоду игральных карт.
В прошлом году математики опубликовали аналогичное исследование всем известной головоломки «15», которая состоит из квадрата 4х4, заполненного 15 скользящими плитками и одним пустым пространством.
Как же разобрать Кубик Рубика?
Типичный человек, пытающийся разобрать кубик Рубика, неоднократно совершал на нем случайные движения. Полученная случайная последовательность состояний является частным случаем того, что математики называют «цепью Маркова». Ключевым свойством является то, что с учетом текущего состояния вероятность того, каким будет следующее состояние, не зависит ни от одного из предыдущих состояний.
Применяя теорию цепей Маркова к разборке куба, из этого следует, что с увеличением числа случайных ходов вероятность оказаться в каком-либо конкретном из возможных состояний становится все ближе и ближе к 1/43 252 003 274 489 856 000. Математики называют это «равномерным распределением вероятностей», поскольку каждое возможное состояние возникает с одинаковой вероятностью.
После любого заданного числа случайных движений состояние куба будет случайным, но его распределение вероятностей не будет точно равномерным; некоторые состояния будут более вероятны, чем другие.
Пусть d (t) описывает, насколько распределение вероятностей после t случайных перемещений отличается от равномерного распределения вероятностей. По мере увеличения числа случайных ходов (t) значение d (t) будет уменьшаться. Разбираемый куб соответствует уменьшению d (t).
Цепь Маркова в методе Монте-Карло
В теории цепей Маркова это уменьшение d (t) называется «перемешиванием». Помимо перетасовки карт и разборки Кубика Рубика теория смешивания цепей Маркова также имеет очень серьезные практические применения. Одним из наиболее важных вычислительных инструментов в современной науке и технике является метод Монте-Карло. Этот метод, как и знаменитое казино, в честь которого он назван, основывается на случайности. По сути, он пытается приблизиться к решению сложных математических задач, используя несколько случайных догадок.
На практике цепочки Маркова часто используются для получения этих случайных состояний. Чтобы понять точность этих методов Монте-Карло с цепью Маркова, ключевая задача состоит в том, чтобы оценить, насколько быстро d (t) уменьшается с ростом t.
Карманный кубик
Изучение проблемы разборки для стандартного Кубика Рубика 3x3x3 в настоящее время является увлекательной нерешенной задачей. Однако, это становится вполне реалистичным, если мы обратим наше внимание на уменьшенную версию 2x2x2, называемую «карманным кубиком».
В этом кубе края и центральные части отсутствуют, и остаются только угловые части. Карманный куб имеет только 3 674 160 возможных состояний, а его число Бога — только 11.
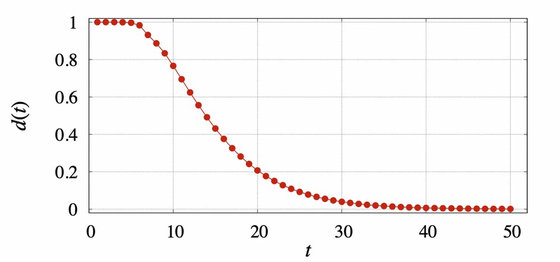
На графике ниже мы строим d (t) для карманного куба. После 11 ходов d (t) по-прежнему очень велико и составляет 0,695. Первое значение t, которое дает значение d (t) ниже 0,25 (часто называемое «временем перемешивания» в теории цепей Маркова), равно 19. После 25 ходов d (t) составляет 0,092; после 50 ходов это 0,0012; и после 100 ходов это 0,00000017.
Удаленность карманного кубика от равномерного распределения после t перемещений.
Так сколько ходов вы должны использовать, чтобы полностью разобрать карманный кубик? Ответ зависит от того, насколько малого вы хотите добиться d (t). Тем не менее, это правда, что ходов числа Бога недостаточно. Как минимум, не следует использовать менее 19 ходов.
Разрушение кубика Рубика
Шаг 1
Поверните верхний ряд так, чтобы каждый угол был примерно посередине между сторонами
Толкайте кусочки вверх, пока они не выскользнут из куба, затем выдвиньте остальные
Повторяйте этот процесс, пока не очистите уровень
Шаг 2
Вы должны быть в состоянии просто вытащить остальные блоки, например, так
У вас будет центральная часть с шестью центрами шести сторон, механизм поворота
Шаг 3
Чтобы собрать, защелкните все части обратно на место и постарайтесь не поворачивать грани.
Это помогает начать с средних частей в первую очередь
Не бойся применять силу!
Когда у вас есть средние части, довольно просто нажать на угловые части
Комментарии
Пока еще нет ниодного комментария, оставьте комментарий первым!
Как собрать кубик Рубика 3х3
Схема сборки кубика Рубика для начинающих. Инструкция состоит из 7 этапов. Длительность урока: 45 минут.
Сборка кубика Рубика – популярное упражнение, которое развивает логику и внимательность. В этой инструкции мы рассмотрим поэтапную сборку, состоящую из 7 основных шагов. Сборка рассчитана на 45 минут. Описанные в данном руководстве действия являются наиболее понятным и распространенным алгоритмом.
Этапы на рисунке выше
Итак, в данном руководстве рассмотрены 7 шагов, в которых работа над сборкой ведется по слоям.
1.Крест на первом слое.
2.Расстановка углов первого слоя (слой собран).
3.Ребра среднего слоя (слой собран).
4.Крест третьего слоя.
5.Ребра третьего слоя.
6.Расстановка углов третьего слоя.
7.Правильный разворот углов третьего слоя (слой собран, кубик собран).
Внимание!
В процессе сборки вы можете столкнуться с некоторыми трудностями. Если на одном из этапов вы зашли в тупик, постарайтесь внимательно проверить свои действия на предыдущих шагах. Также обратите внимание на свой кубик – он мог быть разобран и неправильно собран, что может послужить причиной неудачи в процессе работы. Избежать проблемы можно наверняка, предварительно разобрав кубик и собрав его по цветам.
Шаг 0. Подготовительный этап. Основные понятия.
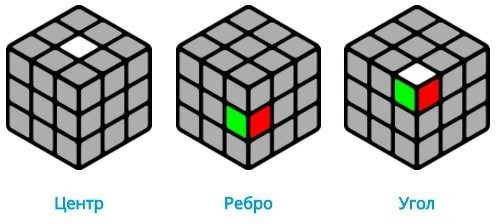
Познакомьтесь с основными элементами кубика Рубика размером 3 на 3. Знание названий составляющих поможет вам с легкостью разобраться в инструкции, нам нужно знать, из чего кубик состоит, как вращается, и как называются его элементы. Итак, Элементы кубика Рубика:
Углы кубика(8 штук) – элементы, содержащие три цвета.
Каркас – это скелет кубика, он представляет собой крестовину, на которой закреплены центры.
U (от UP)
верхняя грань
аналогично:
D (от Down)
нижняя грань.
Обозначение поворотов
Повороты граней осуществляются на 90 градусов и обозначаются по названию грани, которую нужно повернуть.
Тренируемся! Давайте попробуем действовать по формулам. Выполните одну из самых популярных и используемых комбинаций, «четверку».
Найдите Угол с цветами красный-синий-желтый. Возьмите кубик так, чтобы этот угол был справа вверху. Обратите внимание на центр кубика, который обращен к вам (у нас он желтый)
R’ D’ R D
сделайте еще раз эту комбинацию и снова посмотрите на результат. Наш угол прыгнул вверх, но теперь он перекрутился другими цветами
Вывод: угол скачет вверх-вниз и поворачивается разными цветами. Если сделать комбинацию еще 4 раза мы придем к первоначальной ситуации. Попробуйте!
Внимание! Не просто желтый крест вверху, а правильное расположение ребер с учетом других центров кубика.
Начнем с Желто-Синего ребра. Для начала найдем его. Кубик держим синим к себе, желтым к верху.
Возможная ситуация: ребро расположено «наоборот», для того, чтобы развернуть его, делаем F U’ R U.
Поворачиваем кубик следующим (красным) центром к себе и собираем Желто-Красное ребро. Все аналогично. Затем Желто-Зеленое и Желто-Оранжевое.
Результат, которого нужно достичь на этом этапе. Все углы и ребра верхней грани стоят на своих местах.
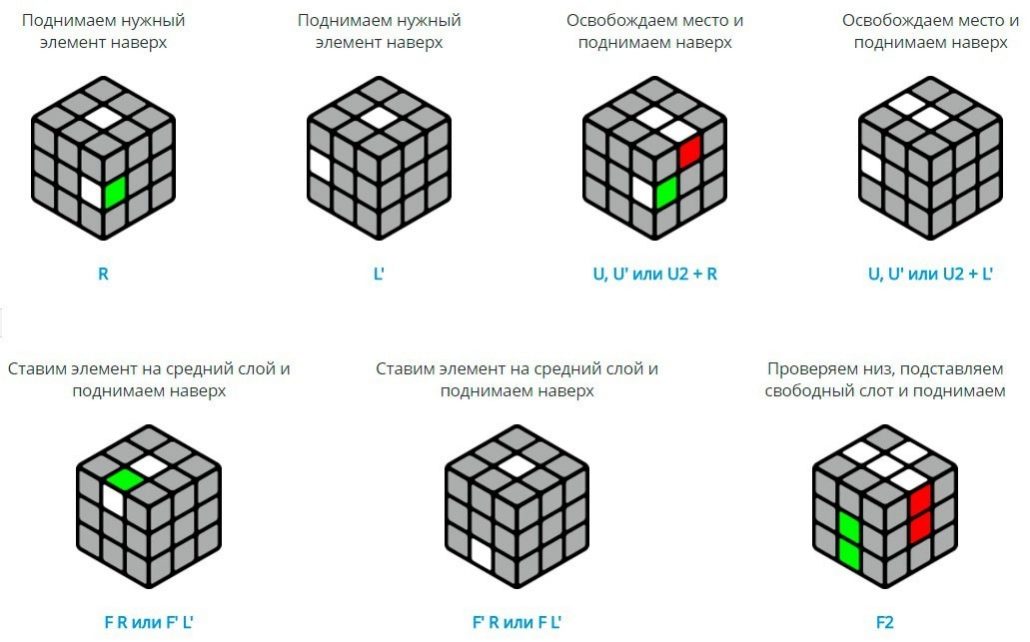
Итак, стратегия второго этапа: опустить нужный элемент вниз, подкрутить низ так, чтобы элемент стал под свое место, поднять элемент вверх на свое место одной из формул.
Шаг 3: сборка среднего слоя кубика Рубика. Ставим 4 ребра на свои места в среднем слое.
Результат 3 этапа. Нам нужно разместить всего 4 ребра по своим местам.
Найдите ребро без белого цвета, к примеру, зелено-оранжевое. Покрутите грань, пока одна из наклеек не встанет к своему центру (зеленый к зеленому).
Если зеленая грань не совмещается с зеленым центром, совместите оранжевый цвет. Т.е. у нас 2 варианта.
U’ L’ U L
U F U’ F’
Выполните эти формулы (ребро переместится вниз и влево).
Наше ребро выскочит наверх и вы уже сможете все сделать так, чтобы поставить его на свое место правильно.
Стратегия этого этапа: ищем нужное ребро, поворотами верха правильно его позиционируем, одной из формул ставим ребро на свое место. Делаем этот алгоритм для всех 4-х ребер. Внимание! При сборке второго слоя первый слой (нижний) сохраняется собранным!
Шаг 4: Собираем «неправильный» белый крест на последнем слое.
Что делать!? Я собрал 2 слоя, но на третьем слое у меня не получается ни одна из ситуаций рис 21-24. Такого на нормальном кубике быть не должно. Это означает, что ваш кубик разбирали на части механическим способом, а назад собрали неправильно. Разберите куб на детали, соберите его правильно и начинайте заново.
Шаг 5. Делаем «правильный» белый крест.
Результат, которого нужно достичь на данном шаге. Верхние ребра совпадают по цветам с центрами.
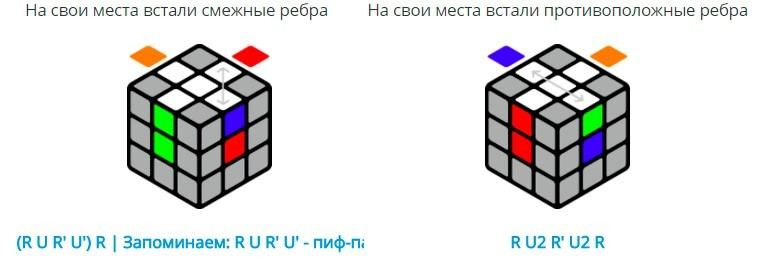
Вращаем верхний слой, чтобы какие-либо ДВА ребра совпали по цветам с центрами из среднего слоя. Может получиться одна из двух ситуаций.
На свои места становятся два противолежащих ребра (у нас бело-синее и бело-зеленое), два остальных нужно поменять местами. Комбинация приведет вас к Рис 28.
R U R’ U R U2 R’
Два собраных ребра, стоят под углом* (у нас бело-синее и бело-оранжевое), два остальных нужно поменять местами комбинацией, при этом кубик держим, чтобы угол* смотрел от вас и вправо.
R U R’ U R U2 R’ U
Шаг 6. Расставляем углы верхнего слоя по своим местам. Не собраны у нас только 4 угловых элемента на верхней грани. Рассмотрите кубик, возможно один из центров уже стоит на своем месте, как на рис 30 или все углы стоят не на своих местах, как на рис 27. Не важно, как повернуты углы, важно только их расположение.
U R U’ L’ U R’ U’ L
Сделайте эту комбинацию, и один из кубиков обязательно станет на свое место, т.е. вы придете к ситуации на Рис 30.
На своем месте стоит один угол. Остальные нужно поменять местами, переместив каждый из них против часовой стрелки, как на Рис 31 или по часовой, как на Рис 32.
Вариант 1. Три несобранные ребра перемещаются против часовой стрелки и становятся на свои места. Собранным углом держим к себе и справа, как на рисунке.
U R U’ L’ U R’ U’ L
Вариант 2. Три несобранные ребра перемещаются по часовой стрелке и становятся на свои места. Собранным углом держим к себе и слева, как на рисунке.
U’ L’ U R U’ L U R’
Частый вопрос на этом этапе: ФОРМУЛА НЕПРАВИЛЬНАЯ!
Этой схеме уже много лет, все тысячу раз проверено, все схемы и формулы рабочие, гарантируем! Будьте внимательны перед выполнением формулы, читайте под формулой, каким цветом нужно держать к себе кубик. Внимательно отнеситесь к предыдущим советам.
R’ D’ R D
Начнем с Красно-Сине-Белого. Держим кубик так, чтобы этот угол смотрел на вас и был справа. Делаем «четверку» 2 или 4 раза, пока угол не развернется.
R’ D’ R D
Перед вами следующий Бело-Сине-Оранжевый угол. Опять разворачиваем его «четверкой». Если так получилось, что следующий угол уже правильно собран, тогда просто поверните верх ЕЩЕ РАЗ и собирайте следующий угол.
Мои поздравления! Вы собрали кубик Рубика!
Вы молодец, у вас получилось собрать кубик Рубика 3х3.
Поделитесь пожалуйста фотографией вашего собранного кубика в комментариях ниже!)
Как правильно чистить и мыть кубик Рубика 3х3
Новички часто задаются вопросом: можно ли мыть кубик в воде?
Но необходимо знать, как это делать, и использовать моющие средства, которые не слишком агрессивно воздействуют на пластик.
Необходимость помыть головоломку может возникнуть по разным причинам. Попал ли внутрь песок, или просто кубик запачкался от частого использования – мешающий сборке мусор и пыль нужно вычистить, чтобы снова наслаждаться мягким ходом граней.
Рассмотрим основные правила и техники промывки (очистки) деталей кубика Рубика 3х3.
Как часто чистить кубик Рубика 3 на 3
Основное правило – кубик Рубика 3х3х3 нужно чистить по мере загрязнения. Вы сами почувствуете, что он нуждается в чистке, по характеру сборки.
Наиболее яркими признаками того, что головоломку необходимо промыть, являются:
Периодичность чистки – дело индивидуальное. У кого-то игрушка хранится дома на полке, носится в чехле, а кто-то роняет ее, или кидает в сумку вместе с кучей вещей, где она пылится и грязнится.
Естественно, во втором случае для качественной, быстрой сборки и продления срока эксплуатации мыть кубик нужно будет гораздо чаще.
Техника чистки кубика Рубика 3х3
Если вы чувствуете, что собирать кубик стало сложнее, но обилия грязи внутри не обнаружено, можно обойтись простой чисткой.
Так вы сможете удалить с граней кубика пыль, кожный жир и прочие незначительные загрязнения.
Для этого используются влажные салфетки. В принципе подойдут любые очищающие, но в идеале нужно приобрести специальные салфетки для очищения техники, мониторов и т.д.

На иллюстрациях изображены салфетки для чистки кубика 3 на 3.





Как и в каком случае нужно мыть кубик Рубика 3 на 3
Необходимость помыть кубик рано или поздно возникает у каждого спидкубера. Она может быть обусловлена просто частым активным использованием и смазыванием головоломки, или внештатными ситуациями – падением ее в грязь, песок, или липкую жидкость, попыткой смазать неподходящим средством и т.д. И в том, и в другом случае требуется тщательная промывка изделия.
Помните, что разобрать головоломку гораздо проще, чем собрать обратно. Если у вас в помощниках нет опытного спидкубера, лучшим решением будет фотографировать каждый этап – так будет проще восстановить последовательность действий при последующей сборке.
Процесс помывки кубика Рубика 3х3
Порядок действий при помывке кубика следующий:
Если данный материал был полезен Вам, оставьте комментарий ниже.
Как собрать кубик Рубика и не умереть. Сейчас научим
Кажется, что Кубик Рубика существовал всегда. Однако его изобрел в 1975 году венгерский скульптор Эрнё Рубик, а головоломке понадобилось меньше 50 лет, чтобы завоевать мир.
Шутка ли: по всему миру продано 450 миллионов копий головоломки, как официальных, так и поддельных (оригинал запатентован, поэтому выпускается определенными тиражами).
Такой популярности не добивались не то что спиннеры. Вероятно, кубик Рубика может поспорить с шахматами и другими древнейшими играми-головоломками-таймкиллерами.
Почему кубик Рубика стал таким популярным?
Секрет популярности прост: кубик Рубика является детской игрушкой только на первый взгляд. На деле это серьезная математическая задача по комбинаторике, воплощенная в форме.
Что такое кубик Рубика известно всем. Что такое собрать его? Это означает привести его в исходное состояние, когда каждая грань заполнена одним цветом. Для этого необходимо менять местами раскрашенные квадраты до полного успеха.
По этой причине у кубика нет однозначного решения: оно требует слишком объемных расчетов, и подчиняется только комбинаторике как подразделу математической статистики. Впрочем, вероятность той или иной конфигурации можно оценить.
Поскольку элементы повторяемы, и для сбора головоломки достаточно собрать по цвету все грани, возможно создать алгоритм, который приведет к правильному решению.
Огромное число возможных решений привело к тому, что все существующие алгоритмы срабатывают только для бОльшей части (80-98%) начальных состояний. Иногда их приходится комбинировать.
Тем не менее, существуют наиболее распространенные, простые и понятные без серьезных математических выкладок (хотя совсем без них не обойдется): именно они позволяют собирать затейливую головоломку чаще всего.
Как умные люди собирают кубик Рубика?
Для сборки или приведения кубика к виду с гранями одного цвета существует несколько официально разработанных методик:
Последний гарантирует, что кубик рано или поздно будет собран и достаточно прост в освоении. Поэтому его сегодня и рассмотрим, оставив прочие варианты для фанатов.
Важно: если кубик упал и рассыпался, то неправильный «ремонт» приведет к невозможности собрать головоломку.
Для ускорения процесса можно воспользоваться Решателем кубика Рубика. Помогает, хотя в некоторых случаях предложенные компьютером варианты не приведут к положительному итогу.
Из чего состоит кубик Рубика. Важно знать, прежде чем собирать
Внутри кубика Рубика прячется крестовидный каркас, на котором закреплены подвижные и статичные элементы головоломки.
Для записи алгоритмов используют упрощенные наименования базовых элементов, которые определяются наблюдателем (человеком, который проводит сборку) относительно самого себя:
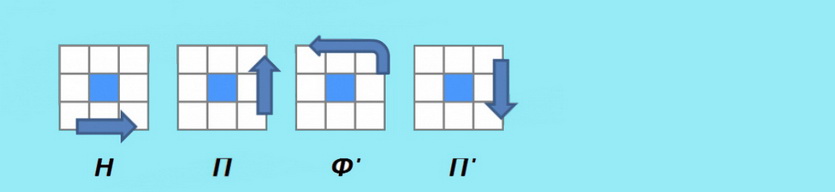
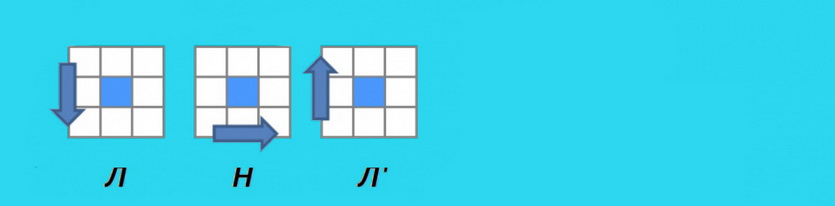
В формуле каждый символ соответствует повороту указанного элемента на 90° по часовой стрелке: Ф, Т, П, Л, В, Н. Поворот против часовой определяет штрих: Ф’, Т’, П’, Л’, В’, Н’. Цифра после буквы обозначает количество повторов операции.
Пример: формула НП’Ф’В2
1. Повернуть нижнюю грань на 90° по часовой (вправо).
2. Повернуть правую грань на 90° против часовой (на себя).
3. Повернуть фасадную грань на 90° против часовой.
4. Повернуть правую грань на 90° по часовой (на себя) дважды, или один раз на 180°.
Все формулы (повороты) выполняются до тех пор, пока не будет получен удовлетворяющий (показанный на рисунке) результат.
Поехали, начинаем собирать кубик Рубика. Инструкция далее.
1. Начинаем. Объемный крест
На первом этапе сборки необходимо определить основной цвет, цвет верхней грани, он же цвет центрального выбранного элемента.
Важно: от выбора цвета дальнейшее решение не зависит.
Далее необходимо поднять элементы того же цвета, чтобы получить так называемый «крест верхней грани»:
1.1 НПФ’П’ — если угловой кубик на нижней грани (поворот боковой грани и несколько поворотов нижней)
1.2 ФФ — если угловой кубик на боковой грани (поворот нижней грани).
Сборка первой части дает понимание процесса и в целом не зависит от формул — эта часть решается без применения комбинаторики простыми вращениями.
2. Продолжаем. Сторона
Для сборки верхней грани нужно поставить 4 угловых кубика выбранного цвета на свои места. В этом случае возможно несколько «фасадов», так как угловой кубик может быть развернут 3 способами относительно граней.
Возможно 3 ситуации, для каждой из которых применяется собственный алгоритм:
2.1 ЛН’Л’ – если кубик выбранного цвета на боковой грани
2.2 Ф’Н’Ф — если кубик выбранного цвета на фронтальной грани
2.3 (Ф’П’)Н2(ПФ) — если кубик выбранного цвета на нижней грани
3. Следующее. Пояс
Этап предполагает 2 возможных раскладки и 2 формулы, с помощью которых необходимо собрать второй от верхней грани слой (пояс).
После последней операции кубик для перестановки в этой находится под центральным элементом фасадной грани. Его нужно вывести на фасад так, чтобы цвет центрального и углового элементов совпадали.
Используется 2 основных алгоритма:
3.1 (НЛН’Л’)(Н’Ф’НФ) — если элемент идет на левую грань
3.2 (Н’П’НП)(НФН’Ф’) — если элемент идет на правую грань
Если нужный кубик находится в среднем слое, необходимо применить любой алгоритм до тех пор, пока кубик не окажется на нижней грани.
4. Теперь – выставка рёбер
Важно: данный этап требует перевернуть кубик на 180° от себя, так, чтобы нижняя грань оказалась вверху, а прочие остались на своих местах.
На данном этапе необходимо правильно выставить с помощью единственной формулы рёберные кубики, за счет чего на нижней грани окажется 2 кубика верного цвета.
4.1 (ВФП)В(П’В’Ф’)
5. Делаем согласованный крест
После этапа 3 возможны 3 базовых начальных позиции, применив к которым формулы этапа, получится необходимая сборка. Если текущая ситуация не подходит ни под один из вариантов, необходимо выполнить алгоритм 5.3 дважды.
Для каждой базовой ситуации имеется свой алгоритм решения? который сводится к повторению одной комбинации:
5.1 (ПС)4 В (ПС)4 В’
5.2 (ПС)4 В’ (ПС)4 В
5.3 (ПС)4 В2 (ПС)4 В2
Внимание: поворот средней грани «С» осуществляется с нижней стороны.
6. Затем – расстановка углов
На этом этапе снова нужно перевернуть, переориентировать кубик таким образом, чтобы в левом дальнем углу верхней грани оказался подходящий по цвету угловой кубик.
Выбор алгоритма зависит от конкретной ситуации и остаётся за «игроком»:
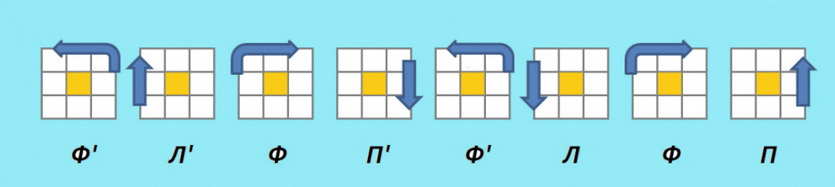
6.1 (П’Ф’Л’Ф)(ПФ’ЛФ) — прямой алгоритм
6.2 (Ф’Л’ФП’)(Ф’ЛФП) — обратный алгоритм
7. Теперь разворот углов
Заключительный этап сборки самый ответственный, поскольку неправильная сборка (выполнение алгоритма) приведет к нарушению конструкции и откату на несколько шагов назад.
В зависимости от сложившейся комбинации, необходимо применить один из алгоритмов, которые сводятся к одному:
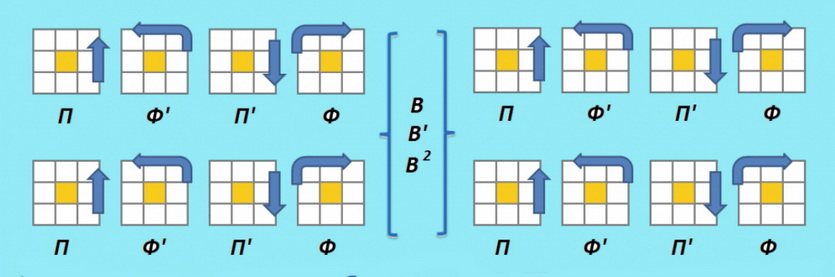
7.1 (ПФ’П’Ф)2 В (ПФ’П’Ф)2
7.2 (ПФ’П’Ф)2 В’ (ПФ’П’Ф)2
7.3 (ПФ’П’Ф)2 В2 (ПФ’П’Ф)2
Каждый выполняется в 2 этапа: первая половина до правильной ориентации углового кубика, вторая половина (после поворота) до возвращения порядка в нижних слоях.
Ура, почти всё. Завершение сборки
Завершается сборка единственным поворотом последней собранной грани на 90° по/против часовой в зависимости от текущей ситуации.
Кубик Рубика собран!
А есть способы проще?
Нет, если вы не гений-рекордсмен. Вначале надо научиться собирать правильно.
Каждый из этапов сборки осуществляется строго из базового положения. Причем, в некоторых случаях кубик необходимо привести к базовому положению самостоятельно, переориентировав его либо повторно выполнив текущий (предыдущий) алгоритм.
Важен не только алгоритм конкретной операции, но и общая последовательность сборки. В противном случае нарушается строй решения задачи и возможен непредсказуемый вариант.
Остаётся ответить самому себе на вопрос: зачем собирать кубик Рубика?
Для основной массы населения планеты ответ очевиден. В отличие от спиннеров и других простых способов занять руки кубик Рубика позволяет тренировать не только руки, но и ум.
Решение (сборка) кубика вслепую невозможны. Вероятность этого события намного меньше, чем появление разумных инопланетян на Земле, начало Звездных войн или самостоятельное возрождение динозавров.
Так что руки в ноги — и за кубиком!
Удивительная математика внутри кубика Рубика
В прошлом году исполнилось 40 лет с того времени, как человечество узнало о кубике Рубика. Эта головоломка сразу смутила умы почти полумиллиарда энтузиастов, которые полагали, что могут раскрыть сумасшедшие секреты этого удивительного кубика, если разберут его на составные части.
В преддверии юбилея кубика Рубика (да, юбилея!) и стартов новых потоков курсов Математика для Data Science и его расширенной версии Математика и Machine Learning для Data Science, пришло время раз и навсегда разгадать эту головоломку, на этот раз с помощью довольно сложной математики. Физические внутренности кубика могут быть изготовлены из пластика, но его виртуальными внутренностями, конечно же, являются числа. Давайте же окунёмся в этот мир чисел.
Разбор кубика Рубика на блоки
Начнем с базовых знаний. Кубик Рубика размером 3x3x3 имеет шесть граней, каждая своего цвета. Центральный кубик каждой грани прикреплён к внутренней крестовине, скрепляющей все элементы куба. Центральные кубики могут только вращаться вокруг своей оси. Одни и те же цвета всегда располагаются напротив друг друга; на стандартном кубе белый цвет находится напротив жёлтого, красный – напротив оранжевого, синий – напротив зелёного.
Если разобрать кубик Рубика, можно увидеть, что он состоит из трёх типов составных блоков. Первый тип: центральная крестовина, на которой удерживаются центральные кубики каждой грани. Второй тип – маленькие кубики размером 1x1x1. Угловые кубики имеют три цветные стороны, бортовые кубики – две. Кубик Рубика имеет одну крестовину, восемь угловых кубиков и двенадцать бортовых кубиков.
С помощью математики мы можем узнать общее количество способов, которыми можно перемешать кубик Рубика: 43 252 003 274 489 856 000. В виде математической формулы это число можно представить следующим образом: (3 8 8!)(2 12 12!)/12. Вот как получается эта формула.
Далее учитываем перемещения каждого углового кубика. Всего угловых пазов восемь, поэтому у первого углового кубика есть восемь вариантов. У второго углового кубика остается семь вариантов, у следующего слева кубика – шесть вариантов и так далее, вплоть до последнего углового кубика, который должен войти в последний угловой паз. Это даёт факториал 8!.
Таким образом, первая часть формулы (3 8 8!) осуществляет подсчёт всех способов, которыми угловые кубики могут размещаться в кубе. Значение 3 8 – это их ориентация, а 8! – их положение.
В следующей части формулы (2 12 12!) применяется тот же принцип, но теперь для ребер. Рёбра имеют только две ориентации, поэтому 12 рёбер могут иметь в общей сложности 2 12 ориентаций. Всего имеется 12 положений, поэтому 12! представляет собой количество способов, которыми кубики могут быть размещены в таких положениях.
Что ещё осталось в формуле (3 8 8!)(2 12 12!)/12? Осталось деление на 12. Деление на 12 связано с одной особенностью кубика Рубика, о которой многим известно, но которую не до конца её понимают. Проведём мысленный эксперимент (который, возможно, вы уже проводили вживую!):
Предположим, вы разобрали кубик Рубика, вытащили из него все кубики, а затем вставили все кубики обратно в случайные пазы (при этом угловые кубики можно установить только в углы, а бортовые кубики – только на рёбра). Вы получите конструкцию, которая выглядит как обычный перемешанный кубик, и на данный момент мы подсчитали все возможные комбинации созданного таким образом куба: (3 8 8!)(2 12 12!). Теперь зададим вопрос, всегда ли можно собрать такой перемешанный кубик, не разбирая его на части?
Здесь кроется ловушка, в которую попадало множество начинающих любителей разгадывать эту головоломку. Если вы тренируетесь и хотите перемешать уже собранный куб, необходимо сохранить куб в целости и собрать его вручную. Если разобрать куб на части и собрать кубики случайным образом, вероятность того, что головоломку можно будет решить, составит всего 1 к 12.
Ответ кроется в алгоритмах
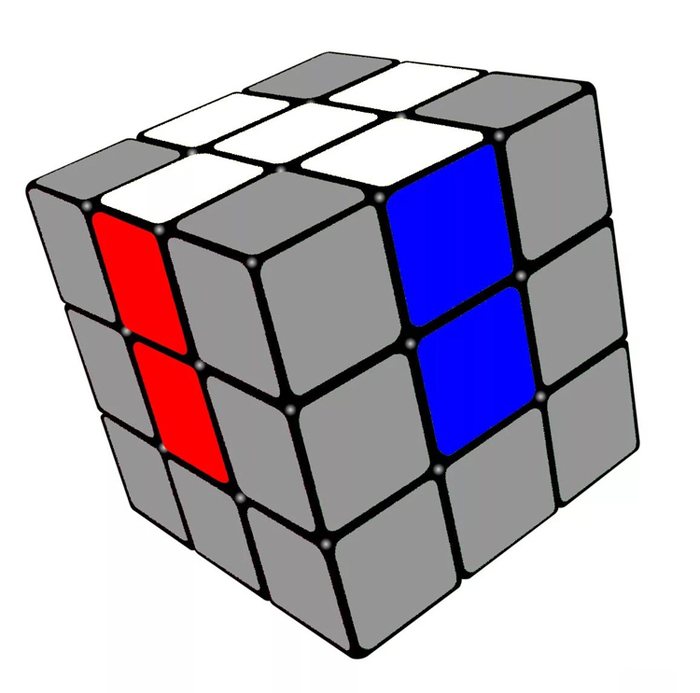
Хотите понять, почему вероятность составит всего 1 к 12? Есть хороший визуальный способ понять, почему вероятность именно такая. Шанс собрать разобранный на составные кубики и снова случайным образом перемешанный большой куб будет равен шансам собрать куб со следующими образцами граней:

Мы разместили их таким образом, чтобы было понятно, как получается коэффициент 12. Ряд 1 имеет нормальные углы. У рядов 2 и 3 один угол повёрнут. Столбец 1 имеет нормальные рёбра. У столбцов 2 и 3 одно ребро повёрнуто. У столбца 3 два ребра поменяны местами. И, наконец, в столбце 4 одно ребро повёрнуто и два ребра поменяны местами.
Таким образом, 12 кубов, представленных выше на фотографиях, не могут быть преобразованы друг в друга. 13-го варианта, который нельзя преобразовать ни в один из таких 12 кубов, не существует. Откуда нам это может быть известно?
Между тем, что может и что не может быть сделано посредством перемещения граней куба, есть связь. Последовательность перемещений граней куба энтузиасты сборки часто называют «алгоритмом». Популярными алгоритмами являются те, которые перемещают лишь несколько кубиков, оставляя остальные нетронутыми. Число 12 возникло по той причине, что на такие алгоритмы накладываются ограничения.
Число 12 составляется из трёх множителей: 12 = 3 * 2 * 2. Откуда берутся множитель 3 и два множителя 2?
Множитель 3: существует алгоритм, который поворачивает каждый из двух разных углов, но нет алгоритма, который поворачивает один угол (оставляя все остальные нетронутыми). Другими словами, если взять обычный кубик Рубика, вынуть один из его углов и заменить его на повёрнутый, такой куб собрать будет невозможно, то есть вы переместитесь из верхнего левого угла нашей диаграммы в одну из клеток прямо под ним.
Однако, если повторить эту операцию и повёрнуть еще один угол, второй множитель 3 не добавится. Теперь, когда в кубе повёрнуто два угла, мы можем последовательно применять алгоритм, поворачивающий два угла, до тех пор, пока не зафиксируется по крайней мере один из углов. Если другой угол случайно встанет на своё место, можем считать, что нам повезло и такой куб можно собрать. Ориентация углов может быть троякой.
Рассуждения относительно первого множителя 2 аналогичны. Существует алгоритм, поворачивающий на свое место каждое из двух разных рёбер, но алгоритма, способного повернуть на своё место только одно ребро, не существует. Таким образом, любое количество повёрнутых ребер может быть сведено к одному ребру, которое в итоге либо окажется, либо не окажется повёрнутым – варианта всего два.
Последний множитель 2 фактически относится к граням и углам, хотя на диаграмме мы показали его с гранями. Существует алгоритм, меняющий местами два угла, одновременно меняя местами два ребра. Но нет ни одного алгоритма, который был бы способен менять местами ни только пару углов, ни только пару рёбер.
Возьмите куб, вытащите два ребра и поменяйте их местами – на диаграмме вы попадёте на столбец, расположенный либо между столбцами 1 и 3, либо между столбцами 2 и 4. Аналогичные рассуждения можно применить, если поменять местами пару углов. Однако перемена местами пары ребер и пары углов уравновешивает баланс, так как алгоритм выхода из таких состояний существует.
Итак, после того как мы объяснили, откуда взялись все множители в коэффициенте 12, можно понять, откуда взялась формула (3 8 8!)(2 12 12!)/12. Число всех возможных положений кубиков в кубе составляет (3 8 8!)(2 12 12!), но только двенадцатая часть таких положений годится для сборки куба. Таким образом, число (3 8 8!)(2 12 12!)/12 обозначает количество способов, которыми можно перемешать кубик Рубика, не разбирая его на части.
Доказательство Популярной механики
Если вы достаточно любопытны, то, наверное, захотите проверить, верны ли сделанные выше утверждения. Существуют ли более сложные математические приемы, которые могут доказать, что «алгоритма, способного повернуть на своё место только один бортовой кубик, не поворачивая любой другой кубик, не существует»? Да, такие математические приёмы существуют. Вот как примерно строится такое математическое доказательство:
При переворачивании грани куба происходит перемещение четырёх бортовых кубиков. Рассмотрим, к примеру, алгоритм из 10 перемещений. Для каждого кубика выполните алгоритм и посчитайте, сколько раз перемещался кубик, и назовите это количество «числом перемещений кубика». Сложите эти числа для каждого бортового кубика, всего должно получиться 40 перемещений кубиков, так как каждое из 10 перемещений добавляет к сумме четверку.
В общем случае для любого алгоритма общее число перемещений бортовых кубиков должно быть кратно 4. Теперь пара важных фактов: если бортовой кубик перемещать чётное количество раз и вернуть его обратно в тот же самый паз, он будет иметь такую же ориентацию. И наоборот, если бортовой кубик перемещать нечётное количество раз и вернуть его обратно в тот же самый паз, он будет иметь перевёрнутую ориентацию.
Естественно, сказанное выше можно доказать с использованием более сложных математических методов, но мы не собираемся сильно углубляться в математику, иначе объём данной статьи превзойдёт все мыслимые и немыслимые пределы. Эти два факта также можно проверить экспериментально, чтобы понять, что всё происходит именно так. (В этом доказательстве поворот на 180 градусов считается двумя перемещениями каждого соответствующего кубика.)
Теперь давайте рассмотрим гипотетический алгоритм, достигающий цели, поворачивающий один бортовой кубик, оставляя при этом в неприкосновенности другой кубик. Одно повёрнутое ребро было перемещено алгоритмом нечётное количество раз, а каждое из 11 остальных рёбер было перемещено чётное количество раз. Сумма 11 чётных чисел и одного нечётного числа всегда нечётна, но мы показали ранее, что такая сумма должна быть кратна 4. Может ли нечётное число быть кратно 4? Нет, не может. Следовательно, такого алгоритма не существует.
Теперь вы понимаете, что число (3 8 8!)(2 12 12!)/12 представляет собой количество возможных состояний куба. Но для изучающего куб математика это лишь предварительная информация. Перед тем как начинать применять более сложные математические методы, задайте себе главный вопрос: «Существуют ли в этой теме математические вопросы, оставшиеся без ответов?»
Число Бога и многое другое
Главной задачей, поставленной изобретателем головоломки, естественно, была сборка куба. Эрно Рубик (Ernő Rubik) создал первый прототип головоломки в 1974 году, и через шесть лет она поступила в массовую продажу. Естественно, он был первым, которому удалось собрать куб.
В 1980 году кубик Рубика стал хитом продаж в магазинах игрушек. Но некоторые математики уже несколько лет экспериментировали с его ранними версиями. Одним из них был доктор Дэвид Сингмастер (David Singmaster) – составитель знаменитого путеводителя «Записки о Волшебном кубике Рубика» и разработавший нотацию для записи операций поворота граней куба. Эта нотация стала стандартом и теперь известна как нотация Сингмастера.
Если бы это была статья писалась в 1980-х годах, то, возможно, стоило бы подробнее объяснить читателям, что такое нотация Сингмастера, и использовать её при описании алгоритмов сборки куба. Множество авторов статей так и делали. Но сегодня на Youtube выложено множество видеоинструкций, поэтому в этой статье мы не будем отвлекаться на описание нотации.
За последние несколько десятилетий рекорд сборки кубика Рубика на время постоянно обновлялся. На сегодня мировой рекорд сборки кубика Рубика человеком составляет 3,47 секунды. В 1997 году доктор Джессика Фридрих разработала самый известный, самый скоростной и самый гибкий метод быстрой сборки кубика Рубика Самые быстрые сборщики кубика Рубика сегодня пользуются разными вариантами сборки от доктора Фридрих.
По мере того как одни пользователи оттачивали мастерство сборки, другие пытались решать важные математические вопросы, связанные с этой головоломкой. За сколько ходов можно собрать куб независимо от того, в каком состоянии он первоначально находился? Если кто-то перемешал куб за 500 ходов, то, естественно, собрать его можно менее чем за 500 ходов. На насколько именно меньше ходов?
Соответственно, была поставлена главная математическая задача: существует ли магическое число, позволяющее сказать: «любой перемешанный куб может быть собран именно за такое количество ходов [или меньше]»? Благодаря остроумному замечанию, что для обретения чувства уверенности нужно божественное вмешательство, это число получило название «Число Бога».
Первая гипотеза о существовании Числа Бога была выдвинута доктором Морвеном Тистлетвэйтом (Morwen Thistlethwaite) в 1981 году, который доказал, что это число существует и не превышает 52. Другими словами, любой перемешанный куб может быть собран за 52 хода или меньше.
В 1990–2000-х годах математики пошли ещё дальше. В июне 2010 года группа из четырёх учёных доказала, что Число Бога равняется 20. На этом веб-сайте, который ведут эти учёные, представлены самые последние знания о кубике Рубика.
Другими словами, какое бы хаотичное первоначальное состояние ни имел Кубик Рубика, его всегда можно собрать за 20 или менее ходов.
Для математиков в теме кубика Рубика остались лишь небольшие лакомые кусочки. Число Бога определено и равняется 20. Но точно неизвестно, сколько именно из 43 252 003 274 489 856 000 комбинаций потребуют для сборки полных 20 ходов.
Количество комбинаций, для сборки которых требуется ровно один ход, составляет 18. Это значение легко рассчитать. Есть шесть граней и три способа поворота каждой из них. Сколько кубов можно собрать ровно за два или три хода? Для математиков эта задача сложности не представляет, но можно предположить, что с увеличением количества ходов также будет увеличиваться сложность вычислений. Сегодня математики уже добрались до числа ходов 15; мы точно знаем количество комбинаций, для сборки которых требуется ровно 15 ходов, но пока не вполне точно представляем количество комбинаций для числа ходов от 16 до 20.
И это – последняя нерешённая задача в математической теме кубика Рубика. Будем ждать, когда кто-либо её решит. Может быть, это будете вы?
Получите нужные знания и навыки на курсе Математика для Data Science и его расширенной версии Математика и Machine Learning для Data Science. А промокод HABR даст скидку 50%.
Узнайте, как прокачаться в других специальностях или освоить их с нуля:
Ломаем систему: что нужно сделать, чтобы полностью перемешать поверхность кубика Рубика?
Выясняем, можно ли перемешать кубик Рубика так, чтобы рядом с каждым квадратом не было квадрата такого же цвета.
С большой вероятностью каждый из нас как минимум держал кубик Рубика в руках, как максимум – пытался его собрать. Это известная во всем мире трехмерная головоломка, цель которой – упорядочить цветные квадратики так, чтобы грани стали одного цвета, что редко удается новичкам. Естественно, время сборки зависит от опыта игрока, и на сегодняшний день рекорд составляет 4 секунды! И несмотря на то, что собрать кубик, в наших глазах, – трудная задача, доцент кафедры математики в университете Монаша (Австралия) Тим Гарони утверждает, что перетасовать его поверхность куда сложнее. Мы предлагаем разобраться в этом вопросе.
Многие ученые всерьез изучали вопрос перемешивания, но чаще всего на примере игральных карт. Например, профессора математики Дейв Бэйер из Колумбийского университета и Перси Диаконис из Гарварда даже опубликовали в 90-х годах научное исследование, которое посвятили изучению распространенного метода перетасовки игральных карт и вывели формулу их случайного смешивания, тем самым сделав значительный вклад в развитие математики и статистики.
По словам ученых, «рифленая тасовка – один из самых действенных способов максимально непредсказуемого распределения карт». То есть колода карт считается хорошо перемешанной, если порядок расположения карт является непредсказуемым, причем каждое возможное положение имеет одинаковую вероятность появления. А для того чтобы добиться нужного результата, необходимо повторить процесс перемешивания 7 раз.
А сколько поворотов граней требуется для того, чтобы полностью перемешать (скремблировать) кубик Рубика?
Число различных конфигураций кубика Рубика оценивается числом из 20 цифр – 4325 2003 274489856000. Несмотря на ужасающие данные, все же в 2010 году было доказано, что кубик Рубика можно собрать из любой конфигурации всего за 20 ходов.
Такой алгоритм решения головоломки и число ходов носит название «число Бога». Очень символично, поскольку все известные методы решения обычно подразумевают значительно больше операций. Но вернемся к противоположному вопросу – как вновь перевести поверхности кубика в случайные позиции? На первый взгляд это кажется очень легко, но на самом деле все обстоит иначе.
Согласно Гарони, механизм кубика Рубика может быть объяснен стохастической моделью – цепью Маркова. Простыми словами, суть модели состоит в следующем: в условиях фиксированного настоящего будущее не зависит от прошлого (вероятность того, каким будет следующее состояние, не зависит ни от одного из предыдущих состояний). Грани в головоломке можно вращать только по трем осям – X, Y и Z – на 90, 180 или 270 градусов.
Применяя теорию цепей Маркова, можно сказать, что с увеличением числа случайных ходов – поворотов граней – вероятность квадратов оказаться в каком-либо конкретном из возможных состояний составляет 1 к 4325 2003 274489856000. Математики называют это «равномерным распределением вероятностей», поскольку каждое из состояний возникает с одинаковой вероятностью.
Используя метод Монте-Карло цепи Маркова, с помощью алгоритма все же можно вычислить количество перетасовки, необходимой для скремблирования кубика. Но и здесь есть загвоздка: применение указанного метода для стандартного кубика Рубика 3х3х3 требует слишком больших и сложных вычислений.
Поэтому до сих пор этот вопрос остается нерешенным. Гарони предлагает использовать «карманную» версию головоломки размерами 2х2х2. В этом случае ситуация несколько проще: общее число конфигураций составляет 3674160, а «число Бога» равно 11.
На графике ниже показано распределение вероятностей перетасовки карманного кубика с помощью моделирования. Значение t на горизонтальной оси – это число манипуляций с гранями, а d(t) на вертикальной оси означает, «насколько далеко мы находимся от поставленной цели (полного непредсказуемого перемешивания поверхности). То есть чем меньше значение d(t), тем больше поверхность «перемешивается».
Показатель «хорошей перетасовки» появляется, когда d(t) имеет значение ниже 0,25, а t равно 19. Проще говоря, если вы повернете грани менее 19 раз, это будет означать, что карманный кубик Рубика перетасован не очень хорошо. Также стоит отметить, что с увеличением числа ходов распределение вероятностей становится более равномерным. Можно увидеть, что значение d(t) составляет 0,092 при количестве ходов в 25 раз, 0,0012 – при 50 разах и 0,00000017 – при повороте граней 100 раз.
В общем, если вам все-таки удалось перемешать свой кубик Рубика и опередить математиков всего мира, все что вам остается сделать – это снова его собрать.
Как собрать кубик Рубика 3×3?
Всем хочется собрать эту неподатливую головоломку, но не все знают как это сделать.
Сначала познакомимся с языком вращения кубика Рубика. Не бойтесь, он несложный!
U — поворот верхней грани по часовой стрелке, U’ — поворот верхней грани против часовой стрелки.
F — поворот передней грани по часовой стрелке, F’ — поворот верхней грани против часовой стрелки.
R — поворот правой грани по часовой стрелке, R’ — поворот правой грани против часовой стрелки.
L — поворот левой грани по часовой стрелке, L’ — поворот левой грани против часовой стрелки.
D — поворот нижней грани по часовой стрелке, D’ — поворот нижней грани против часовой стрелки.
Внимание! Если кубик разбирали механически, появляется вероятность того, что собрать не получится.
Кубик собирается на основе этой формуле:
R U R’ U’
Сборка состоит из семи этапов.
1. Правильный белый крест.
2. Белый цвет.
3. Средний слой.
4. Жёлтый крест.
5. Правильный жёлтый крест.
6. Жёлтые кубики.
7. Финальный.
Готовы? Тогда начнём!
1. Правильный белый крест.
Это должно получиться в итоге.
На этом этапе необходимо собрать белую фигуру, похожую на крест, чтобы эти элементы были одного цвета с центральным. Здесь нет алгоритма: положитесь на свою интуицию. В итоге мы получим то, что видим на картинке.
Теперь белый цвет лежит внизу. Вы не забыли про «пиф-паф»?
Кубик держать левой стороной.
Бывают случаи, когда нужный кубик стоит в среднем слое, (паритеты) но не там, где надо, или не так. В таком случае вытаскиваем его:
4. Желтый крестик.
Здесь надо просто собрать жёлтый крестик, даже если он не правилен. Правильный потом соберём.
5. Правильный жёлтый крестик.
Почему тут белый, а не жёлтый, не знаю. Здесь надо сделать жёлтый крест правильным.
6. Жёлтые кубики
Ставим кубики на место, развернём потом. Повторять, пока на место не встанут!
Наконец-то финал! Если жёлтый лицом к вам, то повторять 2 раза, если справа от вас то четыре раза, а если на верху, то пропускать. Далее, надо верхнюю грань двинуть один раз, и, если там квадратик не на месте, повторить алгоритм. Когда все квадратики на месте, просто верхнюю сторону поставить на место.
P. S. Если не удалось собрать, значит, где-то Вы допустили ошибку или же кубик разбирали механически.
одна из первых ссылок в гугле на эту сборку. посредственный пост. совсем все перестали придумывать новое. только и занимаемся самокопированием.
Головоломка Time Machine
Давно хотел сделать нормальную головоломку
Нет, это не та самая машина. Не Делориан, не Тардис.
Сейчас можно и на разных площадках торговых заказать, но не хочу, дорого=)
По своей сути эта головоломка, простой кубик-Рубика 2х2х2. Но он немного усложнен, двигающимися деталями по каждой стороне куба
В оригинале Time Machine она выглядит так:
Тут не просто нужно собрать по цветам, а ещё и установить порядок деталей от 1 до 12 по часовой стрелке.
У меня на работе было время поработать в компасе. Чертежи и гайды я не искал в интернете (не списывал), просто составлял чертёж. В итоге потов сверился с обычным 2х2х2 и угадал, что механизм такой-же.
Я немного фото скину, для общего обзора
Честно я её сделал, но ещё не собирал=)
Ушла у меня почти вся катушка PLA. Вес около 800 гр. Но результат радует.
По качеству на 4,5 из 5. Присутствует люфт. В этом виноват я, сделал запас, чтобы детали двигались свободно, но вышло не так. Можно было бы сделать фиксирующие магниты или шарики с пружиной, но нужно менять немного конструкцию.
Наклейки заказал в одной из фирм, где фотографии печатают, они мне через плоттер их прогнали, чтобы самому не вырезать.
Решил поделиться своим хобби. Головоломок у меня много (не брендовых)
Это первый нормальный мой пост, регулярно выкладывать не обещаю, мне лень=)
Простите за ошибки, если они есть. Критика приветствуется=)
Спасибо за внимание=)
Кубик Рубика который почти невозможно собрать
Новый уровень сложности
Соберись, кому говорю!
Потешного новобранца мне в коллекцию подарили:
Дополнение к посту «Куб наоборот»
Куб наоборот
Сделал головоломку под Андроид. Представьте: вы находитесь внутри кубика Рубика. Стены, пол и потолок это стороны головоломки. Куб получается вывернутым наизнанку. Теперь не кубик крутится в ваших руках, а вы внутри кубика Рубика. В общем, «замуровали демоны» или «чего только не сделаешь во время самоизоляции».
Белорусский кубик Рубика
Кубик Рубика для слабовидящих
Самая популярная игра-головоломка в мире – тайны кубика Рубика
Кубик Рубика в этом году празднует свое 45-летие и до сих пор остаётся популярным. По оценкам, было продано 350 миллионов экземпляров этой умной игрушки, что позволило ей стать самой продаваемой игрой-головоломкой в мире и, возможно, самой продаваемой игрушкой в мире.
Головоломки Рубика теперь бывают разных форм и размеров, но логика, лежащая в их основе, остаётся той же: собрать каждую сторону кубика одного цвета, и это чрезвычайно сложно.
Согласно тщательному исследованию математиков, существует удивительное количество перестановок в 43 квинтиллиона, которых можно достичь с помощью этой игрушки, и найти правильную очень сложно, особенно потому, что нужно думать на 20 шагов вперед, что непросто для нашего мозга, который привык думать заранее, но не настолько.
Кубик Рубика носит имя своего изобретателя, профессора архитектуры из Венгрии Эрнё Рубика. Он преподавал в Будапештской Школе Коммерческого Искусства, но известен миру не своей профессией напрямую, а своим гениальным изобретением.
Он изучал скульптуру и архитектуру и строил геометрические модели в качестве хобби. Занимаясь своим хобби, он натолкнулся на идею сделать небольшую головоломку, состоящую из 27 деревянных блоков, чтобы изучить со своими учениками трёхмерные объекты.
Самому Рубику понадобился целый месяц, чтобы впервые решить свою головоломку. Куб оказался идеальным для обучения теории алгебраических групп, поэтому он решил запатентовать его в 1975 году.
В 1977 году куб начали производить и продавать в Венгрии в качестве игрушки под названием Magic Cube. После подписания контракта с американским производителем игрушек Ideal Toys в 1979 году головоломка была переименована, и кубик Рубика начал продаваться по всему миру.
В 1980 году цифры взлетели до небес – было продано 4,5 миллиона единиц, и это число продолжало расти. Началось безумство кубика Рубика. К 1981 году он завоевал лучшие награды в области игрушек в Германии, Франции, Великобритании и США, а книги о том, как собрать кубик Рубика, наводнили рынок.
Вскоре повсеместно появились пиратские версии, и их распространение было невозможно контролировать.
Даже несмотря на множество учебных пособий на YouTube и других онлайн-руководств, которые учат нас, как собрать кубик, доступный нам сегодня, люди всё ещё одержимо пытаются разгадать тайну. И испытывают удивительное чувство, по словам тех, кто в этом преуспел.
Ходят даже разговоры о том, что зависимость от кубика Рубика реальна.
Для некоторых разгадка Кубика Рубика стала жизненной целью. Грэхему Паркеру из Гемпшира, Англия, потребовалось 26 лет, чтобы решить эту задачу, так как он отказался «обманывать» и искать ответ в Интернете или в книге. Паркер сказал Би-би-си, что провёл более 27400 часов, ломая голову над кубиком с тех пор, как купил его в 1983 году: «Он заплакал, когда собрал его. Он признался, что это привело к боли в спине и проблемам в семье».
Для многих преданных поклонников одного раза было недостаточно. Они снова и снова собирают кубик Рубика, чтобы улучшить свою скорость, или добавляют дополнительное измерение в задачу, например, завязанные глаза.
1980-е годы были тем временем, когда Кубик Рубика правил миром; ходили легенды о поклонниках, настолько сосредоточенных на разгадке тайны, что их браки распадались. У одного из поклонников якобы развился тендинит в запястьях от постоянного повторения вращательных движений, используемых для того, чтобы собрать кубик.
До сих пор существуют рекорды, которые можно побить, и для фанатов проводятся чемпионаты, на которых люди соревнуются в самом быстром поиске решения.
Соревнования довольно разнообразны: некоторые проводятся с завязанными глазами, под водой, только ногами и т. д. Однако с 1982 года популярность головоломки начала уменьшаться, и в 90-е годы казалось, что кубик был частично забыт, кроме как среди преданных фанатов.
Тем не менее, с бумом Интернета и количеством людей, которые сейчас его используют, кубик Рубика вновь обретает свою популярность.
Популярность игрушки выросла в 2006 и 2007 годах после выхода книги «Погоня за счастьем», в которой Крис Гарднер (Уилл Смит) произвёл впечатление на менеджера крупной биржевой компании, собрав кубик во время совместной поездки на такси, что полностью изменило его жизнь. Кажется, что эта загадка останется с нами навсегда.
Как быстро собрать кубик рубика 3х3 без формул: схема с картинками
Многочисленные попытки сложить кубик Рубика не увенчались успехом? Все представленные инструкции в Интернете написаны профессионалами, а для “чайников” решение кажется очень запутанным? Вы думаете, что решить эту головоломку невозможно? Следуя нашей поэтапной инструкции, вы сможете не только полностью собрать самую популярную головоломку в мире без формул, но и понять, как вы это сделали.
С чего начать
Итак, ваша цель – собрать Кубик Рубик. Сделать это, не зная как он устроен, из чего состоит и как функционирует, не получится.
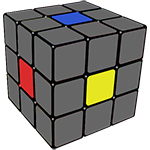
| Центральные элементы | 6 штук, по одному для каждой стороны. Они могут вращаться вокруг оси, но своего положения никогда не меняют, то есть всегда находятся в «правильном» положении. На рисунке они окрашены коричневым цветом. |
| Угловые элементы | 8 штук, каждый из которых имеет 3 разных цвета. На рисунке они– фиолетовые. |
| Ребра | 12 штук с двумя разными цветами. Они находятся между углами – бледно-голубые на картинке. |
При повороте одной стороны, мы видим, что центральные элементы остаются на месте, ребро перемещаются в то место, где должны быть ребра, а угол занимает место в углу.
Из этого следует, что каждый элемент имеет определенный тип, который не меняется после поворота (край остается краем, центр – центром).
Частые «вопросы-ответы»
Если вы не собираетесь участвовать в соревнованиях, можете брать любой кубик. Молодым людям и детям лучше купить головоломку китайских производителей. При выборе, учитывайте следующее:
— Лучше брать кубик последних моделей, в нем предусмотрены недостатки предыдущих версий, и он более усовершенствован.
— Правильный кубик должен легко крутиться, при этом хорошо резать углы.
— Кубики для профессионалов можно разбирать и настраивать.
Классический Кубик состоит из 12 двухцветных бортовых или реберных элементов (12 «ребер»).
Есть много способов сборки Кубика. Есть те, которые позволяют парой-тройкой формул собрать, но за пару часов. Другие при помощи запоминания пары сотен формул позволяют собрать кубик за 1 минуту или даже за 20 секунд.
Основы
Наша цель – поставить все элементы на правильные места. Чтобы определить направление, в котором нужно поворачивать и «правильное место» того или иного квадратика, необходимо все свое внимание обратить на центральные элементы, ведь они, как мы уже говорили, имеют фиксированное положение.
Например, ребро, которое находится, между красным и зеленым центром, соответственно, красно-зеленое, поэтому необходимо ориентироваться на то, чтобы возле зеленого центра разместилось ребро такого же цвета, возле красного центрального элемента – красный край.
Шаг 1. Собираем края одной стороны
Первое, что вам нужно сделать – выбрать цвет, с которого вы будете начинать. В данном примере основной цвет – желтый, он будет представлен на всех схемах. Каждый волен выбирать тот вариант, который ему больше по душе и начинать с него.
Итак, если верхний центральный элемент у нас желтый, то снизу, соответственно – белый (он практически во всех моделях кубика Рубика находится на противоположной стороне).
Этот шаг сложнее всего объяснить тем, кто не знает, как собрать кубик Рубик. Эту задачу проще решить самостоятельно и у вас несомненно это получится сделать, после недолгой тренировки.
Именно на этом шаге большинство новичков и останавливаются – собирают крест, потом одну грань – дальше, к сожалению, мало кто продвигаются.
Если вы собираете куб по схеме эврикак, рекомендуем решить первый шаг самостоятельно, не обращая внимания на приведенные ниже примеры.
Для тех, кто не может этого сделать, ниже представлена схема, как собрать крест. Имейте ввиду вам придется повторить этот шаг 4 раза – по одному для каждой стороны.
а) Желтый «смотрит» вниз
б) Желтый смотрит вперед
в) Ребро в промежуточном слое
После этого край будет находиться в одном из трех вышеописанных положений. Используя схему, поставьте его на «правильное» место. Повторите все действия для каждого желтого края и соберите крест на верхнем слое кубик Рубика.
Шаг 2. Собираем верхнюю грань
Если вы смогли сложить крест, то стоит собрать весь верхний слой, то есть поставить углы на свои места один за другим. Мы не можем ставить их как нам хочется, ведь каждый угол имеет специально отведенное для него место, что и определяют цвета из которых он состоит.
Так же, как и в предыдущем шаге, есть несколько решений, которым мы будем следовать.
а) желтый смотрит влево
б) желтый смотрит вправо
в) желтый находится снизу
Повторите действия для каждого угла, пока не соберете верхний слой полностью.
Шаг 3. Алгоритм сборки второй грани
Мы хотим собрать второй слой кубика. Помните, что центральные элементы – фиксированы, поэтому нет необходимости менять их местами и думать, как разместить. Имейте ввиду, что нижеприведенные действия вам придется повторить 4 раза – по одному для каждого края.
Есть несколько возможных вариантов:
1) Край должен передвинуться вправо с того места, где он находится.
2) Край должен передвинуться влево с того места, где он теперь находится.
Повторите этот шаг 4 раза – по одному для каждого края.
Шаг 4. Второй крест
Итак, мы собрали первые 2 слоя кубика Рубика. Теперь мы должны добиться того, чтобы 4 крайних элемента верхнего слоя имели белый цвет, образуя крест. На данном этапе мы сосредоточимся только на крайних элементах, не обращая внимания на углы.
В верхней грани куба может четыре белых края или два, или ни одного. Если все четыре белые ребра находятся на верхней стороне, то можно этот шаг пропустить и перейти к следующему. Если есть два ребра, то нужно использовать один из следующих вариантов в зависимости от того как они расположены относительно друг друга: рядом или напротив.
2) Противоположные края – белые
3) Ни один белый квадрат не стоит правильно
Если в верхнем слое не оказалось ни одного белого квадрата, проделайте один из двух вышеописанных вариантов и вы получите 2 белых квадрата в верхнем слое. После это проделайте необходимую последовательность действий, в зависимости от полученной ситуации.
Таким образом, мы сложили второй крест.
Шаг 5. Как разместить второй крест
На предыдущем этапе мы сложили второй крест. На этом этапе мы сделаем, чтобы боковые части креста совпадали по цвету с центральными элементами соответствующих граней. Мы сконцентрируем свое внимание только на белых краях куба, не обращая внимания на углы.
б) противоположные края
Таким образом мы разместили правильно второй крест кубика Рубика.
Шаг 6. Размещение углов
Мы уже поставили на свои места все элементы кубика Рубика, кроме угловых частей последнего слоя.
Цель предпоследнего шага – разместить правильно углы, не обращая внимания на их ориентацию. Таким образом, вы должны знать, когда именно угол занял правильную позицию.
Рассмотрим несколько примеров, когда углы размещены неправильно и когда они занимают нужную позицию для того чтобы собрать кубик Рубика.
Вполне возможно, что все 4 угла будут на своих местах с самого начала (смело переходите к следующему шагу), или же только 1 угол размещен правильно, или ни одного. Если только один угол занимает «свое» место, следуйте одному из ниже представленных примеров, выбрав тот, который позволит разместить все элементы на свои места.
1) 3 угла не на своей позиции (а)
2) 3 угла не на своей позиции (б)
3-4) Ни один угол не размещен правильно
Если ни один из 4 углов не занимает «свое» место, проделайте один из вышеописанных примеров – таким образом, вам удастся поставить один из них на место. Далее проделайте действия в зависимости от того, что у вас получилось.
Таким образом мы собрали кубик Рубика 3х3, поставив углы на свои позиции. Последний шаг – вращая углы последнего слоя, мы решим головоломку полностью.
Шаг 7. Как собрать
На предыдущем этапе мы поставили все элементы на свои места. Остается лишь повращать углы, чтобы решить кубик Рубика и собрать его полностью. На данном этапе может остаться два, три или четыре неправильно направленных угла в последнем слое.
Если есть 2 неправильно ориентированных угла, следуйте одному из ниже приведенных примеров в зависимости от ситуации, которая возникла.
Обязательно прочитайте это перед тем, как вращать грани кубика.
Очень важно! Этот шаг не так прост, как другие, но и на много сложнее. Перед тем, как приступить к выполнению, стоит знать несколько моментов. Вариант 1 имеет несколько подвариантов, поэтому прежде всего необходимо понять какой именно подходит вам. Чтобы решить этот шаг проделайте первую последовательность действий. После этого делайте необходимые шаги, в зависимости от варианта красной таблицы, который вы получили.
Вариант 1. Два угла не правильно ориентированы. Обратите внимание на то, что «соседний» угол – нуждается в повороте по часовой стрелке.
Вариант 2-3. Три угла неправильно ориентированы.
Если 2 угла не правильно ориентированы, соберите кубик Рубик, следуя первому примеру – таким образом вы получите всего 2 неправильно ориентированных угла. Наконец проделайте последовательность действий, в зависимости от ситуации, которая у вас вышла.
Вариант 4. Все углы не правильно ориентированы.
Если не один из 4 углов не ориентирован правильно, следуйте первому приведенному примеру. Затем подберите решение, которое подойдет к вашей ситуации.
Если вы сделали все правильно и до сих пор следовали нашей инструкции, то поздравляем! Вы собрали кубик Рубика самостоятельно!
Интересные факты
Если у вас не получилось сложить кубик Рубика с первого раза, не расстраивайтесь и не отказывайтесь от попыток. Не стоит искать легких путей.
Вам будет интересно узнать, что Ерно Рубик – изобретатель всемирно известной головоломки, потратил целый месяц на ее решение.
Проявите терпение и упорство – у вас все непременно получиться! Решив кубик Рубик один раз, не останавливайтесь на достигнутом. Возможно вы – новый рекордсмен. Также, вы можете освоить навыки беспроигрышной игры в домино, шахматные секреты и других логических игр.
А тут, между прочим, есть в чем себя проявить:
Надеемся мы вдохновили вас и помогли понять, как собрать кубик Рубика. Ели вы интересуетесь играми на мышление и головоломками, наверное, вам интересно будет узнать секреты игры в домино или шахматные правила. Эти занятия не только увлекательны, они положительно влияют на вашу память и эффективно способствуют развитию умственных способностей. Хороший вариант интересного времяпровождения с друзьями.
Частые «вопросы-ответы»
Это простой алгоритм, который помогает установить угловые кубики на свои места. Среди спидкуберов он называется “пиф-паф”. Выглядит так: R U R’ U’.
Смазать пластиковые детали кубика для максимально комфортной сборки нужно силиконовой смазкой. Купить ее можно почти в любом магазине радиодеталей. Нужно обратить внимание на ее консистенцию. Она бывает жидкая, густая или очень густая.
Нам подходит смесь вариантов 1 и 2, на крайний случай вариант 2.
Если смазать очень жидкой, его стороны начнут прилегать друг к другу слишком сильно. Густая забирает скорость вращения. Если смешать два вида смазки, именно такая консистенция является оптимальной.
Комментарии экспертов
Я 5 лет занимаюсь сборкой кубиков разных вариантов. Также участвовал в соревнованиях по спидкубингу. По собственному опыту утверждаю, что кубик Рубика сейчас популярен среди людей разных возрастных категорий, и реально его можно собрать за 1 минуту.
Данная статья является отличной инструкцией для тех, кто еще не освоил технику сборки кубика, поскольку здесь описан самый простой механизм сборки. Еще его называют CFOP или метод Джессики Фридрих. Для людей, которые только начинают знакомство с кубиком Рубика, данная информация станет хорошим руководством.
Видео к материалу
Если вы увидели ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Как собрать кубик Рубика 3х3 для начинающих
 Представляем самую простую и понятную схему сборки кубика Рубика 3х3!
Представляем самую простую и понятную схему сборки кубика Рубика 3х3!
А на нашем YouTube канале есть подробное СУПЕР видео Как собрать кубик Рубика — Легко! Методика 2018
Даже если Вы первый раз взяли кубик в руки с этой схемой Вы гарантировано научитесь собирать кубик Рубика не более чем за 20 минут!
Собрать кубик Рубика на самом деле очень просто!
Этапы сборки:
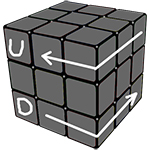
Язык вращений:
Для того чтобы дальше собирать кубик, Вам необходимо будет знать язык вращений.
Важно! Перед началом сборки убедитесь, что Ваш кубик не был разобран на части механическим способом, а затем собран, но не правильно.
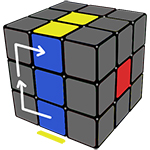
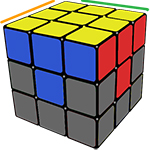
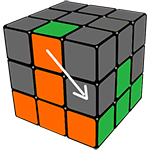
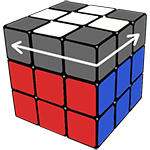
ЭТАП 1. Собираем правильный белый крест:
Первый и самый простой этап сборки кубика Рубика.
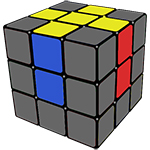
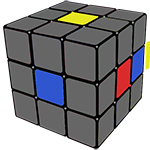
Первое, что необходимо сделать, это просто собрать белый крест, это можно сделать интуитивно.
Но если у вас всё-таки возникли проблемы с данным этапом, то пользуйтесь шпаргалкой ниже:
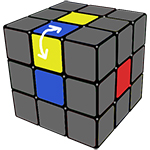
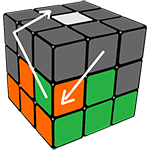
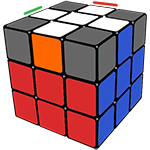
После того, как Вы собрали крест, его необходимо сделать правильным, он будет таким в том случае, если нижний цвет ребра, входящего в наш, уже готовый крест, совпадает с центром, находящимся ниже.
Вот так выглядит правильный крест
Изначально, цвет ребра и цвет центра под ним может не совпадать (если он совпадает, то вам повезло), научимся решать данную ситуацию:
Для начала, выучите простой алгоритм, под названием «пиф-паф», выполняется просто, состоит из 4 действий: RUR’U’.
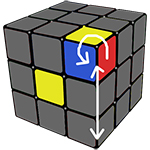
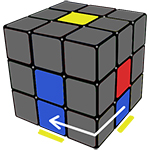
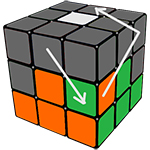
Теперь когда Вы выучили его, повторили несколько раз, Вы готовы идти дальше, а именно, вращать верхнюю грань (UP), до тех пор, пока не увидите, что хотя бы с двух сторон кубика совпали цвета ребра и центра под ним. Держать кубик надо так, чтобы одна из сторон, которые совпали смотрела на Вас, а другая была слева от вас. После этого выполняйте один из алгоритмов, с картинки снизу.
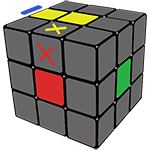
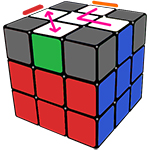
Этап 2. Сборка первого слоя
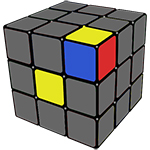
Сборка всего первого слоя не составит большого труда, в основном этот этап будет состоять из обычных «пиф-пафов».
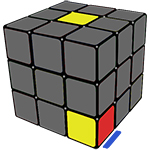
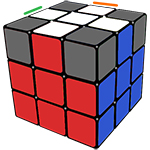
Для начала нам необходимо будет перевернуть кубик на жёлтую сторону и на этой стороне найти углы с белым цветом.
Помимо белого цвета, в угле есть ещё два цвета, например, зелёный и красный, получается, мы имеем бело-красно-зелёный угол.
Теперь его надо поставить на своё место, то есть между зелёным и красным центрами.
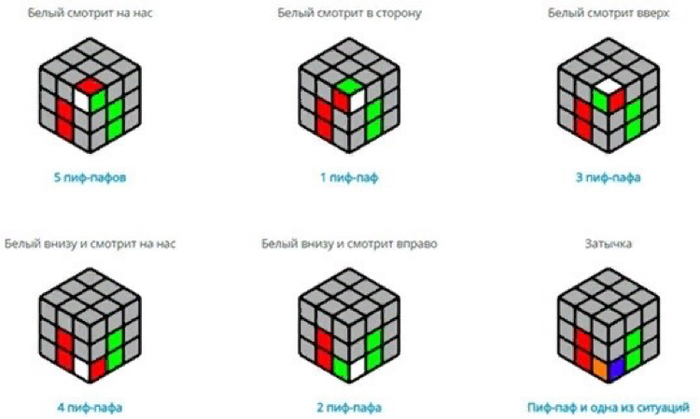
После этого, в зависимости от ситуации, которая вам попалась, вы можете решить её с помощью одного или нескольких «пиф-пафов», на таблице снизу, приведены примеры всех возможных ситуаций и их решение:
После выполнения всех этих действий, Вы установите нужный угол на место, после этого, Вы должны проделать то же самое с тремя оставшимися углами.
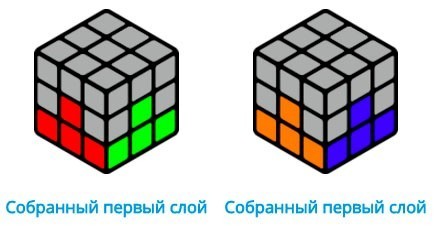
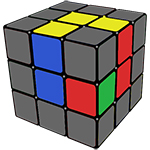
В итоге у Вас получится собранный первый слой:
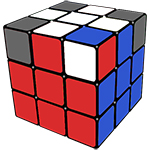
Этап 3. Сборка второго слоя
Сборка второго слоя обычно вызывает определённую сложность, просим Вас быть внимательными и не торопиться.
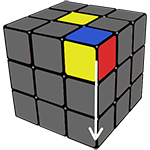
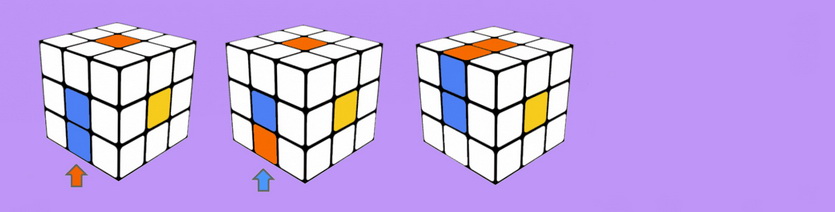
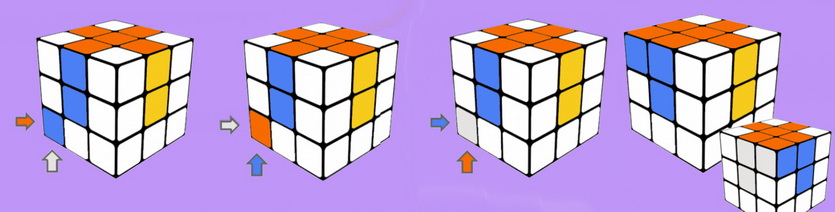
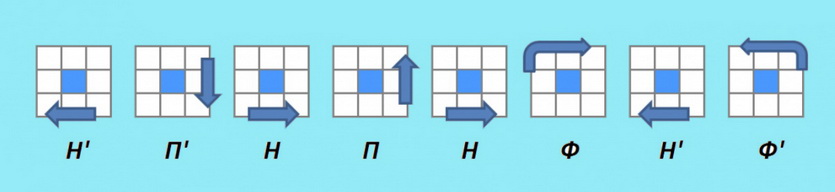
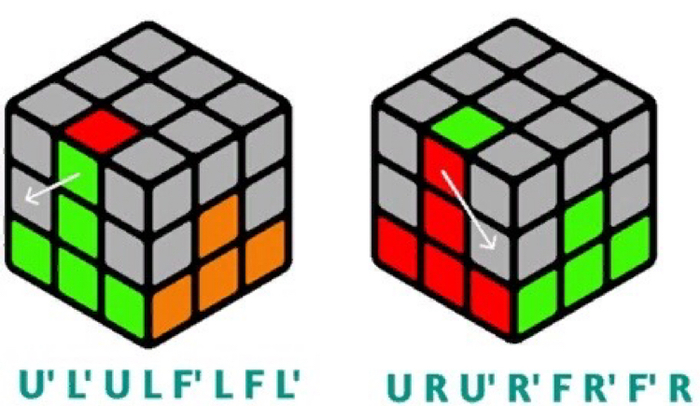
Для начала, на жёлтой стороне, Вы должны найти рёбра без жёлтого цвета, например, Вы нашли зелёно-красное ребро, теперь его необходимо поставить на место, для этого, смотрим на нижний цвет ребра, к примеру, этот цвет зелёный, теперь ты подводим этот цвет к своему центру, так как цвет у нас зелёный, подводим его к зелёному центру и выполняем один из алгоритмов с картинки:
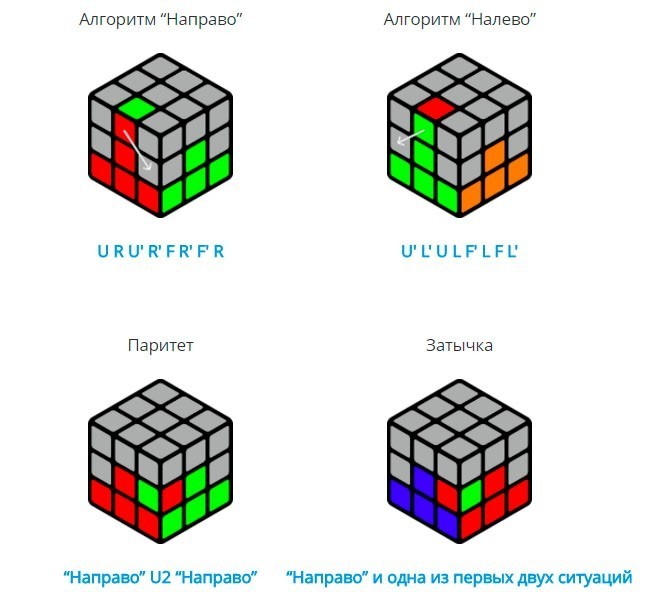
Иногда бывают ситуации, когда ребро без жёлтого цвета стоит на втором слое, но повёрнуто не правильно, либо стоит не на своём месте, эти ситуации называются «паритеты»
На картинке снизу Вы можете увидеть возможные виды паритетов и их решение.
В итоге получится собранный второй слой:
Этап 4. Правильный жёлтый крест
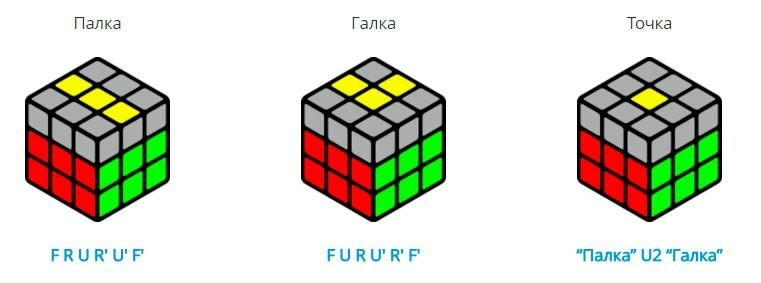
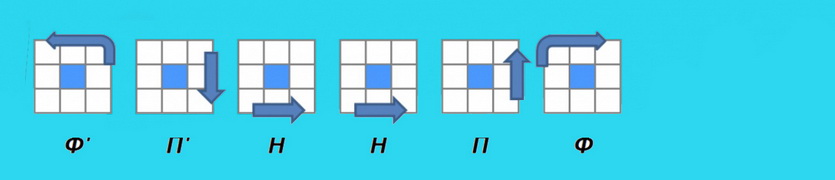
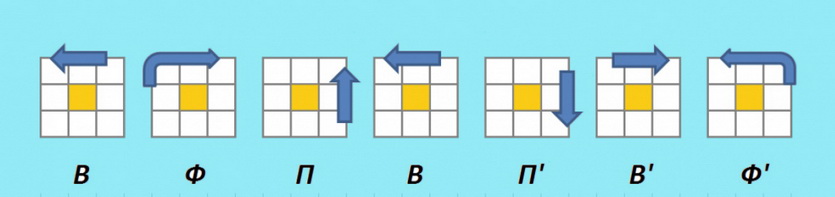
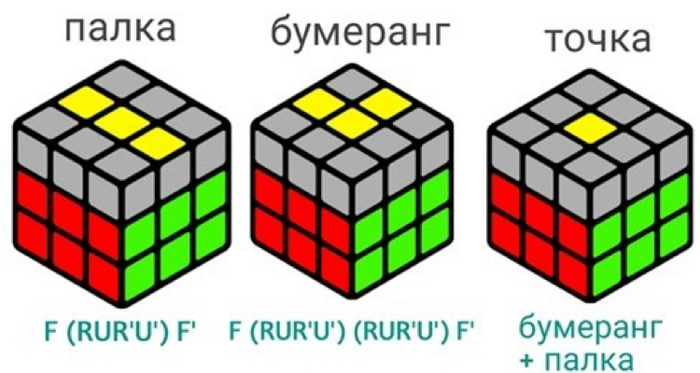
Для начала, Вам необходимо просто собрать крест, но в отличие от первого этапа, здесь крест интуитивно сделать не получится, для этого существуют специальные формулы, которые состоят из обычных пиф-пафов.
Также может быть такое, что крест соберётся сам, и если это произошло, то Вам повезло. А если нет, то пользуйтесь картинкой снизу.
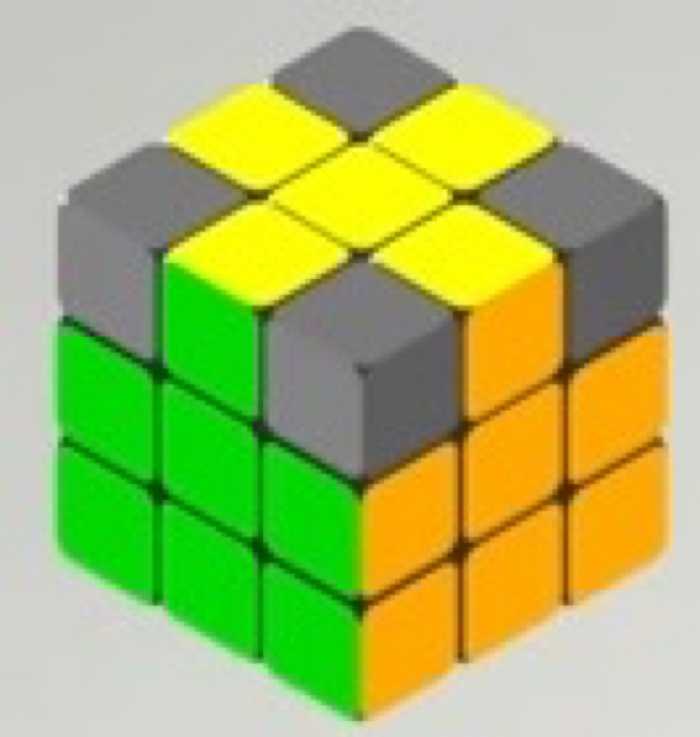
Теперь вам нужно сделать получившийся крест правильным.
Для этого, как и в первом этапе, мы вращаем верхний (жёлтый) слой, до тех пор, пока хотя бы с двух сторон не совпадут цвета ребра и центра под ним (как и в первом этапе).
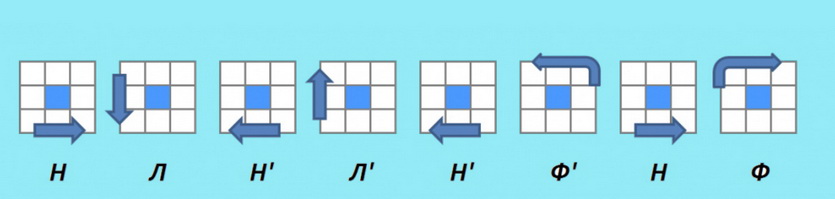
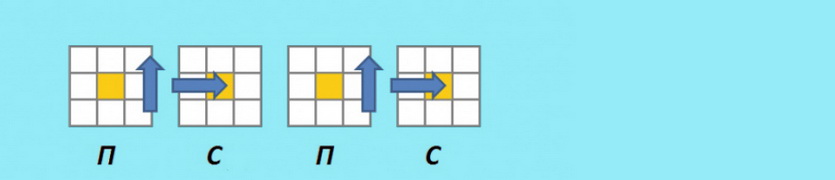
После того, как у Вас совпали две стороны, вам нужно сделать алгоритм, как на картинке снизу (может быть так, что у вас уже правильный крест, а значит Вам снова повезло)
Держать кубик надо так, чтобы сторона, которая не совпала, смотрела на вас, а сторона, которая совпала, была справа.
Этап 5. Ориентирование углов последнего слоя
Для начала разберёмся, как понять, что угол стоит на своём месте:
У угла три цвета, и он стоит правильно только в том случае, если эти цвета совпадают с цветами центров, между которыми стоит угол.
Например: у нас есть синяя красной жёлтый угол, и если он стоит между жёлтым, синим и красным центрами, а если он стоит между другими центрами, например между жёлтым, оранжевым и зелёным, то он не правильный!
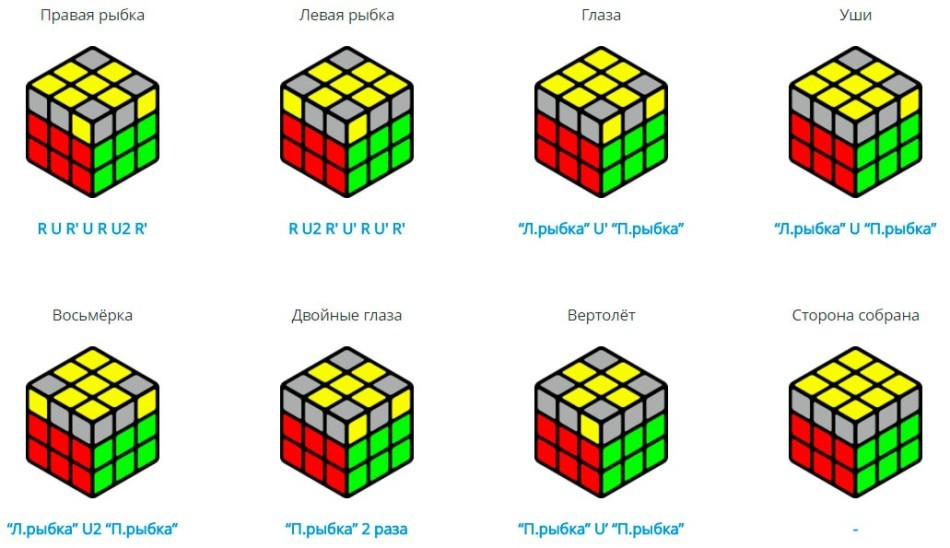
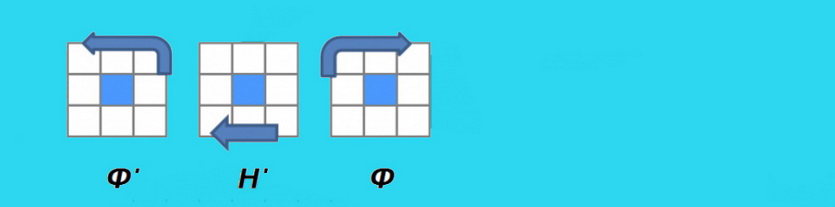
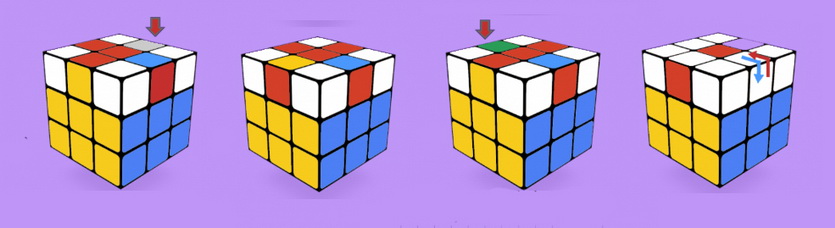
Теперь, на верхнем слое необходимо найди правильный угол, взять кубик так, чтобы этот угол находился слева сверху и выполнить алгоритм (если правильного угла нет, то этот алгоритм надо выполнить с любой из сторон, и хотя бы один из углов станет правильным)
В данном алгоритме используется ход Lw’ – это движение левой грани вместе с центральной против часовой стрелки.
В итоге у Вас получится так:
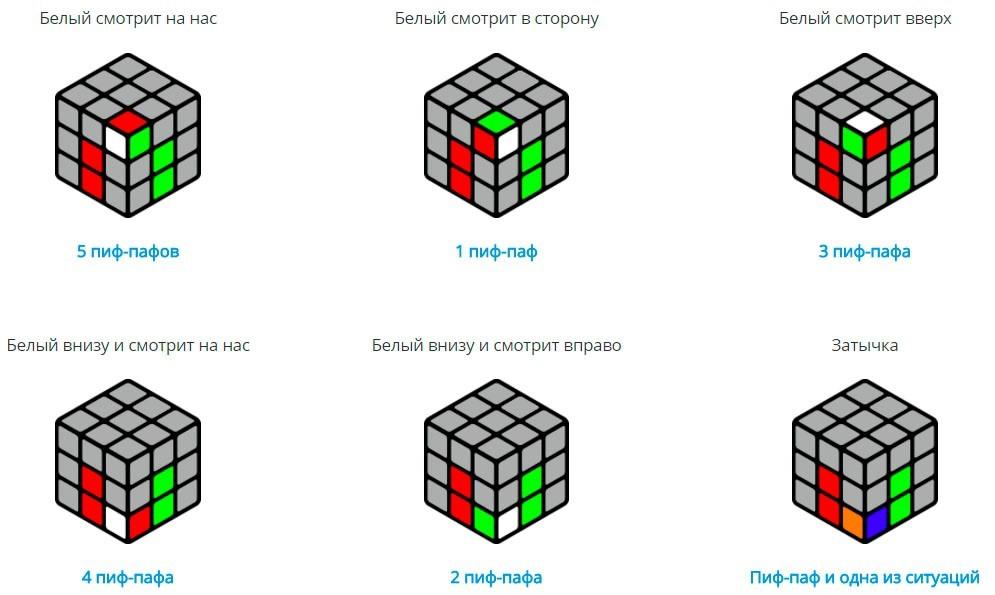
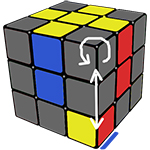
Этап 6. Поворот углов последнего слоя (последний этап)
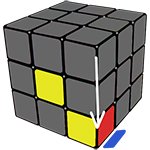
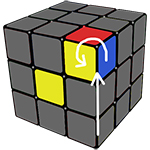
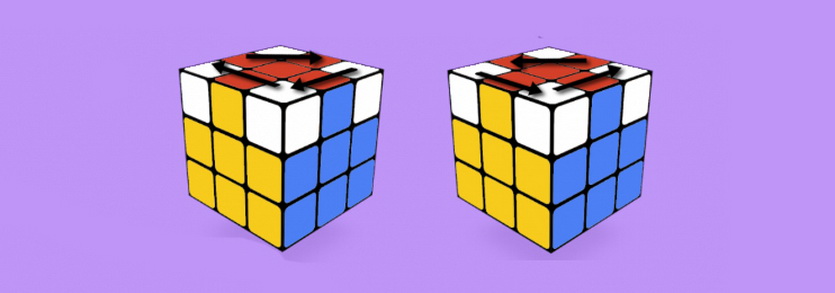
Для того чтобы перевернуть углы на последнем слое, надо будет запомнить простую комбинацию, в ней всего 4 хода (R’D’RD)
ПОЗДРАВЛЯЕМ. Вы собрали кубик Рубика!
P.S. Если кубик не собрался, то начните с начала, не спеша, проверяя результат каждого шага.
И ещё раз убедитесь, что Ваш кубик не был разобран механически.
Схема работает 100%, и проверена миллионами сборок.
Как собрать кубик Рубика. Самая легкая схема
Кубик Рубика на сегодняшний день признан одной из самых популярных в мире головоломок, состоящей из разноцветных секторов, соединенных в одну фигуру. Ее создателем стал венгерский скульптор, который сделал наглядное пособие по теории групп для своих студентов. Сегодня же эта игрушка является наиболее продаваемой в мире.
Строение кубика
Прежде чем понять, как собирать этот кубик, необходимо разобраться с его строением. Сегодня можно встретить самые разные формы и размеры головоломки. Стандартный кубик Рубика состоит из 12 ребер и имеет 8 углов. Внутри имеется крестовина на которой и крепятся все детали.
Концом крестовины является один из квадратов, вокруг которого и собираются другие квадраты с таким же самым цветом. Собранной головоломка считается в том случае, если на каждой из 6 сторон кубика будет один цвет.
В оригинальном кубике желтый цвет в любом случае будет располагаться непосредственно напротив белого. И если по какой-то причине кубик разобрать и потом неправильно сложить, то собрать головоломку уже будет невозможно.
Помимо центра фигуры, ее постоянными составляющими есть углы, на каждом из которых по 3 цвета. Независимо от того, как вы будете менять положение цветов в фигуре, цвет углов будет оставаться одним и тем же. Для сбора головоломки, средние и угловые сектора перемещаются исходя из того цвета, который установлен на центральном секторе.
Каждая из сторон кубика имеет свое название.
При сборке головоломки необходимо не только перемещать его стороны, но и менять пространственное положение кубика. Такие движения получили название перехват. Схематически это можно показать следующим образом.
В Интернете можно найти массу алгоритмов сборки головоломки. Если в нем указана исключительно буква, то положение стороны нужно проводить по часовой стрелке. А знак апостроф (‘) возле буквы указывает на то, что вращать следует против часовой стрелки. Цифра 2 после буквы означает, что сторону следует провернуть дважды. К примеру, D2’ указывает на то, что нижнюю сторону кубика следует дважды провернуть против часовой стрелки.
Инструкция для новичков
Проще всего складывать кубик Рубика следующим образом:
Метод Джессики Фридрих
Данная методика основана на скорости, с которой собирается головоломка. Но такой вариант не подойдет для тех, кто впервые в жизни взял в руки кубик.
Как собрать кубик в 20 ходов
В 1982 году впервые были проведены соревнования по скорости сборки данной головоломки. После чего многие стали самостоятельно разрабатывать различные алгоритмы, способные быстро собрать кубик, используя минимальное количество действий.
Алгоритмом, состоящим из минимального количества ходов признан, так называемый «Алгоритм Бога», который выполняется в 20 ходов.
Секреты сборки головоломки
Если вы поставили перед собой цель научиться очень быстро собирать кубик Рубика, то нужно запомнить несколько секретов:
Кубик Рубика – достаточно хитрая головоломка, которая может заинтересовать не только взрослого, но и ребенка. Чемпионами по скорости его сборки чаще всего становятся подростки. Последний рекорд принадлежит 15-ти летнему Колину Бернсу, который смог полностью собрать кубик за 5,2 секунды.



















































































 Представляем самую простую и понятную схему сборки кубика Рубика 3х3!
Представляем самую простую и понятную схему сборки кубика Рубика 3х3!