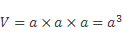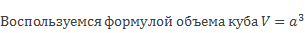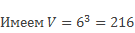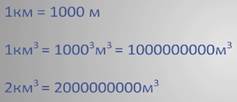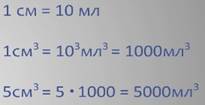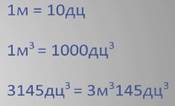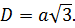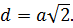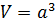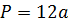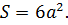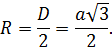Как считается объем куба
Как считается объем куба
Нахождение объема куба: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
Формула вычисления объема куба
1. Через длину ребра
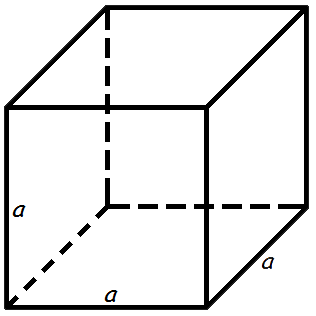
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a 3
2. Через длину диагонали грани
Следовательно, вычислить объем куба можно так:
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Калькулятор для расчета объема куба
Куб или гексаэдр – правильный многогранник, который имеет шесть граней-квадратов. Кубы часто встречаются в реальной жизни, хотя они и не такие популярные, как призмы или параллелепипеды. В любом случае калькулятор объема куба пригодится вам для расчета объема этой распространенной фигуры.
История гексаэдра
Куб относится к классу правильных многогранников, известных человечеству еще с давних времен. Древние цивилизации придавали игральным костям форму куба, а изображения многогранников встречаются на предметах быта, созданных в эпоху неолита. Особое внимание многогранникам, и в частности гексаэдру, уделяли в Древней Греции. Античные греки были неравнодушны к геометрии и числам, выстраивая математические теории создания и функционирования мира. Так, философ Платон использовал образы правильных многогранников для описания природных стихий. Куб в его стройной системе мироздания ассоциировался с землей, так как именно гексаэдр – самый устойчивый правильный многогранник.
Евклид дал полное описание правильных многогранников, в том числе и куба, в «Началах» – своем фундаментальном труде по геометрии. Позднее многогранниками занимался Иоганн Кеплер, который построил модель планетной системы с использованием этих фигур. В кеплеровской модели куб соответствовал Сатурну, вписанному в окружность колец газового гиганта. Гексаэдр, пожалуй, вторая по идеальности фигура после сферы, поэтому она получила важное значение в человеческой культуре.
Геометрия куба
Изучая куб, ученые нашли все его характеристики. Мы давно знаем количество граней (6), ребер (12), вершин (8) или осей симметрии (9). Но с течением времени геометры узнали много нового. Так, в неевклидовой геометрии, которая рассматривает фигуры на сферических или гиперболических поверхностях, прямых углов, следовательно, и привычных нам квадратов и кубов не существует. Одновременно куб – оригинальная фигура, которая существует во всех многомерных пространствах. В отличие от треугольника или параллелограмма, в нульмерном пространстве куб представляет собой точку, в одномерном – простой отрезок, в двухмерном – квадрат, в трехмерном – собственно куб, в четырехмерном – тессеракт, а в пятимерном – пентеракт. Продолжать последовательность можно до десятимерных пространств.
Использование гексаэдров
Кубические фигуры используются не только в архитектуре и строительстве. Куб – эффективная форма для хранения данных, поэтому кубические сетки находят применение в аналитике, программировании, базах данных и прочих научных приложениях. Уникальная форма гексаэдра дает возможность оперировать n-мерными кубами для измерения бесконечно малых объемов или визуализации данных.
Объем куба
Объем любой геометрической фигуры – это количественная характеристика, демонстрирующая, сколько единичных кубов вмещает выбранная фигура. Объем куба, пожалуй, самая простая формула для вычисления этой характеристики. Выглядит она следующим образом:
где a – длина ребра.
Вычислить объем кубической фигуры можно так же при помощи диагонали грани или диагонали самого гексаэдра. Диагональ грани – это диагональ квадрата, которая связана с длиной ребра следующим соотношением:
Диагональ куба связана с длиной ребра похожим соотношением:
Таким образом, рассчитать объем гексаэдра можно оперируя тремя характеристиками фигуры.
Наша программа представляет собой онлайн-калькулятор для вычисления численных характеристик многогранников и тел вращения. Для определения объема достаточно замерить одну характеристику на выбор и ввести это значение в соответствующую ячейку. Программа не только вычислит объем гексаэдра, но и отобразит значения остальных двух неизвестных характеристик.
Естественно, на практике гораздо проще замерить длину ребра куба, однако в школьном курсе стереометрии встречаются задачи на объем куба, в которых даны именно диагонали фигуры. Таким образом, наш калькулятор пригодится в основном школьникам. В быту для вычисления объема достаточно возвести в куб всего один параметр, но если это слишком большое или дробное значение, то для таких вычислений вам и пригодится наша программа.
Рассмотрим пару примеров
К примеру, вы хотите сделать из полимерной глины сплошные игральные кости, которые, естественно, выполняются в форме гексаэдра. Вы хотите сделать пять комплектов, поэтому вам интересно узнать, какой объем глины потребуется для изготовления такой поделки. Стандартный игральный кубик имеет длину ребра 1,6 см. Используя программу, узнаем, что на изготовление одного игрального кубика понадобится V = 4,1 кубических сантиметров полимерной глины. Так как вам необходимо 5 комплектов по 2 кубика в каждом, то общий расход материала составит 41 кубический сантиметр.
Школьная задача
В задаче по стереометрии требуется вычислить объем гексаэдра, диагональ которого равна 5 см. Для решения этой задачи можно использовать формулу, представленную выше, и сначала выразить ребро через диагональ:
Согласно этой формуле, длина ребра куба будет приблизительно равна 5/sqrt(3) = 2,88. Теперь для вычисления объема достаточно возвести полученный результат в третью степень и получить приблизительный результат V = 23,88 кубических сантиметров. Приблизительность вычислений объясняется тем, что корень из трех мы округлили до двух знаков после запятой. Калькулятор использует более точные значения корней, поэтому можно пропустить эти вычисления и просто ввести значение 5 в ячейку D онлайн-калькулятора и получить точный результат V = 24,05.
Заключение
Гексаэдры занимают в человеческой цивилизации большое значение, поэтому не только школьникам требуется вычислять объем этой фигуры. Используйте наши онлайн-калькуляторы для быстрых и точных вычислений характеристик правильных многогранников и тел вращения.
Объем куба
Свойства
Куб представляет собой прямоугольный параллелепипед, у которого все ребра равны между собой. Поэтому объем куба вычисляется не просто произведением всех трех его параметров, а возведением ребра куба в третью степень. Поэтому чтобы вычислить ребро куба через объем необходимо извлечь из последнего кубический корень. a=∛V
Площадь грани куба или одной его стороны равна площади квадрата, стороной которого является ребро куба, поэтому кубический корень из объема необходимо возвести во вторую степень. S=∛(V^2 )
Площадь боковой и полной поверхности куба состоят из четырех и шести таких граней соответственно, поэтому их формулы являются аналогией предыдущей с добавлением необходимых коэффициентов. S_(б.п.)=4∛(V^2 ) S_(п.п.)=6∛(V^2 )
Периметр куба равен сумме двенадцати его ребер, равных между собой, поэтому зная, что каждое ребро представлено в виде кубического корня из объема, необходимо умножить его на двенадцать. P=12a=12∛V
Чтобы вычислить диагональ грани куба, нужно вернуться к формуле диагонали квадрата, которым представлены грани. Согласно ей, чтобы найти диагональ, нужно умножить корень из двух на сторону квадрата – ребро куба в данном случае, или кубический корень из объема. d=a√2=∛V √2
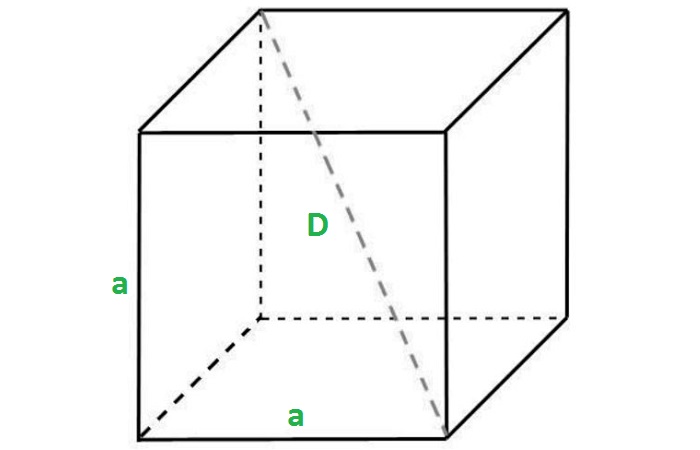
Найти диагональ самого куба немного сложнее. Для этого три вершины – диагонали и прилегающего к ней бокового ребра – соединяются в прямоугольный треугольник через диагональ основания, и по теореме Пифагора выводится формула диагонали куба. (рис.2.1) a^2+d^2=D^2 D^2=a^2+2a^2 D^2=3a^2 D=a√3=∛V √3
Чтобы найти радиус сферы, вписанной в куб, через объем, нужно разделить его кубический корень, представляющий собой ребро куба, на два. (рис. 2.2) r=a/2=∛V/2
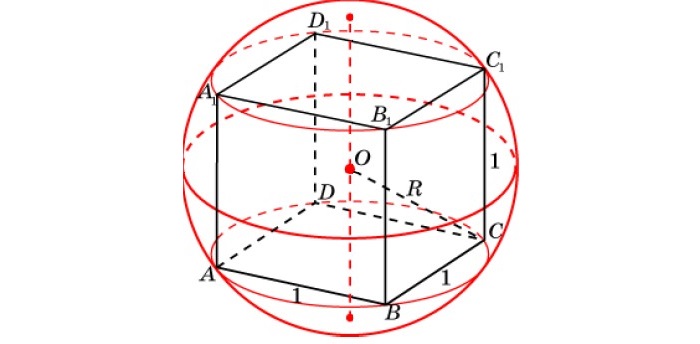
Радиус сферы, описанной вокруг куба, равен половине диагонали куба, поэтому подставив вместо диагонали необходимую формулу через объем, получим следующее выражение: (рис.2.3) R=D/2=(∛V √3)/2
Онлайн калькулятор. Объем куба
Используя этот онлайн калькулятор для вычисления объема куба, вы сможете очень просто и быстро найти объем куба, зная значения длины его стороны.
Воспользовавшись онлайн калькулятором для вычисления объема куба, вы получите детальное решение вашего примера, которое позволит понять алгоритм решения задач и закрепить пройденный материал.
Найти объем куба
| a | = |
Ввод данных в калькулятор для вычисления объема куба
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины, конвертером единиц площади и конвертером единиц объема.
Теория. Объем куба.
Формула для вычисления объема куба
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Расчет объема куба
Куб это геометрическое тело, ограниченное шестью квадратами, которое ещё можно назвать правильный шестигранник, а так же правильный многогранник. Слово «куб» образовано от греческого слова «kybos».
Определение объема куба
Формула расчёта объёма куба
Расчет объема куба можно произвести с помощью следующей формулы:
a – сторона куба
Куб представляет собой правильный многогранник, каждая из граней которого является квадратом. Это геометрическое тело является частным случаем других (а именно – параллелепипеда и призмы) и в повседневной жизни встречается достаточно часто. Инженерам и архитекторам при разработке проектов различных машин и зданий нередко приходится производить расчет объема куба, причем ввиду относительной его простоты решение этой задачи обычно не представляет большой сложности.
На практике с кубами и параллелепипедами чаще всего приходится встречаться в архитектуре. Их форму имеют многие современные здания и сооружения, причем она считается одной из наиболее практичных: такие сооружения проще и быстрее как проектировать, так и возводить. При этом формула объема куба используется преимущественно для точного определения размеров внутренних пространств, что особенно важно для таких зданий, как склады, цеха промышленных предприятий, объекты социально-культурного назначения.
Форму куба нередко имеют различные предметы корпусной мебели, и при их разработке конструкторам требуется определять, в том числе, и такую величину, как объем, для того, чтобы достичь наиболее рациональной компоновки этих элементов. Вычислить объем куба часто бывает необходимо и тем инженерам, которые занимаются созданием проектов контейнеров, железнодорожных вагонов, а также стеллажных систем, использующихся в складском хозяйстве.
Одним из наиболее ярких примеров кубов является знаменитый «магический куб» – оригинальная головоломка, созданная талантливым венгерским преподавателем архитектуры и скульптором Эрне Рубиком и впоследствии названная в его честь. Каждая из граней этого кубика состоит из нескольких квадратов, окрашенных в один цвет. С помощью поворотов их можно комбинировать в различных вариантах, а задача игрока состоит в том, чтобы «разобранную» конструкцию (то есть такую, грани которой содержат квадратики разных цветов) привести в изначальное состояние. Согласно статистике, «Кубик Рубика» за все время своего существования (с 1974 года) был продан в количестве около 350 000 000 экземпляров, и на сегодняшний день является одной из признанных в мире головоломок. Изначально каждая из его граней состояла из девяти квадратов, но впоследствии появились и более сложные варианты (например, содержащие по двадцать пять элементов). В различных странах проводятся соревнования по сборке этой головоломки на время, а также чемпионаты Европы и мира, организатором которого является организация «World Cube Association» («Всемирная ассоциация кубика»).
Форму куба имеют не только рукотворные, но и некоторые природные сущности, например, кристаллические решетки такого минерала, как флюорит, а также обычной поваренной соли. Наконец, следует заметить, что с этими геометрическими телами все мы знакомы еще с детства, поскольку одними из самых любимых игрушек для многих из нас были именно кубики.
Геометрия
Отличие куба от квадрата, разница между ними
Куб и квадрат часто путают, думая, что это тождественные геометрические фигуры. В действительности они отличаются друг от друга, ведь у каждого из этих объектов имеются только им присущие признаки. Какие, нетрудно понять, зная определение куба и квадрата.
Что такое квадрат и что такое куб
Квадрат – фигура, лежащая на плоскости, и она двухмерная. Её можно отобразить в виде прямоугольника с идентичными по длине сторонами. Квадрат можно вырезать из бумаги.
Куб же является трехмерным объектом, имеющим объём и 12 одинаковых граней. Таким образом, это правильный многогранник. Если разложить его на плоскости, то он будет состоять из 6 квадратов. Для наглядности куб можно склеить из плотной бумаги, а лучше слепить из гипса, пластилина.
Фото: разложенный куб на плоскости
В чем разница между кубом и квадратом: сравнение двух фигур
По сравнению с квадратом, куб – более сложная геометрия. Квадрат является фигурой простой, в нём только 4 стороны и 4 угла, между которыми абсолютное равенство. Квадрат можно назвать подвидом прямоугольника, только у которого ширина и длина сторон одинаковы. При этом квадрат всегда плоский. Чтобы посчитать площадь квадрата, достаточно умножить одну его сторону на другую.
Конфигурация куба сложнее, поскольку в нём уже присутствует третья мера – объём. Эта характеристика отражает пространство, которое занимает объект, в нашем случае куб. У куба также есть и третье измерение (параметр) – высота. Между собой ширина, длина и высота у куба равны.
Нахождение объема и площади
Если необходимо посчитать объем фигуры, то для расчета берут длину любого ребра между гранями и возводят её в третью степень. Для нахождения площади трехмерной фигуры куба надо узнать сумму площади всех его сторон. Поскольку они идентичны, то просто площадь одной стороны умножаем на 6. А чтобы найти площадь одной из сторон, умножаем длину ребра на себя же. Допустим, длина ребра 4 см, чтобы найти площадь одной стороны куба, 4 умножаем на 4 – получаем 16. И эту цифру уже увеличиваем в 6 раз. Значит, объём куба будет равен 96 см²
Сложные свойства куба
По сравнению с квадратом куб обладает более сложными, дополнительными характеристиками. Например, геометрический объект имеет четыре сечения, которые представляют собой правильные шестиугольники. Все сечения куба проходят через его центр и располагаются перпендикулярно относительно четырех главных его диагоналей.
Поскольку куб имеет объём, то в него можно вписать различные многогранники – такие как тетраэдр (простейший многогранник с гранями в виде 4-х треугольников), октаэдр (у этого многогранника уже 8 граней), икосаэдр (20 граней многогранника).
Чтобы ещё легче было понять разницу между кубом и квадратом, имеет смысл оценить свойства каждой фигуры наглядно. К примеру, взять обычный детский кубик с наклеенными картинками на его стороны. Так вот, сам кубик – это фигура куб, а каждая наклеенная на его сторону картинка – квадрат.
876 смотрели, 10 сегодня
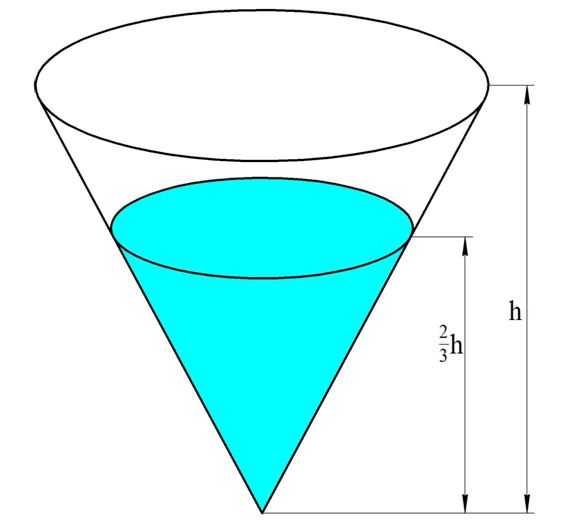
Шаровой сегмент
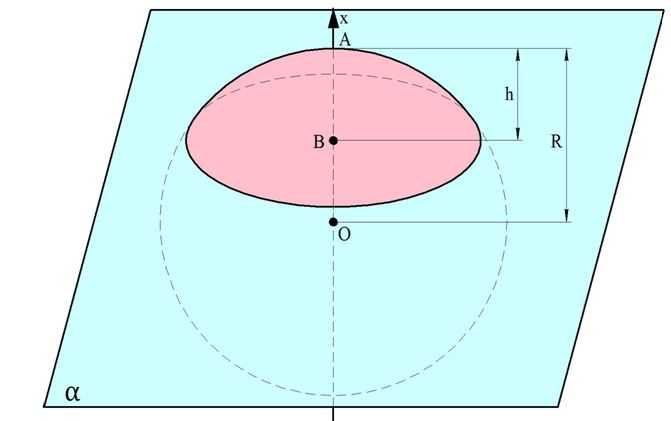
Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:
Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.
Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:
Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.
Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.
Решение. Используем выведенную формулу:
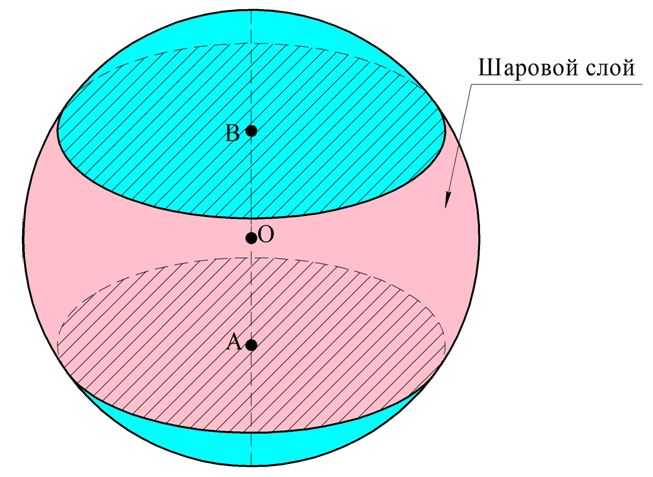
Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?
Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:
Объем куба и прямоугольного параллелепипеда
Докажем важную вспомогательную теорему:
Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР 






Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:
(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).
Умножим это неравенство на длину АК:
Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК 



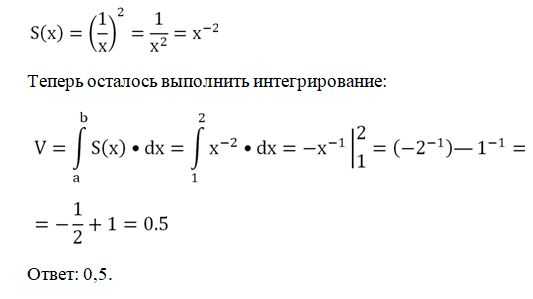




Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.
Построение гиперкуба
Начнём с начала — с 0-мерного куба. Этот куб содержит 0
взаимно перпендикулярных граней, то есть это просто точка.
1-мерный куб
В одномерном пространстве у нас есть только одно направление.
Сдвигаем точку в этом направление и получаем отрезок.
Это одномерный куб.
2-мерный куб
У нас появляется второе измерение, сдвигаем наш одномерный
куб (отрезок) в направлении второго измерения и получаем квадрат.
Это куб в двумерном пространстве.
С появлением третьего измерения поступаем аналогично:
сдвигаем квадрат и получаем обычный трёхмерный куб.
4-мерный куб (гиперкуб)
Теперь у нас появилось четвёртое измерение. То есть в
нашем распоряжении имеется направление, перпендикулярное
всем трём предыдущим. Воспользуемся им точно так же.
Четырёхмерный куб будет выглядеть вот так.
Естественно, трёхмерный и четырёхмерный кубы нельзя
изобразить на двумерной плоскости экрана. То, что нарисовал я — это проекции.
О проекциях мы поговорим чуть позже, а пока немного голых
фактов и цифр.
Что такое гиперкуб и четырёхмерное пространство
В нашем привычном пространстве три измерения.
С геометрической точки зрения это значит,
что в нём можно указать три взаимно-перпендикулярных
прямых. То есть для любой прямой можно найти вторую,
перпендикулярную первой, а для пары можно найти третью
прямую, перпендикулярную двум первым. Найти четвёртую
прямую, перпендикулярную трём имеющимся, уже не удастся.
Четырёхмерное пространство отличается от нашего
только тем, что в нём есть ещё одно дополнительное направление.
Если у вас уже есть три взаимно перпендикулярные прямые,
то вы можете найти четвёртую, такую, что она будет
перпендикуляра всем трём.
Гиперкуб это просто куб в четырёхмерном пространстве.
Примеры расчетов
Чтобы наглядно продемонстрировать применение приведенных выше правил, рассмотрим несколько конкретных примеров.
В кубометрах
Справка. В одном кубометре (1 м3) содержится 106 кубических сантиметров воды.
В литрах
Линейные величины традиционно измеряют в метрах и сантиметрах, а жидкости в литрах. Один литр воды теоретически представляет собой кубик со стороной 10 см. В 1 м3 таких кубиков 1000 штук. Таким образом: 1м3 = 1000 литров.
Масса такого объема воды равна 1 тонне.
Вычисление объема тел вращения
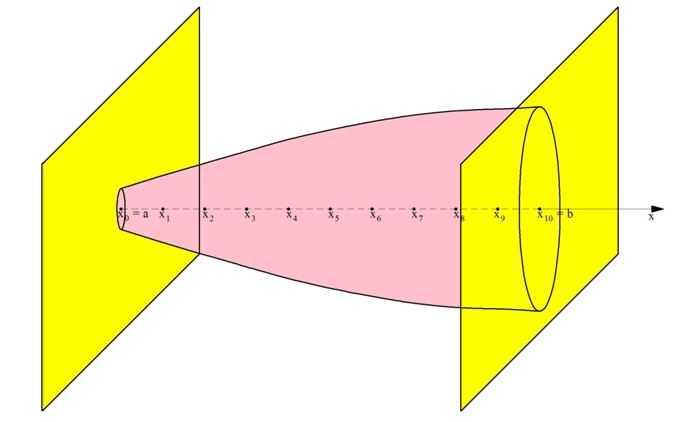
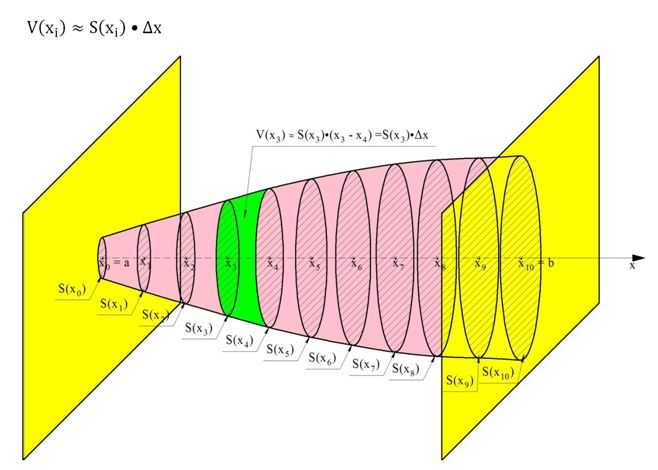
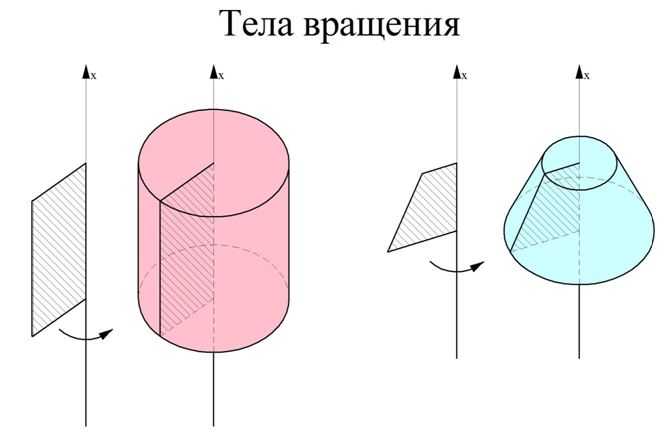
Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.
В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.
Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:
Рассмотрим, как на практике используется эта формула.
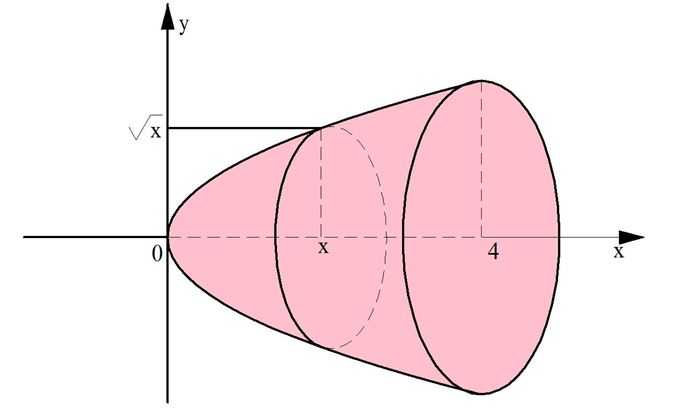
Задание. Объемное тело получено вращением ветви параболы
вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?
Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:
Развёртки
Итак, житель четырёхмерного пространства может увидеть
трёхмерный объект одновременно со всех сторон.
Можем ли мы одновременно со всех сторон увидеть трёхмерный
куб? Глазом — нет. Но люди придумали способ, как
изобразить на плоском рисунке все грани трёхмерного куба одновременно.
Такое изображение называется развёрткой.
Развёртка трёхмерного куба
Как образуется развёртка трёхмерного куба все наверно знают.
Этот процесс показан на анимации.
Для наглядности края граней куба сделаны полупрозрачными.
Следует отметить, что мы способны воспринять эту двумерную картинку
только благодаря воображению. Если рассмотреть фазы разворачивания
с чисто двумерной точки зрения, то процесс будет казаться странным
и совсем не наглядным.





Он выглядит, как постепенное появление сперва очертаний
искажённых квадратов, а потом их расползание на свои места
с одновременным принятием необходимой формы.
Если смотреть на разворачивающийся куб в направлении
одной из его граней (с этой точки зрения куб выглядит как
квадрат), то процесс образования развёртки ещё менее нагляден.
Всё выглядит как выползание квадратов из начального квадрата
(не развёрнутого куба).
Но не наглядна развёртка только для глаз. Как раз
благодаря воображению из неё можно почерпнуть много информации.
Развёртка четырёхмерного куба
Сделать анимированный процесс разворачивания гиперкуба
хоть сколько нибудь наглядным просто невозможно. Но этот
процесс можно представить. (Для этого надо посмотреть на него
глазами четырёхмерного существа.)
Развёртка выглядит так.
Здесь видны все восемь кубов, ограничивающих гиперкуб.
Одинаковыми цветами покрашены грани, которые должны совместиться
при сворачивании. Серыми оставлены грани для которых парных не видно.
После свёртки самая верхняя грань верхнего куба должна совместиться
с нижней гранью нижнего куба. (Аналогично сворачивается развёртка
трёхмерного куба.)
Обратите внимание, что после свёртки все грани восьми кубиков
придут в соприкосновение, замкнув гиперкуб. И наконец, представляя
процесс свёртывания, не забывайте, что при свёртывании происходит не наложение
кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области
Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты
фигурируют в очень многих его картинах. На картине
«Распятие» (1954)
используется развёртка гиперкуба.
Формула площади поверхности куба
П»Ã¾ÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð â ÃÂÃÂþ ÃÂÃÂüüð ÿûþÃÂðôõù òÃÂõàõóþ óÃÂðýõù:
ÃÂûþÃÂðôàúðöôþù óÃÂðýø þôøýðúþòð, ÃÂþ õÃÂÃÂÃÂ:
Sâ² â ÿûþÃÂðôàûÃÂñþù óÃÂðýø úÃÂñð.
âþóôð ÿþûýðàÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð ÷ðÿøÃÂõÃÂÃÂàúðú:
àðÃÂÃÂüþÃÂÃÂøü ýð ÿÃÂøüõÃÂðàÃÂð÷ýÃÂõ ÃÂÿþÃÂþñàòÃÂÃÂøÃÂûõýøàÿþûýþù ÿûþÃÂðôø ÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð.
ÃÂûþÃÂðôàúðöôþù óÃÂðýø úÃÂñð òÃÂÃÂøÃÂûÃÂõÃÂÃÂàúðú ÿûþÃÂðôàúòðôÃÂðÃÂð, ÃÂþ ÃÂÃÂþÃÂþýþù ÃÂõñÃÂð úÃÂñð ÿþ ÃÂþÃÂüÃÂûõ:
a â ÃÂÃÂþÃÂþýð úÃÂñð.
ÃÂÃÂÃÂÃÂôð, þúþýÃÂðÃÂõûÃÂýþ ÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð:
Вычисление объема прямоугольного предмета (в кубических сантиметрах)
Измерьте длину, ширину и высоту предмета (в сантиметрах). Для этого измерьте требуемые величины с помощью линейки или рулетки или конвертируйте известные вам значения в сантиметры.
X
Источник информации
Например, если вы хотите узнать объем холодильника, найдите его длину, ширину и высоту (в сантиметрах). Предположим, что ваш холодильник в высоту имеет 100 см, в ширину — 50 см, в длину — 40 см.
Запишите высоту предмета.
В нашем примере запишите, что высота = 100 см.
Вы можете перемножать величины в любом порядке. Например, начните с высоты.
Умножьте высоту на ширину. Затем умножьте первую величину на какую-нибудь из оставшихся (любую). Например, умножьте высоту на ширину.
X
Источник информации
В нашем примере, умножьте 100 на 50: 100 × 50 = 5000.
Умножьте полученный результат на длину предмета.
В нашем примере, умножьте 5000 на 40: 5000 × 40 =Н 200 000.
Последний шаг — умножьте полученный результат на оставшуюся величину. Например, умножьте произведение высоты и ширины на длину.
Запишите ответ в кубических сантиметрах, чтобы он был понятен любому человеку.
Вычисление объема других фигур
Объем куба V= L3, где V — объем, L — сторона. Куб — прямоугольный параллелепипед, у которого все стороны равны.
X
Источник информации
Таким образом, формулу для вычисления объема куба можно записать в виде: длина × ширина × глубина = длина × длина × длина = длина3. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.
Объем цилиндра V = hπr2, где V — объем, h — высота, r — радиус цилиндра. Цилиндр — геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными круглыми плоскостями.
X
Источник информации
Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.
Объем конуса V = (1/3)hπr2, где V — объем, h — высота, r — радиус конуса. Конус — тело с круглым основанием и вершиной над ним. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.
X
Источник информации
Объем шара V = 4/3πr3, где V — объем, r — радиус шара. Шар — абсолютно круглое тело.
X
Источник информации
Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.
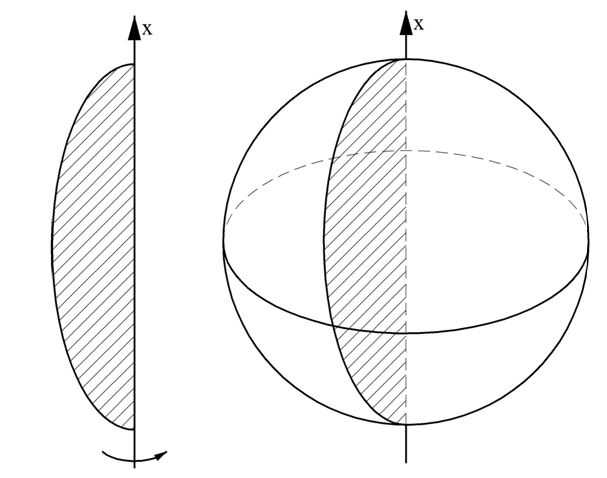
Объем шара
Пришло время разобраться и с таким телом, как шар. Здесь можно использовать тот же метод интегрирования, что и в случае с конусом и пирамидой. Но можно поступить и иначе – использовать выведенную нами для тел вращения формулу
Шар как раз является телом вращения. Он получается при вращении полуокружности вокруг диаметра, на который эта дуга опирается.
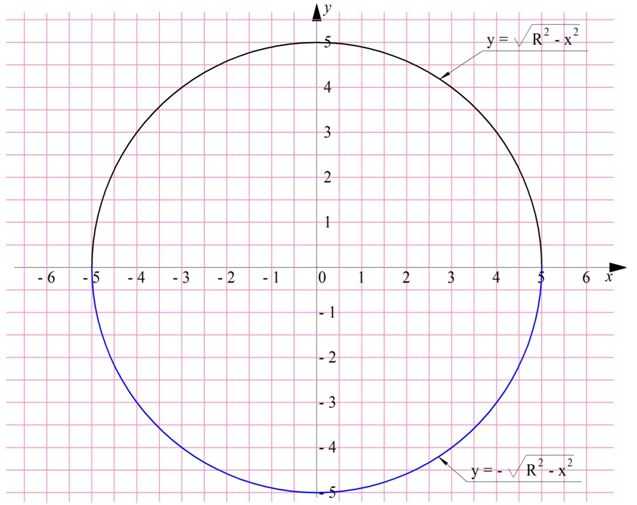
Напомним известное нам уравнение окружности, чей центр совпадает с началом координат:
Здесь надо уточнить, что если у получившейся функции впереди записан знак «+», то ее график соответствует полуокружности, находящейся над осью Ох. Если же используется знак «–», то получается уже нижняя полуокружность, расположенная под осью Ох:
В принципе мы можем поворачивать любую из этих полуокружностей вокруг Ох, но мы выберем верхнюю полуокружность. Заметим, что эта дуга начинается в точке х = – R и заканчивается в точке х = R, эти числа будут пределами интегрирования. Тогда объем шара равен:
Решение. Подставляем радиус из условия в формулу:
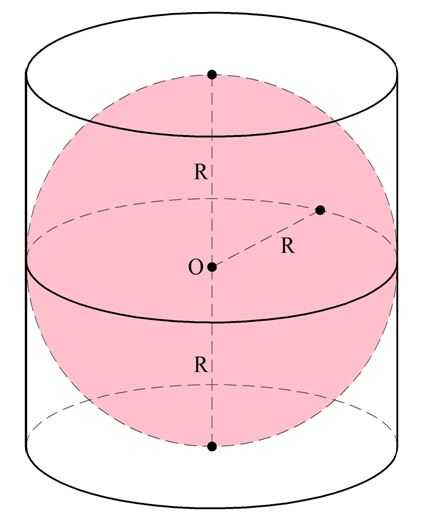
Задание. В цилиндр вписан шар. Во сколько раз объем цилиндра больше объема такого шара?
Решение. Ясно, что так как шар вписан в цилиндр, то радиусы этих тел одинаковы. Обозначим этот радиус как R. Также ясно, что раз шар касается оснований цилиндра, то расстояние между ними (то есть высота цилиндра) равно двум радиусам шара:
Объем пирамиды
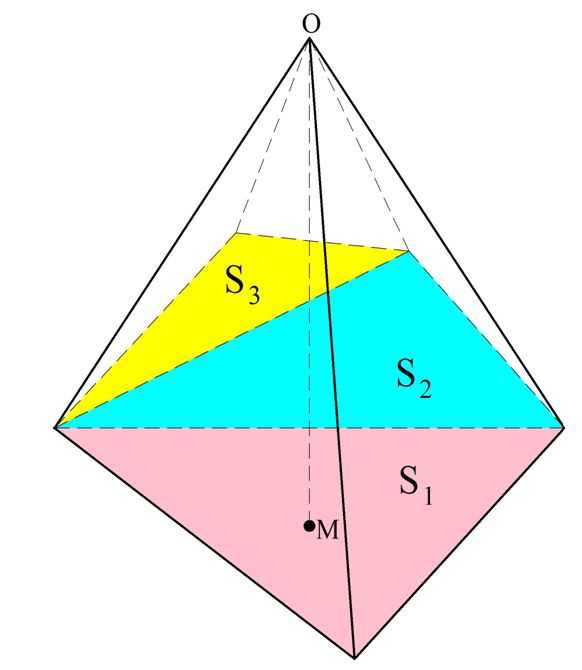
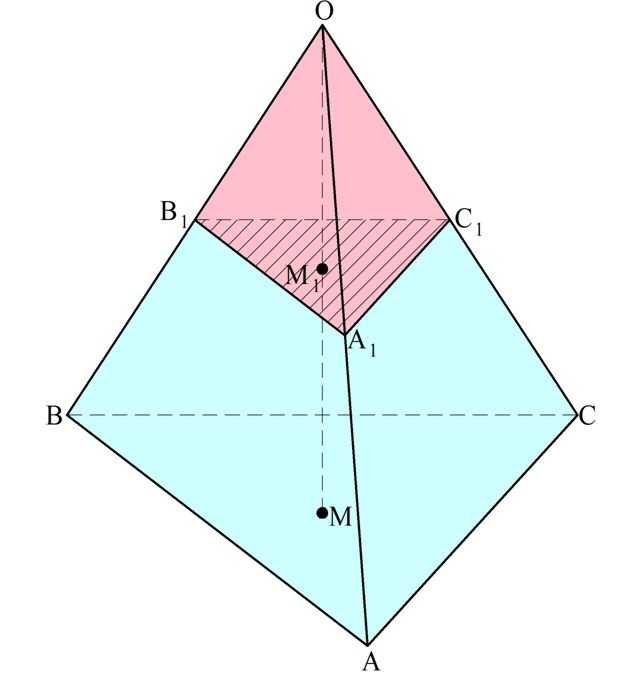
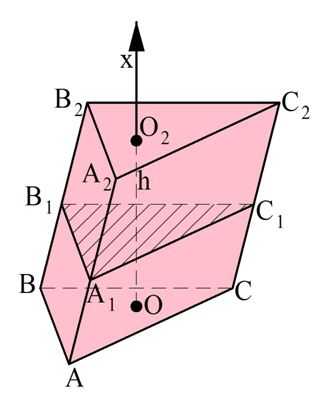
Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.
Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.
Далее построим сечение А1В1С1, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ1. Тогда ОМ1 – это координата х, характеризующая расположение сечения А1В1С1.
Осталось составить выражение для площади ∆А1В1С1. Так как АВ||A1B1, то ∠АВО и ∠А1В1О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А1В1О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что
Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ1В1. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому
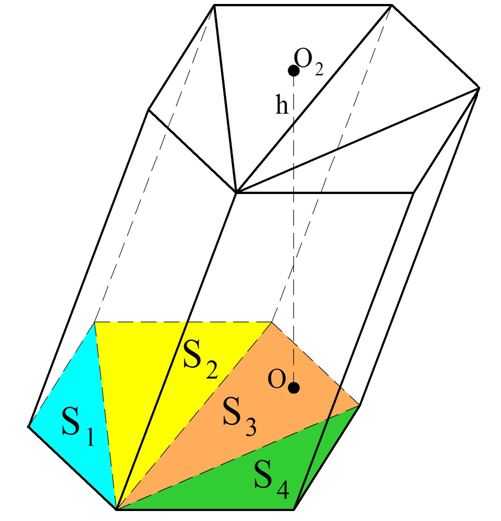
Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:
Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S1, S2, S3…, которые в сумме составляют площадь многоугольника S.
Объем треугольных пирамид рассчитывается по выведенной нами формуле:
Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.
Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:
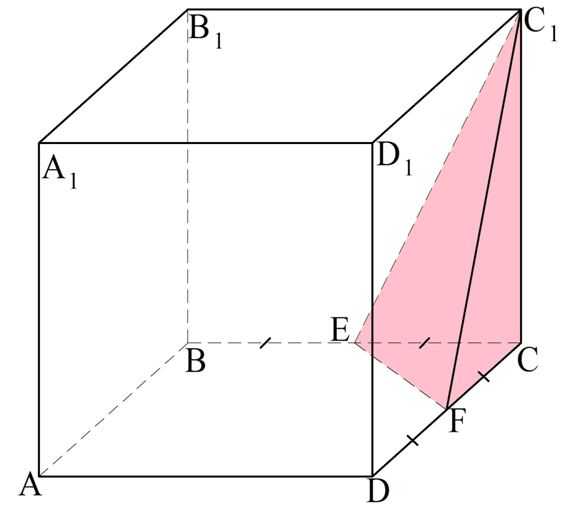
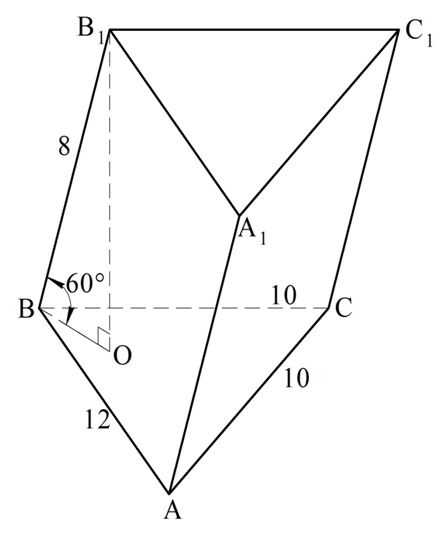
Задание. В кубе АВСDA1В1С1D1 отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С1EFC меньше объема куба?
Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:
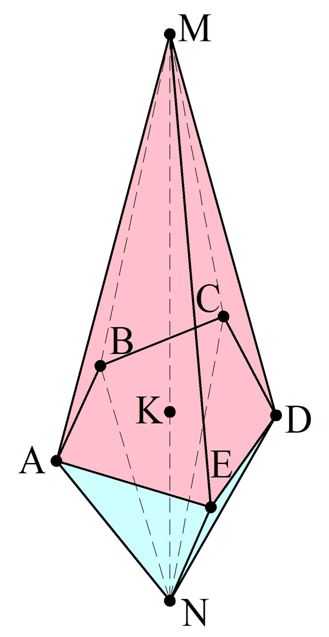

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?
Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.
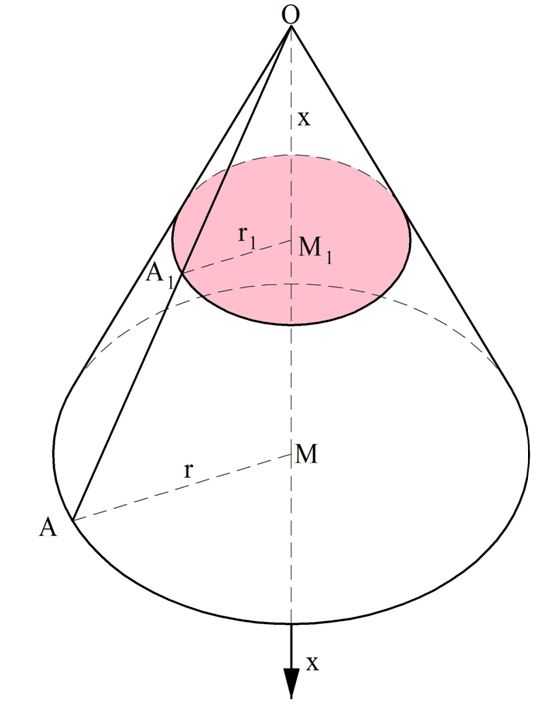
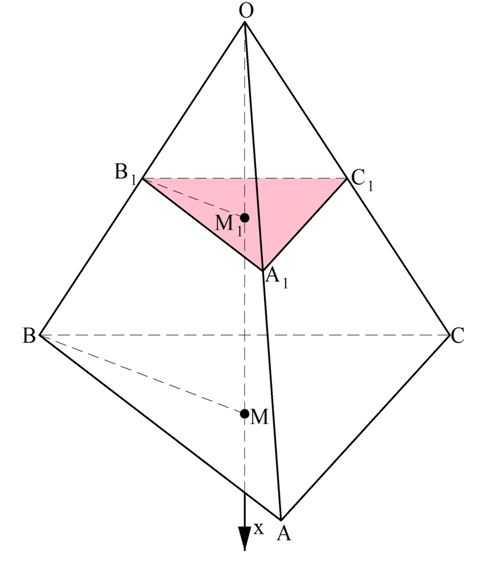
Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.
Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А1В1С1, параллельное основанию.
Обозначим площадь нижнего основания пирамиды как S2, а площадь верхнего основания – как S1. Далее высоту усеченной пирамиды (отрезок ММ1) обозначим как h. Мы уже выяснили ранее, что основания АВС и А1В1С1 – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ1. Тогда можно записать:
Далее используем основное свойство пропорции:
Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:
Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.
Сначала вычислим площади оснований:
Примеры заданий
Задача первая. Дан куб с ребром 12 см. Вычислить его объем и выразить ответ в квадратных метрах.
Задача вторая. Имеется куб с площадью всей его поверхности, равной 600 дм2. Найти объем фигуры и выразить его в кубических метрах.
Для ответа на вопрос этого задания будет нужна формула номер 7. Первым действием известное число делится на 6. В ответе получается 100. Из него легко извлечь квадратный корень, он будет равен 10. Теперь десятку нужно возвести в куб. Так получается, что искомая величина равна 1000 дм3. Осталось перевести его в м3. Как и в предыдущей задаче, деление будет выполняться три раза, только делителем будет 10. Потому что в одном метре десять дециметров. После деления получается ответ равный 1 м3. Ответ: объем равен 1 м3.
Задача третья. Дан куб с длиной диагонали его грани, равной √2 мм. Нужно вычислить объем.
Восьмая формула поможет в том, как найти ответ в этой задаче. Первым делом нужно возвести в куб известную величину. Квадратный корень из 2 в третьей степени даст значение 2√2. После умножения на √2 получится число 4. Последним действием нужно его разделить на 4. Ответ: объем куба 1 мм3.
Задача четвертая. Известно, что диагональ куба равна 3 м. Требуется вычислить его объем.
Будет просто найти ответ на эту задачу по формуле под номером 9. Величину, которая дана в условии, нужно возвести в куб. Получится 27. После его деления на 9 ответ станет равен 3. И последним действием его нужно умножить на квадратный корень из 3. Ответом задачи будет 3√3 м3.
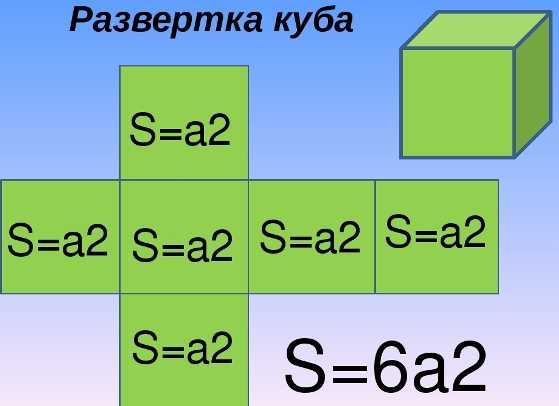
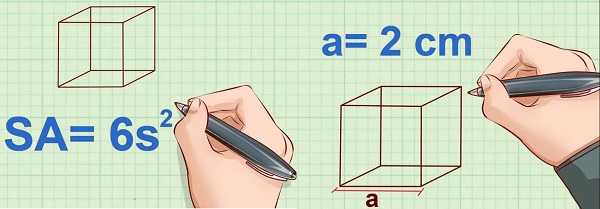
Определение площади поверхности куба.
Определение площади поверхности куба выполняется по формуле SA = 6а2. Куб (правильный гексаэдр) – это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.
Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а2. Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять – a2, где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).
11 Как определить объём сферического изделия
Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.
Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:
Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.
А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу:
Как найти объем куба?
Объем V куба (гексаэдра) со стороной a равен величине этой стороны, возведенной в третью степень: V = a3. Объем куба находят перемножая площади квадрата a2, лежащего в его основании на высоту куба a.
Поскольку объем куба вычисляют как третью степень его стороны, возведение в третью степень называют возведением в куб, а получаемый при этом результат — кубом исходной величины.
Объем куба можно также выразить через величину его большой диагонали D и дианонали d его квадратной грани:
V = a3 = d3/2·√(2) = d3/3·√(3).
Площадь поверхности S куба со стороной a равна сумме площадей шести его квадратных граней, каждая из которых равна a2. Таким образом, плошадь куба S = 6a2.
Суммарная длина ребер куба L = 12a, поскольку у куба 12 ребер, каждое длиной a.
Как найти объем куба – способ 1
Самый простой способ нахождения объема куба – возведение в куб одного из его ребер. Так как у куба все 12 ребер равны, то формула выглядит так V=a3 или V=а*а*а. Если в условии дано ребро, вставьте его значение в формулу и получите правильный ответ. Если длина ребра не дана – придется сначала ее найти. Пример: ребро куба равно 5 см. Найти объем. V = a3 = 53 = 125.Как найти объем куба – способ 2
Найти объем куба можно при помощи формулы площади поверхности куба: S=6a3. Скажем, площадь поверхности куба = 54 см2. Тогда a2 = 54/6 = 9. а, соответственно = 3. V = 33 = 27 см3.Как найти объем куба – способ 3
В случае, если нам известна диагональ одной из грани (важно помнить, что диагональ не куба, а именно грани), то поделив его на √2, вы получите длину ребра куба, то есть а. После этого, по старой доброй формуле возводим а в куб и получаем правильный ответ.
Рассчитать объем куба, площадь и диагональ куба
Рассчитать объем куба. Формула объема, площади и диагонали куба.
Рассчитать объем куба, его площадь и диагональ вы можете по длине его стороны (ребра).
Калькулятор расчета объема куба, его площади и диагонали:
Одновременно рассчитываются объем, площадь и диагональ куба.
Формулы расчета объема, площади и диагонали куба:
Формула расчета объема куба:
V = a · a · a = a 3 ;
Формула расчета площади куба:
S = 6 · a · a = 6a 2 ;
Формула расчета диагонали куба:

а – длина стороны (ребра) куба,
D – диагональ куба.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
How to Calculate the Volume of a Cube?
A block is a 3-layered shape with 6 equivalent sides, 6 countenances, and 6 vertices in the calculation. Each face of a shape is a square. In the 3 – aspects, the shape’s sides are; the length, width, and stature. Normal instances of shapes, in reality, incorporate square ice blocks, dice, sugar 3D shapes, meal, strong square tables, milk containers, and so on. In the above delineation, sides of a block are on the whole equivalent for example Length = Width = Height = a.
The volume of a strong 3D shape is how much space is involved by the strong 3D square. The volume is the distinction in space involved by the block and how much space is inside the 3D square for an empty solid shape.
The volume of a block is characterized as the absolute number of cubic units involved by the solid shape totally. A block is a three-layered strong figure, having 6 square faces. Volume is only the absolute space involved by an item. An article with a bigger volume would consume more space. Allow us to comprehend the volume of a shape exhaustively alongside the recipe and addressed models in the accompanying areas.
Volume of Cube
Volume of Cube Formula
Volume of a 3D square = a 3
Where ‘a’ is the length of the side of the shape.
Volume of Cube Using Diagonal Formula
The volume of the block can likewise be found out straight by another recipe on the off chance that the askew is known.
The corner to corner of a 3D shape is given as, √3a.
Where, ‘a’ is the side length of the block. From this recipe, we can compose ‘a’ as, a = diagonal/√3.
In this way, the volume of a 3D shape condition using diagonal can, at last, be given as:
Volume of the 3D square = (√3 × d 3 )/9
Where d is the length of the corner to corner of the 3D shape.
Note: A typical error is to be kept away from by not befuddling the diagonal of a solid shape with the corner to corner of its face. The diagonal of a block slices through its middle, as displayed in the figure above. While the face diagonal is the corner to corner on each face of the block.
Volume of Cube Using Edge Length
The proportion of the multitude of sides of a solid shape is similar accordingly, we just need to know one side to ascertain the volume of the 3D square. The means to compute the volume of a shape utilizing the side length are,
Volume of Cube Using Diagonal
Given the diagonal, we can follow the means provided beneath to track down the volume of a given 3D shape.
Sample Questions
Question 1: Calculate the volume of a 3D square with a side length of 2 inches.
Solution:
The volume of a 3D square with a side length of 2 inches would have a volume of 3D square,
(2 × 2 × 2) = 8 cubic inches.
Question 2: Calculate the volume of a shape with the diagonal estimating 2 inches.
Solution:
We know, Volume of shape = [√3 × (diagonal) 3 ]/9
⇒ Volume = [√3 × (2) 3 ]/9
Question 3: The edge of a Rubik’s solid shape is 0.08 m. Track down the volume of the Rubik’s block?
Solution:
= (0.08 × 0.08 × 0.08) m 3
Question 4: A cubical box of outer aspects 120 mm by 120 mm by 120 mm is open at the top. Assume the wooden box is made of 4 mm wood thick. Track down the volume of the 3D shape.
Solution:
For this situation, deduct the thickness of the wooden box to get the elements of the 3D square.
Given, the shape is open at the top,
Length = 120 – 4 × 2
Width = 120 – (4 × 2)
Tallness = (120 – 4) mm (a solid shape is open at the top)
Presently compute the volume.
Volume, V = (112 × 112 × 116) mm 3
Question 5: Cubical blocks of length 4 cm are stacked to such an extent that the stature, width, and length of the stack is 30 cm each. Track down the number of blocks in the stack.
Solution:
To get the number of blocks in the stack, partition the stack’s volume by the block volume.
Volume of the stack = 30 × 30 × 30
Volume of the block = 4 × 4 × 4
Number of block = 27000 cm 3 /64 cm 3
Question 6: The number of cubical boxes of aspects 2 cm × 2 cm × 2 cm can be stuffed in an enormous cubical instance of length 20 cm.
Solution:
To observe the number of boxes that can be stuffed for the situation, partition the case’s volume by the volume of the case.
Volume of each container = (2 × 2 × 2) cm 3
Volume of the cubical case = (20 × 20 × 20) cm 3
Question 7: Observe the volume of a metallic solid shape whose length is 40 mm.
Solution:
Volume of a solid shape = a 3
= (40 × 40 × 40) mm 3
Как посчитать см3?
Формула кубических сантиметров для разных единиц
Аналогично, что такое cm3 в математике? В кубический сантиметр (или кубический сантиметр в американском английском) (обозначение единицы СИ: см 3 ; аббревиатуры, не относящиеся к системе СИ: куб.см и куб.см) — общеупотребительная единица объема, соответствующая объему куба размером 1 см × 1 см × 1 см. Один кубический сантиметр соответствует объему в один миллилитр.
Сколько см аметр? Ответ: 1 метр 100 сантиметры.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Как рассчитать м3? Расчет за кубометры осуществляется по умножение длины вашего груза на его ширину и высоту.
Во-вторых, сколько футов составляет метр INA? Ответ: 1 метр равен 3.28084 ноги.
Там 100 сантиметров в 1 метре.
тогда сколько сантиметров нужно для 80 см? Поскольку метр в 10^2 больше сантиметра, это означает, что коэффициент преобразования м в см равен 10^2. Кроме того, 10^2 равно 100. Следовательно, вы можете умножать 80 м на 100 чтобы перевести 80 м в см.
Как найти процент? Процент можно рассчитать, разделив значение на общее значение, а затем умножив результат на 100. Формула, используемая для расчета процента: (значение / общее значение) × 100%.
Какой размер 1м3?
| 1 кубических метров | = 1000 литров (точно) |
|---|---|
| ≈ 1.31 кубических ярдов | |
| ≈ 6.29 баррелей нефти | |
| ≈ 220 британских галлонов | |
| ≈ 264 галлонов жидкости США |
Что больше метр или фут?
Метр приблизительно равна 3.28084 фута. …Помните, в 12 футе 1 дюймов.
Как измерить квадратный фут? Основная формула квадратных футов
Умножьте длину на ширину, и вы получите квадратные футы.. Вот основная формула, которой вы можете следовать: длина (в футах) x ширина (в футах) = площадь в квадратных футах.
Как перейти от см к м?
Чтобы сделать любое преобразование, вы находите взаимосвязь между двумя единицами. В таком случае, 100 см = 1 м.
Каково соотношение 1 метр 100 см?
1 м = 100 см. Таким образом, соотношение 140 см: 100 см.
Сколько сантиметров в миллиграмме? переводная таблица: Миллиграммы в Кубические сантиметры
| Метрическая таблица перевода миллиграммы в Кубические сантиметры | |
|---|---|
| 0.01 мг = 1.0E-5cc | 0.1 мг = 0.0001 см3 |
| 0.02 мг = 2.0E-5 см3 | 0.2 мг = 0.0002 см3 |
| 0.03 мг = 3.0E-5 см3 | 0.3 мг = 0.0003 см3 |
| 0.04 мг = 4.0E-5 см3 | 0.4 мг = 0.0004 см3 |
Сколько см в DCM? Дециметры в Сантиметры таблица
| Дециметры | сантиметров |
|---|---|
| 1 дм | 10.00 см |
| 2 дм | 20.00 см |
| 3 дм | 30.00 см |
| 4 дм | 40.00 см |
Как найти процент снижения?
Как рассчитать процент уменьшения
Что такое процентная формула в Excel? Основная формула расчета процента: = часть / всего. Допустим, вы хотите уменьшить определенную сумму на 25%, например, когда вы пытаетесь применить скидку. Здесь формула будет такой: = Цена * 1-Скидка%. (Думайте о «1» как о замене 100%.)
Как я могу рассчитать неделю беременности?
Большинство беременностей длятся около 40 недель (или 38 недель с момента зачатия), поэтому, как правило, лучший способ оценить дату родов — это отсчитать 40 недель или 280 дней с первого дня последней менструации (ПММ). Вы также можете вычтите три месяца из первого дня последней менструации и прибавьте семь дней.
Как рассчитать размер м3? Формула расчета CBM
Насколько велик кубик?
Как выглядят сантиметры на линейке?
Чтобы прочитать метрическую линейку для измерения сантиметров, посмотрите на длинные линии на линейке, пронумерованные от 1 до 30, которые являются сантиметровыми отметками. Расстояние между ними равно 1 сантиметру. Между большими сантиметровыми линиями есть меньшие линии, которые представляют собой миллиметры.
Сколько см равно 1 см? Один миллилитр определяется как один кубический сантиметр в системе единиц СИ.
.
Эквивалентность другим единицам длины.
| 1 сантиметр | = 10 миллиметры |
|---|---|
| = 0.01 метра | |
| = 0.393700787401574803149606299212598425196850 дюймов | |
| (В одном дюйме ровно 2.54 сантиметра.) |
Что такое 1 см на линейке?
Каждый сантиметр отмечен на линейке (1-30). Пример: вы достаете линейку, чтобы измерить ширину ногтя. Линейка останавливается на 1 см, что означает чтобы ваш ноготь был ровно 1 см шириной. Таким образом, если вы отсчитаете пять линий, например, от 9 см, вы получите 9.5 см (или 95 мм).
Как считается объем куба
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы познакомитесь с формулой объема куба, научитесь переводить кубические метры в кубические дециметры, сантиметры, миллиметры, литры и наоборот.
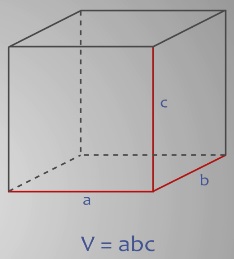
Объем прямоугольного параллелепипеда вычисляется по формуле V =abc, где a, b и с – его измерения: длина, ширина и высота.
А что, если все три измерения в прямоугольном параллелепипеде равны?
Тогда он является кубом.
Значит, чтобы найти объем куба, необходимо также перемножить три его измерения, но поскольку все они равны, то достаточно просто ребро куба возвести в куб.
Т.е. объем куба V равен а умножить на а умножить на а и равно а в кубе, где а – это длина ребра куба.
Давайте выполним следующее задание:
Найдите объем куба со стороной 6 см.
Подставим вместо а длину стороны 6 см.
Ответ: объем куба равен 216 кубическим сантиметрам.
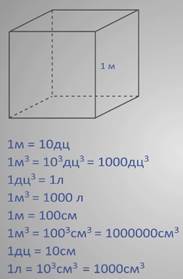
Давайте рассмотрим куб с ребром один метр. Его объем составляет один кубический метр.
А как можно выразить его объем, к примеру, в сантиметрах или дециметрах?
Так как в одном метре 10 дециметров, значит в одном кубическом метре 10 в кубе кубических дециметров, т.е. 1000 кубических дециметров.
Следует вспомнить, что один кубический дециметр равен одному литру, значит один кубический метр составляет 1000 литров.
Так же можно выразить кубический метр в сантиметрах, поскольку в одном метре 100 сантиметров, значит в одном кубическом метре 100 в кубе кубических сантиметров, или миллион кубических сантиметров.
Таким же образом можем найти сколько кубических сантиметров содержится в одном литре. Так как один литр равен одному кубическому дециметру, и в одном дециметре десять сантиметров, значит в одном литре десять в кубе кубических сантиметров, т.е. тысяча кубических сантиметров.
Давайте выполним несколько заданий.
Задание первое: выразите 2 кубических километра в кубических метрах.
Решение: в 1 километре 1000 метров, значит в 1 кубическом километре 1000 в кубе кубических метров, т.е. 1 миллиард кубических метров.
Значит 2 кубических километра содержат 2 миллиарда кубических метров.
Задание второе: выразите 5 кубических сантиметров в кубических миллиметрах.
Решение: так как в одном сантиметре содержится 10 миллиметров, значит в одном кубическом сантиметре содержится 10 в кубе кубических миллиметров, т.е. тысяча кубических миллиметров.
Получаем, что пять кубических сантиметров равно 5 умножить на 1000 равно 5 000 кубических миллиметров.
И последнее задание: выразите 3 145 кубических дециметров в кубических метрах и дециметрах.
Решение: так как в 1 метре 10 дециметров, значит в 1 кубическом метре 1000 кубических дециметров. Следовательно, 3 тысячи 145 кубических дециметров равно 3 кубическим метрам и 145
Таким образом, в этом уроке Вы познакомились с формулой объема куба и научились переводить кубические метры в кубические дециметры, сантиметры, миллиметры а также литры и наоборот.
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
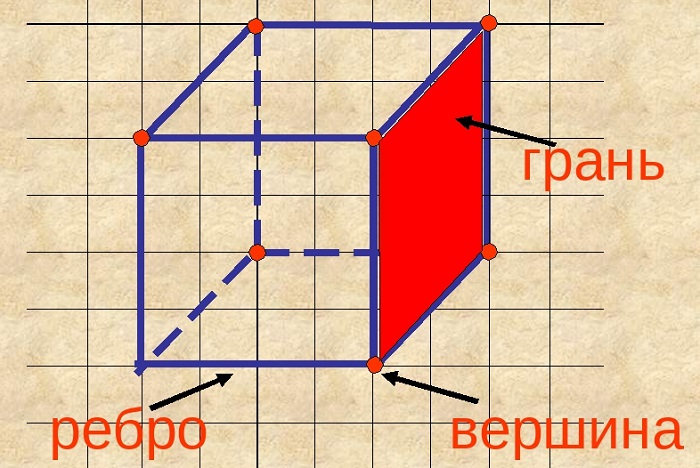
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
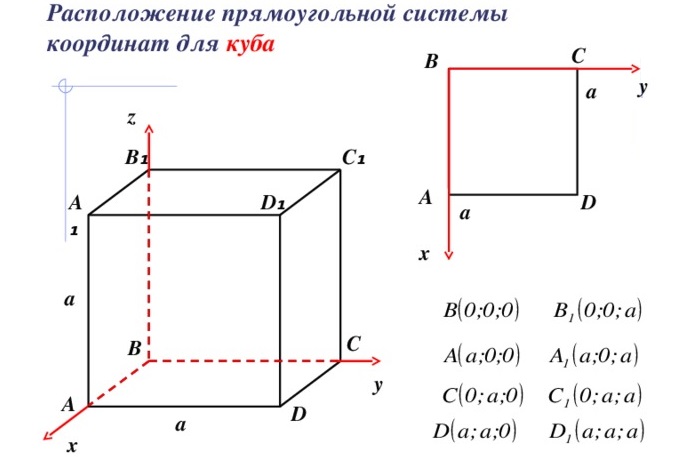
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
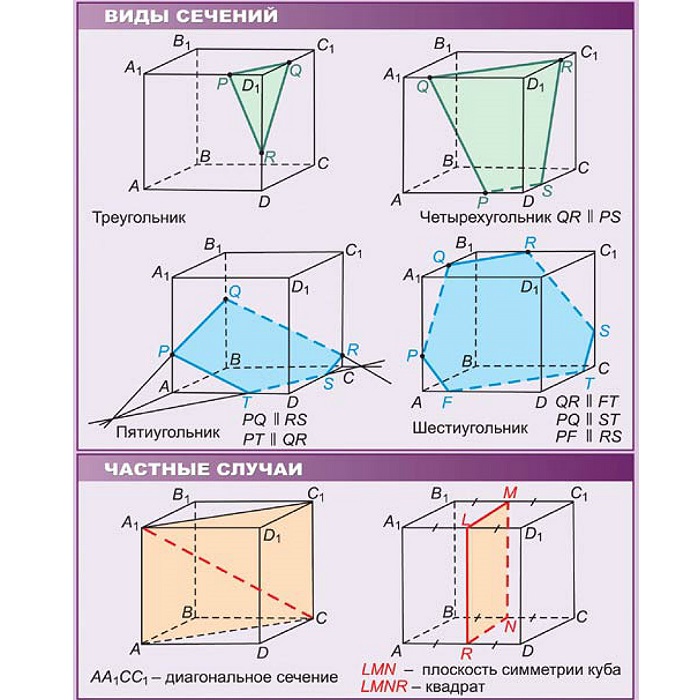
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Как рассчитать объем куба?
Формула для определения объема умножает длину на ширину и высоту. Хорошая новость для куба заключается в том, что измерение каждого из этих измерений точно такое же. Следовательно, длину любой стороны можно умножить в три раза. Это приводит к формуле: Объем = сторона * сторона * сторона.
Аналогично, как найти объем куба?
Каков объем формулы прямоугольного параллелепипеда? Какова формула объема прямоугольного параллелепипеда? Формула объема прямоугольного параллелепипеда = Длина × Ширина × Высота.
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Как найти количество кубиков в фигуре?
Во-вторых, какова формула прямоугольного параллелепипеда? Формулы куба и прямоугольного параллелепипеда
| Cubo,en | Кубоид |
|---|---|
| Объем куба = (Сторона) 3 | Объем кубоида = ( длина × ширина × высота ) |
| Диагональ куба = √3l | Диагональ кубоида = √ (l 2 + b 2 +h 2 ) |
| Периметр куба = 12 сторон | Периметр кубоида = 4 (длина + ширина + высота) |
Что такое кубик 8?
| 1. | Что такое кубический корень из 8? |
|---|---|
| 3. | Является ли кубический корень из 8 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 8 |
Как найти количество кубов прямоугольного параллелепипеда? Чтобы найти количество кубиков в каждом слое прямоугольного параллелепипеда, умножьте длину на ширину. 4 х 3 = 12 и так, в этом слое 12 кубиков.
Как вы решаете задачи на куб и кости?
Как считать кубики в стопке?
Сколько кубиков вы можете определить на данном изображении?
Что такое диагональ кубоида? Объяснение: Пусть «а» — длина стороны куба. Формула диагонали куба = 3⎷a. Пусть «l» — длина, «b» — ширина, а «h» — высота прямоугольного параллелепипеда. Формула диагонали прямоугольного параллелепипеда = ⎷ (l 2 + b 2 + ч 2 )
Является ли куб прямоугольным параллелепипедом?
Куб — это частный случай квадратного прямоугольного параллелепипеда, у которого все шесть граней — квадраты.
.
| Прямоугольный кубоид | |
|---|---|
| Тип | Призма Плезиоэдр |
| Лики | 6 прямоугольника |
| Ребра | 12 |
| вершины | 8 |
Что такое куб 3 7?
| 1. | Что такое кубический корень из 7? |
|---|---|
| 4. | Часто задаваемые вопросы о Cube Root of 7 |
| 1. | Что такое кубический корень из 10? |
|---|---|
| 2. | Как вычислить кубический корень из 10? |
| 3. | Является ли кубический корень из 10 иррациональным? |
Что такое куб от 1 до 10? Числа в кубе от 1 до 100
| Число | Cubo,en |
|---|---|
| 8 | 512 |
| 9 | 729 |
| 10 | 1000 |
| 11 | 1331 |
Как найти диагональ куба и прямоугольного параллелепипеда?
Сколько диагоналей в кубоиде? Кубоид имеет не менее 4 диагоналей.
Сколько кубиков в одном кубоиде?
Разница между кубом и кубоидом
| Cubo,en | Кубоид |
|---|---|
| В кубе все шесть лиц квадраты | У прямоугольного параллелепипеда все шесть граней прямоугольники. |
| Куб, состоящий из 12 диагоналей с одинаковой площадью поверхности | Всего у кубоида 12 диагоналей, из которых 3 диагонали различны по мере. |
Сколько маленьких кубиков в кубоиде? Есть 16 маленьких кубиков прикреплены к наружным стенкам куба.
Сколько кубиков может поместиться в параллелепипед?
Как легко собрать кубик Рубика 3х3?
Как ты делаешь трюк с кубиками?
Как вы решаете кости умственных способностей? DICE REASONING: концепции и хитрости
Как рассчитать кубатуру круглого леса
Что нужно знать, покупая дрова кубами?
Что такое кубометр дров и как его рассчитать?
Когда речь заходит о покупке дров кубами, важно понимать — сколько именно дров вы покупаете, что подразумевается под кубометрами дров и как правильно посчитать кубометр дров на месте. В основном, есть два вида кубометров, которые используются в измерении объемов поставляемых дров:
1. Реальный кубометр
Реальный кубометр — это базовая точка отсчета в измерении дров или объемов других материалов. Возьмем куб, который имеет равные грани (1 метр в длину, 1 метр в ширину и 1 метр в высоту). Так мы получим реальный кубометр. Пространство внутри этого куба имеет объём равный 1 кубическому метру. Реальными кубометрами дров измеряются плотно уложенные в штабель дрова. Если мы плотно уложим колотые дрова в куб с размерами 1м х 1м х 1м, мы получим кубометр дров.
Приведём пример расчета объемов поставки дров. Допустим, у нас есть штабель плотно уложенных колотых дров, размером 2 м х 3 м х 1,5 м. Перемножим габариты, чтобы вычислить количество кубометров дров. 2м х 3м х 1,5м = 9 кубометров.
2. Насыпной кубометр
Насыпными кубометрами измеряются колотые дрова, которые не уложены, а просто насыпаны вразнобой. Для того, чтобы рассчитать количество реальных кубометров насыпных дров, нужно пересчитать их с помощью специальных коэффициентов.
Самые распространённые коэффициенты для пересчета насыпных кубометров колотых дров в реальные кубометры следующие:
Приведём пример. Представим себе, что мы заказали машину неуложенных, колотых дров длиной 25 см, которые просто насыпаны в кузов. Допустим, мы измерили габариты кузова и получили объём в 10 кубометров. Получается, что в кузове 10 насыпных кубометров дров. Теперь переводим насыпные кубометры в реальные кубометры: 10 х 0,8 = 8. То есть, в 10 насыпных кубометрах колотых дров длиной 25 см — 8 реальных кубометров дров.
Как рассчитать цену реального кубометра дров?
Чаще всего продавцы дров указывают цену за реальный кубометр дров, а не за насыпной. Это удобно и продавцу, и покупателю. Выгруженные дрова можно сразу измерить, рассчитать объём поставки и стоимость.
Если продавец дров указывает цену за насыпной кубометр дров, а не за реальный, рассчитать цену реального кубометра дров можно, разделив цену реального кубометра дров на коэффициент пересчета насыпного кубометра в реальный кубометр. Допустим, в нашем примере стоимость насыпного кубометра дров составляет 1500₽. Для того, чтобы узнать цену реального кубометра дров, мы делим 1500₽ на 0,8. Получается, что реальный кубометр дров, в нашем примере, стоит
Расчет объема бревна вручную
Определение объема бревна с помощью компьютерной мерной вилки
Компьютерная мерная вилка определяет объем каждого бревна с помощью измерения диаметра и ввода длины. Использование этого инструмента позволяет избежать утомительной работы с таблицами и многочисленных вычислений. После определения толщины и ввода длины бревна вилка самостоятельно определяет его объем и отображает данные на дисплее. Из-за высокой стоимости этот инструмент применяют лишь на лесоперерабатывающих предприятиях.
Для многих строителей знакома тема расчета количества бревен в кубе. Но для неподготовленного человека это может показаться не только очень далеким, но и непонятным. И очень часто возникают разногласия между самими строителями, а также между строителями и заказчиком о том, сколько бревен в кубе должно быть.
Для того, чтобы разобраться с этой проблемой, обычно используют математический метод, который в несколько минут может дать четкий ответ о том, сколько нужно бревен для определенного количества кубометров.
Как правило, в строительстве деревянных зданий используются оцилиндрованные бревна. Но этот материал может отличаться по размеру, то есть по длине и диаметру. За единицу измерения принято брать сантиметры. В одном кубометре находится один миллион сантиметров. Таким образом, вначале нужно определиться с размерами бревен.
Для того, чтобы измерить размер бревен, потребуется обычная сантиметровая рулетка. Все бревна, как правило, изначально должны быть одного размера, а в дальнейшем, в зависимости от проекта, они распиливаются на необходимые элементы.
Так, измерив с помощью рулетки размер бревна, мы получаем значения длины и диаметра в сантиметрах. Для примера, попробуем высчитать, сколько нужно бревен для одного кубометра, если бревна имеют длину шесть метров, а их диаметр восемнадцать сантиметров.
1 складометр дров сколько это, в чем измеряются дрова
Данная информация позволит избежать лишних трат денег – недобросовестным продавцам будет труднее вас обмануть.
Ни для кого не секрет что в древесине содержится влага, а в только что срубленной древесине она составляет порядка 40-70 процентов и такие дрова можно назвать сырыми.
При сгорании сырых дров часть энергии будет тратиться на выпаривание имеющейся в них влаги, а это значит, что запасов сырого топлива придется делать больше, либо заранее и давать ему просохнуть
При покупке на это стоит обратить особое внимание. Под видом сухих дров, могут продать сырые
Как определить какой объем дров вам привезли? – Это один из самых важных вопросов при покупке.
Для начала ознакомьтесь со способами укладки дров, после чего станет ясно, почему этот вопрос так важен.
Дрова навалом – это когда накидали в машину как попало. Вроде бы смотрите – много, а когда аккуратно сложите в поленницу, то оказывается мало (иногда существенно). Получается так из-за свободного пространства между поленьями, а могут еще и специально складывать в виде шалаша, что увеличивает пустоты.
Дрова в укладку (складометры) – это когда аккуратно сложены полено к полену.
Как видите из картинок дрова аккуратно уложенные имеют намного меньше пустот, поэтому вероятность того что вас обманут (по крайне мере по объему) намного ниже.
При покупке будет достаточно легко контролировать объем визуально. Да и при желании, намного проще посчитать какой объем дров вам привезли.
Способы расчета объема дров
Продавцы дров считают свой товар в плотных метрах (без пустот), а продают уложенные в поленницу (в складометрах). Но, так как дрова обычно перевозятся “навалом”, то объём будет совершенно другим. Посчитать его можно исходя либо из объёма кузова, либо из объёма получившейся кучи.
Куча является, грубо говоря, конусом
Объём конуса, согласно курсу геометрии, находится по формуле:
V=1/3*число ПИ*квадрат радиуса*высота
Итак, если привезли, высыпали и обнаружился конус высотой 1,5 м, а радиусом (мы помним, это половина диаметра) 2 м, то “объём навалом” получится равным 6,28 куб.м.
Чтобы получить объем дров уложенных в поленницу, нужно умножить “объём-навалом” на 0,82.
Наш конус превращается в складометры:
В плотную меру переводят, путем умножения на средний расчетный коэффициент равный 0,6-0,8 (в зависимости от вида и качества древесины, длины и формы дров). Смотрите ГОСТ 3243-88. Дрова.
На практике применяется средний К=0,7.
Таким образом, наш конус превращается в плотный куб: 5,15*0,7=3,6 куб.м.
Или, например, ГАЗ-53 имеет объём кузова 4,8 куб.м.
Значит объём дров “навалом” переводим в складочный, а затем в плотный: 4,8*0,82*0,7= 2,76 куб.м.
Если дрова уложены в штабеля, объём дров посчитать несложно
Формула объёма параллелепипеда всем известна.
Если загрузка идет в неправильной форме, то ориентир держим на объём кузова или на конус при разгрузке.
Помните, есть ГОСТ 3243-88, там на каждый вид дров приводится свой коэффициент. Хотя на практике расчеты производятся условно-приблизительно.
| Вид грузовика | Навалом | В укладку |
| ГАЗ-53 “Газон”ЗИЛ самосвал | 3,95 | 2,76 |
| Газель 3302 | 3,3 | 2,3 |
| КАМАЗ | 7 | 4,9 |
Иногда дрова грузят с горкой, иногда без.
Лучше считать уже выгруженный “конус”.
Как обманывают при продаже дров?
При покупке навалом могут устроить что-то вроде шалаша, тем самым уменьшив фактический объем, вместо 4 кубов продадут 3.
Под видом сухих дров продадут подсушенные, для этого сырые добавят в центр благодаря чему их не будет видно даже после разгрузки (если свалят в кучу, сначала верхняя часть закрывает сырые, а потом нижняя часть закроет).
Разгрузить можно тоже по разному, либо ссыпав кучей, либо равномерно проехав – визуально сразу будет видно где дров меньше.
via The Washinghton Post
Как определить куб дров (кубатуру) или объем при покупке
Последнее обновление: 20-07-2018
Способ расчета кубатуры дров при покупке
Закупка дров всегда связана с определением объема. У продавцов существуют несколько способов продажи.
На складе дрова могут быть уложены в штабеля, но конечному покупателю они продаются навалом прямо с кузова грузовика. Это затрудняет точное определение объема привезенных дров.
Возрастает вероятность заплатить денег за больший объем дров, чем привезли на самом деле. Недобросовестные продавцы часто этим пользуются.
Для определения приблизительного объема закупаемых дров необходимо знать методы замеров.
В конце размещен калькулятор расчета кубатуры дров.
Как измеряется объем дров
Способы расчета кубатуры дров
Очень часто дрова продают без укладки, и определить объем насыпной древесины намного сложнее. Для этого применяют понятие
насыпного или навального кубометра. Такая мера измерения применяется при транспортировке дров навалом в кузове автомобиля или другого транспортного средства.
Объем дров при этом определяется следующим образом:
Это и будет объемом дров в навальных кубометрах.
Зависимость коэффициента от длины поленьев сведена в таблицу:
| Длина полена в метрах | Коэффициент пересчета |
| 0,25 | 0,8 |
| 0,33 | 0,78 |
| 0,50 | 0,75 |
| 0,75 | 0,73 |
Также дрова продаются такими мерами объема, как телега, газон, камаз. Ни один продавец при этом вам не скажет истинного объема дров в кузове.
Намного удобнее и проще было бы покупать дрова по массе, но тут также встает вопрос с влажностью, которую еще сложнее оценить.
Но альтернатива есть. К примеру, древесные брикеты продаются килограммами, тоннами. Тут уж ошибиться можно только с весами.
Как посчитать один кубометр дров: уложенных, навалом и в сетках
Как посчитать один кубометр дров: уложенных, навалом и в сетках
Наверняка каждый человек, кто хоть раз заказывал дрова, задавался вопросом, а не обманули ли его поставщики? Как определить, сколько именно дров вам привезли? Возможно, вы сталкивались, с сельским жителем или бывалым рабочим лесхоза, который с одного многозначительного взгляда на кучу дров, говорил практически верный результат. На самом деле, в определении объема дров, нет ничего сложного, причем это можно делать как на глаз, при должном опыте, так и с высокой точностью, используя расчетный метод. Давайте, именно на нем и остановимся поподробнее.
Первое, на что надо обратить внимание, при подготовке к расчету, это тип укладки дров. Начнем, с самого распространенного – навалом
В этом случае дрова закидываются в кузов или кучу, на первый взгляд оценить объем довольно сложно, ведь поленья лежат не плотно. Для начала требуется вычислить общий объем привезенных дров. С этой целью необходимо обмерить наваленные дрова. Если у вас конусообразная куча, то узнаем ее диаметр и высоту, в случае если дрова находятся в кузове, меряем длину, высоту и ширину, горку лучше предварительно разровнять, для более точных расчетов. Вычислив объем, следует перевести его в складометры, для этого используем коэффициенты. Обычно берется средний 0,7, так как данное число используется в дальнейших расчетах, но при необходимости точного расчета, следует использовать нормативный документ ГОСТ 3243-88. В нем указываются точные коэффициенты, которые зависят от типа древесины, ее состояния, длины и толщины поленьев.
Теперь мы знаем, сколько складочных кубометров нам привезли, но ведь мы заказывали кубические метры, под которыми понимается сплошная древесина без промежутков. Усреднено считается, что один складочный метр, равняется 0,7 кубометра сплошной древесины. Именно этот коэффициент и используется в большинстве случаев, хотя для точных расчетов, следует вернуться к таблице переводов изложенной в ГОСТ 3243-88.
Как видим, ничего сложного в расчетах нет. Для точного определения количества кубометров, достаточно лишь узнать объем привезенных дров, перевести его в складочные метры, а потом, используя коэффициент узнать количество кубов.
А если Вас интересует вес дров, то прочитав нашу статью, вы будете знать те многие параметры которые нужно учитывать при расчете массы древесины: Сколько весят дрова?
Мы работаем без обмана! Мы всегда привозим точное количество заказанных Вами дров!
Заказать дрова в Москве и Московской области у нас очень просто!
Как посчитать кубатуру колотых дров
Древесина отличается уникальными характеристиками, так как ее можно использовать не только как строительный материал, но и источник энергии. Дрова сегодня считаются одним из самых чистых видов топлива.
Многие предприятия осуществляют продажу подобного товара, который может отличаться качеством. Узнать, как правильно выбрать дрова можно на сайте http://дровам.рф/drova-kolotye.html.
Рассчитываем сложенные дрова
Объем древесины считается довольно легко, если она представляет собой пиломатериал, который плотно складывается в стопках. Но дрова невозможно сложить так, чтобы между поленьями не было щелей. Расчет сложенных в стопку данных материалов можно разбить на несколько последовательных шагов:
Насыпные дрова
Но дрова не всегда бывают аккуратно сложенными в правильные конструкции. Многие хотят узнать, какой объем занимает насыпная куча. Эта задача более сложная, особенно если дрова являются нестандартными и отличаются размером полена.
Если вы дома нарубили определенный объем, тогда рассчитать его можно примерно по такой методике:
Как видите, процесс вычисления кубатуры колотых дров довольно простая операция, которая займет у вас немного времени.
Сколько кубов в складометре — важные параметры при расчете. Жми!
Во всем мире существуют единые системы измерения: килограммы для определения веса, метры для размеров вещей и т.д.
При заготовке и перевозке дров и лесов обычно используются измерения кубометр и складометр – между этими величинами существует некоторая разница, о которой знают не все.
Что такое кубометр
В этой величине обычно измеряют газ, воду, снег, песок и другие сыпучие и жидкие материалы.
Однако это величина подходит только для измерения одного целикового куска дерева, например, сосны: ведь, если сложить куб из отдельных дров и досок, между ними все равно останется расстояние, хоть и в несколько миллиметров.
Важно знать: в строительстве в кубометрах также измеряется кубатура древесины: это необходимо при перевозке и хранении стройматериала.
Следовательно, при покупке дров, досок и других «нецеликовых» кусков, кубометры не подходят: пришлось бы измерять каждый брусок со всех сторон и пытаться уложить их в заданные параметры. Это слишком долго и все равно может привести к ошибкам.
Как пересчитать куб дров
Его проще всего представить в виде поленницы размером 1 м х 1 м х 1 м, в которую сложили поленья, подогнав их как можно плотнее друг к другу. Между ними все равно остается какое-то расстояние – небольшое, но значимое при покупке большого количества дров.
Для перевода скадометра в кубометр необходимо вычислить размеры штабеля (длину, высоту и ширину) и умножить на специальный коэффициент, указанный в таблице ниже. Это поможет получить приближенный к истине объем дров.
Значение коэффициента можно найти в специальных таблицах и на фото: они зависят от породы дерева, длины полена и его объема.
Для лиственных деревьев
Для хвойных деревьев
Иными словами, чем короче поленья, чем больше места они могут занять в упаковке, при этом круглые дрова занимают больше объема, чем колотые.
Проще всего увидеть смысл складометра на примере:
Был куплен штабель тонких березовых чурок длиной в 0,75 метра. Габариты самого штабеля составили 1,5 метра * 3 метра * 2,5 метра. Необходимо посчитать итоговый объем занимаемых дров при помощи калькулятора:
Итого разница получилась почти 4 куб. метра. Если бы не было величины скадометр, покупателю пришлось бы значительно переплатить за покупку.
Расчет и вес
В них указан примерный вес 1 кубического метра разных пород. Например, свежий дуб весит 1000 кг, а при естественной влажности в 15% — всего 710 кг.
Было куплено 4 складометра сухих колотых дубовых поленьев длиной в 0,25 метра и влажностью в 15%. Необходимо проверить их вес:
Если же дерево привезли в кузове машины, например, Газели или самосвале, не в поленнице, а накидав кое-как, необходимо объем кузова умножить на 0,8 при длине полена в 0,25 метра и на 0,75 при длине в 0,5 метров. Это средние величины занимаемого воздуха при подобной укладке.
Возьмите на заметку: складометр – это полезная для покупателя величина, позволяющая не платить за «воздух». При покупке дерева кубическими метрами стоит помнить, как правильно рассчитать итог, иначе сумма будет выглядеть несколько завышенной.
Как рассчитать кубатуру, смотрите пример расчета в следующем видео: