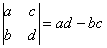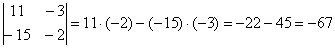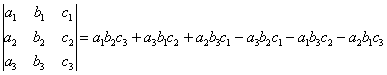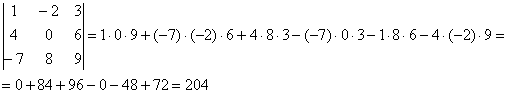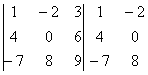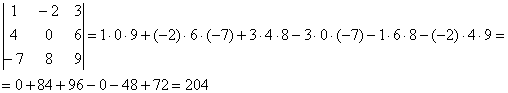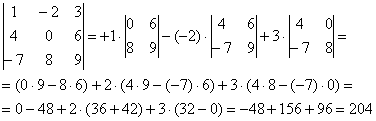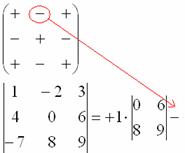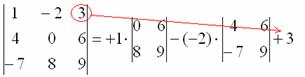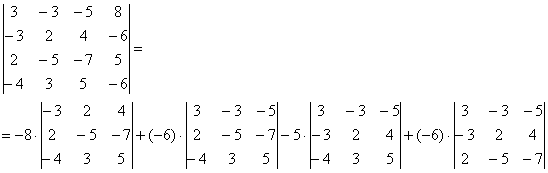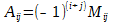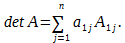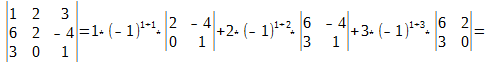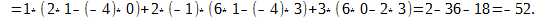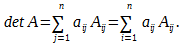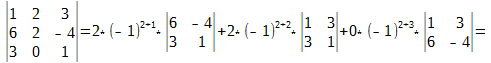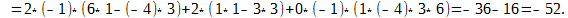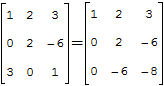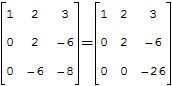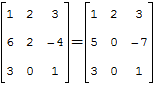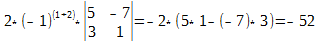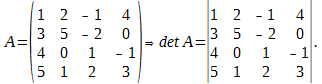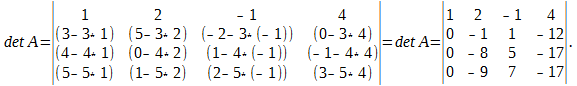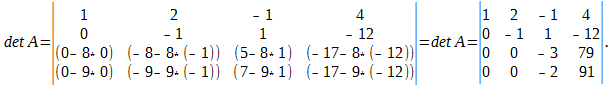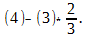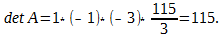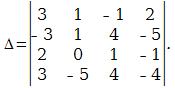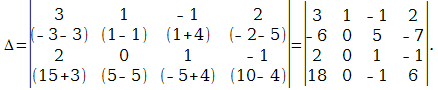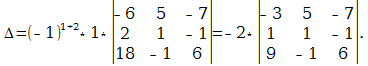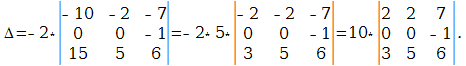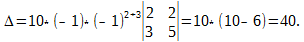Как считать определитель матрицы

Как вычислить определитель?

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)

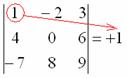
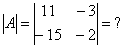
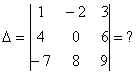
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка 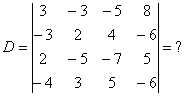тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

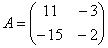
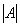
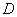
Обозначения: Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два»:

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

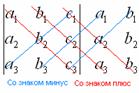
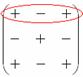
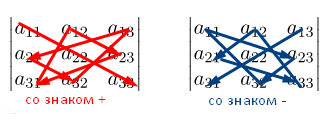
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке.
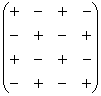
Для этого нам понадобится матрица знаков: 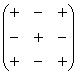. Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот: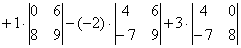
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

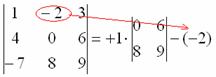
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент: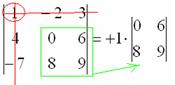

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

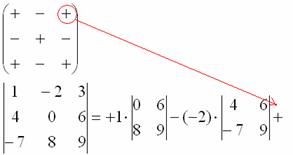
Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент: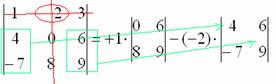

Оставшиеся четыре числа записываем в маленький определитель.

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент: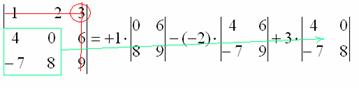

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу:

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Zaochnik.com – профессиональная помощь студентам,

cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys

Источник

Определитель матрицы: алгоритм и примеры вычисления определителя матрицы

Способ вычисления определителя выбирают в зависимости от порядка матрицы.

Определитель матрицы 2-го порядка вычисляют по формуле:

Определитель матрицы 3-го порядка: правило треугольника

Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:

Как найти определитель матрицы 3-го порядка по методу треугольника?

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Разложение матрицы по элементам строки:

Разложение матрицы по элементам столбца:

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Свойства определителя

А = 1 3 4 0 2 1 0 0 5

d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10

Определитель матрицы, который содержит нулевой столбец, равняется нулю.

Источник

Методы вычисления определителей

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:

Решение.

$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Полученный определитель разложим по элементам первого столбца:

$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$

Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

Теорема Лапласа

Источник

Определитель матрицы и его свойства

В этом уроке мы детально рассмотрим несколько ключевые вопросов и определений, благодаря чему вы раз и навсегда разберётесь и с матрицами, и с определителями, и со всеми их свойствами.

Определители — центральное понятие в алгебре матриц. Подобно формулам сокращённого умножения, они будут преследовать вас на протяжении всего курса высшей математики. Поэтому читаем, смотрим и разбираемся досконально.:)

И начнём мы с самого сокровенного — а что такое матрица? И как правильно с ней работать.

Правильная расстановка индексов в матрице

Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.

\[A=\left[ m\times n \right]\]

Какой индекс за что отвечает? Сначала идёт номер строки, затем — столбца? Или наоборот?

При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.

Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:

Введение системы координат на плоскости

А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.

Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:

Наложение системы координат на матрицу

Определение индексов в матрице

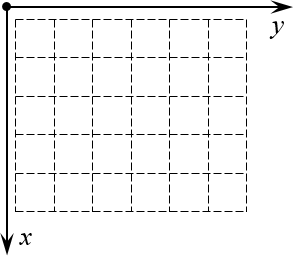
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.

Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)

Геометрическое определение

Ну и что это за характеристика? Что он означает? Всё просто:

Например, определитель матрицы размера 2×2 — это просто площадь параллелограмма, а для матрицы 3×3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.

На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:

Задача. Найдите определители матриц:

Решение. Первые два определителя имеют размер 2×2. Значит, это просто площади параллелограммов. Начертим их и посчитаем площадь.

Определитель 2×2 — это площадь параллелограмма

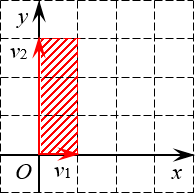
Очевидно, это не просто параллелограмм, а вполне себе прямоугольник. Его площадь равна

Ещё один определитель 2×2

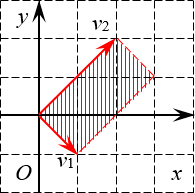
Стороны этого прямоугольника (по сути — длины векторов) легко считаются по теореме Пифагора:

Осталось разобраться с последним определителем — там уже матрица 3×3. Придётся вспоминать стереометрию:

Определитель 3×3 — это объём параллелепипеда

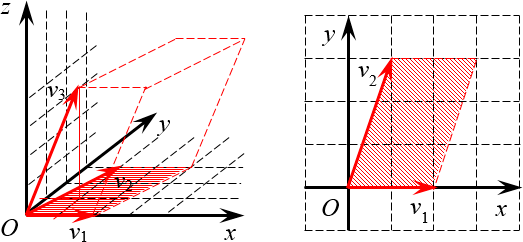
Выглядит мозговыносяще, но по факту достаточно вспомнить формулу объёма параллелепипеда:

Площадь параллелограмма (мы начертили его отдельно) тоже считается легко:

Вот и всё! Записываем ответы.

Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.

Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.

И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем. Но тут есть важное замечание:

В отличие от классического объёма, определитель даст нам так называемый «ориентированный объём», т.е. объём с учётом последовательности рассмотрения векторов-строк.

И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)

Алгебраическое определение

При всей красоте и наглядности геометрического подхода у него есть серьёзный недостаток: он ничего не говорит нам о том, как этот самый определитель считать.

Поэтому сейчас мы разберём альтернативное определение — алгебраическое. Для этого нам потребуется краткая теоретическая подготовка, зато на выходе мы получим инструмент, позволяющий считать в матрицах что и как угодно.

Правда, там появится новая проблема. но обо всём по порядку.

Перестановки и инверсии

Теперь (чисто по приколу) поменяем парочку чисел местами. Можно поменять соседние:

А можно — не особо соседние:

И знаете, что? А ничего! В алгебре эта хрень называется перестановкой. И у неё есть куча свойств.

Далее для простоты изложения будем работать с перестановками длины 5 — они уже достаточно серьёзны для наблюдения всяких подозрительных эффектов, но ещё не настолько суровы для неокрепшего мозга, как перестановки длины 6 и более. Вот примеры таких перестановок:

\[n!=5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120\]

Одной из ключевых характеристик всякой перестановки является количество инверсий в ней.

\[\left( 4;3 \right);\left( 4;2 \right);\left( 5;3 \right);\left( 5;2 \right);\left( 3;2 \right).\]

Что такое определитель

Принципиальным моментом при выборе множителей для каждого слагаемого в определителе является тот факт, что никакие два множителя не стоят в одной строчке или в одном столбце.

\[j=p\left( i \right),\quad i=1,2. n\]

От перестановки множителей произведение чисел не меняется.

Вот только не надо приплетать это правило к умножению матриц — в отличие от умножения чисел, оно не коммутативно. Но это я отвлёкся.:)

Матрица 2×2

Вообще-то можно рассмотреть и матрицу 1×1 — это будет одна клетка, и её определитель, как нетрудно догадаться, равен числу, записанному в этой клетке. Ничего интересного.

Поэтому давайте рассмотрим квадратную матрицу размером 2×2:

Рассмотрим пару примеров:

Решение. Всё считается в одну строчку. Первая матрица:

\[5\cdot 9-8\cdot 6=45-48=-3\]

\[7\cdot 1-14\cdot 12=7-168=-161\]

Впрочем, это было слишком просто. Давайте рассмотрим матрицы 3×3 — там уже интересно.

Матрица 3×3

Теперь рассмотрим квадратную матрицу размера 3×3:

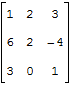
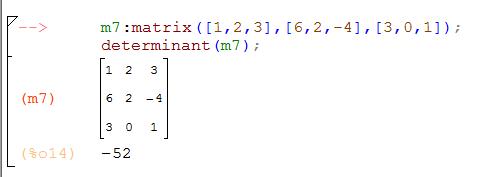
\[\begin & <

_<1>>=\left( 1;2;3 \right)\Rightarrow N\left( <

_<1>> \right)=N\left( 1;2;3 \right)=0; \\ & <

_<2>>=\left( 1;3;2 \right)\Rightarrow N\left( <

_<2>> \right)=N\left( 1;3;2 \right)=1; \\ & <

_<3>>=\left( 2;1;3 \right)\Rightarrow N\left( <

_<3>> \right)=N\left( 2;1;3 \right)=1; \\ & <

_<4>>=\left( 2;3;1 \right)\Rightarrow N\left( <

_<4>> \right)=N\left( 2;3;1 \right)=2; \\ & <

_<5>>=\left( 3;1;2 \right)\Rightarrow N\left( <

_<5>> \right)=N\left( 3;1;2 \right)=2; \\ & <

_<6>>=\left( 3;2;1 \right)\Rightarrow N\left( <

_<6>> \right)=N\left( 3;2;1 \right)=3. \\\end\]

Вот только не надо сейчас садиться и яростно зубрить все эти индексы! Вместо непонятных цифр лучше запомните следующее мнемоническое правило:

. Для нахождения определителя матрицы 3×3 нужно сложить три произведения элементов, стоящих на главной диагонали и в вершинах равнобедренных треугольников со стороной, параллельной этой диагонали, а затем вычесть такие же три произведения, но на побочной диагонали. Схематически это выглядит так:

Определитель матрицы 3×3: правило треугольников

Именно эти треугольники (или пентаграммы — кому как больше нравится) любят рисовать во всяких учебниках и методичках по алгебре. Впрочем, не будем о грустном. Давайте лучше посчитаем один такой определитель — для разминки перед настоящей жестью.:)

\[\left| \begin 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\\end \right|\]

Решение. Работаем по правилу треугольников. Сначала посчитаем три слагаемых, составленных из элементов на главной диагонали и параллельно ей:

\[\begin & 1\cdot 5\cdot 1+2\cdot 6\cdot 7+3\cdot 4\cdot 8= \\ & =5+84+96=185 \\\end\]

Теперь разбираемся с побочной диагональю:

\[\begin & 3\cdot 5\cdot 7+2\cdot 4\cdot 1+1\cdot 6\cdot 8= \\ & =105+8+48=161 \\\end\]

Осталось лишь вычесть из первого числа второе — и мы получим ответ:

Тем не менее, определители матриц 3×3 — это ещё не вершина мастерства. Самое интересное ждёт нас дальше.:)

Общая схема вычисления определителей

Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка.

Что такое минор матрицы

Есть и другое определение. Возможно, кому-то оно больше придётся по душе:

Как говорил мой кот, иногда лучше один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.

Выбирая строку 1 и столбец 2, получаем минор первого порядка:

Выбирая строки 2, 3 и столбцы 3, 4, получаем минор второго порядка:

А если выбрать все три строки, а также столбцы 1, 2, 4, будет минор третьего порядка:

\[<_<3>>=\left| \begin 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\\end \right|\]

Считать этот определитель мне уже в лом. Но он равен 53.:)

Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше.

Алгебраические дополнения

«Ну ok, и что дают нам эти миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.

Уточним один момент: дополнительный минор — это не просто «кусок матрицы», а определитель этого куска.

Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения.

Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример:

\[A=\left[ \begin 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \\\end \right]\]

Выберем минор второго порядка

Капитан Очевидность как бы намекает нам, что при составлении этого минора были задействованы строки 1 и 4, а также столбцы 3 и 4. Вычёркиваем их — получим дополнительный минор:

Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда.

Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте:

Теорема Лапласа

И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны.

Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок.

Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы.

Разложение определителя по строке и столбцу

То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями.

Читайте и наслаждайтесь:

Это и есть формула разложения определителя по строке. Но то же верно и для столбцов.

Из этого следствия можно сразу сформулировать несколько выводов:

Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:)

Что ж, попробуем посчитать одну такую задачку?

\[\left| \begin 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\end \right|\]

Решение. Разложим этот определитель по первой строке:

Задача. Найдите определитель:

\[\left| \begin 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end \right|\]

Решение. Для разнообразия давайте в этот раз работать со столбцами. Например, в последнем столбце присутствуют сразу два нуля — очевидно, это значительно сократит вычисления. Сейчас увидите почему.

Итак, раскладываем определитель по четвёртому столбцу:

И тут — о, чудо! — два слагаемых сразу улетают коту под хвост, поскольку в них есть множитель «0». Остаётся ещё два определителя 3×3, с которыми мы легко разберёмся:

Возвращаемся к исходнику и находим ответ:

Ну вот и всё. И никаких 4! = 24 слагаемых считать не пришлось.:)

Основные свойства определителя

В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было?

Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя:

Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули.

Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше.

Давайте посмотрим, как это работает на практике:

\[\left| \begin 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\end \right|\]

Решение. Нулей тут как бы вообще не наблюдается, поэтому можно «долбить» по любой строке или столбцу — объём вычислений будет примерно одинаковым. Давайте не будем мелочиться и «обнулим» первый столбец: в нём уже есть клетка с единицей, поэтому просто возьмём первую строчку и вычтем её 4 раза из второй, 3 раза из третьей и 2 раза из последней.

В результате мы получим новую матрицу, но её определитель будет тем же:

Теперь с невозмутимостью Пятачка раскладываем этот определитель по первому столбцу:

Понятно, что «выживет» только первое слагаемое — в остальных я даже определители не выписывал, поскольку они всё равно умножаются на ноль. Коэффициент перед определителем равен единице, т.е. его можно не записывать.

Зато можно вынести «минусы» из всех трёх строк определителя. По сути, мы трижды вынесли множитель (−1):

Получили мелкий определитель 3×3, который уже можно посчитать по правилу треугольников. Но мы попробуем разложить и его по первому столбцу — благо в последней строчке гордо стоит единица:

Можно, конечно, ещё поприкалываться и разложить матрицу 2×2 по строке (столбцу), но мы же с вами адекватны, поэтому просто посчитаем ответ:

Вот так и разбиваются мечты. Всего-то −160 в ответе.:)

Парочка замечаний перед тем, как мы перейдём к последней задаче:

Идём дальше. Последняя задача в сегодняшнем уроке.

\[\left| \begin 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\end \right|\]

Решение. Ну, тут первая строка прямо-таки напрашивается на «обнуление». Берём первый столбец и вычитаем ровно один раз из всех остальных:

\[\begin & \left| \begin 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\end \right|= \\ & =\left| \begin 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & 25-5 & 125-5 & 625-5 \\\end \right|= \\ & =\left| \begin 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\\end \right| \\\end\]

Раскладываем по первой строке, а затем выносим общие множители из оставшихся строк:

\[\cdot \left| \begin 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\end \right|=\cdot \left| \begin 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\end \right|\]

Снова наблюдаем «красивые» числа, но уже в первом столбце — раскладываем определитель по нему:

Источник

Определитель матрицы

В высшей математике очень часто при решении задач нужно вычислять определитель матрицы. В данной статье рассмотрим, что такое определитель матрицы и научимся решать определители второго, третьего и четвёртого порядка.

Часто в ВУЗе попадаются задачи по высшей математики, в которых необходимо вычислить определитель матрицы. К слову, определитель может быть только в квадратных матрицах. Ниже рассмотрим основные определения, какими свойствами обладает определитель и как его правильно вычислить.. Также на примерах покажем подробное решение.

Что такое определитель матрицы: вычисление определителя при помощи определения

второго порядка – это число .

Определитель матрицы обозначается – (сокращенно от латинского названия детерминант), или .

Если:, тогда получается

Напомним ещё несколько вспомогательных определений:

Для множества, которое содержит элементов есть факториал (n), который всегда обозначается восклицательным знаком: . Перестановки отличаются друг от друга всего лишь порядком следования. Чтобы вам было понятнее, приведём пример:

Рассмотрим множество из трёх элементов <3, 6, 7>. Всего перестановок 6, так как .:

;

;

;

;

;

Выше мы рассматривали пример с инверсией перестановки, где были числа . Так вот, возьмём вторую строку, где судя по данным числам получается, что , а , так как второй элемент больше третьего элемента . Возьмём для сравнения шестую строку, где расположены числа: . Здесь есть три пары: , а , так как 6″ title=»Rendered by QuickLaTeX.com» height=»13″ width=»42″ style=»vertical-align: 0px;»/>; , так как 3″ title=»Rendered by QuickLaTeX.com» height=»13″ width=»42″ style=»vertical-align: 0px;»/>; , – 3″ title=»Rendered by QuickLaTeX.com» height=»12″ width=»43″ style=»vertical-align: 0px;»/>.

Саму инверсию мы изучать не будем, а вот перестановки нам очень пригодятся в дальнейшем рассмотрении темы.

, где

– перестановка чисел от 1 до бесконечного числа , а – число инверсий в перестановке. Таким образом, в определитель входит слагаемых, которые называются “членами определителя”.

Можно вычислять определитель матрицы второго порядка, третьего и даже четвёртого. Также стоит упомянуть:

определитель матрицы – это число, которое равняется

Чтобы понять данную формулу, опишем её более подробно. Определитель квадратной матрицы x – это сумма, которая содержит слагаемых, а каждое слагаемое является собой произведением определённого количества элементов матрицы. При этом, в каждом произведении есть элемент из каждой строки и каждого столбца матрицы.

Перед определённым слагаемым может появится в том случае, если элементы матрицы в произведении идут по порядку (по номеру строку), а количество инверсий в перестановке множество номеров столбцов нечётно.

Выше упоминалось о том, что определитель матрицы обозначается или , то есть, определитель часто называют детерминантом.

Итак, вернёмся к формуле:

Из формулы видно, что определитель матрицы первого порядка – это элемент этой же матрицы .

Нужна помощь в написании работы?

Вычисление определителя матрицы второго порядка

Чаще всего на практике определитель матрицы решается методами второго, третьего и реже, четвёртого порядка. Рассмотрим, как вычисляется определитель матрицы второго порядка:

В матрице второго порядка , отсюда следует, что факториал . Прежде чем применить формулу

необходимо определить, какие данные у нас получаются:

1. ;

2. перестановки множеств: и ;

4. соответствующие произведения : и .

Исходя из вышесказанного мы получаем формулу для вычисления определителя квадратной матрицы второго порядка, то есть x :

Рассмотрим на конкретном примере, как вычислять определитель квадратной матрицы второго порядка:

Задача

Вычислить определитель матрицы x :

Решение

Итак, у нас получается , , , .

Для решения необходимо воспользоваться ранее рассмотренной формулой:

Подставляем числа с примера и находим:

Ответ

Определитель матрицы второго порядка = .

Вычисление определителя матрицы третьего порядка: пример и решение по формуле

Определитель матрицы третьего порядка – это число, полученное из девяти заданных чисел, расположенных в виде квадратной таблицы,

Определитель третьего порядка находится почти так же, как и определитель второго порядка. Разница лишь в формуле. Поэтому, если хорошо ориентироваться в формуле, тогда и проблем с решением не будет.

Рассмотрим квадратную матрицу третьего порядка * :

Исходя из данной матрицы, понимаем, что , соответственно, факториал = , а это значит, что всего перестановок получается

Чтобы применить правильно формулу , необходимо найти данные:

Итак, всего перестановок множества :

. , количество инверсий в перестановке , а соответствующие произведения = ;

Теперь у нас получается:

Таким образом у нас получена формула для вычисления определителя матрицы порядка x :

.

Нахождение матрицы третьего порядка по правилу треугольника (правило Саррюса)

Как говорилось выше, элементы определителя 3-го порядка расположены в трёх строках и трёх столбцах. Если ввести обозначение общего элемента , тогда первый элемент обозначает номер строки, а второй элемент из индексов – номер столбца. Есть главная (элементы ) и побочная (элементы ) диагонали определителя. Слагаемые в правой части называются членами определителя).

Видно, что каждый член определителя находится в схеме только по одному элементу в каждой строке и каждого столбца.

Вычислять определитель можно при помощи правила прямоугольника, который изображён в виде схемы. Красным цветом выделены члены определителя из элементов главной диагонали, а также члены из элементов, которые находятся в вершине треугольников, что имеют по одной стороне, параллельны главной диагонали (лева схема), беруться со знаком .

Члены с синими стрелками из элементов побочной диагонали, а также из элементов, которые находятся в вершинах треугольников, что имеют стороны, параллельные побочной диагонали (правая схема) берутся со знаком .

На следующем примере научимся, как вычислять определитель квадратной матрицы третьего порядка.

Задача

Вычислить определитель матрицы третьего порядка:

Решение

, , ,

, , ,

, , .

Вычисляем определитель, применяя формулу или схему, которые рассматривались выше:

Ответ

Определитель матрицы третьего порядка =

Рекомендуем запомнить формулы для нахождения определителя матрицы второго и третьего порядка, так как они часто применяются на зачётах и экзаменах.

Основные свойства определителей матрицы третьего порядка

На основании предыдущих определений и формул рассмотрим основные свойства определителя матрицы.

1. Размер определителя не изменится при замене соответствующих строк, столбцов (такая замена называется транспонированием).

На примере убедимся, что определитель матрицы равен определителю транспонированной матрицы:

Вспомним формулу для вычисления определителя:

Вычисляем определитель транспонированной матрицы:

Мы убедились, что определитель транспортированной матрицы равен исходной матрице, что говорит о правильном решении.

2. Знак определителя изменится на противоположный, если в нём поменять местами любые два его столбца или две строки.

Рассмотрим на примере:

Даны две матрицы третьего порядка ( x ):

Нужно показать, что определители данных матриц противоположные.

Решение

В матрице и в матрице поменялись строки (третья с первой, и с первой на третью). Согласно второму свойству определители двух матриц должны отличаться знаком. То есть, одна матрица с положительным знаком, а вторая – с отрицательным. давайте проверим данное свойство, применив формулу для вычисления определителя.

Свойство верно, так как .

3. Определитель равняется нулю, если в нём есть одинаковые соответствующие элементы в двух строках (столбцах). Пусть у определителя одинаковые элементы первого и второго столбцов:

Поменяв местами одинаковые столбцы, мы, согласно свойству 2 получим новый определитель: = . С другой стороны, новый определитель совпадает с изначальным, поскольку одинаковые ответы элементы, то есть = . Из этих равенств у нас получается: = .

4. Определитель равняется нулю, если все элементы одной строки (столбца) нули. Это утверждение выплывает из того, что у каждого члена определителя по формуле (1) есть по одному, и только по одному элементу с каждой строки (столбца), у которого одни нули.

Рассмотрим на примере:

Покажем, что определитель матрицы равен нулю:

В нашей матрицы есть два одинаковых столбца (второй и третий), поэтому, исходя из данного свойства, определитель должен равняться нулю. Проверим:

И действительно, определитель матрицы с двумя одинаковыми столбцами равняется нулю.

5. Общий множитель элементов первой строки (столбца) можно вынести за знак определителя:

.

6. Если элементы одной строки или одного столбца определителя пропорциональны соответствующим элементам второй строки (столбца), тогда такой определитель равняется нулю.

Действительно, за свойством 5 коэффициент пропорциональности можно вынести за знак определителя, и тогда воспользоваться свойством 3.

7. Если каждый из элементов строк (столбцов) определителя является суммой двух слагаемых, то этот определитель можно подать в виде суммы соответствующих определителей:

.

Для проверки достаточно записать в развёрнутом виде по (1) определитель, что в левой части равенства, тогда отдельно сгруппировать члены, в которых содержатся элементы и .Каждая из полученных групп слагаемых будет соответственно первым и вторым определителем с правой части равенства.

8. Значения определения не изменятся, если к элементу одной строки или одного столбца прибавить соответствующие элементы второй строки (столбца), умноженные на одно и то же число:

.

Это равенство получается исходя из свойств 6 и 7.

9. Определитель матрицы , , равняется сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения.

Здесь по подразумевается алгебраическое дополнение элемента матрицы . При помощи данного свойства можно вычислять не только матрицы третьего порядка, но и матрицы более высших порядков ( x или x ).Другими словами – это рекуррентная формула, которая нужна для того, чтобы вычислить определитель матрицы любого порядка. Запомните её, так как она часто применяется на практике.

Стоит сказать, что при помощи девятого свойства можно вычислять определители матриц не только четвёртого порядка, но и более высших порядков. Однако, при этом нужно совершать очень много вычислительных операций и быть внимательным, так как малейшая ошибка в знаках приведёт к неверному решению. Матрицы высших порядков удобнее всего решать методом Гаусса, и об этом поговорим позже.

10. Определитель произведения матриц одного порядка равен произведению их определителей.

Рассмотрим на примере:

Задача

Убедитесь, что определитель двух матриц и равен произведению их определителей. Даны две матрицы:

Решение

Сначала находим произведение определителей двух матриц и .

x = ,

Теперь выполним умножение обеих матриц и таким образом, вычислим определитель:

Ответ

Мы убедились, что

Вычисление определителя матрицы при помощи метода Гаусса

Вспомним, как метод Гаусса помогает находить определитель матрицы: благодаря элементарным преобразованием в матрице все элементы (кроме ) нужно привести к нулю. Однако, такой метод подходит только к тем матрицам, в которых определитель отличен от нуля. Об этом поговорим позже, а сейчас объясним, для чего проделывается такая процедура.

Нулевые элементы необходимы для того, чтобы самым простым способом разложить определитель, исходя из элементов первого столбца. После такого преобразования, исходя из девятого свойства и , получается:

.

Здесь – это минор первого порядка, который получился из матрицы путём вычёркивания элементов первой строки и первого столбца. Такая процедура проделывается до тех пор, пока все элементы первого столбца не превратятся в нулевые элементы.

Конечно же, сразу же назревает вопрос: “А как же получается нулевые элементы?” Рассмотрим алгоритм решения:

Если первый элемент в первой строке и в первом столбце прибавить к соответствующим элементом – ой строки, где . (Метод Гаусса не нужен только в том случае, если все элементы в первом столбцы нулевые). После данного преобразования “новый” элемент матрицы . Определитель “новой” матрицы равен определителю исходной матрицы.

Если , тогда к каждому элементу второй строки прибавляем элемент первой строки, которые заранее умноженные на , а к элементам третьей строки прибавляем определённые элементы первой строки, которые умножаются на . И дальше вычисляем по такой же схеме. Метод Гаусса рассмотрен более подробно в отдельно теме. В итоге получится преобразованная матрица, где все элементы первого столбца окажутся нулевыми. Определитель полученной матрицы будет равен определителю изначальной матрицы.

Напомним, что величина определителя – ого порядка равна сумме произведений элементов какой-либо строки или столбца на соответствующее алгебраическое дополнение.

Рассмотрим записанный сначала формально определитель четвёртого порядка:

Вычёркивая в – тую строку и – тый столбец, на пересечении которого помещается элемент , получим определитель третьего порядка, который называется минором элемента и обозначается . Тогда – алгебраическое дополнение элемента . Определитель 4-го порядка можно обозначить, как размещение по элементам, например, первого столбца:

Пусть введено понятие определителя – ого порядка, тогда определитель – ого порядка:

Можно изобразить, как размещение по элементам первого столбца:

,

где – алгебраические дополнения, а – миноры элементов первого столбца. Последние и есть определители – го порядка.

Чтобы было более понятно, разберём матрицу четвёртого порядка, где нужно найти определитель:

Разберём на примере:

Задача

Нужно вычислить определитель матрицы высшего порядка x :

Решение

Сначала вспомним тему про определители третьего порядка и превратим в нули элементы 1-го столбца, которые принадлежат 2, 3, 4 строкам. Для этого прибавим соответствующие элементы 1 и 2 строк. На месте элементов получим , , , .

Чтобы получить в 3 строке 1-го столбца, умножим на элементы 1-ой строки и прибавим к соответствующим элементам третьей строки:

Умножим элементы 1-ой строки на и добавим к соответствующим элементам 4-ой строки. Получается:

Изначальный определитель впоследствии преобразований получается:

Дальше раскладываем последний определитель за элементами 1-го столбца. Поскольку , а остальные элементы 1-го столбца нули, тогда получим один определитель 3-го порядка.

Ответ

Определитель матрицы четвёртого порядка = .

Вычисление определителя матрицы при помощи теоремы Лапласа

Теорема Лапласа – это глубокое разложение определителя по элементам. При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков.

Напомним – минор – это определитель матрицы, который составлен методом вычёркивания – той строки и – того столбца. А алгебраическое дополнение – соответствующий минор, который берётся со знаком минус . Знаки же зависят от места элемента в определителе и определяются по схеме:

Приведём пример решения алгебраических дополнений по схеме:

Задача

Найти алгебраические дополнения элементов определителя:

Решение

Понятия алгебраического дополнения даёт возможность ещё одного способа определения определителя, который утверждается теоремой Лапласа (про распределение определителя):

Определитель равняется сумме произведения элементов строк (столбца) на их алгебраические дополнения. Например,

. – это равенство проверяется непосредственно

Заметно, как последнее выражение совпадает с выражением из правила треугольника (правила Саррюса). Давайте по теореме Лапласа разберём несколько примеров:

Задача

Вычислить определитель матрицы, разложив его за элементами третьего порядка:

Решение

Ответ

.

Заключение

Итак, определитель квадратной матрицы – это число, полученное при помощи заданных чисел, расположенных в виде квадратной таблицы,которое вычисляется по рассмотренным выше формулам. Мы рассмотрели три основных способа вычисления определителя:

Также были рассмотрены формулы для решения матрицы второго, третьего и высших порядков.

Мы разобрали 10 свойств определителя матриц, благодаря которым можно быстрее и легче найти определитель матрицы.

Удобно решать матрицу третьего порядка методом Гаусса, где нужно выполнить элементарные преобразования матрицы и привести её к ступенчатому виду. Определитель матрицы равняется произведению элементов, которые стоят на главной диагонали.

Источник

Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение

Без преобразования матрицы, определитель легко посчитать только для матриц размером 2×2 и 3×3. Это делается по формулам:

(можно посчитать по любой строке, выше приводиться формула расчёта определителя по первой строке).

Расчёты для матриц размером 4×4 и выше затруднительны, поэтому их нужно преобразовывать в соответствии со свойствами определителя. Нужно стремиться получить матрицу, в которой все значения кроме одного любого столбца или любой строки равны нулю. Пример такой матрицы:

Для неё определитель равен:

Обратите внимание, что

это вычисление детерминанта матрицы, полученой вычетом строки и столбца, на пересечении которых находиться единственное не нулевое числов строки/столбца, по которому мы разлагаем матрицу:

Если привести матрицу к треугольному виду, то её определитель вычисляется как произведение цифр по диагонали. Например, для матрицы

Аналогично следует поступать с матрицами 5×5, 6×6 и другими больших размерностей.

Преобразования матриц нужно выполнять в соответствии со свойствами определителя. Но прежде чем перейти к практике по вычислению определителя для матриц 4×4, давайте вернёмся к матрицам 3×3 и подробно рассмотрим, как вычисляется определитель для них.

Минор

Определитель матрицы не очень прост для понимания, поскольку в его понятии присутствует рекурсия: определитель матрицы состоит из нескольких элементов, в том числе из определителя (других) матриц.

Чтобы не застрять на этом, давайте прямо сейчас (временно) примем, что определитель матрицы

Ещё разберёмся в условных обозначения и в таких понятиях как минор и алгебраическое дополнение.

Буквой i мы обозначаем порядковый номер стоки, буквой j – порядковый номер столбца.

a_ij означает элемент матрицы (цифру) на пересечении строки i и столбца j.

Представим себе матрицу, которая получена из исходной удалением строки i и столбца j. Определитель новой матрицы, которая получена из исходной удалением строки i и столбца j, называется минором M_ij элемента a_ij.

Проиллюстрируем сказанное. Предположим, дана матрица

Тогда для определения минора M₁₁ элемента a₁₁ нам нужно составить новую матрицу, которая получается из исходной удалением первой строки и первого столбца:

И вычислить для неё определитель: 2*1 — (-4)*0 = 2

Для определения минора M₂₂ элемента a₂₂ нам нужно составить новую матрицу, которая получается из исходной удалением второй строки и второго столбца:

Алгебраическое дополнение

Алгебраическим дополнением А_ij для элемента a_ij называется минор M_ij этого элемента, взятый со знаком «+», если сумма индексов строки и столбца (i + j), на пересечении которых стоит этот элемент, чётная, и со знаком «-», если сумма индексов нечётная.

Для матрицы из предыдущего примера

Вычисление определителя для матриц

Определителем порядка n, соответствующим матрице А, называется число, обозначаемое det A и вычисляемое по формуле:

В этой формуле нам всё уже знакомо, давайте теперь посчитаем определитель матрицы для

Каков бы ни был номер строки i=1,2,…, n или столбца j = 1, 2,…, n определитель n-го порядка равен сумме произведений элементов этой строки или этого столбца на их алгебраические дополнения, т. е.

Т.е. детерминант можно вычислить по любому столбцу или по любой строке.

Чтобы убедиться в этом, вычислим определитель для матрицы из последнего примера по второму столбцу

Свойства определителя матриц

Для вычисления определителя любого порядка можно применять метод последовательного понижения порядка определителя. Для этого пользуются правилом разложения определителя по элементам строки или столбца. Еще один способ вычисления определителей заключается в том, чтобы с помощью элементарных преобразований со строками (или столбцами), прежде всего в соответствии со свойствами 4 и 7 определителей, привести определитель к виду, когда под главной диагональю определителя (определяемой так же, как и для квадратных матриц) все элементы равны нулю. Тогда определитель равен произведению элементов, расположенных на главной диагонали.

При вычислении определителя последовательным понижением порядка для уменьшения объема вычислительной работы целесообразно с помощью свойства 7 определителей добиться обнуления части элементов какой-либо строки или какого-либо столбца определителя, что уменьшит число вычисляемых алгебраических дополнений.

Приведение матрицы к треугольному виду, преобразование матрицы, облегчающее вычисление определителя

Показанные ниже методы нецелесообразно использовать для матриц 3×3, но я предлагаю рассмотреть суть методов на простом примере. Воспользуемся матрицей, для которой мы уже считали определитель — нам будет проще проверить правильность вычислений:

Используя 7-е свойство определителя, вычтем из второй строки третью, умноженную на 2:

из третьей строки вычтем соответствующие элементы первой строки определителя, умноженные на 3:

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Как видим, ответ совпал с полученными ранее.

Давайте вспомним формулу определителя матрицы:

Детерминант — это сумма алгебраических дополнений, умноженная на члены одной из строк или одного из столбцов.

Если в результате преобразований мы сделаем так, что одна из строк (или столбец) будет состоять полностью из нулей кроме одной позиции, то нам не нужно будет считать все алгебраические дополнения, поскольку они заведомо будут равны нулю. Как и предыдущий метод, этот целесообразно применять для матриц больших размеров.

Покажем пример на той же самой матрице:

Вычислим определитель по второму столбцу. Нам нужно посчитать только одно алгебраическое дополнение, поскольку остальные заведомо сводятся к нулю:

Вычисление определителя для матриц 4×4, 5×5 и больших размерностей

Чтобы избежать слишком больших вычислений для матриц больших размеров следует делать преобразования, описанные выше. Приведём пару примеров.

Вычислить определитесь матрицы

Р е ш е н и е. Используя 7-е свойство определителя, вычтем из второй строки третью, из четвёртой строки — соответствующие элементы первой строки определителя, умноженные соответственно на 3, 4, 5. Эти действия сокращённо будем обозначать так: (2) — (1) * 3; (3) — (1) * 4; (4) — (1) * 5. Получим:

Далее, в соответствии с ведёнными обозначениями, выполним действия: (3) — (2) * 8; (4) — (2) * 9. Получаем

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Вычислить определитель

Разлагая полученный определитесь по второй строке имеем:

(Затем мы вынесли сомножитель 2 первого столбца на основании свойства 4). Далее прибавим к элементам первого и второго столбца элементы определителя. Получим:

Затем мы вынесли множитель в первом столбце, а затем общий множитель (-1) в первой строке. Разлагая теперь получившийся определитесь третьего порядка по элементам второй строки получим:

Здесь определитесь второго порядка вычислен в соответствии с его определением, по формуле

Вычисление определителя (детерминанта) матрицы wxMaxima и Maxima

В wxMaxima и Maxima для вычисления определителя используется функция determinant:

Для приведения матриц к треугольному виду можно воспользоваться функцией triangularize:

Источник