Как сделать имитационную модель
Простая система имитационного моделирования на Go
Введение
Имитационное моделирование это метод, при котором для проведения экспериментов изучаемая реальная система заменяется моделью. В подобной модели можно проиграть как отдельные ситуации, так и их множество. Собранные статистические данные могут помочь сделать выводы о ходе процессов в системе, а также наметить пути оптимизации.
Имитационное моделирование часто рассматривают как разновидность экспериментальных испытаний, но при этом оно менее затратно, позволяет оперативно менять параметры и наблюдать моделируемую систему в динамике.
Уже порядка полувека при имитационном моделировании используются компьютерные модели. Для их разработки создано огромное множество различных программ и фреймворков, среди которых, на мой взгляд, наибольшее развитие получили средства для моделирования систем массового обслуживания (СМО). Одна из наиболее известных и простых программ для имитационного моделирования СМО – GPSS World (General Purpose Simulation System – система моделирования общего назначения), более подробно можно ознакомится по ссылкам [1], [2].
Концепция этой программы и была положена в основу фреймворка имитационного моделирования на Go.
Моделирование в GPSS
Модель в GPSS представляет собой последовательность блоков (команд), описывающих моделируемые объекты, между которыми перемещаются транзакты. При попадании транзакта в блок генерируются события, приводящие либо к изменению состояния моделируемого объекта, либо изменению состояния/параметров транзакта.
Основных блоков порядка десяти: GENERATE, TERMINATE, ASSIGN, SEIZE, RELEASE, QUEUE, ADVANCE, DEPART, START. Всего блоков порядка трёх десятков. Блоки имеют параметры, в качестве которых могут выступать числа, имена функций, метки в программе моделирования, имена переменных. Более подробно с блоками можно ознакомиться, например, здесь.
Объекты в GPSS имеют набор стандартных числовых атрибутов (СЧА) и стандартных логических атрибутов (СЛА). Например, для очереди, один из СЧА это текущая длина, а примером СЛА для некоего оборудования будет свободно (TRUE) или занято оно (FALSE).
В отдельных версиях GPSS присутствует визуализация процесса моделирования, но чаще всего она отсутствует. По результатам моделирования в GPSS формируется отчёт, с указанием СЧА и СЛА по всем объектам.
Реализация в Go
Реализация в Go представляет собой разработку набора объектов схожих по функциям с блоками GPSS. Первым был создан Pipeline – объект, в рамках которого выполняется симуляция.
Второй важный элемент это собственно компоненты для описания моделирования. Были реализованы: Generator – генерирует транзакты, Advance – создаёт задержки на пути транзакта, Queue – очереди транзактов, Facility – некое устройство, монопольно захватываемое транзактом на некоторое время, Hole – «дыра» в которую проваливаются транзакты в конце пути. Разумеется, такого набора недостаточно для создания сложных имитационных моделей, но для отработки решения и сравнения с результатами GPSS вполне хватает. Все компоненты реализуют интерфейс IBaseObj, который охватывает минимально необходимый функционал.
Для генерации случайных величин при определении времени появления транзакта и создании задержек используются функции ГПСЧ в Go.
Последний ключевой объект это собственно сам транзакт. У него есть идентификатор, время рождения и смерти, владелец (в каком компоненте он сейчас), ряд параметров для вычисления СЧА и СЧЛ.
На рис. 1 приведена структурная схема взаимодействия основных объектов фреймворка при моделировании.
Рис. 1. Обобщённая структурная схема взаимодействия основных объектов при моделировании
Пример моделирования
Допустим надо смоделировать работу парикмахерской. Это известный пример из GPSS. Посетители идут хаотично, с периодичностью 18±6 минут, их количество заранее не известно. Парикмахер у нас один, на стрижку он тратит 16±4 минуты. Итак, сколько всего человек он пострижёт за рабочий день? Сколько будет людей в очереди? Сколько в среднем уйдёт времени на стрижку и сколько времени просидят люди в очереди? Много вопросов и простая симуляция. Структурная схема на рис. 2.
Рис. 2. Структурная схема моделирования парикмахерской
Код для построения модели будет следующий.
Pipeline name » Barbershop »
Simulation time 480
Object name » Chairs »
Max content 1
Total entries 26
Zero entries 11
Persent zero entries 42.31%
In queue 0
Average time/trans 2.58
Average time/trans without zero entries 4.47
Object name » Clients »
Generated 26
Object name » Master »
Average advance 16.46
Average utilization 89.17
Number entries 26.00
Transact 26 in facility
Object name » Out »
Killed 25
Average advance 16.56
Average life 19.44
Обслужили 25 клиентов, 26-ой на момент завершения моделирования был ещё в кресле мастера. В очереди было не более 1 человека, 11 человек не ждали (нулевой проход) и сразу проходили на стрижку. В среднем в очереди люди провели 2,58 минуты, а из тех, кто ждал (не нулевой проход) 4,47 минуты. 89,17% своего времени парикмахер усиленно стриг.
Разумеется, если провести ещё одну симуляцию, результаты изменятся. Но при проведении серии симуляций будет видно общий уровень загрузки мастера и количество обслуженных клиентов. При проведении такой же симуляции в GPSS получаются близкие результаты.
Другой пример. Есть офис, в нём 10 сотрудников и один туалет. Люди желают пойти в туалет каждые 90±60 минут, идти до туалета 5±3 минуты, занимают туалет 15±10 минут, поход обратно в офис 5±3 минуты. Проведём симуляцию в течении 9 часов (8 часов работы + 1 час обед), на рис. 3 приведена структурная схема.
Рис. 3. Структурная схема модели занятости туалета: слева с одним туалетом, справа с двумя
Слева модель с одним туалетом, справа с двумя. Далее приведён код модели.
Pipeline name » Water Closet Simulation »
Simulation time 540
Object name » Office »
Generated 10
Object name » Path from WC »
Average advance 5.77
Object name » Path to WC »
Average advance 5.22
Object name » Queue to the WC »
Max content 4
Total entries 36
Zero entries 8
Persent zero entries 22.22%
Current contents 4
Average content 1.78
Average time/trans 24.11
Average time/trans without zero entries 31.00
Object name » WC »
Average advance 14.69
Average utilization 87.04
Number entries 32.00
Transact 2 in facility
Object name » Wanted to use the toilet »
Average advance 95.85
В очереди было до 4 человек, 8 раз человек сразу попал в туалет, в течении рабочего дня туалет используют на 87,04%. Самое существенное, на мой взгляд, это то, что люди ждут порядка получаса (31 минута) в очереди в туалет. Возможно, это связано с тем, туалет один, а возможно, с тем, что в среднем люди сидят в нём 14,69 минут.
Добавив ещё один туалет, я увидел, что очередь сократилась до 3 человек, 29 раз люди сразу попали в туалет. Но самое главное, почти в три раза уменьшилось ожидание.
Заключение
Созданный на коленке фреймворк достаточно простой и пока ещё ограниченный. В планах повысить его функциональность до уровня GPSS. Практическая ценность фреймворка в возможности просто и быстро собрать на Go имитационную модель и получить результаты.
GPSS-WORLD основы имитационного моделирования на живых примерах
Доброй пятницы уважаемые читатели Хабра.
В данном посте я предлагаю вам бегло ознакомиться с возможностью создания имитационной модели процессов в программе GPSS-WORLD. Данный пост нельзя считать полноценным туториалом, но я поделюсь с Вами теми крупицами, что знаю и вполне возможно что уже через пол часа после прочтения статьи Вы проявив фантазию создадите свою собственную имитационную модель. Как говориться в народе: «Тяжело в учении легко в бою».
И пусть местами, данный «туториал» придерживается принципа: «битый не битого везет», но я всё же донесу до вас те знания, которые у меня есть, ну а вы уж сами вольны решать, стоить ли мне доверять или лучше проверять. В любом случае я буду рад аудиту кода от знатоков GPSS-WORLD. Все материалы статьи размещены на GItHub
Изучать самые азы будем сразу на живых примерах — доступных, понятных и близких сердцу многим сотрудникам проводящим свои законные 8 часов в офисах.
От конкретики перейдем к лирике, пятница традиционно располагает задаваться безумными вопросами, и в этот раз мы с моим коллегой DrZugrik задались вопросом: «Сколько нужно сотрудников тех поддержки, чтобы рассказать, как вкрутить лампочку?».
За подробностями сего мысленного эксперимента прошу под кат.
Написание этого мини туториала вместе с разработкой моделей заняло 6 часов чистого времени.
буду признателен если статья доберется до потенциально заинтересованных читателей.
Во избежания вызова негативных эмоций первоначальная картинка заменена на кота с трубкой и спрятана под спойлер.
Для начала нам понадобиться сам GPSS-World.
Ух, ну вот мы и закончили с описанием первой модели.
Кому интересны результаты, прошу под спойлер. Если вы любите все проверять самостоятельно то еще раз напомню все модели выложены на GItHub
проанализируем результаты
Итак мы видим, что в среднем наш кулер загружен на 33%, то есть в нашей команде из 10 сотрудников получается примерно так как если бы к нему постоянно прикладывался Администратор Петр, Марья Васильевна из бухгалтерии и Менеджер проекта Василий Чуфыркин, ну и еще 0.33 человека, или например — кот. На самом деле этот блок текста не несет смысловой нагрузки, мне просто очень хотелось нарисовать кота и кулер и Марью Васильевну из бухгалтерии (все кроме кота личности сугубо выдуманные)
Хотя черт побери после того как я прочел это, могу смело утверждать, что кулер мог бы напоить 12 милых котиков =)
Но вернемся к теме.
Давайте рассмотрим, результаты выдачи.
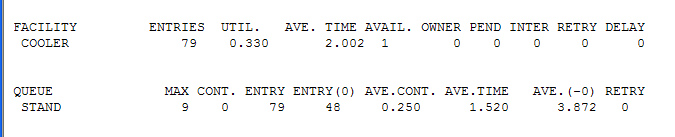
Facility – это список всех наших работающих устройств, в данном случае только кулер.
Entries 79 – означает число подходов на обслуживание к устройству, в данном случае число человек с пустыми чашками составило 79 – за всю рабочую смену.
Util – коэффициент использования оборудования, Он говорит нам о том, что кулер бездествовал (1-0.33)*100%=67% всего времени.
AVE. TIME – среднее время использования кулера 1 человеком 2.002 минуты
AVAIL. – Доступность кулера, не знаю что это значит видимо еденица говрит, что он был доступен
DELAY = 0 – говрит нам о том, что чсло людей которые просто подошли к кулеру, расстроились и ушли с пустыми руками (кружкой), равно нулю.
Теперь переедем к нашей очереди (QUEUE)
Как видите тут указано имя созданной нами ранее очереди,
В которой максимально находилось 9 человек, в которую было 79 входов, и 48 нулевых входов (по всей видимости входов без ожидания в очереди), среднее время проведенное человеком в очереди равно 1.5 минуты. Cont. = 0 говорит нам о том, что на момент окончания моделирования в очереди никого не было.
Ну вот вроде бы все не плохо, но что будет если мы вернемся в сытый 2006
Год и наймем еще 30 сотрудников в наш офис?
Как видно из модели, наш кулер почти перестанет простаивать, а среднее время в очереди составит аж 20 минут, что наводит на мысли либо о том, что нужен второй кулер, либо о том, что пора всех лишать премии за долгие чаепития.
Может быть данная модель, простовата, но даже она при проявлении некоторой фантазии позволяет нам оценить количество кулеров которое необходимо на этаже.
Но на текущий момент мы с вами еще не умеем, разрабатывать многоканальные модели обслуживания. Так убьем же двух зайцев, научимся многоканальному обслуживанию и заодно ответим на вопросов, которым мы с коллегой задались в самом начале статьи. (кто внимательный и помнит — молодец, тому счастья добра и безпохмельных выходных: )
При создании модели операторы call центра и абоненты, зададимся такими условиями
Дано:
2 оператора техподдержки обслуживают пользовталей, которые звонят пимерно раз в две минуты, Если один оператор занят трубку берет другой. Рабочий день составляет 480 минут (8 часов без перерыва на обед так сказать)
Определить:
Коэффициент загруженности сотрудников службы поддержки.
Как и в прошлый раз опишу построчно
В результате получим следующие данные
Структура вывода похожа на структуру вывода первой модели, разве что вместо очереди — накопитель предлагаю вам с ней разобраться самостоятельно. Кстати параметры генерации отчета можно настроить (на этом компьютере у меня не установлен GPSS и нет желания его ставить, поэтому поверьте пока на слово, что в настройках программы есть такая возможность ну, а я если не забуду допишу в понедельник сюда, как это сделать)
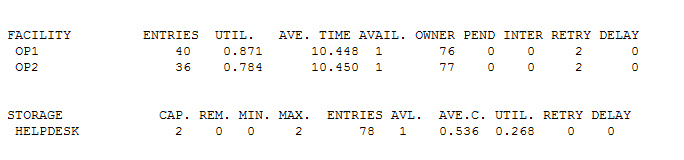
Итак, мы видим, что наши операторы вполне приемлемо загружены примерно на 75% и 87 % соответственно. Будем считать, что двух операторов вполне достаточно, чтобы посоветовать людям как правильно вкрутить лампочку. Но мы же с вами — народ любопытный, давайте посмотрим, что будет если к ребятам подсадить еще одно нахлебника с телефоном.
Для этого рассмотрим немного модифицированную модель. Предлагаю вам разобраться с ней самостоятельно.
Результат под спойлером
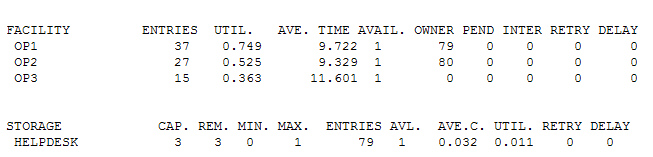
Что же в итоге мы видим, что третий оператор нам явно не нужен и можно смело идти и убирать вакансию, а вместе с ней и всех кандидатов.
На последок хочется вам рассказать о том, что GPSS-WORLD представляет более обширные возможности для моделирования, чем те о которых я вам поведал. Просто ввиду ограниченности моих знаний я не могу вам их адекватно продемонстрировать. Но, тем не менее в качестве бонуса приведу пример работы с переменными
Давайте опять построчно
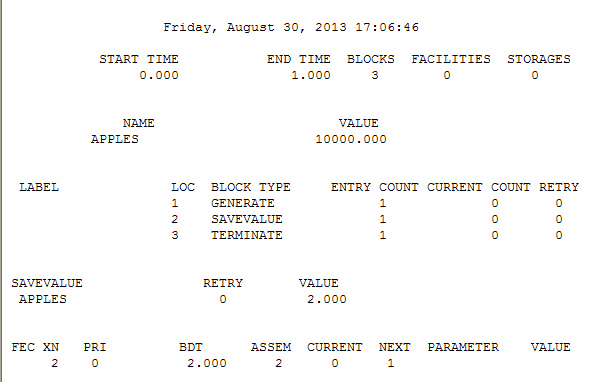
Строка 1 — INITIAL X$APPLES,3 ;1 задаем значение переменной, X$ в данном случае нам как-то указывает на название переменной, а цифра три это значение которое мы запишем в переменю APPLES (кстати я не фанат продукции APPLE просто в тот момент на общем столе лежало 3 яблока, а одно я забрал себе, прям как в детсадовских задачах по математике)
Строка – 2 GENERATE 1 – создадим 1 итерацию
Строка 3 — SAVEVALUE APPLES-,1; – сохраним в переменную яблоки ее значение минус один.
Строки 4-5 помогут нам закончить программу.
Если честно не смотря на то, что данный пример работает и из переменной действительно вычитается единица, полного механизма работы с переменными я не понимаю, поэтому оставлю на откуп профессионалам.
Ну что же теперь вы знаете об одном из инструментов с помощью, которого можно создать имитационную модель процесса, инструмент не самый удобный и уже похоже не дорабатываемый разработчиками, но тем не менее если вы проявите фантазию то за один два дня сможете провести исследование какой-нибудь модели и например опубликовать его в научном журнале или на конференции (об этом я уже писал раньше )
В любом случае теперь у вас есть еще 1 инструмент, чтобы творить, развиваться и делать мир лучше. Право слово это интереснее чем лопать шарике на смартфоне, сидя в общественном транспорте.
Всем хороших выходных, счастья добра и удачи 🙂
Имитационные модели
Имитационная модель воспроизводит поведение сложной системы взаимодействующих элементов. Для имитационного моделирования характерно наличие следующих обстоятельств (одновременно всех или некоторых из них):
· объект моделирования — сложная неоднородная система;
· в моделируемой системе присутствуют факторы случайного поведения;
· требуется получить описание процесса, развивающегося во времени;
· принципиально невозможно получить результаты моделирования без использования компьютера.
Состояние каждого элемента моделируемой системы описывается набором параметров, которые хранятся в памяти компьютера в виде таблиц. Взаимодействия элементов системы описываются алгоритмически. Моделирование осуществляется в пошаговом режиме. На каждом шаге моделирования изменяются значения параметров системы. Программа, реализующая имитационную модель, отражает изменение состояния системы, выдавая значения ее искомых параметров в виде таблиц по шагам времени или в последовательности происходящих в системе событий. Для визуализации результатов моделирования часто используется графическое представление, в т.ч. анимированное.
Детерминированное моделирование
Имитационная модель основана на подражании реальному процессу (имитации). Например, моделируя изменение (динамику) численности микроорганизмов в колонии, можно рассматривать много отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения
и т.д. Эти условия обычно задаются в вербальной форме. Например: по истечении некоторого промежутка времени микроорганизм делится на две части, а по прошествии другого (большего) временноRго отрезка — погибает. Выполнение описанных условий алгоритмически реализуется в модели.
Другой пример: моделирование движения молекул в газе, когда каждая молекула представляется в виде шарика с определенным направлением и скоростью движения. Взаимодействие двух молекул или молекулы со стенкой сосуда происходит согласно законам абсолютно-упругого столкновения и легко описывается алгоритмически. Получение интегральных (общих, усредненных) характеристик системы производится на уровне статистической обработки результатов моделирования.
Такой компьютерный эксперимент фактически претендует на воспроизведение натурного эксперимента. На вопрос: “Зачем это нужно делать?” можно дать следующий ответ: имитационное моделирование позволяет выделить “в чистом виде” следствия гипотез, заложенных в представления о микрособытиях (т.е. на уровне элементов системы), избавив их от неизбежного в натурном эксперименте влияния других факторов, о которых мы можем даже не подозревать. Если такое моделирование включает и элементы математического описания процессов на микроуровне, и если исследователь при этом не ставит задачу поиска стратегии регулирования результатов (например, управления численностью колонии микроорганизмов), то отличие имитационной модели от математической (дескриптивной) оказывается достаточно условным.
Приведенные выше примеры имитационных моделей (эволюция колонии микроорганизмов, движение молекул в газе) приводят к детерминированному описанию систем. В них отсутствуют элементы вероятности, случайности событий в моделируемых системах. Рассмотрим пример моделирования системы, обладающей этими качествами.
Модели случайных процессов
Кому не случалось стоять в очереди и с нетерпением прикидывать, успеет ли он сделать покупку (или заплатить за квартиру, покататься на карусели и т.д.) за некоторое имеющееся в его распоряжении время? Или, пытаясь позвонить по телефону в справочную и натыкаясь несколько раз на короткие гудки, нервничать и оценивать — дозвонюсь или нет? Из таких “простых” проблем в начале XX века родилась новая отрасль математики — теория массового обслуживания, использующая аппарат теории вероятностей и математической статистики, дифференциальных уравнений и численных методов. Впоследствии выяснилось, что эта теория имеет многочисленные выходы в экономику, военное дело, организацию производства, биологию и экологию и т.д.
Компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), играет важную роль. Возможности аналитических методов решения реально возникающих задач массового обслуживания весьма ограничены, в то время как метод статистических испытаний универсален и относительно прост.
Рассмотрим простейшую задачу этого класса. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, то он начинает обслуживать покупателя сразу, если зашло одновременно несколько покупателей — выстраивается очередь. Есть немало других аналогичных ситуаций:
· ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки;
· травмпункт и больные, пришедшие на прием по случаю травмы (т.е. без системы предварительной записи);
· телефонная станция с одним входом (или одной телефонисткой) и абоненты, которых при занятом входе ставят в очередь (такая система иногда практикуется);
· сервер локальной сети и персональные машины на рабочем месте, которые шлют сообщение серверу, способному воспринять разом и обработать не более одного сообщения.
Процесс прихода покупателей в магазин — случайный процесс. Промежутки времени между приходами любой последовательной пары покупателей — независимые случайные события, распределенные по некоторому закону, который может быть установлен лишь путем многочисленных наблюдений (либо для моделирования взят некоторый его правдоподобный вариант). Второй случайный процесс в этой задаче, никак не связанный с первым, — длительность обслуживания каждого из покупателей.
Целью моделирования систем такого вида является получение ответа на ряд вопросов. Относительно простой вопрос — какое в среднем время придется стоять в очереди при заданных законах распределения указанных выше случайных величин? Более сложный вопрос: каково распределение времен ожидания обслуживания в очереди? Не менее сложный вопрос: при каких соотношениях параметров входных распределений наступит кризис, при котором очередь до вновь вошедшего покупателя не дойдет никогда? Если задуматься над этой относительно простой задачей, возможные вопросы будут множиться.
Способ моделирования выглядит в общих чертах так. Используемые математические формулы — законы распределения исходных случайных величин; используемые числовые константы — эмпирические параметры, входящие в эти формулы. Не решается никаких уравнений, которые использовались бы при аналитическом исследовании данной задачи. Вместо этого происходит имитация очереди, разыгрываемая с помощью компьютерных программ, генерирующих случайные числа с заданными законами распределения. Затем производится статистическая обработка совокупности полученных значений величин, определяемых заданными целями моделирования. Например, находится оптимальное количество продавцов для разных периодов времени работы магазина, которое обеспечит отсутствие очередей. Математический аппарат, который здесь используется, называется методами математической статистики.
В статье “Моделирование экологических систем и процессов” 2 описан другой пример имитационного моделирования: одна из многих моделей системы “хищник—жертва”. Особи видов, находящихся в указанных отношениях, по определенным правилам, содержащим элементы случайности, перемещаются, хищники съедают жертв, и те и другие размножаются и т.д. Такая модель не содержит никаких математических формул, но требует статистической обработки результатов.
Пример алгоритма детерминированной имитационной модели
Рассмотрим имитационную модель эволюции популяции живых организмов, известную под названием “Жизнь”, которую легко реализовать на любом языке программирования.
Для построения алгоритма игры рассмотрим квадратное поле из n + 1 столбцов и строк с обычной нумерацией от 0 до n. Крайние граничные столбцы и строки для удобства определим как “мертвую зону”, они играют лишь вспомогательную роль.
Для любой внутренней клетки поля с координатами (i, j) можно определить 8 соседей. Если клетка “живая”, ее закрашиваем, если клетка “мертвая”, она пустая.
Зададим правила игры. Если клетка (i, j) “живая” и ее окружает более трех “живых” клеток, она погибает (от перенаселения). “Живая” клетка также погибает, если в ее окружении находится менее двух “живых” клеток (от одиночества). “Мертвая” клетка оживает, если вокруг нее появляются три “живые” клетки.
Для удобства введем двумерный массив A[0..n, 0..n], элементы которого принимают значение 0, если соответствующая клетка пустая, и 1, если клетка “живая”. Тогда алгоритм определения состояния клетки с координатой (i, j) можно определить следующим образом:
+ А[I + 1, J] + А[I + 1, J + 1] +
Здесь массив B[0..n, 0..n] определяет координаты поля на следующем этапе. Для всех внутренних клеток от i = 1 до n – 1 и j = 1 до n – 1 справедливо сказанное выше. Отметим, что последующие поколения определяются аналогично, стоит лишь осуществить процедуру переприсваивания:
На экране дисплея удобнее выводить состояние поля не в матричном, а в графическом виде.
Осталось лишь определить процедуру задания начальной конфигурации игрового поля. При случайном определении начального состояния клеток подходит алгоритм
Интереснее для пользователя самому задавать начальную конфигурацию, что легко осуществить. В результате экспериментов с этой моделью можно найти, например, устойчивые расселения живых организмов, которые никогда не погибают, оставаясь неизменными или изменяя свою конфигурацию с определенным периодом. Абсолютно неустойчивым (гибнущим во втором поколении) является расселение “крестом”.
Методические рекомендации
В базовом курсе информатики ученики могут реализовать имитационную модель “Жизнь” в рамках раздела “Введение в программирование”. Более основательное освоение имитационного моделирования может происходить в старших классах в профильном или элективном курсе информатики. Далее будет говориться о таком варианте.
Начало изучения — лекция об имитационном моделировании случайных процессов. В российской школе понятия теории вероятностей и математической статистики лишь начинают внедряться в курс математики, и учителю следует быть готовым к тому, чтобы самому сделать введение в этот важнейший для формирования мировоззрения и математической культуры материал. Подчеркнем, что речь идет об элементарном введении в круг обсуждаемых понятий; это можно сделать за 1–2 часа.
Потом обсуждаем технические вопросы, связанные с генерацией на ЭВМ последовательностей случайных чисел с заданным законом распределения. Опираться при этом можно на то, что в каждом универсальном языке программирования есть датчик равномерно распределенных на отрезке от 0 до 1 случайных чисел. На данном этапе нецелесообразно вдаваться в сложный вопрос о принципах его реализации. Опираясь на имеющиеся датчики случайных чисел, показываем, как можно устроить
а) генератор равномерно распределенных случайных чисел на любом отрезке [a, b];
б) генератор случайных чисел под практически любой закон распределения (например, используя интуитивно ясный метод “отбора-отказа”).
Начать рассмотрение описанной выше задачи массового обслуживания целесообразно с обсуждения истории решения проблем массового обслуживания (задача Эрланга об обслуживании запросов на телефонной станции). Затем следует рассмотрение простейшей задачи, которую можно сформулировать на примере формирования и обслуживания очереди в магазине с одним продавцом. Отметим, что на первом этапе моделирования распределения случайных величин на входе можно принять равновероятными, что хоть и не реалистично, но снимает ряд трудностей (для генерации случайных чисел можно просто использовать встроенный в язык программирования датчик).
Обращаем внимание учащихся на то, какие вопросы ставятся в первую очередь при моделировании систем такого вида. Во-первых, это вычисление средних значений (математических ожиданий) некоторых случайных величин. Например, какое среднее время приходится стоять в очереди к прилавку? Или: найти среднее время, проведенное продавцом в ожидании покупателя.
Задача учителя, в частности, состоит в том, чтобы разъяснить, что выборочные средние сами по себе — случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки — не слишком отличающиеся друг от друга). Далее возможны варианты: в более подготовленной аудитории можно показать способ оценивания доверительных интервалов, в которых находятся математические ожидания соответствующих случайных величин при заданных доверительных вероятностях (известными из математической статистики методами без попытки обоснования). В менее подготовленной аудитории можно ограничиться чисто эмпирическим утверждением: если в нескольких выборках равного объема средние значения совпали в некотором десятичном знаке, то этот знак скорее всего верен. Если при моделировании не удается достичь желаемой точности, следует увеличить объем выборки.
В еще более подготовленной в математическом отношении аудитории можно ставить вопрос: каково распределение случайных величин, являющихся результатами статистического моделирования, при заданных распределениях случайных величин, являющихся его входными параметрами? Поскольку изложение соответствующей математической теории в данном случае невозможно, следует ограничиться эмпирическими приемами: построение гистограмм итоговых распределений и сравнение их с несколькими типичными функциями распределения.
После отработки первичных навыков указанного моделирования переходим к более реалистической модели, в которой входные потоки случайных событий распределены, например, по Пуассону. Это потребует от учащихся дополнительно освоить метод генерирования последовательностей случайных чисел с указанным законом распределения.
В рассмотренной задаче, как и в любой более сложной задаче об очередях, может возникнуть критическая ситуация, когда очередь неограниченно растет со временем. Моделирование приближения к критической ситуации по мере возрастания одного из параметров — интересная исследовательская задача для наиболее подготовленных учащихся.
На примере задачи об очереди отрабатываются сразу несколько новых понятий и навыков:
· понятия о случайных процессах;
· понятия и простейшие навыки имитационного моделирования;
· построение оптимизационных имитационных моделей;
· построение многокритериальных моделей (путем решения задач о наиболее рациональном обслуживании покупателей в сочетании с интересами владельца магазина).
Все рекомендации по организационному построению уроков, данные в статье “Математическое моделирование”, в полной мере применимы и в данном случае.