Как сделать инверсию в матлабе

20.03.202313.04.2023 admin 0 Комментариев

Инверсия по методу наименьших квадратов для 2-D

Помогите пожалуйста разобраться с инверсией. Необходимо выполнить инверсию по методу наименьших квадратов для 2-D.
Сначала строю contourf изображение без инверсии:

Как же теперь построить этот же countorf, но с применением инверсии метода наименьших квадратов!?

Буду очень признательна за помощь!!

Нахожение кривой по методу наименьших квадратов
Пожалуйста помогите, написать такую программу, которая способна (1) Используя ginput (), получить.

Графики по методу наименьших квадратов
Здравствуйте. Вылезла ошибка о том, что число с плавающей запятой делится на нуль. Дело в том, что.

Аппроксимация полиномом по методу наименьших квадратов
аппроксимация полиномом по методу наименьших квадратов CLS INPUT “ВВЕДИТЕ СТЕПЕНЬ.

Регрессия 3 порядка по методу наименьших квадратов
реализовать регрессию 3 порядка по методу наименьших квадратов

Я не знаю метода «Инверсии методом наименьших квадратов». Но вот то, что мне удалось нарыть (почти уверен что это не то, что надо) в интернете:

Математическая инверсия —операция, сопоставляющая каждой точке A евклидовой плоскости (в нашем случае наверное пространства), на которой фиксирована окружность (у нас наверное шар) радиуса r с центром O, точку B, «симметричную относительно этой окружности», лежащую на том же выходящем из центра O луче, что и отражаемая точка A, но на тем большем расстоянии от центра O, чем ближе к центру была точка A. |АО|*|ВО|=r^2.

Если нужно это (или близкое к этому) я готов попробовать реализовать.
Просьба, если не трудно, объясните суть метода.

Спасибо за отклик, Алекс!!

Процедура инверсии, которая мне необходима, построена на smoothness-constrained (с ограничениями гладкости) методе наименьших квадратов. Необхлдимо использовать метод наименьших квадратов, основанный на квази-Ньютоновском методе оптимизации. Метод наименьших квадратов smoothness-constrained основан на следующем уравнении
(JTJ + uF)d = JTg
где F = fxfxT + fzfzT
fx = горизонтальный сглаживающий фильтр
fz = вертикальный сглаживающий фильтр
J = матрица частных производных
u = показатель затухания
d = вектор приращений параметров модели
g = вектор невязок

Вот вся информация, которой я пока владею!!
Есть множество литературных источников, но они на английском. При в вводе в гугл
Least square inversion, есть немного о реализации данного метода, но ни примеров, ни кода я не нашла.

Добавлено через 9 минут
Идея метода наименьших квадратов заключается в том, что функцию:

необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений уi. от расчетных Y. была наименьшей.

Источник

Документация

Матрицы в среде MATLAB

Создание матриц

MATLAB имеет много функций, которые создают различные виды матриц. Например, можно создать симметрическую матрицу с записями на основе треугольника Паскаля:

Другим примером является 3 2 прямоугольная матрица случайных целых чисел. В этом случае первый вход к randi описывает область значений возможных значений для целых чисел, и вторые два входных параметров описывают количество строк и столбцов.

Для получения дополнительной информации о создании и работе с матрицами, смотрите Создание, конкатенацию и расширение матрицы.

Добавление и вычитание матриц

Сложение и вычитание требуют, чтобы обе матрицы имели совместимые размерности. Если размерности несовместимы, ошибка заканчивается:

Для получения дополнительной информации см. Массив по сравнению Матричные операции.

Векторные произведения и транспонируют

Если x и y являются оба действительными вектор-столбцами, то продукт x*y не задан, но эти два продукта

Комплексное сопряженное транспонирование z :

Неспрягаемый комплекс транспонирует, где комплексная часть каждого элемента сохраняет свой знак, обозначается z.’ :

Умножение матриц

Прямоугольные умножения матриц должны удовлетворить условия совместимости размерности. Поскольку A имеет размер 3х3, и C 3 2, можно умножить их, чтобы добраться 3 2 результат (общие внутренние отмены размерности):

Однако умножение не работает в обратном порядке:

Можно умножить что-либо со скаляром:

Единичная матрица

Общепринятое математическое обозначение использует прописную букву I, чтобы обозначить единичные матрицы, матрицы различных размеров с единицами на основной диагонали и нулях в другом месте. Эти матрицы имеют свойство, что A I = A и I A = A каждый раз, когда размерности совместимы.

Исходная версия MATLAB не могла использовать I с этой целью, потому что это не различало прописные и строчные буквы, и i уже служил индексом и как комплексной единицей. Таким образом, английская игра слов языка была введена. Функция

возвращает m-by- n прямоугольная единичная матрица, и eye(n) возвращает n-by- n квадратная единичная матрица.

Матричная инверсия

Продукт тензора Кронекера

Кронекеров продукт часто используется с матрицами нулей и единиц, чтобы создать повторенные копии маленьких матриц. Например, если X является матрицей 2 на 2

и I = eye(2,2) является единичной матрицей 2 на 2, затем:

Векторные и матричные нормы

В случаях, где вы хотите вычислить норму каждой строки или столбец матрицы, можно использовать vecnorm :

Используя многопоточное вычисление с функциями линейной алгебры

MATLAB поддерживает многопоточное вычисление во многой линейной алгебре и поэлементных числовых функциях. Эти функции автоматически выполняются на нескольких потоках. Для функции или выражения, чтобы выполниться быстрее на нескольких центральных процессорах, много условий должны быть верными:

Функция выполняет операции, что легко раздел в разделы, которые выполняются одновременно. Эти разделы должны смочь выполниться с небольшой связью между процессами. Они должны потребовать немногих последовательных операций.

Размер данных является достаточно большим так, чтобы любые преимущества параллельного выполнения перевесили время, требуемое разделить данные и управлять отдельными потоками выполнения. Например, большинство функций убыстряется только, когда массив содержит несколько тысяч элементов или больше.

Операция не ограничена памятью; время вычислений не во власти времени доступа к памяти. Как правило сложные функции ускоряют больше, чем простые функции.

Источник

Документация

Обратное быстрое преобразование Фурье

Синтаксис

Описание

Если Y вектор, затем ifft(Y) возвращает обратное преобразование вектора.

Если Y матрица, затем ifft(Y) возвращает обратное преобразование каждого столбца матрицы.

Если Y многомерный массив, затем ifft(Y) обрабатывает значения по первому измерению, размер которого не равняется 1 как векторы и возвращает обратное преобразование каждого вектора.

Примеры

Обратное преобразование вектора

Преобразование Фурье и его обратное преобразование между данными, произведенными во времени и пространстве и данными, производятся в частоте.

Создайте вектор и вычислите его преобразование Фурье.

Заполненное обратное преобразование матрицы

ifft функция позволяет вам управлять размером преобразования.

Создайте случайную матрицу 3 на 5 и вычислите обратное преобразование Фурье с 8 точками каждой строки. Каждая строка результата имеет длину 8.

Спряжение симметричного вектора

Для почти спрягают симметричные векторы, можно вычислить обратное преобразование Фурье быстрее путем определения ‘symmetric’ опция, которая также гарантирует, что выход действителен. Почти спрягайтесь, симметричные данные могут возникнуть, когда расчеты вводят ошибку округления.

Создайте векторный Y это почти сопряжено симметричный, и вычислите его обратное преобразование Фурье. Затем вычислите обратное преобразование, задающее ‘symmetric’ опция, которая устраняет эти почти 0 мнимых частей.

Входные параметры

Y — Входной массив
вектор | матрица | многомерный массив

n — Обратная длина преобразования
[] (значение по умолчанию) | неотрицательный целочисленный скаляр

dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр

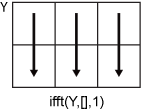
ifft(Y,[],1) возвращает обратное преобразование Фурье каждого столбца.

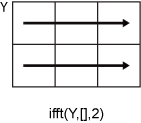
ifft(Y,[],2) возвращает обратное преобразование Фурье каждой строки.

symflag — Тип симметрии
‘nonsymmetric’ (значение по умолчанию) | ‘symmetric’

Больше о

Дискретное преобразование Фурье вектора

W n = e ( − 2 π i ) / n

один из корней из единицы n.

Алгоритмы

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

Выход является комплексным.

Тип симметрии ‘symmetric’ не поддержан.

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Указания и ограничения по применению:

Выход является комплексным.

Тип симметрии ‘symmetric’ не поддержан.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Указания и ограничения по применению:

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Источник

Документация

Инвертируйте порядок элементов

Синтаксис

Описание

Если A вектор, затем flip(A) инвертирует порядок элементов вдоль вектора.

Если A матрица, затем flip(A) инвертирует элементы в каждом столбце.

Примеры

Зеркально отраженный вектор символа

Зеркально отраженная матрица

Зеркально отраженный A не задавая dim аргумент.

Теперь зеркально отраженный A вдоль второго измерения.

Зеркальное отражение массива N-D

Создайте 1 3 2 массивами.

Зеркально отраженный A не задавая dim аргумент.

Теперь зеркально отраженный A по третьему измерению.

Зеркально отраженный массив ячеек

Создайте 3 2 массив ячеек.

Зеркально отраженный A не задавая dim аргумент.

Теперь зеркально отраженный A вдоль второго измерения.

Входные параметры

A — Входной массив
вектор | матрица | многомерный массив | таблица | расписание

Входной массив в виде вектора, матрицы, многомерного массива, таблицы или расписания.

Пример: [1 2 3 4]

Пример: [‘abcde’]

Пример: [1 2; 3 4]

Пример:

Пример: table(rand(1,5),rand(1,5))

dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр

Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.

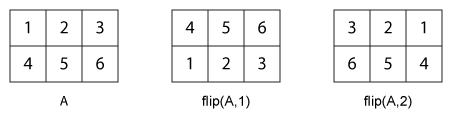
Следующий рисунок показывает различие между dim=1 и dim=2 когда A матрица.

Расширенные возможности

«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Указания и ограничения по применению:

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

Не поддерживает массивы ячеек для первого аргумента.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Смотрите также

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник

Документация