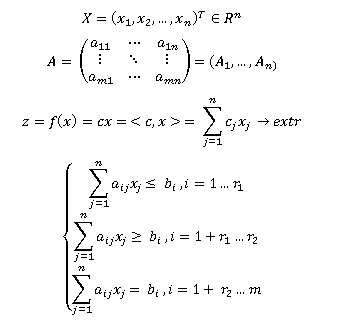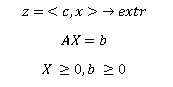Как сделать искусственную общую точку
Подробный разбор симплекс-метода
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
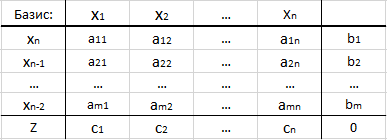
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание: Коэффициенты в строке функционала берутся со знаком “-”.
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение: Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
Условие оптимальности полученного решения:
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Тема: Создаём искусственную точку!
Опции темы
Поиск по теме
Отображение
Создаём искусственную точку!
Давно хотел посоветоваться. Рыбачу на озере с абсолютно ровным дном, ни ям, ни коряг нет, глубина увеличивается очень плавно, в прошлом сезоне облазил всё озеро с эхолотом, ни одной интересной точки. Что, если создать эту точку самому? Хочу весной натаскать на лодке в точку больших веток и затопить их там. Дистанция 120-130м, глубина 3.8-4 м, дно не вонючий ил примерно 5 см. Как думаете если в этом смысл?
присоединяюсь к вопросу,тоже есть водоем,только рельеф немного отличается,там идет резкий свал от берега,а потом ни каких перепадов,иногда местные ставят сети, иногда и бреднем гоняют,думаю может тоже создать рыбе убежище из веток!как это правильно сделать?
Я думаю, смысл есть. По крайней мере сетки там уже не поставят. Была такая мысль сделать то же самое на одном дикарьке. Но льда в этом году толком не было, поэтому ничего не сделал. Как таскать эти коряги по жидкой воде не знаю. Думаю нужно вязать их между собой и потом привязывать надежный груз. Если течения нет, то не унесет, а со временем эти ветки утонут на дно и займут свое место.
Так я сразу там ловить не собираюсь, весной там делать не чего. В течении месяца периодически прикармливать, а в июне уже пробовать ловить. Задача не в том, чтобы приманить карпа, а в том чтобы сделать для него укрытие. А уже потом пытаться его из этого укрытия выманить.
попробую применить ваш совет на практике!
Саша плохого не посоветует, а вообще я с ним согласен меньше браков будет.
значит подожду как потеплеет,и буду строить хату карпам!
Сереж удачи тебе в твоих начинаниян!
спасибо!вам тоже удачи и огромных трофеев!
А за водоёмом наблюдал? Рыб показывался где нибудь? В безветренную погоду утром или вечером места кормления видел?
Наблюдал. Карп если и начинает прыгать, то по всему водоему, определенного места выходов нет.
Тогда искать где кормится. Если долго(много времени проводить на этом водоёме) можно даже определить его маршруты и места где останавливается покушать.
А почему бы просто не затопить корягу? Имхо, деревце 3-4 метра длиной будет самое то. Два-три еще лучше. Он там весь соберется.
Как же так,как? Мы маскируем оснастки, груза под цвет дна, лидкоры, камуфлированные лески, флуорокарбон, крючки с антибликовыми покрытиями, убираем маркер из зоны ловли, а тут целый кусок полиэтилена на дне, да еще и пластиковая бутылка с кирпичем на шнуре?
Квантовая точка — что это такое и как её сделать
Квантовая точка — что это такое и «с чем её едят»
1. Что такое квантовая точка?
1.1. Квантовые точки — искусственные атомы
1.2. Преимущества квантовых точек
2. Как сделать квантовую точку?
2.1. Коллоидные квантовые точки
2.2. Эпитаксиальные квантовые точки
3. Методы компьютерного моделирования квантовых точек
4. Методы характеризации
4.1. Фотолюминесценция
4.2. Рентгеновская дифракция
4.3. Спектроскопия рентгеновского поглощения XANES
5. Источники публикации
Квантовая точка – это нанокристал неорганического полупроводникового материала (кремния, фосфида индия, селенида кадмия). «Нано» – значит измеряющийся в миллиардных долях, размеры таких кристаллов варьируются в пределах от 2 до 10 нанометров. Из-за такого малого размера электроны в наночастицах ведут себя совсем не так как в объемных полупроводниках.
Квантовая точка представляет собой фрагмент проводника или полупроводника (например, CdTe, CdS, CdSe, ZnSe, ZnS и др.), носители заряда которого ограничены в пространстве по всем трем направлениям. Квантовыми их назвали потому, что при столь малых размерах в них проявляются квантовые, то есть, дискретные, свойства электронов.
Физические свойства кристаллов сверхмалых размеров могут принципиально отличаться от массивных кристаллов, например вещество с металлическими свойствами только за счет уменьшения размеров может перейти в диэлектрическое состояние. Уменьшение размеров частиц приводит к увеличению ширины запрещённой зоны. Следовательно, существует возможность варьировать длину волны эмиссии квантовой точки в зависимости от размера частиц. Чем больше радиус частицы, тем меньше излучаемая энергия, тем больше длина волны эмиссии.
Квантоворазмерным эффектом называют изменение термодинамических и кинетических свойств кристалла, когда хотя бы один из его геометрических размеров становится соизмеримым с длиной волны де Бройля электронов.
1. Что такое квантовая точка?
На рисунке 1 представлено строение трехмерной квантовой точки. [4]
Первооткрывателями нанокристаллических полупроводниковых квантовых точек, выполнившими пионерские исследования их электронных и оптических свойств, были наши соотечественники: A. И. Екимов и A. A. Онущенко. В 1981 году они предложили и реализовали первые КТ — микрокристаллы соединений А2B6, сформированные в стеклянной матрице.
Квантовыми точками (КТ) называют частицы с характерными размерами в области наномасштаба — меньше 100 нанометров — во всех трех измерениях, которые содержат электроны проводимости.
При таких размерах квантовая точка уподобляется свойствами атому, ее так часто и называют — искусственный атом. Как известно, в квантовой механике наряду с массой частице присваивается некая длина волны, связанная с ее энергией. В этом проявляется корпускулярно-волновой дуализм. Когда длина волны становится сравнимой с характерными размерами ограничивающего такую частицу пространства, энергетические уровни делаются дискретными, что мы и наблюдаем в атомах и квантовых точках. Благодаря успехам технологии можно получать КТ различного размера, изменяя энергетический спектр. Это дает широкие возможности при формировании наноструктур, в зависимости от поставленных задач. [1]
Рис. 2. Энергетический спектр квантовой точки [3]
Энергетический спектр квантовой точки неоднороден, в нем есть отдельные уровни энергии для электрона (отрицательно заряженной частицы) и дырки. Дыркой в полупроводниках называется незаполненная валентная связь, носитель положительного заряда численно равному электрону, она появляется, когда связь между ядром и электроном разрывается.
Если создаются условия, при которых носитель заряда в кристалле переходит с уровня на уровень, то при этом переходе излучается фотон. Изменяя размер частицы можно управлять частотой поглощения и длиной волны этого излучения. Практически же это значит, что в зависимости от размера частицы точки при облучении они будут светиться разным цветом.
Рис. 3. Изменение цвета (полосы испускания) коллоидного раствора частиц CdSe в оболочке ZnSe в зависимости от размера квантовых точек. [3]
Возможность контролировать длину волны излучения через размер частицы позволяет получать из квантовых точек устойчивые вещества, превращающие поглощаемую ими энергию в световое излучение – фотостабильные люминофоры. [3]
На смену элементам электронных приборов, для которых применимо классическое описание, приходит элементная база наноэлектроники, где необходим последовательно квантовомеханический подход. Квантово-размерные наноструктуры важны не только для наноэлектроники, но и как основа информационных систем нового поколения, они могут применяться для создания магниточувствительных детекторов, на их основе в оптоэлектронике создаются сверхмалые лазерные источники.
Современная субмикронная технология позволяет создавать объекты, в которых движение электронов локализовано в плоскости. Такая ситуация имеет место в полупроводниковых гетероструктурах, на переходе металл-диэлектрик. При приложении достаточно высокого напряжения перпендикулярно слоям гетероструктуры электроны выходят на поверхность и ведут себя как двумерный электронный газ. Если к тому же потенциал ограничивает электроны в одном направлении в плоскости, то электроны могут свободно двигаться только в одном оставшемся — это одномерный газ (квантовые проволоки). Если же ограничивается движение электронов в обоих направлениях, мы получаем квантовую точку. [4. с. 34]
1.1. Квантовые точки — искусственные атомы
Квантовые точки (КТ) — это гигантские (по сравнению с атомами) искусственные атомы с контролируемыми параметрами. Современные технологии позволяют получать и отдельные КТ, и массивы КТ с контролируемыми параметрами, такими как расположение, область локализации, число носителей заряда, крутизна удерживающего потенциала. Если мы сравним КТ и “обычные” атомы, то КТ перспективны из-за возможности управлять их свойствами с помощью магнитного поля (таблица 1). Чтобы значимо изменить свойства обычных атомов, требуются поля, как в нейтронных звездах, а для квантовых точек — вполне доступные в земных лабораториях.
Таблица 1. Сравнение параметров квантовых точек и атомов [4]
Системы же КТ могут рассматриваться как искусственные гигантские молекулы с контролируемо изменяемыми параметрам. Периодические и апериодические массивы КТ — искусственные кристаллы и квазикристаллы.
Рис. 4. Строение двумерной квантовой точки. [4]
Типичный размер квантовой точки — несколько десятков нанометров, однако размер занятой электронами области из-за внешнего потенциала может быть значительно меньше. В такой ситуации становится существенным квантование движения в плоскости границы, так что получается структура, подобная атому (с дискретными уровнями энергии), но роль атомного потенциала выполняет искусственно созданный потенциал квантовой точки, а число электронов может контролируемо изменяться от единиц до нескольких сотен. [4, с. 34]
1.2. Преимущества квантовых точек
Растворы на основе квантовых точек превосходят традиционные органические и неорганические люминофоры по ряду параметров, важных для тех областей практического применения, в которых необходима точная перенастраиваемая люминесценция.
Квантовые точки — фотостабильные люминофоры
• Фотостабильны, сохраняют флуоресцентные свойства в течение нескольких лет.
• Высокая стойкость к фотовыцветанию: в 100 – 1000 раз выше, чем у органических флуорофоров.
• Высоких квантовый выход флуоресценции – до 90%.
• Широкий спектр возбуждения: от УФ до ИК (400 – 200 нм).
• Высокая чистота цвета из-за высоких пиков флуоресценции (25-40 нм).
• Высокая устойчивость к химической деградации.
Еще одним преимуществом, в особенности для полиграфии, является то, что на основе квантовых точек можно делать золи – высокодисперсные коллоидные системы с жидкой средой, в которой распределены мелкие частицы. А значит из них можно производить растворы, пригодные для струйной печати. [3]
Другое не менее важное свойство квантовой точки связано с проявлением дискретности заряда при протекании электрического тока через замкнутую цепь, включающую КТ. При уменьшении размеров квантовой точки увеличивается энергия, необходимая для переноса на нее единичного заряда (вследствие уменьшения емкости КТ пропорционально ее характерному размеру). Это приводит к явлению осцилляции, то есть колебания тока при протекании через КТ, период которых определяется переносом единичного заряда в квантовой точке, что открывает путь к управлению током с точностью до отдельного электрона. Сегодня подобные исследования составляют отдельное направление — одноэлектронику. [1]
2. Как сделать квантовую точку?
Квантовые точки можно получать двумя методами: с помощью коллоидного химического синтеза и эпитаксиальных технологий. Оба способа дают широкие возможности как в получении КТ на основе различных полупроводниковых материалов, так и КТ с различной геометрией. [1]
Достоинства каждого метода — более простого химического синтеза коллоидных и достаточно сложного и дорогостоящего метода роста эпитаксиальных КТ — находят применение в решении различных задач полупроводниковой электроники. [1]
В настоящее время наибольший интерес вызывают гетеронаноструктуры с квантовыми точками на основе арсенида галлия (GaAs) или его твердых растворов разного состава. Основное техническое применение квантово-размерных структур этого типа видится в настоящее время в разработках светоизлучающих приборов, прежде всего лазеров для волоконно-оптических линий связи. Также значительные возможности дает допирование структур на основе полупроводников переходными металлами.
Различие постоянных кристаллических решеток гетеропары, обычно считавшееся ее недостатком, оказалось весьма ценным свойством в технологии получения так называемых самоорганизованных квантовых точек. Под самоорганизацией понимается самопроизвольное возникновение упорядоченных макроскопических структур из менее упорядоченной среды. В основе процесса самоорганизации лежит свойство неравновесных физических систем при приближении к термодинамическому равновесию переходить в состояние, в котором свободная энергия системы минимальна.
Если на поверхности из материала А осажден тонкий однородный слой материала В, то при установлении термодинамического равновесия в слое В возникает атомная структура, и он имеет форму, при которой свободная энергия системы будет минимальна. Факторами, определяющими направление и конечный результат самоорганизации, являются рассогласование постоянных решеток материалов А и В, создающее упругие напряжения в системе и повышающее ее внутреннюю энергию, толщина слоя и некоторые другие. При одних значениях этих параметров может образоваться однородный слой материала В, повторяющий структуру подложки. При других значениях может оказаться более энергетически выгодным, чтобы материал В образовал массив напряженных кластеров определенных размеров и формы или собрался в один большой кластер.
Экспериментально уже давно установлено, что при осаждении из паровой фазы наблюдаются три типа начальной стадии роста слоя на подложке:
1) послойный (двумерный) рост. Он происходит, если материал В смачивает подложку и его постоянная решетки мало отличается от постоянной решетки материала А; [4, с. 34]
2) островковый (трехмерный) рост слоя. Он имеет место при плохом смачивании;
3) промежуточный механизм роста, при котором сначала происходит послойный рост слоя В, который затем сменяется островковым ростом. Этот механизм наблюдается при наличии смачивания и значительном рассогласовании решеток А и В.
Последний механизм используется для получения самоорганизующихся квантовых точек в системе InGaAs/GaAs. Самый важный результат изучения данного механизма — возможность получения массива однородных по размерам, бездефектных, напряженных нанокластеров InGaAs в матрице GaAs, обладающих свойствами квантовых точек.
Часто применяется получение массивов квантовых точек с помощью молекулярно-лучевой эпитаксии, основанное на использовании самосогласованного роста по механизму Странского-Крастанова. Но квантовые точки, полученные в таком процессе, оказываются значительно напряженными. Это приводит к существенным сдвигам спектра электронных состояний и к изменению управляющих параметров.
В зависимости от условий создания квантовых точек могут быть использованы различные виды представления удерживающего потенциала.
Рис. 5. Изменения состояния системы [4]
Для круглой квантовой точки возможно представление потенциала в виде: 
Это достаточно адекватно для не слишком больших квантовых точек. Для больших квантовых точек адекватна модель “жестких стенок”. Но и в том, и в другом случае получается дискретный энергетический спектр, как у атома.
Возможности управлять состоянием отдельных квантовых точек и систем квантовых точек и методы воздействия, схематически изображены на рисунке 5. [4, с. 35]
2.1. Коллоидные квантовые точки
Коллоидные КТ представляют собой полупроводниковые нанокристаллы чаще всего сферической (иногда — эллиптической или более сложной) формы, которые покрывает монослой стабилизатора из органических молекул. [1]
2.1.1. Методы получения коллоидных квантовых точек
В настоящее время для получения квантовых точек существует много различных химических и физико-химических методов синтеза, где отдельные атомы или ионы объединяются в кластеры или наночастицы. На сегодняшний день широко применяются три способа получения квантовых точек: метод электронно-лучевой эпитаксии, мосгидридная газофазовая эпитаксия, метод коллоидного синтеза. Получаемые такими методами частицы имеют узкое распределение по размерам, заданную форму и структуру и воспроизводимыми результатами от синтеза к синтезу. [2]
Метод коллоидного синтеза будет рассмотрен более подробно, потому что он представляет наибольший интерес и с научной, и с производственной точек зрения.
2.1.2. Методы молекулярно-лучевой и мосгидридной газофазовой эпитаксии
Одним из эффективных способов изготовления размерно-ограниченных структур является молекулярно-лучевая эпитаксия. Она представляет собой совершенную технологию выращивания монокристаллических слоев с контролем толщины на уровне атомных размеров, которая позволяет создавать абсолютно новые структуры и приборы. Ее отличие заключается в высоком уровне контроля условий конденсации атомов или молекул и возможности управлять этим процессом с большой точностью.
На полупроводниковую подложку напыляют с высокой точностью слои из другого полупроводника, и по мере наращивания слоев атомы начинают собираться в кластеры, так как при существенном отличии параметра кристаллической решетки подложки от параметра выращиваемого кристалла более энергетически выгодным является образование островков, нежели равномерная поверхность с однородным натяжением.
В последние годы было обнаружено, что при пониженных температурах роста при монослойном росте полупроводника с параметрами кристаллической решетки, отличающимися от параметров решетки подложки, можно получить на поверхности роста почти одинаковые по размеру островки. Островки осаждаемого полупроводника пирамидальной формы практически не содержат дефектов, представляют собой квантовые точки. Движущей силой образования квантовых точек в процессе самоорганизации является уменьшение энергии деформации.
Так, если на подложке из арсенида галлия растить слой арсенида индия, параметры решетки которого больше, то возникнут упругие напряжения, приводящие к росту островков (квантовых точек) InAs на поверхности GaAs. Поверхность покрывается пирамидками InAs с размерами в несколько десятков ангстрем. Оказывается более выгодным формирование островков по сравнению с однородно-напряженной поверхностью. Рост пирамид происходит до полного снятия упругого напряжения на вершине пирамиды.
Благодаря этому стало возможным изготавливать СВЧ и оптические приборы, требующие высокой точности исполнения.
Преимуществом данного метода является возможность создания строго упорядоченных квантовых точек одинаковых размеров и даже их горизонтальных и вертикальных массивов. Однако, существуют и недостатки этого метода: пирамидальная форма не может быть описана моделью шарообразных объектов, а, значит, становится невозможным рассматривать данные структуры как атомоподобные с высокой точностью. Кроме того, такой метод очень сложен и дорог в исполнении.
Рис. 6. Монослойный рост островков пирамидальной формы. [2]
В методе газофазовой эпитаксии на кристаллическую подложку осаждается требуемое вещество, получаемое из газовой фазы в результате химической реакции.
Если осаждать вещество в несколько монослоев, то можно получить поверхность, которую будут покрывать пирамидки — квантовые точки (рис. 6).
Причина их образования – та же самая, что и при росте с помощью молекулярно – лучевой – эпитаксии – уменьшение энергии системы за счет уменьшения энергии упругой деформации. [2]
2.1.3. Метод коллоидного синтеза
Для синтеза коллоидных квантовых точек используются химические методы, основанные на росте нанокристаллов. Это могут быть подходы, основанные как на “дроблении” вещества (сверху-вниз), так и на “выращивании” нанокристаллов (снизу-вверх).
Традиционным методом получения квантовых точек является метод синтеза в неполярных средах (или металлоорганического синтеза). Путь синтеза коллоидных квантовых точек лежит через создание монодисперсных коллоидных растворов первого типа – суспензоидов (иногда их также называют необратимыми или лиофобными коллоидами) методом конденсации фазы из пересыщенного раствора. Коллоидные частицы при этом имеют характерную кристаллическую структуру и высокое стремление к агрегации.
Коллоидный метод относится к методам зернового роста и позволяет сильно варьировать концентрации коллоидных частиц в растворе. В органический растворитель вводят растворы из элементов II и IV групп таблицы Менделеева, которые осаждаются на молекулах растворителя. При проведении таких реакций необходимо тщательно соблюдать ряд параметров, таких как уровень pH и концентрация ряда органических соединений в системе, так как это существенным образом влияет на размеры частиц в коллоиде. За счет разделения этапов нуклеации и роста во времени технология позволила впервые осуществить синтез растворов коллоидных квантовых точек с относительно высокой степенью монодисперсности и квантовым выходом (более 9 %).
Синтез квантовых точек данным методом происходит в несколько этапов:
1) Нуклеация.
2) Рост зародышей.
3) Стадия созревания Оствальда.
Рассмотрим более подробно, как происходит процесс синтеза.
2.1.3.1. Стадия нуклеации
Рис. 7. Изменение концентрации конденсирующегося вещества на этапах нуклеации и роста из сильно пересыщенного раствора. [2]
Согласно классической теории зародышеобразования нуклеация происходит спонтанно: в некоторых нестабильных участках пересыщенного раствора молекулы или ионы растворённого вещества сами по себе способны кристаллизоваться, образуя зародыши (рис. 7). [2]
2.1.3.2. Стадия роста зародышей
Коллоидная теория при интерпретации явлений, связанных с ростом кристаллов, исходит из связи между формой кристалла и поверхностной энергией всех его граней. Согласно диффузионной трактовке роста кристаллов, процесс образования кристаллической грани протекает с большой скоростью и зависит только от скорости диффузии. Поскольку процесс является диффузионным, основным параметром для его регулирования является температура. [2]
2.1.3.3. Стадия созревание Оствальда
Когда реагенты исчерпаны из-за роста частиц начинается процесс созревания Оствальда, при котором большие частицы продолжают расти за счёт растворения более мелких, уменьшая поверхностную энергию системы. При этом происходит дефокусировка. При уменьшении степени пересыщения критический размер зародышей растет, и частицы меньше этого критического размера растворяются. Если реакцию быстро остановить на этой стадии частицы будут иметь широкое распределение по размерам. На этапе созревания Оствальда невозможно получить монодисперсные частицы. Размер оставшихся после полного исчезновения пересыщения частиц может достигать микрометров, поэтому нанокристаллы с хорошим распределением по размерам можно получить лишь при взрывной нуклеации и остановке реакции быстро после ее окончания и до начала созревания Оствальда. Для взрывной нуклеации необходимо создавать высокую степень пересыщения. [2]
2.2. Эпитаксиальные квантовые точки
Эпитаксиальные КТ формируются в два этапа. На первом происходит зарождение и последующий рост ансамбля самоорганизующихся при гетероэпитаксии нанокристаллов (чаще всего пирамидальной формы). На втором — их заращивание материалом подложки в условиях роста кристаллической структуры. В результате нанокристаллы — квантовые точки оказываются встроенными в кристаллическую матрицу подложки и находятся в поле упругих деформаций.
Наиболее часто используются такие полупроводниковые материалы, как: InAs (арсенид индия), InSb (антимонид индия), PbSe (селенид свинца), PbS (сульфид свинца), InP, ZnSe (фосфид индия — селенид цинка), ZnTe, CdS (теллурид цинка — сульфид кадмия), CdSe (селенид кадмия), ZnS, HgTe (сульфид цинка — теллурид ртути), HgSe (селенид ртути), ZnO (оксид цинка), TiO2 (оксид титана). [1]
3. Методы компьютерного моделирования квантовых точек
Одна из основных целей компьютерного моделирования нанообъектов состоит в построении структуры и визуализации нанообъекта, описании характера связи в квантовых точках, расположения атомов, соответствующего самой низкой потенциальной энергии системы.
Особый интерес вызывают квантовые точки на основе халькогенидов кадмия, в частности, на основе теллурида кадмия, благодаря наличию у них целого ряда уникальных свойств и возможности их применения в нанофотонике, фотовольтанике, нанобиологии и наномедицине. Существенно расширить возможности применения квантовых точек можно с помощью их допирования атомами различных типов. В последнее время внимание исследователей привлекли квантовые точки, допированные атомами переходных элементов, имеющие магнитные свойства.
Важным шагом на пути понимания фундаментальных характеристик квантовых точек является установление взаимосвязи особенностей их локальной атомной структуры и электронного строения. Для этой цели хорошо применять точные методики, позволяющие получать информацию об атомной и электронной структурах частиц небольшого размера.
На сегодняшний день разработано большое количество методов моделирования и расчета структуры и свойств нанообъектов. Их условно можно разделить на три группы: ab initio (первопринципные), полуэмпирические методы и эмпирические потенциалы. Все они отличаются необходимыми исходными данными. [2]
4. Квантовая точка. Методы характеризации
Ниже рассмотрены некоторые методы характеризации квантовых точек, такие как фотолюминесценцию, рентгеновскую дифракцию, спектроскопию рентгеновского поглощения.
4.1. Фотолюминесценция
Рис. 8. Фотолюминесценция полупроводниковых нанокристаллов. [2]
Механизм люминесценции в твердом теле различается в зависимости от того, происходит она с участием электронной подсистемы всего кристалла или же внутри примесного центра. Что касается первого типа, межзонной люминесценции, обусловленной электронными переходами между валентной зоной и зоной проводимости, то она уже хорошо и подробно изучена. Однако с уменьшением размеров светоизлучающих нанокристаллов роль межзонной люминесценции заметно снижается – начинает доминировать примесная люминесценция, обусловленная электронными переходами между зонами и донорно-акцепторными уровнями примесных и поверхностных атомов.
Полупроводниковые квантовые точки являются уникальной оптической усиливающей средой, длина волны люминесценции которой зависит от размера квантовой точки. Это дает возможность подстраивать длину волны люминесценции квантовой точки к положению запрещенной зоны фотонного кристалла. Таким образом, возможно организовать лазерный резонатор с трехмерной распределенной обратной связью. [2]
Рис. 9. Изменение спектра светимости коллоидной квантовой точки в зависимости от размера. [2]
4.2. Рентгеновская дифракция
Информация о фазовом составе, а также о среднем размере нанокристаллов может быть получена методом рентгеновской дифракции. Для частиц нанометрового размера рефлексы отражений на дифрактограмме будут уширены. Величина уширения связана со средним размером нанокристаллов (точнее, областей когерентного рассеяния) по формуле Дебая-Шерера. [2]
4.3. Спектроскопия рентгеновского поглощения XANES
Физико-химические свойства соединений в конденсированном состоянии определяются их электронно-энергетическим строением, которое в значительной степени зависит от локальной структуры исследуемого образца. В последнее время важным инструментом для исследования тонких деталей наноразмерной атомной структуры малых квантовых частиц становится спектроскопия рентгеновского поглощения в ближайшей к краю области (XANES-X-ray absorption near edge structure) [8].
XANES-спектроскопия позволяет с высокой точностью получать информацию об электронном строении и трехмерной атомной структуре вокруг исследуемого типа атомов в материалах, в том числе и без дальнейшего порядка в расположении атомов. На основе XANES – спектроскопии длины связей могут быть определены с точностью до 0,001 нм, а углы связей – с точностью до нескольких градусов. Однако XANES – спектроскопия – непрямой метод исследования. Для выделения структурной информации требуется проведение расчетов спектров для структурных моделей, в том числе с использованием суперкомпьютеров и вычислительных кластеров.
Читать или скачать эту статью в формате PDF
Также по теме читайте продолжение этой статьи:
Для экспериментальной регистрации спектров рентгеновского поглощения обычно используется комплекс аппаратуры, основными компонентами которого являются источник излучения, диспергирующий элемент (кристалл или дифракционная решетка) и регистрирующее устройство. Одним из распространенных типов детекторов в настоящее время является полупроводниковые датчики, в том числе построенные в виде координатно- чувствительных детекторов. Они обладают высокой чувствительностью и в комплексе с компьютерной техникой позволяют наблюдать регистрируемый рентгеновский спектр непосредственно во время эксперимента.
К разрешающей способности установки предъявляют высокие требования, это связано с тем, что необходимая структурная информация может быть получена из незначительного изменения энергетического положения относительно интенсивности. [2]
5. Источники публикации
1. Наночастицы с огромным потенциалом [В Интернете] / авт. Двуреченский Анатолий Васильевич // Науки в Сибири. – издание Сибирского отделения РАН, 01 11 2018 г.. – 05 06 2020 г.. – http://www.sbras.info/articles/science/nanochastitsy-s-ogromnym-potentsialom
2. Полупроводниковые коллоидные квантовые точки [Электронное учебное пособие] / авт. Грибкова Н. С. Лесняк В. И.. – Ростов-на-Дону : Южный федеральный университет ; Международный исследовательский центр “Интелектуальные материалы”, 2017 г. http://sneg5.com/wp-content/uploads/2-Полупроводниковые-коллоидные-КТ-5_уч-пособие_ЮФУ_2017.pdf
3. Квантовые точки: полиграфия и другие области применения [В Интернете] / авт. Ольга Филатова // Печатник.com — полиграфический портал. – 08 12 2016 г.. – 05 06 2020 г.. – https://pechatnick.com/articles/kvantovie-tochki-poligrafiya-i-drygie-oblasti-primeneniya
4. Микроэлектроника переходит на квантовые точки [Журнал] / авт. Капуткина Наталия, Алтайский Михаил // Коммерсантъ-Наука. – Москва : АО «Коммерсантъ», 30 11 2015 г.. – № 7. – стр. 34-36.
5. Квантовые точки — что это такое [Видео] Канал администратора общественно-образовательного портала SNEG5.com https://youtu.be/XkJLgQuNfXo
6. Квантовые точки — светодиоды и краски [Видео] Канал администратора общественно-образовательного портала SNEG5.com https://youtu.be/rfTGFsFWPp8
Литература по теме «Квантовая точка»
1. Марков, С.А. Органический синтез коллоидных квантовых точек / С.А. Марков // Окно в микромир. – 2002. – № 4. – С. 18-24.
2. Козлова, М.В. Диссертация на соискание ученой степени кандидата физико- математических наук. Особенности нелинейного поглощения при резонансном одно- и двухфотонном возбуждении экситонов в коллоидных квантовых точках CdSe/ZnS / М.В. Козлова. – Москва, 2015.
3. Ненашев, А.В. Диссертация на соискание ученой степени кандидата физико-математических наук. Моделирование электронной структуры квантовых точек / А.В. Ненашев. – Новосибирск, 2004.
4. Кравцова, А.Н. “In silico исследование атомной и электронной структуры квантовых точек CdTe, допированных атомами редкоземельных элементов” / А.Н Кравцова, А.В. Солдатов, С.А. Сучкова, // Журнал структурной химии. – 2016. – Т. 57, № 3. – С. 508 – 514.
5. Кравцова, А.Н. Допированные квантовые точки семейства CdTe / А.Н Кравцова, А.В. Солдатов, С.А. Сучкова, К.А. Ломанченко, И.А. Панкин, М.Б. Файн, А.Л. Бугаев // Известия РАН. Серия физическая – 2015. – Т. 79, № 11. – С. 1612-1611.
7. Васильев, Р.Б. Методические материалы. Квантовые точки: синтез, свойства, применение // Р.Б. Васильев, Д.Н. Дирин. – М: ФНМ МГУ, 2007.
8. Солдатов, А.В. Методические указания по курсу “Спектроскопия рентгеновского поглощения”. Часть II / А.В. Солдатов. – Ростов-на-Дону. – 2011.