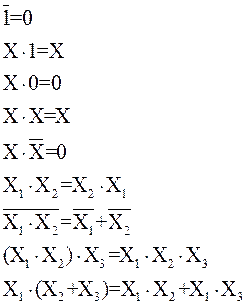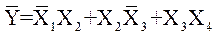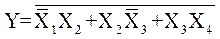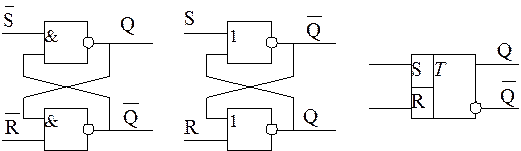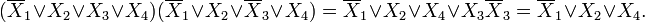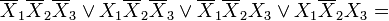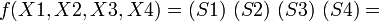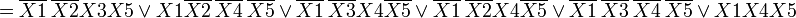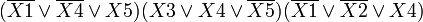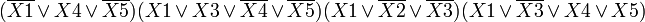Как сделать карту карно
Составить карту Карно
Цель работы
Цель работы – ознакомление с характеристиками основных логических элементов цифровой схемотехники и изучение методов синтеза комбинационных схем.
Логические элементы оперируют с сигналами, которые могут принимать значения только двух уровней – высокого и низкого (нулевого). Обычно сигнал высокого уровня обозначают единицей, низкого уровня – нулем. Для описания поведения логических схем используют специальный раздел алгебры – алгебру логики, или булеву алгебру.
Все переменные в алгебре логики могут принимать два значения – “0” и “1”. Наиболее важными функциями алгебры логики являются функции И, ИЛИ, НЕ.
Функция И называется логическим умножением (X1·X2) и для двух аргументов описывается табл. 1.
| Таблица 1 | Таблица 2 | Таблица 3 | |||||
| Х1 | Х2 | (Х1 Х2) | Х1 | Х2 | (Х1 + Х2) | X |  |
Как видно из таблицы, X1·X2 равно 1 только тогда, когда и аргумент X1, и аргумент X2 принимают значения 1.
Функция ИЛИ называется логическим сложением (X1+X2) и для двух аргументов описывается табл. 2.
Как видно из этой таблицы, (X1+X2) равно 1 тогда, когда или аргумент X1, или аргумент X2 принимает значение 1.
Функция НЕ – это логическая функция одного аргумента. Она также называется логическим отрицанием X и описывается комбинационной табл. 3.
Логическая функция одного аргумента описывается комбинационной таблицей из 2 строк, двух аргументов – таблицей из 4 строк, n аргументов – комбинационной таблицей из 2 n строк.
Логическая функция многих аргументов, описывающая соответствующую комбинационную схему, может определяться не только комбинационной таблицей, но и выражением, включающим в себя определенные выше логические функции, например:
При подстановке в выражение (1) значений аргументов определяется значение функции, например: при X1=0, X2=1, X3=1, X4=1
| f(0, 1, 1, 1)=(0+0)(1+1)+1×1×1=0×1+1=0+1=1 |

|
Синтез выражения логической функции
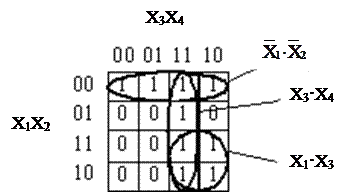
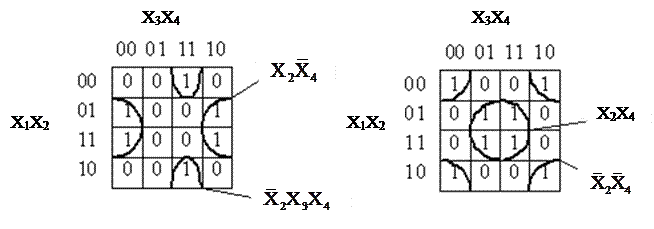
Логические функции с числом переменных не более четырех удобно определять с помощью так называемой карты Карно – формы представления комбинационной таблицы в виде матрицы, строки и столбцы которой соответствуют определению комбинации одной или двух переменных. Например, логическая функция (1), определяемая комбинационной табл. 4, представляется картой Карно (рис. 1).
| Таблица 4 | ||||
| X1 | X2 | X3 | X4 | Y |
| X3X4 |
 X1X2 X1X2 |
Р и с. 1. Карта Карно для функции, представленной табл. 4
Карты Карно удобно использовать при синтезе выражения логической функции, задаваемой комбинационной таблицей.
В одном из методов синтеза выражения рассматриваются элементы, содержащие логическую “1”. Если выбрать на карте Карно достаточное количество групп так, чтобы каждый элемент с логической “1” вошел хотя бы в одну группу, то выражение логической функции может быть определено путем использования функции ИЛИ над функциями И, соответствующими выбранным группам. Разумно выбирая группы, можно получать простые выражения. При выборе группы следует руководствоваться следующими принципами: группа должна быть как можно меньше.
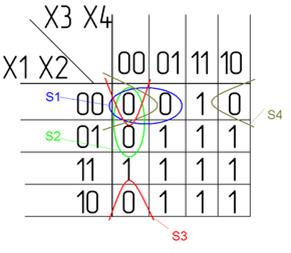
Для приведенного выше примера группы могут быть выбраны в соответствии с рис. 2:
Р и с. 2. Выбор групп на карте Карно для функции,
представленной в табл. 1
В данном случае выбраны три группы
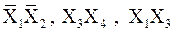
Легко убедиться, что функция принимает единичное значение при X1=0, X2=0 (первая группа); при X3=1, X4=1 (вторая группа); при X1=1, X3=1 (третья группа).
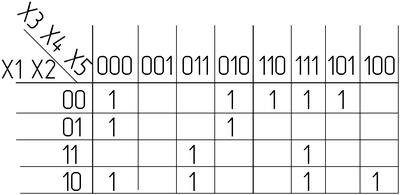
Выражение, описывающее логическую функцию (1), имеет вид:
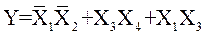
Выбирая группы, необходимо иметь в виду, что крайние столбцы Карно (левый и правый) являются соседними, поскольку Карно является разверткой на плоскость поверхности пространственной фигуры. То же самое можно сказать и про крайние строки (верхнюю и нижнюю).
В этом случае группы могут быть “разорванными” (рис. 3).
Функции, представленные картами на рис. 3, а и рис. 3, б определяются выражениями соответственно
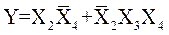
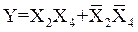
Р и с. 3. Пример карт Карно с разорванными группами
В другом методе синтеза выражения для инверсии логической функции выбираются группы с элементами, содержащими 0.
При выборе групп и синтеза выражения руководствуются принципами, приведенными выше. В качестве примера рассмотрим функцию, представленную картой на рис. 4.
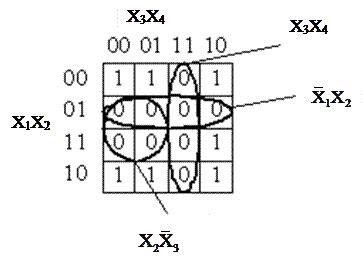 |
Р и с. 4. Карта Карно для функции, содержащей нули в группах
Выражение для инверсии логической функции имеет вид:
Отсюда определяется выражение логической функции
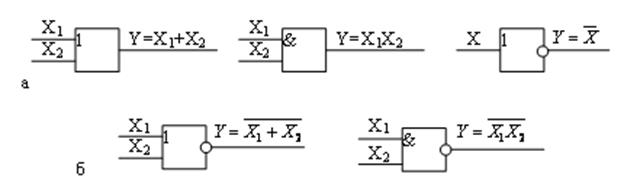
Полученные выражения для логических функций могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ. Обозначения этих элементов на схемах приведены на рис. 5.
Р и с. 5. Обозначение логических элементов:
а – ИЛИ, И, НЕ; б – ИЛИ–НЕ, И–НЕ
Наибольшее распространение получили элементы, реализующие комбинированные функции И–НЕ, ИЛИ–НЕ (рис. 5, б).
При объединении входов любой из этих элементов реализует функцию НЕ. Для рационального построения комбинационной схемы, реализующей синтезированное выражение логической функции и выполненной на элементах И–НЕ, ИЛИ–НЕ, следует преобразовать полученное выражение с использованием теорем (2) таким образом, чтобы оно содержало максимальное количество операций
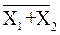
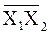
Например, выражение (3) может быть преобразовано следующим образом:
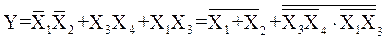
Последнее преобразование следует из теоремы
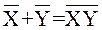
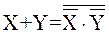
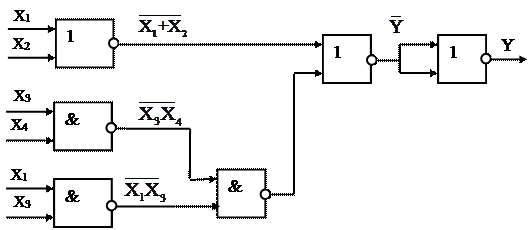
Комбинационная схема, реализующая выражение (3), может иметь вид, представленный на рис. 6.
Р и с. 6. Комбинационная схема, реализующая выражение (3)
Одним из наиболее распространенных узлов вычислительных устройств является триггер – схема с двумя устойчивыми состояниями. Триггер имеет два выхода (прямой Q и инверсный 

Триггеры бывают асинхронные (меняющие свое состояние непосредственно при изменении сигналов на информационных входах) и тактируемые, которые могут менять свое состояние только при поступлении на тактовый вход тактирующего сигнала.
Основным типом триггера является триггер SR-типа, имеющий два входа – S (прямой) и R (инверсный). Работа SR-триггера описывается табл. 5.
| Таблица 5 | ||
| Sn | Rn | Qn+1 |
| X |
SR-триггер реализует уравнение
При поступлении в n-й момент времени на входы S, R нулевых сигналов триггер не меняет своего состояния (Qn+1= Qn), при поступлении на вход S единичного сигнала триггер устанавливается в единичное состояние, при подаче на вход R единичного сигнала триггер устанавливается в нулевое состояние. Комбинация сигналов R=1, S=1 является запрещенной, при подаче такой комбинации на входы триггер устанавливается в неопределенное состояние X.
Схемы SR-триггера, выполненные на логических элементах, и его обозначение представлены на рис. 7.
Р и с. 7. Схемы SR-триггера и его обозначение
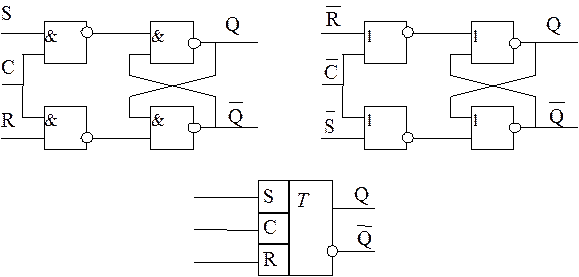
Тактируемые SR-триггеры имеют на входах схемы для разрешения записи информации. Схемы тактируемого SR-триггера, выполненные на логических элементах, а также его условное изображение представлены на рис. 8.
Тактируемый SR-триггер (SRT-триггер) имеет тактовый вход С.
Триггер D имеет один информационный вход D и устанавливается в состояние, соответствующее информации на этом входе: Qn+1=Dn.
Наиболее распространены тактируемые D-триггеры. Схемы таких триггеров и их условное изображение представлены на рис. 9.
Счетный триггер имеет счетный вход С и меняет свое состояние каждый раз, как только на счетном входе появляется единичный сигнал С:
Счетный триггер может быть построен на основе тактируемого D-триггера (рис. 10).
Р и с. 8. Схемы тактируемого SR-триггера и его обозначение
Р и с. 9. Схемы тактируемого D-триггера
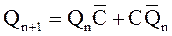
Р и с. 10. Схема счетного триггера
Универсальный JK-триггер имеет информационные входы J, K и тактовый вход С. При комбинации сигналов
JK-триггер ведет себя как счетный триггер, т.е. меняет свое состояние на противоположное:
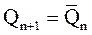
При всех других комбинациях сигналов JK-триггер ведет себя аналогично SR-триггеру (J
R). JK-триггер чаще всего строится по схеме “M-S” (основной-вспомогательный) на основе двух тактируемых SR-триггеров (рис. 11).
При поступлении тактового сигнала на вход С основной триггер “М” воспринимает информацию, подаваемую на входы J, K, затем при поступлении тактового сигнала на вход С2 вспомогательный триггер “S” фиксирует свое состояние. Часто тактовый сигнал С2 определяется инверсией тактового сигнала С1: 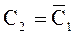
Р и с. 11. JK-триггер, выполненный по схеме “M”-“S”, и его обозначение
При использовании пунктирных связей, изображенных на рис. 11, JK-триггер работает как счетный. Обозначение триггера также приведено на рис. 11.
Дешифраторы и шифраторы
Дешифраторы – схемы, преобразующие код из одного вида в другой, например, двоичный код в десятичный.
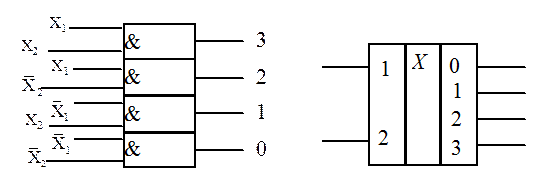
Схема такого дешифратора (рис. 12) может быть легко построена на основе комбинационной табл. 6, в которой представлена функция такого преобразования.
Условное обозначение такого дешифратора также изображено на рис. 12.
| Таблица 6 | ||||
| X1 | X2 | 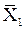 | 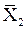 | Y |
Р и с. 12. Схема и условное обозначение дешифратора,
реализующего функцию табл. 6
Шифратор выполняет функцию, обратную дешифратору, например, преобразует унитарный код в двоичный.
Схема шифратора строится на основе комбинационной таблицы преобразования кодов. Для преобразования кодов, соответствующего табл. 6, схема шифратора может иметь вид, изображенный на рис. 13.
Р и с. 13. Схема шифратора, реализующего функцию в табл. 6
2. Описание лабораторного макета
На лицевой панели лабораторного макета размещены условные изображения 4-х логических двухвходовых схем И–НЕ и 4-х логических двухвходовых схем ИЛИ–НЕ, а также входов и выходов этих схем.
Имеются также выводы постоянных сигналов, соответствующих логическим “0” и “1”.
Макет содержит также формирователь одиночных импульсов, управляемый кнопкой, размещенной в нижней части лицевой панели. Здесь же размещены выводы двухфазного выхода формирователя. В правой части лицевой панели размещены выводы, к которым подключается напряжение питания.
К макету прилагается отдельный блок цифрового коммутатора, в котором имеется генератор прямоугольных импульсов с частотами 100 кГц, 50 кГц, 10 кГц, 5 кГц, 2,5 кГц, а также электронный 8-канальный коммутатор для осциллографа.
| 50 кГц | t |
| 10 кГц | t |
| 5 кГц | t |
| 2,5 кГц | t |
Р и с. 14. Диаграммы сигналов на выходах генератора цифрового коммутатора
Диаграммы сигналов на выходах генератора изображены на рис. 14. Кроме макета и блока коммутатора для выполнения работы требуются:
— источник питания типа ВУЛ-2 – 1 шт.;
— осциллограф типа С1-68 – 1 шт.
3. Порядок выполнения работы
В соответствии с комбинационной таблицей логической функции от 4-x переменных представить соответствующую карту Карно. Вариант комбинационной таблицы выбирается преподавателем из указанных в табл. 7.
В представленной карте Карно выбрать группы, содержащие логическую “1” или логический “0”.
Определить выражение, описывающее соответствующую логическую функцию.
| Х1 | Х2 | Х3 | Х4 | Номера вариантов |
Преобразовать его с помощью теорем (2) с целью использования в нем как можно большего числа функций
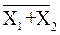
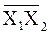
В соответствии с выражением логической функции определить реализующую его комбинационную схему.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Пример Карты Карно на пять переменных
Карта Карно

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
| В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом. |
Принципы минимизации
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких элементов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2 N различных членов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два члена, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировка членов:
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации членов. Например, четыре члена, принадлежащие одной грани куба, объединяются в один член с поглощением двух переменных:
В общем случае можно сказать, что 2 K членов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один член, при этом поглощаются K переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру членов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов членов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им члены можно склеивать.
Описание
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем тоже самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):
 |  |  |  | 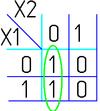 |  |  | 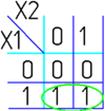 |
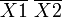 |  | 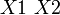 |  |  |  | 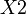 |  |
 | 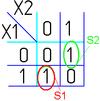 | 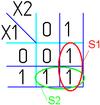 | 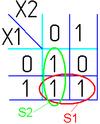 |  |  | ||
 |  |  |  |  |  | ||
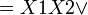 |  |  |  |  |  | ||
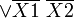 |  |
Для КНФ всё то же самое, только рассматриваем клетки с нулями, не меняющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид: 
В формате КНФ:

Так же из ДНФ в КНФ и обратно можно перейти использовав Законы де Моргана.
Примеры
Пример 1
У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять на улицу если ему разрешат хотя бы двое родителей.
Для краткости обозначим родителей Коли через буквы:
мама — х1
папа — х2
дедушка — х3
бабушка — х4
Условимся обозначать согласие родителей единицей, не согласие нулём. Возможность пойти погулять обозначим буквой f, Коля идёт гулять — f = 1, Коля гулять не идёт — f = 0.
Составим таблицу истинности:
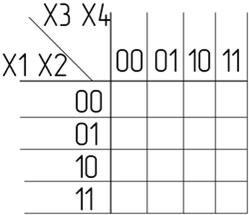
Перерисуем таблицу истинности в 2-х мерный вид:
Переставим в ней строки и столбцы в соответствии с кодом Грея. Получили Карту Карно:
Заполним её значениями из таблицы истинности:
Минимизируем в соответствии с правилами:
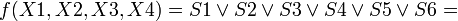

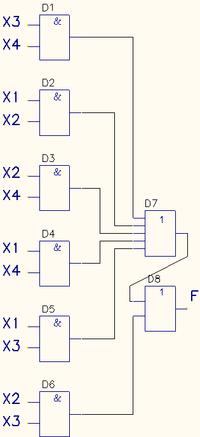
Теперь по полученной минимальной ДНФ можно построить логическую схему:
Из за отсутствия в наличии шести-входового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы(D7, D8).
Пример Карты Карно на пять переменных
Имеем такую таблицу истинности:
Карта Карно будет выглядеть следующим образом (для лучшего визуального восприятия в Карту нули не записываем):
Неправильно (на примере ДНФ):
Правильно, но не оптимально:
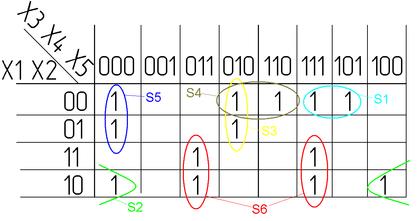
Эта карта Карно минимизирована неоптимально, так как можно объединить единицы, входящие в члены S3 и S5.
Минимизировав эту Карту получаем следующую ДНФ:

Составим минимальную КНФ:


Другой вариант той же самой Карты Карно:
Ничего не меняется только в строках записано три переменных, а в столбцах две.