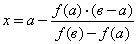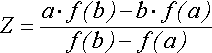Как сделать касательную в excel
Построение графиков в Excel. Практическая работа
Цель работы:
Оборудование:
Фронтальный опрос изученного материала.
Опорный конспект
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.
ПРИМЕР.
(Используется при объяснении материала через проектор.)
Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y
5. Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
Раздаточный материал
Варианты
ВАРИАНТ 1
Построить графики функций y1= x 2 -1, y2= x 2 +1 и y=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
ВАРИАНТ 2
Построить графики функций y1= 
ВАРИАНТ 3
Построить графики функций y1= 

ВАРИАНТ 5
Построить графики функций y1= 

Как построить касательную в excel к точке
Тангенциальная линия – это прямая линия на графике, которая проходит по касательной к кривой линии, составленной из точек данных. В Excel есть возможность автоматически создавать линию тренда, или вы можете вручную нарисовать касательную линию на графике. Тангенциальная линия рисуется касаясь изогнутой линии, так что когда кривая отходит от линии, она равноудалена от линии. В то время как функция линии тренда в Excel покажет тренд всей линии, ручное рисование линии создаст истинную касательную.
Кредит: Драган Радоевич / iStock / Getty Images
Шаг 1
Откройте лист Excel, содержащий данные, которые вы хотите использовать для тангенциальной линии. Изогнутый линейный график основан на наборах двух точек данных, например времени и амплитуды.
Шаг 2
Нажмите и перетащите на электронную таблицу, чтобы выделить данные, которые вы хотите показать, включая метки в вашем выборе.
Шаг 3
Нажмите на вкладку «Вставить», а затем нажмите стрелку вниз рядом с кнопкой «Разброс» в области «Диаграмма». Выберите «Разброс с гладкими линиями». Диаграмма создана в вашей электронной таблице.
Шаг 4
Перейдите на вкладку «Инструменты диаграммы: макет», а затем нажмите кнопку «Линия тренда» справа. Выберите «Линейный», чтобы создать прямую линию, которая приближается к прогрессу изогнутой линии. Он будет пересекать кривую в некоторых точках.
Шаг 5
Нажмите на вкладку «Вставка», а затем нажмите «Фигуры». Выберите «Линия» и нарисуйте линию так, чтобы она просто касалась одной из точек на вашей кривой.
Шаг 6
Нажмите на вкладку «Инструменты рисования: Формат» и нажмите кнопку «Повернуть» справа. Выберите «Дополнительные параметры вращения». Нажмите стрелку «Вверх» или «Вниз» рядом с полем «Поворот» в диалоговом окне, которое появляется, чтобы повернуть линию на кривой. Когда линия будет равноудалена от обеих сторон кривой, нажмите «ОК».
Дубликаты не найдены
ЕСЛИ(условие;выполнить_если_истина;выполнить_если_ложь)
[в eng версии соответственно это IF(. )]
Условие – что угодно, что может интерпретироваться как булевская функция. Например, дано, что a=2, b=3. Тогда IF(a>b;»истина»;»ложь») вернёт «ложь».
Сделать разветвление на несколько вариантов – IF(условие1;действие1;IF(условие2;действие2;..))
В качетсве крайнего «ложь» блока ЕСЛИ можно писать что угодно [если уверены, что рассмотрели все возможные варианты].
Вообще, насколько помню, годная в экселе справка была.. Так что традиционное – RTFM.
В математике много задач связано с вычислением производных функций и использованием геометрической интерпретации первой производной функции. Рассмотрим методику построения касательной к заданной точке функции и определения параметров ее уравнения.
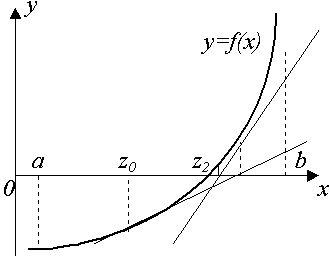
Если задана функция f(x), то первая производная функции в заданной точке с координатами хо и уо является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами хо и уо, имеет вид:
где к = /'(хо) – угловой коэффициент;
Требуется построить график функции /(х) и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс (хмин и хмакс) и ординат (умин и умакс).
Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: (х^у-^) и (х2,у2), которые располагаются на границах прямоугольника.
могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.
Если к Умэкс) П Р И предварительном построении графика заданной функции на основе табулированной функции (В5:С25)
Формируем таблицы начальных условий задачи.
углового коэффициента к = /'(х ) (Н2);
граничных значений диапазонов (хмин, хмакс, умин, умакс) (A2:D5).
Отступив одну ячейку от таблицы функции (В5:С25), рассчитываем координаты точек касательной (В27:С28) с учетом приведенных выше рассуждений (на рисунке в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения уг при хг = хмин и у2 при х2 = хмакс (F8 и G8). Для отображения точки на графике функции добавляем ячейки с ее заданными координатами (ВЗО и СЗО).
Выделив диапазон ячеек (В5:С30), в который включаются ячейки таблицы функции и координат точек касательной, обращаемся к мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы – Точечная, а вид – Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей х и у в диалоговом окне Формат оси.
Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координат. Чтобы установить цвет и толщину линии касательной нужно аккуратно щелкнуть по линии касательной. При появлении маркеров точек касательной вызвать контекстное меню и щелкнуть по пункту Формат точки данных. В диалоговом окне установить тип, цвет и толщину линии касательной.
При необходимости можно дополнительно построить график производной заданной функции.
Метод хорд и касательных в excel
Решение нелинейных уравнений методом хорд в MS Excel
Тема урока: «Решение нелинейных уравнений в MS Excel».
Цель урока: изучение возможностей MS Excel по решению нелинейных уравнений и практическое освоение соответствующих умений и навыков.
Тип урока: комбинированный – урок изучения нового материала и практического закрепления полученных знаний, умений и навыков.
Вид урока: сдвоенный, продолжительность – 1,5 часа.
Задачи урока:
Оборудование урока:
В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft Power Point.
I. Организационный момент
Учитель объявляет тему и цели урока.
II. Актуализация знаний, умений и навыков учащихся – повторение материала прошлого урока по теме «Решение нелинейных уравнений методом половинного деления»
Учащиеся повторяют указанный метод с помощью слайдов, подготовленных в пакете презентационной графики Microsoft Power Point метод половинного деления
Вопросы:
III. Изобразите блок-схему алгоритма. блок-схема
IV. Практическое задание с использованием программы на языке Turbo Pascal (Учащимся разрешено использовать программу, составленную на предыдущем уроке. Было решено уравнение y = x 3 – cos(x)) метод половинного деления TP
Задания для учащихся первой группы
Найти решение уравнения y = x 3 – cos(x) на отрезке [–1;1], при 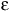
Задания для учащихся второй группы
Найти решение уравнения y = x 3 – cos(x) на отрезке [–1;1], определить на каком шаге циклического алгоритма будет получено решение.
V. Изучение нового материала «Решение нелинейных уравнений методом хорд»
VI. Объяснить алгоритм решения уравнения f(x)=0 на отрезке [а;в] методом хорд с помощью слайдов, подготовленных в пакете презентационной графики Microsoft Power Point. метод хорд
Вопросы:
Этапы решения задачи
Для формализации модели используем математические формулы.
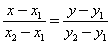
После математических преобразований уравнение примет вид 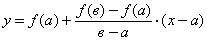
Определим корень уравнения
Метод хорд
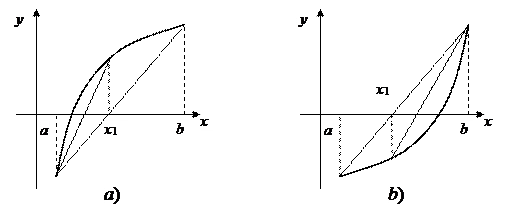
Метод хорд [7] заключается в замене кривой y = f(x) отрезком прямой, проходящей через точки (a, f(a)) и (b, f(b)) (см. рис. 2.6). Абсцисса точки пересечения прямой с осью OX принимается за очередное приближение.
Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая y нулю, найдем x:
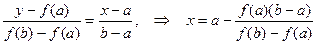
Рис.2.6. Метод хорд
Алгоритм метода хорд:
3) Если f(xk)= 0 (корень найден), то переходим к 5).
5) Выводим значение корня xk.
Замечание.Действия третьего пункта аналогичны действиям метода половинного деления. Однако в методе хорд на каждом шаге может сдвигаться один и тот же конец отрезка (правый или левый), если график функции в окрестности корня выпуклый вверх (рис. 2.6, a)) или вогнутый вниз (рис. 2.6, b)). Поэтому в критерии сходимости используется разность соседних приближений.
Пример 2.6. Применим метод хорд к уравнению sin 5x + x 2 – 1 = 0 и отрезку [0,2; 0,3] для определения корня с точностью до ε = 0,001.
Решение. Проведем расчеты в программе Excel:
1) В ячейки A1:H1 запишем заголовки столбцов как в табл. 2.6;
2) В ячейку B3 запишем формулу =ЕСЛИ(C2*E2
Решение в программе Mathcad:
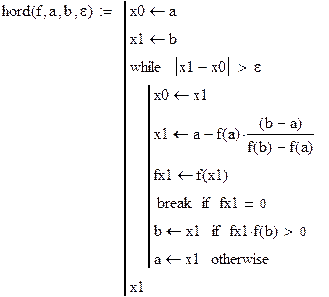 |
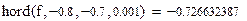 |
 |
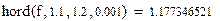 |
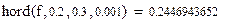 |
Как видим, результаты расчетов согласуются с предыдущими ответами.
Приведем программу, которая реализует метод хорд на языке C++:
typedef double (*PF)(double);
double hord(PF f,double a, double b,double eps, int Kmax);
double a, b, x, eps;PF pf; int Kmax;
x = hord(pf,a,b,eps, Kmax); cout > a;
double f(double x) 0) b = xk1;
Результат расчета для примера 2.6:
Press any key & Enter
Как видим, результат совпадает с предыдущими расчетами.
Дата добавления: 2015-04-25 ; Просмотров: 4005 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Решение уравнений в EXCEL методом половинного деления, методом хорд и касательных.
Скачать:
| Вложение | Размер |
|---|---|
| материал для ученика | 57.5 КБ |
| работа ученика | 27 КБ |
Предварительный просмотр:
Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x
Численные методы позволяют найти приближенное значение корня с любой заданной точностью.
Приближённое нахождение обычно состоит из двух этапов:
1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;
2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.
Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x) определена и непрерывна на отрезке [а.Ь]. Значение х 0 называется корнем уравнения если f(х 0 )=0
Для отделения корней будем исходить из следующих положений:
Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков
Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции
Алгоритм для программной реализации
Запишем уравнение прямой по двум точках:
В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть
, откуда
процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и х п _1 не будет выполняться условие abs(xn-x n-1 ) е — заданная точность
Сходимость метода гораздо выше предыдущего
Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)
Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)
Метод хорд и касательных в excel
Часто в классической математике многое выглядит элементарно. Так, если нужно найти экстремум некоторой функции, то предлагается взять ее производную, приравнять нулю, решить полученное уравнение и т.д. Вне сомнения, что первые два действия в состоянии выполнить многие школьники и студенты. Что касается третьего действия, то позвольте усомниться в его элементарности.
Пусть после взятия производной мы пришли к уравнению tg(x)=1/x. Проведем следующие преобразования:
tg(x)=1/x Ю x tg(x)=1 Ю x2 tg=1 Ю x2= 1 / tg(x) Ю x = ±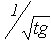
Если в приведённой здесь цепочке преобразований ничто не взволновало вашу мысль, то может быть лучше обучение на этом прекратить и заняться чем-нибудь другим, не требующим уровня знаний выше церковно-приходской школы начала XX века.
В самом деле, мы прекрасно решаем квадратные и биквадратные уравнения, наипростейшие тригонометрические и степенные. Еще водятся «мастодонты», знающие о существовании формул Кардано для кубических уравнений. В общем же случае надежд на простое аналитическое решение нет. Более того, доказано, что даже алгебраическое уравнение выше четвертой степени неразрешимо в элементарных функциях. Поэтому решение уравнения проводят численно в два этапа (здесь разговор идет лишь о вещественных корнях уравнения). На первом этапе производится отделение корней — поиск интервалов, в которых содержится только по одному корню. Второй этап решения связан с уточнением корня в выбранном интервале (определением значения корня с заданной точностью).
1.1. Отделение корней
Возьмем середину отрезка с=(a+b)/2. Если f(a) ґ f(c) Ј 0, то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b.
log2((b-a)/ e ). Например, при исходном единичном интервале и точности порядка 6 знаков ( e
С точки зрения машинной реализации (рис. 2) этот метод наиболее прост и используется во многих стандартных программных средствах, хотя существуют и другие более эффективные по затратам времени методы.
1.3. Уточнение корней методом хорд
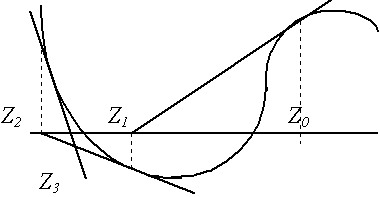
В отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения, метод хорд использует пропорциональное деление интервала (рис. 3).
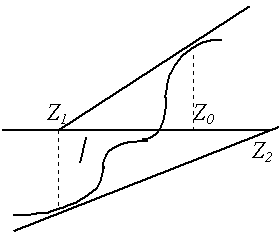
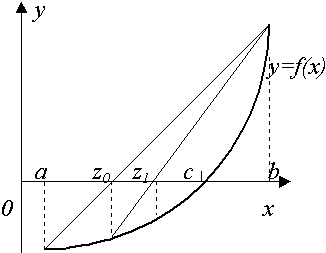 Здесь вычисляются значения функции на концах отрезка, и строится «хорда», соединяющая точки (a,f(a)) и (b,f(b)). Точка пересечения ее с осью абсцисс Можно доказать, что истинная погрешность найденного приближения: 1.4. Уточнение корней методом касательных (Ньютона)Обширную группу методов уточнения корня представляют итерационные методы — методы последовательных приближений. Здесь в отличие от метода дихотомии задается не начальный интервал местонахождения корня, а его начальное приближение. Наиболее популярным из итерационных методов является метод Ньютона (метод касательных).
Геометрически этот метод предлагает построить касательную к кривой y=f(x) в выбранной точке x=Zn, найти точку пересечения её с осью абсцисс и принять эту точку за очередное приближение к корню (рис. 4).
Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий (например при непрерывности и знакопостоянстве первой и второй производной функции в окрестности корня) и при их нарушении либо дает расходящийся процесс (рис. 5), либо приводит к другому корню (рис. 6). Очевидно, что для функций, производная от которых в окрестности корня близка к нулю, использовать метод Ньютона едва ли разумно. Если производная функции мало изменяется в окрестности корня, то можно использовать видоизменение метода Существуют и другие модификации метода Ньютона. 1.5. Уточнение корней методом простой итерацииДругим представителем итерационных методов является метод простой итерации. Здесь уравнение f(x)=0 заменяется равносильным уравнением x= j (x) и строится последовательность значений Если функция j (x) определена и дифференцируема на некотором интервале, причем | j /(x)| j (x) на этом интервале. Геометрическая интерпретация процесса представлена на рис. 7. Здесь первые два рисунка (а, б) демонстрируют одностороннее и двустороннее приближение к корню, третий же (в) выступает иллюстрацией расходящегося процесса (| j /(x)| > 1). | ||||||
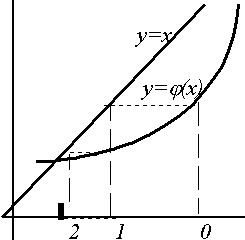 | 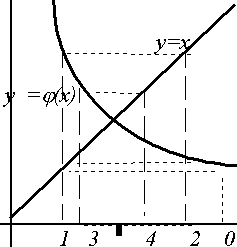 | 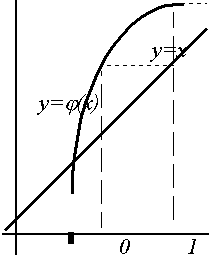 | ||||
| Рис. 7. Геометрическая интерпретация метода простой итерации | ||||||
Если f ‘(x)>0, то подбор равносильного уравнения можно свести к замене x=x- l Ч f(x), т.е. к выбору j (x)= x- l Ч f(x), где l >0 подбирается так, чтобы в окрестности корня 0 j ‘(x)=1- l Ч f ‘(x) Ј 1. Отсюда может быть построен итерационный процесс
Можно и искусственно подобрать подходящую форму уравнения, например:
Заметим, что существуют и другие методы (наискорейшего спуска, Эйткена-Стеффенсена, Вегстейна, Рыбакова и т.д.) уточнения корней, обладающие высокой скоростью сходимости.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter