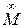Как сделать круг в аксонометрии

Аксонометрические проекции

Согласно ГОСТ 2.317-69, из прямоугольных аксонометрических проекций рекомендуется применять прямоугольные изометрию и диметрию.

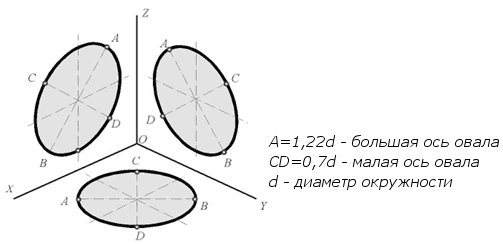
В прямоугольной изометрии размеры предмета по всем трем измерениям сокращаются на 18 %. ГОСТ рекомендует изометрическую проекцию строить без сокращения по осям координат), что соответствует увеличению изображения против оригинала в 1,22 раза.

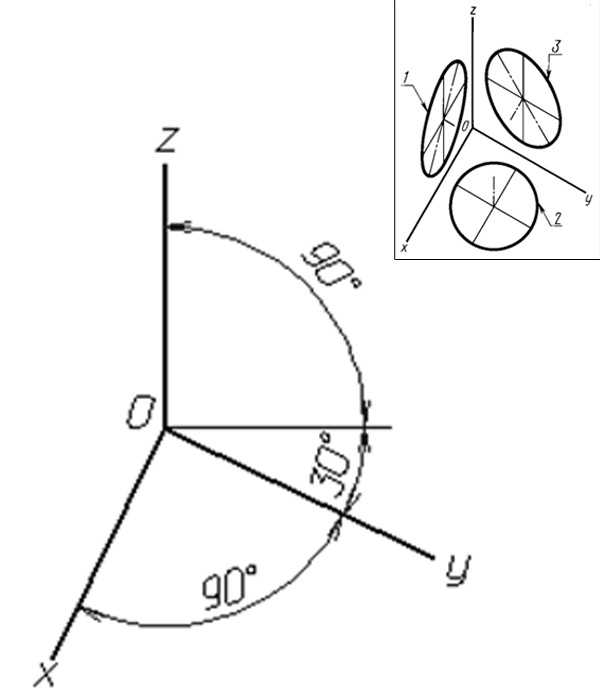
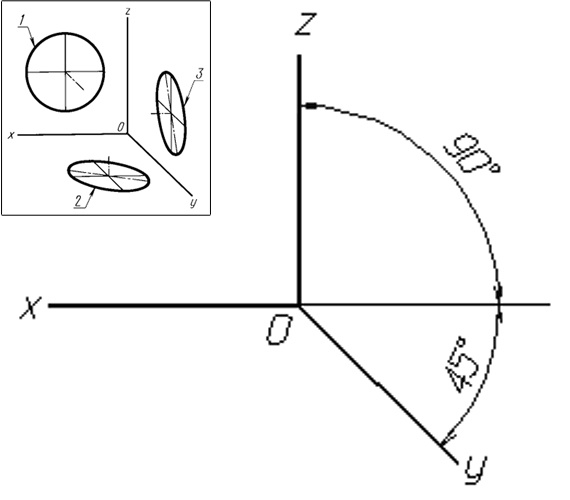
На рисунках 172 и 173 показано расположение осей в изометрии и диметрии.

Построение окружности в аксонометрии

При параллельном проецировании окружности на какую-нибудь плоскость П* получаем ее изображение в общем случае в виде эллипса (рисунок 174).

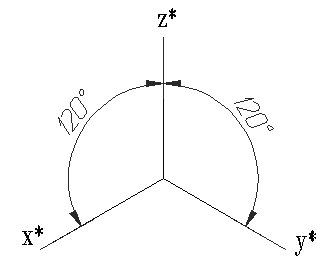
ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций для прямоугольной изометрической проекции (рисунок 175) и для прямоугольной диметрии (рисунок 177).

плоскостях параллельных плоскостям проекций

плоскостях параллельных плоскостям проекций

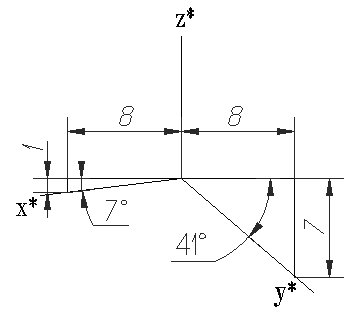
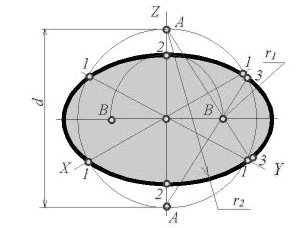
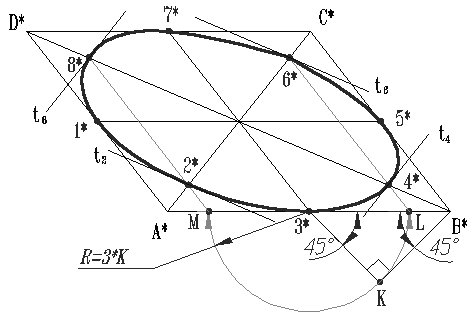
Как бы ни была расположена плоскость окружности, сначала целесообразно построить параллелограмм A*B*C*D* – параллельную проекцию квадрата ABCD, описанного около данной окружности, а затем с помощью восьми точек и восьми касательных вписать в него эллипс. Точки 1, 3, 5 и 7 – середины сторон параллелограмма. На отрезке 3*B*, как на гипотенузе, построить прямоугольный равнобедренный треугольник 3*KB*; из точки 3* радиусом 3*K описать полуокружность, которая пересечет A*B* в точках L и M; эти точки делят отрезок 3*A* и равный ему отрезок 3*B* в отношении 3:7; через точки L и М провести прямые параллельные боковым сторонам параллелограмма, и отметить точки 2*, 4*, 6* и 8* расположенные на диагоналях. Построить касательные к эллипсу в найденных точках. Касательные t₂ и t₆ параллельны BD, а касательные t₄ и t₈ параллельны AC. Получив восемь точек и столько же касательных, можно с достаточной точностью вычертить эллипс (рисунок 179).

Построение аксонометрических изображений

Переход от ортогональных проекций предмета к аксонометрическому изображению рекомендуется осуществлять в такой последовательности:

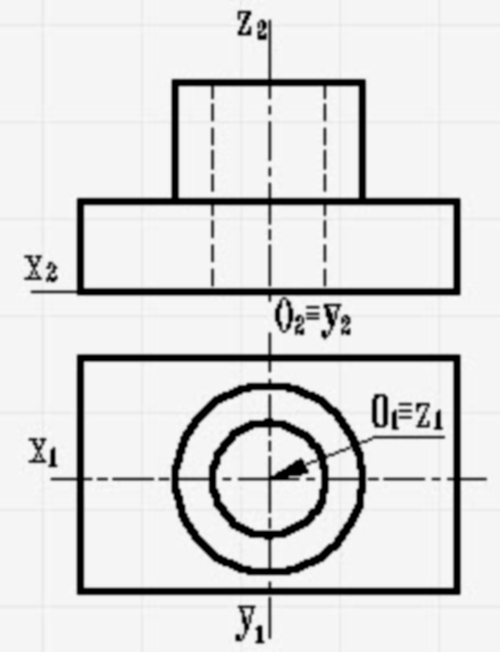
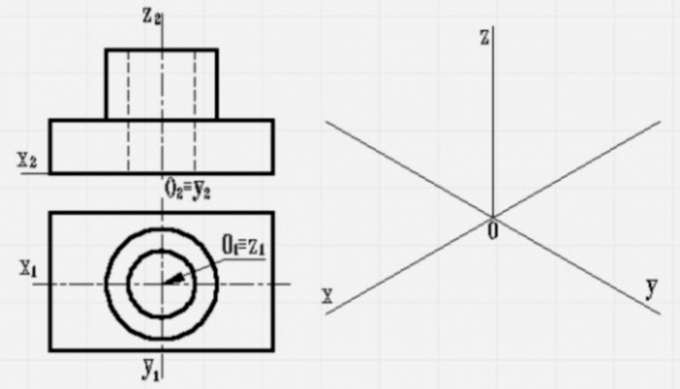
На ортогональном чертеже размечают оси прямоугольной системы координат, к которой и относят данный предмет. Оси ориентируют так, чтобы они допускали удобное измерение координат точек предмета. Например, при построении аксонометрии тела вращения одну из координатных осей целесообразно совместить с осью тела (рисунок 180)

2. Строят аксонометрические оси с таким расчетом, чтобы обеспечить наилучшую наглядность изображения и видимость тех или иных точек предмета.

3. По одной из ортогональных проекций предмета чертят вторичную проекцию.

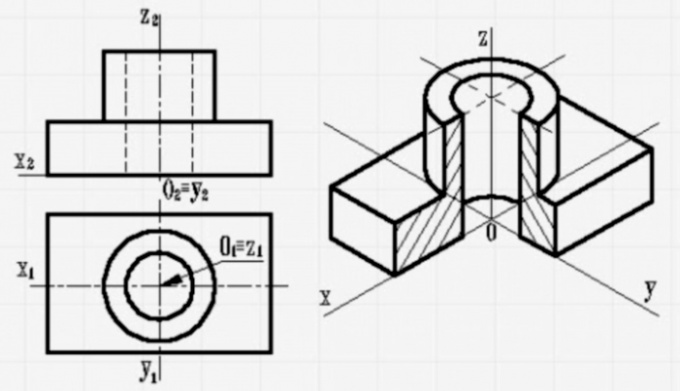
4. Создают аксонометрическое изображение, для наглядности делают вырез четверти.

Штриховка в аксонометрии

Согласно ГОСТ 2.317-68 ЕСКД линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рисунок 181).

При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку.

В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют.

Источник

Как построить окружность в аксонометрии

Аксонометрические проекции используют, дабы передать на чертеже представление о форме предмета с различных сторон. При этом вид предмета с различных сторон проецируется на плоскости куба. Наклон плоскостей в аксонометрической проекции придает окружности форму эллипса. Из-за сложности построения эллипсов на практике их заменяют овалами.

Вам понадобится

Инструкция

2. Ступенчато обозначьте углы построенного ромба точками A, B, C и D. При этом точка A должна располагаться в том углу ромба, тот, что особенно близок к точке пересечения осей на аксонометрической проекции.

3. Начертите диагонали получившегося ромба, объединив отрезками точки A и C, а также B и D. Диагональ AC образует малую ось овала, а диагональ BD – крупную.

4. Пересечение овалов образует центр ромба и окружности на плоскости. Обозначьте его буквой O.

5. Проведите через центр ромба O две линии, которые параллельны осям проекции и разделяют ромб на 4 части.

6. Ступенчато обозначьте точки, в которых линии параллельные осям проекции пересекают стороны ромба буквами E, F, G и H. Точка E должна следовать за точкой A в том же направлении, в котором ступенчато обозначались углы ромба.

7. Объедините точки A и G, а также C и E отрезками.

8. Обозначьте точки, в которых огромная ось ромба пересекает отрезки AG и EC буквами I и J. При этом точка I должна лежать на отрезке EC, а точка J на отрезке EC.

9. С поддержкой циркуля начертите дугу между точками E и F. Центр окружности для дуги размещен в точке I, а её радиус равен длине отрезка EI. Подобно начертите дугу между точками G и H.

10. Начертите две дуги, которые завершат построение овала на проекции. Первая дуга с центром окружности в точке A соединяет точки F и G. Радиус первой дуги равен длине отрезка AG. Вторая дуга с центром окружности, тот, что размещен в точке C, соединяет точки E и H. Ее радиус равен отрезку EC. Когда вы завершите чертить вторую дугу, вы получите построенную окружность на плоскости аксонометрической проекции.

Совет 2: Как возвести окружность

Окружность еще древние греки считали самой идеальной и слаженной из всех геометрических фигур. В их ряду окружность является примитивной косой, а ее безупречность заключается в том, что все составляющие ее точки располагаются на идентичном расстоянии от ее центра, вокруг которого она “скользит сама по себе”. Неудивительно, что методы построения окружности начали волновать математиков еще в древности.

Вам понадобится

Инструкция

1. Самый примитивный и знаменитый с древности и по сей день – построение окружности при помощи особого инструмента – циркуля (от лат. “circulus” – круг, окружность). Для такого построения сперва необходимо подметить центр грядущей окружности – скажем, пересечением 2х штрихпунктирных линий под прямым углом, и выставить шаг циркуля, равный радиусу грядущей окружности. Дальше установите ножку циркуля в подмеченный центр и, поворачивая ножку с грифелем вокруг него, проведите окружность.

2. Без циркуля окружность возвести тоже допустимо. Для этого понадобится карандаш и лист бумаги в клеточку. Подметьте предисловие грядущей окружности – точку А и запомните легкой алгорифм: три – один, один – один, один – три. Для построения первой четверти окружности продвиньтесь из точки А на три клетки вправо и на одну вниз и зафиксируйте точку В. Из точки В – на одну клетку вправо и одну вниз и подметьте точку С. И из точки С – на одну клетку вправо и три вниз в точку D. Четверть окружности готова. Сейчас для комфорта дозволено развернуть лист супротив часовой стрелки так, дабы точка D оказалась вверху, и по тому же алгорифму достроить оставшиеся 3/4 окружности.

3. Но что делать, если нам необходимо возвести окружность большего размера, чем разрешает тетрадный лист и шаг циркуля – скажем, для игры? Тогда нам понадобится веревочка длины, равной радиусу желаемой окружности, и 2 колышка. Колышки привяжите к концам веревки. Один из них воткните в землю, а иным при натянутой веревке начертите окружность.Абсолютно допустимо, что одним из этих методов построения окружности воспользовался и изобретатель колеса – по сей день одного из самых феноменальных изобретений общества.

Видео по теме

Совет 3: Как строить аксонометрию

Инструкция

1. Пускай перед вами стоит задача исполнить построение аксонометрической проекции заданного тела вращения. В первую очередь надобно соотнести данное тело с какой-нибудь прямоугольной системой координат. Потому что дано тело вращения, то в данном случае для комфорта счёта одну из осей системы координат нужно совместить с осью тела вращения.

2. Сейчас необходимо вычертить вторую ортогональную проекцию тела, как показано на рисунке.

3. После этого нужно перейти к построению аксонометрических осей. Учтите, что их необходимо так располагать на листе, дабы большей части поверхности предмета была обеспечена видимость. Для того, дабы упростить задачу построения класснее каждого будет взять координатную ось, используемую в прямоугольной изометрической проекции, изображенную на рисунке. Вследствие такому выбору, показатели искажения по всякой из осей становятся равными единице. Если же делать типовые аксонометрические оси, в которых соседние оси образуют угол в 120 градусов, то показатель искажения станет равен 0,82. Это сделает добавочные трудности при изображении предмета.

4. Все элементы заданной фигуры нужно спроецировать в соотношении один к одному по аксонометрических осей. Для того, дабы изображение было больше наглядным, в ближайшей четверти детали делается вырез, с дальнейшей штриховкой. Линии штриховки по правилам наносят параллельно какой-нибудь из диагоналей условного квадрата, лежащего в рассматриваемой координатной плоскости. Стороны этого квадрата обязаны быть параллельны аксонометрическим осям. В одной детали различные сечения нужно заштриховывать с наклоном в различные стороны.

Полезный совет
Построение аксонометрических проекций предметов во многих учебниках по черчению рекомендуется начинать с построения их оснований, после этого теснее к основаниям понемногу добавляются аксонометрические проекции других элементов: ребер, граней, вершин, оснований.

Совет 4: Как возвести аксонометрическую проекцию

Аксонометрические проекции деталей и узлов машин неоднократно применяются в конструкторской документации для того, дабы наглядно показать конструктивные особенности детали (сборочного узла), представить, как выглядит деталь (узел) в пространстве. В зависимости от того, под каким углом расположены оси координат, аксонометрические проекции подразделяются на прямоугольные и косоугольные.

Вам понадобится

Инструкция

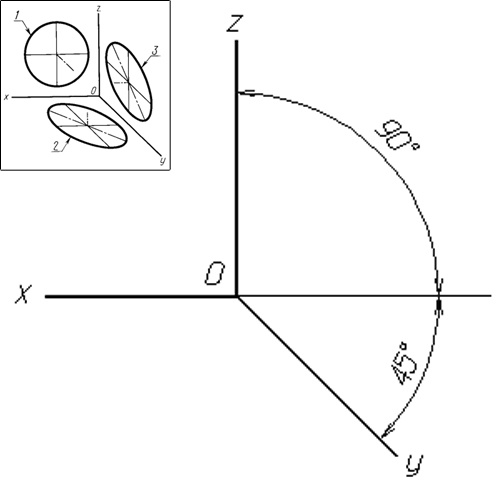
1. Прямоугольные проекции. Изометрическая проекция. При построении прямоугольной изометрической проекции рассматривают показатель искажения по осям X, Y, Z, равный 0,82, при этом окружности, параллельные плоскостям проекций, проецируются на аксонометрические плоскости проекций в виде эллипсов, огромная ось которых равна d, а малая ось – 0,58d, где d – диаметр начальной окружности. Для простоты расчетов изометрическую проекцию исполняют без искажения по осям (показатель искажения равен 1). В этом случае проецируемые окружности будут иметь вид эллипсов с крупной осью, равной 1,22d, и малой осью, равной 0,71d.

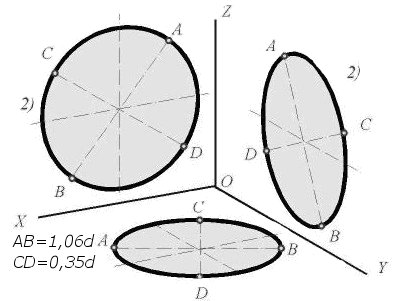
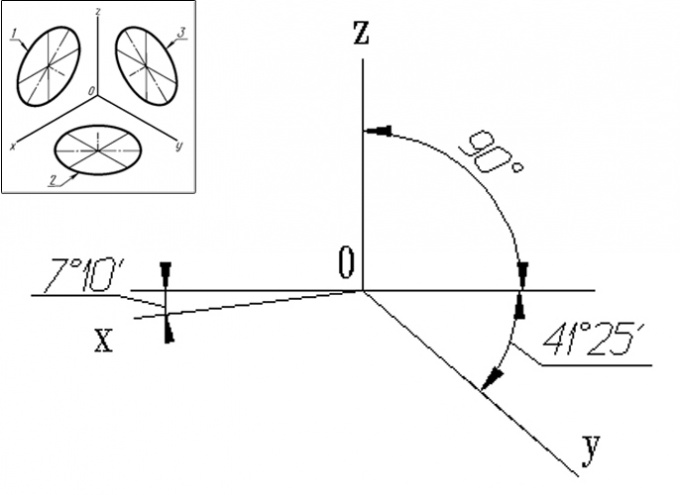
2. Диметрическая проекция. При построении прямоугольной диметрической проекции учитывается показатель искажения по осям X и Z, равный 0,94, а по оси Y – 0.47. На практике диметрическую проекцию упрощенно исполняют без искажения по осям X и Z и с показателем искажения по оси Y = 0,5. Окружность, параллельная общей плоскости проекций, проецируется на нее в виде эллипса с крупный осью, равной 1,06d и малой осью, равной 0,95d, где d – диаметр начальной окружности. Окружности, параллельные двум иным аксонометрическим плоскостям, проецируются на них в виде эллипсов с осями, равными соответственно 1.06d и 0,35d.

3. Косоугольные проекции. Общая изометрическая проекция. При построении общей изометрической проекции эталоном установлен наилучший угол наклона оси Y к горизонтали 45 градусов. Допускаются углы наклона оси Y к горизонтали – 30 и 60 градусов. Показатель искажения по осям X, Y и Z равен 1. Окружность 1, расположенная параллельно общей плоскости проекций, проецируется на нее без искажений. Окружности, параллельные горизонтальной и профильной плоскостям проекций, выполняются в виде эллипсов 2 и 3 с огромный осью, равной 1.3d и малой осью, равной 0,54d, где d – диаметр начальной окружности.

4. Горизонтальная изометрическая проекция. Горизонтальная изометрическая проекция детали (узла) строится на аксонометрических осях, расположенных, как показано на рис. 7. Допускается изменять угол между осью Y и горизонталью на 45 и 60 градусов, оставляя постоянным угол 90 градусов между осями Y и X. Показатель искажения по осям X, Y, Z равен 1. Окружность, лежащая в плоскости, параллельной горизонтальной плоскости проекций, проецируется в виде окружности 2 без искажения. Окружности, параллельные общей и профильной плоскостям проекций, имеют вид эллипсов 1 и 3. Размеры осей эллипсов связаны с диаметром d начальной окружности следующими зависимостями:эллипс 1 – огромная ось равна 1,37d, малая ось – 0, 37d; эллипс 3 – огромная ось равна 1,22d, малая ось – 0.71d.

5. Общая диметрическая проекция. Косоугольная общая диметрическая проекция детали (узла) строится на аксонометрических осях, сходственных осям общей изометрической проекции, но отличаются от нее показателем искажения по оси Y, тот, что равен 0,5. По осям X и Z показатель искажения равен 1. Также возможно метаморфоза угла наклона оси Y к горизонтали до значений 30 и 60 градусов. Окружность, лежащая в плоскости, параллельной общей аксонометрической плоскости проекций, проецируется на нее без искажений. Окружности, параллельные плоскостям проекций горизонтальной и профильной, вычерчиваются в виде эллипсов 2 и 3. Размеры эллипсов от размера диаметра окружности d выражаются зависимостью:огромная ось эллипсов 2 и 3 равна 1,07d; малая ось эллипсов 2 и 3 равна 0,33d.

Видео по теме

Полезный совет
Плоскость, на которую производится проецирование, именуется аксонометрической либо картинной. Аксонометрическая проекция именуется прямоугольной, если при параллельном проецировании проецирующие лучи перпендикулярны картинной плоскости ( =90 ) и косоугольной, если лучи составляют с картинной плоскостью угол 0

Вам понадобится

Инструкция

1. Аксонометрия может быть исполнена как в прямоугольной проекции, так и в косоугольной. Для начала постройте куб в прямоугольной изометрической проекции, то есть проецирование происходит перпендикулярно плоскости проекции и масштаб по каждой оси идентичен. Обыкновенно, для простоты показатель искажения тут принимают равным 1. Нарисуйте три оси координат. Для этого с помощью линейки и карандаша нарисуйте вертикальную линию приблизительно от середины листа вверх. С помощью транспортира от этой линии отложите угол в 120 градусов в обе стороны и проведите соответствующие линии. Получилась ось координат в пространстве. Сейчас на этих осях отложите идентичные отрезки. Из полученных точек проведите линии, параллельные оси координат. Для этого вновь нужно от каждой точки отложить по 120 градусов в обе стороны. И на каждом луче с помощью линейки отложите отрезок той же величины, что и раньше. Сейчас объедините получившиеся точки параллельными линиями. Получился куб в прямоугольной изометрической проекции. Она еще носит наименование ортогональной.

2. Дабы получить прямоугольную диаметрическую проекцию, сбережете размеры в по любым двум осям, а по оставшейся — исказите в нужной либо произвольной степени. Реально куб превращается в прямоугольный параллелепипед. Помимо прямоугольной существуют косоугольные проекции, при которых проецирование происходит под любым иным углом к плоскости, помимо прямого. Различают фронтальную изометрическую проекцию, фронтальную диметрическую и горизонтальную изометрическую проекцию.

3. Для того дабы возвести фронтальную косоугольную проекцию, отложите следующие углы между осями: между вертикальной и горизонтальной — 90 градусов, а третью ось наклоните касательно вертикальной на 135 градусов. Помимо того, допускаются и другие отклонения — на 120 либо 150 градусов. Позже этого постройте проекции подобно предыдущему случаю, но лишь во фронтальной проекции сбережете пропорции. Для горизонтальной проекции пропорции сбережете в горизонтальной плоскости.

Обратите внимание!
При изометрических проекциях сложно оценить глубину и высоту рисунка.

Полезный совет
Аксонометрия почаще каждого применяют в машиностроительном черчении и САПР и в компьютерных играх для построения трёхмерных объектов и панорам.

Источник

Построение овалов как аксонометрических проекций окружности

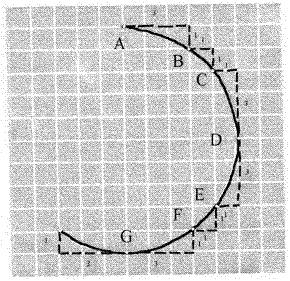
Практически для построения прямоугольной аксонометрии окружности, расположенной в координатной плоскости (или плоскости уровня), строят овалы, условно аппроксимирующие эллипсы в прямоугольной аксонометрии. Работа с ними намного упрощает (и ускоряет!) процесс построения аксонометрических изображений, содержащих круглые формы (рис. 39).

a) b)

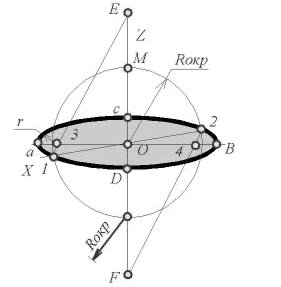
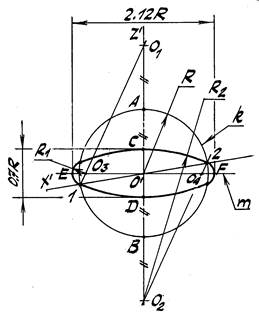
Задача 1. Построить прямоугольную изометрию окружности k радиуса R, расположенной в горизонтальной плоскости π’₂ (рис. 40 a,b).

1. Строим окружность с центром в т. О’, через которую проводим аксонометрические оси x’, y‘ и z’ (рис. 40a).

a) b)

2. Отмечаем точки пересечения О₁ и О₂ окружности и оси z’ (рис. 40b).

3. Из т. Е пересечения оси y’ и данной окружности проводим дугу радиуса R’= ЕО₁ до её пересечения с горизонтальной прямой h в т. О₃.

Дальнейшее построение четырехцентрового овала с точками стыка 1, 2,

3 и 4 понятно из рис. 40b.

Следует заметить, что ориентация овалов в разных аксонометрических плоскостях (или плоскостях, параллельных им), а также соотношения величин их осей, зависит от направления стороны треугольника следов, расположенной в соответствующей аксонометрической плоскости.

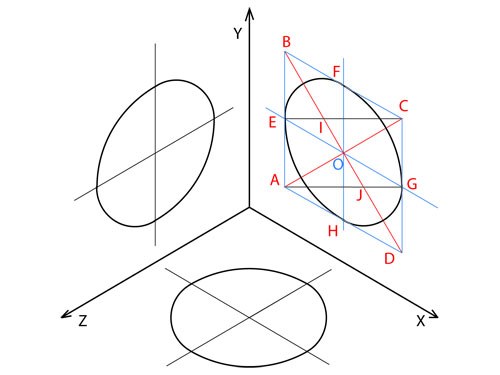
Например, если овал на рис. 40b располагать на аксонометрических плоскостях в изометрии (рис. 41), то:

· большая ось h овала, расположенного в плоскости π’₁ будет параллельна следу А’В’ треугольника следов А’В’С’ (рис. 41);

· большая ось h овала, расположенного в плоскости π’₂ будет параллельна следу А’С’;

· большая ось h овала, расположенного в плоскости π’₃ будет параллельна

При этом овалы в изометрии, лежащие в разных аксонометрических плоскостях равны при равенстве большой оси овала 1,22d, а малой – 0,58d, где d – диаметр исходной окружности.

В других видах аксонометрии соотношения величин осей овалов в разных аксонометрических плоскостях, могут различаться.

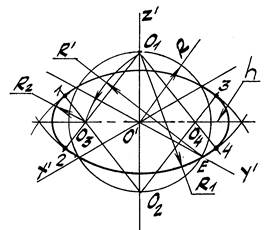
Задача 2. Построить прямоугольную диметрию окружности k, радиуса R, лежащей в горизонтальной плоскости π’₂ (рис. 42).

1. Строим окружность заданного радиуса R с центром в т. О’.

2. От тт. А и В её пересечения с осью z’ откладываем вверх и вниз отрезки

3. Находим тт. 1 и 2 пересечения заданной окружности с осью х’.

5. В пересечении горизонтальной прямой m É О’ с прямыми О₁1 и О₂2

Применяя их для построения дуг, как показано на рис. 37, строим овал,

большая и малая оси которого с достаточным приближением равны

На рис. 43 для построения прямоугольной диметрии окружности того же радиуса R, лежащей во фронтальной плоскости π’₁, через концы 1, 2, 3 и 4 (точки стыка) сопряжённых диаметров, параллельных осям х’ и z’ проводим горизонтальные прямые, которые пересекают взаимно-перпендикулярные оси МN и LК овала в четырёх центрах – О₁, О₂, О₃ и О₄. Окончательное проведение четырёхцентровой кривой несложно уяснить из чертежа.

Следует иметь в виду, что ось LК овала в плоскости π’₂ параллельна диметрической оси y’ и равна 1,9R, другая ось MN равна 2,12R. Обе величины с достаточным приближением соответствуют осям эллипса, лежащего в плоскости π’₁.

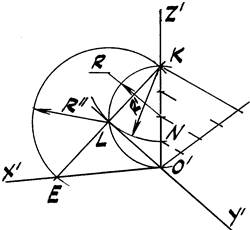
Дополнение. Построение углов между осями в прямоугольной диметрии в «приведённом» виде (рис. 44а) выполняется следующим образом (рис. 44b):

1. На оси z’ от заданного начала О’ откладываем отрезок О’К.

2. На отрезке О’К как на диаметре строим полуокружность радиуса R.

3. Из т. К проводим дугу радиуса R’= КN=3/4 О’К.

4. На пересечении двух дуг находим т. L, которая вместе, с т. О’ определит ось у’.

5. Из т. L проведём полуокружность радиуса R», которая пересечёт прямую КL в т. Е (КL=LЕ).

6. Искомая ось х’ проходит через тт. ЕО’.

3.3. Построение циркульных спиралей

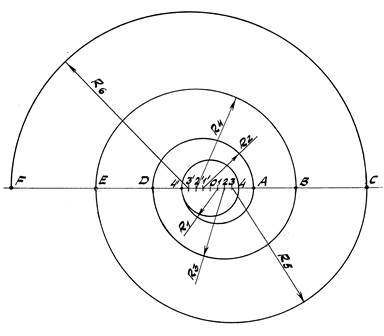
Точка, которая вращается в плоскости около некоторого центра и удаляется от него по определённому закону, описывает траекторию, представляющую собою спираль. Спирали относятся к односвязным линиям, не имеющим никаких разветвлений и простирающимся до бесконечности. Спирали широко используются в архитектурном декоре и имеют долгую художественную и сакральную традицию.

Циркульная спиральная кривая, состоящая из последовательных сопряжённых дуг, называется завитком.

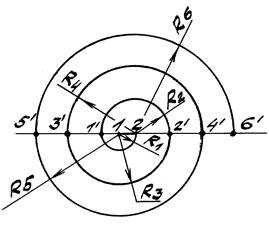
Задача 1. Построить завиток по двум центрам 1 и 2 – концам заданного отрезка (рис. 45).

1. Из центра 1 проводим полуокружность 1′-2 радиуса R₁, равного величине исходного отрезка 1-2.

2. Из центра 2 проводим полуокружность 1′-2′ радиуса R₂.

3. Из центра 1 проводим полуокружность 2′-1′ радиуса R₃.

Дальнейшие построения аналогичны и их легко понять из чертежа.

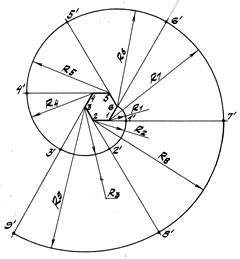
Задача 2. Построить завиток по трём центрам 1, 2 и 3 – вершинам равностороннего треугольника (рис. 46).

1. Из центра 1 проводим дугу 3-1′, равную трети окружности радиуса R₁.

2. Из центра 2 проводим дугу 1′-2′, равную трети окружности радиуса R₂.

3. Из центра 3 проводим дугу 2′-3′, равную трети окружности радиуса R₃.

Дальнейшие построения несложно продолжить аналогичным образом.

Задача 3. Построить завиток по четырём центрам 1, 2, 3 и 4 – вершинам квадрата (рис. 47).

1. Из центра 1 проводим дугу 4-1′ радиуса R₁, равного стороне исходного квадрата.

2. Следующую дугу 1′-2′ радиуса R₂ проводим из центра 2.

3. Очередную дугу 2′-3′ проводим из центра 3 радиусом R_3.

Далее построения выполняются сходным образом, при этом на каждом этапе центры сопряжения сменяются последовательно (в данном случае, по часовой стрелке).

Построение шестицентрового завитка предлагается разобрать самостоятельно (рис. 48).

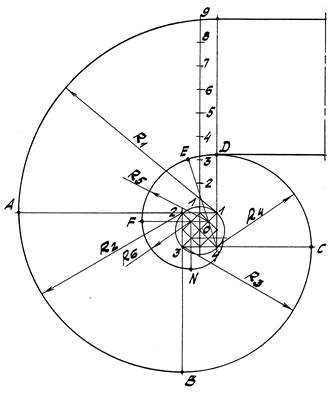
Задача 4. Построить завиток по заданному диаметру 4-4′ окружности с известным центром О (рис. 49).

1. Поделим заданный диаметр 4-4′ на n равных частей по n/2 на радиус.

2. Тогда при n=8 радиусом R₁=1-4′ из точки 1 проводим

3. Радиусом R₂ =1′-А из точки 1′ проводим полуокружность АD.

4. Далее из центра 2 проводим полуокружность DB радиусом R₃ = D-2.

Последующие построения проводятся аналогичным образом.

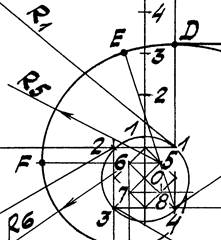
Задача 5. Построить завиток по заданному отрезку ОА, где О – центр завитка (рис. 50a, b).

1. Делим отрезок ОА на n равных частей, например на n=9.

2. Около центра О описываем окружность радиуса, равного 1/9 ОА,

и вписываем в неё квадрат 1—2—3—4 (обход вершин против часовой

3. Соединяем середины сторон полученного квадрата и, таким образом,

находим ещё один квадрат, вписанный в предыдущий, в который, в свою очередь, аналогичным образом вписываем очередной квадрат 5—6—7—8 (обход вершин также против часовой стрелки) и т.д. (рис. 50b).

4. Строим дугу 9-А радиуса R₁= 1—9 из центра 1; т. А лежит на продолжении

стороны квадрата 1—2.

5. Строим дугу АВ радиуса R₂=2—А, причем т. В лежит на продолжении

стороны 2-3 квадрата. Далее построения ведутся аналогичным образом.

Точку Е стыка двух смежных дуг радиусов R₄ и R₅ находим на продолжении отрезка 4—5.

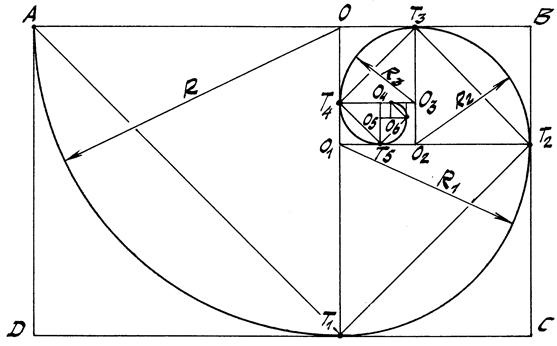
АВ/ВС = 1+

В этом прямоугольнике его стороны АВ и DC делятся точками О и Т₁ в отношении 5/3. В результате прямоугольник оказывается разделённым на квадрат АОТ₁ D и прямоугольник ОВСТ₁ стороны ОТ₁ и ВС которого, в свою очередь, так же делятся в отношении 5/3. Очередной и последующие прямоугольники продолжают делить аналогичным образом.

В каждом квадрате, полученном таким образом, можно последовательно провести дуги окружностей из центров О, О₁, О₂, О₃, О₄, О₅, …, которые образуют завиток, построение которого традиция приписывает Архимеду.

3.4. Дополнение: сопряжения, выполняемые посредством коник

Кривые 2-го порядка (коники) широко применяются в технике строительстве и архитектуре. Форма коники и её положение на плоскости определяются заданием пяти параметров, например, пятью касательными, никакие три из которых, не должны пересекаться в одной точке или пятью точками, никакие три из которых не должны лежать на одной прямой. В число пяти параметров может входить любая комбинация из касательных и точек, отвечающих указанным выше условиям.

При задании коники пятью параметрами вид кривой (эллипс, парабола или гипербола) предусмотреть заранее трудно. Поэтому кривую удобнее задавать двумя касательными к ней с точками касания на них и графическим или инженерным дискриминантом.

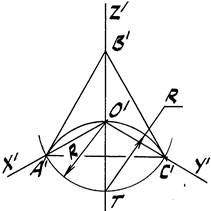
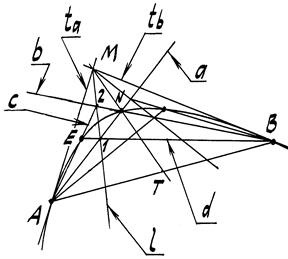
Пусть касательные t_a и t_b касаются кривой в тт. А и В и пересекаются в т. М (рис. 52).

Найдём середину Т хорды АВ и проведём медиану МТ. Выберем на медиане некоторую точку N и зададим тем самым значение дискриминанта. Тогда коника может считаться заданной.

Дискриминантом f коники называется отношение отрезков NM к ТМ, т.е. f= NM/ ТМ. При этом, если f 0,5 – гиперболой.

Поскольку при подсчёте величина дискриминанта окажется, в нашем случае, равной f = 0,42, то искомой кривой будет эллипс. Для построения эллипса необходимо отыскать некоторое множество его текущих точек в следующем порядке:

1. Проводим прямые a =А 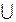N и b = В N.

2. Через т. М проводим произвольную прямую l, которая пересечёт прямые

a и b соответственно в точках 1 и 2.

3. Точку Е кривой находим на пересечении прямых с (А-2) и d (В-1).

4. Пучок прямых l i c центром в т. М позволяет найти сколько угодно

точек Е i кривой при аналогичных построениях.

Задача 2. Построить арочную кривую, которая определена парой взаимно-параллельных касательных t_a и t_b с точками касания А и В на них и точкой N подъёма (рис. 54).

проходящих через несобственную т. позволяет найти сколько

Источник