Как сделать круг в проекции

Как сделать круг в проекции

§ 14. Построение аксонометрических проекций окружности

Рассмотрите рис. 92. На нем дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями.

Рис. 92. Фронтальные диметрические проекции окружностей, вписанных в грани куба

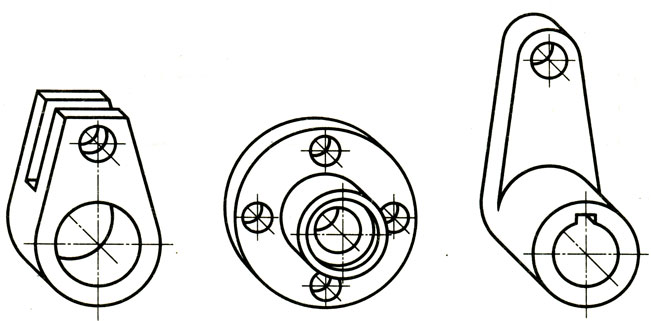
Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем. Поэтому фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подооных представленными на рис. 93.

Рис. 93. Фронтальные диметрические проекции деталей

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием. Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 94, а).

2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 94, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.

Рис. 94. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 94, в).

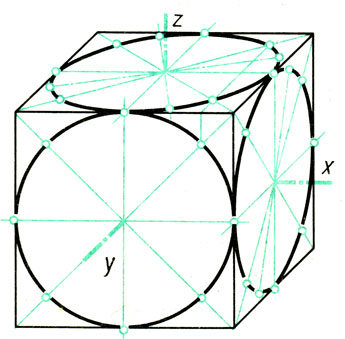
Изометрические проекции окружностей. Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 95), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.

Рис. 95. Изометрические проекции окружностей, вписанных в грани куба

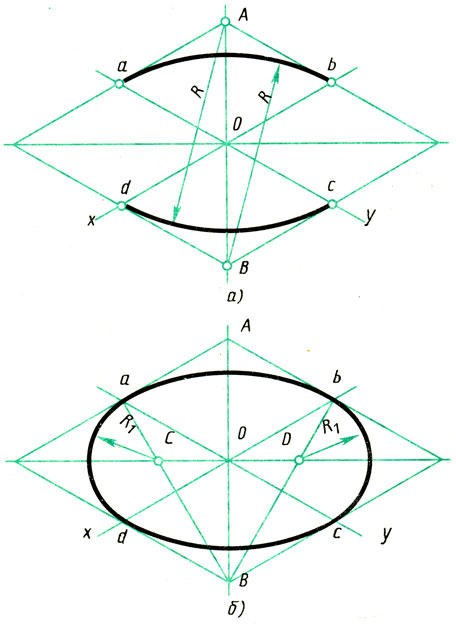
Построение овала, вписанного в ромб.

1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 96, а). Для этого через точку О проводят изометрические оси х и у и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, w, с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.

Рис. 96. Построение овала в плоскости, перпендикулярной оси z

Рис. 97. Построение овала в плоскостях, перпендикулярных осям х и у

Построение изометрической проекции детали с цилиндрическим отверстием.

Как применить рассмотренные построения на практике?

Дана изометрическая проекция детали (рис. 98, а). Нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани.

Построения выполняет следующим образом.

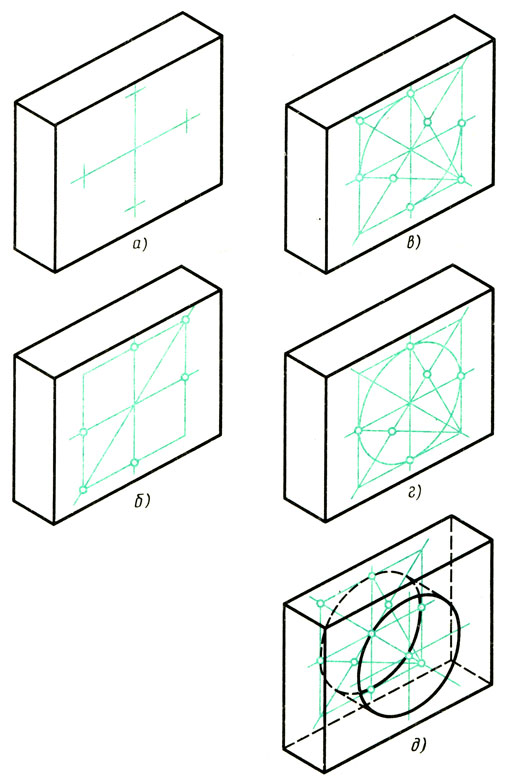
1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 95.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 98, а).

2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 98, б).

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 98, в).

4. Проводят малые дуги (рис. 98, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 98, д).

Рис. 98. Построение изометрической проекции летали с цилиндрическим отверстием

Ответьте на вопросы

1. Какими фигурами изображаются во фронтальной диме-трической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х и у?

2. Искажается ли во фронтальной диметрической проекции окружность, если ее плоскость перпендикулярна оси у?

4. Какими фигурами изображаются в изометрической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х, у, z?

5. Какими фигурами в практике заменяют эллипсы, изображающие окружности в изометрической проекции?

6. Из каких элементов состоит овал?

7. Чему равны диаметры окружностей, изображенных овалами, вписанными в ромбы на рис. 95, если стороны этих ромбов равны 40 мм?

Задания к § 13 и 14

Упражнение 42

Рис. 99. Задание для упражнений

Упражнение 43

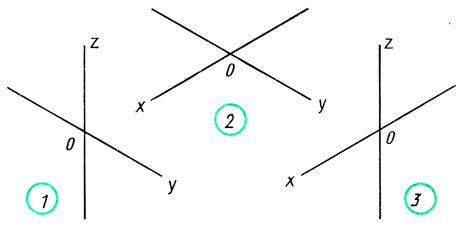
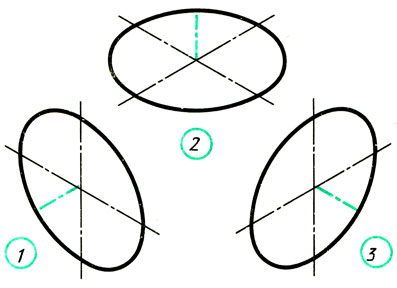
Запишите, какой оси (х, у или z) перпендикулярны плоскости овала на рис. 100. В какой аксонометрической проекции даны здесь окружности?

Рис. 100. Задание для упражнений

Упражнение 44

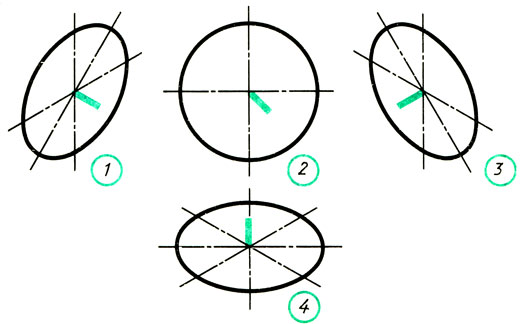
В каких аксонометрических проекциях даны окружности на рис. 101? Какой оси перпендикулярна плоскость каждой из них?

Рис. 101. Задание для упражнений

Упражнение 45

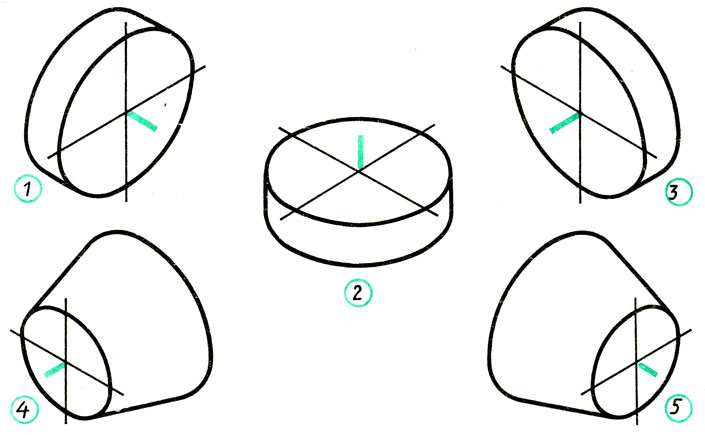
Запишите, в каких аксонометрических проекциях даны геометрические тела на рис. 102.

Каким осям (х, у или z) параллельна высота каждого из них?

Рис. 102. Геометрические тела для задания для упраждений

Упражнение 46

5 ПРИЧИН КОТОРЫЕ ОТТАЛКИВАЮТ КЛИЕНТОВ: КАК МОЖНО ВСЁ ИСПРАВИТЬ здесь.

Источник

Проецирование окружности

Окружность с центром О, рассматриваемая как плоская фигура, проецируется без искажения на ту плоскость, которой она параллельна (рис. 6.5). При этом две другие ее проекции есть отрезки, параллельные осям проекций и равные по длине диаметру окружности.

Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси зависит от угла наклона плоскости окружности к плоскости проекций.

Окружность, изображенная на рис. 6.6, перпендикулярна плоскости проекций П и наклонена к плоскости проекций к₂, поэтому ее фронтальная проекция — эллипс. Большая ось этого эллипса С «И « представляет собой проекцию диаметра окружности, который без искажения проецируется на плоскость проекций л₂. Таким образом, она перпендикулярна плоскости проекций Л1 и параллельна плоскостям проекций 7^2 и Лз. Малая ось эллипса является проекцией диаметра АВ, перпендикулярного СИ. Ее величину на плоскости проекций п₂ определяют с помощью линий проекционной связи, проведенных через точки А’ и В’.

Промежуточные точки эллипса находят с помощью дополнительной плоскости проекций тс₄, которую располагают параллельно плоскости окружности, поэтому окружность проецируется на нее без искажения. Вначале строят новую проекцию центра окружности — точку О™ и на плоскости тс₄ описывают заданную окружность. Затем на окружности намечают 8 или 12 произвольных точек и находят их проекции в системах плоскостей щ/щ и щ/л₂. На рис. 6.6 приведено построение только для двух промежуточных точек 1 и 2; остальные строят аналогично.

Окружность, расположенная в плоскости общего положения, проецируется на все основные плоскости проекций в виде эллипсов, большие оси которых равны ее диаметру. Величины малых осей обычно различны и зависят от углов

наклона заданной плоскости, в которой расположена окружность, к плоскостям проекций.

Если эллипс представляет собой проекцию окружности, то на горизонтальной проекции его большая ось расположена на горизонтальной прямой плоскости, на фронтальной — на фронтальной прямой и на профильной — на профильной прямой.

Построение в плоскости общего положения а(И_а п /_а) (рис. 6.7) проекций окружности с центром в точке О, расположенной на горизонтальной прямой /г_а, и с радиусом, равным /?, начинают с определения проекций осей эллипса.

Для фронтальной проекции окружности через точку О « проводят проекцию прямой, параллельной^’, и на ней вправо и влево от точки О » откладывают радиус окружности Я, получая точки Е «, Е». Сделав замену плоскостей проекций П/П2 —> П2/Л5, где п₅ Е/_а, и построив новую проекцию окружности в виде отрезка, равного диаметру окружности, строят на фронтальной проекции с помощью точек 1У, малую ось эллипса.

Таким образом, на каждой проекции есть по четыре точки, принадлежащие проекции окружности: точки Л ‘, ВС‘, В‘ и Е «, Е», К «, Ь». Проводя из них линии проекционной связи, получают восемь точек для построения горизонтальной и фронтальной проекций эллипса.

Источник

Урок 18. Построение окружности в аксонометрии

Лист 1. Тема урока: Построение окружности в аксонометрии.
Лист 2. Фронтальная диметрическая проекция (см. рис. 18.1).

Рис. 18.1 Рис. 18.2
Лист 3. Изометрическая проекция (см. рис. 18.2).
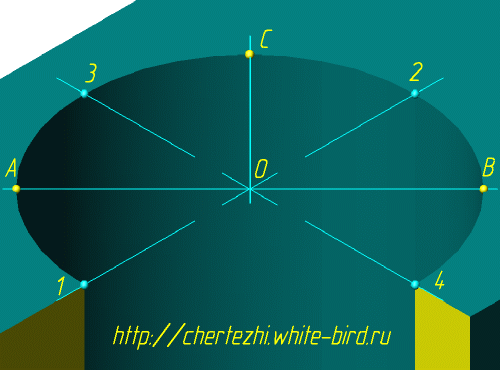
Лист 4. Центровые оси (см. рис. 18.3). Для выполнения построений учащимся выдаются распечатанные заготовки (см. приложение 8).

Рис. 18.3 Рис. 18.4
Лист 5. Обозначения осей для построения овала в плоскости V, W, H (см. рис. 18.4).

Лист 6-7. Построение овала в горизонтальной плоскости проекции. Обозначение оси Z – главная ось (см. рис. 18.5), на пересечении окружности и осевой обозначаем точки (см. рис. 18.6), из них проводим вспомогательные радиусы (синие стрелки) до пересечения с осевыми линиями (см. рис. 18.7).

Лист 8-14. Проводим две большие дуги овала, для этого ножку циркуля ставим в точки, раствор циркуля равен длине стрелки (см. рис. 18.8, 18.9).

Рис. 18.10 Рис. 18.11
Строим две малые дуги овала. Центры малых дуг лежат на пересечении двух левых и двух правых стрелок. Радиус равен остатку стрелки (см. рис. 18.10). Овал в горизонтальной плоскости построен (см. рис. 18.11).
Лист 15 – 20. Построение овала во фронтальной плоскости проекции. Обозначение оси Y – главная ось (см. рис. 18.12), на пересечении окружности и осевой обозначаем точки (см. рис. 18.13), из них проводим вспомогательные радиусы до пересечения с осевыми линиями (см. рис. 18.14). Строим большие дуги овала (см. рис. 18.15). Затем малые дуги овала (см. рис. 18.16).

Рис.18.14 Рис.18.15 Рис. 18.16
Лист 21 – 25. Построение овала в профильной плоскости проекции. Обозначение оси X – главная ось, на пересечении окружности и осевой обозначаем точки, из них проводим вспомогательные радиусы до пересечения с осевыми линиями.

Рис. 18.19 Рис. 18.20 Рис. 18.21
Лист 26. Домашнее задание (см. рис. 18.22).

Файл проекта урока для интерактивной доски MIMIO Скачать

Источник

Как сделать круг в проекции

Как начертить окружность в изометрии?

>

В предыдущем уроке мы попытались разобраться, как построить изометрию. Если с построением плоских линий и форм все понятно, то построение цилиндрических и конусовидных элементов может вызвать дополнительные вопросы. Итак, рассмотрим окружность в изометрии.

Вы можете сказать «спасибо!» автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»

Автор комментария: Елена
Дата: 2011-08-03

Молодцы! Отличный ресурс! Облазила много сайтов посвященных инженерной графике, но объяснения приведенные здесь показались мне самыми доступными. Теперь смогу объяснить все дочери 🙂

Автор комментария: николай
Дата: 2012-04-14

СПАСИБО!урок очень помог.я уже было собирался «на глаз» чертить.

Автор комментария: Леон
Дата: 2012-05-25

Превосходный сайт! Благодарю авторов этого сайта.

Автор комментария: Аида
Дата: 2012-07-11

черчение не мое, но придется любит, работа такая

Автор комментария: е%лан палыч
Дата: 2012-10-08

все четко е$%ть колотить на%

Автор комментария: константин.
Дата: 2013-03-24

спасибо. вспомнил молодость,чертя для внучки. и это хорошее воспоминание..

Автор комментария: Андрей
Дата: 2013-04-12

Полагаю, что вы имели ввиду недостаточно описанную технологию построения эллипса, но это уже есть в другом уроке, ссылка на него есть в тексте.

Автор комментария: Дмитрий
Дата: 2016-06-07

Здравствуйте. А как изображается резьба у гайки в изометрии?

Автор комментария: Зоя
Дата: 2016-12-16

Спасибо! Тоже бабушка, несущая свет

Автор комментария: 123
Дата: 2019-03-06

Источник

§ 8. Аксонометрические проекции предметов, имеющих круглые поверхности

8.1. Фронтальные диметрические проекции окружностей. Если на аксонометрическом изображении хотят некоторые элементы. например окружности (рис. 64), сохранить неискаженными, то применяют фронтальную диметрическую проекцию. Построение фронтальной диметрической проекции детали с цилиндрическим отверстием, два вида которой даны на рисунке 64, а, выполняют так:

Рис. 64. Построение фронтальной диметрической проекции

Постройте в рабочей тетради фронтальную диметрическую проекцию детали, изображенной на рисунке 64, а. Ось у направьте в другую сторону. Величину изображения увеличьте примерно в два раза.

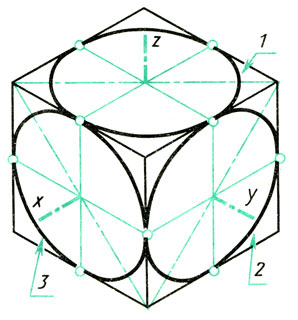
8.2. Изометрические проекции окружностей. Изометрической проекцией окружности (рис. 65) является кривая, которая называется эллипсом. Эллипсы строить трудно. В практике черчения вместо них часто строят овалы. Овал — замкнутая кривая, очерченная дугами окружностей. Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.

Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб

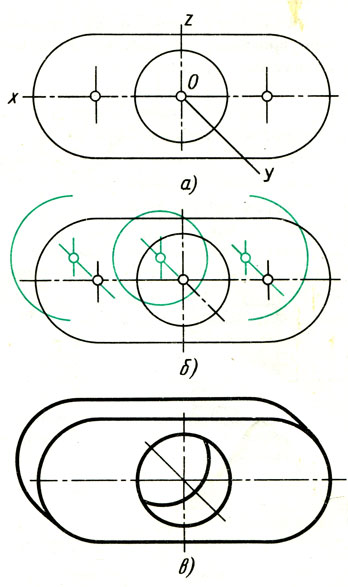
Построение овала, вписанного в ромб, выполняют в такой последовательности.

Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб.

Рис. 66. Построение овала

Большая ось овала располагается на большой диагонали ромба.

После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б).

Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала.

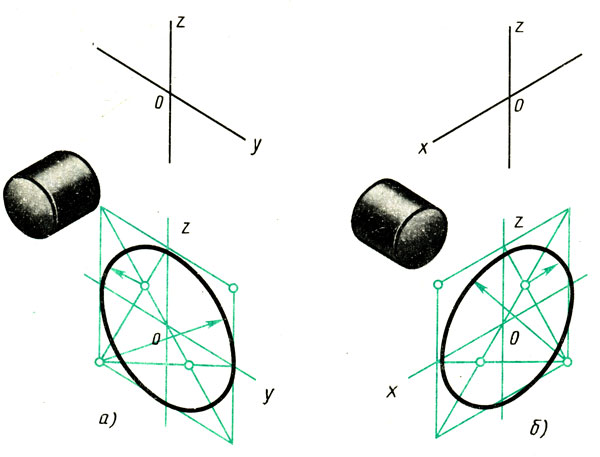
Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике.

Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x

Рис. 68. Построение изометрической проекции детали с цилиндрическим отверстием

Источник