Как сделать куб эшера

Как нарисовать невозможный 3д куб Эшера поэтапно – Рисуем невероятные фигуры

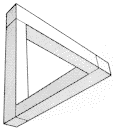
Что такое невозможный куб? Эта оптическая иллюзия, также называемая иррациональным кубом, была создана голландским художником М.С. Эшером в 1958 году. Его литографическая печать « Бельведер» изображает здание, основанное на невозможном кубе, которое, кажется, бросает вызов законам геометрии.

Невозможный куб определяется как «двумерная фигура, внешне напоминающая перспективный чертеж трехмерного куба, элементы которого непоследовательно нарисованы так, как они выглядят в реальном кубе». Другими словами, изображение выглядит как куб, который соединяется и перекрывается невозможным образом.

Невозможный куб связан с кубом Неккера — чертежом, на котором передняя грань куба может выглядеть как один из двух разных квадратов, в зависимости от того, как вы на него смотрите.

Пересечение верхней балки невозможного куба напоминает одну ориентацию куба Неккера, а нижние — как другую. Результатом является, казалось бы, трехмерный объект, который не может существовать в реальной жизни.

Многие художники экспериментировали с невозможным кубом, часто создавая отвлекающие оптические иллюзии. Некоторые статуи даже соответствуют этому описанию, если смотреть под определенным углом. В 1966 году в журнале Scientific American была показана фотография, изображающая невозможный куб .

Как работают оптические иллюзии, подобные этой? Человеческий глаз имеет тенденцию воспринимать двухмерные рисунки как трехмерные объекты. Поэтому линии на бумаге, кажется, представляют собой настоящий, осязаемый объект.

Иллюзии также полагаются на то, что мы уже знаем о мире. Наш глаз может быть обманут в применении общей геометрии или размеров к изображению. В случае невозможного куба мы делаем предположения о прямых углах и прочности балок.

Хотите нарисовать невозможный куб? Это простое пошаговое руководство по рисованию куба поможет вам. Все, что вам нужно, это карандаш, лист бумаги и ластик. Вы также можете покрасить свой законченный рисунок.

Если вам понравился этот урок, см. Также следующие руководства по рисованию: Бейсбол, Футбол и Футбольный шлем.

Пошаговая инструкция по рисованию невозможного куба

1. Начните рисовать три прямые, вертикальные линии. Линии должны быть одинаковой длины, но средняя линия должна располагаться ниже, чем остальные. Затем соедините линии внизу, используя прямые линии. Это формирует боковые и нижние края куба.

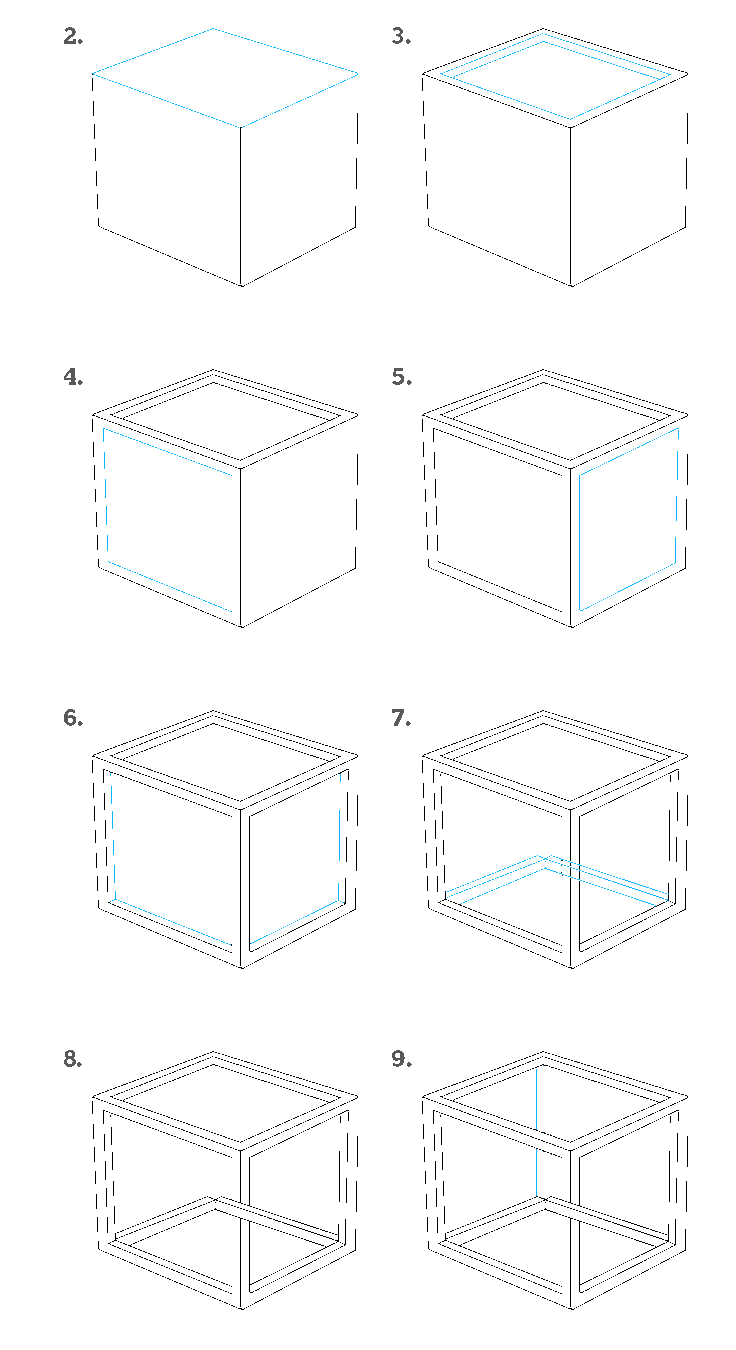
2. Нарисуйте четырехугольник или четырехстороннюю форму в верхней части куба.

3. Далее подробно опишите верхнюю панель куба. Нарисуйте меньший квадрат в верхней части куба. Протяните короткую прямую линию от самого верхнего угла этого квадрата. Затем нарисуйте две прямые линии, идущие от этой линии, параллельно сторонам квадрата.

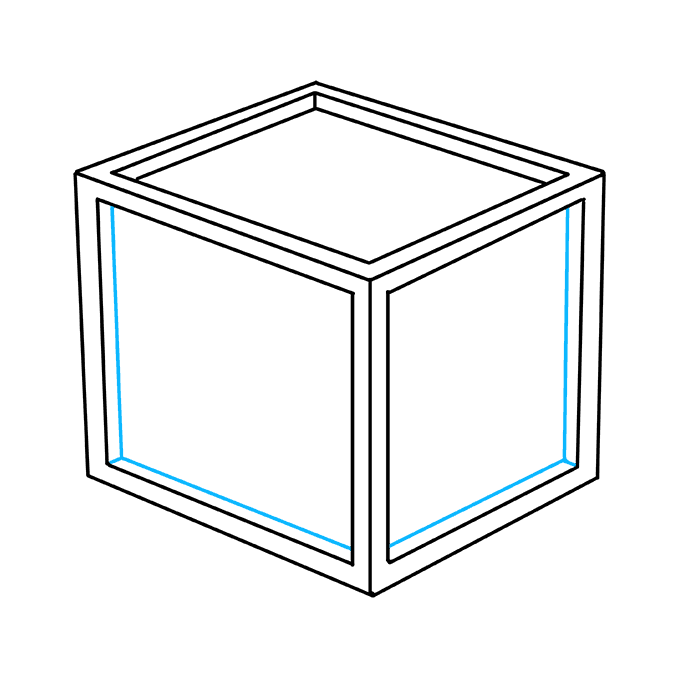
4. Нарисуйте квадрат внутри одной из боковых панелей куба.

ДРУГИЕ ЛЕГКИЕ РУКОВОДСТВА ПО ЧЕРТЕЖАМ:

5. Нарисуйте квадрат в оставшейся боковой панели куба.

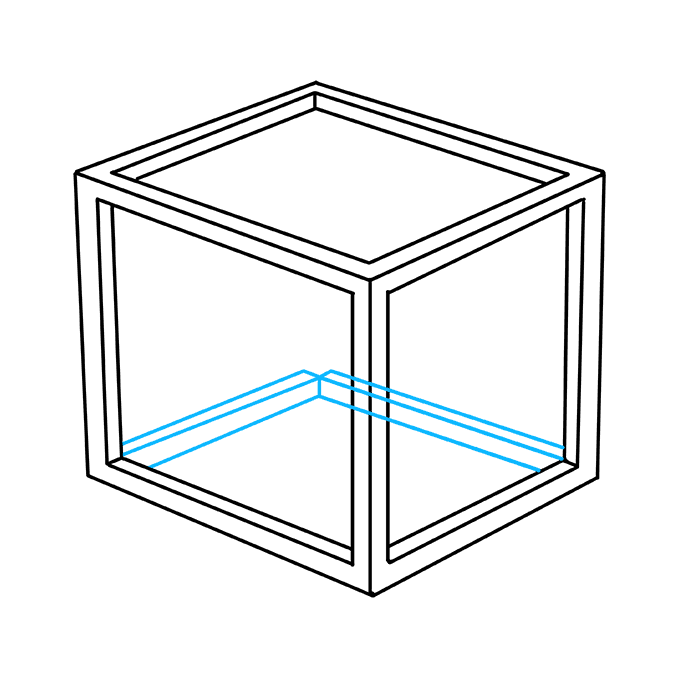
6. Нарисуйте короткие прямые линии, идущие от противоположных углов квадратов. Затем нарисуйте две прямые линии, идущие от каждой из коротких линий. Эти линии должны быть параллельны сторонам квадрата.

7. Вытяните три прямые линии из нижнего левого угла куба. Затем вытяните три прямые линии из нижнего правого угла куба. Позвольте нижней и средней линии встретиться. Затем соедините концы линий, образуя прямоугольники.

8. Сотрите направляющие линии из фигур, нарисованных на предыдущем шаге

ДРУГИЕ ЛЕГКИЕ РУКОВОДСТВА ПО ЧЕРТЕЖАМ:

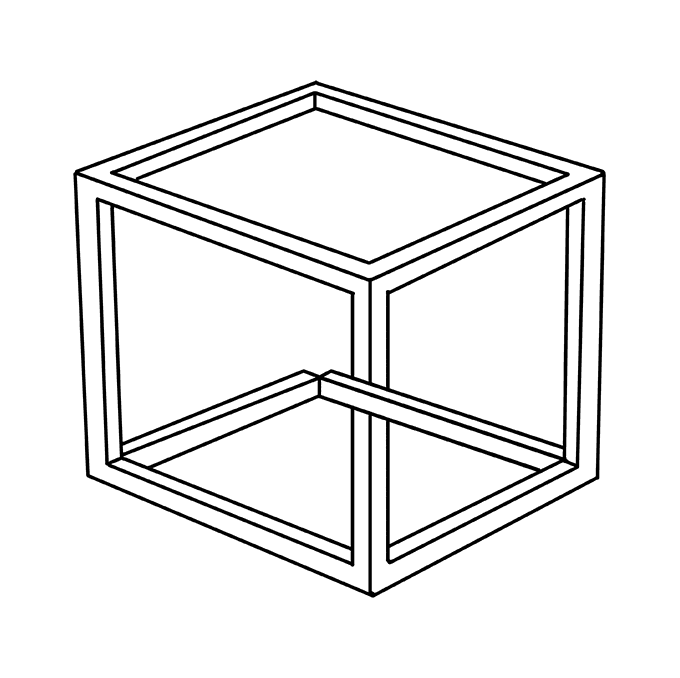
9. Нарисуйте последнюю сторону невозможного куба. Нарисуйте три прямые, параллельные линии, соединяющие верхний и нижний задние углы куба.

10. Раскрась свой невозможный куб.

Ознакомьтесь с нашими руководствами по рисованию искусственных объектов для получения дополнительной информации

Полное руководство по рисованию невозможного куба в одном изображении

Понравилось руководство по рисованию?

Оставьте комментарий ниже или следуйте на Pinterest.

Источник

Математическое искусство М.К. Эшера

Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Когда он учился в школе, родители планировали, что он станет архитектором, но плохое здоровье не позволило Морицу закончить образование, и он стал художником. До начала 50-х годов он не был широко известен, но после ряда выставок и статей в американских журналах (Time и др.) он получает мировую известность. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования.

В процессе своей работы он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии, о чем будет рассказываться ниже. Он был очарован всевозможными парадоксами и в том числе «невозможными фигурами». Парадоксальные идеи Роджера Пенроуза были использованы во многих работах Эшера. Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости и логика трехмерного пространства.

Мозаики

Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него «богатейшим источником вдохновения». Позже в 1957 году в своем эссе о мозаиках Эшер написал:

В математических работах регулярное разбиение плоскости рассматривается теоретически. Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней.

Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. (Нерегулярных вариантов разбиения плоскости гораздо больше. В частности в мозаиках иногда используются нерегулярные мозаики, в основу которых положен правильный пятиугольник.) Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.

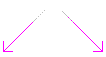Регулярное разбиение плоскости птицами	Рептилии	Цикл	Эволюция 1

В гравюре «Рептилии» маленькие крокодилы играючи вырываются из тюрьмы двухмерного пространства стола, проходят кругом, чтобы снова превратиться в двухмерные фигуры. Мозаику рептилий Эшер использовал во многих своих работах. В «Эволюции 1» можно проследить развитие искажения квадратной мозаики в центральную фигуру из четырех ящериц.

Многогранники

Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.

Форма пространства

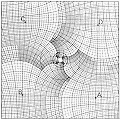
Под влиянием рисунков в книге математика Х. Коксетера Эшер создал много иллюстраций гиперболического пространства. Один из примеров можно увидеть в работе «Предел круга III». Здесь представлен один из двух видов неевклидового пространства, описанных французским математиком Пуанкаре. Чтобы понять особенности этого пространства, представьте, что вы находитесь внутри самой картины. По мере вашего перемещения от центра круга к его границе ваш рост будет уменьшаться также, как уменьшаются рыбы на данной картине. Таким образом путь, который вам надо будет пройти до границы круга будет казаться вам бесконечным. На самом деле, находясь в таком простарнстве вы на первый взгляд не заметите ничего необычного в нем по сравнению с обычным евклидовым пространством. Например, чтобы достичь границ евклидового пространства вам также необходимо пройти бесконечный путь. Однако, если внимательно присмотреться, то можно будет заметить некоторые отличия, например, все подобные треугольники имеют в этом пространстве одинаковый размер, и вы не сможете там нарисовать фигуры с четырьмя прямыми углами, соединенными прямыми линиями, так как в этом пространстве не существует квадратов и прямоугольников. Странное место, не правда ли?

Логика пространства

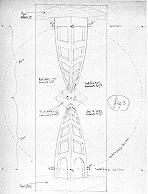
Под «логикой» пространства мы понимаем те отношения между физическими объектами, которые обычны для реального мира, и при нарушении которых возникают визуальные парадоксы, называемые еще оптическими иллюзиями. Большинство художников, экспериментирующие с логикой пространства, изменяют эти отношения между объектами, основываясь на своей интуиции, как, например, Пикассо.

Водопад

Самовоспроизведение и информация

В заключение мы рассмотрим аспекты творчества Эшера, относящиеся к теории информации и искусственному интеллекту. Эта область творчества художника широко освещена во многих статьях и книгах. Наиболее полное исследование этого вопроса освещено в книге Дугласа Хофстадтера (Douglas R. Hofstadter) «Гёдель, Эшер, Бах: Бесконечная золотая нить» (Godel, Escher, Bach: An Eternal Golden Braid), выпущенной в 1980 году и награжденной пулитцеровской премией.

Центральная идея самовоспроизведения, взятая на вооружение Эшером, обращается к загадке человеческого сознания и способности человеческого мозга обрабатывать информацию так, как не сможет обработать ни один компьютер. Литографии «Рисующие руки» и «Рыбы и чешуйки» используют эту идею разными способами. Самовоспроизведение является направленным действием. Руки рисуют друг друга, создавая самих себя. При этом сами руки и процесс их самовоспроизведения неразделимы. В работе «Рыбы и чешуйки» концепция самовоспроизведения представлена более функционально, и в данном случае она может быть названа самоподобием. В этом смысле данная работа описывает не только рыб, а все живые организмы, в том числе и человека. Конечно, мы не состоит из уменьшенных копий самих себя, но каждая клетка нашего тела несет в себе информацию обо всем теле в виде ДНК.

Заключение

Мы рассмотрели лишь небольшую часть работ из сотен набросков и литографий и гравюр, оставшихся после смерти Эшера в 1972 году. Еще многое будет сказано и уже сказано о значении и важности его работ. С каждым годом появляется все больше и больше книг, где освещается творчество художника, анализируются различные аспекты его творчества. Надеемся, что мы заинтересовали вас творчеством Эшера.

Перевод Влада Алексеева.

Дополнение переводчика

Спирали

Иной способ представления спирали использован в работе «Сферические спирали», где четыре полосы расположены на поверхности шара, проходя от одного полюса шара к другому. Похожий путь может пройти самолет, летящий с северного полюса земного шара на южный.

Здесь мы привели основные виды спиралей, использованных Эшером в своих работах. Различные их модификации можно обнаружить и на многих других литографиях художника.

Заключение 2

Использование Эшером различных математических фигур и законов не ограничивается лишь вышеприведенными примерами. Внимательно изучая его картины, можно обнаружить и другие, не упомянутые в данной статье, геометрические тела или визуальную интерпретацию математических законов.

Закончить хотелось бы картиной «Узлы», изображающей замкнутые фигуры, которые нельзя отнести к какому-либо разделу данной статьи.

Источник

Можно ли использовать медь в самогоноварении? Медный самогонный аппарат: причуда или необходимость

По свидетельству историков, первыми были медные самогонные аппараты, и не потому, что медь имеет особенные свойства (мы о них еще поговорим), а по более прозаичной причине. В 15 веке, когда начало развиваться самогоноварение, медь была самым доступным металлом.

Из меди изготавливалась посуда, предназначенная для нагревания на огне. Стали в том виде, в котором мы знаем ее сегодня (нержавеющей) не существовало. Человечество только училось обрабатывать сталь, изделия из нее были чрезвычайно дороги и не использовались для приготовления пищи, тем более – самогона.

Современный аппарат из меди

Модификация такого устройства, как самогонный аппарат из меди, в наши дни претерпела некоторые изменения. Конструкция поделена на отдельные составляющие. Она получила название «аламбик». Таким агрегатам присуще оригинальное исполнение. Зачастую их выполняют своими руками.

Есть модели, которые включают в себя ряд материалов. К примеру, наряду с медью применяются нержавейка и стекло. Достаточно часто встречается устройство, где из металла сделаны только трубка и купол.

Самогонный аппарат из меди, отзывы о котором в большинстве своем положительные, имеет самую высокую стоимость. В особенности по сравнению с экономичными вариантами, произведенными из подручных материалов своими руками.

Развертка и схема куба из бумаги

Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой. Скачать:
Контрольные для 1 класса по учебнику Моро М.И.(PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 1 класса
Тренажер к учебнику Моро М.И. Электронное пособие к учебнику Моро М.И.

Геометрия и куб

Куб – это фигура, которые мы встречаем не только на уроках геометрии и изобразительного искусства, но и в нашей повседневной жизни. Другое название куба – правильный гексаэдр. Кубом называется правильный многогранник, каждая грань которого является квадратом. Куб можно назвать объемный, трехмерным или даже 3D квадратом. Куб имеет 8 вершин, 6 граней, 12 ребер. Куб – это удивительная геометрическая фигура, в которую можно спрятать или вписать другие фигуры, например такие: октаэдр, тетраэдр, икосаэдр и другие.

Удивительная фигура «куб»

Куб или гексаэдр также называют кубом Неккера, назван он так в честь швейцарского кристаллографа Луиса Альберта Неккера. В 1832 году Неккер предложил иллюзию, вглядываясь в куб с гранями можно заметить, что маленькая черная точка появляется то на переднем, то на заднем плане, то в углу или в центре. Она перемещается из одного места в другое, как бы движется. Еще одна особенность куба Неккера в том что, его параллельные боковые ребра кажутся расходящимися. Можно перекрасить одну из граней в другой цвет, и посмотреть, как эта цветная грань фантастическим образом перемещается.

Еще один необычный куб – это куб художника Маурица Эшера. Это куб, который невозможен.

Еще одно интересное открытие, имеющие отношение к кубу, было сделано в 1966 году благодаря фотографу Чарльзу Ф. Кокрану. Он сделал фотографию, которую окрестили «сумасшедший ящик». Что же из себя представляет «сумасшедший язык»? Это вывернутый наизнанку каркас фигуры гексаэдра (куба). «Сумасшедший ящик» основывается на неправильных соединениях, которые допустили при рисовании фигуры.

В список самых удивительных и странных фигур можно занести: интегральный куб, разрастающийся куб (также может называться бесконечным кубом), повторяющиеся кубы, кубическую снежинку, парящие кубы, двухэтажный куб и многие, многие другие. Все эти фигуры завораживают, от них не возможно оторвать глаз. Каждый, кто их видит, хочет понять, как они устроены.

Куб всегда таил в себе много загадок – удивительно сложная и в тоже время удивительно простая геометрическая фигура, помогающая заглянуть в глубины сознания. Еще в древности Платон называл ее священной фигурой и относил к знаку Земли, потому что это самая устойчивая фигура из всех других. Куб является фигурой сакральной геометрии. Еще в 16 веке немецкий математик и астроном Иоганн Кеплер составил модель солнечной системы, в которую вписал куб.

Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб. Самая знаменитая игрушка-головоломка, которую хотя бы раз в жизни каждый ребенок держал в руках, а некоторым даже удалось ее собрать, это кубик Рубика. Название говорит само за себя. В 1975 году венгерский архитектор Эрне Рубик создал игрушку-головоломку, которая стала популярной во всем мире. Кубик-рубик представляет собой куб, сделанный из пластмассы, который в свою очередь состоит из 26 кубиков. И когда «Кубик-рубик» собран, каждая его грань окрашивается в один определенный цвет.

Различные вещества кристаллизуются в форме куба, например поваренная соль, минерал флюорит и другие.

Инструменты и материалы, чтобы сделать куб из бумаги

Особенности медного приспособления

Каковы отличительные особенности такого агрегата? Оборудование для производства алкоголя отличается не только внешним видом, но и своими технологическими и химическими процессами, происходящими при изготовлении напитка.

Самогонный аппарат из меди обладает следующими показателями:

Поделки из бумаги – увлечение на всю жизнь

Что-то делать руками всегда интересно и полезно, особенно если получается красиво. Ручная несложная работа помогает успокоить нервы после тяжелого трудового дня и развивает фантазию (особенно у детей). В Китае данный вид творчества известен как оригами, и давно с успехом помогает лечить душевнобольных людей и детишек, страдающими нервными заболеваниями. Такие занятия повсеместно применяются на уроках труда в школах или в старших группах в детских садах, что позволяет развить усидчивость, воображение и мелкую моторику, которая в свою очередь развивает умственную деятельность. Часто детские журналы предлагают схемы различных зверюшек, фигурок для совместной работы взрослых с детьми. Мы предлагаем схемы кубиков из бумаги или картона с различными вариантами картинок. Такие поделки будут интересны как малышам, так и школьникам, их можно преподнести в качестве подарка, сделанного своими руками. Взрослые так же могут использовать сделанные по нашим разверткам кубики, например кубик-календарь.

Пошаговая инструкция: как сделать куб из картона

1. Распечатайте необходимое количество шаблонов, например для кубика-календаря – необходимо оба варианта, а для кубиков с алфавитом – распечатайте столько, сколько нужно для складывания слов. 2. Аккуратно вырежьте схему куба. Вырезать удобнее ножницами, но можно воспользоваться и канцелярским ножом. 3. Согните вырезанный шаблон куба по линиям, чем аккуратнее вы согнёте схему куба, тем лучше будет смотреться ваше изделие. 4. Смажьте затемненные участки клеем и сторону за стороной соберите весь куб.

И еще немного о кубиках из бумаги

Сейчас детские магазины переполнены всякими игрушками, в том числе и развивающими. Можно найти практически всё на любой возраст и кошелёк. Но иногда бывет трудно найти кубики, которые нам знакомы с детства. Кубики – это своего рода конструкторы, с которыми с удовольствием играют детишки. По рекомендациям педагогов, психологов и педиаторов малышам до 1 года уже можно давать игрушки-кубики. Они отлично развивают не только координацию, воображение, но при этом задействуют практически все мышцы рук, что прекрасно развивает мелкую моторику малыша. Из какого только материала не делают кубики – и из пластика, из дерева, из стекла, мы предлагаем вам сделать кубики из бумаги. Кубики с картинками с изображением цифр или букв будут прекрастным подспорьем для родителей и воспитателей в процессе подготовки ребёнка к школе. Более того, игра с кубиком даст малышу представление о геометрическх фигурах, в частности о кубе, о его свойствах. Если вы распечатаете и другие объемные геометрические фигуры (пирамиды, тетраэдр и т.д.), это значительно расширит кругозор ребёнка и поможет в процессе обучения в школе. Совместные занятия взрослых и детей очень сближают и укрепляют семью.

Сейчас практически в каждом доме есть компьютер и принтер, т.е. ваши затраты – это стоимость бумаги, формата А4. Приведённые на данной странице шаблоны куба можно редактировать, т.е. взяв чистую развёртку куба, вы можете смело вставлять свои картинки и распечатать новый вариант. В качестве картинок можно взять рисунки или фотографии зверей, животных, машин, а так же фотографии знаменитостей или своих родственников, полет фантазии безграничен. Успехов вам в творчестве и в воспитании!

Развертка и схема куба из бумаги

Как выглядит аппарат из меди?

Он совсем не похож на аналогичные устройства, выполненные из другого материала. Они, как правило, сделаны из нержавейки и баков. Оборудованию присущи декоративные элементы. Прибор может быть сооружен своими руками, обладать изяществом и компактностью.

Некоторые зарубежные производители выпускают подобные агрегаты. Они получили название «аламбик». Приспособления обладают высоким уровнем производительности. Их отличает разное дизайнерское исполнение. Поверхность таких приборов тщательно отполирована. Готовые изделия можно приобрести при помощи интернет-магазинов.

Цена на эксклюзивные приборы достаточно высока. К примеру, в Португалии есть мастера, которые делают аппараты посредством старинного метода. Металл подлежит тщательной отборке, а пайка производится серебром.

Как правило, чаще употребляются агрегаты смешанной конфигурации, В них использована трубка из меди, а основные детали произведены из нержавейки и специального пластика.

Бытует мнение, что медь не подходит для пищевых целей и, несмотря на надежность этого металла, он может быть вреден для организма человека. Тем не менее, многие фирмы выпускают приборы, выполненные полностью из него, и урон здоровью от него статистика не подтверждает.

С чего начать работу?

Начать работу стоит с создания чертежей и заготовок, особенно если в изготовлении приборов из нержавейки или металла нет особых навыков.

Итак, с чего начать работу:

Листы можно резать ножницами для металла или работать болгаркой — большой разницы в этом нет. Затем стоит приступить к пайке, можно работать паяльником или сваркой, но, главное, следить за герметичностью и надежностью пайки. После того как куб будет готов, стоит проверить, насколько качественно припаян кран. Если работа сделана хорошо, то можно примерить крышку к кубу.

Крышка должна выступать по краям на 1–2 миллиметра. Чтобы повысить герметичность устройства, к крышке приделывают уплотнитель. В качестве него используют резину, ее стоит нарезать тонкими полосками. После стоит заняться монтажом крепежей, за счет которых крышка будет плотно прилегать к кубу.

Последним этапом монтируем датчик температур, его стоит прикрутить сбоку емкости или вмонтировать в крышку — это поможет получить точные показатели и отследить колебания температур.

Несмотря на то что процесс изготовления емкости кажется легким и простым, в процессе работы могут возникнуть трудности. По этой причине многие любители готовить самогон в домашних условиях предпочитают приспособить под куб уже готовую емкость.

Изготовление змеевика своими руками

Змеевик считается очень важной деталью. Для его изготовления потребуется труба из меди, а также большая труба, на которую он будет накручен. Так ему будет придана форма. Чтобы форма трубы нее была нарушена, ее набивают песком или же другим уплотнителем. После этого можно приступать к накручиванию с соблюдением нужного расстояния. При конце процесса следует закрепить другой конец трубки. После этого труба освобождается от песка или же другого материала.

Следует отметить, что труба со змеевиком будет располагаться в охладительной трубе. Поэтому следует заранее учесть ее диаметр. После окончания работы змеевик помещается в холодильник. В нем делаются отверстия и ставятся заглушки. Поверхность герметизируется для того, чтобы из нее не происходила утечка жидкости.

Почему медь нужно чистить

И вот мы подобрались к самому важному – медь в обязательном порядке нужно чистить. Окислы, которые постепенно скапливаются на медных поверхностях, препятствуют контакту спиртовых паров с металлом. Окислительно-восстановительные реакции сводятся к минимуму, страдают теплообменные свойства. Есть несколько простых, но действенных способа очистить медь от налёта солей, при этом не нужно использовать ни какой бытовой химии, остатки которой на внутренних поверхностях дистиллятора могут повлиять на качество самогона:

Для поддержания меди в «рабочем состоянии» её чистку нужно проводить регулярно, в идеале после каждой перегонки или при появлении на поверхностях видимого налёта. Также рекомендуется чистить медные элементы снаружи, что не только влияет на внешний вид изделия, но и сохраняет его высокую теплопроводность. Особенно это актуально для медного шлема аламбика, стенки которого, посредством охлаждения воздухом, выступают в роли некого дефлегматора. Для внешней чистки можно использовать специальные чистящие средства для меди или воспользоваться одним из народных средств.

Внешнюю поверхность меди можно отполировать пастой собственного приготовления на основе обычной муки, соли и уксуса. Для этого нужно смешать четверть стакана муки и четверть стакана соли, а затем добавлять уксус, с постоянным перемешиванием, до образования густой пасты. Для полировки достаточно нанести пасту, используя мягкую ткань, на медные поверхности, подождать примерно 30 минут до её высыхания и просто смыть водой.

Изготовление сухопарника

Самогонные аппараты из меди с сухопарником обладают более завершенной конструкцией.

Сухопарник (дефлегматор или прикубник) не является обязательной составляющей. Деталь посредством трубок присоединяется к кубу для перегонки и змеевику. Она служит для физической очистки спиртного от вредных примесей.

Конфигурация самодельного дефлегматора может быть унифицированной.

Почему медь – это опасно

Одновременно с очисткой и улучшением самогона, в медных самогонных аппаратах образуются растворимые медные окислы, которые токсичны и могут сильно навредить здоровью пьющих. Чтобы предотвратить контакт солей меди с продуктами питания, медную посуду покрывают слоем олова (лудят). Но от луженой меди в самогонных аппаратах толку мало – с парами или флегмой она не контактирует, ни каких реакций не происходит. Тупик? Не совсем.

Окислы меди могут попасть в дистиллят лишь в момент конденсации спирта внутри медного холодильника – до этого нелетучие соли меди или оседают на шлеме аламбика и медных комплектующих царги-дефлегматора бражной колонны, или смываются флегмой обратно в куб. Следовательно, использование луженого холодильника (или изготовленного из нержавеющей стали) решает описанную выше проблему без вреда общему делу. Тем более медный холодильник, что было доказано лабораторными исследованиями, оказывает минимальное влияние на удаление ДМТС (но положительно влияет на превращение вонючего диметилсульфида (ДМС) в менее ароматный сульфид).

Сувенир «Сердечко» из медной проволоки

Можно совмещать проволоку и с другими материалами. Например, незамысловатое, но очень милое сердечко из медной проволоки можно зафиксировать на деревянном брусочке.

Складываем сердечко

Перекручиваем проволоку у основания сердечка.

Перекручиваем проволоку

Выкладываем проволоку второй раз. Фиксируем конец проволоки в нижней части сердечка.

Двойное сердечко из проволоки

Делаем отверстие в деревянном кубике, наливаем туда немного клея и вставляем туда проволоку с сердечком. Получится замечательный сувенир, который, кстати, удобно использовать в качестве подставки для записок, визиток и даже фотографий.

Сувенир из проволоки с сердечком

Бабочка из медной проволоки

Во-первых, нужно научиться делать из проволоки завитки. Удобно с этой целью использовать специальные щипчики.

Делаем щипчиками завиток

Только на основе таких завитков можно сделать замечательный вариант поделки из проволоки для детей – изящную бабочку с невесомыми ажурными крылышками.

Закручиваем с помощью щипчиков второе крылышко.

Закручиваем крылышко

Приклеиваем по центру крупную бусину.

Приклеиваем бусину

Лайфхак-самоделка 3: Трубка-завивальщица

На этот раз трубка пригодится и без продольных разрезов. С помощью плоскогубцев всего лишь приплющим ее на некотором расстоянии от края.

Длинный конец трубки вставляем в кулачок дрели, а в короткий сплюснутый – концы зачищенного от изоляции провода, которые необходимо скрутить при выполнении электропроводки.

Включаем дрель на небольшую скорость и в итоге получаем плотно скрученные концы.

Каждый лайфхак из тех, которые мы перечислили выше, очень прост в исполнении. Однако полученная с его помощью самоделка будет очень полезна для вас при выполнении довольно большого числа операций. А в дополнение к этому и металлическая трубочка, которая валялась у нас без дела и которую очень хотелось выбросить, нашла себе вполне достойное применение.

Самоделки из двигателя от стиральной машины:

1. Как подключить двигатель от старой стиральной машины через конденсатор или без него 2. Самодельный наждак из двигателя стиральной машинки 3. Самодельный генератор из двигателя от стиральной машины 4. Подключение и регулировка оборотов коллекторного двигателя от стиральной машины-автомат 5. Гончарный круг из стиральной машины 6. Токарный станок из стиральной машины автомат 7. Дровокол с двигателем от стиральной машины 8. Самодельная бетономешалка

30 идей самоделок из труб (яркая фотоподборка)

ПВХ и алюминиевые трубы можно использовать не только по прямому назначению. Из них можно сделать мебель, стеллажи для гаража, кладовки или комнаты, декоративные элементы и даже украшения. Смотрите подборку вещей из ПВХ и алюминиевых труб, выбирайте то, чего не хватает вашему дому, и пробуйте сделать своими руками.

Источник

• ← Как сделать куб чертеж
• Как сделать кубанку своими руками →