Как сделать кубическую параболу
Кубическая функция
Куби́ческая фу́нкция в математике — это числовая функция 
где 
Содержание
Аналитические свойства
Производная кубической функции 






График
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 




Кроме того, кубическая парабола
Коэффициент при кубе
Коэффициент при квадрате
Коэффициент при первой степени
Применение
Кубическую параболу иногда применяют для расчёта переходной кривой на транспорте, так как её вычисление намного проще, чем построение клотоиды.
См. также
Литература
Смотреть что такое «Кубическая функция» в других словарях:
Кубическая парабола — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция вида где Другими словами кубическая функция задаётся многочленом третьей степени … Википедия
Кубическая кривая Безье — Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов… … Википедия
КУБИЧЕСКАЯ ГИПЕРПОВЕРХНОСТЬ — проективное алгебраич. многообразие, задаваемое однородным уравнением 3 й степени с коэффициентами из нек рого основного поля k. Кубические кривые. Неприводимая кубич. кривая является либо гладкой (в этом случае ее канонич. класс равен 0, а род… … Математическая энциклопедия
Парабола кубическая — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция вида где Другими словами кубическая функция задаётся многочленом третьей степени … Википедия
Список математических функций — Эта страница информационный список. В математике, многие функции и группы функций настолько важны, что заслужили право на собственные имена. Ниже приведён список статей, которые содержат подробные описания некоторых из таких функций … Википедия
Кубические простые числа — Кубические простые числа это простые числа, которые являются решением одного из двух кубических уравнений третей степени от переменных x и y. Первое из них: [1] и первые несколько таких кубических простых чисел: 7, 19, 37, 61, 127, 271, 331 … Википедия
Линия — I Линия (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной… … Большая советская энциклопедия
Кривые Безье — были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.… … Википедия
Кубические кривые Безье — Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов… … Википедия
Приближение и интерполирование функций — раздел теории функций, посвященный изучению вопросов приближённого представления функций. Приближение функций нахождение для данной функции f функции g из некоторого определённого класса (например, среди алгебраических… … Большая советская энциклопедия
Кубическая парабола
Куби́ческая фу́нкция в математике — это числовая функция 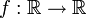
где 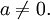
Содержание
Аналитические свойства
График
Кроме того, кубическая парабола
См. также
Литература
Смотреть что такое «Кубическая парабола» в других словарях:
КУБИЧЕСКАЯ ПАРАБОЛА — алгебраическая кривая 3 го порядка: y = x3 … Большой Энциклопедический словарь
кубическая парабола — алгебраическая кривая 3 го порядка: у = х3. * * * КУБИЧЕСКАЯ ПАРАБОЛА КУБИЧЕСКАЯ ПАРАБОЛА, алгебраическая кривая 3 го порядка: y = x3 … Энциклопедический словарь
КУБИЧЕСКАЯ ПАРАБОЛА — алгебр кривая 3 го порядка (рис.): у = х3 … Естествознание. Энциклопедический словарь
Кубическая парабола — плоская кривая; см. Линия … Большая советская энциклопедия
КУБИЧЕСКАЯ ПАРАБОЛА — плоская кривая (см, рис.), выражаемая в прямоугольной системе координат уравнением у=ах 3 … Математическая энциклопедия
Парабола кубическая — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция вида где Другими словами кубическая функция задаётся многочленом третьей степени … Википедия
Кубическая функция — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция … Википедия
Парабола — У этого термина существуют и другие значения, см. Парабола (значения). Парабола, её фокус и директриса Коническое сечение … Википедия
Парабола (значения) — Парабола: Парабола геометрическое место точек, равноудалённых от данной прямой и данной точки. Кубическая парабола числовая функция, задаваемая многочленом третьей степени. Полукубическая парабола (парабола Нейла) плоская алгебраическая кривая.… … Википедия
Кубическая кривая Безье — Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов… … Википедия
Как построить параболу
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
Построить график функции y=x²+2x-3.
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
Построить график функции y=x²+5x+4.
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Вершина (-1,5; 2,25) — первая точка параболы.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x ² +c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Куб графика – График кубической функции. Построить кубическую функцию. Кубическая парабола график.
График кубической функции. Построить кубическую функцию. Кубическая парабола график.
Как построить график кубических функций вида \(y = a (x − h)3 + k\). В этой статье мы покажем как построить график кубических функций путем построения точек. Общая формула кубической функции:
где \(a, b, c\) и \(d\) являются действительными числами и \(a\) не равно нулю.
Построим график кубических функций путем построения точек.
Пример 1. Постройте график \(y = x^3 + 3\) на промежутке \(-3 ≤ x ≤ 3\).
Пример 2. Постройте график \(y = x^3-9x + 5\) на промежутке \(-4 ≤ x ≤ 4\):
Решение. Строим график аналогично первому примеру:
1) когда \(x = 1.6, \;y≈ –5.3\)
2) когда \(y = 12, \;x ≈ –0.8 \) или \( x ≈ –2.5\)
Теперь выведем правила построения графиков кубических функций вида \(y = a (x − h)^3 + k\).
Академический рисунок куба. Основные правила поэтапного рисования
Изображение куба – самое простое и первое задание по изображению предметов в пространстве. Для этого вам уже нужно знать правила передачи тонов, а также воздушной и линейной перспективы. Пропускать это академический рисунок куба нельзя, ведь именно на нём закладываются основы передачи объема и пространства. Уже на этом задании многие ученики делают массу ошибок, если их вовремя не исправить, то они переползут на будущие работы.
Общие правила рисования
Напоминаем, что задача изображения куба – тренировка умения видеть пропорции, оттенки и отображать их на листе бумаги. Поэтому при рисовании следуйте нескольким правилам, без них вы не приобретете нужного навыка.
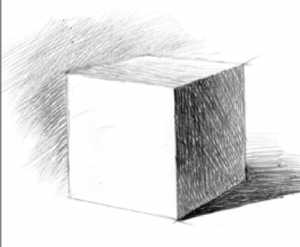
 Границы и перспектива в академическом рисунке
Границы и перспектива в академическом рисунке
Сначала легкими линиями изображаем положение куба на листе бумаги. Предмет вместе с тенью должен находиться по центру листа. Сначала изображаем тонкими линиями грани куба, они у него параллельны. Но по законам отображения объема все параллельные линии в перспективе соединяются в одной точке на горизонте. Кажется, что для такого небольшого размера как куб это правило не важно, но оно обязательно для выполнения.

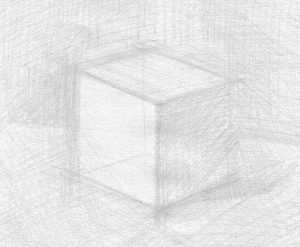
Штриховка и объем

Рисуем куб. | Рисуем вместе
Начнем ab ovo что в нашем случае означает с куба:).
Вы, должно быть, знаете, что традиционно самое первое и самое простое задание по рисунку — это нарисовать куб. Задание действительно самое простое, но уже при его выполнении можно сделать массу ошибок (которые в дальнейшем переползают в более сложные постановки). Поэтому, скучное и неинтересное задание на самом деле очень полезно сделать.
Рисовать разумеется, лучше с натуры, так что, если вы не рисуете куб в учебном заведении, можно его просто склеить из листа ватмана. Оптимальный размер стороны 18-20 см. Готовый кубик нужно поставить на стул или стол, который предварительно можно накрыть темной тканью. Красивые складки выкладывать не обязательно, для начала наша задача разобраться с простой геометрией. Источник света традиционно находится слева и сверху, лучше свет натуральный, то есть от окна. Но лампа тоже сгодится. Осталось выбрать себе место и начать!
На выборе места, кстати, хотелось бы остановиться отдельно. Во-первых, не стоит слишком приближаться. Посмотрите, какого примерно размера то, что вы будете изображать (не сам куб, а все, что попадает в кадр — вместе с краем стола и драпировкой).
Расстояние от изображаемых предметов до художника должно быть в 2-3 раза больше размера этих предметов.
Это справедливо для любой постановки, будь это натюрморт или человек. Объект должен попадать в поле зрения целиком, так, чтобы его увидеть, не приходилось крутить головой. Мольберт или доску нужно поставить также с расчетом на то, что она не будет закрывать обзор. В идеале вы можете видеть рисунок и натюрморт одновременно и только переводите взгляд с одного на другое.
Кроме того, желательно выбрать место так, чтобы вы видели 3 грани кубика (то есть, смотрите на него не в лоб, а сбоку). Боковые грани куба (как и край стола) в рисунке не должны быть параллельны листу — это не слишком хорошо воспринимается в готовой работе. Итак, сели.
На первом этапе вы просто намечаете положение в листе. В случае с кубом (и любым другим неодушевленным предметом в количестве 1 шт.), вы располагаете его так, чтобы справа и слева расстояние до края листа было одинаковым, а сверху пространства оставалось немного больше, чем снизу. На сколько больше? На глаз. Или читаем про композицию)
Далее, в тонких линиях намечаются грани. Помним про линейную перспективу. Вертикальные линии параллельны друг другу, остальные должны сходиться на горизонте. Линию горизонта найти достаточно просто, она всегда находится на уровне глаз. То есть, высота линии горизонта величина не постоянная и зависит от того, лежите вы, стоите или залезли на стремянку. Не стоит брать слишком высокий или слишком низкий горизонт. В первом случае будет впечатление вывернутости и искаженной перспективы, во втором — верхняя плоскость будет или вообще не видна, или так сильно сократится, что будет трудно ее рисовать.
Не нужно стараться рисовать идеально ровный куб. Мы только намечаем грани, далее линии построения будут уточняться.
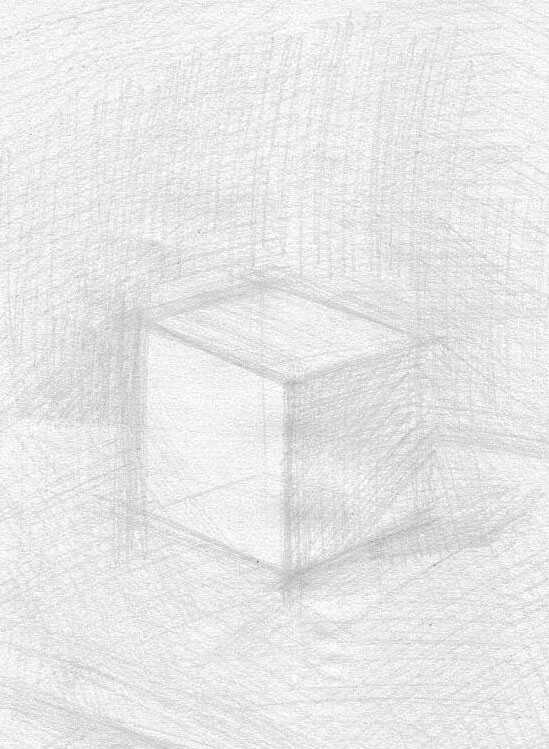
Следующий и заключительный этап — светотеневая моделировка. Если вы не уверены в отличном качестве штриха, набирайте тон постепенно, твердым карандашом, постепенно меняя на более мягкие. Не штрихуйте каждую часть отдельно, золотое правило художника — работа на каждом этапе может быть остановлена. То есть, карандаш летает по всему рисунку, тон накладывается равномерно.
Не старайтесь штриховать строго по форме, направление штриховки не так принципиально. На данном этапе ваша задача — набрать тон.
По мере проработки тоном становятся видны ошибки в построении, уточняем направление и положение граней.
Выравниваем тон. Очень полезно по ходу работы отходить и смотреть на рисунок издалека. Так можно заметить ошибки, которые не заметны «в упор». Снова уточняем положение граней куба.
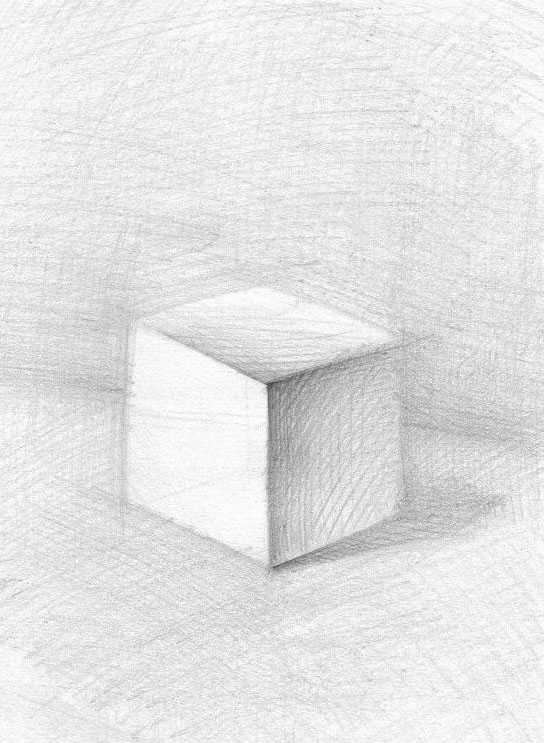
Чтобы работа выглядела выразительней, можно добавить контраста. В рисунке самый яркий контраст лежит там, где предмет приближается. В нашем случае — это ближний к нам угол куба. Вот и все, действительно очень просто.Результат может быть приблизительно такой)
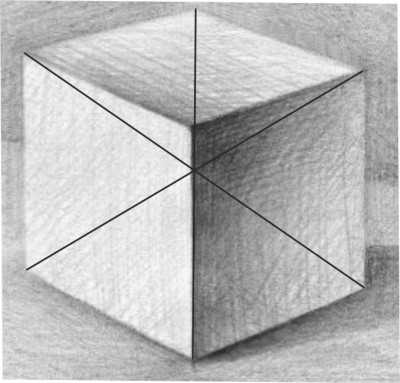
Для самопроверки можно провести диагонали куба — как известно, диагонали должны пересечься в одной точке. Для перспективы это правило также справедливо.
Разумеется, все, что написано выше относится не только к рисованию куба. Просто куб — самый подходящий пример для иллюстрации и самый простой предмет в исполнении для начала.
Если получилось, можно переходить к более сложным предметам. Следующая ступень: Рисуем шар.
Вернуться на главную страницу
Кубическая функция
Кубическая функция – это функция вида Y=X³.
Построим график функции y = x3. Составим таблицу соответственных значений x и y, округляя значения y до сотых:
| X | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 |
| Y | -8 | -3.38 | -1 | -0.13 | 0 | 0.13 | 1 | 3.38 | 8 |
Из таблицы видно, что графиик функции в начале координат почти сливается с осью x.
Выясним некоторые свойства функции Y=X³ :
• График функции неограниченно продолжается вверх справа от оси y и неограниченно продолжается вниз слева от оси y.
• Если x = 0, то y = 0. То есть график функции проходит через начало координат
• Если x > 0, то y > 0, если x
• Противоположным значениям x соответствует противоположные значения y. Это следует из того, что (-x)³=-x³ для любого значения x. Значит, точки графика, имеющие противоположные абсциссы, симметричны относительно начала координат.
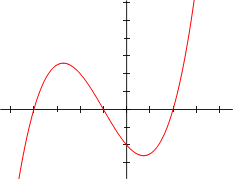
Теперь немного поговорим о графиках многочленов. График любого многочлена третьей степени y=ax³+bx²+cx+d (a≠0) принципиально имеет следующий вид:
Тот же график, но в уменьшенном масштабе имеет следущий вид:
Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014
Задача видеоурока: научиться рисовать куб, правильно компоновать куб на листе бумаги, как нарисовать объемный куб.
Из этого урока вы узнаете не только о том, как нарисовать сам куб, но и:
В уроке рассказано и показано рисование куба, и как нарисовать куб карандашом. В уроке показывается как нарисовать куб поэтапно.
Как правильно разместить (закомпоновать) рисуемый объект на листе бумаги;
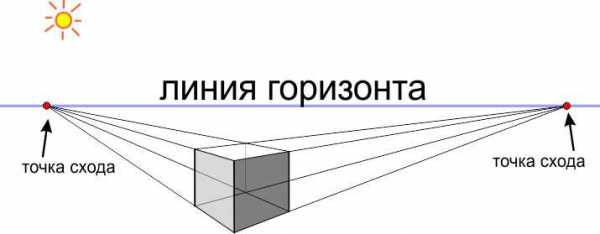
Что такое точки схода граней, почему они должны быть и что вообще такое перспектива;
Как выбрать формат листа для рисунка;
Геометрический и оптический центр, зачем они нужны, и как верно их выбрать;
Штриховка, учимся её рисовать правильно;
Расположение источника света, распространенные ошибки студентов в его размещении и последующая работа с ним;
Объясняется понятие Светотень, раскрывается, зачем она нужна, и что в неё входит: падающая тень, собственная тень, полутень, рефлекс, блик, свет.
Немножко о заточке карандаша и почему так важно правильно его заточить;
Как правильно искать ошибки в рисунке и устранять их. Не бойтесь проверять себя! Не бойтесь ошибок: их не делает только тот, кто ничего не делает!
Как рисовать и чем отличаются грани на переднем и на заднем плане и почему их нужно рисовать по-разному.
Почему в художественном рисунке параллельные линии сходятся (в геометрии то они не сходятся!).
Почему так важен правильный нажим карандаша.
Также из этого урока вы сделаете для себя интересные выводы:
Как правильно нарисовать куб!
На до же, тени оказывается неравномерные!
Куб в геометрии и художественном рисунке отличается не только отсутствием или наличием линейки!
И многие другие полезные и интересные умозаключения.
В общем, приятного просмотра!
P.S. от Анны Кошкиной: для лучшей усвояемости материала я бы рекомендовала сначала просмотреть весь видеоурок, и лишь потом, после его окончания, начинать рисовать куб. Самые нетерпеливые могут начинать его рисовать со мной, после того, как я взяла второй листок бумаги.
Итак выкладываю урок как нарисовать куб видео.
Почему Вы не сможете сделать такое же точно построение, если будете рисовать с натуры, спросите Вы. Да потому, что Вам нужно будет оставить место на длину линий, которые стремятся в точки схода. И фактически у Вас на листе куб получится очень маленьким, когда Вы сотрёте линии построения, которые продолжаются после куба, которые идут в точки схода.
Из этого урока Вы узнаете как нарисовать куб с тенью.
Домашнее задание:
1.Нарисовать куб в разных положениях.
2. Нарисовать спичечную коробку в разных положениях, для лучшего понимания перспективы. Думаю, спичечная коробка есть у всех, поэтому модель будет у всех в наличии. Вот так вышло у меня домашнее задание по рисованию спичечной коробки, на первом курсе.
После рисования куба вместе со мной, и последующей его доводкой светотеневой, то есть штриховкой, возьмите обычный спичечный коробок и, кладя его в разных ракурсах, по отношению к вашей точке зрения порисуйте его. Можно на формате А4. Так, как это у меня показано на моём рисунке. Это моя работа (домашнее задание) за первый курс ВУЗа.
Обратите внимание, геометрические предметы в академическом рисунке рисуются напросвет (как будто бы Вы видите их насквозь). Это делается для того чтобы предметы были изображены верно и Вы представляли себе, как они располагаются в пространстве по отношению к Вам.
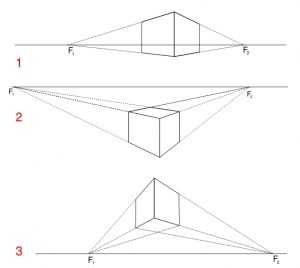
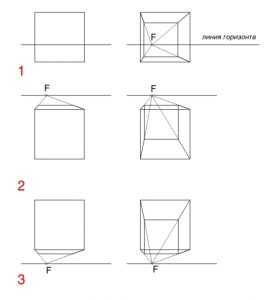
Как нельзя рисовать куб? Есть некоторые точки зрения, с которых куб смотрится неубедительно или некрасиво на бумаге, постарайтесь их избегать. Вот они: В рисунке 1 куб похож на клеточку в тетради, потому, что использована фронтальная перспектива. В рисунке 2 использовано неудачное положение по композиции, так как куб разделили ровно посередине на две части, все его углы и грани получились чётко противолежащими. Такое положение кажется уж слишком симметрично, похоже на чертёж, как в геометрии.
Для обычной срисовки Вам будет достаточно книги Н. П. Костерина «Учебное рисование», там написано и нарисовано очень просто, но немного поверхностно. Но вот если Вы хотите понять, почему рисовать нужно именно так, а не иначе, и как правильно нарисовать не только куб, но и другие предметы в перспективе, то я бы порекомендовала Вам книгу Николая Ли «Основы учебного академического рисунка».
Н. П. Костерин «Учебное рисование»
Николай Ли «Основы учебного академического рисунка»






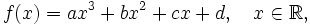
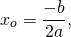
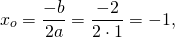
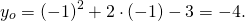

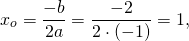
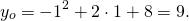

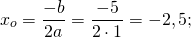
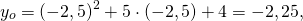



 Границы и перспектива в академическом рисунке
Границы и перспектива в академическом рисунке