Как сделать кумуляту в экселе
Использование Excel для расчета статистических характеристик случайной величины
Разделы: Математика
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Выполнение задания в ППП MS Excel
Значения каждого из трех признаков должны быть упорядочены, что реализуется с помощью сортировки (отдельно каждого из признаков): выбираем вкладку ДАННЫЕ – СОРТИРОВКА (традиционно по возрастанию).
Для выполнения структурной равноинтервальной группировки сначала определяем величину интервала по формуле:
где R – размах вариации, 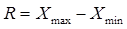
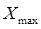

Число групп определяется следующими факторами: задачами исследования, основанием группировки, численностью совокупности, степенью вариации (изменчивости) признака.
Как ориентир для определения количества групп может быть использована формула Стерджесса:
где N – число единиц совокупности.
Если признак варьирует незначительно, может быть взято и меньшее число групп. И наоборот, если вариация велика, для более подробного ее описания лучше выбрать большее число групп.
Далее определяются границы каждого интервала по следующей схеме:
| № интервала | Границы интервала | |
| нижняя | верхняя | |
 |  | |
 | 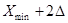 | |
| … | ||
| k |  |  |
Например, пусть статистическая совокупность состоит из 40 туристических компаний, показатели выручки которых варьируют от 50 млн. у.е./год до 650 млн. у.е./год, что является, соответственно, минимальным и максимальным значениями признака. Тогда по формуле Стерджесса получаем: 

После определения границ интервалов рассчитываются частоты, для чего используется функция ЧАСТОТА(вводится как формула массива, т.е. комбинацией клавиш CTRL + SHIFT + ВВОД). Выделяем столбец, в который должны поместиться частоты, соответствующие каждому интервалу. Вызываем функцию (из категории «Статистические») :
= ЧАСТОТА(массив_данных;массив_интервалов)
где массив_данных – это столбец исходных значений признака, для которых вычисляются частоты;
массив_интервалов – это столбец верхних границ интервалов с 1-го по k-1 –й (т.е. без последнего). Функция ЧАСТОТА предполагает формирование верхних границ по принципу «включительно», а нижних – «исключительно».
Сумма частот должна быть равна объему совокупности:
где 
Далее оценивается относительная структура совокупности через расчет частостей:
где 
В результате получаем структурную равноинтервальную группировку.
Группировки с равными интервалами предпочтительнее, но характер изменения большинства социально-экономических явлений не отвечает требованиям, предъявляемым к равноинтервальной группировке.
Если в результате построения равноинтервальной группировки большая часть совокупности попала в один-два смежных интервала, а остальные содержат незначительное число наблюдений, это свидетельствует о том, что исследуемый признак варьирует неравномерно. В данном случае может быть использован «прогрессивный» подход к определению границ интервалов.
В этом случае величина интервалов определяется формулами:
где 



q – константа геометрической прогрессии, для возрастающих интервалов 
Описанные выше технические способы определения величины интервалов не гарантируют, что не появятся группы малочисленные или вообще «пустые», в которые не попало ни одно наблюдение. Если это произошло, необходимо изменить число групп и/или величины интервалов, так как подобная группировка является некорректной.
Для обеспечения статистической устойчивости показателей, исчисляемых для отдельных групп, может использоваться равнонаполненная группировка, в которой число наблюдений в каждой группе примерно одинаковое и определяется по формуле:

Если полученное n не целое и/или в совокупности есть повторяющиеся значения признака, то число наблюдений в каждой группе может различаться. При этом надо стремиться к тому, чтобы эти различия были незначительны.
Если для реализации задач исследования необходимо устанавливать границы групп там, где количество переходит в новое качество, пользуются специализированными интервалами.
Границы групп могут определяться и произвольно, когда ни один из вышеописанных методов не дал хороших результатов.
В результате на основе итоговой группировки формируется вариационный ряд распределения (см. табл. 1).
Таблица 1. Ряд распределения выручки туристических компаний, млн. у.е./год
| Границы интервала | Частота | Частость | Плотность абсол. | Плотность отснос. |
| нижняя | верхняя | |||
| 0,300 | 0,12 | 0,00300 | ||
| 0,250 | 0,10 | 0,00250 | ||
| 0,200 | 0,08 | 0,00200 | ||
| 0,125 | 0,05 | 0,00125 | ||
| 0,100 | 0,04 | 0,00100 | ||
| 0,025 | 0,01 | 0,00025 | ||
| Итого | — | — |
Для неравноинтервального вариационного ряда распределения сравнение частот по группам неправомерно. В данном случае необходимо избавиться от влияния величины интервала путем перехода от частот/частостей к абсолютной/относительной плотности распределения:
где 


Далее строится кумулятивный ряд распределения, для чего рассчитываются накопленные частоты/частости к концу каждого интервала:
где 

Построение гистограммы и кумуляты выполняется с указанием названия графика и каждой оси. Для кумуляты в таблице рассчитываем накопленные частоты/частости (см. табл.2):
где 

Таблица 2. Кумулятивный ряд распределения выручки туристических компаний, млн. у.е./год
| Границы интервала | Частота | Частость | Накопленная частота | Накопленная частость |
| нижняя | верхняя | |||
| 0,30 | 0,300 | |||
| 0,25 | 0,550 | |||
| 0,20 | 0,750 | |||
| 0,13 | 0,875 | |||
| 0,10 | 0,975 | |||
| 0,03 | ||||
| Итого | — | — |
Гистограмма– графическое изображение интервального вариационного ряда распределения, дающее представление о характере изменения его частот (рис. 1).
Рис. 1. Гистограмма распределения выручки туристических компаний
Рис. 2. Кумулята распределения выручки туристических компаний
Кумулята – графическое изображение кумулятивной кривой, дающее представление о характере изменения накопленных частот/частостей (рис. 2).
Выводы должны давать общую картину распределения: однородность совокупности («похожесть» единиц совокупности друг на друга), концентрация значений вокруг средней величины, «типичное» значение, симметричность распределения (преобладание больших или малых значений).



























