Как сделать линейку треугольник

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Построение отрезка, равного данному

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Деление отрезка пополам

Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Построение угла, равного данному

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Источник

Как построить высоту треугольника — основные способы

Для решения многих геометрических задач учащемуся нужно уметь быстро построить высоту треугольника. Сделать это можно несколькими простыми для восприятия способами, которые подходят для фигуры разной формы и размера. Весь процесс состоит из определённой последовательности действий, правильно выполнить которые сможет каждый школьник.

С применением циркуля

Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.

Способ начертить искомый отрезок:

Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.

С помощью линейки

Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.

В остроугольном треугольнике

Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.

Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.

Правильная последовательность действий:

В тупоугольной фигуре

Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.

Порядок действий:

В прямоугольном и равнобедренном

В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.

Пошаговая инструкция:

Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.

Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.

Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.

Источник

Как построить высоту треугольника

Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.

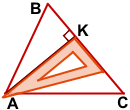
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.

AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.

BF⊥AC.

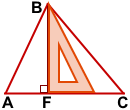
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.

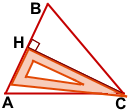
CH — высота треугольника ABC, проведённая из вершины C к стороне AB.

Все высоты треугольника пересекаются в одной точке.

В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

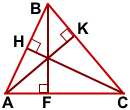
Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.

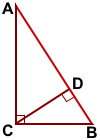
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.

Угольник прикладываем прямым углом так, чтобы одна сторона проходила через гипотенузу, а другая — через прямой угол.

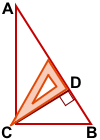
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.

Точка пересечения высот прямоугольного треугольника — вершина прямого угла.

Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.

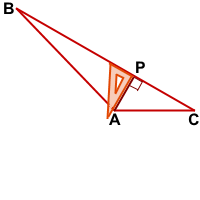
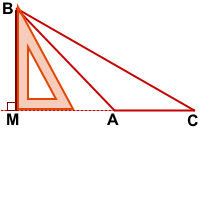
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.

Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.

AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.

Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.

Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.

Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.

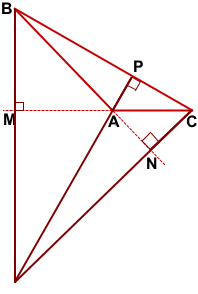
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.

CN⊥AB,

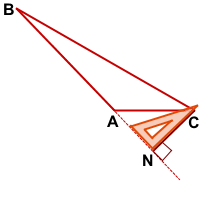
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.

Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.

Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.

Мы рассмотрели, как строить высоты треугольника с помощью угольника.

Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».

Источник

Как нарисовать равносторонний треугольник без циркуля

Смотрите видео

Построение различных треугольников – обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

Построение равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

Построение равнобедренного треугольника

Данный тип треугольников можно построить по основанию и боковым сторонам.

Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

Построение прямоугольного треугольника

Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.

Построение тупоугольного треугольника по углу и двум прилегающим сторонам

Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

Построение остроугольного треугольника

Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

Вписанный треугольник

Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного – на середине гипотенузы.

Чертим описанный треугольник

Описанный треугольник – это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.

Спонсор размещения P&G Статьи по теме «Как нарисовать правильный треугольник» Как оформить титульный лист школьного реферата Как найти радиус описанной около треугольника окружности Как найти площадь многоугольника

Теперь, беря пересечения каждой из двух последовательных окружностей, мы получаем места, где мы должны поместить деревья в строки, параллельные первой. С полученными точками пересечения мы работаем так же, как и с первыми, тем самым получим, что все деревья размещены, образуя равносторонние треугольники.

Это самый эффективный способ? В книге «Творчество математики» Микель Альберти комментирует, что, по словам Гил-Альберта, садовод будет делать иначе. Мы помещаем один конец веревки в первую точку, где мы хотим посадить дерево, и мы развертываем расстояние, которое мы хотим оставить между последовательными деревьями, установив эту точку в качестве области для посадки дерева и создания метки на веревке. Теперь, начиная с первой точки, мы вытягиваем расстояние, равное удвоенному расстоянию, которое мы хотим оставить между последовательными деревьями, мы помещаем конец этих 2 метров во второй фиксированной точке и затягиваем веревку, потянув отметку 1 метра, мы сделали прежде.

Нарисовать правильный треугольник можно двумя способами. Один из них потребует циркуль и линейку, другой — две линейки. Выберите способ в зависимости от того, что имеете под рукой.

Рассмотрим способ с линейкой и циркулем. Построим треугольник АВС. С помощью линейки начертите линию АВ, это будет одна из сторон треугольника, а точки А и В его вершинами.

Используя циркуль, нарисуйте окружность, центр которой будет в точке А, а радиус равен отрезку АВ.

С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.

Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.

Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.

Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.

Не сдвигая линейки после построения отрезка ОК, приложите перпендикулярно к ней еще одну линейку. Проведите прямую m пересекающую отрезок ОК в середине.

С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.

Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки. Как просто

Другие новости по теме:

Задачи на геометрические построения весьма хорошо развивают пространственное и логическое мышление и потому являются одной из основных частей школьной программы обучения. Как и в любой предметной области, существуют типовые и нетиповые задачи. К типовым задачам можно отнести, например, построение

Среди всех возможных задач планиметрии, связанных с геометрическими построениями, можно выделить наиболее типовые. Их решения представляют собой четкий алгоритм действий и используются в качестве составных частей решений более сложных задач. К подобному типа относится и задача о том, как начертить

Медианой треугольника называется отрезок, соединяющий любую из вершин треугольника с серединой противоположной стороны. Поэтому задача построения медианы с помощью циркуля и линейки сводится к задаче нахождения середины отрезка. Вам понадобится — циркуль — линейка — карандаш Спонсор размещения

Геометрические задачи на построение, в которых использовались только циркуль и линейка, зародились еще в древней Греции. Уже во времена Евклида и Платона математики умели решать множество геометрических задач. Например, строить правильные треугольники, квадраты, разбивать отрезки на равные части и

Если окружность касается всех трех сторон данного треугольника, а её центр находится внутри треугольника, то ее называют вписанной в треугольник. Вам понадобится линейка, циркуль Спонсор размещения P&G Статьи по теме «Как вписать треугольник в окружность» Как построить окружность, вписанную в

У любого равностороннего треугольника одинаковы не только стороны, но и углы, каждый из которых равен 60 градусам. Однако чертеж такого треугольника, построенный при помощи транспортира, не будет обладать высокой точностью. Поэтому для построения данной фигуры лучше воспользоваться циркулем. Вам

В этой статье вы научитесь рисовать в фотошопе разные виды треугольника: равносторонний, равнобедренный, разносторонний и прямоугольный.

Как нарисовать равносторонний треугольник

У равностороннего треугольника все три стороны равны.

Выберите этот инструмент и на панели настроек сразу укажите количество сторон — 3.

Следующим этапом нужно определиться каким должен быть будущий треугольник: векторной фигурой, растровым со сплошной заливкой или нужен только контур. Рассмотри все варианты.

Векторный треугольник

Теперь можно рисовать и сам треугольник. Во время создания вы будете видеть его границы. Это нужно для того, чтобы рассчитать его размеры. Также, пока не отпустили клавишу мыши, можно его крутить.

Растровый треугольник со сплошной заливкой

Получится такой же треугольник, что и примером выше, но он будет сразу в растре.

Теперь рисуйте фигуру и она будет как самый обычный элемент растрового изображения.

Как нарисовать контур равностороннего треугольника

Откроется диалоговое окно. Радиус растушевки оставьте 0. Жмите Ок.

Как нарисовать равнобедренный треугольник

У равнобедренного треугольника две стороны равны.

Разберем пример, когда нужно нарисовать равнобедренный треугольник заданных размеров. Допустим, основание 300 пикселей и высота 400 пикселей.

Равнобедренный треугольник по заданным размерам нарисован!

В прямоугольном треугольнике один из углов равен 90 градусов.

Если нужен прямоугольный треугольник с заранее известными размерами, например, размеры катетов 200 и 300 пикселей, то проще всего сделать следующим образом:

Создайте новый документ в фотошопе с высотой и шириной равными размерам катетов: например, ширина пусть 300 пикселей, а высота 200 пикселей.

Рабочая область в фотошопе всегда прямоугольной формы, поэтому угол в 90 градусов будет уже обеспечен. Две стороны прямоугольника — его катеты. Останется только провести диагональ — это будет гипотенузой.

Теперь обводим линией по краям и соединяем две точки по диагонали:

На палитре слоев опять три слоя-фигуры. Их можно объединить в один слой (команда Объединить слои ).

Прямоугольный треугольник готов, можно закрасить его в какой-нибудь цвет:

Главная » Планиметрия » Как начертить равнобедренный треугольник в круге. Как нарисовать треугольник в фотошопе

Шаг 1

Нарисовать отрезок, длина которого АВ=а будет четным числом.

Как построить правильный треугольник с помощью линейки. Шаг 1

Шаг 2

Через центр отрезка провести перпендикулярную прямую.

Как построить равносторонний треугольник с помощью линейки. Шаг 2

Шаг 3

Взять линейку и от точки А отложить отрезок, равный длине АВ, таким образом, чтобы конец этого отрезка лег на проведенный перпендикуляр. Точку пересечения обозначить буквой С.

Как построить равносторонний треугольник с помощью линейки. Шаг 3

Шаг 4

Соединить точку В с концом отрезка АС.

В результате будет построен правильный треугольник АВС со стороной равной а.

Как построить равносторонний треугольник с помощью линейки. Шаг 4

Источник