Как сделать линейный алгоритм
Повседневная жизнь каждого человека заключается в решении огромного количества задач различной сложности на работе или во время учебы. Некоторые задачи являются настолько простыми, что при их выполнении мы делаем определенные действия автоматически, даже не задумываясь. Решение любой задачи, даже самой простой, как правило, осуществляется последовательно за несколько шагов. Такого рода последовательность при решении задач называется алгоритмом. Сегодня мы рассмотрим, что такое линейные алгоритмы, как изображается их структура, как осуществляется их решение и программирование.
Алгоритмический язык
Это понятие представляет собой точное предписание для исполнителя совершить определенную последовательность действий, которая направляется на решение поставленной задачи.
Данный язык является средством описания алгоритмов, которые ориентированы обычно на пользователя.
Если говорить на компьютерном языке, так обозначается точное предписание, определяющее вычислительный процесс. Он, в свою очередь, ведет от начальных данных, которые варьируются, к исходному результату.
Свойства алгоритма
Среди свойств выделяют:
Линейные алгоритмы. Информатика 9 класса
Мы уже рассмотрели определения и свойства данного понятия. Теперь поговорим о его видах:
Нас интересуют линейные алгоритмы. Что они собой представляют? Они содержат команды, которые должны выполняться одна за другой в четкой последовательности.
Линейная структура алгоритма может быть записана в словесной и графической форме.
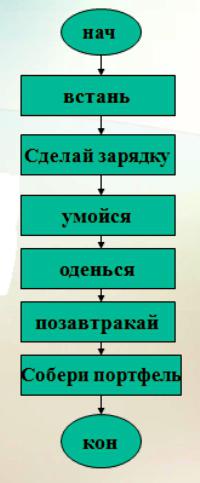
Приведем такой пример, записанный в словесной форме. Итак, задача: соберись в школу. Решение:
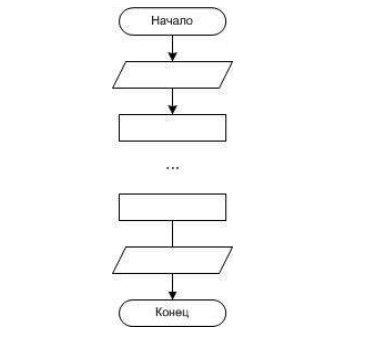
Графическая форма вышеописанного процесса будет предсатвлять собой следующее:
Линейный алгоритм в виде блок-схемы
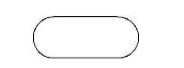
Блок-схема представляет собой иллюстративное изображение алгоритма, при котором каждый отдельный этап изображается с помощью блоков, представленных в виде разнообразных геометрических фигур. К тому же связь между этапами (иными словами, последовательность поэтапного выполнения) обозначается с помощью стрелок, которые соединяют фигуры (блоки). Каждый блок сопровождается надписью. Для типичных действий в линейном алгоритме используются следующие геометрические фигуры:
Вот с помощью таких блок-схем изображается решение линейных алгоритмов. Далее поговорим об особенностях присваивания значений.
Линейные вычислительные алгоритмы
Основное элементарное действие в вычислительном алгоритме – это присваивание переменной величине определенного значения. В случае, когда значение константы определяется видом ее записи, переменная величина получит конкретное значение исключительно в результате присваивания. Это может быть выполнено с помощью двух способов: при помощи команды присваивания; при помощи команды ввода.
Пример решения линейного алгоритма
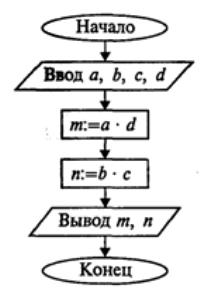
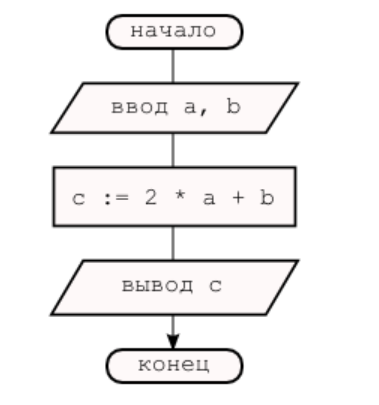
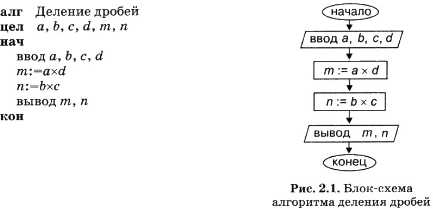
Приведем пример описания правил деления обыкновенных дробей с помощью линейного алгоритма, которые в школьных учебниках имеют такое содержание:
Итак, построим для ЭВМ алгоритм деления дробей. Чтобы не запутаться, будем использовать для переменных те самые обозначения, что и в формуле, которая была указана выше. а, b, с, d– исходные данные в виде целочисленных переменных. Результатом также будут целые величины. Решение на алгоритмическом языке будет следующим:
алг Деление дробей
цел а, b, с, d, m, n
Графическая форма решения
Схема линейного алгоритма, описанного выше, выглядит так:
Команда присваивания значения имеет следующий формат:
Знак «:=» читается как присвоить.
Присваивание – это команда, которая необходима для выполнения компьютером следующих действий:
Приведенный выше алгоритм содержит две команды в качестве присваивания. В блок-схеме команду присваивания нужно записывать в прямоугольнике, который называется вычислительным блоком.
Когда описываются линейные алгоритмы, нет особой необходимости в обязательном соблюдении строгих правил при записи выражений. Можно их записывать с помощью обычной математической формы. Ведь это не строгий синтаксис языка программирования.
В приведенном примере алгоритма есть также команда ввода:
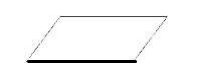
Команда ввода в блок-схеме записывается в параллелограмме, то есть в блоке ввода-вывода. Выполняя эту команду, процессор прерывает работу, пока пользователь не осуществит определенные действия. А именно: пользователю нужно на устройстве ввода (клавиатуре) набрать вводимые переменные (их значения) и нажать Enter, которая выступает клавишей ввода. Важно, чтобы значения вводились в таком же порядке, что и расположенные в списке ввода соответствующие переменные.
Линейный алгоритм. Его программирование
Как уже говорилось в начале статьи, линейные программы могут включать такие операторы:
То есть с помощью перечисленных операторов осуществляется программирование линейных алгоритмов.
Итак, оператор присваивания на программном языке записывается так:
LET А = В, где А – переменная, В – выражение. Например, А = У + 20.
Оператор ввода имеет следующий вид:
INPUT, к примеру: INPUT С
Оператор вывода данных, значений, записывается в таком виде:
PRINT. К примеру PRINT С.
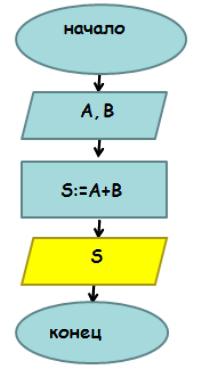
Приведем простой пример. Нам нужно написать программу, которая будет находить сумму вводимых с клавиатуры чисел А и В.
На языке программирования мы получим программу, текст которой изображен ниже.
Операторы ввода, вывода в языке программирования Паскаль
Паскаль не выделяет специальных операторов, обозначающих операции ввода или вывода, которые используют линейные алгоритмы. В программах обмен информацией осуществляется с помощью встроенных процедур. Поскольку нет нужды в предварительном описании стандартной процедуры, она доступна каждой программе, содержащей обращение к ней. Также названием упомянутой процедуры не выступает какое-либо зарезервированное слово.
При вводе данных используют такие операторы для обращения к стандартной процедуре ввода данных, которая уже встроена в программу.
Read (А, В, С), где А, В, С – переменные, которые нужно ввести в оперативную память для запоминания.
Readlnn (х1, у, х2) – закончив ввод, курсор переходит на начало новой строки.
Вывод на экран монитора данных осуществляется с помощью таких операторов:
Write (А, В, С) – указав значения А, В, С в одной строке, курсор не покидает текущей строки.
Writeln (z, у, z2) – закончив вывод значений, курсор в данной позиции перейдет на новую строку.
Вот с помощью таких простых операторов и осуществляется ввод и вывод данных в языке Паскаль.
Линейный алгоритм. Понятие и особенности. Блок-схема
Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.
Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.
Алгоритмический язык
Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы; — разработку алгоритма; — составление программы решения на алгоритмическом языке; — ввод данных; — отладку программы (возможны ошибки — их надо исправить); — выполнение на ПК; — анализ результатов.
Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.
Свойства алгоритма
Их несколько: — конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов; — однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия; — результативность. Итог работы — результат, полученный за конечное число шагов; — универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.
Линейная структура
Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.
Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.
Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим: — принести пылесос к месту уборки; — включить; — пропылесосить; — выключить; — унести пылесос.
И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.
Теперь поговорим про графическую форму представления.
Блок-схема
Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.
Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):
Арифметический блок (отображает арифметическую операцию/группу операций):
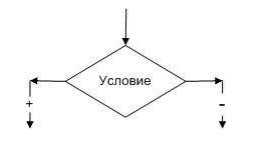
Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:
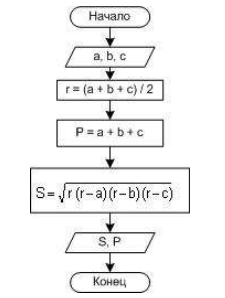
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.
Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.
Примеры линейных алгоритмов
Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:
И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:
Как составить программу линейной структуры?
Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.
На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!
Содержание урока
Линейные вычислительные алгоритмы











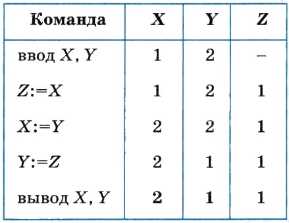
 Переменная величина получает значение в результате присваивания.
Переменная величина получает значение в результате присваивания.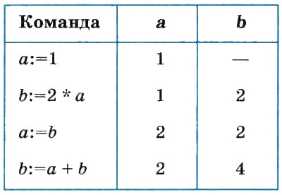
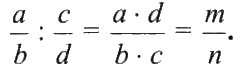
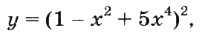
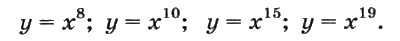

 Компьютерный практикум ЦОР. Линейные вычислительные алгоритмы
Компьютерный практикум ЦОР. Линейные вычислительные алгоритмы