Как сделать линейный модуль
Сборка линейного светодиодного светильника
Сейчас одним из самых популярных и модных решений освещения являются линейные светодиодные светильники. В этой статье мы разберемся, как устроены современные LED системы освещения и соберем один светильник своими руками.
Конструкция
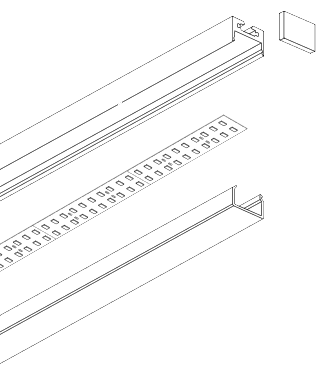
Линейный светильник включает в себя: алюминиевый светодиодный профиль с поликарбонатным светорассеивающим стеклом, источник света (светодиодная лента или светодиодная линейка), LED драйвер. Так же к профилям предлагается огромное множество комплектующих (подвесы, заглушки, крепления и многое др.)
Из плюсов такой простой конструкции можно отметить широкие возможности конфигурации и выбора. Практически каждый такой светильник является уникальным. Неоспоримое преимущество линейных систем освещения заключается в том, что мы можем делать светильники любой длины.
Разновидности
Линейные светильники бывают: встраиваемые, подвесные, накладные. Отличаются они по способу монтажа, который предусмотрен производителем.
Приступим
Выбор корпуса
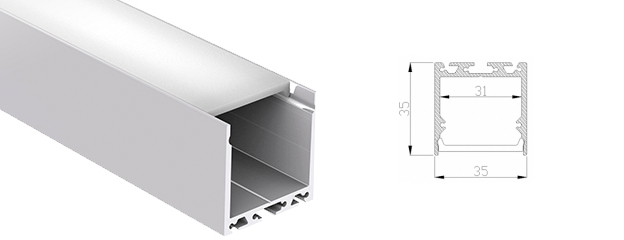
Мы приняли решение собрать подвесной светильник, который найдет свое применение как в гараже, так и в офисе. Среди широкого ассортимента алюминиевых светодиодных профилей мы нашли подходящий. Наш выбор остановился на профиле который называется U-S35. Габариты этого профиля 35*35*2500мм.
Выбор источника света
Изучив рынок светодиодных лент, посмотрев обзоры и прочитав отзывы, мы захотели применить в нашем будущем светильнике новинку.
Японский светодиодный модуль HOKASU. Модуль обладает огромным преимуществом перед светодиодной лентой.
Злейший враг светодиодов это тепло. От температуры, которую выделяют мощные LED’ы, светодиоды деградируют, теряют проценты своей первоначальной яркости. Очень важен мгновенный отвод точечного тепла, которое концентрируется у самого основания кристалла. Так как, светодиодная лента — это гибкий проводник с smd- светодиодами, при монтаже их на охлаждающую поверхность у нас получается тепловой зазор. Лента не очень плотно клеится к поверхности, мгновенному отводу тепла мешает клей (двойной скотч 3M). Линейки лишены этого недостатка, т.к плата на заводе припаяна к алюминиевой полосе, которая в свою очередь уже крепится к поверхности.
Итак, характеристики в студию:
Комплектация
Из материалов мы использовали
Для сборки нам понадобится
Сборка
Для начала мы примерим линейки в профиле и обрежем их до нужного нам размера.
Кстати, их можно резать каждые 4 см.
После того как мы обрезали линейку, желательно проверить её на сопротивление, т.к после первой попытки, когда я резал обычной пилой, линейка замыкала с самого края.
Это связано с тем, что основание изготовлено из алюминия и проводит ток. И при неаккуратном разрезе с торца медные дорожки задевают подложку.
Далее мы проклеиваем линейки (у них предусмотрен клейкий слой 3M):
Сейчас наш светильник практически готов, нам осталось запаять все линейки между собой. Как заявляет производитель: допустимо последовательное соединение до 3м. (Это мы проверим позже, замерив общую мощность готового линейного светильника.)
Припаиваем с одного конца провод и закрываем экран. (Для провода нужно сделать отверстие и вывести его за профиль, но мы пока делать этого не будем.)
Я подключил светильник к лабораторному источнику питания для того, чтобы посмотреть какой ток потребляют светодиоды. Довольно распространенная проблема, что при подключении мощных лент более 2м идет потеря мощности. Это связано с недостаточной проводимостью медных дорожек. У меня получилось, что суммарная мощность светильника 2.7*24 = 64.8Вт (26 Вт/м).
Показатели скакали от температуры, но усреднено 26 Вт/м. С учетом того, что заявленная мощность одного модуля 26Вт, я считаю это идеальный показатель.
Применимость
Для наглядности я повесил светильник над рабочим столом и сделал несколько фотографий. В будущем найду ему постоянное место.
Стоимость
Линейный светильник 65Вт, 2.5м.
Одного такого светильника хватит на 2 или даже на 3 рабочих места. Его можно разрезать пополам и установить над разными столами, подключив к одному источнику питания.
Производители

Новые линейные модули линейного перемещения для российских условий
В статье пойдет речь о первом российском производителе модулей линейного перемещения различного назначения.
На данный момент на российском рынке модулей линейного перемещения представлены в основном японские, европейские и тайваньские производители. В России до сегодняшнего момента подобные модули не производились. Далее мы расскажем о новых российских модулях линейного перемещения, производимых подмосковной компанией «Завод мехатронных изделий» (ЗМИ).
Основной сферой компании «ЗМИ» является производство уникальных несерийных станков и машин для автоматизации производства заказчиков. В процессе работы компания ощутила острую необходимость в готовых модулях линейного перемещения для конструирования своих уникальных станков и решения задач автоматизации. Импортные модули обладали высокой ценой и долгими сроками поставки, поэтому было принято решение начать проектирование своих модулей. При их разработке учитывались не только высокие технические характеристики, но и отечественные особенности эксплуатации. В 2008 году были разработаны основные серии модулей и налажено опытное производство, в 2009 году они были запущены в серийное производство, как для продажи, так и для использования в проектах.
Дадим определение понятию «модуль линейного перемещения».
Модуль линейного перемещения является исполнительным механизмом, передающим воздействие от управляющего устройства на объект управления, и предназначен для осуществления точного и плавного перемещения устанавливаемых на него объектов по прямой траектории.
Первый российский модуль линейного перемещения
Конструктивно модули производства «ЗМИ» состоят из основания (несущий силовой элемент) с закрепленными на нем рельсовыми или цилиндрическими направляющими качения. На фланцевых опорах установлена трансмиссия, крутящий момент к которой передаётся от двигателя через компенсирующую муфту. В качестве трансмиссии может выступать ШВП, трапецеидальный винт или рейка. За счёт движения трансмиссии происходит перемещение каретки модуля, которая в свою очередь служит базовой платформой для крепления на ней всевозможных изделий и механизмов. Материал фланцев, каретки – алюминиевый сплав Д16Т. Для основания может применяться сталь.
Смазка направляющих и ШВП осуществляется через ниппели, расположенные непосредственно на каретках и гайке ШВП. Основание и каретка модуля снабжены специальными технологическими элементами (отверстиями, шпоночными канавками), упрощающими процесс сборки и монтажа системы линейного перемещения. В стандартной комплектации модуль оснащен аварийными упорами. Опционально устанавливаются концевые выключатели, выводы с которых заведены в стандартный разъем D-Sub.
Линейный модуль – это готовая ось для линейного перемещения, с помощью которой можно с большой легкостью конструировать любые системы линейного перемещения, обладающие высокой точностью позиционирования.
По сути, покупатель может самостоятельно собрать модуль линейного перемещения. Для этого необходимо взять алюминиевый профиль, линейную направляющую, ШВП (ремень или рейку). Готовый же модуль позволяет сэкономить время, затрачиваемое на сборку, а также получить систему, обладающую большей жесткостью и точностью.
Основные серии модулей «ЗМИ»
Серия СТМ-1
Данная серия является основной в семействе модулей, производимых ЗАО «ЗМИ», и наиболее востребованной на данный момент. В серии СТМ-1 применяются рельсовые линейные направляющие и ШВП. Модули серии СТМУ-1 обладают повышенной нагрузочной способностью, снабжены четырьмя танкетками и удлиненной кареткой (длина 170 мм).

Серия СТМЛ-1
Данная серия является самой бюджетной из всей линейки модулей «ЗМИ». Низкая цена достигается за счет применения цилиндрических направляющих вместо рельсовых и использования трапецеидального винта. Модуль на основе трапецеидального винта обладает меньшей точностью чем на ШВП и подходит для транспортных применений.

Серия МТР-1
В данной серии в качестве трансмиссии используется рейка, а приводом для этого модуля служит синхронный двигатель вместе с точным планетарным редуктором. Данный модуль обладает самой большой скоростью перемещения из всех модулей и имеет самый большой возможный ход.

Серия СТМТ
Линейные модули серии СТМТ-1 обладают повышенной грузоподъемностью и предназначены для перемещения крупных тяжёлых объектов по прямой траектории с высокой точностью. В отличие от остальных модулей, серия СТМТ-1 имеет сварное стальное основание.

Технические характеристики модулей «ЗМИ»
| Характеристика/Серия | СТМ-1/СТМУ-1 | СТМЛ-1 | МТР-1 | СТМТ-1 |
| Тип механической передачи | ШВП/ШВП | ШВП или трапецеидальный винт | Рейка | ШВП |
| Повторяемость, мкм. | ±10 | +10- ШВП/ +100 – трап. винт | ±0,05 | ±0,02 |
| Максимальная перемещаемая масса в горизонтальном положении, кг | 30 / 40 | 10 | 200 | 200 |
| Максимальная перемещаемая масса в вертикальном положении, кг | 20 | 10 | 40 | 100 |
| Максимально возможный ход модуля по упорам (S), мм * | 1230 / 1170 | 460 | 5640 | 2190 |
| Скорость быстрого перемещения, мм/сек | 125 (с шагом винта ШВП 5мм) 250 (с шагом винта ШВП 10мм) 400 (с шагом винта ШВП 16мм) | 125 (с шагом винта 5мм) 100 (с шагом винта 4мм) 75 (с шагом винта 3мм) | 1000 | 250 (с шагом винта ШВП 5мм) 1000 (с шагом винта ШВП 20мм) |
Опции для модулей
Для модулей доступна защита, имеющая два варианта исполнения: в виде неподвижных кожухов и гофрозащиты (кроющей гармошки). Неподвижный кожух предназначается для защиты элементов трансмиссии модуля от попадания, раскаленной стружки, окалины от сварки, грязи, предотвращает повреждения трансмиссии посторонними предметами. Щель между верхним и боковым кожухами составляет 9мм. Данный вид защиты наиболее эффективен при горизонтальном монтаже модуля (каретка сверху). Материал кожухов – нержавеющая сталь.
Гофрозащита предназначается для защиты элементов трансмиссии модуля от попадания пыли, шлаков, песка, мелкой и крупной неметаллической стружки, грязи, брызг СОЖ, предотвращает повреждения трансмиссии посторонними предметами. Материал гофрозащиты – тканевая основа с резиновым покрытием. Жесткие вставки из ПВХ находятся в каждой складке. Максимальная температура эксплуатации составляет 90 o С. При совместном применении модулей «ЗМИ» и сервопривода СПШ, производимого «Сервотехникой» получается полноценный актуатор. Все необходимые элементы для состыковки двигателя и модуля уже входят в комплект.
На все модули, комплектуемые защитой, устанавливаются закрытые переходные стаканы, обеспечивающие защиту муфты.
Преимущества
Среди преимуществ модулей, производимых ЗАО «ЗМИ» можно выделить следующие. Модули «ЗМИ» имеют оптимальные показатели по точности и прямолинейности перемещения за счет высокой точности обработки базовых элементов и набора качественных комплектующих как зарубежного, так и отечественного производства. Модули собираются в России, поэтому имеют небольшой срок поставки.
Гибкие производственные возможности компании «ЗМИ» позволяют в кратчайшие сроки изготовить линейный модуль необходимой длины или даже целую систему (X-Y, X-Z, X-Y-Z).
Для модулей «ЗМИ» доступны такие опции как: защита направляющих и винта ШВП, установка датчика линейного положения, изменение размеров каретки согласно требованиям заказчика, подготовка дополнительных резьбовых отверстий и др.
Модули линейного перемещения «ЗМИ» можно применять в следующих областях: лабораторное оборудование, медицинские приборы, испытательные стенды, технологические координатные столы, транспортные системы, манипуляторы.
На данный момент компания «ЗМИ» производит четыре вида модулей линейного перемещения. В дальнейшем планируется расширять линейку производимых модулей.
Как решать уравнения с модулем: основные правила
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
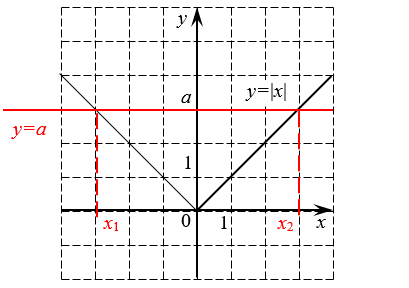
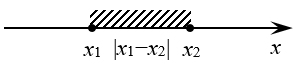
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
\[\left| f\left( x \right) \right|=a\]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
\[\left| 2x+1 \right|=5\Rightarrow 2x+1=5\]
\[2x+1=5\Rightarrow 2x=4\Rightarrow x=2\]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
\[2x+1=-5\Rightarrow 2x=-6\Rightarrow x=-3\]
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
\[\left| f\left( x \right) \right|=a\Rightarrow f\left( x \right)=\pm a\]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
Опять раскрываем модуль с плюсом и минусом:
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
\[\left| f\left( x \right) \right|=g\left( x \right)\Rightarrow \left\< \begin
Применительно к нашему уравнению получим:
\[\left| 3x-2 \right|=2x\Rightarrow \left\< \begin
Поэтому решим-ка само уравнение:
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
\[\left| f\left( x \right) \right|=g\left( x \right)\]
И решается оно точно так же:
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
\[\left| f\left( x \right) \right|=\left| g\left( x \right) \right|\Rightarrow f\left( x \right)=\pm g\left( x \right)\]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\]
Элементарно, Ватсон! Раскрываем модули:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left( 2x-7 \right)\]
Рассмотрим отдельно каждый случай:
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
\[2x+3=-2x+7\Rightarrow 4x=4\Rightarrow x=1\]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
\[\left| x-1 \right|=\left| <
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
\[\left[ \begin
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
\[x-<
\[<
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
\[3x-5 \gt 0\Rightarrow \left| 3x-5 \right|=3x-5\]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
\[3x-5=5-3x\Rightarrow 6x=10\Rightarrow x=\frac<5><3>\]
\[x=\frac<5><3>\Rightarrow 3x-5=3\cdot \frac<5><3>-5=5-5=0\]
\[3x-5 \lt 0\Rightarrow \left| 3x-5 \right|=5-3x\]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
\[3x-5 \lt 0\Rightarrow 3x \lt 5\Rightarrow x \lt \frac<5><3>\]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
\[3x-5=0\Rightarrow \left| 3x-5 \right|=0\]
\[0=3x-5\Rightarrow 3x=5\Rightarrow x=\frac<5><3>\]
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
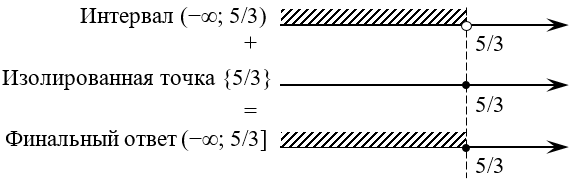
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:

Ну и какие тут интервалы? Понятно, что их три:
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)