Как сделать логарифмическую шкалу

Основные свойства счетной линейки и в первую очередь правило пропорций вытекают из того, что шкалы счетной линейки являются логарифмическими.

Шкала называется логарифмической, если на ней нанесены логарифмы чисел, а отметками шкалы являются сами числа.

На рисунке представлена логарифмическая шкала х рядом с равномерной шкалой у, на которой нанесены десятичные логарифмы чисел х.

Логарифмическая шкала простирается неограниченно в обе стороны. Слева от точки х=1 находятся положительные числа, меньшие 1, десятичные логарифмы которых отрицательны. (Мы здесь и в дальнейшем будем употреблять термины «точка х» и «число х» как равносильные, подобно тому как это делается при работе с числовой осью.)

Основные шкалы А и В счетной линейки представляют собой только один отрезок [1, 10] логарифмической шкалы. Шкалы С и D представляют собой отрезок [1, 100] логарифмической шкалы, а шкала К — отрезок [1, 1000] той же шкалы.

Шкала L представляет собой равномерную шкалу, точки 0 и 1 которой находятся соответственно против чисел 1 и 10 шкалы В из сказанного выше, а также из рисунка ясно, что шкала L дает десятичные логарифмы чисел шкалы В.

1. Вывод правила пропорций (см. раздел «Правило пропорций»). Сначала найдем расстояние ρ [а, b] между двумя точками х = а и x = b (b > а) логарифмической шкалы. Воспользуемся для этого равномерностью шкалы у = lgx длина отрезка шкалы у, совпадающего с отрезком [а, b] шкалы х пропорциональна разности lgb — lga.

Обозначая коэффициент пропорциональности через λ, получим

В частности, расстояние любой точки х логарифмической шкалы от точки 1 пропорционально десятичному логарифму числа х

Коэффициент λ равен длине отрезка [1, 10] логарифмической шкалы (т. е. единице масштаба оси у), как видно из формулы

Возьмем теперь две одинаковые и параллельно расположенные логарифмические шкалы, которые мы обозначим через А и В. Сместим шкалу А относительно шкалы В и рассмотрим любые пары чисел а₁ и b₁ а₂ и b₂, которые окажутся друг против друга на этих шкалах (см. раздел «Правило пропорций»).

Это значит, что для рассматриваемых чисел имеет место пропорция

Эта пропорция равносильна пропорции

которая и выражает доказываемое правило:

При любом смещении шкал А и В все числа шкалы А пропорциональны расположенным против них числам шкалы В.

Отметим, что доказанное правило пропорций относится ко всей бесконечной логарифмической шкале. Если бы мы имели возможность построить такую шкалу на счетной линейке, то мы могли бы вести расчеты с числами без их предварительной нормализации и без переброски движка. Необходимость нормализации исходных данных и применяемые в расчетах переброски движка вызваны тем, что на основных шкалах счетной линейки имеется только один отрезок логарифмической шкалы.

2. Свойство «периодичности» логарифмической шкалы. Из правила пропорций вытекает, что если шкалу А сдвинуть относительно шкалы В вправо на длину отрезка [1, 10], то все числа шкалы В будут в 10 раз больше расположенных против них чисел шкалы А:

Наконец, свойство периодичности позволяет нанести логарифмическую шкалу на окружность, что вообще снимает вопрос о перебросках движка. Такие круговые логарифмические шкалы реализованы в конструкциях логарифмического диска «Спутник» (см. раздел «Решение пропорций») и описываемой в приложении 3 Круговой логарифмической линейки КЛ-1.

3. Постоянство относительной погрешности. Погрешность установки чисел на шкале определяется тем расстоянием, на которое по техническим правилам допускается смещение штрихов шкалы. Так как смещение штрихов, не превышающее допуска, может встретиться на любом участке шкалы, то для равномерной шкалы абсолютная погрешность установки чисел будет одна и та же на всем протяжении шкалы. Иначе обстоит дело на логарифмических шкалах. Здесь оказывается постоянной не абсолютная, а относительная погрешность установки чисел. Это означает следующее. Пусть при установке чисел а и b на логарифмической шкале их абсолютные погрешности А_а и А_b вызваны тем, что отметки а и b смещены на одно и то же расстояние. Тогда из равенства этих расстояний

как и в пункте 1, вытекает пропорция

что и выражает равенство относительных погрешностей установки чисел а и b.

По существующим техническим правилам смещение штрихов на обычных счетных линейках не должно превосходить 0,2 мм. Это значит, что предельное допустимое смещение любой отметки а составляет

Отсюда по формуле расстояний получаем

Для основных шкал А к В нормальной линейки коэффициент дающий длину отрезка [1, 10] шкалы, равен 250 мм, поэтому

а значит, относительная погрешность установки чисел на основных шкалах А и В нормальной счетной линейки составляет около 0,2%.

На шкалах С и D коэффициент К вдвое меньше (125 мм) и поэтому относительная погрешность установки чисел на этих шкалах вдвое больше (≈ 0,4%).

4. Построение шкал степенных функций. Рассмотрим сначала соответствие между шкалами В и С корпуса. Шкала В представляет собой отрезок [1, 10] логарифмической шкалы с масштабным коэффициентом λ₁ = 250 мм. Шкала С представляет собой отрезок [1, 100] логарифмической шкалы с масштабным коэффициентом λ₂ = λ₁/2 = 125 мм причем 1 шкалы С находится против 1 шкалы В.

Поэтому если точка u шкалы С находится против точки х₀ шкалы В, то из равенства расстояний

Вот почему шкала С является шкалой квадратов для шкалы В. Аналогично строится шкала кубов К с масштабным коэффициентом λ₃ = λ₁/3.

Шкала квадратов и шкала кубов являются простейшими шкалами степенной функции. Легко построить шкалу степенной функции u = х r при любом показателе r > 0. Для этого достаточно параллельно шкале В аргумента х поместить еще одну логарифмическую шкалу с масштабным коэффициентом

и установить число u = 1 этой шкалы против числа х = 1 шкалы В. Действительно, при этом для соответственных точек х и u по формуле расстояния имеем

Таким путем можно построить на счетной линейке шкалу функции х r не только при любом целом, но и при любом дробном и даже иррациональном значении r. На обычных линейках ограничиваются случаями целых значений r = 2 и r = 3.

На обычных линейках подобные шкалы встречаются только для случая г = — 1 (шкала обратных величин).

Источник

Логарифмическая линейка

Логарифмическая линейка – устройство, предназначенное для упрощения и ускорения работы с логарифмическими таблицами. Использование логарифмической линейки значительно упрощало операции умножения, деления, возведение в степень, извлечения корня и расчет тригонометрических и логарифмических функций. Различного вида логарифмические линейки широко использовались вплоть до начала восьмидесятых годов, пока небыли вытеснены электронными калькуляторами.

Содержание

1. История создания логарифмической шкалы.

Первую попытку упростить и ускорить работу с логарифмическими таблицами предпринял Эдмунд Гюнтер, профессор астрономии Грэшемского колледжа. Он разработал шкалу, состоящую из нескольких отрезков, располагающихся параллельно на деревянной или медной пластине. На каждый отрезок наносились деления, соответствующие логарифмам чисел или тригонометрических величин.

Рассмотрим пример построения логарифмической шкалы. Возьмем за основу отрезок АВ (рисунок ниже) и примем его за единицу. Следовательно, его можно принять за lg 10, так как lg 10 = 1; Теперь рассчитаем длины отрезков, соответствующих десятичным логарифмам чисел 1,2,…9, c точностью до тысячных долей:

Нанесем эти отрезки на шкалу, учитывая, что отрезок АВ = 1:

Для вычисления с помощью этой шкалы необходимо определить сумму или разность длин от начала шкалы до логарифмов исходных чисел. Далее находим логарифм, соответствующий полученной длине, и по его значению определяем произведение или частное. Например, для умножения 2 на 4 надо сложить длину отрезка для числа 2 (0.301) с длинной отрезка для числа 4 (0.602). Далее находим значение, соответствующее длине отрезка 0.903. Это будет число 8. Таким образом, 2*4 = 8. Обычно такая шкала использовалась вместе с двумя циркулями, позволяющими быстро и точно определять длину результирующего отрезка.

Описание логарифмической шкалы Эдмунд Гюнтер опубликовал в 1620 году, так же в этой книге были опубликованы таблицы логарифмов синусов и котангенсов. Изобретение Гюнтера пользовалось большой популярностью и описывалось во многих книгах. Так, например, описание логарифмической шкалы встречается в книге французского механика Н. Биона «Конструкция и применение математических инструментов», опубликованной в 1723 году. Шкала, описанная в этой книге, имела длину 600 мм и ширину 37. Она состояла из шести частей, предназначавшихся для операций с числами, синусами, тангенсами, синусами-верзусами (sin ver a = 1 – cos a), синусами и тангенсами малых углов, синусами и тангенсами румбов. Так же на шкале предусматривались участки для работы с равномерными величинами – «линия меридиана» и «линия равных частей».

2. История создания логарифмической линейки.

Логарифмическая шкала Гюнтера являлась прародителем логарифмической линейки и подвергалась многократным доработкам. Так в 1624 году Эдмунд Уингейт издал книгу, в которой описал модификацию шкалы Гюнтера, позволяющую легко возводить числа в квадрат и в куб, а также извлекать квадратные и кубические корни. Для этого Уингейт поместил две шкалы, построенные в масштабе 1:2, на одной прямой и три шкалы в масштабе 1:3 – на другой. Перенося с помощью измерительного циркуля отрезки с обычной шкалы на шкалу с масштабом 1:2 или 1:3 и наоборот, можно возводить числа в квадрат или в куб и извлекать квадратные или кубические корни.

Дальнейшие усовершенствования привели к созданию логарифмической линейки, однако, авторство этого изобретения оспаривают два ученых Уильям Отред и Ричард Деламейн.

Впервые о своем изобретении Отред рассказал в 1630 году своему ученику и другу Уильяму Фостеру, учителю математики из Лондона. На тот момент Отред изготовил два типа логарифмических линеек – прямоугольную и круглую. Эти изобретения настолько поразили Фостера, что он уговорил передать ему описание изобретения для последующей публикации.

Осенью этого же года Отред рассказал об изобретении круговой логарифмической линейки своему бывшему ассистенту и учителю математики Ричарду Деламейну, который в ответ на рассказ заявил: «Подобное изобретение сделал и я!» и в этом же 1930ом году опубликовал книгу «Граммелогия, или Математическое кольцо», в которой описал круговую логарифмическую линейку и правила ее использования.

Линейка Деламейна содержала до 13 шкал и состояла из вращающегося внутри кольца круга. Так же на линейке располагался указатель, который передвигался вдоль радиуса, облегчая использование инструмента. В книге так же описывалась методика гравировки таких линеек и способы проверки их точности.

Книга Фостера и Отреда, посвященная описанию круглой логарифмической линейки, была издана в Лондоне только в 1632 году и называлась «Круги пропорций». Линейка, описанная в этой книге, содержала восемь шкал (одна шкала была равномерная, а семь остальных – шкалы логарифмов чисел, синусов и тангенсов), выгравированных на медной пластинке. Для облегчения счета на пластинке закреплялись два указателя (см. рисунок справа).

В следующей книге Фореста «Дополнение к использованию инструмента, называемого Кругами Пропорций», изданной в 1633 году, описывалась прямоугольная логарифмическая линейка Отреда. Она состояла из двух частей, на каждой из которой была нанесена логарифмическая шкала. При вычислении эти части линейки зажимались левой рукой, и правой рукой одна из частей сдвигалась относительно другой.

Авторы логарифмических линеек оспаривали первенство изобретения. Так Деламейн обвинял Отреда в воровстве, утверждая, что он не изобрел круговую линейку, а все сведения о ней почерпнул из его (Деламейна) книги. В ответ на подобные заявления Отред подробно описал историю своего изобретения и заметил, что оно было сделано около 12 лет назад. Кто из них прав так и не удалось выяснить. Видимо придется признать, что изобретение логарифмической линейки было сделано независимо друг от друга Уильямом Отредом и Ричардом Деламейном.

Примерно в те же годы Томасом Брауном была разработана плоская спиральная логарифмическая линейка, позволяющая, благодаря увеличению длины шкалы, повысить точность вычислений. Однако, это изобретение не получило широкой известности и вскоре было забыто. Вновь этот тип логарифмических линеек был изобретен в 1748 году Джорджем Адаме. Линейка Адаме размещалась на медной пластинке диаметром 305 мм и имела 10 витков шкалы.

Примерно 1650 году Милбурн предложил способ увеличения длины шкалы логарифмической линейки путем нанесении спиралевидной шкалы на боковую поверхность цилиндра.

В 1654 году англичанин Роберт Биссакер разработал прямоугольную логарифмическую линейку, состоящую из трех частей длинной 60 см, закрепленных параллельно друг другу. Две внешние части были неподвижно закреплены с помощью медных оправ, а третья (движок) свободно передвигалась между ними. Каждой шкале на неподвижных частях соответствовала аналогичная шкала на движке. Причем шкалы были на обоих сторонах логарифмической линейки.

Независимо от Роберта Биссакера аналогичную структуру линейки разработал в 1657 году Сет Патридж, учитель математике из Лондона.

Следующее усовершенствование линейки произвел Томас Эверард. Во-первых, он применил на практике идеи Уингента, расположив на линейке двойные и тройные шкалы для возведения чисел в квадрат и куб, извлечения квадратного и кубического корней.

Во-вторых, он отметил на шкалах особые точки – числа, наиболее часто встречающиеся при расчетах:

— сторона квадрата, вписанного в круг диаметра 1 (0,707);

— сторона квадрата, равновеликого кругу диаметра 1 (0,886);

— длина окружности с диаметром 1 (3.14);

— объем стандартного галлона вина в кубических дюймах (231);

— объем стандартного бушеля солода (2150,42);

— объем стандартного галлона эля (282).

Основное предназначение линейки Эверарда было определение объема сосудов. Универсальная линейка была разработана в 1779 году Джейсом Уаттом, шотландским изобретателем-механиком.

Джеймс Уатт в то время занимался разработкой паровых машин и для их расчета пользовался логарифмическими шкалами, нанесенными на линейки. Подобные линейки были широко известны, однако, их точность оставляла желать лучшего. Мистер Уатт и мистер Соутерн разработали удобное расположение логарифмических шкал для универсального использования и пригласили опытнейших специалистов своего времени для градуировки первого образца. Копии этого образца были переданы мастерам, работающим над паровой машиной.

В 1850 году девятнадцатилетний французский офицер Амедей Маннхейм создал прямоугольную логарифмическую линейку, ставшую прообразом современных линеек и обеспечивающую точность до трех десятичных знаков. Этот инструмент он описал в книге «Модифицированная вычислительная линейка», изданной в 1851 году. В течение 20-30 лет эта модель выпускалась только во Франции, а затем ее стали изготавливать в Англии, Германии и США. Вскоре линейка Маннхейма завоевала популярность во всем мире.

Логарифмическая линейка долгие годы оставалась самым массовым и доступным прибором индивидуального вычисления, несмотря на бурное развитие вычислительных машин. Естественно, она обладала небольшой точностью и скоростью решения по сравнению с вычислительными машинами, однако, на практике большинство исходных данных были не точные, а приближенные величины, определенные с той или иной степенью точности. А, как известно, результаты вычислений с приближенными числами будут всегда приближенные. Этот факт и высокая стоимость вычислительной техники позволили Логарифмической линейке просуществовать практически до конца 20 столетия.

3. Устройство логарифмической линейки.

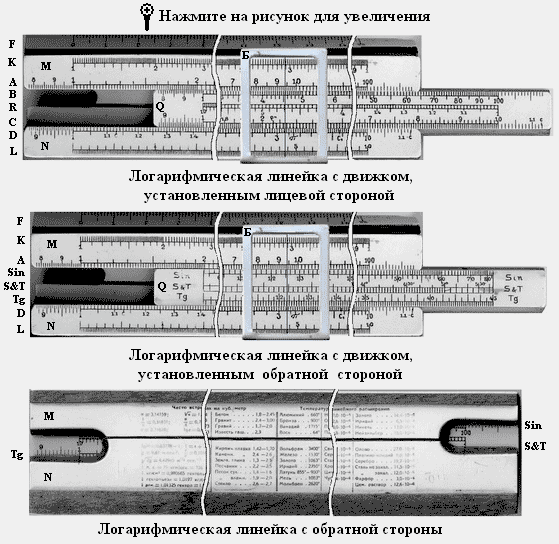
Рассмотрим логарифмические линейки, используемые во второй половине 20 века в России. Стандартная логарифмическая линейка состояла из трех, покрытых белым целлулоидом, частей: корпуса (M,N), движка (Q) и бегунка (Б). На корпусе линейки наносилось шесть шкал длиной по 25 см каждая. Длина шкалы в 25 см позволяла получить результаты с точностью до четырех значащих цифр с ошибкой, не превосходящей единицы последнего знака.

На движке так же было нанесено шесть неравномерных шкал длиной 25 см, по три с лицевой и обратной сторон.

Бегунок представлял собой прямоугольную рамку со стеклом, на середине которого нанесена тонкая черта – указатель. Бегунок удерживался на линейке зацепляясь краями рамки. Между бегунком и линейкой устанавливалась пружинка, помогающая свободно перемещаться бегунку и удерживаться ему на линейке.

На обратной стороне линейки приводились справочные данные: математические и физические константы, коэффициенты линейного расширения, модули упругости, удельные веса тел и другие данные.

Рассмотрим назначение шкал линейки.

Шкала А служит для вычисления квадратов чисел, откладываемых на шкале D. Так же можно с помощью шкал А и В вычислять квадратные корни чисел.

Шкала В точно такая же, как шкала А. На этих шкалах нанесены отрезки, пропорциональные (m/2)*lg X. Цена наименьшего деления на участках от 1 до 2, от 2 до 5, от 5 до 10, от 10 до 20, от 20 до 50, от 50 до 100 равна соответственно 0.02, 0.05, 0.1, 0.2, 0.5 и 1.

Шкала L – равномерная. На ней отложены мантиссы (дробная часть десятичного логарифма) логарифмов шкалы D. Наименьшее деление этой шкалы соответствует 0.002, а метки, обозначенные цифрами 1,2,3,4. читаются как 0.1, 0.2, 0.3, 04…

Шкалы D и С называются основными. На них нанесены отрезки, пропорциональные m*lg X, при Х изменяемом от 1 до 10. Значение наименьших делений этих шкал на участке от 1 до 2 означает 0.01, на участке от 2 до 4 они означают 0.02, на участке от 4 до 10 – 0.05.

Шкала R – это шкала обратных значений. Она представляет собой шкалу С (D), но в перевернутом виде. Таким образом, метка 10 этой шкалы будет на левом конце, а 1 – на правом. На этой шкале любой отрезок P от начала шкалы равняется 250-250* lg p = 250* lg (1/p).

Шкалы Sin, S&T и Tg используются при вычислениях с тригонометрическими функциями. Отрезки на этих шкалах пропорциональны следующим функциям:

Для шкалы синусов (Sin): y = k ( lg sin Vs + 1 ),

Для шкалы синусов и тангенсов (S&T): y = k [ lg 1/2( sin V + tg V ) +2],

Для шкалы тангенсов (Tg): y = k ( lg tg Vt + 1 ),

Следует помнить, что каждая метка (риска) на шкалах линейке имеет не одно определенное значение, а всякое другое, которое может быть получено умножением этого значения на 10 в любой степени. То есть, числа … 1525, 152.5, 15.25, 1.525, 0.1525 … будут расположены в одном месте логарифмической линейки.

4. Работа с логарифмической линейкой.

С помощью логарифмической линейки можно производить умножение, деление, возведение в степень и извлечение корней, определять натуральные значения тригонометрических функций заданных углов и по заданным натуральным значениям тригонометрических функций находить соответствующие им углы, определять логарифмы и антилогарифмы чисел, находить логарифмы тригонометрических функций и производить различные вычисления.

Рассмотрим подробно правила выполнения перечисленных выше операций с помощью логарифмической линейки и начнем с умножения и деления.

4.1. Умножение и деление.

Умножение и деление с помощью линейки основывается на свойстве логарифмов:

lg X*Y = lg X + lg Y lg X/Y = lg X – lg Y

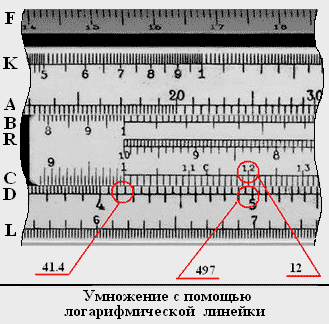
Следовательно, операция умножения сводится к сложению соответствующих отрезков на логарифмических шкалах C и D, а операция деления – к вычитанию этих отрезков. Рассмотрим пример, в котором требуется вычислить X = 41.4 x 12 = 496,8:

1. Ставим указатель бегунка на деление 41.4 на шкале D.

2. Передвигаем движок вправо так, чтобы крайняя левая цифра шкалы C (1) была под указателем бегунка.

3. Ставим указатель бегунка на деление 12 на шкале C.

4. По указателю бегунка считываем число на шкале D (497).

5. Приблизительный результат умножения 497.

Рассмотрим деление на примере y = 5.15/1.31 = 3.931…:

1. Устанавливаем указатель бегунка на деление 5.15 шкалы D.

2. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с делением 1.31 шкалы С.

3. Устанавливаем указатель бегунка на левую крайнюю цифру шкалы С (1).

4. По указателю бегунка считываем число на шкале D (393).

5. Приблизительный результат деления будет 3.93.

4.2. Возведение в степень и извлечение корня.

Для возведения в квадрат или в куб числа М устанавливают указатель бегунка на деление шкалы D, соответствующее числу М. По указателю бегунка на шкале А считывают квадрат числа М, а на шкале К – куб числа М. При этом необходимо вручную учитывать порядок результата.

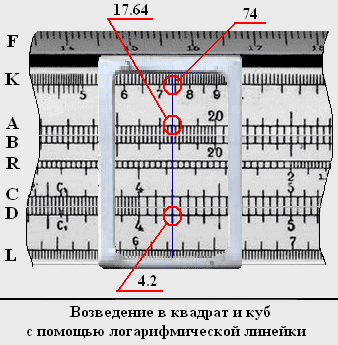
Рассмотрим пример возведения числа 42 в куб и квадрат с помощью логарифмической линейки:

1. Устанавливаем бегунок на деление 4.2 шкалы D.

2. По указанию бегунка считываем число на шкале А (17.64).

4. Приблизительный результат возведения числа 42 в квадрат будет 17.64*10 2 = 1764.

5. По указанию бегунка считываем число на шкале К (74).

6. Определяем порядок результата возведения в куб. В этом случае n = 1, m = 3, следовательно, порядок результата будет 1*3 = 3.

7. Приблизительный результат возведения числа 42 в куб будет 74*10 3 = 74000.

Извлечение корня – действие, обратное возведению в степень, поэтому для того, чтобы извлечь квадратный корень из числа устанавливают указатель бегунка на деление, соответствующее этому числу на шкале А, а результат извлечения смотрят по указателю бегунка на шкале D. Для извлечения кубического корня указатель устанавливают по шкале К, а результат опять же будет на шкале D. Так же, как и при возведении в степень, порядок результата необходимо рассчитывать вручную.

4.3. Работа с логарифмами.

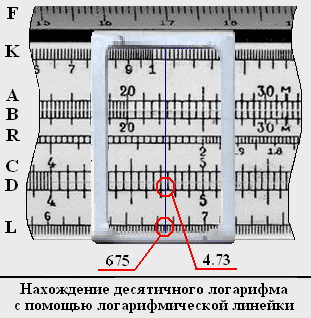
Для нахождении десятичного логарифма числа необходимо указатель бегунка установить на деление шкалы D, соответствующее этому числу. И по указателю бегунка на шкале L определить мантиссу (дробная часть) логарифма. Затем спереди приписать к ней характеристику (целая часть) логарифма. Рассмотрим пример нахождения десятичного логарифма числа 473 (lg 473 = 2.67486…):

1. Устанавливаем указатель бегунка на деление шкалы D, соответствующее числу 473. В нашем случае это будет деление 4.73.

2. Определяем значение мантиссы на шкале L по указателю бегунка (675).

4. Приблизительный результат вычисления десятичного логарифма числа 473 будет 2.675.

Для нахождения числа по заданному десятичному логарифму (потенцирование) устанавливают указатель бегунка на деление шкалы L, соответствующее мантиссе логарифма. По указателю бегунка определяют число, соответствующее мантиссе. Далее вручную определяют порядок результата, исходя из характеристики логарифма.

Рассмотрим пример определения числа, заданного десятичным логарифмом 2.675:

1. Устанавливаем указатель бегунка на деление шкалы L, соответствующее мантиссе заданного десятичного логарифма (675).

2. Определяем по указателю бегунка значение на шкале D (4.73).

4. Приблизительный результат потенцирования: 4.73*10 2 = 473.

4.4. Тригонометрические расчеты.

Логарифмические шкалы Sin, S&T и Tg позволяют производить разнообразные действия над формулами, содержащими тригонометрические функции. Однако, эти шкалы предназначались только для работы с синусами и тангенсами, поэтому при работе с косинусами и котангенсами было необходимо предварительно выразить их через синусы и тангенсы по формулам:

ctg a = 1/tg a, для а от 0 0 до 45 0 ;

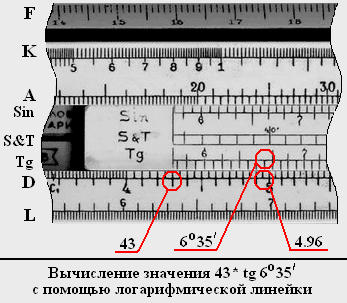
Рассмотрим на примерах методы работы на логарифмической линейке при вычислении тригонометрических функций. Для начала вычислим значение 43*tg6 0 35` = 4.9625…:

1. Устанавливаем указатель бегунка на деление 4.3 шкалы D.

2. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с началом шкалы Tg.

3. Устанавливаем указатель бегунка на деление 6 0 35` шкалы Tg.

4. По указателю бегунка считываем ответ со шкалы D. В нашем примере это будет примерно 4.96.

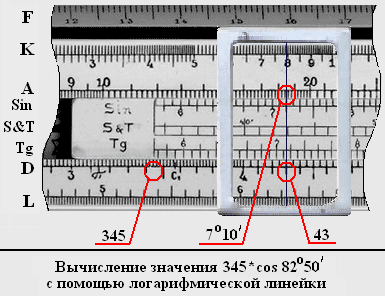
Аналогичные действия необходимо предпринять и при работе с синусами и косинусами. Рассмотрим пример 345*cos 82 0 50` = 43.0408…:

1. Преобразуем косинус в синус: 345*cos 82 0 50` = 345*sin 7 0 10`.

2. Устанавливаем указатель бегунка на деление 3.45 шкалы D.

3. Перемещаем движок логарифмической линейки влево до совпадения указателя бегунка с началом шкалы Sin.

4. Устанавливаем указатель бегунка на деление 7 0 10` шкалы Sin.

5. По указателю бегунка считываем ответ со шкалы D. В нашем случае это будет примерно 43.

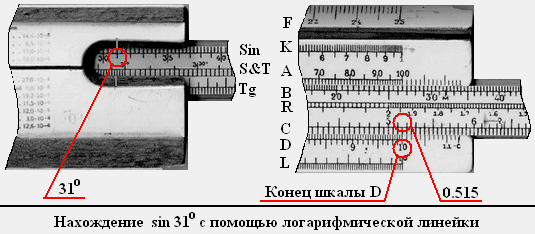
Если же под верхний штрих правого выреза установить, например, 31 0 шкалы Sin, то на шкале С (напротив правого крайнего штриха (цифра 10) шкалы D) будет значение sin 31 0 (примерно 0.515).

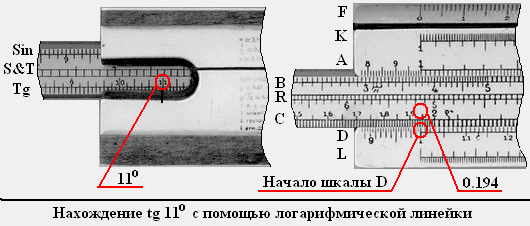
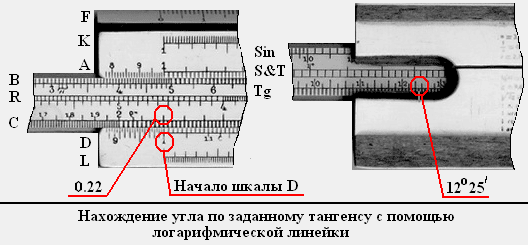
Так же с помощью логарифмической линейки можно находить углы по значениям синуса или тангенса. Рассмотрим пример нахождения угла, которому соответствует tg a = 0.22:

1. Находим на шкале С значение заданного тангенса (0.22).

2. Совмещаем найденное деление шкалы С с началом шкалы D.

Для нахождения угла по заданному синусу (например, sin a = 0.56) совмещаем деление шкалы С, соответствующее синусу (0.56), с концом шкалы D. Переворачиваем линейку и на шкале Sin в правом вырезе напротив верхнего штриха считываем значение искомого угла (примерно 34 0 ).

Стоит помнить, что при определении угла по значению тригонометрической функции, необходимо вручную учитывать в какой четверти находится искомый угол.

Часто при расчетах требуется переводить углы из градусов в радианы. Для этих целей на линейке предусмотрена специальная отметка 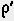. Рассмотрим использование отметки на примере перевода 36 0 12` в радианы:

1. Выражаем заданный угол в минутах (36 0 *60+12` = 2172`).

2. Устанавливаем бегунок на деление 2.172 шкалы D.

3. Подводим под указатель бегунка штрих шкалы С, отмеченный знаком .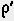

4. Считываем ответ на шкале D напротив конца шкалы C (примерно 0.632 рад).

Рассмотрим перевод угла из радиан в градусы на примере 0.35 рад:

1. Устанавливаем бегунок на деление 3.5 шкалы D.

2. Подводим под указатель бегунка конец шкалы С.

3. Устанавливаем бегунок на деление шкалы С, отмеченное символом .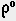

4. По указателю бегунка со шкалы D считываем ответ (примерно 1.2).

5. Ответ считан в минутах без учета порядка. Переведем ответ в градусы и учтем порядок: 1.2/60 = 0.02. С учетом порядка ответ будет примерно 20 градусов.

5. Виды логарифмических линеек.

Часто на логарифмические линейки наносили дополнительные шкалы со значениями функций часто употребляемых на практике, например, в электротехнических, геодезических и других расчетах. Большое распространение имели и дисковые логарифмические линейки. Ниже приведены различные виды логарифмических линеек.

На логарифмических линейках закончим обзор домеханического этапа и перейдем к следующему этапу истории развития ЭВМ – Механическому этапу.

Источник