Как сделать ломаный отрезок
Ломаная линия
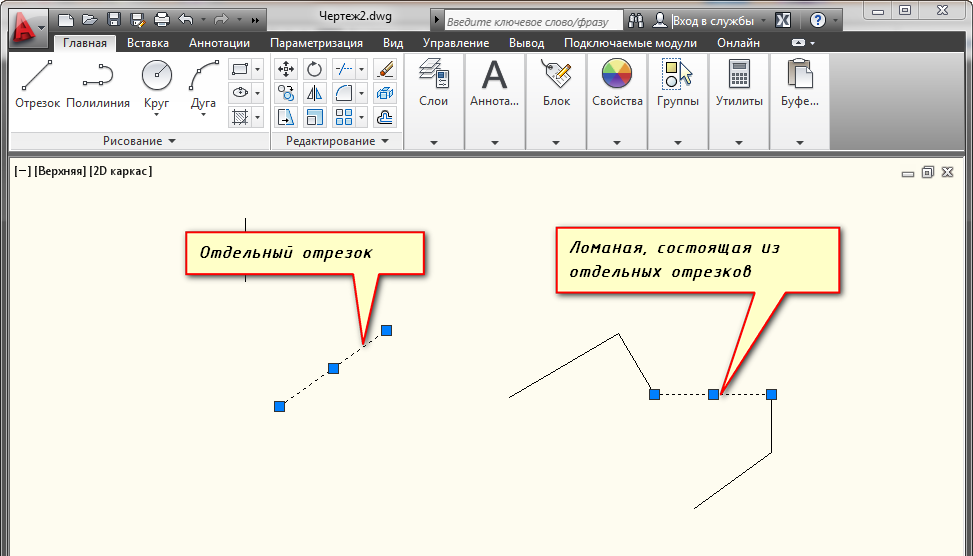
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Инструмент Отрезок в Автокаде (Autocad)
Построение отрезков в Автокаде производится щелчками левой кнопки мыши (далее ЛКМ). Тем самым мы задаем конечные точки отрезка в необходимых местах.
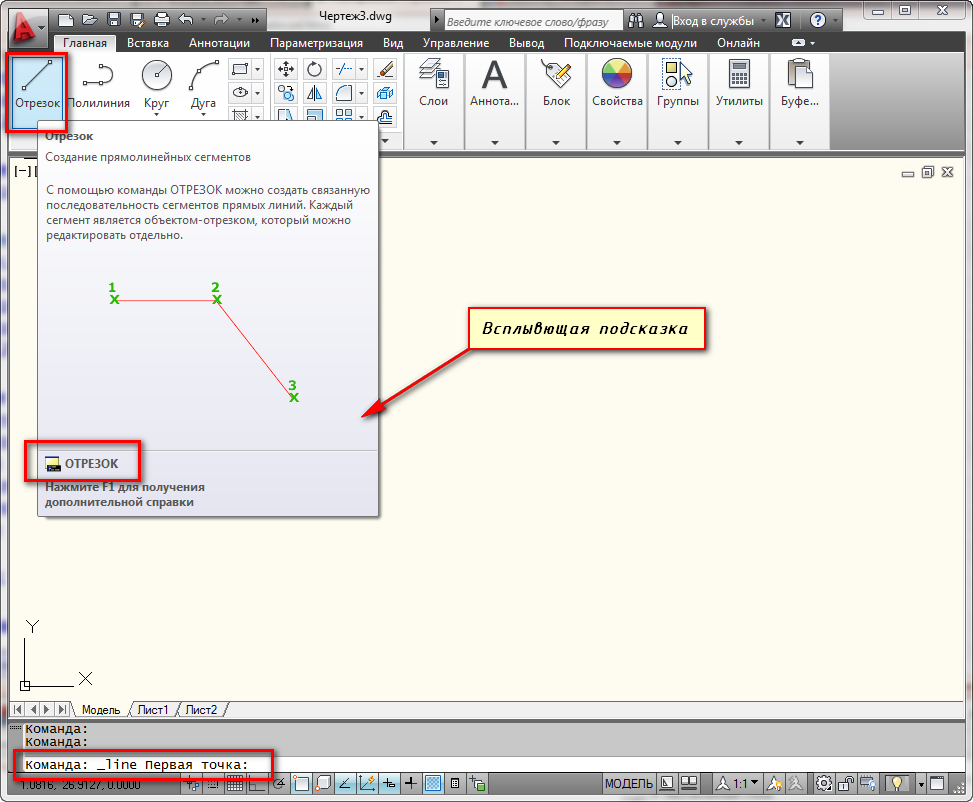
На вкладке “Главная” в окне “Рисование” наведите указатель мыши на инструмент “Отрезок”. Не спешите щелкать по кнопке. Подождите некоторое время, и программа выведет подсказку (всплывающее окно). Там будет указана Команда вызова инструмента. В нашем случае это команда «ОТРЕЗОК».
Как построить отрезок в Автокаде?
Теперь нажмите ЛКМ по кнопке “Отрезок”, либо просто на клавиатуре начните вводить слово Отрезок (или “_line”). Достаточно напечатать лишь ‘Отр”, и программа сама вам предложит вариант Отрезок. Чтобы вызвать команду, нажмите клавишу «Enter».
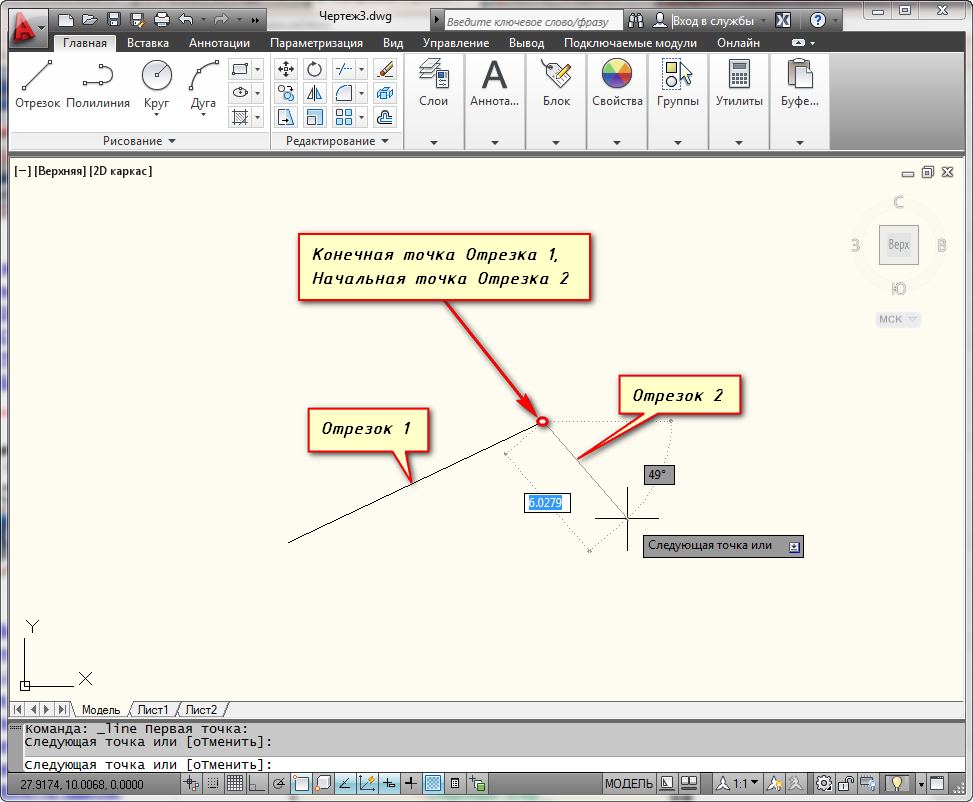
Теперь обратите внимание на командную строку! Там появился запрос: _line Первая точка. Программа Автокад просит нас указать первую точку отрезка. Для этого ставим курсор в необходимое место на экране и производим щелчок ЛКМ. Затем указываем вторую точку так же с помощью ЛКМ. И отрезок в Автокаде построен.
На этом выполнение команды Отрезок в Автокаде не закончится. Далее будет предложено продолжить построение отрезков. При этом конечная точка первого отрезка будет начальной точкой второго отрезка. Посмотрите другие наши уроки по Автокаду для начинающих, чтобы более детально разобраться в программе.
Теперь узнаем, как разделить отрезок в Автокаде. В ходе выполнения построений можно отменить задание последней точки отрезка, а также закончить построение отрезка.
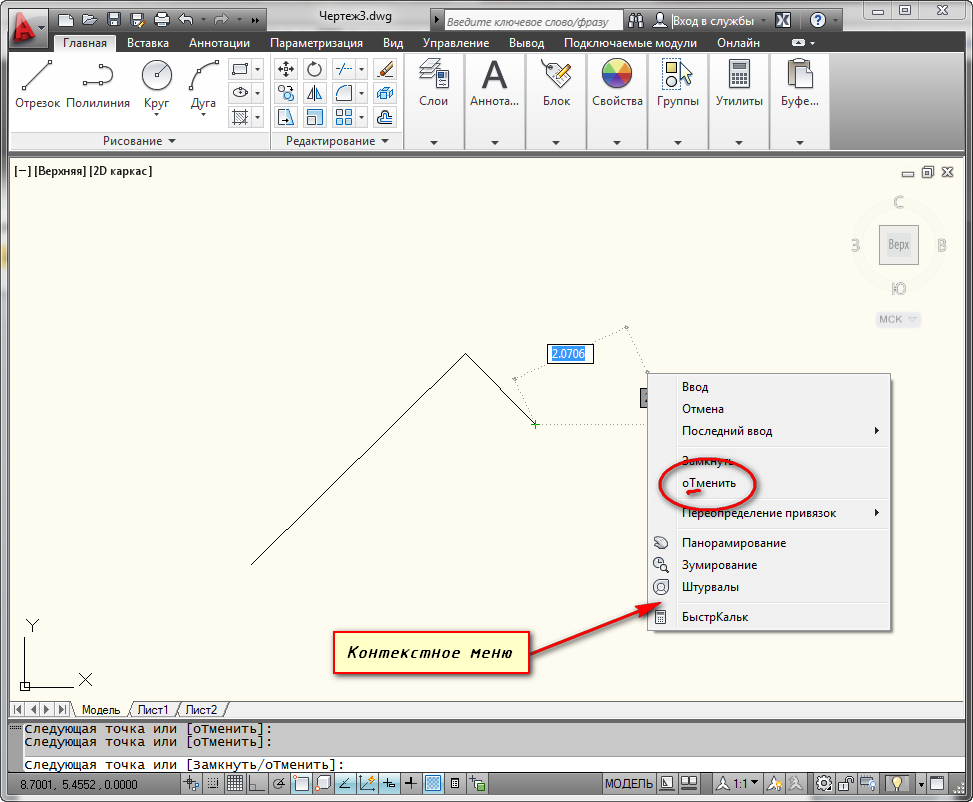
Отмену последней введенной точки можно произвести из контекстного меню. Для этого нажмите правой кнопкой мыши (ПКМ) и выберите действие “ Отменить”. При этом последняя построенная точка удалится.
Чтобы не тратить время на вызов контекстного меню, Вы всегда можете воспользоваться ключевыми буквами вызова команды. В нашем случае буква “Т” (а затем нажатие “Enter”) отменяет построение последней точки отрезка.
Чтобы закончить построения, выберите из контекстного меню опцию “Ввод”, либо “Отмена” или нажмите клавишу “Enter” (ещё можно использовать”Esc”).
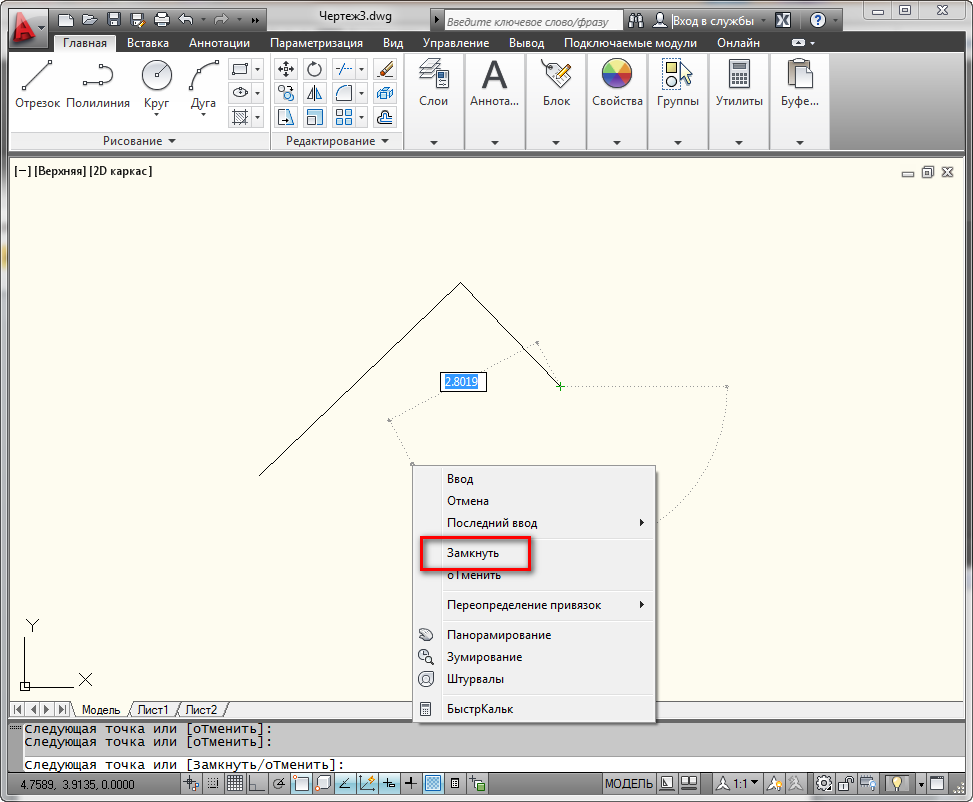
Также в ходе выполнения команды Отрезок доступна еще опция “Замкнуть”, то есть создать отрезок в полилинию Автокад. Она становится доступна при построении хотя бы двух отрезков. И предназначена для замыкания начальной точки первого отрезка и конечной точки последнего отрезка. Вызывается из контекстного меню при нажатии ПКМ. Вы можете использовать ключевую букву “З” на клавиатуре.
Точные построения отрезков и ломаных в Автокаде
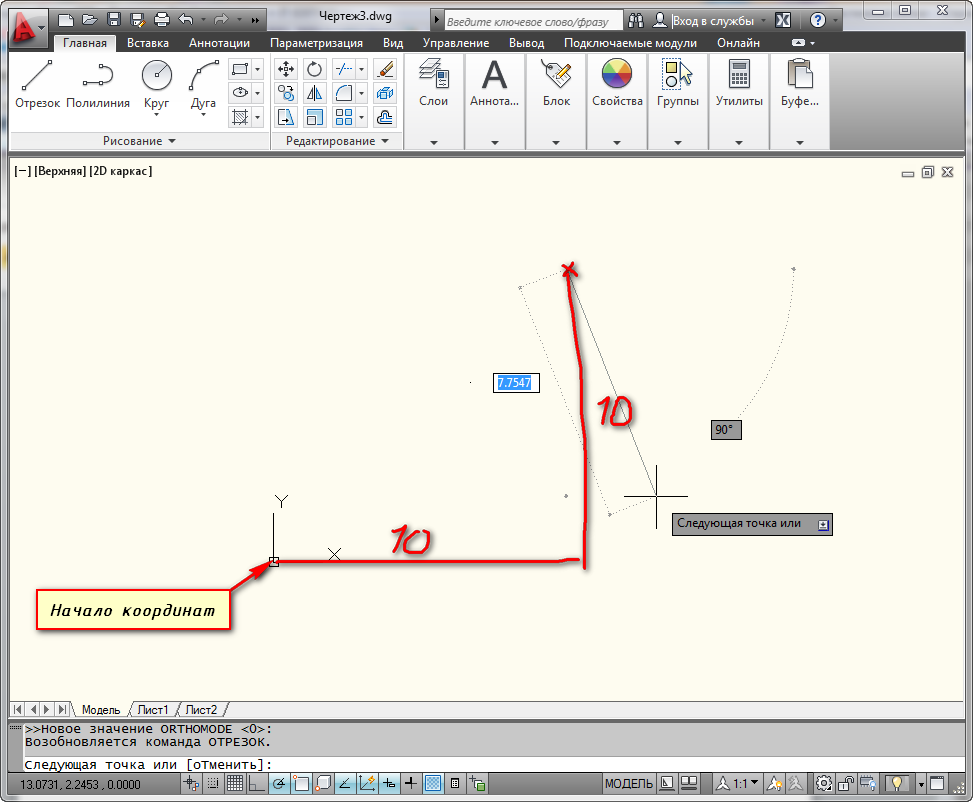
Выбираем инструмент «Отрезок». И на запрос командной строки указать первую точку отрезка, вводим в нее координаты, например, (10,10) и нажимаем “Enter”.
Как видно на рисунке, первая точка построилась в точке с координатами х=10мм и y=10мм от начала координат.
Внимание! Между координатами X и Y необходимо ставить знак запятой, так как точка воспринимается программой как разделитель между целой и дробной частью числа.
Конечную точку отрезка давайте построим в начале координат. Для этого в командной строке вводим значения (0,0). И не забываем нажать “Enter”.
Как быть, если нам надо построить отрезок в Автокаде заданной длины?
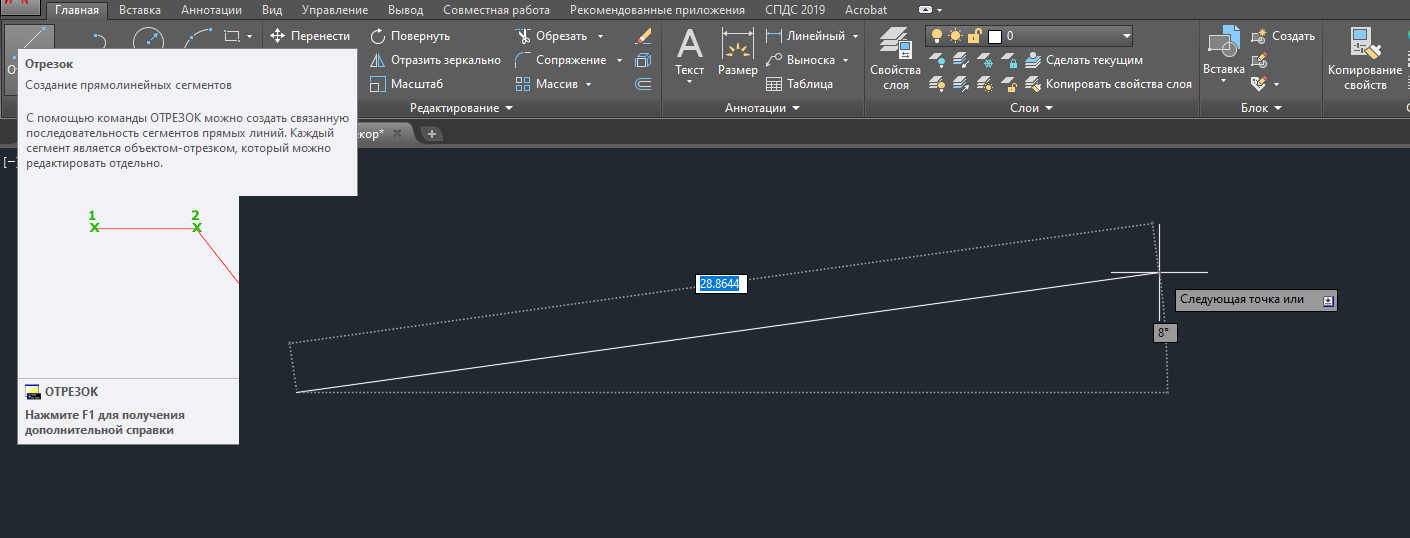
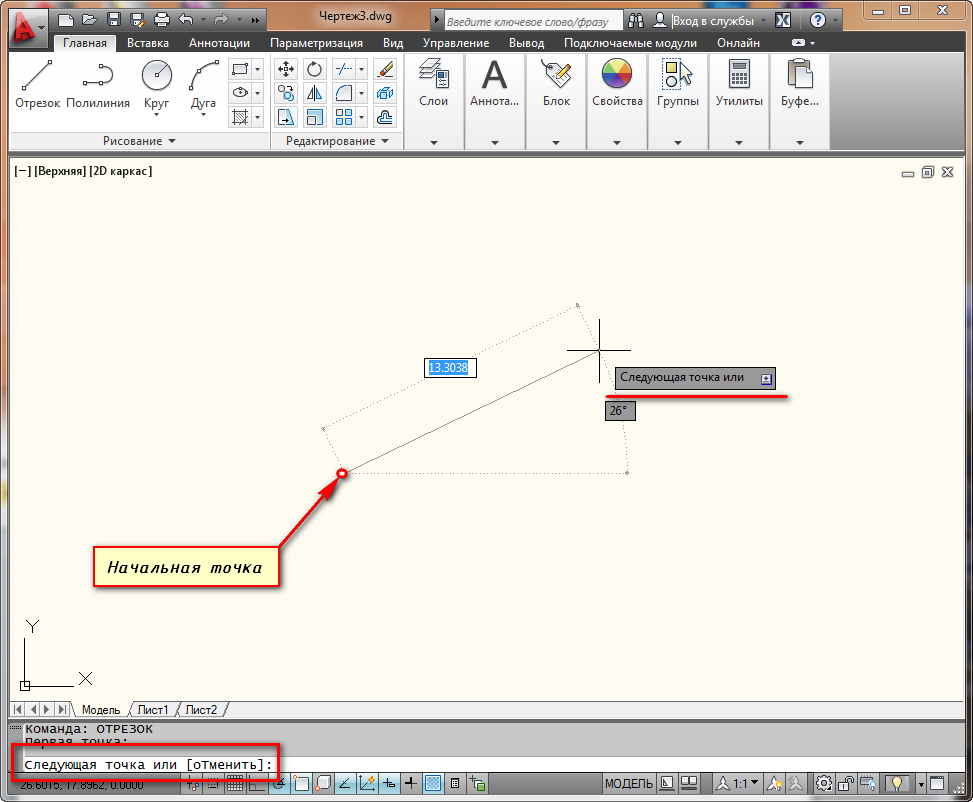
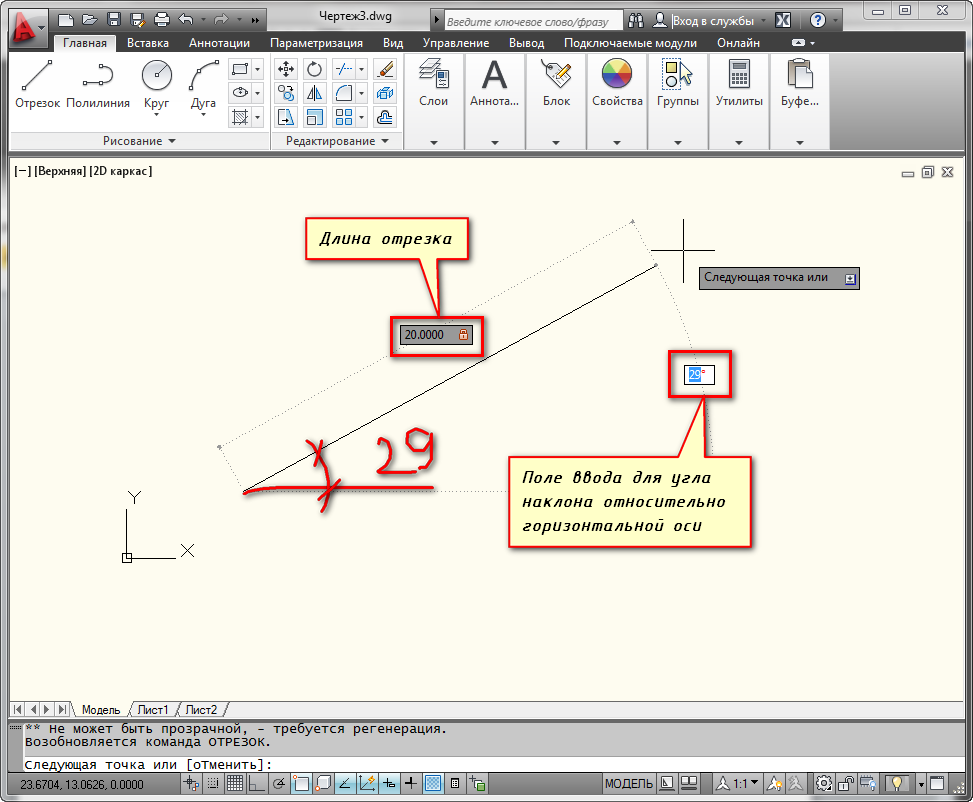
Строим первую точку. Можно задать её произвольно или с помощью координат. А теперь обратите внимание на подсказки в виде полей для ввода значений. На рисунке я выделил их красным цветом.
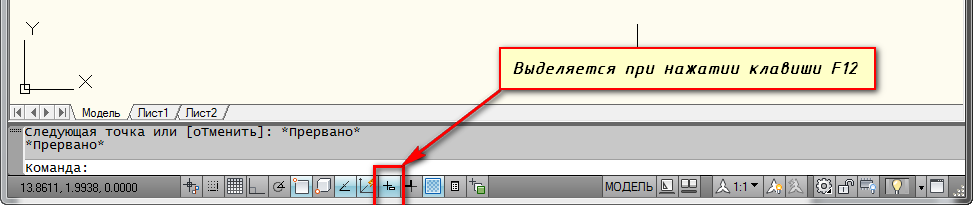
Если у Вас они не показываются, то необходимо выбрать параметр “динамический ввод”. Для этого нажмите на клавишу F12. Либо выберите значок в строке состояния.
Эти поля показывают значение длины отрезка в Автокаде и угла наклона отрезка. При этом поле длины по умолчанию активно.
Теперь попробуйте ввести какое-нибудь значение длины отрезка с клавиатуры, например, 20. Оно автоматически показывается в поле-подсказке. Теперь нажимаем “Enter”. И отрезок в Автокаде, заданной длины 20 мм, построен.
Если Вы знаете угол наклона, то можете ввести и его. Для этого после ввода длины отрезка в Автокаде нажмите клавишу “Tab” на клавиатуре и попадете в поле для ввода угла наклона отрезка. Вводите значение и нажимаете “Enter”.
Мы с Вами разобрались, как строить отрезки в Автокаде, в. т.ч. как преобразовать отрезок в полилинию Автокад.
Теперь Вы сможете построить отрезки в Автокаде с помощью координат, задания значений длины отрезка в Автокаде или просто с помощью мыши.
В следующем уроке продолжим рассмотрение простейших примитивов, в частности, прямых (лучей). Как научиться работать в Автокаде, расскажет наш курс!
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 1
Оценок пока нет. Поставьте оценку первым.
Так как вы нашли эту публикацию полезной.
Подписывайтесь на нас в соцсетях!
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше? Отправить отзыв
1 класс. Математика. Точка. Прямая, кривая и ломаная линии.
1 класс. Математика. Точка. Прямая, кривая и ломаная линии.
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
На данном уроке Вы изучите простейшие геометрические понятия, о которых вам расскажет мама дракончиков. Вместе с дракончиками Вы изучите такие основные понятия, как прямая линия, луч, отрезок, угол, ломаная и кривая линия. У Вас будет возможность изучить предложенный материал на наглядных примерах.
Тема: Наглядная геометрия
Урок: Начальные геометрические понятия
1. Начало сказки о дракончиках
На этом уроке будут изучены простейшие геометрические понятия. Для лучшего понимания рассмотрим сказку про дракончиков.
Далеко-далеко в горах живет большая-большая семья драконов: папа-дракон, мама-дракониха и много маленьких дракончиков. Когда дракончики были маленькие, они учились ползать, бегать, летать, прыгать, узнавали, что такое снег, дождь, звёзды, учились в горах ориентироваться, учились даже огнём дышать. Когда дракончики немножко подросли, мама решила их научить математики, в том числе геометрии. Дракончики очень удивились, они не поняли о чём идет речь. Мама предложила им сесть на площадке перед большой скалой и смотреть, что она будет рисовать. Она начала рисовать мелом на этом плоском куске скалы различные геометрические вещи, начиная с самых простых. Вначале мама-дракониха нарисовала линию, которая изображена на рисунке. (рис. 1)
Мама-дракониха сказала, что эта линия называется прямая. Это такое геометрическое понятие.
2. Изображение и определение прямой
Прямая линия – это линия, которая совершенно бесконечна.
Прямая линия идет бесконечно в одну сторону и в другую сторону. Есть такое даже выражение «Летит в небе по прямой».
Потом мама нарисовала точку и от неё провела линию. (рис. 2)
3. Изображение и определение луча
Она объяснила, что точка – это начало, от нее идет линия в бесконечность. Это называется луч.
Луч — это полупрямая, которая имеет точку начала и не имеет конца.
Он так называется потому, что она как луч света. У луча света всегда есть начало. Он всегда начинается либо на солнце, либо на свечки, либо в фонарике, либо на звезде далекой. Дракончики поняли, что такое луч.
4. Изображение и определение отрезка
Потом мама-дракониха попросила представить дракончиков, что они от прямой отрежут кусочек. Такая фигура называется отрезок. (рис. 3)
Отрезок может быть длинным или коротким. Дракончики сразу не поняли. Тогда мама нарисовала еще несколько отрезков: длинные и короткие. (рис. 4)
Это всё отрезки. Теперь дракончики все поняли.
5. Изображение и определение угла
Потом мама-дракониха из одной точки отложила два луча, получилась фигура, которая называется угол. (рис. 5)
Причем углом называется как вся фигура, так и что находится внутри неё.
Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
6. Изображение ломаной
Потом мама-дракониха решила нарисовать еще одну форму линии. (рис. 6)
Такая линия называется ломаная линия. Потому что взяли фактически прямую линию и поломали ее. И каждый кусочек на этой линии называется звено. Ломаные линии могут быть самые разные, по разному поломанные.
7. Изображение кривой
Следом мама нарисовала загогулину. (рис. 7)
Это кривая линия. Таких кривых линий можно нарисовать много-много самых разных.
8. Окончание сказки о дракончиках
Потом мама-дракониха спросила у маленьких дракончиков, по какой линии они летаете в небе. Дракончики задумались. И один сказал, что он летает по кривой линии, он делает всякие пируэты, закладывает спирали, петли делает. А другой дракончик сказал, что когда они в снежки играли, он повисал в воздухе, махал крылышками, а в него кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
И тут мама заметила, что дракончики уже стали скучать и как-то вертеться, уже плохо её слушают. Она поняла, что пора их отпустить, она сказала, что урок закончен. Дракончики замахали крылышками, взлетели в небо, разлетелись над горами, весело кричали, смеялись. Мама смотрела на них и улыбалась, махала им лапой.
Итак, на уроке мы выучили такие простейшие геометрические понятия, как прямая линия, отрезок, луч, угол. Также мы рассмотрели ломаную и кривую линию. После изученного урока Вы будете знать простейшие геометрические понятия не хуже маленьких дракончиков.
Источник конспекта: http://interneturok.ru/ru/school/matematika/1-klass/beksperimentb/nachalnye-geometricheskie-ponyatiya?seconds=0
Источник видео: https://www.youtube.com/watch?v=o8Pu_Q8YFjk
Файлы
Нет дополнительных материалов для этого занятия.