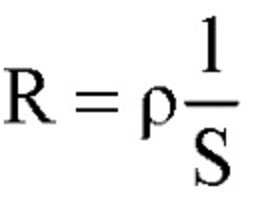Как сделать сопротивление своими руками
Низкоомный резистор своими руками
Для изготовления низкоомных резисторов необходимо по данным справочника по электротехнике (или справочника радиолюбителя) определить, какой длины нужно взять медный (в изоляции) провод, чтобы сопротивление этого отрезка провода было равно сопротивлению требуемого резистора.
Затем зачищают и облуживают начало и конец отрезка провода и припаивают их к проволочным выводам стандартного резистора, номиналом от единиц до сотен килоом. Полученную петлю из провода, которая в зависимости от сечения провода и требуемого сопротивления резистора может иметь длину от нескольких сантиметров до нескольких метров, складывают вдвое посередине петли и затем спаренный провод наматывают (это так называемая бифилярная намотка) внавал на корпус использованного стандартного резистора. Намотанный провод закрепляют нитками.
После этого проверяют номинал вновь изготовленного резистора. Обычно отклонение от номинала составляет более 5 что вполне достаточно для большинства схем. Для изготовления резисторов номиналом от 0,05 до 10 Ом достаточно использовать провода диаметром от 0,08 до 0,35 мм. Габариты изготовленных таким образом резисторов в основном определяются размером использованного для намотки стандартного резистора, а мощность рассеяния оказывается достаточной для большинства электрических схем.
Разумеется, что в качестве каркаса для намотки можно использовать не только стандартные резисторы большого номинала, но и другие нетокопроводящие материалы и средства, например, спички, диэлектрические прутки и т.п. Если мощность полученного резистора окажется недостаточной (он будет нагреваться выше 60°), то потребуется взять медный провод большего диаметра вплоть до 1-1,5 мм. В этом случае увеличится требуемая длина провода, а, следовательно, и габаритные размеры изготовленного резистора.
Возможно потребуется использование специального каркаса для размещения в нем всей массы провода. Но в любом случае намотка провода обязательно должна быть бифилярной, так как это сводит к минимуму индуктивность резистора и повышает диапазон частот, на которых возможно его использование.
В качестве примера определения требуемой длины медного провода рассмотрим следующий: требуется резистор номиналом 2 Ом. Имеется провод ПЭЛ диаметром 0,14мм. Из справочника [1] определяем, что сопротивление 1 м провода данного диаметра равно 1,14 Ом. Следовательно, для определения искомой длины требуемого отрезка провода (X) необходимо решить пропорцию 1/1,14 Ом = Х(м)/20 Ом. Отсюда Х(м) = 1 м х 2 Ом/1,14 Ом = 1,75 м.
Как сделать самодельный низкоомный резистор, электрическое сопротивление своими рукам. Расчет диаметра и длины провода для намотки проволочного сопротивления.
Тема: как можно самому намотать постоянный резистор на малое сопротивление.
Порой возникает необходимость в намотке самодельного резистора на достаточно малое электрическое сопротивление, порядка 0,1-1000 ом. Допустим в моем случае мне нужен был низкоомный резистор аж на 0,1 ом, это мало, и даже очень мало. Он должен стоять на схеме электронной нагрузки в эмиттерной цепи мощных силовых транзисторов, для снятия тока на отрицательную обратную связь, что была на операционном усилителе. Ехать на радиорынок из-за одного резистора как-то было лень. Мне проще было самому намотать нужное сопротивление своими руками поверх обычного резюка, с большим сопротивлением. В этой статье я расскажу о некоторых тонкостях и нюансах, касающиеся процесса этой самой самодельной намотке.
Длину медного провода, для получения нужного сопротивления, можно вычислить по следующей формуле:
Но, вот когда дело имеешь с очень маленьким сопротивлением (как в моем случае 0,1 ом), то длину пожалуй лучше определить практическим путем. То есть, беру, например, один метр нужного по диаметру провода и обычным мультиметром измеряю его сопротивление. Ну, а далее уже по пропорции можно легко найти нужную длину, зная что 1 метр провода равен определенному значению сопротивления. Или совсем просто, если сопротивление в этом метре больше нужного, постепенно начинаем откусывать от провода лишнии куски. Проводим измерения. Опять откусываем. Опять измеряем. И так до тех пор, пока не останется кусок провода с нужным сопротивлением.
То есть, когда мы намотаем катушку на резистор и поставим его в схему, то при скачках напряжения или его снятия с этого резистора на нем будет образовываться всплески напряжения, которые по своей амплитуде могут превышать напряжение питания, аж в несколько раз. Эти скачки, помимо прочего, будут иметь обратную полярность, относительно источника питания. Такой вот нехороший процесс может крайне негативно влиять на другие элементы электронной схемы, особенно чувствительны к таким скачкам напряжения маломощные полупроводники (диоды, транзисторы, тиристоры, стабилитроны, микросхемы и т.д.). В лучшем случае схема может давать сбои, работать с отклонениями, ну, а в худшем такие всплески напряжения могут вовсе вывести определенные узлы схемы из строя.
Видео по этой теме:
Резистор
Здравствуйте уважаемый читатель блога Моя лаборатория радиолюбителя.
В сегодняшнем материале хотелось бы освятить довольно таки нужную тему о резисторах, в особенности вопрос о том, что такое резистор, возникает у новичков радиолюбителей. В этой обширной статейке я довольно таки подробно постараюсь объяснить, что такое резистор, как он выглядит и где применяется.
И так начнем повествование о резисторах, поэтому усаживаемся поудобнее за нашими мониторами, желательно сделать себе кофе и погрузиться в мир радиоэлектроники 🙂
—Что такое резистор? Резистор – это пассивный элемент электрической схемы, создающий сопротивление электрическому току.
Где применяются резисторы? Применяются резисторы во всех схемах, и чаще, в количественном отношении, чем другие элементы схемы. С помощью резисторов регулируют значения тока и напряжения.
Единица измерения сопротивления – Ом. Измерения записываются в сторону увеличения: Ом, кОм(1000Ом)-килоом, мОм(1.000.000Ом)-мегаом и Гом(1.000.000.000Ом)-гигаом.
Типы резисторов:
Постоянные резисторы – это резисторы имеющие постоянное, неизменное, сопротивление независимое от воздействия окружающих воздействий, таких как свет, температура.
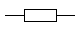
Переменные резисторы — это резисторы меняющее свое сопротивление в зависимости от положения движка переменного резистора.
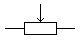
Такие переменные резисторы используются в многой бытовой технике вокруг нас, старые телевизоры, где звук регулировали крутя ручку звука и подобные
Подстроечные резисторы — это те же самые переменные резисторы, но используемые для точных настроек токов и напряжений схем. Устанавливаются преимущественно на самих печатных платах.
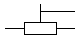
Фоторезисторы – это резисторы меняющие свое сопротивление под действием света.
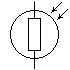
Терморезисторы – резисторы меняющие свое сопротивление в зависимости от температуры, приложенной к нему
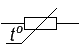
— Маркировка резисторов:
Заграничный ГОСТ
Тут немного проще. По американским стандартам маркируются резисторы 3 буквами, две первые указывающие номинал, а третья — количество нулей добавляемых к номиналу
Например: 0,33Ом –R33, 33Ом-330, 33кОм-333, 330кОм-334, 33мОм-336.
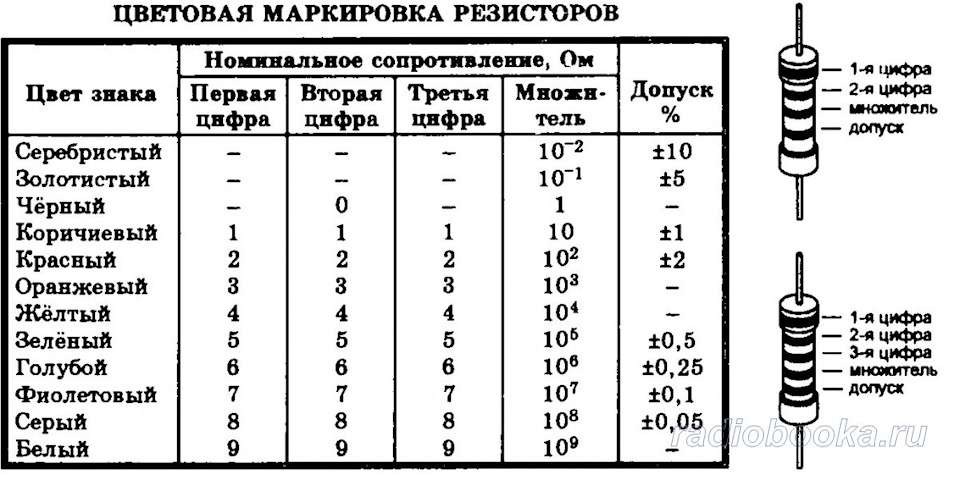
Цветовая маркировка резисторов
На мой взгляд самая удобная и простая в использовании. Обозначается она разноцветными полосками на резисторе. Полосок бывает 4 и 5. Научится читать резисторы цветной маркировки очень просто:
-Первые две полосы указывают номинал резистора.
-Третья полоска, у резисторов с 4 полосами, указывает множитель, а у резисторов с 5 полосами, указывает третью цифру номинала.
-Четвертая полоса в 4 полосной маркировке говорит о точности номинала, а в 5 полосной указывает на множитель номинала.
-Пятая полоса указывает на точность
Что бы удобно было ориентироваться, вот табличка с цветовой кодировкой резисторов
| Цвет | Число | Множитель | Точность |
| Черный | 0 | 1 | — |
| Коричневый | 1 | 10 | 1 % |
| Красный | 2 | 100 | 2 % |
| Оранжевый | 3 | 1 000 | — |
| Желтый | 4 | 10 000 | — |
| Зеленый | 5 | 100 000 | 0,5 % |
| Синий | 6 | 1 000 000 | 0,25 % |
| Фиолетовый | 7 | 10 000 000 | 0,1 % |
| Серый | 8 | 100 000 000 | — |
| Белый | 9 | 1 000 000 000 | — |
| Серебристый | — | 0,01 | 10 % |
| Золотой | — | 0,1 | 5 % |
К примеру, резистор номиналом 1 кОм с погрешностью 1% будет иметь код — коричневый черный красный коричневый
— Мощность резисторов и рассеиваемая мощность
Каждый резистор, пропуская через себя напряжение, создает определенное падение напряжение, что обусловлено законом Ома (R=U\I). Из-за этого на резисторе начинает рассеиваться тепло — это и есть рассеиваемая мощность. Эту мощность мы рассчитываем для сбережения целостности резистора, потому-то резистор имеют свою определенную рассеиваемую мощность, то есть сколько тепла он сможет выделить при падении на нем напряжения. Рассчитывается мощность по формуле P= I*U либо эти две для вычисления промежуточного параметра P=I^2*R или P=U^2/R
Для примера нам нужно рассчитать балластный резистор для блока питания 5В с током нагрузки 0,1А. Сначала по закону Ома рассчитаем, какое сопротивление резистора нам нужно R=5/0.1=50(Ом). Имея сопротивления резистора, рассчитываем мощность резистора P=5*0.1=0.5Вт.
То есть наш балластный резистор должен быть сопротивлением 50Ом и рассеиваемой мощностью 1ВТ, а 1 Вт — потому что всегда нужно брать резисторы с запасом в 1.5-2 раза, что бы небыло ситуаций как на этой очень удачно подобранной картинке 🙂
Поэтому запоминаем, что необходимо брать мощность резистора в 2 раза большей от расчетной!
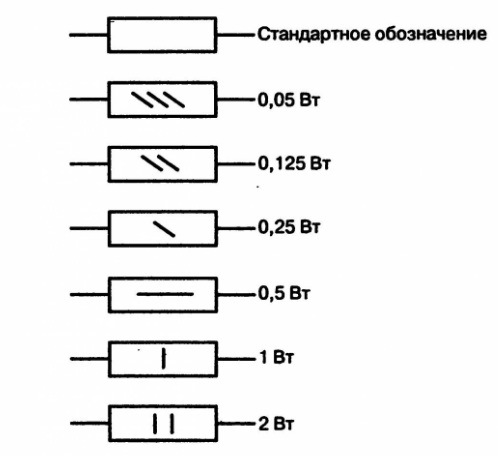
Мощность резисторов на схемах указываются так:

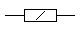

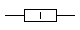
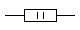
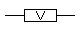
Есть и далее продолжение маркировки, но это уже не обязательно, потому что это саамы ходовые мощности и больше редко используются в схемах
— Последовательное и параллельное соединение резисторов
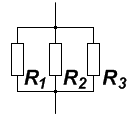
Так же для достижения нужного нам сопротивления мы можем подключать последовательно резисторы
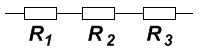
И подключать резисторы параллельно
— Делитель напряжения на резисторе
Делитель напряжения на резисторах часто используется в схемах для получения нужного напряжениях в отдельных цепях схемы.
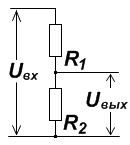
И прежде чем мы начнем рассматривать формулы, давайте выясним один очень важный момент.
Что бы четко рассчитывать нужное нам напряжение на выходе, используйте R2 сопротивлением в 100 раз меньше сопротивления нагрузки подключенной к выходу делителя
Рассмотрим самые нужные формулы для расчета делителя:
1. Нам известно входящее напряжение Uвх и сопротивление R1 и R2.
Uвых=Uвх*R2/(R1+R2)
Например, входящее напряжение 12В, резисторы R1=2.2к и R2=1к. Uвых=12В*1000Ом/3200Ом=3.75В
2. Известно нужное Uвых и сопротивление R1 и R2.
Uвх=Uвых*(R1+R2)/R2
Например, нам нужно получить 5 вольт для питания, резисторы R1=2.2к и R2=1к. Uвх=5В*3200Ом/1000Ом=16В
3. Определим значение R1 при известном Uвх, Uвых
R1=Uвх*R2/Uвых-R2
Например, входящее напряжение 12 вольт, выходящее напряжение 5В, значение R2=1к
R1= 12В*1000Ом/5В – 1000Ом=1400Ом
4. Определим значения R1 и R2, зная их суммарное сопротивление Rобщ и Uвх и Uвых
R2=Uвых*Rобщ/Uвх, R1= Rобщ-R2
Например R2=5В*3200Ом/12В=1333Ом, R1= 3200-1333=1867(Ом)
Это самые ходовый формулы, которые я использую уже около года, с тех пор, как только узнал о них
— Делитель тока на резисторе
Делитель тока на резисторах необходим для того, что бы определенную нужную часть тока перевести в другое плече делителя и после вернуть его обратно.
Делитель тока это параллельно соединенные резисторы, делящие между собой протекаемый ток. 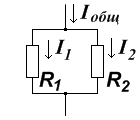
Применяют делители тока для измерительных приборов, когда основной ток проходит через шунтирующий резистор, а малая часть тока проходит через катушки измерительного прибора, которая является вторым сопротивлением в схеме. Так же применяется для усиления тока, когда одного резистора не хватает
Формула расчета шунта для измерительных приборов R2 =I1*R1/(Iобщ-I1),где R1 это сопротивление прибора, а I1 это ток отклонения катушки прибора.
Расчет делителя проходит по формуле I1=Iобщ*R2/(R1+R2) и I2=Iобщ*R1/(R1+R2)
Для примера. Рассчитаем токи, проходящие через R1=0,1Ом и R2=0,2Ом, если сумарный ток 5А.
I1=5А*0,2Ом/0,3Ом=3,33А и I2=5А*0,1Ом/0,3Ом=1,66А, определили проходящие токи, а теперь рассчитаем рассеиваемую мощность по формуле P=I^2*R. P1=3.33*3.33*0.1=1.1(Вт), P2=1.66*1.66*0.2=0.55Вт
И на этой ноте можно заканчивать материал. Изучайте, понимайте, задавайте вопросы.
С ув. Admin-чек
Box77 › Блог › Основы автоэлектрики. Часть2. Резисторы. Провода. Подробнее о сопротивлении
Ранее мы изучили самые базовые основы электротехники:
Основы автоэлектрики. Часть1. Основные законы
Сегодня мы поговорим о таком простом и популярном электронном компоненте как резистор, немного о проводах и о законах сопротивления.
Оглавление сегодняшнего материала:
1. Резистор постоянный.
2. Провод как резистор.
3. Последовательное включение резисторов.
4. Параллельное включение резисторов.
5. Смешанное (последовательно-параллельное) включение резисторов.
6. Преобразование «звезда-треугольник».
7. Маркировка резисторов.
Данный материал служит продолжением описания некоторой фундаментальной базы знаний по автоэлектрике. Не обязательно приведённые формулы и правила маркировки элементов автоэлектрик должен знать наизусть. Но иметь представление об этом материале, знать, где искать эту информацию и как ей правильно пользоваться, должен каждый электрик или электронщик.
1. Резистор постоянный.
Резистор постоянный — это электронный компонент с постоянным сопротивлением.
Его основными характеристиками являются:
— Номинальное значение сопротивление, Ом
— Допускаемое производителем отклонение от номинального значения, %
— Максимально допустимая мощность рассеяния (о мощности мы погорим позже), Вт
Его обозначение на схемах (условное графическое обозначение) выглядит следующим образом:
Резисторы могут иметь несколько видов корпусов:
2. Провод как резистор
Во многих идеализированных схемах провод имеет сопротивление, равное 0 Ом. На практике же это не совсем так (или даже: сосем нетак). Если постоянно принимать значение провода, равным нулю, можно попасть в очень неприятные ситуации, особенно, когда речь идёт об автоэлектрике. Дело в том, что проводник обычно подбирают таким, чтобы его значение было значительно ниже сопротивление цепи, тогда можно будет принимать значение его сопротивления, равным нулю.
Сопротивление проводника считается по формуле, которую мы изучили в прошлый раз:
, где l — длины проводника, S — площадь поперечного сечения проводника, р — удельное сопротивление.
Основные выводы из данной формулы:
— чем длиннее провод, тем выше его сопротивление.
— чем больше сечение (толще провод), тем ниже сопротивление.
Когда проводник выполняет функцию провода (кабеля, шнура), то с точки зрения электротехники работает правило «Чем меньше сопротивление, тем лучше». И идеальный провод — это проводник с сопротивлением 0 Ом. Но мы живём в реальном мире, в котором такого проводника не существует.
По этой причине провод следует рассматривать как резистор с неким сопротивлением.
О том, почему горят провода, как правильно подбирать провод и почему помогает в некоторых вопросах элементарная замена, казалось бы, целого провода или переобжимка его клемм, мы поговорим более детально дальше, когда будем касаться вопроса мощности. Но сразу скажу, что связь с сопротивлением провода тут прямая.
3. Последовательное включение резисторов
Первый из законов сопротивлений, который мы сегодня рассмотрим, связан с последовательным включением резисторов и проводов.
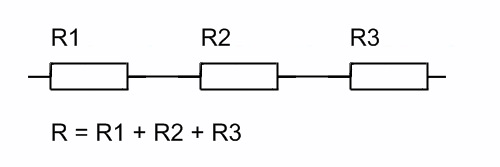
Последовательное включение резисторов приводит к суммированию сопротивлений.
На схеме это может выглядеть так:
Если, к примеру, мы имеем три резистора сопротивлением 10 кОм, то суммарное сопротивление всей цепи от начала до конца будет равно 30 кОм.
4. Параллельное включение резисторов
Второй закон сопротивлений связан с параллельным включением резисторов и проводов:
Общее сопротивление цепи, состоящей из параллельных резисторов, считается по формуле:
1/R = 1/R1 + 1/R2 + … + 1/RN.
Пусть мы имеем три резистора сопротивлением 3 кОм, включенных параллельно. Тогда общее сопротивление полученной цепи вычисляется по следующей формуле:
1/R = 1/R1 + 1/R2 + 1/R3
1/R = 1/3000 + 1/3000 + 1/3000 = 3/3000 = 1/1000
Откуда:
R = 1000 Ом, или же R = 1кОм.
Когда все резисторы в параллельной цепи имеют одинаковое сопротивление (т.е. R1=R2=…=RN), суммарное сопротивление высчитывается легко:
R = R1/N, где N — количество резисторов.
При параллельном включении ВСЕГДА суммарное сопротивление всей цепи ниже, чем сопротивление любого из включенного в цепь резистора. Отсюда следует вывод, что параллельное включение — это один из способов снижения суммарного сопротивления цепи. Данное применение можно увидеть в многожильном кабеле:
Следует отметить, что обламывание отдельных жил в таком кабеле приводит к увеличению сопротивления провода.
5. Смешанное (последовательно-параллельное) включение резисторов.
Если существует два изученных типа включений, то возникает вопрос, почему не может существовать смешанное включение? Ответ на вопрос очевиден: может и, более того, существует.
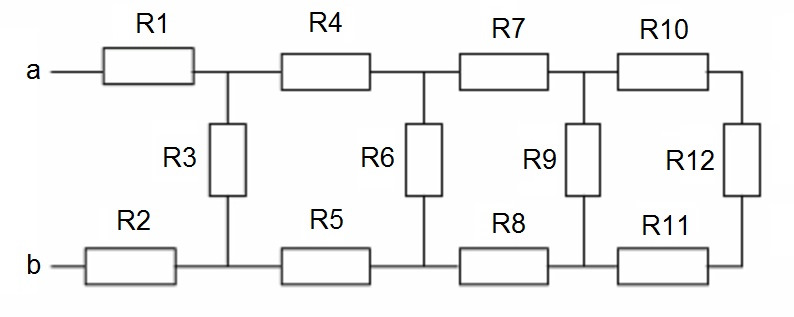
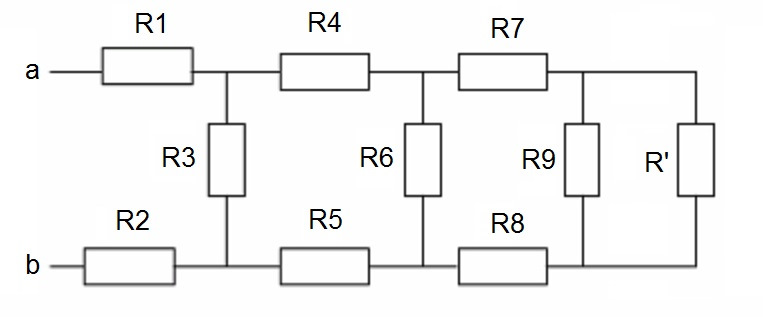
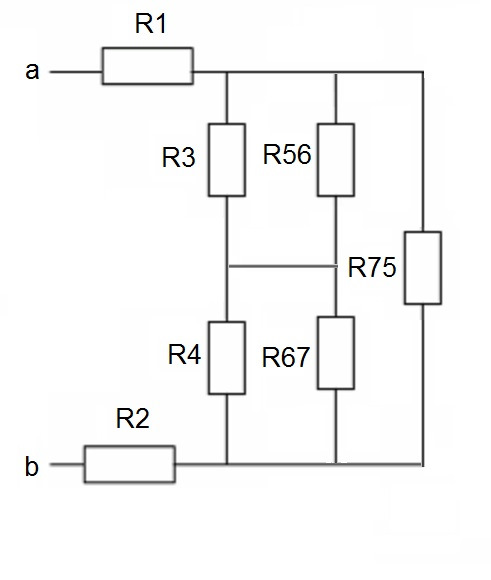
Представим себе одну из таких цепей, состоящей из двенадцати резисторов:
И нам необходимо понять, какое сопротивление всей цепи, если подключимся Омметром к точкам «a» и «b».
Неподготовленному зрителю картинка может показаться ужасающей. Но не всё так сложно, когда мы знаем правила параллельных и последовательных включений.
Смотрим на схему:
Первое, что следует отметить — это последовательное включение трёх резисторов: R10, R11 и R12.
Значит их суммарное сопротивление будет равно:
R’ = R10 + R11 + R13.
Эквивалентно на схеме эти три резистора можно заменить на одно с сопротивлением R’:
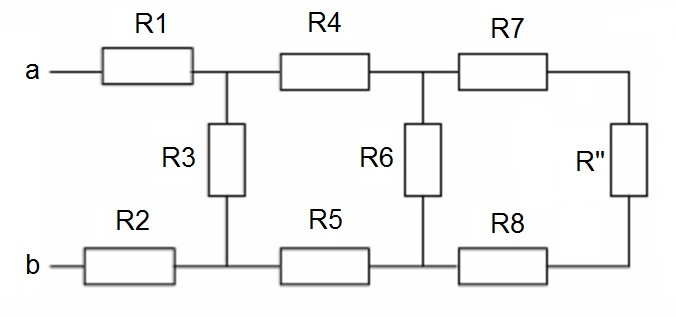
Далее мы видим, что R9 и R’ включены параллельно. Т.е. их суммарное сопротивление будет равно:
Далее опять можно заменить резисторы R9 и R’ на одно эквивалентное сопротивление R»:
Ну, а дальше все аналогичным образом:
Ну, и в конечном счете:
Как видно, ничего сложного в задачах подобного рода нет. Кроме того, на втором курсе университета с упоением считал настолько сложные конфигурации из решебника, даже те, что не задавались на дом=)
Это напоминает своего рода игру — лабиринт или судоку=)
6. Преобразование звезда-треугольник.
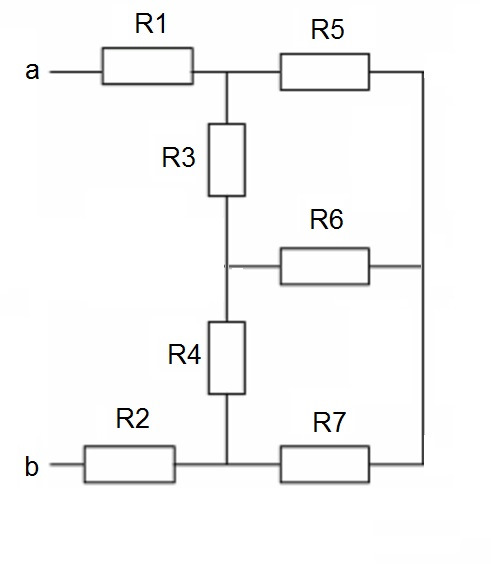
Представьте ситуацию: вы смотрите на смешанное включение резисторов, но понять как вести расчет, используя правила для последовательного и параллельного включения, вы не можете:
Тут не видно явных параллельных и последовательных включений.
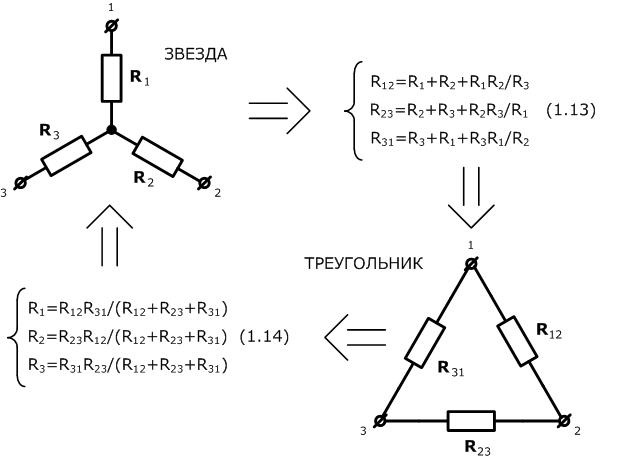
В таких случаях на помощь приходит замечательный механизм преобразований «звезда-треугольник»:
Возвращаемся к нашему рисунку и мы видим, что R5, R6 и R7 образуют звезду.
Преобразовав в треугольник, мы получим следующее:
R56 = R5 + R6 + R5*R6/R7
R67 = R6 + R7 + R6*R7/R5
R75 = R7 + R5 + R7*R5/R6
Ну, а дальше схема приобретает вид, который спокойно решается правилами последовательного и параллельного включения:
R’ = 1/(1/R3 + 1/R56)
R» = 1/(1/R4 + 1/R67)
R»’ = R’ + R»
R»» = 1/(1/R75 + 1/R»’)
7. Маркировка резисторов
Решать задачи, конечно, хорошо. Кому очень хочется порешать задачи такого рода, может обратиться в любой книжный магазин и приобрести задачник по электротехнике или скачать таковой с просторов сети.
Но мы опять же с Вами возвращаемся в реальность — в наши квартиры, офисы, гаражи, где перед нами появилось устройство с резисторами. Как же определить номинал? Напомню (об этом упоминалось в прошлой части курса), что для проверки сопротивления Омметром необходимо не только обесточить цепь, но и извлечь и цепи резистор (хотя бы отпаять одну ножку). Почему необходимо извлекать резистор (лампочка накала, кстати, тоже отчасти резистор), ясно из проведённых схемных преобразований. Попытка проверить Омметром приведет к значению на неких двух точках А и В, которое нужно высчитать, зная значения всех сопротивлений цепи.
Если на выводном (т.е. с ножками) резисторе имеются буквы, то гадать долго не придётся:
12Ω, 12J, 12 — означают 12 Ом
12kΩ, 12k — означают 12 кОм
1k2Ω, 1k2 — означают 1,2 кОм
R12 — означает 0,12 Ом
И так далее.
Также для выводных резисторов характерно обозначение цветами:
Тогда читать их нужно так:
Для чип-резисторов характерно трехзначное цифровое обозначение, типа 123, 560 и так далее:
123 — это 12*10^3 Ом, т.е. 12 кОм.
560 — это 56*10^0 Ом, т.е. 56 Ом
Если на чип-резисторе 4 цифры, типа 7122, то считается это так:
7122 = 712*10^2 = 71,2 кОм
Если же маркировка на чипе буквено-цифровая (две цифры и буква или буква и две цифры), то тут всё гораздо сложнее и для получения значения потребуется воспользоваться специальными таблицами типа EIA-96).
Логике особой сходу значения не поддаются, поэтому гадать даже не пытайтесь.
К примеру,
D12 — это 300 кОм,
12D — это 130 кОм
B51 — это 1,5 кОм
51B — это 3320 Ом