Как сделать сопряжение двух окружностей

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

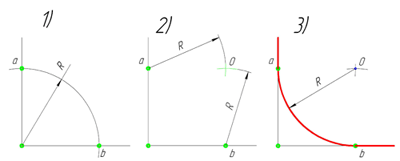
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
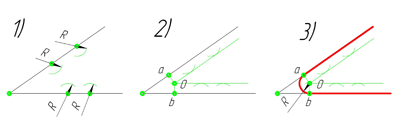
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

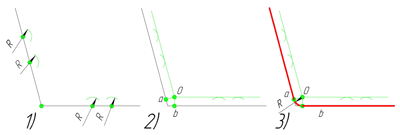
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

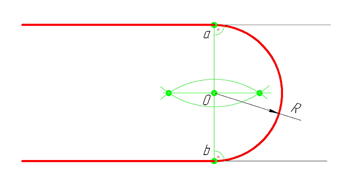
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

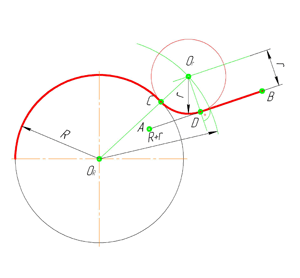
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

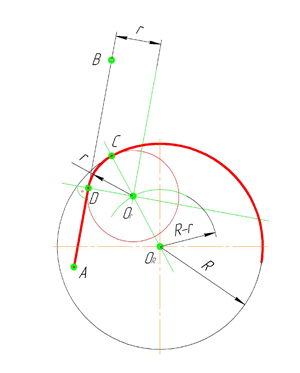
Внутреннее сопряжение прямой линии с дугой

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

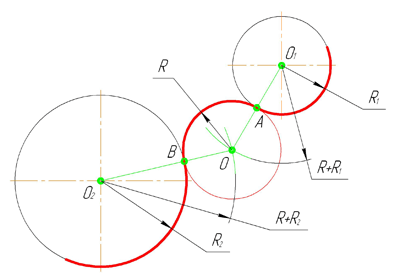
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

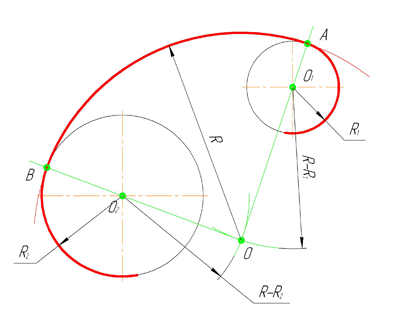
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Источник

Как сделать сопряжение двух окружностей

При вычерчивании деталей машин и приборов, кон­туры очертаний которых состоят из прямых линий и дуг окружностей с плавными переходами от одной линии в другую, часто применяют сопряжения. Сопря­жением называется плавный переход одной линии в другую. На рис. 60 показаны примеры применения сопряжений.

Контур рычага (рис. 60а) состоит из отдельных линий, плавно переходящих одна в другую, например, в точках А, А₁ виден плавный переход от дуги окруж­ности к прямой линии, а в точках В, В₁ — от дуги одной окружности к дуге другой окружности (рис. 60, б). На рис. 60, в изображен двурогий крюк. На чертеже кон­тура крюка (рис. 60, г) в точке А виден плавный пере­ход от дуги окружности D=200 к прямой линии, а в точке В — от дуги окружности радиуса R460 к дуге ра­диуса R260.

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях.

СОПРЯЖЕНИЕ ДВУХ СТОРОН УГЛА ДУГОЙ ОКРУЖНОСТИ ЗАДАННОГО РАДИУСА

При выполнении чертежей деталей, показанных на рис. 62, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 62, а выполнено построение сопряжения сто­рон острого угла дугой, на рис. 62, в — тупого угла, на рис. 62, д — прямого.

Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса R выполняют следующим образом (рис. 62, а и в).

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса Я, т. е. центром сопряже­ния. Из центра О описывают дугу, плавно переходя­щую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n₁ которые являются Основаниями перпендикуляров, опущенных из центра О на сто­роны угла.

СОПРЯЖЕНИЕ ПРЯМОЙ С ДУГОЙ ОКРУЖНОСТИ

Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внутренним касанием (рис. 63, в) и дуги с внешним касанием (рис. 63, а).

На рис. 63, а показано сопряжение дуги окружности радиусом R и прямой линии А В дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, рав­ном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности

радиусом, равным сумме радиусов и r, до пересече­ния ее с прямой ab в точке О₁ Точка О₁ является цент­ром дуги сопряжения.

Точку сопряжения с находят на пересечении прямой 00 ₁ с дугой окружности радиуса R. Точка сопряжения C₁ является основанием перпендикуляра, опущенного из центра О₁ на данную прямую При помощи ана­логичных построений могут быть найдены точки 0₂,

На рис. 63, б показан кронштейн, при вычерчивании контура которого необходимо выполнить построения, описанные выше.

На рис. 63, в выполнено сопряжение дуги радиуса R с прямой А В дугой радиуса r с внутренним касанием. Центр дуги сопряжения О₁ находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогатель­ной окружности, описанной из центра О радиусом, рав­ным разности R—r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О₁ на данную прямую. Точку сопряжения с находят на пересечении прямой ОО₁ с сопрягаемой дугой. Такое сопряжение выполняют, например, при вычерчивании контура маховика, показанного на рис. 63, г.

СОПРЯЖЕНИЕ ДУГИ С ДУГОЙ

Сопряжение двух дуг окружностей может быть вну­тренним, внешним и смешанным.

При внутреннем сопряжении центры O и O₁ сопря­гаемых дуг находятся внутри сопрягающей дуги ради­уса R (рис. 64, б).

При внешнем сопряжении центры и сопрягае­мых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (рис. 64, в).

При смешанном сопряжении центр О, одной из сопрягаемых дуг лежит внутри сопрягающей дуги

радиуса R, а центр О другой сопрягаемой дуги вне ее (рис. 65, а).

На рис. 64, а показана деталь (серьга), при вычерчи­вании которой необходимо построение внутреннего и внешнего сопряжения.

Построение внутреннего сопряжения.

а) радиусы сопрягаемых окружностей R₁ и R₂

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения s₁ и s

в) провести дугу сопряжения.

Построение сопряжения показано на рис. 64, б. По заданным расстояниям между центрами 1₁ и l₂ на чер­теже намечают центры О и O₁ из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ про­водят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂, а из центра О — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁ Вспомогательные дуги пересекутся в точке 0₂ которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку 0₂ соеди­няют с точками О и О₁ прямыми линиями. Точки пере­сечения продолжения прямых 0₂0 и 0₂0 с сопрягае­мыми дугами являются искомыми точками сопряжения (точки S и s₁).

Радиусом R из центра О_г проводят сопрягающую дугу между точками сопряжения s и s₁

Построение внешнего сопряжения.

б) расстояния и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения и s₁;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рис. 64, в. По заданным расстояниям между центрами l₁ и l₂ на чертеже находят точки О и О₁ из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁, и сопряга­ющей R, а из центра О₁ — радиусом, равным сумме

радиусов сопрягаемой дуги R₂ и сопрягающей R. Вспо­могательные дуги пересекутся в точке O₂, которая будет искомым центром сопрягающей дуги Для нахождения точек сопряжения центры дуг сое-

диняют прямыми линиями 00₂ и 010₂. Эти две пря­мые пересекают сопрягаемые дуги в точках сопряже­ния S и s1

Из центра 0₂ радиусом R проводят сопрягающую ду­гу, ограничивая ее точками сопряжения и

Построение смешанного сопряжения. Пример сме­шанного сопряжения приведен на рис. 65, и где изображены кронштейн и его чертеж.

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

а) определить положение центра 0₂ сопрягающей дуги;

б) найти точки сопряжения s и s₁

в) провести дугу сопряжения.

По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры 0 и 0₁, из которых описы­вают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁ и сопрягающей R, а из центра 0₁ — радиусом, равным разности радиусов R и R₂. Вспомогательные дуги пересекутся в точке 0₂, которая будет искомым центром сопряга­ющей дуги.

Соединив точки О и 0₂ прямой, получают точку сопряжения соединив точки О₁ и 0₂, находят точку сопряжения s. Из центра 0₂ проводят дугу сопряжения от s до s₁

При вычерчивании контура детали необходимо разо­браться, где имеются плавные переходы, и предста­вить себе, где надо выполнить те или иные виды сопря­жения.

Для приобретения навыков построения сопряжения выполняют упражнения по вычерчиванию контуров сложных деталей. Перед упражнением необходимо просмотреть задание, наметить порядок построения сопряжений и только после этого приступить к выпол­нению построений.

На рис. 66, а изображена деталь (кронштейн), а на рис. 66, б, в, г показана последовательность выполне­ния контурного очертания этой детали с построением различных видов сопряжений.

Источник

Урок инженерной графикм. Тема: «Сопряжение»

Модуль: Графическое оформление чертежей.

Результат 1: Уметь оформлять форматы стандартных листов в соответствии с ГОСТ 2.303 – 68. Иметь навыки по вычерчиванию контуров деталей, уметь наносить размеры, уметь выполнять надписи в соответствии с ГОСТ 2.303 – 68.

Результат 2: Знать правила построения и иметь навыки по построению сопряжения. Уметь объяснять правила построения.

1. Правила оформления форматов, правила заполнения основной надписи в соответствии со стандартом.
2. Правила нанесения размеров, типы линий.
3. Правила выполнения надписей шрифтами в соответствии с ГОСТ 2.303 – 68.
4. Правила вычерчивания контуров технических деталей. Геометрические построения.
5. Правила вычерчивания и построение сопряжений.

Тема урока: Правила построения сопряжений.

1. Организационно-мотивационный этап – 10 минут.

1.2. Деление группы на подгруппы по 5-6 человек (на четыре подгруппы).

Всем студентам группы предлагается выбрать из четырех видов геометрических фигур одну на выбор, после того, как выбор сделан, студенты объединяются в подгруппы, для самостоятельной работы в подгруппах.
Студентам сообщается, какую тему им предстоит изучить, познакомиться с правилами построения сопряжений, которые помогут им понять, как строятся плавные переходы (сопряжения). Каждой группе предлагается изучить и представить один из видов сопряжения (преподаватель каждому раздает материал по теме занятия по разделам).

2. Организация самостоятельной деятельности учащихся по теме урока – 25 минут.

2.1. Понятие сопряжения.
2.2. Общий алгоритм построения сопряжений.
2.3. Виды сопряжения. Правила их построения.
2.3.1. Сопряжение между двух прямых.
2.3.2. Сопряжение внутреннее и внешнее между прямой и дугой окружности.
2.3.3. Сопряжение внутренне и внешнее между двух дуг окружностей.
2.3.4. Смешанное сопряжение.
3. Подведение итогов, доклады групп по теме после самостоятельной работы в подгруппах- 25 минут.
4. Проверка степени усвоения материала – 10 минут.
5. Заполнение дневников (о проведенном занятии ) – 5 минут.
6. Оценка деятельности учащихся.

Сопряжение – это плавный переход одной линии в другую.

Общий алгоритм построения сопряжения:

1. Необходимо найти центр сопряжения.
2. Необходимо найти точки сопряжения.
3. Построить сопряжение (плавный переход одной линии в другую)
2. 3.1. Построение сопряжения двух сторон угла окружности заданного радиуса.

Сопряжение двух сторон угла (острого и тупого) дугой заданного радиуса R выполняют следующим образом:

Сопряжение – это плавный переход одной лини в другую.

Общий алгоритм построения сопряжения:

1. Необходимо найти точку сопряжения.
2. Необходимо найти точки сопряжения.
3. Построение сопряжения (плавного перехода одной линии в другую).
2.3.2 Построение внутреннего и внешнего сопряжения между прямой и дугой окружности.

Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внутренним касанием дуги и внешним касанием. На рисунке 2(а, б) показано сопряжение дуги окружности радиусом Rи прямой линии АВ дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, равному радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой ab в точке О1. Точка О1 является центром дуги сопряжения. Точку сопряжения с находят на пересечении прямой ОО1 с дугой окружности радиуса R. Точка сопряжения О1 на данную прямую АВ. При помощи аналогичных построений могут быть найдены точки О2, с2, с3. На рисунке 2(а, б) показан кронштейн, при вычерчивании которого необходимо выполнить построения, описанные выше.

При вычерчивании маховика, выполнено сопряжение дуги радиуса R с прямой АВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О1 находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из центра О радиусом, равным разности R-r. Точка сопряжения с 1 является основанием перпендикуляра, опущенного из точки О1 на данную прямую. Точку сопряжения с находят на пересечении прямой ОО1 с сопрягаемой дугой. Пример построения сопряжения прямой с дугой окружности показан на рисунке 3.

Сопряжение – это плавный переход одной лини в другую.

Общий алгоритм построения сопряжения:

1. Необходимо найти центр сопряжения.
2. Необходимо найти точки сопряжения.
3. Построение линии сопряжения (плавного перехода одной лини в другую).

2.3.3. Построение сопряжения между двух дуг окружностей.

Сопряжение двух дуг окружностей может быть внутреннее и внешнее.
При внутреннем сопряжении центры О и О1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R. При внешнем сопряжении центры О и О1 сопрягаемых дуг радиусов R1 и R2 находятся вне сопрягающей дуги радиуса R.
Построение внешнего сопряжения:

а) радиусы сопрягаемых окружностей R и R1;
б) расстояния между центрами этих дуг;
в) радиус R сопрягающей дуги;

а) определить положение центра О2 сопрягающей дуги;
б) найти точки сопряжения s и s1;
в) провести дугу сопряжения;

Построение внутреннего сопряжения:

Построение внутреннего сопряжения:

а) радиусы R и R1 сопрягаемых дуг окружностей;
б) расстояния между центрами этих дуг;
в) радиус R сопрягающей дуги;

а) определить положение О2 сопрягающей дуги;
б) найти точки сопряжения s и s1;
в) провести дугу сопряжения;

Построение внешнего сопряжения показано на рисунке 4(в). По заданным расстояниям на чертеже находят точки О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R2 и сопрягающей R. Вспомогательные дуги пересекутся в точке О2, которая будет искомым центром сопрягающей дуги. Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО2 и О1О2. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения s и s1. Из центра О2 радиусом Rпроводят сопрягающую дугу, ограничивая ее точками S и S1.

2.3.4. Построение смешанного сопряжения.

Пример смешанного сопряжения показан на рисунке 5.

а) Заданы радиусы R и R1 сопрягаемых дуг сопряжения;
б) расстояния между центрами этих дуг;
в) радиус R сопрягающей дуги;

а) определить положение центра О2 сопрягающей дуги ;
б) найти точки сопряжения s и s1;
в) провести дугу сопряжения;

По заданным расстояниям между центрами на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R1 и сопрягающей R, а из центра О1 – радиусом, равным разности радиусов R и R2. Вспомогательные дуги пересекутся в точке О2, которая будет искомым центром сопрягающей дуги. Соединив точки О и О2 прямой, получают точку сопряжения s1; соединив точки О1 и О2, находят точку сопряжения s. Из центра О2 проводят дугу сопряжения от s до s1. На рисунке 5 показан пример построения смешанного сопряжения.

3. Подведение итогов самостоятельной работы студентов в группах. Доклады студентов по каждому разделу темы занятия у доски.
4. Проверка степени усвоения знаний учащихся. Студенты каждой из групп задают вопросы студентам другой группы.
5. Заполнение дневников. Каждому студенту по итогам занятия предлагается заполнить дневник.

Для того чтобы получить хороший объем знаний, важно зафиксировать, насколько успешно прошло занятие. Этот дневник дает возможность записывать в течение занятия каждую деталь вашей работы при изучении модуля. Если вы довольны, удовлетворены, разочарованы тем, как пошло ваше занятие, то отметьте ваше отношение к элементам урока в соответствующей клетке анкеты.

КомментарииПростота и доступность раздаточного материала.Понятны ли были задания.Насколько комфортно вы себя чувствовали во время занятия.Интересен ли был данный урок.Как вы оцениваете свою работу на уроке.

В этом месте вы можете сделать любые пометки к уроку __________________________________________________________________________

6. Подведение итогов занятия, оценка работы студентов на занятии.

Источник