Как сделать сопряжение тупого угла
Сопряжение тупого угла
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4
ТЕМА: СОПРЯЖЕНИЕ ПРЯМЫХ И ОКРУЖНОСТЕЙ
СОПРЯЖЕНИЯ, ПРИМЕНЯЕМЫЕ В КОНТУРАХ ТЕХНИЧЕСКИХ ДЕТАЛЕЙ
Сопряжением называется плавный переход одной линии в другую.
Точка, в которой одна линия переходит в другую, называется точкой сопряжения.
Дуги, при помощи которых осуществляется плавный переход одной линии в другую, называются дугами сопряжений.
Касательнойназывается прямая, имеющая с замкнутой кривой только одну общую точку. Это предельное положение секущей, точки пересечения которой с кривой, стремясь друг к другу, сливаются в одну точку — точку касания.
Построение сопряжений основано на свойствах касательных к кривым и сводится к определению положения центра сопрягающей дуги и точек сопряжения (касания), т.е. точек, в которых заданные линии переходят в сопрягающую дугу
СОПРЯЖЕНИЕ УГЛОВ (СОПРЯЖЕНИЕ ПЕРЕСЕКАЮЩИХСЯ ПРЯМЫХ)
Сопряжение прямого угла
(Сопряжение пересекающихся прямых под прямым углом)
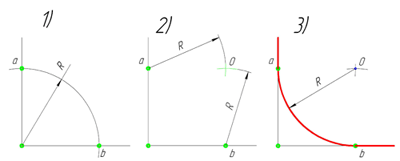
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла
(Сопряжение пересекающихся прямых под острым углом).
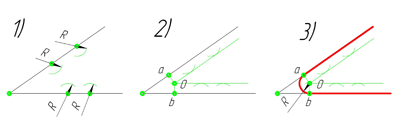
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение острого угла. Для построения сопряжения острого угла раствором циркуля, равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a и b. Сопряжение острого угла построено.
Сопряжение тупого угла
(Сопряжение пересекающихся прямых под тупым углом)
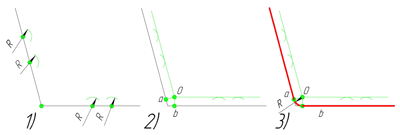
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Сопряжения
В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Сопряжение параллельных прямых линий
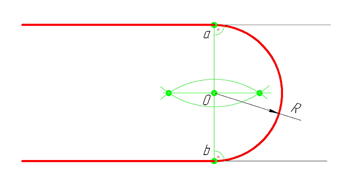
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
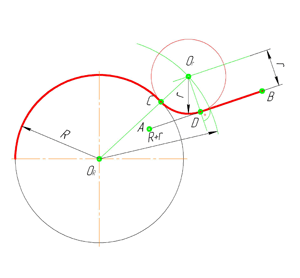
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
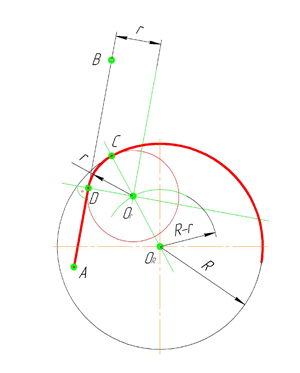
Внутреннее сопряжение прямой линии с дугой
Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Сопряжение окружностей (дуг)
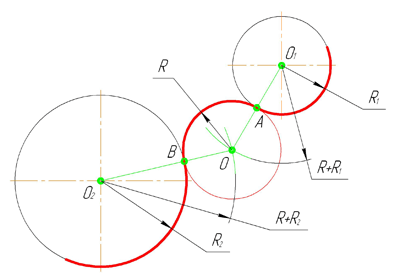
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
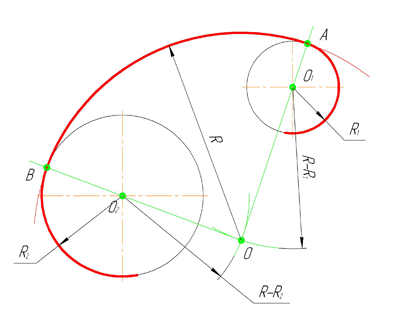
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение параллельных прямых линий
Внешнее сопряжение дуги и прямой линии
Внутреннее сопряжение прямой линии с дугой
Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Смешанное сопряжение дуг окружностей
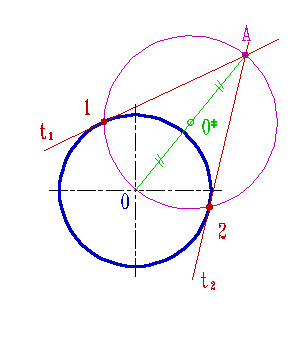 | Касательную из точки А к окружности можно провести следующим образом: 1. На отрезке ОА как на диаметре строят окружность радиуса R=0,5[OA]; 2. Точки 1 и 2 пересечения полученной окружности с заданной определяют положение точек касания; 3. Отрезки [1A]и [2A] определяют положение касательных t1 и t2 проведенных из точки А к окружности. |
7) Сопряжения. Построение сопряжения двух прямых дугой заданного радиуса.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
1. Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение параллельных прямых линий
Внешнее сопряжение дуги и прямой линии
Внутреннее сопряжение прямой линии с дугой
Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Смешанное сопряжение дуг окружностей
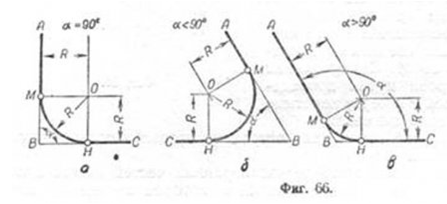
Даны пересекающиеся прямые AB и ВС и радиус сопряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в).
Сопряжение будет возможным, если прямые AB и ВС будут касательными к окружности радиуса R. Для нахождения центра этой окружности
необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О.
8) Сопряжения. Построение сопряжения двух окружностей дугой заданного радиуса.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
1. Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение параллельных прямых линий
Внешнее сопряжение дуги и прямой линии
Внутреннее сопряжение прямой линии с дугой
Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Смешанное сопряжение дуг окружностей
При построении сопряжения двух окружностей дугой третьей окружности заданного радиуса возможны три варианта: внешнее сопряжение, внутренне сопряжение и сочетание внешнего и внутреннего сопряжений.
Внешнее касание.
Из центра окружности О1 описываем дугу вспомогательной окружности радиусом R1+R3.
Из центра окружности О2 описываем дугу вспомогательной окружности радиусом R2+R3.
Пересечение дуг вспомогательных окружностей даст точку О3, которая является центром дуги сопряжения
(окружности с радиусом R3).
Точки касания К1 и К2 находятся на линиях О1О3 и О2О3.
Внутреннее касание
Из центра окружности О1 описываем дугу вспомогательной окружности радиусом R3-R1.
Из центра окружностиО2 описываем дугу вспомогательной окружности радиусом R3— R2.
Пересечениедуг вспомогательных окружностей даст точку, которая является центром дуги сопряжения
(окружности с радиусом R3).
9) Изображения: виды, разрезы, сечения. Условности и упрощения при выполнении изображения.
Изображения.
Изображение в общем случае можно рассматривать как проекцию пространственного объекта на плоскость. Изображения на чертеже в зависимости от их содержания разделяются на виды, разрезы, сечения.
Количество изображений (видов, разрезов, сечений) должно быть наименьшим, но обеспечивающим полное представление о предмете при применении установленных в соответствующих стандартах условных обозначений, знаков и надписей.
Вид— изображение обращенной к наблюдателю видимой части поверхности предмета. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности предмета при помощи штриховых линий.
| Устанавливаются следующие названия видов, получаемых на основных плоскостях проекций: |
1- вид спереди (главный вид);
Названия видов на чертежах надписывать не следует, за исключением случая, когда виды сверху, слева, справа, снизу, сзади не находятся в непосредственной проекционной связи с главным изображением (видом или разрезом, изображенным на фронтальной плоскости проекций).
При нарушении проекционной связи, направление проектирования должно быть указано стрелкой около соответствующего изображения. Над стрелкой и над полученным изображением (видом) следует нанести одну и ту же прописную букву. Чертежи оформляют так же, если перечисленные виды отделены от главного изображения другими изображениями или расположены не на одном листе с ним. Если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, непараллельных основным плоскостям проекций. Дополнительный вид должен быть отмечен на чертеже прописной буквой, а у связанного с дополнительным видом изображения предмета должна быть поставлена стрелка, указывающая направление взгляда, с соответствующим буквенным обозначением. Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим изображением, стрелку и обозначение вида не наносят. Изображение отдельного, ограниченного места поверхности предмета называется местным видом. Местный вид может быть ограничен линией обрыва, по возможности в наименьшем размере, или не ограничен. Местный вид должен быть отмечен на чертеже подобно дополнительному виду.
Разрезы разделяются, в зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций, на:
горизонтальные – секущая плоскость параллельна горизонтальной плоскости проекций).
вертикальные – секущая плоскость перпендикулярна горизонтальной плоскости проекций
наклонные –секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого. В зависимости от числа секущих плоскостей разрезы разделяются на:
простые – при одной секущей плоскости
сложные – при нескольких секущих плоскостях
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций и профильным, если секущая плоскость параллельна профильной плоскости проекций. Сложные разрезы бывают ступенчатые, если секущие плоскости параллельны, и ломанным, если секущие плоскости пересекаются. Разрезы называются продольными, если секущие плоскости направлены вдоль длины или высоты предмета, и поперечными, если секущие плоскости направлены перпендикулярно длине или высоте предмета.
Положение секущей плоскости указывают на чертеже линией сечения. Для линии сечения должна применяться разомкнутая линия. При сложном разрезе штрихи проводят также у мест пересечения секущих плоскостей между собой. На начальном и конечном штрихах следует ставить стрелки, указывающие направление взгляда; стрелки должны наноситься на расстоянии 2-3 мм от конца штриха.
Начальный и конечный штрихи не должны пересекать контур соответствующего изображения.
В случаях, подобных указанному на стрелки, указывающие направление взгляда, наносятся на одной линии.
У начала и конца линии сечения, а при необходимости и у мест пересечения секущих плоскостей ставят одну и ту же прописную букву русского алфавита. Буквы наносят около стрелок, указывающих направление взгляда, и в местах пересечения со стороны внешнего угла.
Разрез должен быть отмечен надписью по типу «А-А» (всегда двумя буквами через тире).
В строительных чертежах у линии сечения взамен букв допускается применять цифры, а также надписывать название разреза (плана) с присвоенным ему буквенным, цифровым или другим обозначением.
Когда секущая плоскость совпадает с плоскостью симметрии предмета в целом, а соответствующие изображения расположены на одном и том же листе в непосредственной проекционной связи и не разделены какими – либо другими изображениями, для горизонтальных, фронтальных и профильных разрезов не отмечают положение секущей плоскости, и разрез надписью не сопровождают.
Фронтальным и профильным разрезам, как правило, придают положение, соответствующее принятому для данного предмета на главном изображении чертежа. Горизонтальные, фронтальные и профильные разрезы могут быть расположены на месте соответствующих основных видов.
При ломаных разрезах секущие плоскости условно повертывают до совмещения в одну плоскость, при этом направление поворота может не совпадать с направлением взгляда.
Если совмещенные плоскости окажутся параллельными одной из основных плоскостей проекций, то ломаный разрез допускается помещать на месте соответствующего вида. При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, с которой производится совмещение. Разрез, служащий для выяснения устройства предмета лишь в отдельном, ограниченном месте, называется местным. Местный разрез выделяется на виде сплошной волнистой линией или сплошной тонкой линией с изломом. Эти линии не должны совпадать с какими-либо другими линиями изображения. Часть вида и часть соответствующего разреза допускается соединять, разделяя их сплошной волнистой линией или сплошной тонкой линией с изломом. Если при этом соединяются половина вида и половина разреза, каждый из которых является симметричной фигурой, то разделяющей линией служит ось симметрии.
Допускается соединять четверть вида и четверти трех разрезов: четверть вида, четверть одного разреза и половину другого и т. п. при условии, что каждое из этих изображений в отдельности симметрично.
Сечение — изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости.
Сечения, не входящие в состав разреза, разделяют на:
вынесенные; наложенные.
Вынесенные сечения являются предпочтительными и их допускается располагать в разрыве между частями одного и того же вида.
Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями, а контур наложенного сечения – сплошными тонкими линиями, причем контур изображения в месте расположения наложенного сечения не прерывают.
В случае, подобных указанному при симметричной фигуре сечения линию сечения не проводят.
Во всех остальных случаях для линии сечения применяют разомкнутую линию с указанием стрелками направления взгляда и обозначают её одинаковыми прописными буквами русского алфавита. Для несимметричных сечений, расположенных в разрыве или наложенных, линию сечения проводят со стрелками, но буквами не обозначают. Сечение по построению и расположению должно соответствовать направлению, указанному стрелками