Как сделать совокупность однородной
Задача по статистике. Определение однородности совокупности. Правило «трех сигм». Показатели цента распределения
Определение однородности совокупности
Определим средний Уровень экономической активности по формуле средней арифметической простой:
Дисперсия определяется по формуле:
Среднее квадратическое отклонение:
Коэффициент вариации составит:
Совокупность однородна, т.к. коэффициент вариации менее 0,33
Правило «трех сигм»
Исключение из массива первичной информации всех резко выделяющихся единиц по уровню факторного признака производится по правилу «трех сигм»: исключаются все единицы, у которых уровень признака-фактора не попадает в интервал:
xmax, xmin — максимальное и минимальное значение
n – число групп
Произведем группировку с равными интервалами
| Интервалы | Диапазон по уровню ВРП | Число регионов, f |
| 1 | 56,5 — 59,7 | 2 |
| 2 | 59,7 — 63 | 2 |
| 3 | 63 – 66,2 | 17 |
| 4 | 66,2 – 69,4 | 32 |
| 5 | 69,4 — 72,6 | 22 |
| 6 | 72,6 — 75,9 | 5 |
| 7 | 75,9 — 79,1 | 2 |
В 1,2 и 7 интервалы попадает менее 3 субъектов. При сокращении интервалов на 1 в последний попадет 2 субъекта. Сократим число интервалов и примем n = 5
| Интервалы | Диапазон по уровню экономической активности | Число регионов, f | накопленная частота | доля |
| 1 | 56,5 — 61 | 3 | 3 | 3,7% |
| 2 | 61 – 65,5 | 16 | 19 | 19,5% |
| 3 | 65,5 – 70,1 | 38 | 57 | 46,3% |
| 4 | 70,1 – 74,6 | 22 | 79 | 26,8% |
| 5 | 74,6 – 79,1 | 3 | 82 | 3,7% |
3. Проанализировать полученный в п.2 ряд распределения значений признака Y. Для этого построить таблицу, содержащую интервальные группы, число субъектов в каждой группе и частоты групп (f), по сгруппированным данным рассчитать статистические показатели, характеризующие
Дополнить расчеты описательными выводами и способами графического представления рядов распределения.
Показатели цента распределения
Определим средний уровень экономической активности по формуле средней арифметической взвешенной :
X’ — середина интервала
Дисперсия определяется по формуле
Составим расчетную таблицу
Совокупность можно считать однородной, т.к. коэффициент вариации менее 33%
Расчет моды и медианы
Интервал, имеющий наибольшую частоту, будет являться модальным, а конкретное (дискретное) значение моды будет находиться внутри него. Рассчитать конкретное, значение моды в интервальном ряду можно по следующей формуле:
где: ХМо — нижняя граница модального интервала,
i — длина модального интервала,
fMo — частота модального интервала,
fMo-1 — частота, соответствующая предшествующему интервалу,
fMo+1 — частота, соответствующая последующему интервалу.
Самая большая частота — 38, соответствует варианту 65,5 – 70,1. Этот интервал является модальным.
Медиана применяется для количественной характеристики структуры и равна такому варианту, который делит ранжированную совокупность на две равные части. У одной половины совокупности признаки не больше медианы (меньше или равны), у второй — не меньше медианы (больше или равны).
Если рассматриваемый ряд интервальный, то накопленные частоты покажут нам медианный интервал. Конкретное значение медианы рассчитывается по формуле:
i — длина медианного интервала,
fMe’ — накопленная частота в интервале, предшествующем медианному,
fMe — частота медианного интервала.
Для нахождения медианного интервала нужно знать половину частот, то есть 82 : 2 = 41. Во 2-м интервале частот накопилось менее половины, модальным является 3-й интервал 65,5 – 70,1
Размах вариации составит: R = xmax — xmin = 79.1-56.5=22.6% (абсолютная вариация)
Построим график распределения
Получаем примерное равенство моды, медианы и средней, т.е. распределение близко к нормальному
Показатели степени дифференциации
Децильный коэффициент дифференциации
Децильный коэффициент дифференциации рассчитывается так:
Д9 – дециль №9;
Д1 – дециль №1.
дециль №1 (10%) находится в интервале 61 – 65,5, где удельный вес субъектов с уровнем экономической активности
хн – нижняя граница децильного интервала
hд — шаг интервала
Fд-1 — сумма накопленных удельных весов до децильного интервала
fд — удельный вес децильного интервала
дециль №9 (90%) находится в интервале 70,1 – 74,6
Вывод: Значение децильного коэффициента менее 1,2, то можно говорить о слабой дифференциации по уровню экономической активности.
Как сделать совокупность однородной
Средняя выборочная вычисляется по формуле (1.4):
По таблице 1.5 видно, что значения признака отклоняются от средней выборочной в основном в отрицательную сторону.
С помощью формулы (1.3) находится дисперсия, у 2 = 3422825485.
Расчетная таблица для вычисления дисперсии по величине себестоимости проданных товаров, продукции, работ, услуг
Группы предприятий по себестоимости проданных товаров, продукции, работ, услуг, тыс. руб.
Число предприятий ni
Середина интервала xi
Значения себестоимости в основном не превышают среднюю выборочную.
Расчетная таблица для вычисления дисперсии по величине коммерческих и управленческих расходов
Группы предприятий по величине коммерческих и управленческих расходов, тыс. руб.
Число предприятий ni
Середина интервала xi
По таблице видно, что значения признака отклоняются от средней выборочной также в основном в отрицательную сторону.
Для того чтобы рассчитать коэффициент вариации для группы предприятий по величине выручки от продажи товаров, продукции, работ, услуг нужно рассчитать среднее квадратическое отклонение у по формуле (1.6):
Среднее квадратическое отклонение у = 58504,92, то есть величина выручки в среднем отклоняется на 58504,92 тыс. руб.
Исходя из этого, коэффициент вариации равен:
Vв = (58504, 92 / 177166,1) * 100% = 33 %
Величина Vв оценивает интенсивность колебаний вариантов относительно их средней величины. Принята следующая оценочная шкала колеблемости признака:
Для нормальных и близких к нормальному распределений показатель Vв служит индикатором однородности совокупности: принято считать, что при выполнимости неравенства
совокупность является количественно однородной по данному признаку. Так как коэффициент вариации не превышает 33%, то можно считать совокупность предприятий по выручке достаточно однородной.
Коэффициент вариации для остальных признаков равен:
1) Для группы предприятий по себестоимости проданных товаров, продукции, работ, услуг Vв = 33,4%. Колеблемость незначительная.
2) Для группы предприятий по величине коммерческих и управленческих расходов Vв = 32,7%. Колеблемость незначительная. Совокупность можно считать однородной.
Так как коэффициент вариации группировки предприятий по себестоимости незначительно превышает 33%, то можно сказать, что совокупность достаточно однородна, а превышение можно объяснить небольшим объемом выборки, аномальностью некоторых значений и влиянием внешних и внутренних факторов.
Вопрос 1. Статистическая совокупность. Однородность совокупности
Вопрос 1. Статистическая совокупность. Однородность совокупности
Статистическая совокупность—это совокупность социально-экономических объектов или явлений общественной жизни, объединенных некоей качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Таковы, например, совокупность домохозяйств, совокупность семей, совокупность предприятий, фирм, объединений и т. п.. Совокупности могут быть однородными и разнородными.
Совокупность называется однородной, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Совокупность оказывается однородной именно с точки зрения этих признаков.
Единица совокупности— это первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счета.
Вопрос 2. Признаки и их классификация
Признак— это качественная особенность единицы совокупности. По характеру отображения свойств единиц изучаемой совокупности признаки делятся на две основные группы;
признаки, имеющие непосредственное количественное выражение, например возраст, стаж работы, средний заработок и т. д. Они могут быть дискретными и непрерывными;
признаки, не имеющие непосредственного количественного выражения. В этом случае отдельные единицы совокупности различаются своим содержанием (например, отрасли — древесина, минеральные продукты, продтовары и т. д.). Такие признаки обычно называют атрибутивными (в философии «атрибут» — неотъемлемое свойство предмета).
Особенностью статистического исследования является то, что в нем изучаются только варьирующие признаки, т. е. признаки, принимающие различные значения (для атрибутивных признаков) или имеющие различные количественные уровни у отдельных единиц совокупности.
Вариация — это изменение величины либо значения признака при переходе от одного объекта (или группы объектов) к другому; точнее говоря — от одной единицы совокупности к другой. Обычно под вариацией мы понимаем обусловленное перекрещивающимся влиянием различных факторов на данное явление изменение величин только в пределах однородной совокупности.
Если же изменения изучаемого явления происходят в разные периоды времени, причем носят характер закономерности, то говорят уже не о вариации признака, а о его динамике.
Вопрос 3. Статистический показатель, система статистических показателей
Задачами статистики в этом направлении являются:
а) правильное определение содержания статистического показателя (валового национального продукта, национального дохода, экспорта, импорта и т. п.);
б) разработка методологии расчета статистического показателя.
Атрибуты статистического показателя:
1. Качественная сторона: объект, его свойство, категория.
2. Количественная сторона: число и единицы измерения.
3. Территориальные, отраслевые и иные границы объекта.
4. Интервал или момент времени.
Система статистических показателей—это совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Для каждой общественно-экономической формации характерна определенная система взаимосвязи общественных явлений. Поэтому образуют систему и статистические показатели.
Система статистических показателей охватывает все стороны жизни общества на различных уровнях: страны, региона — макроуровень; предприятий, фирм, объединений и т. д. — микроуровень.
Системы статистических показателей имеют следующие особенности:
1) они носят исторический характер — меняются условия жизни населения, общества, меняются и системы статистических показателей;
2) методология расчета статистических показателей непрерывно совершенствуется.
Вопрос 4. Статистическая закономерность. Закон больших чисел
Статистическая закономерность – причинно-следственные связи, проявляющиеся в последовательности, повторяемости, регулярности массовых явлений и процессов общественной жизни, относящихся к определенному пространству и времени.
Закономерности, в которых необходимость неразрывно связана в каждом отдельном явлении со случайностью и лишь во множестве явлений проявляет себя как закон, называются статистическими.
Статистические закономерности обладают свойством устойчивости, т.е. стабильности и повторяемости при повторных наблюдениях.
Статистические закономерности изучают распределение единиц статистического множества по отдельным признакам под воздействием всей совокупности факторов.
Статистическая закономерность выступает как объективная закономерность сложного массового процесса и является формой причинной связи. Она обнаруживается в итоге массового статистического наблюдения. Этим обуславливается ее связь с законом больших чисел.
Статистическая закономерность с определенной вероятностью гарантирует устойчивость средних величин при сохранении постоянного комплекса условий, порождающих данное явление.
Свойство статистических закономерностей — проявляться лишь в массе явлений при обобщении данных по достаточно большому числу единиц, получило название закон больших чисел.
Закон больших чисел в наиболее простой форме гласит, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе.
Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными, отражающими действия постоянных и существенных фактов в данных условиях места и времени.
Тенденции и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного случая.
Он характеризует лишь одну из форм проявления закономерностей в массовых количественных отношениях.
Вопрос 7. Классификация стат.сводки и группировки.
Классификация сводки
от глубины обработки первичной информации, полученной в результате статистического наблюдения:
Простая сводка предусматривает подсчет общих итогов по всей совокупности единиц статистического наблюдения. При этом определяется общий объем изучаемого явления.
Сложная сводка представляет собой комплекс процедур, которые включают группировку единиц совокупности, подсчет итогов характеристик единиц совокупности по каждой группе и по совокупности в целом, а также представление полученных результатов в виде статистических таблиц.
По признаку формы обработки информации:
В зависимости от техники исполнения:
Классификация группировки
В зависимости от числа положенных в их основание признаков:
Группировка, выполненная по одному признаку, называется простой.
Многомерная (сложная) группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации.
По отношениям между признаками:
Неиерархические (например, группировка по товарным группам в разрезе таможен или стран и т.д.).
По очередности обработки информации:
· первичные (составленные на основе первичных данных)
· и вторичные, являющиеся результатом перегруппировки ранее уже сгруппированных данных.
Статистические группировки и классификации делятпо преследуемым целям:
· типологическая, выделения качественно однородных совокупностей
· структурная, изучения структуры совокупности
· аналитическая (факторная)исследования существующих зависимостей
Вопрос 9. Ряды распределения. Атрибутивные и вариационные ряды распределения
Результаты сводки или группировки стат.наблюдения представляют собой статистические ряды распределения.
При этом ряды распределения образованные по качественному признаку называют атрибутив.(например, распределение экспорта или импорта по товарным группам, по таможням, характеру сделки, категориям участников ВЭД).
Если в качестве группировки выступает количественный признак, то получается вариационный ряд распределения.
Атрибутивные ряды распределения
Изучение структуры в разрезе атрибутивных признаков целесообразно проводить по объемным показателям, таким как экспорт, импорт. Так, экспорт (импорт) можно подразделять по всем тем признакам, которые отражены в ГТД (товарные группы, страны, отрасли промышленности, таможенные режимы и т.д.).
Элементом структуры атрибутивного ряда являются группы значений, объединенных по качественному признаку (структура отраслей промышленности, страна, товарная позиция). Для более наглядного описания структуры ряда распределения используют относительные величины (доли, %). Еще более наглядным является графическое изображение.
Любой вариационный ряд состоит из элементов: вариантов и частот.
Вариантами (х) называются отдельные значения признака, которые он принимает в вариационном ряду, т.е. значения варьирующего признака.
Частость, или относительная частота (м)-это отношение частоты к объему всей совокупности, т.е. частота, выраженная в процентах к итогу.
При проведении вариационного анализа исходные данные группируются в виде ряда распределения, рассчитываются статистические характеристики, описывающие форму распределения, строится его график. Затем делается вывод о соотношении закономерности и случайности.
В статистике вариационные ряды делятся на дискретные, в которых значения признака выражены в виде изолированных величин (чаще всего целых), и интервальные (непрерывные), где значения признака заданы определенным интервалом. Например, участники ВЭД по товарообороту разделены на группы: 1000-10000 долл., 10000-20000 долл.
Простые таблицы
Простые таблицы имеют в подлежащем перечень единиц совокупности, времени или территорий.
Групповые таблицы
Групповыми называются таблицы, имеющие в подлежащем группировку единиц совокупности по одному признаку.
Комбинационные таблицы
Комбинационные таблицы имеют в подлежащем группировку единиц совокупности по двум или более признакам.
По характеру разработки показателей сказуемого различают:
§ таблицы с простой разработкой показателей сказуемого, в которых имеет место параллельное расположение показателей сказуемого.
§ таблицы со сложной разработкой показателей сказуемого, в которых имеет место комбинирование показателей сказуемого: внутри групп, образованных по одному признаку, выделяют подгруппы по другому признаку.
Для достижения наибольшей выразительности статистической таблицы необходимо при ее оформлении придерживаться определенных правил
1 Форма статистической таблицы должна быть согласована с ранее существующими таблицами для обеспечения возможности сравнения данных за ряд отрезков времени
2 Название таблицы (общий заголовок) должна кратко и точно характеризовать основное ее содержание Это требование в равной степени касается и названий подлежащего и сказуемого таблицы Если общий заголовок недостаточно подробно сформулирован, то можно сделать примечания к нему.
3 В таблице должно быть указано, какой территории или какого периода или момента времени к приведенные данные, а также характер этих данных (фактич,норматив.,расчетные и т д.).
4 Показатели таблицы должны иметь единицы измерения
5 Все числовые значения данного показателя отмечаются с одинаковой точностью и др.
Относительные величины
Относительные величины представляют собой частное от деления двух величин и характеризуют количественное соотношение между ними.
В завис-ти от базы сравнения- результат отношения может быть выражен в форме коэффициента или %.
Если значение основания или базы сравнения принимается за единицу (приравнивается к единице), то относительная величина (результат сравнения) является коэффициентом и показывает, во сколько раз изучаемая величина больше основания. (только если сравниваемая величина существенно больше той, с которой она сравнивается.) Если значение основания или базу сравнения принять за 100%, результат вычисления относительной величины будет выражаться также в %.
По своему значению они подразделяются на относительные величины структуры, сравнения, динамики, интенсивности, координации.
Относительные величины структурыхарактеризуют состав изучаемых совокупностей, исчисляются как отношение абсолютной величины каждого из элементов группировки к общему объему, т.е. как отношение части к целому. Сравнивая относительные величины структуры за разные периоды можно проследить структурные изменения. (Удел.вес (долю) экспорта и импорта в объеме внешнеторгового оборота…. а на долю экспорта – 3:4*100=75%).
Относительные величины динамики характеризуют изменение изучаемого явления во времени, т.е. показывают во сколько раз или на сколько %, уровень отчетного периода больше или меньше уровня базисного периода. (базис или цепной)
координации— соотношение между отдельными частями стат. совокупности, и показывает во сколько раз сравниваемая часть больше или меньше части, которая принимается за базу сравнения. Относительная величина координации рассчитывается следующим образом.650 : 6500= 10%, т.е. на 10 человек с высшим образованием приходится 1 чел. со средним техническим.
Средние величины
Сред. величина измер-ся в той же размер-ти, что и признак.
Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку.
Средняя арифметическая используется для характеристики абсолютных величин.
1. Если каждое значение признака в ряду встречается по одному разу, расчет производится по формуле простой (сумма всех значений, деленная на число этих значений 
2. Если одно и то же значение признака встречается несколько раз, используют формулу средней арифметической взвешенной. 
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Средней гармонической величинойназывают величину, рассчитанную из обратных значений варьирующего признака. Она применяется и как обобщающая характеристика относительных величин.
Средняя гармоническая простая:
Средняя гармоническая взвешенная:

Средней геометрической принято именовать величину, исчисляемую как корень n–ной степени из произведения n отдельных вариантов признака.
Она также обычно используется для характеристики относительных величин и рассчитывается по формуле:

В случаях, когда некоторые либо все варианты (коэффициенты темпов роста, например) относятся к периодам, не одинаковым по продолжительности:
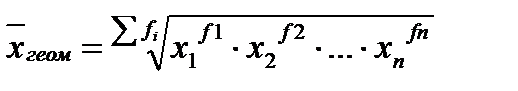
Определить длину интервала
Вопрос 1. Статистическая совокупность. Однородность совокупности
Статистическая совокупность—это совокупность социально-экономических объектов или явлений общественной жизни, объединенных некоей качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Таковы, например, совокупность домохозяйств, совокупность семей, совокупность предприятий, фирм, объединений и т. п.. Совокупности могут быть однородными и разнородными.
Совокупность называется однородной, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Совокупность оказывается однородной именно с точки зрения этих признаков.
Единица совокупности— это первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счета.























