Как сделать степень в маткаде

Как сделать степень в маткаде

Некоторые команды из меню Символика позволяют выполнять алгебраические действия. Можно упрощать выражения, разлагать их на члены и сомножители, объединять подобные члены выражения, находить коэффициенты полиномаhigh, разлагать выражение в ряд, или изменять все вхождения переменной на содержимое буфера обмена.

При преобразовании выражений, содержащих комплексные числа, можно выбрать команду Вычислить 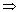В комплексном виде из меню Символика. Это предпишет Mathcad выражать результаты в форме a + ib. Рисунок 8 показывает соответствующий пример.

Обычно символьный процессор возвращает результаты, перестраивая переменные. Таким образом, когда Mathcad преобразует выражение, содержащее p или e, он будет обычно возвращать другое выражение, содержащее p или exp(x). Чтобы предписать Mathcad возвратить числовые значения p или e, выберите Вычислить 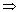N плавающей запятой из меню Символика.

Появится диалоговое окно, в котором можно определить число цифр справа от десятичной точки. По умолчанию это число равно 20.

Рисунок 8: Символьное преобразование выражений, использующее подкоманды, доступные из пункта меню Вычислить в Mathcad PLUS.

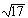
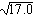
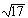
Рисунок 9 показывает некоторые примеры того, как наличие десятичной точки влияет на ответы, получаемые от символьного процессора. В этом примере обратите внимание, что возвращается неизменённым, так как это число не является рациональным. Но возвращается как десятичная аппроксимация к иррациональному числу .

Когда символьная операция дает приближенный ответ в виде десятичной дроби, этот ответ всегда отображается с 20 значащими цифрами. На это отображение не воздействует ни локальный, ни глобальный числовой формат Mathcad.

Рисунок 9: Численные ответы в символьных вычислениях.

Команда Упростить выполняет основные алгебраическое и тригонометрическое упрощения выбранного выражения. Упростить выполняет арифметические преобразования, сокращает общие множители, использует основные тождества для тригонометрических и обратных функций, и упрощает квадратные корни и степени.

Можно упрощать как части выражений (например, знаменатель дроби, или один член суммы), так и всё выражение целиком. Можно также упрощать выражения, содержащие массивы, например, суммы или произведения матриц. Для этого заключите требуемую часть выражения в выделяющую рамку прежде, чем выберете Упростить.

Mathcad иногда может упростить части выражения, даже если он не может упростить выражение целиком. Если преобразование всего выражения не дает желаемый ответ, попытайтесь выделить и упростить часть выражения. Рисунок 10 иллюстрирует некоторые результаты применения команды Упростить.

Рисунок 10: Некоторые результаты упрощения.

Команда Разложить по степеням из меню Символика разлагает все степени и произведения сумм в выделенном выражении. Если выражение — дробь, числитель будет разложен, и выражение будет представлено как сумма дробей. Синусы, косинусы и тангенсы сумм переменных, или целого числа, умноженного на аргумент, будут разложены, насколько возможно, в выражения, включающие только синусы и косинусы одиночных переменных. См. Рисунок 12.

Разложения выражений в ряды

Рисунок 11 показывает некоторые примеры разложений, полученных с использованием этой команды меню. Относительно альтернативного метода выполнения разложений в ряды см. о ключевом слове series в разделе “Символьные преобразования” ранее в этой главе.

Рисунок 11: Разложение в ряд.

Разложение выражения на множители

Команда Разложить на множители. из меню Символика разлагает на множители выбранное выражение. Если выражение представляет целое число, Mathcad разложит его на множители по степеням простых чисел. В остальных случаях Mathcad будет пытаться преобразовывать выражение в произведение. Эта команда будет объединять сумму дробей в одну дробь и будет упрощать многоэтажную дробь с несколькими дробными чертами.

Обратите внимание, что при использовании этой команды Mathcad разлагает на множители “только то, что выделено”. Например, если выделить всё выражение

ab + ac + x

a(b + c) + x

Разлагая на множители, всегда можно немного упростить выражение, выбирая и разлагая на множители подвыражения, даже если выражение в целом не факторизуемо. Команду Разложить на множители. следует использовать также, чтобы объединить сумму дробей в одну дробь или упростить сложную дробь. См. примеры на Рисунке 12.

Поскольку выделяющая рамка следует структуре выражения, может понадобиться прежде вставить скобки, чтобы удалось выделить требуемое подвыражение. Например, чтобы выделить ac + x в выражении, приведенном выше, необходимо вставить левую скобку перед вторым a и правую скобку — после x.

Приведение подобных членов

Команда меню Разложить по подвыражению. объединяет члены, содержащие одинаковые степени выделенного подвыражения. Результатом является полином от подвыражения. Выбираемое подвыражение должно быть либо простой переменной, либо встроенной функцией вместе с аргументом. См. пример на Рисунке 12.

Рисунок 12: Разложение по степеням, разложение на множители и приведение подобных членов.

Разложение на элементарные дроби

Символьный процессор будет пытаться разлагать знаменатель выражения на линейные или квадратичные множители, имеющие целочисленные коэффициенты. Если это удастся, он будет разлагать выражение в сумму дробей с этими множителями в качестве знаменателя. Все константы в выделенном выражении должны быть целыми числами или дробями: Mathcad не будет разлагать выражение, которое содержит десятичные точки. См. некоторые примеры на Рисунке 13.

Рисунок 13: Разложение на элементарные дроби.

Нахождение коэффициентов полинома

Mathcad возвращает вектор, содержащий коэффициенты требуемого полинома в порядке возрастания степеней. Первое выражение на Рисунке 14 показывает пример такой операции.

Если нужно, чтобы символьнай процессор рассматривал выражение как полином относительно функции, заключите в выделяющую рамку функцию. Второе выражение на Рисунке 14 показывает пример разложения по степеням sin(x).

Mathcad подставит выражение из буфера обмена вместо выделенной переменной. Если переменная появляется более чем один раз в преобразуемом выражении, Mathcad заменит все её вхождения на содержимое буфера обмена. Рисунок 15 показывает некоторые примеры.

Обратите внимание, что команда Заменить переменную не может подставлять векторы или матрицы. Чтобы подставить скалярное выражение вместо переменной, которая находится в матрице, поместите выражение в буфер обмена, используя команду Копировать. Затем щёлкните кнопкой мыши на каждом элементе матрицы, который содержит заменяемую переменную, и выберите Заменить переменную.

Рисунок 15: Замена переменной выражением.

Вычисление произведения по индексу производится аналогично, за исключением того, что требуется напечатать [Ctrl][Shift]3, чтобы получить оператор произведения. Если при суммировании или вычислении произведения используются числовые пределы, убедитесь, чтобы верхний предел был больше или равен нижнему.

Вычисление других функций и операторов

Как правило, можно символьно преобразовать любую комбинацию встроенных функций Mathcad. Если результат может быть вычислен точно — sin( p ), например, — появится точный ответ. В противном случае Mathcad будет возвращать в качестве ответа первоначальное выражение. Рисунок 16 иллюстрирует различные результаты символьного вычисления.

Рисунок 16: Символьное вычисление сумм, произведений и функций.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Как сделать степень в маткаде

Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.

Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 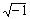, Mathcad вернёт i.

Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.

При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.

Специальные операции над комплексными числами

В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:

Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.

Рисунок 2: Комплексные числа в Mathcad.

При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.

Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.

Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.

Рисунок 3: Нахождение вещественных корней n—ой степени из отрицательного числа.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Урок 4. Использование Mathcad в качестве калькулятора

Mathcad является хорошим калькулятором, особенно удобным при использовании цифровой клавиатуры. Несмотря на то, что Mathcad требует некоторого времени для освоения, он имеет одно неоспоримое преимущество – в нем можно сохранять результаты всех вычислений и выводить их на печать.

Бинарные операторы

Большую часть вычислений можно провести с помощью так называемых «бинарных» операторов (операторы для двух чисел):

возведение в степень [^]

Кроме того, существует оператор деления «в строку» [?], который по функции аналогичен обычному оператору деления. Все эти операторы находятся на вкладке Математика –> Операторы, но намного быстрее использовать для их ввода клавиатуру:

Использование бинарных операторов в Mathcadаналогично их использованию в обычном калькуляторе. Сначала щелкните мышью в пустой области, введите первое число, затем оператор, затем второе число. Для вывода результата следует нажать [=]. Например, ввод выражения [2/3=] приведет к следующему результату:

При использовании бинарных операторов Mathcad использует обычные правила старшинства операций. Попробуйте вычислить следующие выражения:

Правила старшинства операций и скобки

Используя скобки, можно изменить правила старшинства операций. В вычислениях скобки набираются сразу парой. В математической области введите открывающуюся скобку [(], и появится пара скобок:

В появившийся местозаполнитель вводите символы дальше, например, [3+7]:

Нажмите на стрелку вправо на клавиатуре, чтобы выделить закрывающую скобку, затем введите оператор деления: [?/]

Закончите вычисление, набрав [10=]:

Следующие выражения можно вычислить, набрав следующие комбинации клавиш [(2+3/5?*7=] и [2+3/5??*7=]:

При вводе бинарных операторов без чисел Вы получите оператор и два местозаполнителя:

При вводе сложных выражений часто бывает проще сначала ввести скобки и операторы, а затем вводить числа:

При вводе сложных выражений можно допустить ошибку. Как их можно исправить, мы обсудим в уроке 6 «Редактирование выражений». А пока просто удаляйте неправильные выражения, выделяя их и нажимая [Delete].

Унарные операторы

Существует несколько «унарных» операторов, применение которых требует только одно число: квадратный корень [\], модуль [|], факториал [!]. Примеры:

Оператор корня может быть как унарным, так и бинарным. Если не заполнять местозаполнитель над знаком корня, используется квадратный корень:

Оператор [-] также может использоваться для двух случаев: как оператор вычитания и как оператор отрицания. При внимательном рассмотрении видно, что оператор отрицания находится ближе к числу, следующему за ним:

Константы

Стандартные константы Mathcad (доступны на вкладке Математика –> Операторы и символы –> Константы):

Странная, но полезная константа – NaN (Not a Number– Не число). Ее можно использовать, чтобы избегать пропущенные или ошибочные значения:

Многие другие константы также находятся на вкладке Математика –> Операторы и символы –> Константы. В следующем уроке мы научимся определять собственные константы.

Функции

Mathcad включает в себя большое число функций. Весь список можно увидеть, нажав Функции –> Все функции:

Вот пример некоторых использования некоторых из них (обратите внимание, что у некоторых из них не совсем привычные названия, например, функцию арккосинуса следует набирать acos, а не arccos):

Форматирование чисел

Чтобы изменить формат числа, следует щелкнуть по числу и выбрать нужный формат на вкладке Форматирование формул –> Результаты. Первое меню включает в себя пять форматов: Общий, Десятичный, Научный, Проектирование, Процент:

Второе меню позволяет настроить число знаков после запятой.

Продемонстрируем эти настройки на следующих числах (здесь используется оператор присваивания :=, о котором мы поговорим в следующем уроке):

Чаще всего используют общий формат – число от 0.001 до 1000 представляется в привычной записи, для остальных чисел используется стандартная запись (число от 1 до 10, умноженное на 10 n ):

Десятичный формат представляет все числа в привычной десятичной форме:

Научный формат представляет все числа в стандартной записи:

На него похож инженерный формат (формат Проектирование), но показатель степени кратен трем:

В процентном формате число умножается на 100 и отображается со знаком процента:

Источник